| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A176 | |
| Number of page(s) | 9 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202346802 | |
| Published online | 18 October 2023 | |
Dynamic cosmography of the local Universe: Laniakea and five more watershed superclusters
1
Korea Institute for Advanced Study, 85, Hoegi-ro, Dongdaemun-gu, Seoul 02455, Republic of Korea
e-mail: adupuy@kias.re.kr
2
Université Claude Bernard Lyon 1, IUF, IP2I Lyon, 4 rue Enrico Fermi, 69622 Villeurbanne, France
Received:
3
May
2023
Accepted:
29
August
2023
This article delivers the dynamical cosmography of the local Universe within z = 0.1 (1 giga light-years). We exploited the gravitational velocity field computed using the CosmicFlows-4 catalog of galaxy distances in order to delineate superclusters as watersheds, publishing for the first time their size, shape, main streams of matter, and the location of their central attractor. We confirm the size of Laniakea, our home supercluster, to be 2 × 106 (Mpc h−1)3. We dynamically define five more known superclusters in the same way as Laniakea: Apus, Hercules, Lepus, Perseus-Pisces, and Shapley. Additionally, we found the central repellers of the Bootes and Sculptor voids, and based on our analysis, the Dipole and Cold Spot repellers appear as a single gigantic entity. Interestingly, the observed superclusters are an order of magnitude larger than the theoretical ones predicted by cosmological ΛCDM simulations.
Key words: large-scale structure of Universe
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Cosmography is the science that maps and measures the large-scale structures in the observed Universe that are built from the tug between gravitation and space expansion. Mapping the position and spatial extents of clusters, filaments, walls, superclusters, and voids of galaxies is most frequently and most easily done using the Hubble-Lemaître law on redshift datasets. However, such positions and sizes are distorted by the local gravitational velocity field that curves clusters of galaxies and elongates them radially to the observer. This local effect also squeezes the thickness of the walls of galaxies so that they appear more concentrated and less thick in redshift space than they are in real space. Several methodologies have been developed to counter these distortions that will become dominant as ever larger datasets arrive.
However, in the local Universe (i.e., below z = 0.1), the cosmography can be studied using direct distance measurements of galaxy positions, which are much less affected by redshift space distortion effects, but distance measurements are numerically much fewer and consequently prone to strong incompleteness biases, collected under the name of “Malmquist biases”. The gravitational (also known as peculiar) velocity field derived from direct galaxy distances reconstructs the underlying distribution of mass responsible for these motions, hence allowing for a dynamic cosmography of the (dark and luminous) matter distribution.
Such a dynamical mapping of the local Universe volume also provides an evolution in the semantic segmentation of large-scale structures with the possibility to compute watersheds, basins of attraction, and basins of repulsion. Static filaments, walls, and voids are embedded into a more global view of large dynamical superclusters delineated by empty regions. The main advantage of mapping superclusters as watershed basins in the divergence velocity field is the robustness of the definition. For example, it allows for quantitative comparison of the observed sizes with the predicted ones in cosmological simulations (Peñaranda-Rivera et al. 2021), enabling superclusters to be used as cosmological probes.
In contrast, in the hierarchy of structures, voids are regions empty of galaxies that can be described as large coherent volumes evacuating flows of matter (Aragon-Calvo & Szalay 2013; Courtois et al. 2023a). Dynamic mapping can thus also promote the use of cosmic voids as probes of cosmology and galaxy evolution models (Platen et al. 2007; Fiorini et al. 2022; Domínguez-Gómez 2023).
In this study, large-scale structures are defined as regions of space with gravitationally induced coherent inward or outward motions, which, in this way, describe basins of attraction or basins of repulsion, respectively. In other words, a gravitational basin is the volume of space containing all the motions of mass going toward a common center defined as an attractor, in the case of basins of attraction, or a repeller, for basins of repulsion. As per this definition, basins may also be described as “watersheds”. There are then two tessellations of the velocity field into gravitational basins: into basins of attraction on one side and into basins of repulsion on the other side. A point in space belongs to at most one basin of attraction and one basin of repulsion.
This article presents the cosmography of the local Universe within z = 0.1 by partitioning the volume of space into gravitational watersheds and delivering the positions of core attractors, main cosmic streams, and strong repellers at the center of voids. Section 2.1 presents the computation of the peculiar velocity field using the CosmicFlows-4 (CF4) catalog of galaxy distances Courtois et al. (2023b). The methodology to define superclusters as basins of attraction Dupuy et al. (2019) is explained in Sect. 2.2. Section 3 delivers the sizes and locations of the newly defined local large-scale structures as basins of attraction. A short analysis of streamlines and gravitational valleys is presented in Sect. 4. Structures defined as repellers and basins of repulsion are discussed in Sect. 5. Conclusions are drawn in Sect. 6.
2. Methods
2.1. Data: Three-dimensional velocity field
The CF4 catalog (Tully et al. 2023) is currently the latest and largest compilation of reliable distances of galaxies and groups of galaxies independent of redshift obtained through eight methodologies, including the Tully–Fisher relation for spiral galaxies (TF; Tully & Fisher 1977) and the fundamental plane for elliptical galaxies (FP; Dressler et al. 1987b; Djorgovski & Davis 1987). The catalog provides distances for 55 877 galaxies (Table 2 in Tully et al. 2023) and distances for 38 065 groups constructed from the groups of Kourkchi & Tully (2017), Tully (2015), Tempel et al. (2017; Table 3 in Tully et al. 2023) with a uniform coverage of the sky up to approximately 8000 km s−1. Two FP samples provide more distant coverage in two distinct patches of the sky: up to 16 000 km s−1 in south celestial hemisphere (6dF Galaxy Survey, or 6dFGSv; Springob et al. 2014) and up to 30 000 km s−1 in the region covered by the Sloan Digital Sky Survey (SDSS; York et al. 2000; Howlett et al. 2022).
From the CF4 galaxy and group distances, it is possible to reconstruct the three-dimensional overdensity δ and related peculiar velocity v fields by using the method introduced in Courtois et al. (2023b). The algorithm uses a Hamiltonian-Monte-Carlo (HMC) algorithm that derives the 3D overdensity and velocity fields through an exploration of a range of free parameters (e.g., matter density parameter Ωm, and bias). We refer the reader to Courtois et al. (2023b) for more details regarding the reconstruction methodology. In this article, all reconstructions have been derived by considering a ΛCDM cosmology for the initial values: Ωm = 0.3 and a value of the Hubble constant H0 = 74.6 km s−1 Mpc−1, compatible with the CF4 assembly of distances as stated in Tully et al. (2023). In order to reach a stable convergence on the free parameters, about 10 000 HMC steps were computed, and the resulting overdensity and peculiar velocity fields were obtained by averaging all steps (except the burning steps).
We include in this article two 3D reconstructions of the overdensity and velocity fields: one reconstruction is derived from the galaxy sample of the CF4 dataset, and the other reconstruction is obtained from groups of galaxies also provided by the CF4 compilation. Both reconstructions were computed in a grid with a size of 1283 and a side length of 1000 Mpc h−1, hence reaching a resolution of 7.8 Mpc h−1. Figures displaying the overdensity and velocity fields reconstructed from both CF4 galaxies and groups are included in Appendix A. Figure A.1 shows three-dimensional visualizations of the reconstructed overdensity field through four levels of isosurfaces ranging from white to dark red. The reconstruction from CF4 galaxies is shown in the top panel of the figure, while the reconstruction from CF4 groups is shown in the bottom panel. The related peculiar velocity field is represented by streamlines. The orientation of the visualization is given by the red, green, and blue arrows of length 50 Mpc h−1 directed along the supergalactic cartesian SGX, SGY, and SGZ axes, respectively, and located at the center of the reconstructed cube. More details on this plot are given in Appendix A. One can recognize known structures in both reconstructions, such as Norma close to the center, the Shapley supercluster in −SGX and +SGY, the Perseus-Pisces supercluster on the +SGX side, as well as the Apus, Pisces-Cetus, and Hercules superclusters. However, the two reconstructions differ since the grouped version shows a strong accent on the more distant SDSS region in +SGY. The grouped reconstruction is therefore less satisfying than the ungrouped one since we noticed a “ring” that appears due to a lack of constraints in the ortho-radial direction around the observer and also arising from the intrinsic shape and size of the SDSS galaxy distances catalog.
2.2. Watersheds and gravitational basins
The methodology we used to identify attractors, repellers, and their respective gravitational basins in this article was introduced in Dupuy et al. (2019). In the case of a time-independent linear velocity field, streamlines are paths that are always tangent to the local value of the velocity field. They are computed by spatially integrating the components of the peculiar velocity field, starting from a given seed point. The integration is performed by the fourth order Runge-Kutta (RK4) numerical integrator. Streamlines converge toward the critical points of the velocity field (i.e., attractors or repellers). Hence, depending on the direction of integration considered, either forward (integrating v) or backward (integrating −1 × v), we can identify the positions of attractors or repellers by finding the points of convergence of streamlines. Subsequently, a gravitational basin can be defined as a set of seed points whose streamlines converge toward the same critical point of the velocity field: an attractor for basins of attraction or a repeller for basins of repulsion.
As the peculiar velocity is available as a grid, streamlines are actually computed for each voxel (a cell in three dimensions) of the velocity grid with a fixed number of RK4 iterations. Attractors (or repellers) are then identified as the voxels where most streamlines are terminated, also called “ending points”. The velocity grid is then segmented into basins of attraction (or repulsion) defined as sets of (seed) voxels whose streamlines share the same ending point. As streamlines are computed with a fixed number of iterations, they may be terminated before reaching a critical point of the velocity field. Hence several iterations are needed when matching voxels to basins, making the basins “grow” around the attractors or repellers. Finally, we obtained two tessellations of the velocity field: into basins of attraction and into basins of repulsion, depending on the direction of integration. Each voxel of the velocity field belongs to, at most, one basin of attraction and one basin of repulsion. Since the considered peculiar velocity grid does not have periodic boundary conditions, seed voxels whose streamlines go out of the computational grid do not belong to any basin. More details on the basin segmentation algorithm can be found in Dupuy et al. (2019). More extensive testing of this methodology has been conducted using cosmological simulations in Dupuy et al. (2020).
Additionally, the methodology of segmenting basins allows the definition of a new quantity that helps visualize gravitational valleys. Instead of analyzing the convergence of streamlines to tessellate the velocity field into gravitational basins, one can simply construct a histogram from the streamlines by counting how many streamlines are passing through each voxel and assigning that value to the associated voxel to build the histogram. This cube, which is of the same size and resolution as the grid containing the velocity field, produces a map of the density of streamlines with regions high or low in streamline concentrations showcasing gravitational valleys. This definition allowed a kinematic confirmation of the Vela supercluster, which is known to be hidden within the zone of avoidance (Courtois et al. 2019). We also refer the reader to Dupuy et al. (2019) to find more details about that algorithm.
3. Watersheds of the local Universe and their core attractors
The methodology of segmenting watersheds of basins of attraction was performed on both versions of the CF4 catalog (ungrouped and grouped galaxies), and we present the most robust analysis obtained using individual galaxy distances (ungrouped CF4). All results for the grouped version are available in detail in Appendix A. Nine basins of attraction were found in the velocity field reconstructed from the CF4 individual galaxies, and they are presented in Fig. 1. The new basin of attraction of our home supercluster Laniakea is shown in red. Other basins, namely, the five superclusters that we dynamically define as watersheds (Apus, Hercules, Lepus, Perseus-Pisces, and Shapley) and basins identified in the area covered by SDSS, are shown in purple. Streamlines were computed from each individual CF4 galaxy, which are themselves represented by tiny dots. The gradient of color (from red to yellow and purple to white for Laniakea and other basins, respectively) is related to the density of streamlines. White or yellow streamlines denote a high concentration of streamlines in that area. Each basin of attraction is annotated by the name of the associated supercluster. For practical purposes, the three supergalactic cartesian orientation axes (SGX, SGY, and SGZ) are respectively displayed at the bottom left of the figure, rendered as red, green, and blue arrows of 50 Mpc h−1 in size.
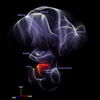 |
Fig. 1. Visualization of the basins of attraction of Laniakea (in red) and the five superclusters that are now dynamically defined as watershed in the same way, namely Apus, Hercules, Lepus, Perseus-Pisces and Shapley, as well as the basins identified further away in the SDSS area (both in purple). The basins shown are obtained from the ungrouped CF4 velocity field. Each galaxy from the CF4 catalog is positioned at its redshift and represented by tiny dots, red for galaxies part of the Laniakea basin of attraction and purple otherwise. Streamlines are also computed for each galaxy with the same color code. The gradient of color is related to the density of streamlines. Streamlines colored white or yellow indicate a high density of streamlines. Each identified basin of attraction is annotated by the associated structure name. For reference, the three supergalactic cartesian orientation axes SGX, SGY, SGZ are drawn in the bottom left, represented respectively by red, green and blue arrows of size 50 Mpc h−1. |
The basin of attraction corresponding to the Laniakea supercluster is only identified in the ungrouped reconstruction. In the grouped reconstruction, it appears as part of the Shapley basin of attraction. The segmented Laniakea basin has a volume of 1.9 × 106 (Mpc h−1)3. It can be compared to the earliest estimates from the CosmicFlows-2 (CF2) dataset: eye-ball measurement computed a decade ago giving 1.7 × 106 (Mpc h−1)3 in Tully et al. (2014) and using the segmentation algorithm on CF2 data gives 2.3 × 106 (Mpc h−1)3. The Laniakea central attractor is located at [ − 62, −8, 39] Mpc h−1 in supergalactic cartesian coordinates, equivalent to sgl = 187°, sgb = 32°, and cz = 7370 km s−1. This is in full accordance with the direction of the Great Attractor (Dressler et al. 1987a).
Similar to Laniakea, the Apus supercluster is only identified as a single basin of attraction in the velocity field when reconstructed from individual CF4 galaxies. Its associated attractor is found to be located at [ − 125, −23, −31] Mpc h−1, while the segmented basin has a volume of 9.5 × 106 (Mpc h−1)3.
The attractor coordinates for the Hercules supercluster show a great coherence between the two different reconstructions, being detected at [ − 39, 70, 78] Mpc h−1 and [ − 47, 78, 78] Mpc h−1 for ungrouped and grouped galaxies, respectively, although the volumes of the basin differ a lot (3.1 × 106 (Mpc h−1)3 for individual galaxies and 0.8 × 106 (Mpc h−1)3 for galaxy groups), mainly due to a stronger emphasis of the SDSS data in the grouped CF4. The Hercules attractor coordinates can be compared to the position of the Abell cluster A2151 (Abell & Corwin 1989), also known as the Hercules cluster of galaxies, with a right ascension and declination of RA = 241° and Dec = +17°.
The Lepus supercluster is a basin of attraction in both reconstructions, with a volume of 8.1 × 106 (Mpc h−1)3 for individual galaxies and 6.9 × 106 (Mpc h−1)3 for galaxy groups. Its attractor is positioned at [ − 62, −39, −109] Mpc h−1 and [ − 47, −55, −125] Mpc h−1, for galaxies and groups, respectively.
The Perseus-Pisces supercluster basin of attraction displays a volume of 4.8 × 106 (Mpc h−1)3 in the individual galaxies reconstruction and a volume of 2.0 × 106 (Mpc h−1)3 in the reconstruction obtained from CF4 galaxy groups. Its central attractor is located at [47, −23, −31] Mpc h−1 and [47, −23, −39] Mpc h−1 for CF4 galaxies and groups, respectively, showing an important consistency between the two reconstructions. The coordinates of the Perseus-Pisces attractor differ from the location of the richest cluster in the Perseus-Pisces supercluster, the Abell cluster A426, with RA = 50° and Dec = +41° (also see Jõeveer et al. 1978; Tully 2015). However, due to the low resolution of the reconstructions considered in this work (7.8 Mpc h−1), the positions derived from the segmentation method are not accurate and cannot be compared to redshift positions of clusters.
Last, we also identified the Shapley supercluster as a basin of attraction around an attractor located at [ − 141, 62, −16] Mpc h−1 in both velocity fields. The position of the attractor is in good agreement with, for example, two Abell clusters known to be part of the Shapley supercluster: A3570, located at RA, Dec = (207° , − 37° ), and A3575 at RA, Dec = (208° , − 32° ). The volume of Shapley is evaluated to be 7.9 × 106 (Mpc h−1)3 and 27.0 × 106 (Mpc h−1)3 for CF4 ungrouped and grouped galaxies, respectively. In both cases, the basin includes the Coma supercluster. This may be an indication that the Coma supercluster could be a sub-basin of the Shapley supercluster. Shapley’s basin found using the CF4 grouped version is much larger than in the galaxy reconstruction, as it also encompasses the Apus and Laniakea superclusters, each of which were identified as separate basins in the reconstruction from CF4 ungrouped galaxies.
A few attractors were also identified in the more distant region covered by the SDSS addition to the CF4 catalog. However, the computed basins of attraction cannot be constrained correctly because streamlines overflow up to the borders of the computational box due to the lack of more distant data needed to delimit the basins on their far side. Also, the errors on the galaxy distance data are proportional to distance. For this reason, we do not comment on the volumes of the basins, though the instability in the values between the two reconstructions is easy to notice. For the sake of clarity, we classified the SDSS attractors into two groups depending on their position in the SDSS reconstructed overdensity. In the ungrouped reconstruction, only three attractors were identified. They are labeled SDSS-1a, located at [117, 227, −227] Mpc h−1; SDSS-2a/b, identified accordingly at [ − 102, 297, 102] Mpc h−1; and [31, 289, 156] Mpc h−1.
The main source of error in the current cosmography is the difference between the two CF4 catalog’s variations: individual galaxies and groups of galaxies. The fact of grouping or not grouping galaxy distances strongly impacts the resulting peculiar velocity fields. More work is needed in the preparation of catalogs of galaxy distance in order to mitigate this problem. The grouped version of CF4 gives too much importance to the SDSS subset of data, inflating the signal in the more distant region where the errors in the data are harder to constrain. This results in an overestimation of the sizes of the SDSS basins.
4. Streamlines and gravitational valleys
Figure 2 shows the density of streamlines computed from the peculiar velocity field reconstructed from CF4 individual galaxies (left panel) and groups of galaxies (right panel). Both panels of the figure correspond to a supergalactic cartesian SGX-SGY slice centered on SGZ = 0 Mpc h−1. Regions with a high concentration of streamlines are shown in yellow, while regions with less streamlines are shown in black. One can notice how the density of streamlines depicts a “skeleton” of the peculiar velocity field, as the superclusters present in this slice can be spotted. The gradient of yellow and purple present around each structure also helps visually identify the coverage of the associated basins of attraction, as described earlier in this work.
 |
Fig. 2. Gravitational valleys in the Local Universe. Left and middle: both panels show a supergalactic cartesian SGX-SGY slice of width 7.8 Mpc h−1, centered on SGZ = 0 Mpc h−1, of the density of streamlines, derived from the ungrouped (left) and grouped (right) CF4 velocity field. Yellow represents voxels highly concentrated in streamlines, while black represents a low concentration of streamlines. Right: density of streamlines from a ΛCDM simulation constrained with the CF2 data, with the same color code. Structures are annotated in the figure. Note that the scale of the axes is different from the two other panels. As a matter of fact, the CF2 catalog was much sparser in data (seven times less data) and much smaller in cartographied volume (ten times smaller compared to CF4), thus this simulation is loosely constrained on scales up to 150 Mpc h−1 maximum. Also at that time, we had poor coverage of the southern hemisphere large-scale structures. |
5. Repellers of the local Universe
Repellers and associated basins of repulsion can be identified in a mirroring way as attractors and basins of attraction by simply computing streamlines in the backward direction (i.e., integrating −1 × v). The segmenting algorithm detected three repellers (with their associated basin of repulsion) in the ungrouped reconstruction.
A basin of repulsion was identified in the Sculptor Void region, centered on a repeller located at [23, −109, −16] Mpc h−1 and encompassing a volume of 1.3 × 106 (Mpc h−1)3. Similarly, a repeller in the SDSS area was detected near the Bootes Void region at [ − 31, 125, 8] Mpc h−1. A huge basin of repulsion was spotted at [133, −133, 62] Mpc h−1 (or sgl = 315°, sgb = 18°, and cz = 19 800 km s−1). This direction is about 20° away from the direction of the Dipole Repeller at sgl ∼ 334°, sgb ∼ 39°, and cz = 14 000 km s−1, and 50° away from the direction of the Cold Spot Repeller at sgl ∼ 287°, sgb ∼ −16°, and cz = 23 000 km s−1 (Hoffman et al. 2017; Courtois et al. 2017). The Dipole and Cold Spot repellers now appear as a single gigantic extended entity with a volume of 163 × 106 (Mpc h−1)3.
In the grouped reconstruction, two smaller new regions evacuating matter were identified: one in the zone of avoidance and one within the SDSS surveyed volume. A full table is available in Appendix A, accompanied by three-dimensional visualizations of the detected repellers and their related basins of repulsion.
6. Conclusion
This article presents the dynamic cosmography of the local Universe up to z = 0.1 by analyzing the gravitational velocity field reconstructed from the CF4 galaxy distances. This analysis allows for the identification of the large-scale structures of the Universe as gravitational basins. A decade after its discovery, we confirm the shape, size, and coordinates of the attractor of our home supercluster, Laniakea, which now englobes a volume of 1.9 × 106 (Mpc h−1)3. We dynamically defined for the first time as basins of attraction, or watersheds, five known superclusters, namely Apus, Hercules, Lepus, Perseus-Pisces, and Shapley, as well as structures detected in the region covered by SDSS. We note that the supercluster Coma is part of the basin of Shapley, hinting that it may be a substructure of Shapley. Superclusters and gravitational basins can also be visualized as gravitational valleys, shown in Fig. 2. The coverage of CF4 also allows a few basins of repulsion to be defined, such as the basins of the Sculptor Void and a basin near the Bootes Void, in the region covered by SDSS and in the zone of avoidance. The Dipole Repeller and the Cold Spot Repeller are now defined as a single gigantic entity.
We find that it is worth pointing out that the observed superclusters defined in this article are larger than the ones found in cosmological ΛCDM simulations. In this work, we used the same segmentation algorithm as that of the Dupuy et al. (2020) study of basins of attraction detected in a constrained cosmological simulation. An SGX-SGY slice (centered on SGZ = 0 Mpc h−1) of the density of streamlines derived from this simulation and extracted from Dupuy et al. (2020) is shown in the right panel of Fig. 2 with the same color code. The authors of the previous work showed that the typical size of basins of attraction is within 1 × 105 and 1 × 106 (Mpc h−1)3. Because their simulation was constrained by the Cosmicflows-2 (CF2) dataset, they defined the simulated basins of Laniakea and Perseus-Pisces as containing a volume of 5 × 105 (Mpc h−1)3 and 7 × 105 (Mpc h−1)3. This difference in volume between the simulated and observed volumes may come from the fact that we are comparing structures from a simulation constrained with the CF2 data to structures detected in reconstructions from CF4, which has a much larger coverage and larger number of galaxies than CF2.
Errors on the definition of large-scale structures as gravitational basins can be derived in this work from the difference between the two reconstructions of the local velocity field considered, namely, from the distances of galaxies and of groups of galaxies, as grouping galaxies and their distances has a direct impact on the resulting peculiar velocity field. In particular, the grouped version of CF4 gives too much importance to the SDSS subset of data, overestimating the SDSS basin sizes.
Identifying attractors of the gravitational watersheds of the local Universe as known rich galaxy clusters may define an interesting follow-up study of this work. For example, the attractor of the SDSS-2c basin of attraction may point to the very rich A2142 Abell cluster described in Einasto et al. (2020). However, as mentioned above, the current resolution of the reconstruction may be too low to obtain accurate attractor positions, which are comparable to redshift positions of rich clusters.
At this point in time, the main contingency regarding the identification of large-scale structures comes from the inclusion of the SDSS data into the CosmicFlows catalog, which is a composite of several sources of observations. There is great hope that upcoming large, independent surveys in the next few years, such as WALLABY (Widefield ASKAP L-band Legacy All-sky Blind surveY; Koribalski et al. 2020), which will bring 90 000 galaxies up to z = 0.1; DESI (Dark Energy Spectroscopic Instrument; DESI Collaboration 2016); and the 4HS (4MOST Hemisphere Survey; de Jong et al. 2019), each of which will deliver 500 000 galaxies up to z = 0.15, will further enrich the cosmography of our Universe.
The main part of our article discusses only two figures. However, a more detailed description is given in Appendix A, along with additional figures, a table summarizing all detected basins of attraction and repulsion, and links to interactive three-dimensional visualizations.
Acknowledgments
H.C. is grateful to the Institut Universitaire de France for its huge support which enabled this research. H.C. also acknowledge support from the CNES. A.D. is supported by a KIAS Individual Grant (PG087201) at Korea Institute for Advanced Study. A. Dupuy is the author to whom correspondence and material requests should be addressed. The authors declare no competing interests. The datasets generated during and/or analyzed during the current study are available online on the CosmicFlows project page (https://projets.ip2i.in2p3.fr/cosmicflows/). Grids are of the same size as the velocity field discussed in this manuscript (1000 Mpc h−1 and 1283) and are filled with integers from 0 to n where n is the number of basins detected. Each integer labels a single basin (in the same order as listed in Table A.1, ignoring blank lines), and the value of all voxels part of a given basin is set to that same integer. Voxels set to 0 are not part of any basin. For example, in the case of basins of attraction in the CF4 galaxy velocity field: voxels filled with 1 are part of Laniakea, 2 of Apus, 3 of Hercules, etc.
References
- Abell, G. O., Corwin, Harold G., Jr., & Olowin, R. P., 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Aragon-Calvo, M. A., & Szalay, A. S. 2013, MNRAS, 428, 3409 [NASA ADS] [CrossRef] [Google Scholar]
- Courtois, H. M., Tully, R. B., Hoffman, Y., et al. 2017, ApJ, 847, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Courtois, H. M., Kraan-Korteweg, R. C., Dupuy, A., Graziani, R., & Libeskind, N. I. 2019, MNRAS, 490, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Courtois, H. M., van de Weygaert, R., Aubert, M., et al. 2023a, A&A, 673, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Courtois, H. M., Dupuy, A., Guinet, D., et al. 2023b, A&A, 670, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
- DESI Collaboration (Aghamousa, A., et al.) 2016, ArXiv e-prints [arXiv:1611.00036] [Google Scholar]
- Djorgovski, S., & Davis, M. 1987, ApJ, 313, 59 [Google Scholar]
- Domínguez-Gómez, J. 2023, Nature, 619, 269 [CrossRef] [Google Scholar]
- Dressler, A., Faber, S. M., Burstein, D., et al. 1987a, ApJ, 313, L37 [CrossRef] [Google Scholar]
- Dressler, A., Lynden-Bell, D., Burstein, D., et al. 1987b, ApJ, 313, 42 [Google Scholar]
- Dupuy, A., Courtois, H. M., Dupont, F., et al. 2019, MNRAS, 489, L1 [CrossRef] [Google Scholar]
- Dupuy, A., Courtois, H. M., Libeskind, N. I., & Guinet, D. 2020, MNRAS, 493, 3513 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, M., Deshev, B., Tenjes, P., et al. 2020, A&A, 641, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiorini, B., Koyama, K., & Izard, A. 2022, J. Cosmol. Astropart. Phys., 2022, 028 [CrossRef] [Google Scholar]
- Hoffman, Y., Pomarède, D., Tully, R. B., & Courtois, H. M. 2017, Nat. Astron., 1, 0036 [NASA ADS] [CrossRef] [Google Scholar]
- Howlett, C., Said, K., Lucey, J. R., et al. 2022, MNRAS, 515, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Jõeveer, M., Einasto, J., & Tago, E. 1978, MNRAS, 185, 357 [Google Scholar]
- Koribalski, B. S., Staveley-Smith, L., Westmeier, T., et al. 2020, Ap&SS, 365, 118 [Google Scholar]
- Kourkchi, E., & Tully, R. B. 2017, ApJ, 843, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Peñaranda-Rivera, J. D., Paipa-León, D. L., Hernández-Charpak, S. D., & Forero-Romero, J. E. 2021, MNRAS, 500, L32 [Google Scholar]
- Platen, E., van de Weygaert, R., & Jones, B. J. T. 2007, MNRAS, 380, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Springob, C. M., Magoulas, C., Colless, M., et al. 2014, MNRAS, 445, 2677 [Google Scholar]
- Tempel, E., Tuvikene, T., Kipper, R., & Libeskind, N. I. 2017, A&A, 602, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tully, R. B. 2015, AJ, 149, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Tully, R. B., Courtois, H., Hoffman, Y., & Pomarède, D. 2014, Nature, 513, 71 [Google Scholar]
- Tully, R. B., Kourkchi, E., Courtois, H. M., et al. 2023, ApJ, 944, 94 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., & Anderson, John E., Jr., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Attractors and repellers
The methodology described above was applied to both reconstructions obtained from CF4 individual galaxies and CF4 groups. Structures identified as basins of attraction and repulsion in each reconstruction are listed in the first column of Table A.1 along with their volume in units of 106 (Mpc h−1)3 in columns 5 and 9 as well as the supergalactic cartesian coordinates of the respective attractors and repellers in Mpc h−1 in columns 2 to 4 and 6 to 8. The respective attractors are plotted as black spheres in Figure A.1 with their associated basin of attraction annotated with the name of the corresponding structure. The reconstruction from CF4 galaxies is shown in the top panel, and the reconstruction from CF4 groups is shown in the bottom panel. The orientations of the two visualizations are given by the red, green, and blue arrows that have a length of 50 Mpc h−1 and are respectively directed along the supergalactic cartesian SGX, SGY, and SGZ axes and located at the center of the reconstructed cube. We restate that the four levels of isosurfaces ranging from white to dark red display the reconstructed overdensity field, while streamlines represent the related peculiar velocity field. Additionally, for clarity, streamlines were computed by considering only voxels that are part of all basins of attraction as seed points, allowing us to focus on basins identified in the velocity field and to remove extra noise caused by streamlines going out of the computational box (hence not part of any basin). For each basin of attraction, the streamlines converge nicely toward their respective core attractor. Figure A.2 shows an SGX-SGY slice centered on SGZ = 0 Mpc h−1 of the overdensity field associated with the velocity field reconstructed from CF4 distances of galaxies (left panel) and groups (right panel). The overlapping contours represent the gravitational basins obtained from the tessellation of the velocity field into basins of attraction (filled contours without borders) and basins of repulsion (empty contours with borders). The names of each associated structure are also shown.
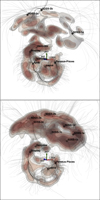 |
Fig. A.1. Attractors in the local universe reconstructed from the CF4 galaxies (top panel) and groups (bottom panel). The reconstructed overdensity field is represented by four levels of isosurfaces from white to dark red: 0.75, 1, 1.4, and 1.75 for CF4 galaxies, and 0.5, 0.8, 1.2, and 1.5 for CF4 groups. Streamlines were derived by integrating the reconstructed peculiar velocity field in the forward direction. For clarity purposes, extra noise has been removed by only showing streamlines part of basins of attraction identified with the segmentation algorithm, listed in the top part of Table A.1. Black spheres are located at the coordinates of attractors identified in the velocity field (i.e., at the points where the streamlines converge). The center of the reconstructed cube is indicated by the red, green, and blue arrows of length 50 Mpc h−1 directing along the supergalactic cartesian SGX, SGY, and SGZ axes, respectively. Sketchfab interactive visualizations are available for both analyses (i.e., https://skfb.ly/oL976 and https://skfb.ly/oL977). |
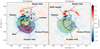 |
Fig. A.2. SGX-SGY slice centered on SGZ = 0 Mpc h−1 and of width 7.8 Mpc h−1 of the overdensity field reconstructed from CF4 galaxies (left panel) and groups (right panel) overlapped with the gravitational basins identified in the associated velocity field. Basins of attraction are indicated with filled contours with no border line, and basins of repulsion are shown with empty contours with solid, dashed, or dotted black lines. The name of each corresponding structure is also included. |
Gravitational basins identified in the peculiar velocity field reconstructed from the CF4 individual galaxies and groups.
Figure A.3 shows zoomed-in visualizations of the basins of attraction of six different superclusters: Laniakea, Apus, Hercules, Lepus, Perseus-Pisces, and Shapley. The left and right columns show basins obtained from the ungrouped and grouped reconstructions, respectively, except for the first row (ungrouped version only in this case). In each panel, the overdensity field is represented by four levels of isosurfaces (see Figure A.1 for more details). Streamlines were also computed from the velocity field by only considering voxels part of the basin as seed points. In the figure, the volume of each basin is shown in blue. In the case of Laniakea, in yellow, we also show the volume obtained previously from the peculiar velocity field reconstructed from the CF2 catalog (Dupuy et al. 2019), which allowed its discovery.
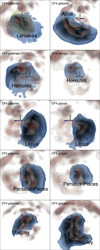 |
Fig. A.3. Gravitational watersheds identified in the peculiar velocity field reconstructed from CF4 galaxies and groups. Each watershed is indicated with a blue contour and streamlines. In the case of Laniakea, the basin of attraction found in the CF2 reconstruction is also shown in yellow. The reconstructed overdensity field is represented by four levels of isosurfaces. The center of the reconstruction is indicated by the red, green, and blue arrows of length 50 Mpc h−1, each directing along SGX, SGY, and SGZ. |
Repellers detected in both reconstructions are shown in Figure A.4. In the top panel are the repellers in the ungrouped reconstruction, and in the bottom panel are those in the grouped reconstruction. In order to focus on repellers and underdensities, overdensities are only represented by the three highest levels of isosurfaces, as in Figure A.1. Additionally, underdensities are plotted as two levels of isosurfaces. The red, green, and blue arrows pointing toward SGX, SGY, and SGZ respectively indicate the orientation of the visualization. The black spheres in the figure are at the coordinates of the repellers detected in each reconstruction, and the velocity field inside the associated basins of repulsion is represented by streamlines, computed in the backward direction and hence converging at the locations of the repellers. The two gray spheres in the figure indicate the positions of the Dipole and Cold Spot Repeller (Hoffman et al. 2017; Courtois et al. 2017).
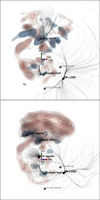 |
Fig. A.4. Repellers in the local universe reconstructed from the CF4 galaxies (top panel) and groups (bottom panel). Overdensities are represented in different red shades by three levels of isosurfaces: 1, 1.4, and 1.75 for CF4 galaxies, and 0.8, 1.2, and 1.5 for CF4 groups. Underdensities are highlighted in less transparent blue shades and represented by two levels of isosurfaces: -1.27 and -1.6 for CF4 galaxies, and -1 and -1.35 for CF4 groups. Streamlines were derived by integrating the reconstructed peculiar velocity field in the backward direction (i.e., integrating −1 × v). For the sake of clarity, extra noise has been removed by showing only streamlines part of basins of repulsion identified with the segmentation algorithm, listed in the bottom part of Table A.1. Black spheres are located at the coordinates of repellers identified in the velocity field (i.e., at the points where the streamlines converge). The center of the reconstructed cube is indicated by the red, green, and blue arrows of length 50 Mpc h−1 and directing along the supergalactic cartesian SGX, SGY, and SGZ axes, respectively. Sketchfab interactive visualizations are available for both CF4 reconstructions https://skfb.ly/oL97q and https://skfb.ly/oL978). |
All Tables
Gravitational basins identified in the peculiar velocity field reconstructed from the CF4 individual galaxies and groups.
All Figures
 |
Fig. 1. Visualization of the basins of attraction of Laniakea (in red) and the five superclusters that are now dynamically defined as watershed in the same way, namely Apus, Hercules, Lepus, Perseus-Pisces and Shapley, as well as the basins identified further away in the SDSS area (both in purple). The basins shown are obtained from the ungrouped CF4 velocity field. Each galaxy from the CF4 catalog is positioned at its redshift and represented by tiny dots, red for galaxies part of the Laniakea basin of attraction and purple otherwise. Streamlines are also computed for each galaxy with the same color code. The gradient of color is related to the density of streamlines. Streamlines colored white or yellow indicate a high density of streamlines. Each identified basin of attraction is annotated by the associated structure name. For reference, the three supergalactic cartesian orientation axes SGX, SGY, SGZ are drawn in the bottom left, represented respectively by red, green and blue arrows of size 50 Mpc h−1. |
| In the text | |
 |
Fig. 2. Gravitational valleys in the Local Universe. Left and middle: both panels show a supergalactic cartesian SGX-SGY slice of width 7.8 Mpc h−1, centered on SGZ = 0 Mpc h−1, of the density of streamlines, derived from the ungrouped (left) and grouped (right) CF4 velocity field. Yellow represents voxels highly concentrated in streamlines, while black represents a low concentration of streamlines. Right: density of streamlines from a ΛCDM simulation constrained with the CF2 data, with the same color code. Structures are annotated in the figure. Note that the scale of the axes is different from the two other panels. As a matter of fact, the CF2 catalog was much sparser in data (seven times less data) and much smaller in cartographied volume (ten times smaller compared to CF4), thus this simulation is loosely constrained on scales up to 150 Mpc h−1 maximum. Also at that time, we had poor coverage of the southern hemisphere large-scale structures. |
| In the text | |
 |
Fig. A.1. Attractors in the local universe reconstructed from the CF4 galaxies (top panel) and groups (bottom panel). The reconstructed overdensity field is represented by four levels of isosurfaces from white to dark red: 0.75, 1, 1.4, and 1.75 for CF4 galaxies, and 0.5, 0.8, 1.2, and 1.5 for CF4 groups. Streamlines were derived by integrating the reconstructed peculiar velocity field in the forward direction. For clarity purposes, extra noise has been removed by only showing streamlines part of basins of attraction identified with the segmentation algorithm, listed in the top part of Table A.1. Black spheres are located at the coordinates of attractors identified in the velocity field (i.e., at the points where the streamlines converge). The center of the reconstructed cube is indicated by the red, green, and blue arrows of length 50 Mpc h−1 directing along the supergalactic cartesian SGX, SGY, and SGZ axes, respectively. Sketchfab interactive visualizations are available for both analyses (i.e., https://skfb.ly/oL976 and https://skfb.ly/oL977). |
| In the text | |
 |
Fig. A.2. SGX-SGY slice centered on SGZ = 0 Mpc h−1 and of width 7.8 Mpc h−1 of the overdensity field reconstructed from CF4 galaxies (left panel) and groups (right panel) overlapped with the gravitational basins identified in the associated velocity field. Basins of attraction are indicated with filled contours with no border line, and basins of repulsion are shown with empty contours with solid, dashed, or dotted black lines. The name of each corresponding structure is also included. |
| In the text | |
 |
Fig. A.3. Gravitational watersheds identified in the peculiar velocity field reconstructed from CF4 galaxies and groups. Each watershed is indicated with a blue contour and streamlines. In the case of Laniakea, the basin of attraction found in the CF2 reconstruction is also shown in yellow. The reconstructed overdensity field is represented by four levels of isosurfaces. The center of the reconstruction is indicated by the red, green, and blue arrows of length 50 Mpc h−1, each directing along SGX, SGY, and SGZ. |
| In the text | |
 |
Fig. A.4. Repellers in the local universe reconstructed from the CF4 galaxies (top panel) and groups (bottom panel). Overdensities are represented in different red shades by three levels of isosurfaces: 1, 1.4, and 1.75 for CF4 galaxies, and 0.8, 1.2, and 1.5 for CF4 groups. Underdensities are highlighted in less transparent blue shades and represented by two levels of isosurfaces: -1.27 and -1.6 for CF4 galaxies, and -1 and -1.35 for CF4 groups. Streamlines were derived by integrating the reconstructed peculiar velocity field in the backward direction (i.e., integrating −1 × v). For the sake of clarity, extra noise has been removed by showing only streamlines part of basins of repulsion identified with the segmentation algorithm, listed in the bottom part of Table A.1. Black spheres are located at the coordinates of repellers identified in the velocity field (i.e., at the points where the streamlines converge). The center of the reconstructed cube is indicated by the red, green, and blue arrows of length 50 Mpc h−1 and directing along the supergalactic cartesian SGX, SGY, and SGZ axes, respectively. Sketchfab interactive visualizations are available for both CF4 reconstructions https://skfb.ly/oL97q and https://skfb.ly/oL978). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


