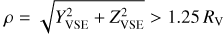EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A142 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A142
Number of page(s) 7
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202346989
Published online 20 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Venus has no intrinsic magnetic field, but the interplanetary magnetic field (IMF) piles up and drapes around the conductive ionosphere, forming an induced magnetosphere (Luhmann et al. 2004). The three-dimensional configuration of the draped magnetic field near Venus is guided by the IMF clock angle (Saunders & Russell 1986; Du et al. 2013), which is the IMF azimuthal angle in the plane perpendicular to the solar wind flow (Ramstad et al. 2020). This 3D configuration is important because it concerns the energy transfer from solar wind to planetary particles, including the pickup process on the dayside (Wei et al. 2017; Xu et al. 2023), the wave-particle interaction in the magnetosheath and bow shock (Jarvinen et al. 2020; Hadid et al. 2021; Dimmock et al. 2022), the occurrence of Kelvin-Helmholtz instability at the terminator region (Dang et al. 2022), the ion acceleration by magnetic tension force (Dubinin et al. 2013; Allen et al. 2021), and the magnetic reconnection in the magnetotail (Zhang et al. 2012; Volwerk et al. 2021).

Within the induced magnetosphere, the field strength is asymmetric with respect to the upstream solar wind electric field (E; Phillips et al. 1987; Zhang et al. 1991; Xiao & Zhang 2018): in the +E hemisphere where the solar wind convection electric field points away from the planet, the magnetic field is stronger than that in the opposite −E hemisphere. When the draped magnetic field lines are stretched and slip over the magnetic “pole” into the nightside to fill the magnetotail (Luhmann 1986; Phillips & McComas 1991; Ma et al. 2013), the field lines in the +E hemisphere of the magnetotail sink towards the −E direction (Rong et al. 2014; Zhang et al. 2022), the reversal of clock angle appears (Zhang et al. 2010; Xiao et al. 2016), and the cross-tail magnetic field exhibits a looping configuration (Chai et al. 2016; He et al. 2021).

However, most previous studies concentrated on the Venusian induced magnetosphere (Du et al. 2013; Jarvinen et al. 2013), and a thorough examination of the magnetic field morphology within the Venusian magnetosheath remains to be carried out. It seems that the cross-flow IMF component could maintain its direction to some extent as it traverses the bow shock into the Venusian magnetosheath (Phillips et al. 1986). Nevertheless, the asymmetry in the magnetic field configuration associated with ±E has not been extensively explored within the sheath region. In this work, we aim to analyze the magnetic field clock angle and its variability specifically within the Venusian magnetosheath, drawing insights from both observations and simulations.

thumbnail Fig. 1

Comparison of the IMF clock angles under the steady IMF and the normal solar wind. The magnetic field, the three components of the magnetic field, and the local magnetic field clock angle under the cases of (a) the steady IMF and (b) the normal solar wind. The vertical lines mark the BS and the induced magnetosphere boundary (IMB). The region of the induced magnetosphere is shaded in yellow.

2 Data and MHD model

We use the magnetic field data with 1 s resolution from the MAG (Zhang et al. 2006) of Venus Express (VEX; Svedhem et al. 2007). The IMF clock angle (0° < Φ < 360°) is defined as the counterclockwise angle from the +Y direction in YZ plane of the Venus-Solar-Orbital (VSO) coordinates, where the XVSO axis points from the center of Venus to the Sun, lyso points in the opposite direction to the planet’s direction of motion, and ZVSO completes the right-handed system. To study the 3D magnetic field morphology of Venusian magnetosheath, the magnetic field is organized in the Venus-Solar-Electrical (VSE) coordinate system, in which the XVSE is antiparallel to the solar wind velocity, the ívsE points along the cross-flow magnetic field component of the upstream IMF, and the Zvse is along the solar wind motional electric field. The direction of solar wind velocity VSW is assumed to be aligned with the Sun–Venus line (a 5° aberration due to the orbital motion of Venus is taken into account). To construct the 3D magnetic field configuration, we selected orbits under the condition of a steady IMF where the influence of IMF variability can be minimized. Figure 1 shows that the magnetic field clock angle is relatively steady in the magnetosheath when the upstream IMF shows little variation. For each orbit, we denoted the average IMF clock angle 10 min before (after) the inbound (outbound) bow shock (BS) crossing as Φ1 (Φ2) and chose the orbits with relatively steady IMF clock angles, where the differences of Φ1 and Φ2 do not exceed 30° (Rong et al. 2016; Delva et al. 2017). The YVSE direction of each orbit was defined as the angle bisector of Φ1 and Φ2, and about 200 orbits from May 2006 to November 2014 were picked out.

A 3D single-fluid multi-species global magnetohydrodynamics (MHD) model of Venus (Ma et al. 2013, 2020; Xu et al. 2022) within the BATS-R-US (Block Adaptive Tree Solar Wind Roe-Type Upwind Scheme) code (Tóth et al. 2012) is used in this study. The input parameters, including the solar wind number density of 6.9 cm−3 (Xu et al. 2021), the solar wind temperature of 2.1 × 10s K (Bader et al. 2019), the solar wind velocity of 384 km s−1 (Rojas Mata et al. 2022) anti-parallel to the +Xvse direction, and the IMF magnitude of 6.5 nT (Chang et al. 2018), represent the average solar minimum condition of Solar Cycle 24. We ran the model with a time-dependent scheme for a one-hour simulation to achieve a steady state.

3 The clock angle distributions in the magnetosheath

To ensure statistical significance, we ignore the bins that contain fewer than ten data points in Figs. 2a–c. The magnetotail radius is approximately ρ=YVSE2+ZVSE2=1.25RV$\rho = \sqrt {Y_{{\rm{VSE}}}^2 + Z_{{\rm{VSE}}}^2} = 1.25{R_{\rm{V}}}$ (Zhang et al. 2010; Xu et al. 2021), within which the data points are ignored in Figs. 2b,c. We note that this straightforward separation of magnetosheath and magnetotail at ρ = 1.25RV might involve some data points that were actually measured in the region of magnetotail. ΔΦ is the sheath magnetic field clock angle departure, which is defined as counterclockwise rotation of local field clock angle from the IMF. The maps of ΔΦ show almost symmetric distributions with respect to the Zvse direction. The mean |ΔΦ| with standard deviation of the bins are 7 + 5° on the dayside (1 < Xvse <1.5RV), 12 ± 8° on the terminator (−0.5 < XVSE < 0.5RV), and 12 ± 9° on the nightside (−5 < XVSE < −l·RV)· The configurations of sheath magnetic field in YZVSE planes are also presented in Figs. 2d–f, which display corresponding maps of the ΔΦ obtained from the simulation with Bjmf = [0.0, 6.5, 0.0] nT. The sheath field clock angle on the dayside is almost identical to that of the IMF (Fig. 2d), and both exhibit maximum values of approximately 30° on the terminator and nightside (Figs. 2e,f). Additionally, the maps also reveal that the |ΔΦ| tends to be higher for smaller ρ values. One likely explanation could be the more significant draping and bending of magnetic field lines in the inner part of magnetosheath adjacent to the induced magnetosphere, as shown in Fig. 3. Another contributing factor is that our definition of the magnetosheath region, separated at ρ = 1.25RV, might encompass a portion of the magnetotail region. Even though, the |∆Φ| is, overall, not significant.

An IMF clock angle proxy can be used to organize data in VSE coordinates when the spacecraft is located downstream of the bow shock (Hurley et al. 2018; Ruhunusiri et al. 2018; Dong et al. 2019). Considering the small IMF clock angle departure as discussed above, we expect any measurement taken within the magnetosheath can be a proxy for the IMF clock angle. The magnitude of the deviation |∆Φ| can be regarded as the uncertainty associated with this proxy. To assess its effectiveness, all data points above the empirical induced magnetosphere boundary (Xu et al. 2021) and downstream of the bow shock are examined. The median value and 90th percentile of |∆Φ| for these data points are determined to be 16° and 43°, respectively.

thumbnail Fig. 2

Spatial distributions of the Venusian magnetosheath magnetic field clock angle departures (∆Φ) on the dayside, terminator, and nightside. (a)–(c) Average ∆Φ and average magnetic field directions labeled by arrows in the YZVSE planes (ρ=YVSE2+ZVSE2>1.25RV$\rho = \sqrt {Y_{{\rm{VSE}}}^2 + Z_{{\rm{VSE}}}^2} > 1.25{R_{\rm{V}}}$ for (b) and (c)). A bin size is 0.5 × 0.5 RV, and the black circle in each panel corresponds to the position of Venus. (d)–(f) The same values from the simulation run on the slices of XVSE = 1.25 Rv, 0 Rv and −3 Rv.

4 Response time of the sheath field to IMF rotation

Although the magnetosheath field clock angle departure is not substantial under steady IMF conditions, the instances during the unsteady IMF need to be further investigated. However, inferring the unsteady IMF becomes challenging when the VEX is located downstream of the bow shock. Fortunately, during smoothly rotating interplanetary coronal mass ejections (ICMEs), if the response of the sheath field to IMF rotation is fast, the upstream IMF clock angle can be inferred based on the rotation speed of sheath field clock angle (the slope of clock angle variation). As shown in Fig. 4, Venus encountered a strong ICME on 10 Sep. 2006 (Zhang et al. 2008). Three distinct time intervals from 10 Sep. 2006 20:30:00 to 11 Sep. 2006 02:30:00, 11 Sep. 2006 04:00:00 to 06:00:00 and 09:00:00 to 13:00:00 were chosen, and the periods during which the spacecraft was located in the solar wind and magnetosheath region are marked at the top of Fig. 4a. In each time interval, the rotation of IMF clock angle is fitted by a dashed cyan line based on the data collected in the solar wind. Simultaneously, the slope of sheath field variation is fitted based on the downstream measurements, enabling us to estimate the upstream IMF when the spacecraft located in the magnetosheath. The cyan and magenta dashed lines exhibit remarkable alignment in the three time intervals. This alignment suggests that the inferred IMF clock angle closely corresponds to the measured IMF, highlighting the swift reaction of magnetosheath field to changes in the IMF orientation. The time delay in the magnetosheath should be related to how far the magnetic field has propagated downstream of the bow shock, where in this case the distance is relatively short due to the bow shock flapping back and forth across the spacecraft.

In order to determine the exact response time of the magnetic field within the magnetosheath, a time-dependent MHD simulation is conducted. The simulation with an initial BIMF = [0.0, 6.5, 0.0] nT proceeds for 1 h to reach a stationary state, and subsequently the IMF is altered gradually to [−3.6, 0.0, 5.4] nT over about 40 s. Figure 5a provides examples of clock angle variations in several regions, including the solar wind represented by red dashed lines, and the inner and outer magnetosheath depicted by blue and green lines, respectively. Each region is further categorized into the dayside, terminator, and nightside, which are marked by circle, triangle and square symbols. The blue and green lines are the simnulation results at six specific locations, as depicted in Fig. 5b. The rotated IMF arrives at Venus at approximately 1:01:30–1:01:40, and by around 1:02:10, the IMF clock angle has shifted by 90°. Although the dayside sheath field direction cannot synchronize with the IMF rotation, there is only a slight time delay of a few seconds (indicated by the distances between the lines). On the terminator and night-side, the time delay ranges from 0 to 20 s. This time delay can also be estimated from Fig. 5b, which shows the flow velocity near Venus. The solar wind undergoes deceleration from 384 to 100 km s−1 upon encountering the subsolar bow shock, and it shows higher velocity with increasing solar zenith angle. The flow speeds exceed 300 km s−1 on the terminator and nightside, and the white lines mark the flow directions. It is worth noting that the magnitude and direction of the bulk velocity from our model results align well with the observations by Bader et al. (2019), Rojas Mata et al. (2022), and Xu et al. (2023). We use two yellow points to label a time period of approximately 16 s. For instance, the solar wind takes 79 s to propagate from XVSO = 2RV to XVSO = −3 RV, while there are 5.4 time intervals (85 s) for the green point and 5.9 time intervals (93 s) for the blue point at XVSO = −3 RV. These time delays are consistent with the distances between the lines in Fig. 5b, indicating that the flow velocities determine the time delays in the magnetosheath. Moreover, the outer region of magnetosheath adjacent to the bow shock reacts more quickly compared to the inner region closer to the induced magnetosphere, showing agreement with Romanelli et al. (2018, 2019).

Figure 6 shows the magnetic field configurations projected on the YZVSO plane at different moments. The nightside magnetosheath achieves a balance at 1:03:50 (Fig. 6i), just 20–30 s after the outside IMF turns to 90° (Fig. 6h). Figures 6f,i show the asymmetry of the magnetic field clock angle departure between the sectors downstream of the quasi-parallel and quasi-perpendicular bow shocks (Fang et al. 2018; Dong et al. 2019; Li et al. 2023).

thumbnail Fig. 3

Example of the draping of magnetic field lines. The field lines are color-coded according to the clock angle departure (∆Φ), and the XZVSE plane is color-coded according to the magnetic field strength (|B|). The black line denotes the empirical induced magnetosphere boundary (IMB; Xu et al. 2021), which separates the magnetosheath and the induced magnetosphere.
thumbnail Fig. 4

Rotation of the magnetic field clock angle during an ICME. (a) Magnetic field strength. (b) Three components of the magnetic field. (c) Local magnetic field clock angle in the solar wind and the Venusian magnetosheath. Three time intervals from 10 Sep. 2006 20:30:00 to 11 Sep. 2006 02:30:00, 11 Sep. 2006 04:00:00 to 06:00:00 and 09:00:00 to 13:00:00 are focused on. For each time interval, the clock angle variations are fitted with cyan and magenta dashed lines based on the data gathered in solar wind and magnetosheath, respectively. The rotation speeds are indicated by the slopes of the dashed lines.
thumbnail Fig. 5

Temporal evolution of the Venusian magnetosheath magnetic field clock angle under an IMF variation from [0.0, 6.5, 0] nT to [−3.6, 0.0, 5.4] nT. (a) IMF (red dashed lines) probed on the dayside [X, Y, Z]vso = [1.25, 0, 5] Rv (circle symbol), terminator region [X, Y, Z]VSO = [0, 0, 5] Rv (triangle), and nightside [X, Y, Z]VSO = [−3, 0, 5] Rv (square). The magnetic field in the inner and outer parts of magnetosheath (blue and green and lines) are probed at [X, Y, Z]VSO = [1.25, 0, 0] Rv, [0, 0, 1.5] Rv, [−3, 0, 2] Rv, and [X, Y, Z]VSO = [1.25, 0, 0.5] Rv, [0, 0, 2] Rv, [−3, 0, 3] Rv. The six positions are labeled by blue and green points in (b). The white lines mark the flow directions, and an interval between two yellow points corresponds to a time period of about 16 s.
thumbnail Fig. 6

Spatial distributions of Venusian magnetosheath magnetic field clock angle Φ under an IMF variation from [0.0, 6.5, 0] nT to [−3.6, 0.0, 5.4] nT on the (a–c) dayside XVSO = 1.25 RV, (d–f) terminator XVSO = 0RV and (g–i) nightside XVSO = −3 RV.

5 Discussion and conclusions

In this work, we conducted observations of the IMF clock angle departures within the magnetosheath of Venus. The magnetosheath field clock angle exhibits a symmetrical distribution with respect to the direction of solar wind electric field. This feature was further confirmed by MHD simulations. Additionally, the simulations depicted the magnetic field line draping in the vicinity of Venus (Fig. 3). To a great extent, the sheath field just passes the planet without significant pileup, resulting in the symmetric sheath field morphology, in contrast with the magnetotail (Zhang et al. 2010) where the magnetic field is greatly anchored by planetary ions. Furthermore, our simulation produces an asymmetry of the magnetic field clock angle departure between the sectors downstream of the quasi-parallel and quasi-perpendicular bow shocks, which is attributed to the different magnetosheath field and flow geometries associated with the two sectors (Fang et al. 2018). The median value and 90th percentile of IMF clock angle departure |∆Φ| of all data points are 16° and 43°. The insignificant |∆Φ| in the Venusian magnetosheath is also validated by MHD model.

A case study illustrates a continuous and uniform rotation of the IMF clock angle during an ICME, as shown in Fig. 4. The rotation of the sheath field aligns with the rotation of the IMF, which suggests that the response time of the sheath field to changes in the IMF should be relatively short. In order to characterize the precise response time of the sheath field, we conducted a time-dependent MHD simulation lasting 1 hour to reach a stationary state. Subsequently, we deliberately rotated the IMF clock angle by 90°. The sheath field clock angle closely followed the changes in the IMF clock angle, particularly on the dayside. As compared with the response time of the Venusian induced magnetosphere and magnetotail associated with IMF rotation (~ 10 min; Benna et al. 2009; Slavin et al. 2009; Xu et al. 2022), the sheath field’s reaction to changes in the IMF takes no longer than 1 min, which is similar to the time delay determined within the Martian magnetosheath (Romanelli et al. 2018, 2019). Moreover, the response time varies depending on the specific regions within the magnetosheath. In particular, the timescale for changes in the inner part of the magnetosheath, which is adjacent to the induced magnetosphere, is longer compared to the outer part. Our suggestion is that the primary factor governing the response timescale in the Venusian magnetosheath is the local bulk velocity. If the downstream magnetic field direction remains relatively stable for a duration of at least 1 minute, it can serve as a proxy for the upstream IMF clock angle. Conversely, if the magnetic field within the sheath region were found to exhibit rotation, this would suggest that the direction of the upstream IMF is changing. Furthermore, observations of the plasma distributions in the magnetosheath, based on this proxy (Xu et al. 2023), also support the effectiveness of using measurements taken within the magnetosheath as a proxy.

Acknowledgements

This work is supported by NSFC (42122061 and 42241112), Guangdong Basic and Applied Basic Research Foundation (2022A1515110383), and The Science and Technology Development Fund, Macau SAR (File nos. 0098/2022/A2 and 0003/2022/AFJ). This work is also supported by Pandeng Program of National Space Science Center, Chinese Academy of Sciences. L. Xie is supported the Youth Innovation Promotion Association of the Chinese Academy of Sciences. We acknowledge Venus Express team for the MAG data (https://archives.esac.esa.int/psa/ftp/VENUS-EXPRESS/MAG/). We especially appreciate Y. J. Ma at UCLA for the model used in this work (https://doi.org/10.1029/2012JA018265).

References

  1. Allen, R. C., Cernuda, I., Pacheco, D., et al. 2021, A&A, 656, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bader, A., Stenberg Wieser, G., André, M., et al. 2019, J. Geophys. Res. SpacePhys., 124, 3312 [NASA ADS] [CrossRef] [Google Scholar]
  3. Benna, M., Acuña, M. H., Anderson, B. J., et al. 2009, Geophys. Res. Lett., 36, L04109 [NASA ADS] [CrossRef] [Google Scholar]
  4. Chai, L., Wei, Y., Wan, W., et al. 2016, J. Geophys. Res. Space Phys., 121, 688 [NASA ADS] [CrossRef] [Google Scholar]
  5. Chang, Q., Xu, X., Zhang, T., et al. 2018, ApJ, 867, 129 [Google Scholar]
  6. Dang, T., Lei, J., Zhang, B., et al. 2022, Geophys. Res. Lett., 49, e96961 [NASA ADS] [CrossRef] [Google Scholar]
  7. Delva, M., Volwerk, M., Jarvinen, R., & Bertucci, C. 2017, J. Geophys. Res. Space Phys., 122, 10396 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dimmock, A. P., Khotyaintsev, Y. V., Lalti, A., et al. 2022, A&A, 660, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Dong, Y., Fang, X., Brain, D. A., et al. 2019, J. Geophys. Res. Space Phys., 124, 4295 [NASA ADS] [CrossRef] [Google Scholar]
  10. Du, J., Wang, C., Zhang, T. L., & Kallio, E. 2013, J. Geophys. Res. Space Phys., 118, 6915 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dubinin, E., Fraenz, M., Zhang, T. L., et al. 2013, J. Geophys. Res. Space Phys., 118, 7624 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fang, X., Ma, Y., Luhmann, J., et al. 2018, Geophys. Res. Lett., 45, 3356 [Google Scholar]
  13. Hadid, L. Z., Edberg, N. J. T., Chust, T., et al. 2021, A&A, 656, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. He, M., Vogt, J., Dubinin, E., Zhang, T., & Rong, Z. 2021, ApJ, 923, 73 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hurley, D. M., Dong, Y., Fang, X., & Brain, D. A. 2018, J. Geophys. Res. SpacePhys., 123, 9612 [NASA ADS] [CrossRef] [Google Scholar]
  16. Jarvinen, R., Kallio, E., & Dyadechkin, S. 2013, J. Geophys. Res. Space Phys., 118, 4551 [NASA ADS] [CrossRef] [Google Scholar]
  17. Jarvinen, R., Alho, M., Kallio, E., & Pulkkinen, Tuija, I. 2020, Geophys. Res. Lett., 47, e87462 [NASA ADS] [CrossRef] [Google Scholar]
  18. Li, G., Lu, H., Li, Y., Cao, J., & Li, S. 2023, MNRAS, 521, 1849 [NASA ADS] [CrossRef] [Google Scholar]
  19. Luhmann, J. G. 1986, Space Sci. Rev., 44, 241 [NASA ADS] [CrossRef] [Google Scholar]
  20. Luhmann, J. G., Ledvina, S. A., & Russell, C. T. 2004, Adv. Space Res., 33, 1905 [Google Scholar]
  21. Ma, Y. J., Nagy, A. F., Russell, C. T., et al. 2013, J. Geophys. Res. Space Phys., 118, 321 [NASA ADS] [CrossRef] [Google Scholar]
  22. Ma, Y., Toth, G., Nagy, A., Luhmann, J., & Russell, C. 2020, Geophys. Res.Lett., 47, e87593 [NASA ADS] [Google Scholar]
  23. Phillips, J. L., & McComas, D. J. 1991, Space Sci. Rev., 55, 1 [Google Scholar]
  24. Phillips, J. L., Luhmann, J. G., & Russell, C. T. 1986, J. Geophys. Res. SpacePhys., 91, 7931 [NASA ADS] [CrossRef] [Google Scholar]
  25. Phillips, J. L., Luhmann, J. G., Russell, C. T., & Moore, K. R. 1987, J. Geophys.Res. Space Phys., 92, 9920 [NASA ADS] [CrossRef] [Google Scholar]
  26. Ramstad, R., Brain, D. A., Dong, Y., et al. 2020, Nat. Astron., 4, 979 [CrossRef] [Google Scholar]
  27. Rojas Mata, S., Stenberg Wieser, G., Futaana, Y., et al. 2022, J. Geophys. Res. Space Phys., 127, e29611 [NASA ADS] [CrossRef] [Google Scholar]
  28. Romanelli, N., Modolo, R., Leblanc, F., et al. 2018, J. Geophys. Res. Space Phys., 123, 5315 [NASA ADS] [CrossRef] [Google Scholar]
  29. Romanelli, N., DiBraccio, G., Modolo, R., et al. 2019, Geophys. Res. Lett., 46, 10977 [NASA ADS] [CrossRef] [Google Scholar]
  30. Rong, Z. J., Barabash, S., Futaana, Y., et al. 2014, J. Geophys. Res. Space Phys., 119, 8838 [NASA ADS] [CrossRef] [Google Scholar]
  31. Rong, Z. J., Stenberg, G., Wei, Y., et al. 2016, J. Geophys. Res. Space Phys., 121, 10978 [NASA ADS] [CrossRef] [Google Scholar]
  32. Ruhunusiri, S., Halekas, J. S., Espley, J. R., et al. 2018, Geophys. Res. Lett., 45, 10855 [NASA ADS] [CrossRef] [Google Scholar]
  33. Saunders, M. A., & Russell, C. T. 1986, J. Geophys. Res. Space Phys., 91, 5589 [NASA ADS] [CrossRef] [Google Scholar]
  34. Slavin, J. A., Acuña, M. H., Anderson, B. J., et al. 2009, Geophys. Res. Lett., 36, L09106 [Google Scholar]
  35. Svedhem, H., Titov, D. V., McCoy, D., et al. 2007, Planet. Space Sci., 55, 1636 [Google Scholar]
  36. Tóth, G., van der Holst, B., Sokolov, I. V., et al. 2012, J. Comput. Phys., 231, 870 [Google Scholar]
  37. Volwerk, M., Horbury, T. S., Woodham, L. D., et al. 2021, A&A, 656, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Wei, Y., Fraenz, M., Dubinin, E., et al. 2017, Sci. Bull., 62, 1669 [NASA ADS] [CrossRef] [Google Scholar]
  39. Xiao, S. D., & Zhang, T. L. 2018, Planet. Space Sci., 158, 53 [Google Scholar]
  40. Xiao, S. D., Zhang, T. L., & Baumjohann, W. 2016, J. Geophys. Res. Space Phys., 121, 4542 [NASA ADS] [CrossRef] [Google Scholar]
  41. Xu, Q., Xu, X., Zhang, T. L., et al. 2021, A&A, 652, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Xu, Q., Xu, X., Zuo, P., et al. 2022, ApJ, 931, 95 [NASA ADS] [CrossRef] [Google Scholar]
  43. Xu, Q., Xu, X., Zuo, P., et al. 2023, Geophys. Res. Lett., 50, e2022GL102401 [NASA ADS] [CrossRef] [Google Scholar]
  44. Zhang, T. L., Luhmann, J. G., & Russell, C. T. 1991, J. Geophys. Res. Space Phys., 96, 11145 [NASA ADS] [CrossRef] [Google Scholar]
  45. Zhang, T. L., Baumjohann, W., Delva, M., et al. 2006, Planet. Space Sci., 54, 1336 [Google Scholar]
  46. Zhang, T. L., Pope, S., Balikhin, M., et al. 2008, J. Geophys. Res. Planets, 113, E00B12 [Google Scholar]
  47. Zhang, T. L., Baumjohann, W., Du, J., et al. 2010, Geophys. Res. Lett., 37, L14202 [NASA ADS] [Google Scholar]
  48. Zhang, T. L., Lu, Q. M., Baumjohann, W., et al. 2012, Science, 336, 567 [CrossRef] [Google Scholar]
  49. Zhang, C., Rong, Z., Klinger, L., et al. 2022, J. Geophys. Res. Planets, 127, e07334 [NASA ADS] [Google Scholar]

All Figures

thumbnail Fig. 1

Comparison of the IMF clock angles under the steady IMF and the normal solar wind. The magnetic field, the three components of the magnetic field, and the local magnetic field clock angle under the cases of (a) the steady IMF and (b) the normal solar wind. The vertical lines mark the BS and the induced magnetosphere boundary (IMB). The region of the induced magnetosphere is shaded in yellow.
In the text
thumbnail Fig. 2

Spatial distributions of the Venusian magnetosheath magnetic field clock angle departures (∆Φ) on the dayside, terminator, and nightside. (a)–(c) Average ∆Φ and average magnetic field directions labeled by arrows in the YZVSE planes (ρ=YVSE2+ZVSE2>1.25RV$\rho = \sqrt {Y_{{\rm{VSE}}}^2 + Z_{{\rm{VSE}}}^2} > 1.25{R_{\rm{V}}}$ for (b) and (c)). A bin size is 0.5 × 0.5 RV, and the black circle in each panel corresponds to the position of Venus. (d)–(f) The same values from the simulation run on the slices of XVSE = 1.25 Rv, 0 Rv and −3 Rv.
In the text
thumbnail Fig. 3

Example of the draping of magnetic field lines. The field lines are color-coded according to the clock angle departure (∆Φ), and the XZVSE plane is color-coded according to the magnetic field strength (|B|). The black line denotes the empirical induced magnetosphere boundary (IMB; Xu et al. 2021), which separates the magnetosheath and the induced magnetosphere.
In the text
thumbnail Fig. 4

Rotation of the magnetic field clock angle during an ICME. (a) Magnetic field strength. (b) Three components of the magnetic field. (c) Local magnetic field clock angle in the solar wind and the Venusian magnetosheath. Three time intervals from 10 Sep. 2006 20:30:00 to 11 Sep. 2006 02:30:00, 11 Sep. 2006 04:00:00 to 06:00:00 and 09:00:00 to 13:00:00 are focused on. For each time interval, the clock angle variations are fitted with cyan and magenta dashed lines based on the data gathered in solar wind and magnetosheath, respectively. The rotation speeds are indicated by the slopes of the dashed lines.
In the text
thumbnail Fig. 5

Temporal evolution of the Venusian magnetosheath magnetic field clock angle under an IMF variation from [0.0, 6.5, 0] nT to [−3.6, 0.0, 5.4] nT. (a) IMF (red dashed lines) probed on the dayside [X, Y, Z]vso = [1.25, 0, 5] Rv (circle symbol), terminator region [X, Y, Z]VSO = [0, 0, 5] Rv (triangle), and nightside [X, Y, Z]VSO = [−3, 0, 5] Rv (square). The magnetic field in the inner and outer parts of magnetosheath (blue and green and lines) are probed at [X, Y, Z]VSO = [1.25, 0, 0] Rv, [0, 0, 1.5] Rv, [−3, 0, 2] Rv, and [X, Y, Z]VSO = [1.25, 0, 0.5] Rv, [0, 0, 2] Rv, [−3, 0, 3] Rv. The six positions are labeled by blue and green points in (b). The white lines mark the flow directions, and an interval between two yellow points corresponds to a time period of about 16 s.
In the text
thumbnail Fig. 6

Spatial distributions of Venusian magnetosheath magnetic field clock angle Φ under an IMF variation from [0.0, 6.5, 0] nT to [−3.6, 0.0, 5.4] nT on the (a–c) dayside XVSO = 1.25 RV, (d–f) terminator XVSO = 0RV and (g–i) nightside XVSO = −3 RV.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.