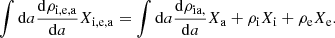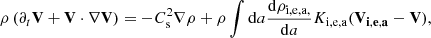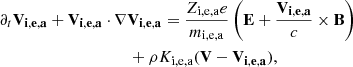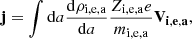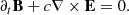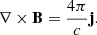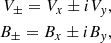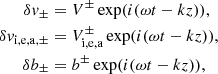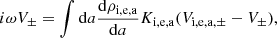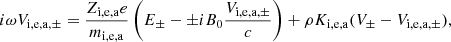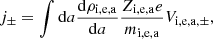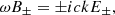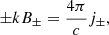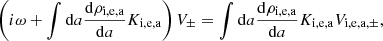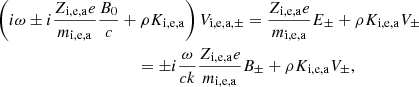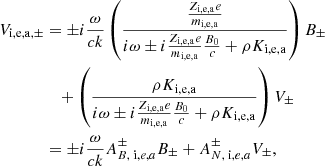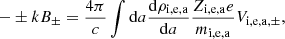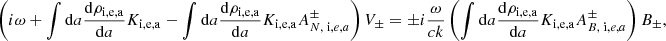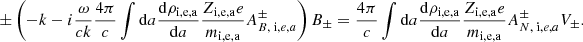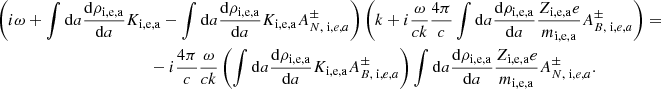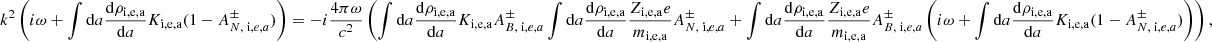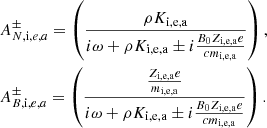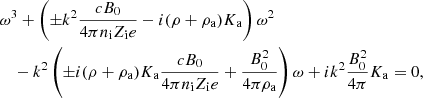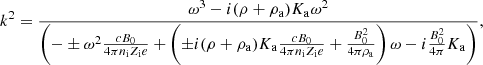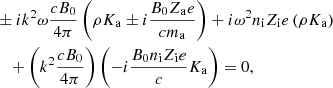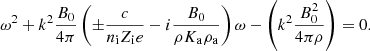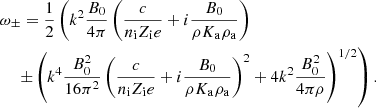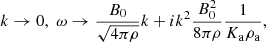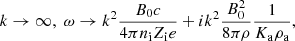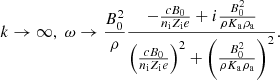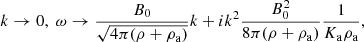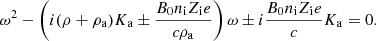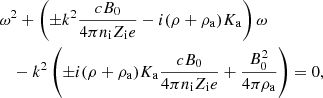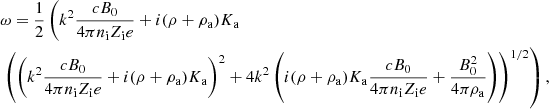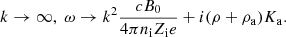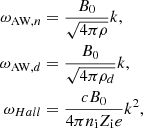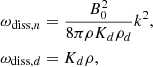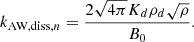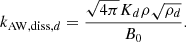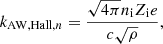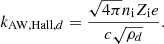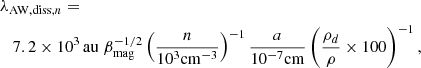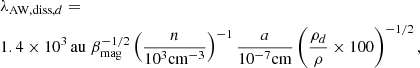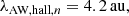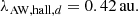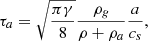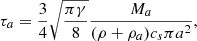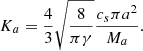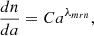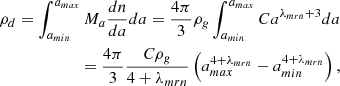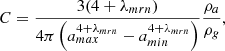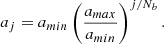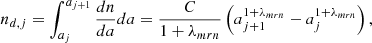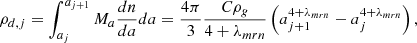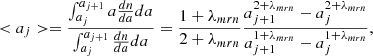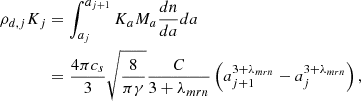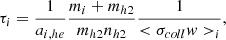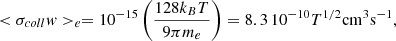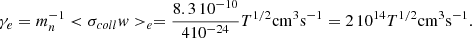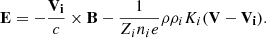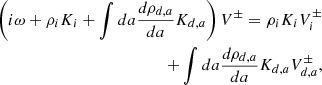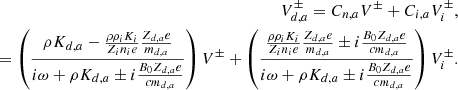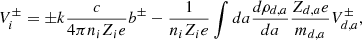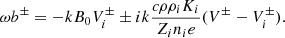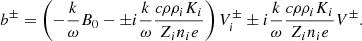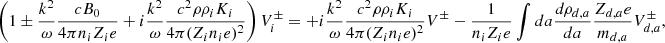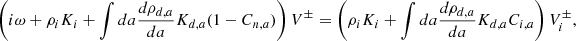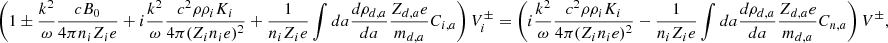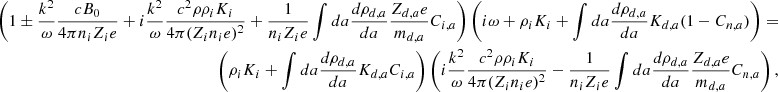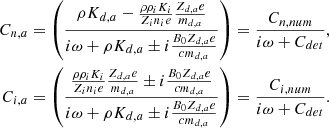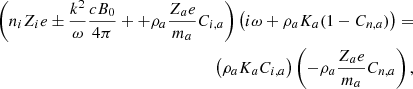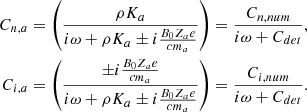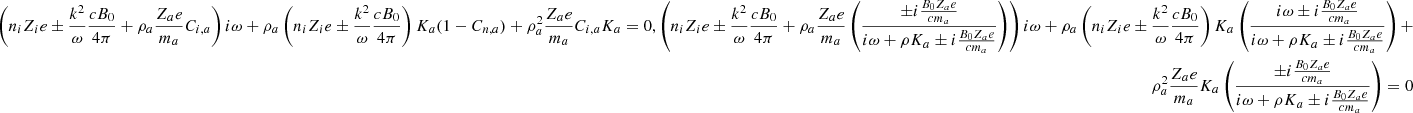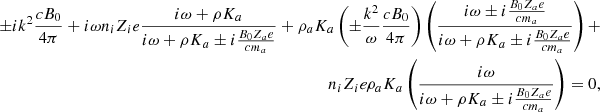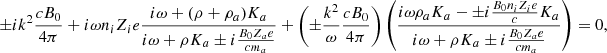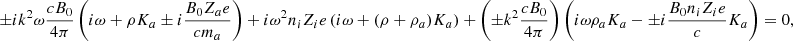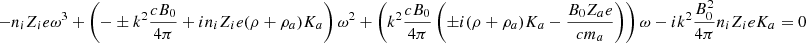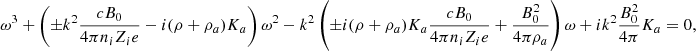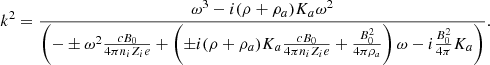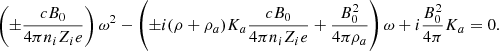| Issue |
A&A
Volume 674, June 2023
|
|
|---|---|---|
| Article Number | A149 | |
| Number of page(s) | 19 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202245120 | |
| Published online | 15 June 2023 | |
Propagation of Alfvén waves in the dusty interstellar medium
Can we neglect dust inertia in molecular clouds?
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris Diderot, Sorbonne Paris Cité, 91191 Gif-sur-Yvette, France
e-mail: patrick.hennebelle@cea.fr
Received:
2
October
2022
Accepted:
14
April
2023
Context. Alfvén waves are fundamental magnetized modes that play an important role in the dynamics of magnetized flows such as the interstellar medium (ISM).
Aims. In a weakly ionized medium, their propagation critically depends on the ionization rate as well as on the charge carriers. Depending on the gas density, these may be ions, electrons, or dust grains. The latter are particularly well known to have a drastic influence on the magnetic resistivities in the dense ISM, such as collapsing dense cores. Yet, in most calculations, for numerical reasons, the grain inertia is usually neglected.
Methods. We carried out an analytical investigation of the propagation of Alfvén waves both in a single-size and multi-size grain medium such as the ISM and we obtained exact expressions giving wavenumbers as a function of wave frequencies. These expressions were then solved analytically or numerically by taking into account or neglecting grain inertia.
Results. At long wavelengths, neglecting grain inertia is a very good approximation, however, the situation is rather different for wavelengths shorter than a critical value, which broadly scaled as 1/n, with n being the gas density. More precisely, when inertia is neglected, the waves do not propagate at short wavelengths or, due to the Hall effect, they develop for one circular polarization only, namely, a whistler mode such that ℛe(ω) ∝ k2. The other polarization presents a zero group velocity, namely, ℛe(ω) ∝ k0. When grain inertia is accounted for, the propagation of the two polarizations tend to be more symmetrical and the whistler mode is only present at density higher than ≃108 cm−3. At a lower density, it is replaced by a mode having ℛe(ω) ∝ k≃1.2. Interestingly, one of the polarization presents a distribution, instead of a single ω value. Importantly, for short wavelengths, wave damping is considerably reduced when inertia is properly accounted for.
Conclusions. To properly handle the propagation of Alfvén waves at short wavelengths, it is necessary to self-consistently treat grain inertia. We discuss the possible consequences this may have in the context of diffuse and dense molecular gas regarding turbulence, magnetic braking, and protoplanetary disk formation as well as cosmic ray propagation in the dense ISM.
Key words: waves / magnetohydrodynamics (MHD) / stars: formation / dust, extinction
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
It is now widely recognized that the magnetic field plays a fundamental role in many astrophysical contexts with regard to galaxies as well as stars and planets. In a weakly ionized medium such as the interstellar medium (ISM), its impact on the gas depends on its coupling with the neutrals. This coupling is related not only to the ionization degree but also to the charge carriers, namely, ions and electrons as well as dust grains. One difficulty that arises with the latter is that unlike ions and electrons, they present a distribution of sizes that span several orders of magnitude.
While few studies have addressed this problem in fully ionized plasma (Tripathi & Sharma 1996; Cramer et al. 2002), so far most of the works in the context of the dense ISM have not accounted for the grain dynamics but have factored in their impact on magnetic resistivities. Studies in this area include works by Nishi et al. (1991), Nakano et al. (2002), Kunz & Mouschovias (2009), Zhao et al. (2016), Marchand et al. (2016, 2021), Wurster et al. (2016), Guillet & Hennebelle (2020), and Tsukamoto & Okuzumi (2022). It has generally been found that the magnetic resistivities in the dense ISM are controlled by the grain distributions, particularly by the small ones, namely, of a size equal to a few nm. Ambipolar diffusion and the Hall effect, due to the decoupling of neutrals and ions with magnetic field, respectively, have been consistently found to play a significant role and are dominant over Ohmic dissipation up to densities of about ≃1011 cm−3.
Aside from the context of protoplanetary disks, where grains play a fundamental role regarding planet formation and are the subject of intensive studies over recent decades (e.g., Drazkowska et al. 2022), the dynamics of the grains has been recognized to be significant in such contexts as ISM shocks (Ciolek & Roberge 2002; Guillet & Forêts 2007), collapsing dense cores (Lebreuilly et al. 2019) or diffuse ISM (Hopkins & Lee 2016). These works constitute important attempts towards fully consistent ISM studies, particularly when the magnetic field is taken into account.
Indeed, grains follow their own dynamics and since they carry a fraction of the electric charges, they influence the propagation of magnetic waves and, more generally, the coupling between the gas and the magnetic field. Therefore, a more fully consistent approach should eventually be considered. In the present paper, we aim at progressing along this line, by addressing self-consistently the very fundamental magnetic waves, namely, the Alfvén waves. Indeed, Alfvén waves are certainly the most fundamental novelty that magnetic field introduces compared to an unmagnetized plasma. This is because Alfvén waves are transverse, incompressible modes that carries momentum and even angular momentum in rotating and magnetized flows.
For instance, Alfvén waves are likely responsible of the magnetic braking (Mouschovias & Paleologou 1979; Joos et al. 2012; Hirano et al. 2020) which appears to play a fundamental role in the formation of protoplanetary disks (Allen et al. 2003; Hennebelle et al. 2016, 2020; Wurster & Li 2018; Zhao et al. 2020; Maury et al. 2022). A detailed analysis of Alfvén waves propagating in the dense ISM, that is to say, one that accounts for the proper resistivities (e.g., Nakano et al. 2002), has been conducted by Wardle & Ng (1999). In particular, these authors stress the role of the Hall effect, which deeply modifies the propagation of Alfvén waves and introduce a strong difference between the two circularly polarized modes. While one of them present, at short wavelengths, λ, a dispersion relation such that ℛe(ω) ∝ λ−2 (with ω being the frequency of the wave), which is typical of whistler modes; the other circular polarization is such that ℛe(ω) ∝ λ0. This latter mode therefore has a zero group velocity (ZGV) and as a result, it does not transport momentum and energy. This strong effect has turned out to have consequences regarding the formation of protoplanetary disks, since aligned and anti-aligned rotators are not subject to the same magnetic braking (e.g., Braiding & Wardle 2012; Tsukamoto et al. 2015; Wurster et al. 2016). These analyses have so far neglected grain inertia and the question arises: to what extent this may modify this effect and more generally what the impact of this approximation is with regard to the wave propagation.
Interestingly, Kulsrud & Pearce (1969) have shown that in a partially ionized medium, when the inertia of ions is accounted for, Alfvén waves whose propagation is impossible at intermediate wavelengths can propagate at short wavelengths (see also Roberge & Ciolek 2007; Soler et al. 2013). This is because the ion-neutral friction is negligible in the long and short wavelength limit but may become dominant at intermediate wavelengths. Since the dense ISM is very weakly ionized, with ion abundances below 10−7, the ion fluid mass is rather low compared to the neutral one and we may expect the regime for which ions dynamics play a role, to occur at very short wavelengths. Since they carry electric charges, similar processes are expected for dust grains. However, the total mass of dust is about hundred times below the mass of the neutrals. While this still is a small fraction, it is nevertheless much greater than the total mass of the ions. In particular, it is worth remembering that since the Alfvén velocity is proportional to the square-root of the density, it is typically only ten times greater for waves propagating in the dust fluid than in the neutral one. Moreover, due to dynamical effects, dust enrichment by a factor of a few, has been obtained in collapse calculations (Lebreuilly et al. 2020). Therefore, it seems important to investigate the role that dust dynamics may have on Alfvén wave propagation.
The paper is organized as follows. In Sect. 2, the equations and the physics of grains in the ISM are discussed and presented. Then, the dispersion relation for Alfvén waves propagation in a multi-size grain medium is obtained. Section 3 is dedicated to the simpler but enlightening case of a single-size grain medium. The physics of the various waves is discussed as well as the possible consequences in term of momentum transport by the waves. In Sect. 4, a multi-size grain medium is considered. Several densities as well as ionization and grain distributions are explored and discussed. In Sect. 5, we discuss the possible consequences of our results regarding the development of magnetized turbulence and the magnetic braking occurring in dense cores and controlling the formation of protoplanetary disks. In Sect. 6, we present our conclusions.
2. Equations and grain properties
2.1. Fluid equations
The equations describing the dynamics of a magnetized fluid are well known. The situation is rendered significantly more complicated when a continuum of dust grains is considered. To simplify the notations and take advantage of the similarities between the various equations describing charged particles, we note as Xi, e, a any quantity like density or velocity associated to ions, electrons, or charged grains, respectively, of size a. By convention, we note:
The momentum equation for neutrals is
where ρ, ρi, e, a are the neutral and charged particle density, V, Vi, e, a are the velocities, Cs is the sound speed, Ki, e, a are the friction coefficients of the charged particles and a represents the grain size. In practice, since there is a continuity of grain size, ρa and Va are distributions.
The momentum equation for charged particles is
where E and B are the electric and magnetic fields respectively. Then, Zi, e, a and mi, e, a are the charge and mass of the charged particles. We note that we do not consider a population of neutral grains because the timescale for charge fluctuation is shorter than the grain Larmor timescale 1/ω (see for instance Fig. 5 of Guillet & Hennebelle 2020), meaning that all grains possess an effective mean charge.
The electric current is given by:
and the Maxwell-Faraday equation
The Maxwell-Ampère equation is
We have not considered the continuity equations at this stage since Alfvén waves are incompressible.
2.2. Grain and ionization
As grains are important charge cariers, their physical properties and ionization are fundamental in the context of Alfvén wave propagation.
2.2.1. Grain properties
Grain characteristics vary a great deal with the environment. For instance, in the diffuse interstellar medium, the size typically goes from a few nanometers to a few hundreds of nanometers and roughly follows the so-called MRN distribution (Mathis et al. 1977) such like dn/da ∝ aλmrn, where a is the grain size and λmrn ≃ −3.5. The reality is however likely more complex (Jones et al. 2017) particularly in the dense interstellar medium, which is the subject of the investigation presented here. In dense environments, the grain size distribution is less known but it appears that the grains coagulate and grow in mass and size, possibly becoming as big as hundreds of micrometers or possibly even larger (Valdivia et al. 2019). The matter of how this coagulation proceeds is still being investigated, but several teams have recently been stressing the active role of the charged particles-neutral slip induced by the magnetic field (Guillet & Hennebelle 2020; Silsbee et al. 2020; Marchand et al. 2021; Kawasaki et al. 2022; Lebreuilly et al. 2023) together with the turbulent processes (Ormel & Cuzzi 2007). The resulting grain distributions appear to be complicated and to depend on the magnetic intensity and the collapsing time. Therefore, to keep the discussion simple enough at this stage, we will restrict the investigation to few configurations. For the single-size grain models, two sizes are being used namely a = 3 nm and a = 30 nm. For multiple size grains, we chose amin = 1 nm and amax = 100 nm or amin = 10 nm, and amax = 1000 nm. This latter case is typically used at high density when grain growth is expected to have occurred. Except for one case, we always assume λmrn = −3.5. The details of grain binning and related properties (which are all standard) are given in Appendix A.
2.2.2. Ionization models
For the ionization, we made two assumptions. When a single-size grain is investigated (Sect. 3), we simply assume 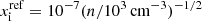 (Shu et al. 1987). Since the number of charges carried on small grains cannot be larger than one, we assume that the numbers of electrons is such that ne= max(ni − ng, 0).
(Shu et al. 1987). Since the number of charges carried on small grains cannot be larger than one, we assume that the numbers of electrons is such that ne= max(ni − ng, 0).
When grain distribution is studied (as described in Sect. 4), the ionization is self-consistently calculated using the model presented in Marchand et al. (2021), which is based on the model of Draine & Sutin (1987). In this model, the charge carried by the grains varies with their size and typically increases with it.
Figure 1 shows the ion, electron and charged grain abundances as a function of density and for the two different grain distribution, amin = 1 nm and amax = 100 nm (top panel) or amin = 10 nm and amax = 1000 nm (bottom panel). In the first case, the negative charges are essentially carried by the grains except at low density whereas in the second case they are carried by the electrons except at high density.
 |
Fig. 1. Abundances of ions, electrons, and charged grains as a function of gas density for two grain distributions. The size grain distribution is assumed to be a power law, dn/da ∝ aλmrn, with λmrn = −3.5 and grains of size between amin and amax are considered. The ionization rate is assumed to be 5 10−17 s−1. |
2.3. Alfvén waves propagation
We consider the propagation of Alfven waves along a uniform magnetic field B = B0k. Introducing, as variables, the two polarization modes respectively denoted by “+” and “−”, we have:
and considering the following perturbations
the momentum equation for charge species:
electric current:
Maxwell-Faraday equation:
Maxwell-Ampère equation:
from which we get
or, equivalently,
and thus:
The dispersion relation follows
It can also be written as:
where
Equations (20) and (22) constitute a complex dispersion relation. Due to the presence of ω at the denominator of AN, i, e, a and AB, i, e, a, which are part of integrals over the grain size distribution, the dispersion relation is, strictly speaking, not a polynomial expression; however, because of the finite number of grain size eventually considered, it is effectively a higher order polynomial. While Eq. (21) explicitly gives k as a function of ω, getting ω as a function of k (that is to say a real k) is obviously more complex as will be seen below. We stress that the only difference between the “+” and “−” modes is the term i(ω ± B0Zi, e, ae/(cmi, e, a)) that represents the Hall effect. We therefore expect that these two modes should present important differences for frequencies close to the grain gyro frequencies B0Zi, e, ae/(cmi, e, a). In particular, since the grain are negatively charged, we see that for the “+” mode a kind of resonance is expected to occur (whose amplitude is limited by the friction).
2.4. Dispersion relation for a single-size grain
Equations (20) and (22) are rather complex and it is therefore enlightening to start considering a system that is as simple as possible. This allows us to verify that simple regimes and behaviors are indeed recovered. We therefore study the single-size grain case and since our main goal here is to gain insight on the problem, we further neglect the ion inertia and ion-neutral friction. This case is therefore equivalent to the standard electron-ion-neutral case, originally considered by Kulsrud & Pearce (1969), where the electrons and the ions have been replaced by the ions and charged grains respectivelly.
The derivation has been obtained in Appendix C via a simplification of Eqs. (B.10) and (B.11). The corresponding dispersion relation (single-size grain and Ki = 0) is:
which is a third degree polynomials meaning that three roots are to be found.
This relation can also be expressed as
which implies that for a given ω, there are two possible k solutions of Eq. (24).
3. Single-size grain case
As the multi-size grain case obviously appears to be more complex, we start with a single-size grain fluid for which a simple analysis can be enlighteningly performed.
3.1. Some simple asymptotic behaviors
3.1.1. Neglecting grain inertia
It is worth first discussing the behavior obtained when the grain intertia is being neglected. This latter approximation is accomplished by removing the terms iω in Eq. (C.2) at the numerator of Eq. (C.2). This leads to replace Eq. (23) via:
and this leads to (using niZi = −naZa):
The two solutions describing waves propagating along positive z are
We note that the other solutions of Eq. (26) are physically equivalent to the two solutions ω± as they simply correspond to propagation toward negative z.
In the limit of long wavelengths, we get
with the two modes propagating at the Alfvén speed. The dust friction leads to a dissipation proportional to k2.
In the limit of short wavelengths, two different modes are found (Wardle & Ng 1999):
and
The first one presents a frequency proportional to k2 which is characteristic of the Hall effect. These modes are known as the whistler modes. For the second one, the frequency tends toward a constant, meaning that the group velocity ∂kℛe(ω) = 0 and so these waves do not transport energy.
3.1.2. Effect of the inertia
A first and immediate difference between Eqs. (23) and (26), which includes and excludes, respectively, grain inertia is that the former is of a degree of three, whereas the latter is of a degree of two. As expected there are fewer degrees of freedom and, thus, fewer modes when grain inertia is neglected. Again, it is worth studying the asymptotic behaviors.
In the limit ω → 0, k → 0, we have:
which is almost identical to the limit with no inertia, as stated by Eq. (28), except for a minor correction in the densities.
In the limit k → ∞, we see that if ω remains finite, it must satisfy a second order equation that is independent of k, namely:
We thus get two modes, which in the limit k → ∞ tend to a constant ω and therefore have a vanishing group velocity.
In the limit ω → ∞, k → ∞, we see that Eq. (23) becomes:
which, for relevant solutions, admits:
and thus
Comparing this expression with Eq. (29), namely, the asymptotic behavior when grain inertia is neglected, we see a fundamental difference. While the real parts are identical, the imaginary ones are different. More precisely, the dissipation is proportional to k2 when inertia is neglected and to k0 when it is taken into account. This is a major difference, indicating that inertia cannot be neglected at short wavelengths.
To summarize, we see that in the long wavelength limit, the grain inertia does not play a significant role, it cannot be neglected, however, at scales that are sufficiently small.
3.2. Orders of magnitude
The asymptotic analysis allows us to anticipate the most important regimes regarding the Alfvén waves. We have three modes of propagation:
which correspond to the Alfvén velocity for the neutrals, the Alfvén velocity for the grains (about 10 times larger than ωAW, n), and the velocity of the whistler mode, respectively.
There are two modes of dissipation
where the latter is the relevant dissipation at large k whereas the former is valid at small k.
By comparing the various expressions, we can infer different cases. First, we have the transition between the neutral Alfvénic regime and the dissipation dominated mode above which Alfvén waves do not propagate. This occurs when ωdiss, n ≃ ωAW, n at a wavenumber of kAW, diss, n
Then, we have the dust Alfvénic regime and the dissipation-dominated mode below which Alfvén waves do not propagate, that is, ωdiss, d ≃ ωAW, d giving:
Another fundamental regime comes from the transition between Alfvén and whistler propagation. This leads to two wavenumbers
and
For convenience, writing 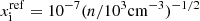 and
and 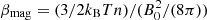 , we obtain
, we obtain
Several interesting trends can already be inferred. First, the dissipation wavelengths scale with the density as n−1 and therefore vary significantly during the collapse. In particular, given than the Jeans length varies as n−1/2, the dissipation length becomes continuously smaller with respect to the Jeans length. The dissipation wavelengths also increase with the grain size. Second, the Hall wavelengths do not depend on density nor on the grain size (assuming that the ionization is as stated by 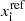 ). The consequence this may have in the context of collapsing cloud are discussed in Sect. 5.2.
). The consequence this may have in the context of collapsing cloud are discussed in Sect. 5.2.
3.3. Solving for the dispersion relation ω versus λ
We now solve the dispersion relations both with and without grain inertia, as stated by Eqs. (23) and (26). This is achieved by simply finding the roots of the second and third degree polynomials.
We assumed a temperature of 10 K and a magnetic βmag = 0.1, which define the value of B0. We also recall that the ionization is prescribed as explained in Sect. 2.2.2. For a = 3 × 10−7 cm, the number of grains is large and thus the number of electrons is assumed to be 0. For a = 3 × 10−6 cm, the number of grains is much smaller and thus ne = ni − ng > 0. However, since (as described in Sect. 3), both the inertia and the friction of ions and electrons are neglected, the only consequence it has on Eq. (23) is to replace ni by ni − ne = ng. This also means that when a = 3 × 10−6 cm, the ionization is given by ng/n0.
3.3.1. n0 = 106 cm−3 and a = 3 × 10−7 cm
Figure 2 displays results for n0 = 106 cm−3 and a = 3 × 10−7 cm. The black, blue and red lines of top panel correspond to the three roots of Eq. (23), the solid lines represent the real parts and dashed lines the imaginary ones. The yellow, green, pink and orange vertical lines stand for λAW, diss, n, λAW, diss, d, λAW, hall, n, λAW, hall, d respectively (as stated by Eqs. (41)–(44)).
 |
Fig. 2. Wave frequency as a function of wavelengths for n0 = 106 cm−3 and a single grain size of a = 3 × 10−7 cm. In the top panel, the grain inertia is considered and the three modes are displayed (dark, blue, and red lines). Both the real (solid lines) and the imaginary (dashed lines) parts are shown. In the bottom panels, the grain inertia is neglected and the two corresponding modes are displayed (cyan and purple). The modes of top panel have been drawn in the bottom panel (thin lines) for ease of comparison. At large wavelengths, inertia does not play any role. However at a scale smaller than about 10 au, the inertia drastically modify the Alfvén wave propagation. The yellow, green, pink, and orange vertical lines represent λAW, diss, n, λAW, diss, d, λAW, hall, n and, λAW, hall, d, respectively (see Eqs. (41)–(44)). We note that in this particular case, λAW, diss, d = λAW, hall, n and so, the pink line is not visible. |
For λ > λAW, diss, n au, the red and blue lines are identical. They correspond to the two usual Alfvén modes and they behave as stated by Eq. (31). The black lines represent a very dissipative mode which has a very low group velocity. This corresponds to a mode for which the dust is decoupled from the neutral and is very dissipative. At about λ = λAW, diss, n (yellow line), the dissipation is very intense and the wave propagation is significantly reduced. In particular we see that the group velocity changes sign. At about λ ≃ λAW, diss, d (green line), the waves propagate as classical Alfvén waves however at the Alfvén speed of the dust, which is ten times the Alfvén speed of the neutrals. The two Alfvén waves, which we recall, represent the two circularly polarized modes, behave similarly. At λ ≃ λAW, hall, d (orange line), we see that the two branches split due to the Hall effect as predicted by Eqs. (32) and (34).
Bottom panel of Fig. 2 shows the solutions obtained when grain inertia is neglected as described by Eq. (26). The cyan and purple lines display the two roots. For convenience the thin lines reproduce the results of top panel. For λ > λAW, diss, n au, the solutions with and without inertia are essentially identical. However, for λ < 10 au, major differences between the cases with and without inertia appear. First of all, we see that only the cyan mode has a non-vanishing group velocity. Indeed, the purple root is identical to the red one and has a vanishing group velocity. It therefore does not transport energy. Thus, for 1 au < λ < 10 au, neglecting inertia predicts an unphysically strong difference between the two circularly polarized modes. Second, the real part of the cyan mode has a slope much stiffer than the black and blue ones: it is a whistler wave. The reason is that since the grain inertia is neglected, the Alfvénic grain modes do not exist. We also see that the imaginary part of the cyan root is much higher than for the blue and black ones. This is because the grain-neutral friction is considerably overestimated.
3.3.2. n0 = 106 cm−3 and a = 3 × 10−6 cm
Figure 3 portrays the case n0 = 106 cm−3 and a = 3 × 10−6 cm. Because the grain size is ten times bigger than the case of Fig. 2, then λAW, diss, n is correspondingly ten times larger than in Fig. 3. Overall, the dispersion relations are similar except that they are shifter toward longer wavelength when a = 3 × 10−6 cm.
 |
Fig. 3. Same as Fig. 2 for n0 = 106 cm−3 and a = 3 × 10−6 cm. The difference between the inertia and no inertia cases is important below 100 au. |
The difference with the waves corresponding to the no inertia case (bottom panel) is again very pronounced. Again, the cyan mode is a whistler wave which is completely asymmetrical with the other polarization represented by the purple one. At small wavelengths, the real part agrees well with the case with inertia, however, the imaginary one is far too high, implying that the waves dissipate too rapidly if inertia is neglected. More physical interpretations are given for this case in Sect. 3.5, where the velocities of the various species are analyzed.
3.3.3. n0 = 108 cm−3 and a = 3 × 10−6 cm
Figure 4 portrays the case n0 = 108 cm−3 and a = 3 × 10−6 cm. Due to the high density, λAW, diss, n is 100 times smaller than in Fig. 3. Consequently, it is smaller than λAW, hall, n and, thus, we have a transition between two Alfvén waves and a whistler mode together with a zero group velocity wave (red mode). As expected, bottom panel reveals that the no inertia wave constitutes a good approximation of the exact case, except at small scales below 1 au, where deviations between the two cases are significant.
 |
Fig. 4. Same as Fig. 2 for n0 = 108 cm−3 and a = 3 × 10−6 cm. The difference between the inertia and no inertia cases is important below 1 au. |
3.4. λ versus ω
A complementary description to the dispersion relation ω(λ) is provided by the λ(ω) relation, as stated by Eq. (24), which we see is a simple second-order polynomial. The difference between the two approaches is that in the classical ω(λ), λ is kept real, while it is ω for the λ(ω) relation. Physically, this could represent the waves generated by a perturbation at a fix spatial position and at a real frequency. The imaginary part of k then indicates the length over which the waves propagate.
Figure 5 shows λ as a function of ω for a = 3 × 10−6 cm and n0 = 106 cm−3. The top panel shows the two modes, where “+” is represented by dark lines whereas “−” is by red lines. Interestingly, a major difference, already noted by Soler et al. (2013), with the ω(λ) description can be seen. The waves propagates at any wavelength including inbetween λAW, diss, d ≃ 120 au, and λAW, diss, n ≃ 300 au unlike what happens in the ω(λ) description (strictly speaking the “+” mode propagates, but its group velocity appears to be low). There is no contradiction, since the two descriptions correspond to two different physical situations. We see, however, that for λ ≃ 200 au, the derivative ∂ωλ is shallower. Also in this region as expected, the dissipation is more significative as revealed by the imaginary part, which is comparable to the real one. At λ ≃ λAW, hall, n ≃ 10 au, the two modes split and for the “−” polarization we get λ ∝ ω1/2 whereas for the “+” one (dark lines), the waves are quickly damped.
The bottom panel of Fig. 5 displays the no inertia case (purple line). For comparison, the results of the top panel have been reproduced (thin lines). Neglecting inertia appears to be a good approximation for λ < 100 au. At smaller scales, we see that the purple lines strongly differ from black and red ones. In particular, at a given ω, the real part of λ is lower when the inertia is accounted for (except for high values of ω and for the “+” case). This indicates for instance that neglecting grain inertia leads to underestimate the group velocity.
3.5. Ion and grain velocities
To get more insight regarding the physical meaning of the various waves, we look at the velocities of the various species. Figure 6 portrays the ratio of the ion over neutral velocities, Vi/V (solid lines) and grain over neutral velocities, Vd/V (dashed lines). The two cases displayed in Figs. 3 and 4 are shown with identical color coding.
 |
Fig. 5. Wavelength as a function of wave frequency for n0 = 106 and a grain size a = 3 × 10−6 cm as stated by Eq. (24). In the top panel, the red and black lines represent the two solutions with grain inertia accounted for whereas on bottom panel the cyan and purple lines (which cannot be distinguished in this particular case) represent the solutions without grain inertia. For ease of comparison, the solutions of top panel have been reported (thin lines) on bottom panel. |
The top panel corresponds to n0 = 106 cm−3 and a = 3 × 10−6 cm. For λ > λAW, diss, n (vertical yellow line) and for the two Alfvén modes (dark and red lines), the grains, the ions, and the neutrals have the same velocities, since Vi/V and Vd/V are both equal to 1. The blue lines reveal that the corresponding mode is of different nature and why it is so dissipative. While Vi and Vd are roughly equal, Vd/V is about 100. This means that this modes correspond to dust and ions oscillating in almost static neutrals, thus leading to heavy dissipation. At scales smaller than λAW, diss, n, whereas Vi and Vd are almost equal, Vd/V is no longer equal to 1. The neutrals and the dust are not dynamically coupled. For the dark and blue modes, the neutral velocity is much smaller than the dust one meaning that the Alfvén waves are carried by the dust grains whereas the neutrals are almost static. As seen from Fig. 3, the dissipation is nevertheless limited (and drops with density) because the grains and the neutral are not dynamically well coupled. For the red mode, the neutrals are moving whereas the dust and the ions remain nearly static. Since the former do not feel directly the magnetic field, it is clear that no propagation is possible and thus the group velocity vanishes. At λ < λAW, hall, d, the blue and dark modes (Alfvén waves carried by the dust) split. The ions and neutrals decouple and acquire different velocities.
In bottom panel, the case n0 = 108 cm−3 and a = 3 × 10−6 cm is displayed. Interestingly, in these conditions, λAW, hall, n > λAW, diss, n. Thus, the ion and dust velocities are different, whereas in this range of densities, the Alfvén waves are still carried by the neutrals that is to say the Alfvén speed is still given by 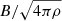 . At λ ≃ λAW, hall, d, the black and blue modes eventually split due to the Hall effect. The velocity ratios remain much smaller than in the case presented in top panel (which has n0 = 106 cm−3) because at a density of 108 cm−3, the dust grains are much more efficiently coupled to the gas.
. At λ ≃ λAW, hall, d, the black and blue modes eventually split due to the Hall effect. The velocity ratios remain much smaller than in the case presented in top panel (which has n0 = 106 cm−3) because at a density of 108 cm−3, the dust grains are much more efficiently coupled to the gas.
Altogether, we see that at long wavelengths, the dust grains, ions, and neutrals are strongly coupled and have same velocities, but at short wavelengths, they have completely different dynamics. More precisely, we expect that at wavelengths lower than the maximum between λAW, diss, n and λAW, hall, n, the ions and the grains would have a velocity dispersion that is larger than the one of the neutrals.
3.6. Group velocity and flux of momentum
As we note in the introduction, in the context of protoplanetary disk formation, magnetic braking is believed to play a fundamental role (Zhao et al. 2020). In essence, magnetic braking is related to the flux of angular momentum that is carried away by Alfvén waves. This is a question that merits particular consideration and investigation. At high wavelengths, the neutrals and the dust grains are well coupled, however, this is not the case at small scales. This is illustrated in Sect. 3.5, where the neutrals have velocities which become gradually smaller compared to the grains and ions ones, as the wavelength decreases. On the other hand, at small scales, the waves present a group velocity, vg, which is higher than its value at large scales. This is because at small wavelengths, the waves propagate either at the Alfvén speed of the dust, namely, 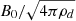 or at the velocity of whistler modes, namely, cB0/(2πniZie)k, which increase with k. Since the flux of momentum is proportional to vgvn, it is therefore not straightforward to anticipate the actual trend.
or at the velocity of whistler modes, namely, cB0/(2πniZie)k, which increase with k. Since the flux of momentum is proportional to vgvn, it is therefore not straightforward to anticipate the actual trend.
Figure 7 shows the product vgvn as a function of λ for the two cases displayed in Figs. 2 and 4. To calculate vn, it is assumed that b = 1, which is therefore assumed to be a reference. The color coding is identical as the one of Figs. 2 and 4. The dark and deep blue correspond to the case with inertia, while the cyan and purple (not seen because identical to the red mode) ones to the case without inertia. For n0 = 106 cm−3 (top panel), for λ < λAW, diss, d (green vertical lines), the flux of momentum, vgvn, increases with λ, meaning that magnetic braking is likely more efficient at larger scales. Interestingly, we see that at wavelengths between 3 and 10 au, the flux of momentum, vgvn, is slightly larger than its value at larger wavelengths. We note that the spikes (seen for instance in top panel of Fig 6) around 50 au are due to the stiff variations of ω with k.
 |
Fig. 6. Ion (solid lines) and grain (dashed line) velocities over neutral velocities as a function of wavelength. Top panel displays the case of Fig. 3, i.e., n0 = 106 cm−3 and a = 3 × 10−6 cm. Bottom panel shows the one of Fig. 4, i.e., n0 = 108 cm−3 and a = 3 × 10−6 cm. The color coding is the same than the one used in Figs. 3 and 4. At high wavelengths, the grains and the gas are dynamically coupled, but at small scales, they become substantially different. |
 |
Fig. 7. Group velocity times neutral velocity (assuming a magnetic field b = 1) as a function of wavelength. This quantity represents the flux of momentum transported by the wave. |
The cases with and without inertia are again quite different for λ < λAW, diss, d. First, we see that whereas the dark and deep blue modes have similar vgvn (for λ > λAW, hall, d), the behavior of the cyan one is very different. Also at λ ≃ 7 au, the momentum flux, vgvn, is more than an order of magnitude smaller when inertia is neglected than when it is taken into account. This may indicate that when inertia is taken into account (as it should be), the flux of angular momentum is more symmetrical for the two polarizations, therefore, possibly leading to less asymmetry for the disk formed in the aligned and anti-aligned configurations (e.g., Tsukamoto et al. 2015; Wurster et al. 2016; Lee et al. 2021).
The situation for n0 = 108 cm−3 (bottom panel) is different. For λ > λAW, hall, d (orange line), the deep blue (with inertia) and cyan (without intertia) modes are almost identical. One difference is that for λ < λAW, diss, n (yellow line), the black mode (which corresponds to waves carried by dust) is not negligible, implying here, again, that two modes are contributing to the transport of momentum when inertia is accounted for, instead of one when inertia is not taken into account.
4. Alfvén waves propagation in the dense ISM
We now investigate the more complex but more realistic multi-size grain ISM.
4.1. Method
The dispersion relation for the multi-grain Alfvén waves is given by Eqs. (20) and (22), which are complex equations. In particular, whereas from Eq. (21), it is straightforward to compute k once ω is specified, getting ω for a given k is considerably more complex. Indeed, Eq. (20) is an integral equation. When the number of bin of grains is finite, Eq. (20) is formally a high order polynomials. To get the dispersion relation, we use an iterative method. First, we specify a real part for ω and a series of 200 imaginary parts logarithmically distributed between ℛe(ω) × 10−4 and ℛe(ω) × 104. For all these values, we calculate k using Eq. (21). As the goal is to obtain a dispersion relation, we seek for real values of k. Thus we select the ω for which the imaginary part of k is changing sign between two values of ℐm(ω). We then carry out iterations, using a simple dichotomy iterative method, until convergence is reached. We have varied the number of bins of imaginary parts and found that increasing their number above 200 leads to identical results. We stress, in particular, that while the total number of existing roots is proportional to the number of grain bins, most of these roots are not likely to be found because they are very dissipative weakly propagative waves and are therefore outside the search interval: (‖log(ℛe(ω)/ℐm(ω))‖ < 4).
In spite of the complexity of Eq. (20), in many cases we found a unique solution (for each sign “±”). In particular, we did not find the highly dissipative zero group velocity waves identified with single-size grain. It is likely that this is because the range of search for ℐm(ω) is overly restricted. It seems likely that there are many of this type of modes when a large number of size of grains is considered.
Various configurations are explored below. We used 1000 bins of grains and asked for a convergence on ℐm(ω) better than 10−3. In Appendix D, we explore the influence of these parameters. To assess the method, we checked that for single-size grain, Eqs. (20) and (23) give indisguishable results.
4.2. A fiducial case: n0 = 106 cm−3, amin = 10−7 cm, and amax = 10−5 cm
We start by discussing in detail a case that we consider as being sufficiently typical. The parameters are n0 = 106 cm−3, amin = 10−7 cm, amax = 10−5 cm, λmrn = −3.5, βmag = 0.1, and ζ = 5 × 10−17.
Figure 8 portrays ω as a function of λ. First-top panel is for the “+” mode (pm = 1) and grain inertia is accounted for, that is to say, Eqs. (20)–(22) are being solved. The second-top panel is identical to the top one, except that grain inertia is neglected, which mathematically means that in Eq. (22), the terms iω in 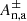 and
and 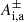 have been dropped.
have been dropped.
 |
Fig. 8. Wave frequency as a function of wavelengths for n0 = 106 cm−3 and amin = 1 × 10−7 cm amax = 1 × 10−5 cm. First panel displays the real and imaginary part of the frequency for the “+” circularly polarized mode. Second panel shows the result when grain inertia is neglected. Third and fourth panels same as the first and second, but displaying the “–” circularly polarized mode. |
At large wavelengths, namely, λ > 100 au, we have a standard Alfvén wave, almost identical to the single-size grain case. Neglecting the inertia here is entirely justified, the real and imaginary parts are almost identical with and without inertia.
At scales of λ < 100 au, we see a new behavior in the top panel. A branch that presents a dispersion relation (ω vs. λ) that is broadly similar to an Alfvén wave carried by the grains (i.e., 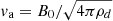 ) is found. However, at a given λ, there seems to be many (likely a continnum) of ω values. Mathematically, this is a clear consequence of the non-polynomial nature of Eqs. (20)–(22) which allows a large number of solutions. Physically, this clearly comes from the grain distribution. Each bin of grains has its own Alfvén velocity and coupling with the gas. At large wavelengths, the grains are synchronized by their coupling with the neutrals but at small wavelengths, particularly for λ < λAW, diss, n we do not expect this to be necessarily the case. As what has been found with single-size grains (Fig. 2), the discrepancy with the no inertia case is obvious. No solution, apart for the ZGV ones, were found for λ < 100 au. This is because when grain inertia is neglected, the grains cannot carry waves independently of the neutrals. As for single-size grain, this implies that at small scales, waves can propagate and therefore angular momentum for instance could possibly be transported whereas this is not possible if inertia is neglected.
) is found. However, at a given λ, there seems to be many (likely a continnum) of ω values. Mathematically, this is a clear consequence of the non-polynomial nature of Eqs. (20)–(22) which allows a large number of solutions. Physically, this clearly comes from the grain distribution. Each bin of grains has its own Alfvén velocity and coupling with the gas. At large wavelengths, the grains are synchronized by their coupling with the neutrals but at small wavelengths, particularly for λ < λAW, diss, n we do not expect this to be necessarily the case. As what has been found with single-size grains (Fig. 2), the discrepancy with the no inertia case is obvious. No solution, apart for the ZGV ones, were found for λ < 100 au. This is because when grain inertia is neglected, the grains cannot carry waves independently of the neutrals. As for single-size grain, this implies that at small scales, waves can propagate and therefore angular momentum for instance could possibly be transported whereas this is not possible if inertia is neglected.
Because of the grain size distribution, the meaning of λAW, diss, n is less obvious. The yellow line represents the value of λAW, diss, n obtained for amin. The agreement between its value and the λ at which the group velocity vanishes, is much less good than in Fig. 2 for instance, as λAW, diss, n is about ten times lower. This is because larger grains have a larger λAW, diss, n.
Even more importantly, we do not see a sign of a change of behavior around λAW, hall, n or λAW, hall, d. Although the distribution of ω values precludes a clear measurement, the mean ω appears to be broadly proportional to λ−1.1-λ−1.2, which seems to be intermediate between the standard Alfvén and whistler waves.
The third-top panel portrays the “−” mode (pm = −1). For λ > 100 au, it behaves as the “+” mode. The behavior for λ < 100 au, differs from the “+” mode (first-top panel). For all λ, including below 100 au, there is now a unique ω. Interestingly, we find that whereas for large wavelengths, ℛe(ω) ∝ λ−1, at short wavelength we approximately get ℛe(ω) ∝ λ−1.2, which again indicates a behavior between standard Alfvén and whistler modes.
On the other hand, the bottom panel, which displays the case without grain inertia, reveals that at short wavelength, ω ∝ λ−2 as expected for whistler modes. This clearly shows that at short wavelengths, neglecting inertia leads to incorrect predictions.
4.3. The effect of density
We now discuss the dependence of the waves on gas density. We recall that from Eqs. (41)–(42), we expect the non-ideal magnetohydrodynamical (MHD) behavior to occur at wavelengths that scale as ≃n−1. Figures 9 and 10 portray the dispersion relation for n0 = 103 cm−3 and n0 = 108 cm−3, respectively. We note that for n0 = 108 cm−3, we have used amin = 10−6 cm and amax = 10−4 cm instead of amin = 10−7 cm and amax = 10−5 cm because it is very likely that due to the differential motions between grains induced by magnetic drift, small grains disappear as the collapse proceed (Guillet & Hennebelle 2020; Lebreuilly et al. 2023).
The two dispersion relations appear to be similar to the one of Fig. 8, once a rescaling is performed (as suggested by Eq. (41)). For n0 = 103 cm−3, Alfvén waves would barely propagate for λ < 3 × 104 au without grain inertia (as seen from second-top and bottom panel). On the contrary, first and third-top panels show that the waves do propagate except in a relatively narrow range of wavelengths. The “+” and “−” modes present the same characteristic than in Fig. 8, that is to say the “+” mode has a distribution of ω and its mean value appears to be close to the dispersion relation obtained for the “−” mode. At short wavelengths, the dependence of ℛe(ω) is again given by ω ∝ λ−1.2.
For n0 = 108 cm−3, the agreement between the case with and without inertia is very good for λ > 2 − 3 au. Interestingly, since λAW, hall, n > λAW, diss, n, represented by the pink and yellow lines, respectively, a clear whistler regime develops for 2 au < λ < 20 au.
4.4. Effect of grain size and ionization
To investigate the influence that grain distribution and ionization may have on the dispersion relation, we present two cases: one with an ionization rate five times lower than the one used in Fig. 8 and one with λmrn = −2.1, instead of λmrn = −3.5 as usually assumed. With λmrn = −2.1, there are more large grains and less small grains.
The dispersion relation seen in Fig. 11 is very similar to the one presented in Fig. 8, in spite of the fact that the model has a lower ionization rate. The main difference appears to be the imaginary part of ω, which is inversely proportional to the dissipation rate, that is a about two times higher.
 |
Fig. 11. Wave frequency as a function of wavelengths for n0 = 106 cm−3 and amin = 1 × 10−7 cm amax = 1 × 10−5 cm as well as a low ionization rate of 10−17 s−1. The yellow, green, pink, and orange vertical lines represent λAW, diss, n, λAW, diss, d, λAW, hall, n, and λAW, hall, d, respectively (see Eqs. (41)–(44)). |
Figure 12 presents more difference with Fig. 8. First, the dissipation rate is also larger than for λmrn = −3.5 (Fig. 8). Second, regarding the “+” mode, the distribution of ω seen for λ < 100 au is significantly broader. This is expected since bigger grains have more inertia. Third, the wavelength at which classical Alfvén waves stop propagating, is about five times higher in Fig. 12 than in Fig. 8.
 |
Fig. 12. Same as Fig. 11 for n0 = 106 cm−3 and amin = 1 × 10−7 cm amax = 1 × 10−5 cm as well as with λmrn = −2.1. |
4.5. Grain velocities
Figure 13 portrays the velocity range of the ions (pink points) and of the grains for various size from amin (dark points) to amax (red points). The blue, cyan, and purple points correspond to grains of intermediate size (in increasing order). As expected at long wavelengths, the grains and the neutrals have the same velocities because they are dynamically coupled. At short wavelengths, the smaller the grains, the larger their velocities. As for the single-size grain case, we therefore expect that at short wavelengths, the small grains and the ions present a velocity range that is larger than the one of the neutrals and of the big grains.
 |
Fig. 13. Velocities of ions and various grains relative to the amplitude of the neutral velocity for n0 = 106 cm−3. The pink points correspond to the ion velocities, the dark points to the smallest grains, namely, of size amin whereas the red points correspond to grain of size amax. The blue, cyan, and purple points correspond to grain of intermediate sizes evenly distributed (logarithmically) between amin and amax. |
5. Discussion
Although the results obtained in this paper are restricted to Alfvén waves only, nevertheless, they represent a very fundamental mode of magnetized flows and it is worth discussing the effect this may have.
5.1. Consequences for magnetized turbulence in molecular clouds
It has sometimes been speculated that the ion-neutral friction prevent the propagation of waves below λdiss, n (≃0.1 pc for n0 = 103 cm−3), possibly even suppressing the turbulent cascade at λ < λdiss, n. Our results suggest that the waves are likely not cut at λdiss, n because the grains lead to the propagation of Alfvén waves at the Alfvén speed of the dust, 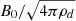 (i.e., roughly ten times the Alfvén speed of the neutrals). Our results suggest that through the grain-neutral friction, the grains may transfer some momentum to the neutrals often more efficiently (depending of densities and wavelengths) that if the grains had no inertia, though this momentum diminishes with wavelengths and tends toward 0 in the short wavelength limit. Very importantly, the Alfvén wave dissipation is considerably reduced when grain inertia is properly accounted for.
(i.e., roughly ten times the Alfvén speed of the neutrals). Our results suggest that through the grain-neutral friction, the grains may transfer some momentum to the neutrals often more efficiently (depending of densities and wavelengths) that if the grains had no inertia, though this momentum diminishes with wavelengths and tends toward 0 in the short wavelength limit. Very importantly, the Alfvén wave dissipation is considerably reduced when grain inertia is properly accounted for.
Qualitatively this suggests that in molecular gas of density ≃103 cm−3 at scale below ≃0.1 pc (see Fig. 9), the ion velocity, could be larger than the velocity of the neutrals at least if Alfvén modes are sufficiently representative of motions in molecular clouds. Interestingly, Pineda et al. (2021) have recently reported that the velocity dispersion of NH are systematically larger by ≃0.015 km s−1 than the one of NH3. They discuss the possibility that this may be due to the injection of Alfvén waves, although they stress that the waves are quickly damped and therefore would need to be continuously injected. While it is likely that the motions in molecular clouds are fully turbulent, therefore, implying energy cascade, it is likely that at scale below the dissipative scale, λdiss, n, the charged dust and the ions acquire velocities larger than the ones of the neutrals.
are systematically larger by ≃0.015 km s−1 than the one of NH3. They discuss the possibility that this may be due to the injection of Alfvén waves, although they stress that the waves are quickly damped and therefore would need to be continuously injected. While it is likely that the motions in molecular clouds are fully turbulent, therefore, implying energy cascade, it is likely that at scale below the dissipative scale, λdiss, n, the charged dust and the ions acquire velocities larger than the ones of the neutrals.
Indeed, while it is now largely accepted that molecular clouds are both turbulent and magnetized (e.g., Hennebelle & Falgarone 2012), the nature of this turbulence at small scales is presently unclear precisely because it is expected that below ≃0.1 pc (due to ambipolar diffusion) dissipation may become important. The various attempts to study this turbulence have either used the so-called strong coupling approximation which consists in neglecting entirely the ion inertia (e.g., Ntormousi et al. 2016) or the so-called heavy ion approximation (e.g., Meyer et al. 2014; Burkhart et al. 2015), where it is assumed that the ions have a mass that is several orders of magnitude larger than their actual values, allowing then to limit the high Alfvén velocity that they would otherwise present. In principle, our results show that even when the charges are carried by the ions and electrons (bottom panel of Fig. 1), the Alfvén speed at wavelengths shorter than λdiss, n, corresponds to the one of the dust grain and not the one of the ions. Since the latter is typically three orders of magnitude larger than the Alfvén speed of the neutral, this suggests that a full modeling of molecular clouds at small scales may be performed without requiring the use of heavy ion approximation, although the size distribution remains a serious difficulty. In this respect, we note, nevertheless, that the single-size grain and the multi-size grain cases studied in this paper present strong similarities, suggesting that the former may constitute a fruitful approach.
5.2. Consequences for magnetic braking and disk formation
In astrophysical problems where rotation is a dominant process, the magnetic field is usually an important mechanism through which angular momentum can be transported. This is particularly true for the formation of planet-forming disks where the magnetic field plays a crucial role (Zhao et al. 2020; Maury et al. 2022).
Magnetic braking is basically a flux of angular momentum carried away by torsional Alfvén waves. It operates at all densities as the collapse proceeds. For instance, Fig. 4 of Joos et al. (2012) reveals that at all times, the angular momentum of the gas above 108 cm−3 is significantly higher for a low magnetic field (μ = 17) than for a strong field (μ = 2). This implies that the magnetic braking has already occurred before the gas reaches this density.
To determine whether or not grain inertia may influence magnetic braking in collapsing cores, we estimate the scale at which magnetic braking applies. We assume that the gas density is given by 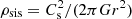 , namely, the density of the singular isothermal sphere. This leads to rsis = Cs/(ρ2πG)1/2. The relevant scale for magnetic braking is the thickness of the pseudo-disk, which depending of the magnetization has an aspect ratio of ≃5–10 (Li & Shu 1996; Hennebelle & Fromang 2008).
, namely, the density of the singular isothermal sphere. This leads to rsis = Cs/(ρ2πG)1/2. The relevant scale for magnetic braking is the thickness of the pseudo-disk, which depending of the magnetization has an aspect ratio of ≃5–10 (Li & Shu 1996; Hennebelle & Fromang 2008).
From Fig. 8, we see that at 106 cm−3, the wave propagation for wavelengths below 100 au is not correctly described if inertia is neglected. We also see that this scale is about 10 λdiss, n (yellow lines). To estimate the typical density below which grain inertia may affect magnetic braking, we thus write rsis/10 ≃ 10λdiss, n. This leads to 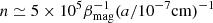 cm−3. Since, in dense cores, βmag is generally small (about 0.1 or less) and that grain growth is expected, we see that grain inertia could possibly affect magnetic braking up to relevant densities during collapse. From the conclusions given in Sect. 4, it seems possible that magnetic braking is enhanced and more symmetrical between the aligned and anti-aligned configurations which have been found different because of the Hall effect (Tsukamoto et al. 2015; Wurster et al. 2016; Lee et al. 2021). Obviously, this is still a rough estimate at this stage, but it advocates for considering grain dynamics during collapse.
cm−3. Since, in dense cores, βmag is generally small (about 0.1 or less) and that grain growth is expected, we see that grain inertia could possibly affect magnetic braking up to relevant densities during collapse. From the conclusions given in Sect. 4, it seems possible that magnetic braking is enhanced and more symmetrical between the aligned and anti-aligned configurations which have been found different because of the Hall effect (Tsukamoto et al. 2015; Wurster et al. 2016; Lee et al. 2021). Obviously, this is still a rough estimate at this stage, but it advocates for considering grain dynamics during collapse.
5.3. Consequences for propagation of cosmic rays in the dense gas
Finally, we discuss the consequences that our results may have on the propagation of cosmic rays within the ISM. Several recent studies have included GeV cosmic rays in ISM and galaxy simulations (e.g., Pfrommer et al. 2017; Dubois et al. 2019; Dashyan & Dubois 2020; Girichidis et al. 2022), showing that (as expected) cosmic rays have an impact on galaxy evolution. Cosmic rays having a bulk velocity larger than the Alfvén speed, excite Alfvén waves through gyroresonance, and tend to be well-coupled to these waves (Kulsrud 2005; Everett & Zweibel 2011; Thomas & Pfrommer 2019; Hopkins et al. 2021). Since the streaming velocity is proportional to the Alfvén speed of the charge carriers, the influence of charged dust may change the picture significantly in the dense gas. Indeed, since the ionization ranges from 10−4 to 10−10 depending on the gas density, the Alfvén speed would range in the absence of charged dust, from 30 to 105 the Alfvén speed within the neutral gas. Instead, since the gas-to-dust ratio is about 1/100, the Alfvén speed is typically ten times the Alfvén speed within the neutral gas. The other fundamental consequence is obviously the presence and the intensity of the Alfvén waves, which depends on the damping that they are subject to. The latter is much reduced in the presence of charge carriers. The consequences that cosmic rays propagation in the dense gas may have in ISM clouds have been recently investigated by Bustard & Zweibel (2021). For instance, their Figs. 3 and 4 illustrate how the variations of ion abundance may affect a cloud evolution.
To illustrate further the effect that charged grains may have in this context, we have computed the dispersion relation for gas more typical of the cold HI. We adopted n0 = 100 cm−3 and an ionization of xi ≃ xe = 10−4. For the abundance of charged grains, we considered two cases. For the first, we adopted ng/n0 = 10−7, which is close to the value given by Eq. (C14) of Wolfire et al. (2003). For the second, we assume that there is no grain, that is to say: all charges are carried just by ions and electrons.
Figure 14 shows the results. Top and middle panel display the dispersion relation for “+” and “−” modes when grains are accounted for whereas bottom panel shows the dispersion relation when grains are ignored (the “+” and “−” modes are almost identical and only the “+” is shown). As can be seen, the dispersion relations present significant differences. In particular, the dissipation rate of the Alfvén waves is lower when grains are included therefore the wave intensity excited by the cosmic ray propagation may be larger in the presence of grains. We note that the differences between the dispersion relations with and without grains nevertheless present similarities. This is because with an ionization of 10−4 and given that the mass of the ions is about 10 Mp the mass of the charged fluids differ by a factor of about 10 only. In the molecular gas where the ionization rate is significantly lower, the differences would be far more pronounced.
 |
Fig. 14. Wave frequency as a function of wavelengths for n0 = 102 cm−3. An ionization of 10−4 is assumed. Bottom panel corresponds to the case with no dust, i.e., only ions and electrons (the “+” and “–” modes are indistinguishable). For the top and middle panels (respectively “–” and “+” modes), dust is included a standard MRN distribution, with amin = 1 × 10−7 cm amax = 1 × 10−5 cm is assumed. |
6. Conclusion
In this paper, we calculate how Alfvén waves propagate in a weakly ionized and dusty medium, represented by the ISM. We obtain the exact dispersion relation taking into account a continuous grain size distribution. For the sake of simplicity and to interpret our results with grain size distribution, we also computed the single-size grain case for which we obtain and discuss the wave behavior in the short and long wavelength limit. From these asymptotic behavior, we obtain simple estimates for the relevant wavelengths which separate the various propagation regimes of the waves.
Importantly, we account for the grain inertia and we systematically compare the results with what is inferred when inertia is neglected. At long wavelengths, it is generally found that neglecting grain inertia is always a valid approximation. This remains correct up to the scale at which grain-neutral friction is so strong that the wave propagation is considerably reduced or even suppressed. At short wavelengths, the situation is however different. When grain inertia is neglected, it is found that due to the Hall effect, the two circularly polarized Alfvén waves behave differently. While one has a zero group velocity implying no wave propagation, the other presents a dispersion relation typical of whistler modes. When grain inertia is accounted for and at density lower than ≃108 cm−3, the two modes tend to be more symmetrical and are essentially standard Alfvén waves propagating at the Alfvén velocity of the grains although with ℛe(ω) ∝ k≃1.2. Interestingly, we found that one of the two polarization modes (“+”) present a distribution of ω, rather than a single value. At long wavelengths, the grains, the ions and the neutrals have nearly identical velocities, whereas at short wavelengths, the ions and the small grains present velocities that are far higher than those of the neutrals.
Acknowledgments
We thank the anonymous referee for constructive and helpful comments that have improved the manuscript. P.H. acknowledges discussions with Jaime Pineda and Alexei Ivlev. This research has received funding from the European Research Council synergy grant ECOGAL (Grant: 855130).
References
- Allen, A., Li, Z.-Y., & Shu, F. H. 2003, ApJ, 599, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Braiding, C. R., & Wardle, M. 2012, MNRAS, 422, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Burkhart, B., Lazarian, A., Balsara, D., Meyer, C., & Cho, J. 2015, ApJ, 805, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Bustard, C., & Zweibel, E. G. 2021, ApJ, 913, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Ciolek, G. E., & Roberge, W. G. 2002, ApJ, 567, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Cramer, N. F., Verheest, F., & Vladimirov, S. V. 2002, Phys. Plasmas, 9, 4845 [NASA ADS] [CrossRef] [Google Scholar]
- Dashyan, G., & Dubois, Y. 2020, A&A, 638, A123 [EDP Sciences] [Google Scholar]
- Draine, B. T., & Sutin, B. 1987, ApJ, 320, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Roberge, W. G., & Dalgarno, A. 1983, ApJ, 264, 485 [CrossRef] [Google Scholar]
- Drazkowska, J., Bitsch, B., Lambrechts, M., et al. 2022, ArXiv e-prints [arXiv:2203.09759] [Google Scholar]
- Dubois, Y., Commerçon, B., Marcowith, A., & Brahimi, L. 2019, A&A, 631, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Everett, J. E., & Zweibel, E. G. 2011, ApJ, 739, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Pfrommer, C., Pakmor, R., & Springel, V. 2022, MNRAS, 510, 3917 [NASA ADS] [CrossRef] [Google Scholar]
- Guillet, V., Forêts, Pineau Des. G., Jones, A. P., 2007, A&A, 476, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillet, V., Hennebelle, P., Pineau des Forêts, G., et al. 2020, A&A, 643, A17 [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&A Rev., 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., Commerçon, B., Chabrier, G., & Marchand, P. 2016, ApJ, 830, L8 [Google Scholar]
- Hennebelle, P., Commerçon, B., Lee, Y.-N., & Charnoz, S. 2020, A&A, 635, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirano, S., Tsukamoto, Y., Basu, S., & Machida, M. N. 2020, ApJ, 898, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., & Lee, H. 2016, MNRAS, 456, 4174 [Google Scholar]
- Hopkins, P. F., Squire, J., Chan, T. K., et al. 2021, MNRAS, 501, 4184 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Köhler, M., Ysard, N., Bocchio, M., & Verstraete, L. 2017, A&A, 602, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joos, M., Hennebelle, P., & Ciardi, A. 2012, A&A, 543, A128 [CrossRef] [EDP Sciences] [Google Scholar]
- Kawasaki, Y., Koga, S., & Machida, M. N. 2022, MNRAS, 515, 2072 [NASA ADS] [CrossRef] [Google Scholar]
- Kulsrud, R., & Pearce, W. P. 1969, ApJ, 156, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Kulsrud, R. M. 2005, Plasma Physics for Astrophysics (Princeton, NJ: Princeton University Press) [Google Scholar]
- Kunz, M. W., & Mouschovias, T. C. 2009, ApJ, 693, 1895 [Google Scholar]
- Lebreuilly, U., Commerçon, B., & Laibe, G. 2019, A&A, 626, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebreuilly, U., Commerçon, B., & Laibe, G. 2020, A&A, 641, A112 [EDP Sciences] [Google Scholar]
- Lebreuilly, U., Vallucci-Goy, V., Guillet, V., Lombart, M., & Marchand, P. 2023, MNRAS, 518, 3326 [Google Scholar]
- Lee, Y.-N., Marchand, P., Liu, Y.-H., & Hennebelle, P. 2021, ApJ, 922, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z.-Y., & Shu, F. H. 1996, ApJ, 472, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Marchand, P., Masson, J., Chabrier, G., et al. 2016, A&A, 592, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchand, P., Guillet, V., Lebreuilly, U., & Mac Low, M. M. 2021, A&A, 649, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
- Maury, A., Hennebelle, P., & Girart, J. M. 2022, Front. Astron. Space Sci., 9, 949223 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, C. D., Balsara, D. S., Burkhart, B., & Lazarian, A. 2014, MNRAS, 439, 2197 [Google Scholar]
- Mouschovias, T. C., & Paleologou, E. V. 1979, ApJ, 230, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Nakano, T., Nishi, R., & Umebayashi, T. 2002, ApJ, 573, 199 [Google Scholar]
- Nishi, R., Nakano, T., & Umebayashi, T. 1991, ApJ, 368, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Ntormousi, E., Hennebelle, P., André, P., & Masson, J. 2016, A&A, 589, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., & Cuzzi, J. N. 2007, A&A, 466, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfrommer, C., Pakmor, R., Schaal, K., Simpson, C. M., & Springel, V. 2017, MNRAS, 465, 4500 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J. E., Schmiedeke, A., Caselli, P., et al. 2021, ApJ, 912, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Roberge, W. G., & Ciolek, G. E. 2007, MNRAS, 382, 717 [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Silsbee, K., Ivlev, A. V., Sipilä, O., Caselli, P., & Zhao, B. 2020, A&A, 641, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, R., Carbonell, M., Ballester, J. L., & Terradas, J. 2013, ApJ, 767, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, T., & Pfrommer, C. 2019, MNRAS, 485, 2977 [NASA ADS] [CrossRef] [Google Scholar]
- Tripathi, K. D., & Sharma, S. K. 1996, Phys. Plasmas, 3, 4380 [NASA ADS] [CrossRef] [Google Scholar]
- Tsukamoto, Y., & Okuzumi, S. 2022, ApJ, 934, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Tsukamoto, Y., Iwasaki, K., Okuzumi, S., Machida, M. N., & Inutsuka, S. 2015, ApJ, 810, L26 [Google Scholar]
- Valdivia, V., Maury, A., Brauer, R., et al. 2019, MNRAS, 488, 4897 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, M., & Ng, C. 1999, MNRAS, 303, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [Google Scholar]
- Wurster, J., & Li, Z.-Y. 2018, Front. Astron. Space Sci., 5, 39 [Google Scholar]
- Wurster, J., Price, D. J., & Bate, M. R. 2016, MNRAS, 457, 1037 [Google Scholar]
- Zhao, B., Caselli, P., Li, Z.-Y., et al. 2016, MNRAS, 460, 2050 [Google Scholar]
- Zhao, B., Tomida, K., Hennebelle, P., et al. 2020, Space Sci. Rev., 216, 43 [CrossRef] [Google Scholar]
Appendix A: Grain and ion properties
Here, we give a detailed description of the model and assumptions that are made in the paper.
 |
Fig. A.1. Wave frequency as a function of wavelengths for n0 = 106 cm−3 and amin = 1 × 10−7 cm amax = 1 × 10−5 cm. All panels display the real and imaginary part of the frequency for the "+" circularly polarized mode. The top panel uses 103 bins of grains, second-top panel 100, third-top panel 10, and bottom panel only 1 bin of grains. |
Ka, the friction coefficient, is generally written as Ka = 1/((ρ + ρa)τa) (e.g., Marchand et al. 2016; Lebreuilly et al. 2019), where
where ρg = Ma/(4π/3a3) is the grain density assumed to be ρg = 2.4g cm−3.
where γ is the adiabatic index, a is the grain radius and Ma its mass.
Thus,
The grain distribution is given by
where typically λmrn = −3.5.
The normalization constant C is determined through the dust density
Leading to
The total number of grains is given by:
We consider Nb logarithmic bins of grains given by:
The mean size, number, density, and mass of grains in bin j is
While the friction coefficient is given by:
For the ions we consider (Draine et al. 1983):
and Ki = γad = 3.5 × 1013 g−1 cm3 s−1.
For the electrons, we have
and
Appendix B: Neglecting the ion inertia
Here, we provide the dispersion relation when the ion inertia is neglected. Since the ionization is very small (typically below 10−7) in the dense ISM, the inertia of ions is negligible and thus we have:
The momentum equation for the neutrals leads to:
The dynamical equation of the grains gives 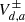 as a function of V± and
as a function of V± and 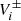 and can be rewritten as
and can be rewritten as
With Eq. (4), we obtain:
Finally with Eq. (B.1), we obtain
which can be recast as
With Eq. (B.4), we obtain
With Eq. (B.3), Eq. (B.2) and Eq. (B.7) become
The dispersion relation follows
where
Appendix C: Derivation in the single grain case
The dispersion relation as stated by Eq. (B.10) is not a polynomial. Here, we infer the dispersion relation for a single-size grain fluid for which we have the usual polynomial form. Although it is straightforward, the calculation is a bit cumbersome and some details are given below.
where we used the fact that niZi = −naZa.
This relation can also be expressed as:
In the limit k → ∞, we see that if ω remains finite, it must satisfy a second order equation that is independent of k, namely:
Appendix D: Influence of numerical parameters on the dispersion relation in the multi-size grain case
Here, we investigate the influence of the number of bins of grains on our results, particularly on the "+" mode as we saw that it presents a distribution of ω instead of a single value. Figure 1 displays the dispersion relation for 1000 (top panel), 100 (second-top panel), 10 (third-top panel), and 1 (bottom panel) bins of grains. The long wavelengths are barely affected by a change of bin number. However at short wavelengths, clearly the bin distribution evolves from a single value (bottom panel) to discrete bands of ω to an apparent continuum (top and second-top panels).
All Figures
 |
Fig. 1. Abundances of ions, electrons, and charged grains as a function of gas density for two grain distributions. The size grain distribution is assumed to be a power law, dn/da ∝ aλmrn, with λmrn = −3.5 and grains of size between amin and amax are considered. The ionization rate is assumed to be 5 10−17 s−1. |
| In the text | |
 |
Fig. 2. Wave frequency as a function of wavelengths for n0 = 106 cm−3 and a single grain size of a = 3 × 10−7 cm. In the top panel, the grain inertia is considered and the three modes are displayed (dark, blue, and red lines). Both the real (solid lines) and the imaginary (dashed lines) parts are shown. In the bottom panels, the grain inertia is neglected and the two corresponding modes are displayed (cyan and purple). The modes of top panel have been drawn in the bottom panel (thin lines) for ease of comparison. At large wavelengths, inertia does not play any role. However at a scale smaller than about 10 au, the inertia drastically modify the Alfvén wave propagation. The yellow, green, pink, and orange vertical lines represent λAW, diss, n, λAW, diss, d, λAW, hall, n and, λAW, hall, d, respectively (see Eqs. (41)–(44)). We note that in this particular case, λAW, diss, d = λAW, hall, n and so, the pink line is not visible. |
| In the text | |
 |
Fig. 3. Same as Fig. 2 for n0 = 106 cm−3 and a = 3 × 10−6 cm. The difference between the inertia and no inertia cases is important below 100 au. |
| In the text | |
 |
Fig. 4. Same as Fig. 2 for n0 = 108 cm−3 and a = 3 × 10−6 cm. The difference between the inertia and no inertia cases is important below 1 au. |
| In the text | |
 |
Fig. 5. Wavelength as a function of wave frequency for n0 = 106 and a grain size a = 3 × 10−6 cm as stated by Eq. (24). In the top panel, the red and black lines represent the two solutions with grain inertia accounted for whereas on bottom panel the cyan and purple lines (which cannot be distinguished in this particular case) represent the solutions without grain inertia. For ease of comparison, the solutions of top panel have been reported (thin lines) on bottom panel. |
| In the text | |
 |
Fig. 6. Ion (solid lines) and grain (dashed line) velocities over neutral velocities as a function of wavelength. Top panel displays the case of Fig. 3, i.e., n0 = 106 cm−3 and a = 3 × 10−6 cm. Bottom panel shows the one of Fig. 4, i.e., n0 = 108 cm−3 and a = 3 × 10−6 cm. The color coding is the same than the one used in Figs. 3 and 4. At high wavelengths, the grains and the gas are dynamically coupled, but at small scales, they become substantially different. |
| In the text | |
 |
Fig. 7. Group velocity times neutral velocity (assuming a magnetic field b = 1) as a function of wavelength. This quantity represents the flux of momentum transported by the wave. |
| In the text | |
 |
Fig. 8. Wave frequency as a function of wavelengths for n0 = 106 cm−3 and amin = 1 × 10−7 cm amax = 1 × 10−5 cm. First panel displays the real and imaginary part of the frequency for the “+” circularly polarized mode. Second panel shows the result when grain inertia is neglected. Third and fourth panels same as the first and second, but displaying the “–” circularly polarized mode. |
| In the text | |
 |
Fig. 9. Same as Fig. 8 for n0 = 103 cm−3 and amin = 1 × 10−7 cm amax = 1 × 10−5 cm. |
| In the text | |
 |
Fig. 10. Same as Fig. 10 for n0 = 108 cm−3 and amin = 1 × 10−6 cm amax = 1 × 10−4 cm. |
| In the text | |
 |
Fig. 11. Wave frequency as a function of wavelengths for n0 = 106 cm−3 and amin = 1 × 10−7 cm amax = 1 × 10−5 cm as well as a low ionization rate of 10−17 s−1. The yellow, green, pink, and orange vertical lines represent λAW, diss, n, λAW, diss, d, λAW, hall, n, and λAW, hall, d, respectively (see Eqs. (41)–(44)). |
| In the text | |
 |
Fig. 12. Same as Fig. 11 for n0 = 106 cm−3 and amin = 1 × 10−7 cm amax = 1 × 10−5 cm as well as with λmrn = −2.1. |
| In the text | |
 |
Fig. 13. Velocities of ions and various grains relative to the amplitude of the neutral velocity for n0 = 106 cm−3. The pink points correspond to the ion velocities, the dark points to the smallest grains, namely, of size amin whereas the red points correspond to grain of size amax. The blue, cyan, and purple points correspond to grain of intermediate sizes evenly distributed (logarithmically) between amin and amax. |
| In the text | |
 |
Fig. 14. Wave frequency as a function of wavelengths for n0 = 102 cm−3. An ionization of 10−4 is assumed. Bottom panel corresponds to the case with no dust, i.e., only ions and electrons (the “+” and “–” modes are indistinguishable). For the top and middle panels (respectively “–” and “+” modes), dust is included a standard MRN distribution, with amin = 1 × 10−7 cm amax = 1 × 10−5 cm is assumed. |
| In the text | |
 |
Fig. A.1. Wave frequency as a function of wavelengths for n0 = 106 cm−3 and amin = 1 × 10−7 cm amax = 1 × 10−5 cm. All panels display the real and imaginary part of the frequency for the "+" circularly polarized mode. The top panel uses 103 bins of grains, second-top panel 100, third-top panel 10, and bottom panel only 1 bin of grains. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.