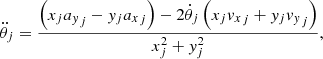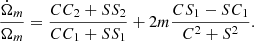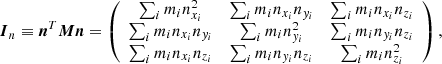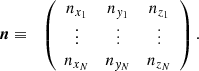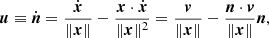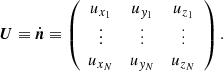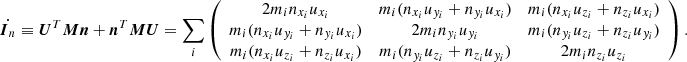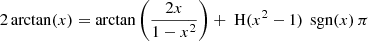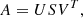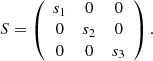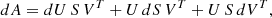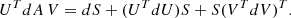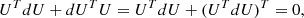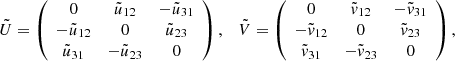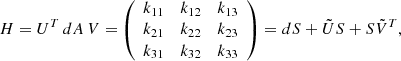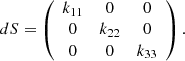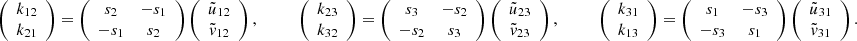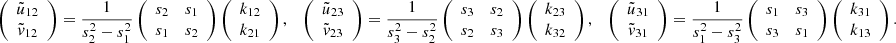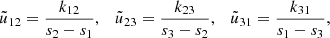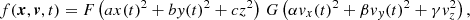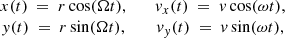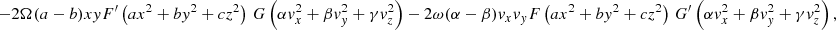| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 16 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202245463 | |
| Published online | 28 April 2023 | |
Five methods for determining pattern speeds in galaxies
I. Methods
1
University of Geneva, Geneva Observatory, chemin Pegasi 51, 1290 Versoix, Switzerland
e-mail: daniel.pfenniger@unige.ch
2
Inter-University Centre for Astronomy and Astrophysics, PostBag 4, Ganeshkhind, Pune 411007, India
3
National Astronomical Observatory of Japan, Mitaka, Tokyo 181-8588, Japan
Received:
14
November
2022
Accepted:
27
January
2023
Context. After matter distribution and kinematics, the bar or spiral pattern speeds are the next fundamental parameters determining the dynamics of a galaxy.
Aims. New or refined methods for determining instantaneous scalar and vector pattern speeds from a restricted domain are developed for applications in N-body simulations or in galaxies such as the Milky Way, for which the stellar coordinates become increasingly better known.
Methods. The general feature used throughout follows from the fact that the time derivative of a function of the coordinates is linearly proportional to its rotation rate and its particle velocities. Knowing these therefore allows retrieving the instantaneous pattern speed vector by linear optimization. Similarly, if an invariant function depends on the position and velocities, then its instantaneous rotation vectors in space can be retrieved. Knowing the accelerations also allows determining the pattern rotation of velocity space.
Results. The first three methods are based on the assumed rotational invariance of functions at each point in space or velocity space: (1) the 6D invariant function method, measuring the pattern speed vectors in space and velocity space, (2) the differential/regional 3D Tremaine-Weinberg method, evaluated over regions with a high signal-to-noise ratio, (3) the 3D Jacobi integral method, yielding the potential pattern speed. Extensions to derive the rotation center position, speed, and acceleration are introduced in the first and third methods. The last two methods are based on the assumed invariance of average functions of the particle coordinates: (4) the 2D and 3D moment of inertia methods by using the derivative of the singular value decomposition, (5) the 2D Fourier method (3D for m = 2 mode), giving the mode rotation speeds. Pattern speed accelerations are also derived in the fourth and fifth methods.
Conclusions. Depending on the available data in specific problems, the different methods provide a choice of approaches.
Key words: Galaxy: fundamental parameters / Galaxy: kinematics and dynamics / galaxies: fundamental parameters / galaxies: kinematics and dynamics / methods: numerical / methods: data analysis
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The rotation frequency Ωp, also called the pattern speed, of morphological features such as bars or spiral arms is a crucial parameter in most dynamical studies of disk galaxies because it allows describing the local dynamics in a rotating frame where time dependence is reduced. Physical and numerical reality is more complicated, however, because most self-consistent galaxy models, even when they do not include a dissipative gas component, show that several flexible patterns with distinct speeds coexist (Sparke & Sellwood 1987; Wozniak 2015, 2020; Wu et al. 2016, 2018). This implies that the system is not strictly time-invariant at meso- and macro-scales in any rotating frame. Therefore, periodic or secular angular speed variations must be expected, and the amplitude of the time fluctuations is an aspect of galactic dynamics that needs to be better examined. The constancy of spiral arm pattern speeds has been a fundamental assumption in the density wave theory of Lin & Shu (1964) all along, but this theory has been challenged (Sellwood 2011): Spiral arms might be winding up, or be transient (Toomre 1991) in view of the efficient swing amplification of small perturbations in cold disks (Julian & Toomre 1966). Long-lived (∼5 Gyr) spirals are not excluded (Saha & Elmegreen 2016) in particular conditions, however. More quantitative numerical investigations of these questions in fully consistent models are therefore required. In the meanwhile, evaluations of the instantaneous pattern speeds of spatially limited features are required in order to be able to verify whether long-time pattern speed averages, as commonly calculated, make sense for disk dynamics, and to quantitatively determine the errors when assuming a single global pattern speed.
For solid bodies, there is no internal streaming, thus the instantaneous rotation speed and instantaneous pattern speed are identical. More realistically, in stellar and fluid systems, the mean rotation of their matter and the rotation of one or several patterns may all be different, and differ spatially, as was clearly demonstrated in Wu et al. (2018), because bars and spirals may be flexible structures.
The precise definition of “pattern speed” is rarely specified, while a “pattern” may mean different things: it can be just a special morphological feature, or the shape of a mass distribution in space, kinematical space, or phase-space, or in more abstract spaces, such as frequency (Fourier) space. To characterize a shape, the gradient of observable quantities, such as the mean mass distribution, must be available. The motion of this gradient allows us to follow the shape in time, and, if it rotates uniformly around a center, it can describe the pattern rotation speed. Assuming a single pattern rotation speed therefore assumes that all gradients of the observable quantity over the examined region rotate rigidly, at the same angular speed, around a common center.
That a stellar or particle system displays a single pattern speed everywhere is very particular. Typical galaxies or N-body models of galaxies may display an approximate constant pattern speed over only a subset of the whole. When a pattern speed is estimated, it therefore is important to understand the possible bias introduced by selecting a specific particle subset. Unless a continuous differentiable function is involved, in which case the motion of the function gradient at any point yields a speed, a pattern in galaxies or in simulations is a statistical property over many particles. Choosing a specific subset may therefore introduce a selection bias. For example, the pattern speed of a single particle can only be its speed. The pattern speed of a well-grouped set of particles (a cluster) is its average speed. The pattern speed of a ring of particles is not the average circular speed of its particles, but the speed of a density gradient moving as a single wave. Depending on the subset selection, the speed of a compact subset of stars may therefore reflect the local streaming motion of this subset more than the motion of a pattern of larger size.
In numerical work, most often, in N-body simulations, full information about the particle distribution and properties is available, so that the assumptions made for galaxies can in principle be checked in detail. A popular approach to determine an average pattern speed is to Fourier transform, over angle and time, the particle distribution in radial bins (Sellwood & Athanassoula 1986; Masset & Tagger 1997; Rautiainen & Salo 1999). Because the simulations are not time periodic, a finite time window is used that is longer than the pattern period, but shorter than the simulation length. Power peaks of a given Fourier mode in the time domain at a given radius reveal the average mode pattern speed(s) over the chosen time window. The power spectrum indicates whether a single or multiple distinct patterns coexist on average at any given radius. The sampling of shortest and longest time-intervals bounds the examined average frequencies, but also introduce aliases. Strictly, any power spectrum different from a single sharply peaked function (the width of which should be consistent with the particle noise) then indicates time variability.
A direct straight method for finding the almost instantaneous bar pattern speed has been used, for instance, by Pfenniger & Friedli (1991). The method consists of measuring the angle of its inertia tensor major axis separated by a short time interval, where the inertia tensor is calculated with the particles within a cylinder as large as the bar. This method provides an almost instantaneous pattern speed averaged over a time step, but the result may depend on the adopted cylinder size. Its drawback is that it requires two particle snapshots, which is unnecessary, as we show in Sect. 6.
The current most popular method to find the instantaneous Ωp has been proposed by Tremaine & Weinberg (1984, hereafter TW), with some modifications in Merrifield et al. (2006) and Meidt et al. (2008), where radial variations are considered. The conservation of the observed population projected in the galactic plane is assumed. Integrating spatial gradients over lines allows recovering the bar pattern speed when only the line-of-sight velocity component and the disk inclination angle are known. The problem with the TW method is that the pattern speed is assumed to be uniform over the whole observed disk, which is questionable in view of the known pattern speed differences between the bar and the spiral arms in N-body simulations (Sparke & Sellwood 1987; Rautiainen & Salo 1999). The possible interaction between the bars and spiral arms might also affect the pattern speed measurement (Hilmi et al. 2020). Furthermore, nested double bars are common (Erwin 2004), and are expected to rotate at very distinct speeds (Pfenniger & Norman 1990), and was indeed found in simulations (e.g., Friedli & Martinet 1993; Debattista & Shen 2007; Saha & Maciejewski 2013; Wu et al. 2016, 2018). A more flexible method giving the instantaneous pattern speed over a spatial domain relevant for the addressed problem appears to be required.
Methods based on the kinematic signature of specific resonances, such as the Milky Way bar outer Lindblad resonance observed in a star sample around the Sun (e.g., Monari et al. 2017), are global and implicitly assume that the disk dynamics at the Sun is not strongly perturbed by the local spiral arms, which rotate possibly with a distinct pattern speed, as is frequently observed in N-body simulations. The mere presence of self-gravitating spiral arms around the Sun suggests the opposite, however: Local forces are substantially dominated by the influence of local disk matter.
Offset bars, now seen in more than a dozen galaxies (de Swardt et al. 2015; Kruk et al. 2017), present another kind of problem. Because the offset bar may not necessarily be at the kinematical center of the host galaxy or at the geometrical center of the outer disk, the bar pattern, including its central density peak, may rotate both about itself and as a whole about the galaxy center, performing a kind of epicyclic motion around the center of mass, a superposition of two or more rotational motions.
Here we concentrate on methods providing a single instantaneous pattern speed and possibly local pattern speeds in N-body models because the information contained in a particle snapshot should be sufficient to find them in principle, and, in some cases, their pattern acceleration as well. In case of multiple rotational components, to first order, we search only for the fastest rotational component in the system and its instantaneous rotation center. The slower additional rotational components are then approximated to first order with a constant translation of the rotation center. Proceeding beyond first order may be vain as the pattern speed invariance hypothesis is likely to be invalid over longer time intervals.
Some of these methods may hopefully be useful for interpreting astrometric data of the Milky Way. Precise astrometric surveys, such as the Gaia survey (Gaia Collaboration 2018), start to provide full phase-space coordinate information for large Milky Way star samples. Alternative methods to determine a pattern speed, in particular of the Milky Way bar, for which a number of methods and tracers already exist (e.g., Debattista et al. 2002; Gerhard 2011; Minchev et al. 2007; Sanders et al. 2019; Clarke & Gerhard 2022), may be found to be useful and complementary.
It might be thought that any method should give the same pattern speed value. Using three of methods exposed here, Wu et al. (2018) showed that according to the adopted shape definition, somewhat different pattern speeds are found in the same model because different methods measure different characteristics of the not strictly rigidly and constantly rotating pattern. This is especially relevant for the double-bar galaxy models used in Wu et al. (2018), or for non-rigidly rotating spiral arms. In regions in which the system is strongly time dependent with respect to the local dynamical time, for example, at the interface between two nested bars or between a bar and the surrounding spiral arms around the corotation radius, methods based on the assumption of a constant pattern speed obviously break down, as shown in Wu et al. (2016, 2018), because the single steady pattern assumption is incorrect.
In Sect. 2 we discuss a naive method along with its shortcomings. In Sect. 3 we derive the scalar or vector pattern speed in space and velocity space from any observable function of space and/or velocity space that is assumed invariant by rotation and translation, with a possibly unknown rotation center. In Sect. 4, as a generalization of the TW method, we examine the local and regional TW methods (herafter LTW and RTW), and describe the criterion where in observations, the derived pattern speed is a priori the least affected by measurement errors. Then, in Sect. 5, we use the Jacobi integral, or equivalently, the rotational invariance of the mean potential, to determine the potential pattern speed. In Sect. 6 we consider how second-moment tensors in ordinary space, or velocity space, allow us to determine Ωp, when the rotation axis direction is known or not. In Sect. 7 we use the Fourier space phase information to analyze how circular wave modes rotate, which is for mode 2 a similar but distinct approach from the moment methods. Finally, we conclude in Sect. 8.
2. Morphological feature method
A direct method (not counted in the five methods) is to use a clear morphological feature, assumed to be corotating with the figure. For example, a barred spiral can display a straight bar and a symmetric two-arm spiral apparently starting at the ends of the bar. The intersection points of a logarithmic spiral fitted along the spiral arms and a straight line along the bar major axis define two symmetric points that can be assumed to corotate with the bar. Dynamically, the most obvious explanation for this feature is that these points represent the stationary Lagrange points L1, 2 of the bar pattern (Pfenniger 1990). Other examples in the literature attempted to use the Lagrange points L4, 5 (e.g., Shimizu & Yoshii 2012), the location of which can be inferred from various tracers, such as a star-forming region or a local minimum of surface brightness in case of unstable L4, 5 for strong bars.
When we know both the position (x, y) and the velocity in an inertial frame (vx, vy) of one of these points in the galaxy plane, the angle is found by
and the pattern speed is its time derivative,
where vt is the tangential velocity component of the point (x, y), and R = (x2 + y2)1/2 is its distance to origin.
This method clearly relies on the assumption that the chosen point is indeed stationary in some rotating frame. For N-body bars, Wu et al. (2016) have shown that the instantaneous equilibrium points between a bar and spiral arms may oscillate with a substantial amplitude in any rotating frame, including the bar frame. No strict Lagrange points therefore exist because of the perturbation by the adjacent spiral pattern that rotates at a different speed. The assumptions made about the pattern that we wish to measure are therefore clearly crucial. In some cases, no strictly constant pattern speed even exists.
3. Invariant function method
A pattern can be defined by the mean of a function f(x, v, t) (e.g., the phase-space distribution function of stars, the mass density of a particular stellar population, or the mean gravitational potential). This function is assumed to be invariant either (1) after an infinitesimal time dt, or (2) at fixed time t after an infinitesimal rigid rotation dt Ω about some rotation center in configuration space {x}, and likewise an infinitesimal rigid rotation dt ω about some rotation center in velocity space {v}.
3.1. Rotation about the origin
First, we start with the simplest case. The rotation center is assumed to be fixed and located at the origin. We generalize the derivation used by TW in their pioneer paper to more cases. The function f(x, v, t) invariance, either after an infinitesimal time displacement or after an infinitesimal solid rotation about the origin, reads
A priori, the pattern speeds Ω and ω do not need to be equal. For the sake of rigor, we verify in Appendix B the mere existence of such functions by displaying an explicit class of these.
Expanding both sides of the equation to first order in time leads to a linear equation for Ω and ω that can be reformulated more conveniently by using the dot and cross products property a ⋅ (b ∧ c) = (c ∧ a)⋅b,
If the direction unit vector n of the rotation axis is known, Ω = Ωn, and the two frequencies are the same, ω = Ω, we can then attempt to solve this linear equation for Ω provided the partial derivatives of f are known at a given phase space point (x, v) at time t. Rotating the axes such that n = (0, 0, 1), we find
If n is not known and ω = Ω, we need n ≥ 3 independent positions (xi, vi), i = 1, 2, …n to solve by linear optimization, such as the least-squares method, the linear system of equations
where fi means f(xi, vi, t). In the presence of noise, no reliable solution exists if the n × 3 left-hand side matrix is degenerate, however.
The least-squares solution of a linear system Ax ≈ b, where A is the n × m matrix (n > m), and b the n × 1 vector, is the unique solution for the m vector x minimizing the Euclidian L2 norm ||Ax − b||2, and, when A is degenerate, the minimum ||x||2. In addition to the traditional least-squares method, methods that minimize other norms are available, such as the L1 norm, which may be less sensitive to outlier data points (Boyd & Vandenbergh 2004). In contrast to the L2 norm, however, a L1 norm solution may not always exist.
If ω ≠ Ω, we need n ≥ 6 independent positions (xi, vi), i = 1, 2, …n to solve the linear system as above,
In these linear optimization problems, each line of Eqs. (6) and (7) can always be multiplied left and right by a weight wi to weight the data points differently. For example, the weight can be inversely proportional to the error σi expected on the ith data point, 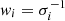 . For the L2 norm, this weight is equivalent to performing a χ2 minimization.
. For the L2 norm, this weight is equivalent to performing a χ2 minimization.
3.2. Incompressible function f
If f conserves phase-space density, such as for Boltzmann’s collisionless equation, where f(x, v, t) is the phase-space distribution function,
where 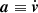 is the acceleration, then ∂tf can be eliminated.
is the acceleration, then ∂tf can be eliminated.
When ω = Ω, we obtain
and when ω ≠ Ω,
Thus, when f depends on v, we need to also know the acceleration (or force) field a, which is typically minus the gradient of the gravitational potential Φ(x). When f does not depend on v, all the ∂vfi terms cancel, a is not needed, and as it should, ω then remains undetermined.
3.3. Mass-conserving function f(x, t)
Likewise, when f conserves mass in space, for instance, the mass density in a fluid, often called ρ, and u = u(x, t) is the velocity field, ∂tf can be eliminated by the continuity equation
Because u is a function of x, it rotates in space at the same speed as in velocity space, so that Ω = ω. Determining Ω then requires knowing only the spatial gradients of f and u at time t.
3.4. Translation and rotation about a known center
When f is invariant only when it rotates about the center at frequencies Ω and ω, and when in addition, the center moves at velocity V and acceleration A, Eq. (3) is modified as
Expanding both sides of the equation as before to first order in time leads to a linear equation system for V, A, Ω, and ω,
As above, we can replace the ∂tfi terms if f follows a conservation law. In principle, we can therefore quantify by how much the system center of rotation moves or accelerates with the same data required to solve Eq. (10) by solving Eq. (13) for Ω, V, and A with at least n ≥ 12 data points by linear optimization.
Because Eq. (13) is dimensionally inhomogeneous, it may be useful to scale the left-hand side matrix columns and vector lines by appropriate constants. For example, when we use length and velocity scale factors R0 and V0, the system becomes
and V = R0Υ, A = V0Λ.
3.5. Translation and rotation about an unknown center
When the center of rotation is unknown both in space and velocity space, the true centers of rotation would be x0 and v0, respectively. The invariant f would follow the following constraint to first order in dt,
Expanding both sides of the equation as before to first order in time leads to a quadratic (hyperbolic) equation system for x0, v0, Ω, and ω, and linear for V, A,
Rearranging the terms, we can separate the linear and quadratic parts,
An iterative approach to determine a least-squares solution for this system might be to start by guessing initial values for x0, v0, and then to solve Eq. (16) for Ω, ω, V, and A by linear least-squares. Using these values, we could then solve for x0, v0 Eq. (17) by linear least-squares. Iterating this process a number of times might converge to a solution. Otherwise, quadratic or nonlinear least-squares algorithms could be required. In general, we expect either no, one, or several real solutions with quadratic problems.
4. Local and regional 3D Tremaine-Weinberg methods (LTW and RTW methods)
The TW method is based on a particular case of invariant function, as discussed in Sect. 3, where the surface density
is a projection of a thin distribution function f in the galactic plane of a tracer assumed to verify the continuity equation ∂tΣ + ∂x ⋅ (Σu) = 0, where u(x, y) is the local mass-weighted average velocity in the plane x − y. Because Σ does not depend on v, this method does not require knowledge of the force field. In the original method, the direction of the rotation axis n is assumed to be known. Using Eq. (9) at a single position, and integrating over all velocities,
In principle, a single local calculation at x is therefore sufficient to find ΩLTW. Because this calculation involves gradients, however, observational errors may be an issue, as taking the gradient of data, for example, by finite differences, typically amplifies errors. Furthermore, even when precise gradients are available, the coefficient x ∧ ∂xΣ in Eq. (19) may vanish (e.g., when the azimuthal density profile is an extremum, or more generally, when it is tangent to a circle centered at the origin), so that large errors are contributed by all the regions that are locally rotationally symmetric. This occurs, for example, close to the main axes of a bar, but also in the disk. By weighting each data point line in Eq. (19) by a coefficient wi proportional to the error inverse, we can thus achieve a χ2 minimization.
The original TW method attempts to minimize noise by using weighted averages of Eq. (19) along lines. In these line integrals, the high-noise segments mostly contribute to increasing errors, the above-noise signal segments alone do contribute to finding Ω. Extending the integration interval to infinity and performing integration by parts avoids formally dealing with gradients in the integrals, but this does not remove the measurement noise, and it necessarily includes contributions outside the relevant region and in this way, it may add systematic errors in case of multiple pattern speeds. Since N-body bars and real galaxies have different pattern speeds in their bar(s) and surrounding spiral arms (Sellwood & Sparke 1988; Wu et al. 2016, 2018), and double-bar systems are frequent (Erwin 2004), it is therefore necessary to consider local or regional evaluations of pattern speeds.
Local methods use data gradients, however, which, if done without attention, are prone to amplifying noise. In the literature, many approaches exist for evaluating gradients of noisy data. For the systems considered here, methods that smooth data locally have to be preferred over methods that use global characteristics of noise. One of the oldest local method is the Savitzky-Golay filter (Savitzky & Golay 1964). Spectral methods that smooth the gradient operator instead of smoothing data are intrinsically nonlocal. In astrophysical particle systems, the smoothed-particle hydrodynamics technique (Gingold & Monaghan 1977; Lucy 1977) is frequently used to evaluate the density gradients and other physical quantities attached to particles. A smoothing kernel convolved spatially over the particle data provides smooth density and velocity functions. In numerical mathematics, more advanced methods have been proposed that not only provide accurate gradients, but also preserve discontinuities (e.g., Chartrand 2011, 2017). We refer to Van Breugel et al. (2020) for a recent short review of the problem. In view of the general need in science and engineering to extract derivatives of data, the question will continue to progress in the following years. Below we assume that the problem of taking gradients of data has been sufficiently well mastered.
4.1. Local method (LTW)
An alternative approach to TW is to choose a number of selected locations with a high signal-to-noise ratio instead of lines, which consequently excludes the regions in which azimuthal gradients are too small, below the observational noise.
When we do not assume n as known, we can determine the vector ΩLTW by least-squares using three or more distinct positions xi, i = 1, …n, for the 3D space density, and solve the equation system by linear optimization,
where
and
In principle, if these positions provide a nondegenerate set of linear equations, the full rotation vector ΩLTW can be retrieved.
Thus the LTW method consists in choosing a finite number of locations well in which the azimuthal density gradient ∝|x∧∂xρ(x)| has a high signal-to-noise ratio. In bars, the maximum signal is to be sought in the off-axis regions, a butterfly shape, determined by preferentially accepting the data points where |x∧∂xρ(x)| is above the noise. Typically, locations near the principal axes of a bar should be rejected: because the density gradient is radial, these regions add noise to the linear system. Because this involves measuring the gradient of ρ and ρu, it can be used in N-body bars where errors are under control.
4.2. Regional method (RTW)
However, if gradients are too noisy, we can proceed as in TW by integrating data over a volume. We do this here in 3D. Instead of the TW infinite line in the galaxy plane, we generalize by integrating over an arbitrary finite contiguous volume V bounded by an oriented surface S in one or several favorable high signal-to-noise regions.
The 3D local equation for the mass density equation ρ(x) in a velocity file 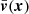 is
is
Integrating over V, noting that ∇ρ ∧ x = ∇ ∧ (ρx), and using the divergence and curl theorems of vector calculus1, we obtain an integral over the surface S on both sides of the equation,
These integrals amount to the total mass flux through surface S, one expressed with the supposed unknown uniform rotation of the system2, the other by the measured mass flux parallel to S. When S is chosen poorly, this flux may vanish in all cases, which is thus a degenerate configuration to be avoided. For example, a sphere centered on the origin sees all x being parallel to the surface elements dS, so (ρx)∧dS = 0 for any ρ, Eq. (24) reduces to 0 ⋅ ΩRTW = 0.
The RTW method can be considered to be a method that replaces the gradient of data evaluation at a point by directly integrating data over a finite surface. The optimal volume size is determined by the noise in the available data. Since only the information present on the surface of V is used, there is no interest in taking overly large regions.
4.3. Multiple regional method (MRTW)
In principle, we can therefore combine the two previous approaches by a multiple RTW method (MRTW), for which several distinct signal-rich regions inside volumes bounded by surfaces S1, S2, …Sn are used, allowing us to solve a series of Eq. (24) by linear optimization for ΩMRTW,
For the Milky Way, using full 6D astrometric data from Gaia in volume-limited regions around the Sun where extinction is under control, we might in principle attempt to evaluate the pattern speed of local spiral arms, and possibly more.
5. Jacobi integral, or potential method
Here we develop a method that does not require density gradients, but requires the individual kinematic data of test particles, or stars. This method was already briefly described in Wu et al. (2018).
In a gravitational mean potential Φ that rotates uniformly with angular frequency Ω, a test particle moving in this potential always has the Jacobi integral HJ as the global integral of motion (Binney & Tremaine 2008),
where x(t) is the position of the particle, and v(t) the velocity in the inertial frame instantaneously aligned with the rotating frame at time t. The quantity 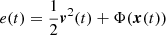 is the particle specific energy in the inertial frame, and l(t) = x(t)∧v(t) is its specific angular momentum, also in the inertial frame.
is the particle specific energy in the inertial frame, and l(t) = x(t)∧v(t) is its specific angular momentum, also in the inertial frame.
5.1. Pattern speed knowing its direction
When we know the direction of the rotation axis n, Ω = Ω n, we can in principle determine Ω from the motion of a single particle because along an orbit
that is,
In principle, provided the torque (x∧a) is nonzero and not orthogonal to n, a single particle has the information about Ω in the values of its instantaneous position, velocity, acceleration and the time-derivative of its potential along the trajectory, 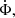 at any time along its trajectory. At some locations along a trajectory, the tangential acceleration may become low (the torque term x ∧ a in Eq. (28) almost vanishes). Then Ω is ill defined. In nonaxisymmetric systems, these locations are exceptional. Thus the best moments for determining Ω along a trajectory occur when angular momentum varies the most, that is, when the torque is strong.
at any time along its trajectory. At some locations along a trajectory, the tangential acceleration may become low (the torque term x ∧ a in Eq. (28) almost vanishes). Then Ω is ill defined. In nonaxisymmetric systems, these locations are exceptional. Thus the best moments for determining Ω along a trajectory occur when angular momentum varies the most, that is, when the torque is strong.
Alternatively, the above derivation leading to Eq. (28) can be obtained without invoking Jacobi’s integral by assuming that the potential Φ is an invariant function in some rotating frame, and using the equations developed in Sect. 3. Replacing f by Φ in Eq. (9), and noting that 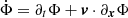 , so
, so 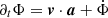 , we retrieve Eq. (28), with nΩ replaced by Ω.
, we retrieve Eq. (28), with nΩ replaced by Ω.
5.2. Pattern speed vector
Using three or more independent particles, we can form the linear system
which can be solved for Ω by linear optimization. Furthermore, as in Eq. (13), we can extend the search for the motion of the system rotation center at speed V,
The particularity of this method is that 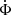 must be determined. In usual N-body simulation codes, all the other values except for
must be determined. In usual N-body simulation codes, all the other values except for 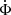 are calculated at each time step. With a small increase in computation cost, the force algorithm can also calculate Φ, so that
are calculated at each time step. With a small increase in computation cost, the force algorithm can also calculate Φ, so that 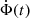 can be approximated to second order in Δt by finite difference in time and two additional potential calculations,
can be approximated to second order in Δt by finite difference in time and two additional potential calculations,
where Δt is a positive time step. In a pure N-body system, and similarly, for other potential solvers, the time derivative of the potential can be calculated directly with little additional expense simultaneously with the potential and forces by
In an N-body system, however, the potential is clearly never strictly time independent. It differs from a mean potential because nearby particles eventually contribute to strong fluctuations of the potential over the background of slowly varying contributions from particles that are far away. The distribution of the found Ω obtained from a set of selected particles can help to quantify the force fluctuations from the nearest particles with respect to the smoother mean field force: if the distribution of found Ω is broad, it means that there is no single frame with a uniformly rotating potential, or that the fast local fluctuating forces dominate the more constant force from the mean rotating potential. In a smooth mass distribution, the contribution to force fluctuations from nearby particles becomes particularly important near the potential minimum (near the center), or everywhere in extended nearly homogeneous distributions like in cosmology.
6. Second-order moment methods
6.1. Moment of inertia tensor
In mechanics, the polar moment of inertia tensor I is a simple 3 × 3 tensor characterizing the second moments of the mass distribution with respect to the origin. It is set at the location at which the center of mass and center of rotation coincide. It can be seen as the covariance matrix weighted by the mass of the particle positions. For an N particle distribution, it is defined as
where x is the N × 3 matrix composed of the stacked particles in Cartesian coordinates xi,
and M is the N × N mass diagonal matrix, with its diagonal filled with the particle masses mi,
When only the average particle distribution is rigid except for a uniform rotation about an axis, we can still use the axial moment of inertia tensor in use in solid body mechanics (e.g., Goldstein 1971) even though each particle moves nonrigidly with respect to each other to relate the rotation of the particle distribution to its constant total angular momentum vector L = ∑imixi ∧ vi and its axial moment of inertia tensor, which is given by
Then the angular speed Ωs of the solid body is related to L by
As the system rotates, I and therefore 𝕀 vary: the non-diagonal terms, for example, vanish when the Cartesian coordinates are aligned with the principal axes of the mass distributions. Ωs must still be constant, however, because L is conserved and its value should not change under a rotation of the coordinates about L. This means that knowing the particle distribution and its total angular momentum allows us to find a unique Ωs that describes the instantaneous rotation rate as if the particles were moving as a solid. When the particle distribution does not rotate rigidly, then Ωs can clearly change, still respecting Eq. (37).
The only technical problem is to find a well-behaved invert of 𝕀 for all possible configurations. Pfenniger (2019) gave an explicit procedure for finding the inverse 𝕀−1, or more generally, the pseudo-inverse 𝕀† in degenerate cases,
For a body with internal streaming, however, such as a bar in a galaxy, Ωs is not necessarily the pattern speed because its value does not depend on any feature of the mass distribution and also works with axisymmetric systems rotating about the symmetry axis.
The polar moment of inertia tensor I described above is a simple 3 × 3 tensor characterizing the second moments of the mass distribution with respect to the origin, set at the center of mass. If the system globally keeps its shape over time while rotating uniformly, the eigenvalues of I remain constant, and its rotating eigenvectors may be used to determine the pattern speed.
6.1.1. Pattern speed of the 3D system vector
In principle, the real eigenvalues and eigenvectors can be calculated analytically for a 3 × 3 symmetric matrix, but the expressions are huge because the eigenvalues are solutions of a cubic polynomial. It is more practical to use well-established numerical methods to determine them (Anderson et al. 1999; Trefethen & Bau 1997).
For a symmetric positive definite matrix A, the eigenvalue problem, which consists of finding the orthogonal eigenvector matrix V and the diagonal eigenvalue matrix Λ for which A = VΛVT, is identical to the singular value decomposition (SVD) problem for a general (nonsquare) matrix: A = USVT-pagination, where S is the diagonal matrix of (real) singular values and U and V are two orthogonal matrices. For positive definite symmetric matrices U = V, the eigenvalue problem is thus equivalent to the SVD problem. In contrast to standard SVD algorithms, however, common eigenvalue–eigenvector algorithms do not sort eigenvalues and eigenvectors in a standard way because they may be complex or real negative. It is therefore more convenient to use the SVD algorithm. For small matrices, the difference in computational cost is negligible.
After decomposing I with SVD: I = USUT-pagination, we obtain a real orthogonal rotation matrix U made of the three orthogonal unit vectors ni, where i = 1, 2, 3, U = [n1, n2, n3], which gives the direction of the eigenvectors, and a diagonal real matrix S with singular values s1 ≥ s2 ≥ s3 ≥ 0 in decreasing order, giving the second-order moment amplitudes in the respective directions. If the second-order moments are invariant, S does not depend on time, but 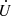 , the time derivative of U, is a matrix giving the speed of the eigenvectors.
, the time derivative of U, is a matrix giving the speed of the eigenvectors.
To evaluate 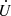 , we first need İ(t), which is obtained using the particle positions x and velocities V (assuming mass conservation, Ṁ = 0),
, we first need İ(t), which is obtained using the particle positions x and velocities V (assuming mass conservation, Ṁ = 0),
A safe, accurate method for calculating he derivative of the SVD, knowing İ is described in Appendix A. To do this, knowing the SVD decomposition of İ, the symmetric matrix H = UTİU is first calculated. Its diagonal is the diagonal of 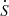 , while its nondiagonal elements allow us to build an auxiliary antisymmetric matrix
, while its nondiagonal elements allow us to build an auxiliary antisymmetric matrix 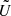 -pagination. The time derivative of U is then found by
-pagination. The time derivative of U is then found by 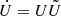 -pagination. The singular value derivative matrix
-pagination. The singular value derivative matrix 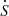 allows us to check the radial rigidity of the rotating pattern, which is small by hypothesis. Along the respective eigenvector i, each
allows us to check the radial rigidity of the rotating pattern, which is small by hypothesis. Along the respective eigenvector i, each 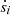 provides a check of rigidity, and
provides a check of rigidity, and 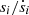 a timescale for substantial radial change.
a timescale for substantial radial change.
Then, using the unit vectors ni and ṅi, i = 1, …3, of U = (n1,n2,n3) and 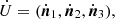 respectively, corresponding to the singular values si, we derive the instantaneous rotation frequency vector of each of the principal axes along ni,
respectively, corresponding to the singular values si, we derive the instantaneous rotation frequency vector of each of the principal axes along ni,
If the particle ensemble rotates as a rigid figure, and if the axis of rotation is not aligned with any ṅi, the three ΩIi should be almost identical within the numerical errors. However, figures frequently rotate close to around one of the principal axes, in which case the corresponding |ṅj|, thus |ΩIj|, is small or zero. In the frequent case that the figure rotates around the shortest axis, ΩI1 and ΩI2 are almost identical and provide the sought pattern speed. Determining the instantaneous vector ΩI of distinct subsets of particles allows us to quantify as a function of time by how much the rotation axes of these subsets may tilt with respect to each other.
6.1.2. Pattern speed of the 2D system
When the direction of the rotation axis is known and constant, for instance, along the z-axis, we can evaluate Ω explicitly avoiding SVDs. Noting
we calculate the eigenvalues λ± by solving the characteristic polynomial of I,
which gives two solutions for λ: λ± = I+ ± P. The eigenvalue ratio is a measure of the moment-of- inertia ellipsoid axis-ratio squared, thus the ellipticity reads
The eigenvectors ξ± only depend on the ratio ζ ≡ Ixy/I− ,
The two vectors can be verified to be orthogonal, that is, ξ+ ⋅ ξ− = 0. Using identity 1.626.3 in Gradshteyn et al. (2007)3, the angle ϕ at time t between one of the eigenvectors and the x-axis in the x − y plane is
The constant is 0, or ±π/2, which is irrelevant for our aim because it disappears when we differentiate ϕ with respect to time. We find
The instantaneous angular speed of the moment of inertia at any time can therefore be calculated directly with the position and position-velocity moments given in Eq. (41).
When the particle distribution is close to axisymmetric, for instance, Ixy ≈ 0 and I− ≈ 0, Ωz is undetermined, as it should. This also occurs when the distribution, while not axisymmetric, has strictly no bisymmetric component, however, such as a pure four−arm spiral pattern. This method was briefly described in Wu et al. (2018).
6.1.3. Pattern acceleration of the 2D system
The time derivative of ΩIz can be calculated similarly, knowing the particle accelerations, which are calculated in N-body simulations in any case. This can be useful for estimating the timescale over which the pattern speed can be approximated as constant. Differentiating Eq. (46), we obtain the relative pattern acceleration after simplifications,
where
Dimensionless estimators of the pattern speed invariance can be obtained by dividing Eq. (47) by a reference frequency, such as the solid-body speed Ωs, or the pattern speed ΩIz itself. When the dimensionless estimator is of order unity or more, the constant pattern speed assumption is no longer valid.
6.2. Kinetic tensor rotation
The velocity distribution can rotate in velocity space with an angular speed that is distinct from the angular speed in position space. Exactly the same discussion as in Sect. 6.1.1 for the inertia tensor method can be carried out for the second-order moment tensor of velocities, the kinetic tensor (where the velocity origin is set at the velocity center of mass),
All the calculations for finding the 3D pattern speed with SVD decomposition can be made to obtain the pattern speed of the velocity ellipsoid by replacing positions by velocities, and velocities by accelerations, as in Sect. 6.1.1. We therefore do not elaborate further.
Likewise, for the 2D case, using these notations,
we obtain the pattern speed of the velocity ellipsoid,
To evaluate the pattern acceleration, we would need to know the particle jerk (ȧ).
7. Fourier method
A 2D mass distribution can have a simple angular Fourier decomposition where a low-order mode may capture the nonaxisymmetric shape of the distribution. This is commonly used to measure the strength, phase, and length of a bar, for instance, where the dominant m = 2 mode is often exclusively considered, while the m = 4, 6 and 8 modes are still non-negligible. The m = 2 and higher-order modes are thought to rotate at the same angular velocity as the mass distribution. In this case, we can attempt to determine the pattern speed by measuring just the mode phase velocity.
Below we describe the Fourier method introduced in Wu et al. (2018) more extensively. An inverse Fourier decomposition in the plane x − y of the mass-weighted azimuthal positions of a distribution of particles sampled in a ring reads
where the azimuth angle θj of particle j depends on the Cartesian coordinates xj, and yj, θj = arctan(yj, xj), and m is the Fourier mode. The summation runs over the number of particles in the ring. The phase of the Fourier transform is
where
7.1. 2D Fourier mode velocity
Because the mode phase goes from 0 to 2π when the particle positions rotate in space by 2π/m, the mode velocity in space is the phase velocity divided by m,
where
and
Explicitly, defining the following trigonometric sums,
we obtain the compact expression,
When several modes superpose with different mode velocities, the mass distribution is time-dependent and no single pattern speed characterizes the distribution well. Determining how well the large amplitude (C2 + S2)1/2 mode velocities coincide is therefore a way to verify the time-independence of the pattern.
7.2. Fourier mode acceleration
Another way to confirm time dependence is to calculate the instantaneous mode acceleration. Differentiating Eq. (55), and defining
with
we obtain the relative mode acceleration,
Thus we can also calculate the instantaneous variation of the mode phase velocity from the particle coordinates, velocities, and accelerations at any time.
7.3. 3D extension for the m = 2 mode
Extending a Fourier-like decomposition for 3D distributions in order to determine a given mode speed vector is not straightforward. For example, choosing a decomposition in spherical harmonics or a double Fourier expansion over the sphere predetermines the positions of the poles and therefore breaks isotropy.
For the m = 2 mode in 2D, however, the Fourier method is equivalent to the moment of inertia method, as shown by substitution, where the positions xi are replaced by unit vectors ni = xi/∥xi∥. We showed above that the moment of inertia method works for 3D naturally using a SVD decomposition and differentiation. We can therefore use this method to replace the position vectors by unit vectors weighted by the mass.
The angular moment of inertia tensor In reads
where n is the N × 3 matrix composed of the particles unit vector coordinates ni = xi/∥xi∥,
To determine ṅ, we first calculate the time derivatives of a unit vector n,
which is just the angular speed of the unit vector n. Therefore,
Thus
Knowing İn and the SVD decomposition of In allows us to proceed exactly as in Sect. 6, therefore, we do dot elaborate further.
8. Conclusions
We have presented five different formal methods for determining the instantaneous pattern speed of sets or subsets of particles, or of stars, under the assumption that at the broad scale, these sets or subsets possess gradients that rigidly rotate around some axis. This is only a first approximation of the more complex reality in simulations and in galaxies.
The methods include checks that the pattern acceleration is low, or that different modes in a Fourier decomposition rotate at the same speed. The local methods are useful for probing the spatial variations of instantaneous local pattern speeds in real situations, allowing us to estimate the intrinsic errors made in assuming a constant global pattern speed. Some methods require knowing, or estimating, the particle accelerations, which for the present time are difficult to measure in the Milky Way, but should become increasingly more available in the future. Accelerations in the Milky Way can currently best be inferred from mass modeling and by solving Poisson’s equation.
We have already used and successfully tested some of these methods in published (Wu et al. 2016, 2018) or unpublished works. In a sequel paper, we plan to present tests, checks, and code of the most useful methods we presented here.
An extended collection of matrix derivative results for forward and reverse mode algorithmic differentiation, Mike Giles, (2008), https://people.maths.ox.ac.uk/gilesm/files/NA-08-01.pdf
PBA2014: SVD differentiation, Ladislav Kavan, 2014, https://www.youtube.com/watch?v=1cCwKsgsFX8
Differentiating the Singular Value Decomposition, James Townsend, 2016, https://j-towns.github.io/papers/svd-derivative.pdf
Acknowledgments
DP thanks both the Inter-University Centre for Astronomy and Astrophysics, Pune, India, and the Academia Sinica Institute of Astronomy and Astrophysics, Taipei, Taiwan, for hospitality for a number of stays where this work was extended. KS thanks Geneva observatory for the kind hospitality during 2013 and subsequent years when the initial phase of this work started. YTW thanks Geneva observatory for hospitality for a number of visits in 2015 and subsequent years when this work was extended.
Note added in proof. An older web publication, besides the ones cited in Appendix A, by Mike Giles4, has been found which describes, among others, the derivatives of eigenvalue and singular value decompositions, including computer code. In particular the eigenvalue decomposition derivative is an equivalent but slightly more efficient method than the SVD method presented here.
The initial phases of our work, including the original moment and Fourier methods, was openly presented many times in seminars and workshops, such as the 2013, 2014 and 2016 Gaia Challenge Workshops5. The methods have been developed over the years, and some of the methods briefly described and applied in Wu et al. (2016, 2018). While submitting this article, Dehnen et al. (2023) published a paper using very similar Fourier and moment methods to Sects. 6–7. They add a smoothing weight function to their derivations, while keeping our C and S notations used in Wu et al. (2018) and in Eq. (58). This is not a coincidence, because we publicly disclosed our single snapshot Fourier and moment methods years before.
Their weight function correction, using the additional mass conservation assumption, may be a useful option to add to the moment and Fourier methods in Sects. 6 and 7 whenever sharp windowing of particles is used. However, in a particular N-body simulation we have found that the radial flux correction for a ring containing less than about 105 particles was an illusory improvement because the noise introduced by the mass flux correction terms was comparable to the intended bias correction. This calls for more testing of the respective approaches.
References
- Anderson, E., Bai, Z., Bischof, C., et al. 1999, LAPACK Users’ Guide, 3rd edn. (Philadelphia: Society for Industrial and Applied Mathematics) [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edn. (Princeton: Princeton University Press) [Google Scholar]
- Boyd, S., & Vandenbergh, L. 2004, Convex Optimization (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Chartrand, R. 2011, Nonsmooth Data, ISRN Applied Mathematics, 11 [Google Scholar]
- Chartrand, R. 2017, in 2017 IEEE Global Conference on Signal and Information Processing (GlobalSIP), 244 [CrossRef] [Google Scholar]
- Clarke, J. P., & Gerhard, O. 2022, MNRAS, 512, 2171 [NASA ADS] [CrossRef] [Google Scholar]
- Debattista, V. P., & Shen, J. 2007, ApJ, 654, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Debattista, V. P., Gerhard, O., & Sevenster, M. N. 2002, MNRAS, 334, 355 [Google Scholar]
- Dehnen, W., Semczuk, M., & Schönrich, R. 2023, MNRAS, 518, 2712 [Google Scholar]
- de Swardt, B., Sheth, K., Kim, T., et al. 2015, ApJ, 808, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Erwin, P. 2004, A&A, 415, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friedli, D., & Martinet, L. 1993, A&A, 277, 27 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Katz, D., et al.) 2018, A&A, 616, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerhard, O. 2011, Mem. Soc. Astron. It. Suppl., 18, 185 [Google Scholar]
- Gingold, R. A., & Monaghan, J. J. 1977, MNRAS, 181, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, H. 1971, Classical Mechanics (Addison-Wesley) [Google Scholar]
- Gradshteyn, I. S., Ryzhik, I. M., Jeffrey, A., & Zwillinger, D. 2007, Table of Integrals, Series, and Products (Academic Press) [Google Scholar]
- Hilmi, T., Minchev, I., Buck, T., et al. 2020, MNRAS, 497, 933 [Google Scholar]
- Julian, W. H., & Toomre, A. 1966, ApJ, 146, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Kruk, S. J., Lintott, C. J., Simmons, B. D., et al. 2017, MNRAS, 469, 3363 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C. C., & Shu, F. H. 1964, ApJ, 140, 646 [Google Scholar]
- Lucy, L. B. 1977, AJ, 82, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F., & Tagger, M. 1997, A&A, 322, 442 [NASA ADS] [Google Scholar]
- Meidt, S. E., Rand, R. J., Merrifield, M. R., Debattista, V. P., & Shen, J. 2008, ApJ, 676, 899 [Google Scholar]
- Merrifield, M. R., Rand, R. J., & Meidt, S. E. 2006, MNRAS, 366, L17 [NASA ADS] [Google Scholar]
- Minchev, I., Nordhaus, J., & Quillen, A. C. 2007, ApJ, 664, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Monari, G., Kawata, D., Hunt, J. A. S., & Famaey, B. 2017, MNRAS, 466, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Pfenniger, D. 1990, A&A, 230, 55 [NASA ADS] [Google Scholar]
- Pfenniger, D. 2019, Celest. Mech. Dyn. Astron., 131, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Pfenniger, D., & Friedli, D. 1991, A&A, 252, 75 [NASA ADS] [Google Scholar]
- Pfenniger, D., & Norman, C. 1990, ApJ, 363, 391 [Google Scholar]
- Rautiainen, P., & Salo, H. 1999, A&A, 348, 737 [NASA ADS] [Google Scholar]
- Saha, K., & Elmegreen, B. 2016, ApJ, 826, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, K., & Maciejewski, W. 2013, MNRAS, 433, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. L., Smith, L., & Evans, N. W. 2019, MNRAS, 488, 4552 [NASA ADS] [CrossRef] [Google Scholar]
- Savitzky, A., & Golay, M. J. E. 1964, Anal. Chem., 36, 1627 [Google Scholar]
- Sellwood, J. A. 2011, MNRAS, 410, 1637 [NASA ADS] [Google Scholar]
- Sellwood, J. A., & Athanassoula, E. 1986, MNRAS, 221, 195 [NASA ADS] [Google Scholar]
- Sellwood, J. A., & Sparke, L. S. 1988, MNRAS, 231, 25P [Google Scholar]
- Shimizu, T., & Yoshii, Y. 2012, ASP Conf. Ser., 458, 341 [NASA ADS] [Google Scholar]
- Sparke, L. S., & Sellwood, J. A. 1987, MNRAS, 225, 653 [NASA ADS] [Google Scholar]
- Toomre, A., & Kalnajs, A. J. 1991, in Dynamics of Disc Galaxies, ed. B. Sundelius (Göteborg Univ. Press), 341 [Google Scholar]
- Trefethen, L. N., & Bau, I., D. 1997, Numerical Linear Algebra (SIAM) [CrossRef] [Google Scholar]
- Tremaine, S., & Weinberg, M. D. 1984, ApJ, 282, L5 [Google Scholar]
- Van Breugel, F., Kutz, J. N., & Brunton, B. W. 2020, IEEE Access, 8, 196865 [CrossRef] [Google Scholar]
- Wozniak, H. 2015, A&A, 575, A7 [Google Scholar]
- Wozniak, H. 2020, A&A, 642, A207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, Y.-T., Pfenniger, D., & Taam, R. E. 2016, ApJ, 830, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y.-T., Pfenniger, D., & Taam, R. E. 2018, ApJ, 860, 152 [Google Scholar]
Appendix A: SVD differentiation
For any matrix A, here illustrated for a 3 × 3 matrix, the singular value decomposition
consists of two orthogonal matrices U and V, and a diagonal real matrix S where the non-negative singular values s1, s2, … are sorted in decreasing order s1 ≥ s2 ≥ … along the diagonal,
The goal here is to explicitly describe the behavior of the SVD when the matrix A is perturbed to A + dA. We have found very little useful literature on this topic. The derivation below is based on web publications by Ladislav Kavan6 and James Townsend7.
For symmetric (square) matrices, the singular-value problem is the same as the eigenvalue problem AV = VS because then U = V. We therefore show the case for general 3 × 3 matrices below. Townsend’s article contains the matrix expressions for the fully general rectangular case of any size.
Differentiating Eq. (A.1),
and multiplying left and right by UT and V, we obtain
When A, U, V, S, and dA are known, the task is now to explicit the differential part of the SVD decomposition, namely dS, dU, and dV. The orthogonality of U and V ensures that UTU = 1, and VTV = 1. Differentiating UTU,
we see that the matrix UTdU is antisymmetric. The same holds for VTdV. Naming 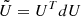 and
and 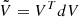 , and writing element-wise,
, and writing element-wise,
and
we see that in Eq. (A.7) the diagonal part consists of dS, and the nondiagonal part consists of 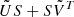 . Thus dS is made by the diagonal of H,
. Thus dS is made by the diagonal of H,
For the nondiagonal part, we obtain three linear systems of two equations,
When we solve these systems for nondegenerate cases s1 > s2 > s3, the explicit solution reads
In case of degenerate cases, we can always solve Eqs. (A.9) using the pseudo-inverse instead, yielding the least-norm solution. Thus we can always obtain the matrices 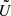 and
and 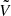 .
.
When A is symmetric, U = V, 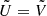 , and H is symmetric as well, so that Eqs.(A.10) reduce to
, and H is symmetric as well, so that Eqs.(A.10) reduce to
yielding the nonzero components of 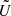 .
.
Finally, because 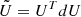 , and U−1 = UT (and similar for
, and U−1 = UT (and similar for 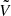 ), with a last matrix product, the differential matrices dU and dV are obtained,
), with a last matrix product, the differential matrices dU and dV are obtained,
Appendix B: Class of distribution functions with distinct space and velocity pattern speeds
Here we confirm with a particular class of functions that distribution functions exist that have different pattern speeds, Ω in space and ω in velocity space. We adopt a product of ellipsoidal distribution functions F and G in space and velocity space, respectively,
where a, b, c, α, β, and γ are constants, and
where r and v are constants. Clearly, the distribution function rotates at distinct speeds Ω and ω in space and velocity space around the z− and vz-axes, respectively. Direct evaluation of both sides of Eq. (4) verifies that the two sides read the same:
where F′ and G′ are the derivatives of F and G. The only constraint on F and G therefore is that they should be differentiable.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



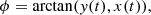
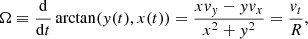
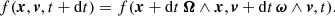
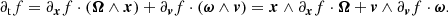
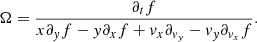
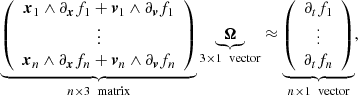
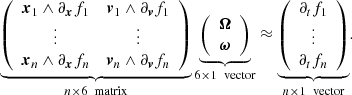
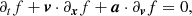
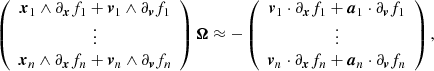
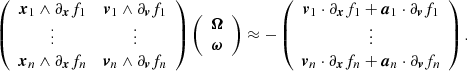
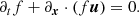
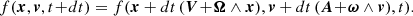
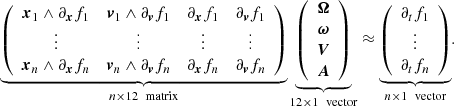
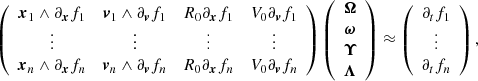
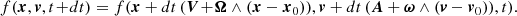
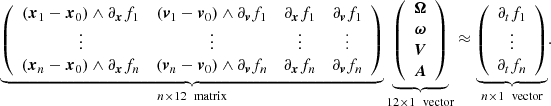
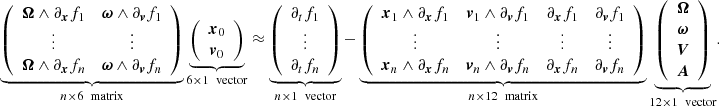
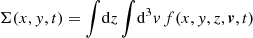
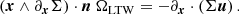
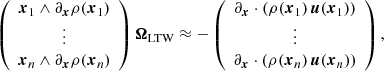
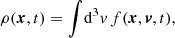
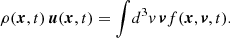
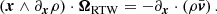
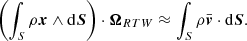

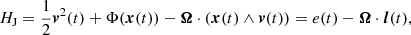
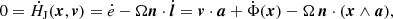
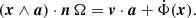
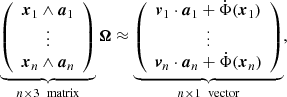
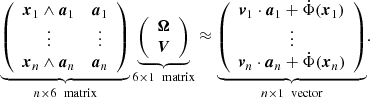
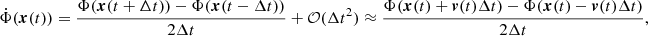
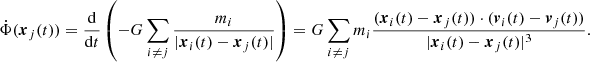
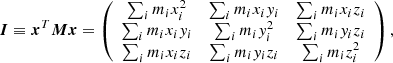
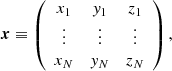
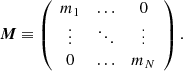
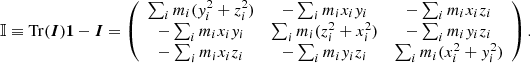
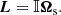
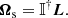
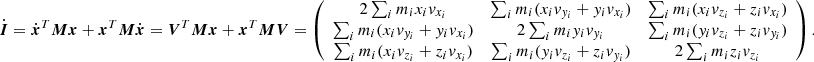
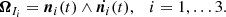
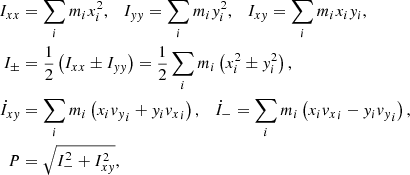
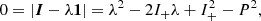
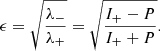
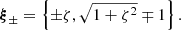
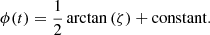
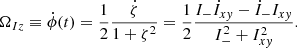
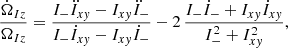
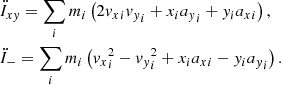
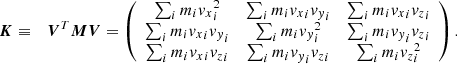
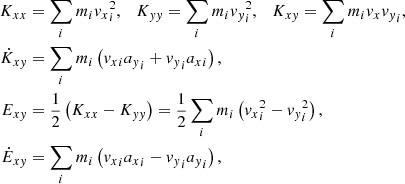
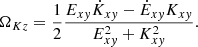
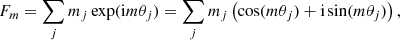
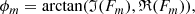
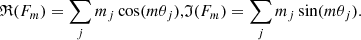
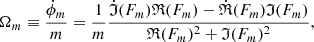
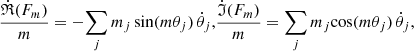
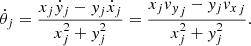
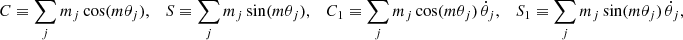
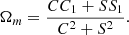
![$$ \begin{aligned} C_2 \equiv \sum _j m_j \left[ \cos ( m \theta _j)\,\ddot{\theta }_j - m \sin ( m \theta _j)\,\dot{\theta }_j^2\right],\quad S_2 \equiv \sum _j m_j \left[ \sin ( m \theta _j)\,\ddot{\theta }_j + m \cos ( m \theta _j)\,\dot{\theta }_j^2\right], \end{aligned} $$](/articles/aa/full_html/2023/05/aa45463-22/aa45463-22-eq79.gif)