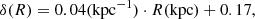EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) A58 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number A58
Number of page(s) 11
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202243714
Published online 30 March 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The past few years have witnessed remarkable observations in the field of multi-messenger astrophysics, especially in the cosmic-ray (CR) and γ-ray channels. The Tibet ASγ experiment reported the observation of diffuse γ-ray emission from the Galactic plane (25° < l <  100° and 50° < l <  200°, both for |b|< 5°) with energy up to the PeV (Amenomori et al. 2021). This finding was confirmed by the Large High Altitude Air Shower Observatory (LHAASO) collaboration (Zhao et al. 2021) for the innermost region. If not originating in currently active unresolved sources (see, e.g., Casanova & Dingus 2008 and the more recent Vecchiotti et al. 2022 for an alternative interpretation), the presence of truly diffuse γ-rays at PeV levels is likely due to ∼𝒪(10) PeV CRs injected by PeV accelerators that were active in the past called PeVatrons. The ability to explore the knee region (ECR ∼ a few PeV) of the CR spectrum is of outstanding importance for our understanding of CR physics. If we assume the conventional scenario of supernova remnants (SNRs) as the bulk of Galactic CRs (see Gabici et al. 2019 for a recent review), it is a theoretical challenge to even achieve particle acceleration at the level of ∼𝒪(100) TeV, and only for a short time in the evolution of the remnant (Lagage & Cesarsky 1983a,b). To overcome this problem, stellar clusters have recently come back as a viable explanation for such high-energy particle acceleration (Cesarsky & Montmerle 1983; Morlino et al. 2021), although it is not clear to what extent in the locally observed CRs. Therefore, whether the knee in the CR spectrum is due to a change in the CR acceleration mechanism or to a transport effect is still matter of debate.

The Tibet ASγ and LHAASO measurements offer a new valuable approach to study the origin and the propagation of Galactic CRs that complement direct measurements, which above ∼𝒪(100) TeV are performed with Extended Air Shower (EAS) experiments. As witnessed by the large discrepancies in the energy spectra observed by different collaborations (see Fig. 1), these measurements suffer from large systematic errors, mostly associated with modeling hadronic interaction within the Earth’s atmosphere. Another valuable advantage of measuring the Eγ ≥ TeV γ-ray diffuse emission of the Galaxy is that it may allow us to test whether features in the CR spectra, such as the hardening at ∼300 GeV/n found by CREAM (Ahn et al. 2010), PAMELA (Adriani et al. 2011), and AMS (Aguilar et al. 2015a,b), and the softening at ∼10 TeV/n measured by DAMPE (An et al. 2019) and CREAM (Yoon et al. 2017), are due to local sources or if they are representative of the whole Galaxy, due to transport effects (Blasi et al. 2012). Moreover, the detection of the diffuse emission at low Galactic longitudes gives crucial information on how CR propagation behaves in the inner regions of the Galaxy, where the conditions for CR transport are expected to be different than in the average disk, noticeably leading to a radial (galactocentric) dependence for the CR spectra. In the last years a huge experimental effort has allowed us to strongly reduce the uncertainties on the CR transport parameters within a horizon of a few kpc around the Solar System; however, it should be noted that very little is still known about CR propagation beyond that distance. In this regard, the study of weakly interacting messengers such as γ-rays and neutrinos originating in the scattering of CRs with the interstellar medium (ISM) and the interstellar radiation field (ISRF) offers a valuable probe of CR transport in those distant regions.

thumbnail Fig. 1.

Proton (left panel) and helium (right panel) local spectra computed for the γ-optimized scenario are plotted against a representative set of data. For each species the spectra as predicted using the Max and Min source spectrum setups are shown. The corresponding lines computed for the Base scenario are not shown since they are almost coincident with those reported here above 10 GeV n−1 (at the Solar System position).

In Gaggero et al. (2015b), Cerri et al. (2017) the authors argue that the hardening of the γ-ray diffuse emission found by Fermi-LAT above 10 GeV (Ackermann et al. 2012; Acero et al. 2016; see also Yang et al. 2016) can be explained in terms of a radially dependent CR spectrum. Based on that interpretation, in Gaggero et al. (2015a) the authors predict a diffuse flux that is much higher than expected from conventional transport models at low Galactic longitudes and very high energies E ≫ 1 TeV. They show that this also allows us to consistently reproduce Fermi-LAT and Milagro (Abdo et al. 2008) measurements in the inner Galaxy, as well as the H.E.S.S. (Gaggero et al. 2017) observed diffuse-emission in the central molecular zone (Abramowski et al. 2016), although the CR population in that small region may be affected by one or more PeVatrons close to the Galactic Center (GC).

Recently, a phenomenological model inspired by that scenario, where the energy and spatial dependence of the CR spectrum are non-factorized, has been studied (Lipari & Vernetto 2018; hereafter LV non-factorized model) and used by Tibet ASγ to interpret their results (Amenomori et al. 2021). For reference, the authors also considered a conventional (LV factorized) model with a radially independent CR spectrum. LV models also account for γ-ray absorption, which is significant above 100 TeV, due to pair production by scattering onto the CMB and the dust emitted infrared photon background (Vernetto & Lipari 2016). Both LV models are designed to reproduce AMS-02 and CREAM proton and helium data below 100 TeV. As shown in Amenomori et al. (2021), the LV non-factorized (spatial dependent) model seems to be in better agreement with Tibet ASγ results than the factorized (conventional) model. Preliminary LHAASO data (Zhao et al. 2021), however, are slightly lower than Tibet in some energy bins. More importantly, they have significantly smaller statistical errors and extend down to 10 TeV where they are less scattered, and the uncertainties on the CR spectral elemental shapes are smaller. As we show in this paper, this may have relevant implications for their interpretation.

In this work we model the γ-ray diffuse emission of the Galaxy from 10 GeV up to PeV levels trying to assess the effect of the uncertainties due to the choice of the CR spectra, hence on the choice of the transport scenario. Differently from what is done in Lipari & Vernetto (2018), we make extensive use of Fermi-LAT results, and show their relevance to constrain CR transport properties, and use physically motivated models. CR transport is modeled with the DRAGON2 numerical code (Evoli et al. 2017, 2018) in two transport scenarios, assuming a spatially independent or dependent diffusion coefficient. Additionally, we use the newly released HERMES code (Dundovic et al. 2021) to integrate along the line of sight the CR spatial and energy distributions obtained with DRAGON2 using detailed IS gas emission maps, updated ISRF models, and γ-ray production cross sections, to get high-resolution sky maps of the diffuse emission at all relevant energies, which provide more accurate and robust results than the analytical gas models used in Lipari & Vernetto (2018). Moreover, we account for a wider set of CR data above 10 TeV (but see Vernetto & Lipari 2021) and, in order to cope with the large discrepancies among different data sets (see also Koldobskiy et al. 2021b), we consider two setups for the CR injection spectra (see Table 1). We then compare our predictions with the Tibet ASγ and LHAASO results, with ARGO-YBJ (Bartoli et al. 2015) at lower energy, and with IceCube (Aartsen et al. 2019b) and CASA-MIA (Borione et al. 1998) upper limits between 100 TeV and 2 PeV in regions closer to the GC, and also with Fermi-LAT data in several Galactic plane (GP) quadrants.

Table 1.

Spectral indexes at injection for the Max and Min models.

We show that Tibet ASγ and, if confirmed, LHAASO data in combination with Fermi-LAT favor a spatially dependent transport scenario.

2. Relevant data

The high-precision measurements provided by recent cosmic-ray missions such as AMS-02 (Aguilar et al. 2014, 2015a,b) and DAMPE (Ambrosi et al. 2017; An et al. 2019) together with the increasing quality and quantity of gamma-ray data, thanks to the Fermi-LAT (Ackermann et al. 2012, 2015), HAWC (Albert et al. 2020; Abeysekara et al. 2019) and H.E.S.S. (Aharonian et al. 2008; Abdalla et al. 2018) experiments, require improved models of particle acceleration and transport for their interpretation (Serpico 2018).

2.1. Local cosmic-ray data

In the low to intermediate energy range (10 GeV ≲ ECR ≲ 10 TeV), CR data are collected by space-born or balloon experiments, which are less affected by systematic uncertainties. In this energy band we consider the results from AMS-02 (Aguilar et al. 2015a,b), DAMPE (An et al. 2019; Alemanno et al. 2021), CALET (Adriani et al. 2019), ATIC-2 (Panov et al. 2009), CREAM-III (Yoon et al. 2017), and NUCLEON (Atkin et al. 2018).

As shown in Fig. 1, measurements are in good agreement with each other for both protons and helium nuclei, and show a power-law structure up to ∼𝒪(100 − 500) GeV, where a spectral hardening is reported by all the experiments, typically interpreted as a consequence of a new phenomenon occurring in particle transport rather than in the acceleration (see Gabici et al. 2019 and references therein). Another structure that is clearly visible in the proton and helium spectra is a pronounced softening reported by DAMPE at a rigidity of ∼𝒪(10) TV (An et al. 2019; Alemanno et al. 2021), confirming previous claims by CREAM-III (Yoon et al. 2017) and NUCLEON (Atkin et al. 2018).

It is important to note that since the highest-precision measurements come from experiments that are not ground based, for which it is challenging to achieve energies above ∼10 TeV with significant statistics, the highest energies currently reached do not allow us to determine whether the softening is a (i) local feature or (ii) a global structure. In scenario (i) the particle spectra in the Galaxy would follow the trend after the hardening at a few hundred GeV and proceed up to the knee at ∼5 PeV, where it undergoes a cutoff in the form of a sharp softening; the bump is then typically interpreted as a signature of a nearby source contributing to the primary CRs (Fornieri et al. 2021). Throughout the paper we refer to this setting as the Max setup. For the case (ii) we would expect a softening above ECR ∼ 𝒪(10) TeV and a cutoff as a pronounced break at the knee (at ∼ a few PeV). We refer to this setting as the Min setup.

For the highest-energy band (1 PeV ≲ Eγ ≲ 1 EeV), such energies can be achieved at the moment only by ground-based experiments measuring extensive air showers (EASs), which imply much larger uncertainties and a strong dependence on models of the hadronization occurring in the Earth’s atmosphere, specifically on their Monte Carlo-based simulations (see Pierog et al. 2006; Parsons et al. 2011 for a discussion on the model-dependent uncertainties of the hadronic showers). In particular, we consider data points from KASCADE (Antoni et al. 2005) and KASCADE-Grande (Apel et al. 2013), or, alternatively, from IceTop (Aartsen et al. 2019a), being the two data sets incompatible with each other. We report the break positions and spectral indexes of the power laws used to parameterize the injection spectra of CRs from the sources in Table 1.

In what follows we compute the γ-ray emission in the Galaxy for both the Min and the Max spectral setups. As shown in Fig. 1, our procedure is addressed to bracket the uncertainties due to the poor knowledge of the CR spectrum in the highest-energy range.

As an additional comment, we do not account for CR species heavier than helium since, under reasonable conditions, their contribution to the gamma-ray source term is subdominant (less than 10%) with respect to the expected flux due to proton plus helium production rate (see, e.g., Breuhaus et al. 2022 for a recent analysis).

2.2. Fermi-LAT data

The LAT is a pair-conversion telescope that has been providing gamma-ray data since August 2008 in a range of energies ranging from ∼20 MeV to a few hundred GeV (Atwood et al. 2009). In this work we make use of ∼149 months of data (from 2008 August 04 to 2020 December 31), selecting CLEAN events from the PASS8 data. We selected events from good-quality time intervals and removed the intervals when the LAT was subtended at rocking angles θr <  52deg ((DATA_QUAL>0) && (LAT_CONFIG==1) && ABS(ROCK_ANGLE< 52)), and in addition applied the zenith-angle cut θz <  100deg in order to avoid contamination with the Earth albedo. We considered front- and back-converted events in order to minimize statistical errors. We employed the P8R3_CLEAN_V3 version of the instrument response functions. The extraction of Fermi data and calculation of exposure maps was performed using the most up-to-date version of the ScienceTools1 (2.0.8; released on 2021 January 20). In this work our γ-ray model is optimized to reproduce Fermi-LAT data in different windows of galactic longitude in the energy range between ∼10 and ∼300 GeV, under the hypothesis of a spatially dependent spectral index of the diffusion coefficient (see details in Sect. 3.2), considering the recent Fermi 4FGL-DR2 catalog in order to account for the source’s γ-ray emission.

2.3. Very high-energy gamma-ray data

A dedicated section is necessary for the very high-energy band, namely for the photons detected with energy Eγ ≥ 100 TeV that can be probed via the deconvolution of the EAS ground-based detectors. In particular, we note the observations of PeV γ-rays by the LHAASO (Cao et al. 2021) and Tibet ASγ (Amenomori et al. 2021) Collaborations. LHAASO reports the detection of ∼530 photons above Eγ = 100 TeV at σ ≥ 7 significance from 12 regions with overlapping known sources. Among these, source J2032+4102, which is associated with the stellar cluster Cygnus-OB2 and is considered a probable PeV-acceleration site (Aharonian et al. 2019), deserves special attention as it is where the highest-energy photon (Eγ = 1.42 ± 0.13 PeV) originates. In addition, Tibet observes ten events in the energy bin 398 ≤ Eγ(TeV)≤1000, four of which originate around the OB2 cluster. However, in order to remove the cluster contribution to the total detected photons, in Tibet they use a Gaussian profile with width σOB = 0.5° (consistent with the angular extension exploited by LHAASO; Cao et al. 2021), motivated by the profiles σHAWC ≤ 0.3° used by the HAWC Collaboration for sources above Eγ = 56 TeV (Abeysekara et al. 2020). On the other hand, for the specific case of the Cygnus cocoon, HAWC reports an extension of σOB,  HAWC = 2.1° (Abeysekara et al. 2021), which implies that most of the diffuse emission from the Cygnus region could actually be coming from the single source. This information is used in Liu & Wang (2021) to interpret the neutrino counterpart expected from the region, which would otherwise be in tension with the IceCube observations on the GP (Aartsen et al. 2017).

As a result, it is possible that the highest-energy γ-ray point in the Tibet observations actually should show a flux that is lower than currently estimated. Future analyses will certainly help to clarify the picture.

3. The models

The diffuse γ-ray sky is the superposition of a number of different components. They include the isotropic background, the unresolved point-like (or extended) source emission, and the secondary emission of Galactic CRs.

  • The isotropic background component captures the contribution from extragalactic diffuse emission, unresolved extra-galactic sources, and residual (mis-classified) cosmic-ray emission. We adopt here a reference isotropic spectral template provided by the Fermi-LAT collaboration (iso_P8R3_CLEAN_V3_v1)2.

  • For the unresolved point-like, or extended, source emission the contribution of unresolved sources is derived from population synthesis, using the model for the Galactic gamma-ray population following a four-arm spiral distribution described in Steppa & Egberts (2020). This source model for fluxes at 1 TeV is translated to the energy range of the Fermi-LAT data using a spectral index of −2.4 for the TeV energy range as the mean spectral index of the H.E.S.S. Galactic source catalog (Abdalla et al. 2018) and for lower energies a spectral index of −2.27 as mean of the Fermi-LAT 4FGL (Abdollahi et al. 2020) with a transition regime between 100 GeV and 1 TeV. Source populations are simulated, and their sources are classified as detectable or unresolved according to the Fermi-LAT sensitivity of the 4FGL. The sample of detectable sources is used as verification; both the cumulative spectrum and the log N − log S distribution of detectable sources are well matched in simulations and data in the energy range considered in the Fermi analysis. As a model for the unresolved emission we use the mean of 200 realisations, which results in a flux in unresolved sources of around 1% of the detected sources. Individual realizations exhibit large fluctuations, manifested in a standard deviation in the simulated fluxes of > 100%.

  • The secondary emission of Galactic CRs, at the energies relevant for this paper (E ≫ 10 GeV), can be further divided in the hadronic component, due to the decay of neutral pions produced by CR scattering onto the IS gas (mostly hydrogen and helium), and the inverse-Compton (IC) emission of CR electrons and positrons onto the ISRF.

The relative contributions of these components depend on the Galactic coordinates and on the energy. On the GP and at energies higher than 10 TeV, the hadronic emission by CRs is expected to be dominant although a significant contribution due to IC emissions cannot be excluded (see Linden & Buckman 2018).

Here we focus mainly on modeling the secondary diffuse emission due to interaction of Galactic CRs during their propagation. We do this with the HERMES code (Dundovic et al. 2021), which at each given energy bin and for each relevant CR species performs a numerical integration along the line of sight of the product of the CR differential energy flux, of the IS gas density (or the ISRF for the IC emission), and of the γ-ray production cross section. More details on the cross sections and the gas distributions (hydrogen and helium) used in this work will be given in Sects. 3.2 and 3.1 respectively.

In the following subsection we discuss how the CR energy and spatial distributions are computed.

3.1. The interstellar gas

Our model consists of a set of column density maps in (l, b) Galactic coordinates for atomic and molecular gas, associated with galactocentric rings. The atomic gas model is based on the 21 cm line emission data observed by the recent HI4PI survey that covers the whole sky with 1/12 deg binning (HI4PI Collaboration 2016). For molecular gas, the decomposition is based on the observations of the CO rotational line at 115 GHz from the CfA survey (Dame et al. 2001; Dame & Thaddeus 2004). The profile decomposition is discussed in Remy et al. (in prep.), Fermi-LAT (2021). In our framework, every galactocentric ring can be associated with a value of the CO-H2 conversion factor (XCO). In our model, we adopt the values of [1.8, 3.5, 4.0, 4.5, 7.5, 8.0] in units of 1020 cm−2 K−1/(km s−1) in the following galactocentric radial intervals: [0 − 3 kpc; 3 − 5 kpc; 5 − 6 kpc; 6 − 7 kpc; 7 − 15 kpc; 15 − 30 kpc]. We assume here that the ISM gas is a mixture of hydrogen and helium nuclei with uniform density ratio fHe = 0.1.

3.2. CR transport: Conventional and γ-optimized scenarios

We determine the energy and spatial distribution of each relevant CR species, solving numerically the transport equation with the DRAGON2 code (Evoli et al. 2017, 2018). We assume that the observed CR spectrum can be approximated as a steady-state solution for a smooth distribution of continuous sources, which we fix on the basis of SNR catalogs; here we use the SNR distribution reported in Ferriere (2001). For a given source spectrum, generally a broken power law tuned against locally measured CR spectra, as output the code provides the propagated spectra of each primary and secondary species in each point of the Galaxy. In addition to several astrophysical quantities, as input the code needs to receive the CR diffusion coefficient D(ρ, x) as a function of the particle rigidity ρ and of the spatial coordinates. In the conventional scenario this is assumed to be a single power-law function of the particle rigidity with a spatially dependent slope, parameterized as

D ( ρ , x ) = D 0 · β ( ρ ρ 0 ) δ ( x ) , $$ \begin{aligned} D(\rho , \boldsymbol{x}) = D_0 \cdot \beta \left(\frac{\rho }{\rho _0}\right)^{\delta (\boldsymbol{x})}, \end{aligned} $$(1)

where D0 is its normalization at a reference rigidity ρ0 = 4 GV,3 and β is the velocity of the particles in units of the speed of light. The index δ, being poorly known a priori, is inferred from the comparison with the measured secondary-to-primary CR flux ratios, the boron-to-carbon (B/C) ratio being the most common. Works based on multi-channel analysis (Génolini et al. 2019; Fornieri et al. 2020; Luque et al. 2021) of the AMS-02 results (Aguilar et al. 2016), including others based on antiproton data (Di Bernardo et al. 2010; De La Torre Luque 2021), found that at the Solar System δ(R⊙)≃0.5. A different scenario arises if δ = δ(x), which turns into a non-factorized dependence of the propagated CR spectra on energy and position. For the models studied here the Alfvèn velocity is taken to be VA = 13 km s−1, the normalization of the diffusion coefficient is D0 = 6.1 × 1028 cm2 s−1 and the halo size is H = 6.7 kpc, in agreement with recent analyses of 10Be ratios (De La Torre Luque et al. 2021). We checked that passing to the γ-optimized scenario has no effect on the local B/C (see, e.g., Gaggero et al. 2015b), or on other secondary-to-primary CR ratios, which indeed are correctly reproduced with this setup. We note that adopting a different value of H and rescaling D0 to keep their ratio, and thus the CR grammage, unchanged would have no significant effect on the CR propagated spectra and the γ-ray diffuse emission along the GP. For the vertical (with respect to the GP) z dependence of the diffusion coefficient, we assume here a simple step function D(ρ, R, z)=D(ρ, R)Θ(H − |z|). Since the target gas is concentrated in a thin disk with zgas ≪ H, varying the value of H within the errors or using a smoother vertical profile would not have a significant effect on the line-of-sight integrated γ-ray emission.

Probing only the spectra of CR reaching the Solar System, the detection of charged CRs does not allow us to discriminate between the factorized (conventional) and non-factorized scenarios. The first evidence supporting the non-factorized scenario was found in Gaggero et al. (2015b) on the basis of the Fermi-LAT results showing an excess of the diffuse γ-ray emission of the Galaxy above 10 GeV in the inner GP with respect to the predictions of the conventional scenario. In that work it was shown that the Fermi-LAT results are reproduced if δ has a linear dependence on the galactocentric radius R, which turns into a harder spectrum of CR protons at low R, hence of secondary γ-rays at low Galactic longitudes (see also Acero et al. 2016). For this reason, in the following we call this the γ-optimized scenario. It should be understood, however, that the optimization is performed only on the parameters setting the CR diffusion coefficient in addition to XCO. Afterward, it was shown (Cerri et al. 2017) that this scenario is theoretically motivated and arises as a consequence of the growing poloidal component of the Galactic magnetic field at small galactocentric radii (see, e.g., Jansson & Farrar 2012).

In the following we consider two transport setups: the Base setup, which is representative of the conventional scenario, and the γ-optimized setup. The main parameters of these models are listed in Table 1. For the γ-optimized setup we find

δ ( R ) = 0.04 ( kpc − 1 ) · R ( kpc ) + 0.17 , $$ \begin{aligned} \delta (R) = 0.04(\mathrm{kpc^{-1}}) \cdot R(\mathrm{kpc}) + 0.17, \end{aligned} $$(2)

for R <  R⊙ = 8.5 kpc and δ(R)=δ(R⊙) for R ≥ R⊙. As discussed at the end of Sect. 2.1, for each model we use two different choices (Min and Max setups) of the CR proton and helium source spectra, which we enter to determine the spectra propagated to the Earth, to bracket the experimental uncertainties above 10 TeV (see Fig. 1). This arrangement effectively also accounts for the scenario in which the features in the propagated spectra are originated by transport rather than by the acceleration mechanism close to the sources. CR electron source spectra are also tuned to match local experimental data, up to a few TeV (see Fig. B.1).

Both models are implemented with the DRAGON2 code (Evoli et al. 2017, 2018), which was designed to enforce spatially dependent diffusion, using the same cross sections and IS gas and ISRF as discussed below. Hadronic emission maps due to CR interactions on IS hydrogen and helium, We adopt the γ-ray production cross section described in Kelner & Aharonian (2008; based on SYBILL) with the updated parameterization of the proton-proton total inelastic cross section reported in Kafexhiu et al. (2014; SYBILL version). The results obtained with these cross sections were also compared to the γ-ray emissivities extracted from the AAfrag package (Koldobskiy et al. 2021a); we find a maximum 20% difference in normalization and a negligible impact on the slope in the energy range of interest for this work. For helium we assume that it contributes with a geometrical weight estimated considering its atomic radius as a function of the atomic mass A, R(A)≃A1/3 R0, being R0 the reference proton radius. Since its contribution appears due to the pp interaction cross section, then its geometrical weight becomes 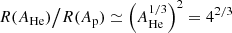R ( A He ) / R ( A p ) ≃ ( A He 1 / 3 ) 2 = 4 2 / 3 $ R(A_{\mathrm{He}}) \big/ R(A_{\mathrm{p}}) \simeq \left( A^{1/3}_{\mathrm{He}} \right)^{2} = 4^{2/3} $ with respect to protons. At high energies the absorption by pair-production on the spatially independent CMB photon field is computed as shown in Dundovic et al. (2021). The effect of the infrared galactic background is negligible compared to the uncertainties, and we neglect it in this work.

In Fig. 2 we compare our models with the spectrum of the diffuse emission below 300 GeV obtained from Fermi-LAT data, as described in Sect. 2.2. To avoid overcrowding the figure, for the Base transport model only the Max setting is shown. A more comprehensive comparison is presented in Fig. A.1. As mentioned above, the γ-optimized setups provide a better agreement with Fermi-LAT results at low Galactic longitudes.

thumbnail Fig. 2.

Average spectrum of the γ-ray diffuse emission along the galactic plane (|b|< 5°) compared with Fermi-LAT data in three longitude intervals. The “Sources” component comprises the sources included in the 4FGL Fermi Catalog as well as unresolved sources and the interstellar galactic background light (IGB) component comprises the extra-galactic background light and Fermi’s instrumental background.

We note that simplified versions of the Base and γ-optimized models considered in this work, adopting an exponential cutoff at 5 PeV n−1 and neglecting absorption, were used in Acharyya et al. (2021).

4. Results

We computed the full-sky maps of the diffuse gamma-ray emission associated with π0 decay, inverse-Compton scattering and Bremsstrahlung with the HERMES code (Dundovic et al. 2021). We chose an angular resolution characterized by the Healpix resolution pararameter nside = 512, corresponding to a mean spacing between pixel of ≃0.11° (Górski et al. 2005), nicely matching the angular resolution of the gas models adopted to compute the hadronic emission. For illustrative purposes, we show the Mollweide projection of the total emission associated with the γ-optimized Min model in Fig. 3, in a lower resolution.

thumbnail Fig. 3.

Mollweide projection of the all-sky map of Galactic diffuse emission flux above 100 TeV obtained for the Min γ-optimized model. The contours of the regions probed by Tibet/LHAASO and by IceCube (IC-86) are shown. J represents the differential flux of γ-rays per unit of solid angle.

In order to directly compare our models to the different experimental results described above, we considered several regions of interest, directly associated with the spectral data provided by the experiments focused on the very high-energy domain. In particular, we show in the same figure the contours of the regions observed by LHAASO (coincident with Tibet ASγ and ARGO) and IceCube-86.

We obtain the integrated flux in these regions, and compare it to the experimental data without any further ad hoc tuning and post-processing. We note once again that all the details of the setup (in particular, the ring-by-ring normalization of the molecular gas density, and the CR transport setup) are set by the comparison with both local data on charged CRs and Fermi-LAT data in the GeV–TeV domain, as commented in greater detail in the Appendix. The results are presented in Figs. 4, 5 and 6. The absorption due to γ − γ scattering is accounted for as described at the end of Sect. 3.2. Its effect is shown in Fig. 7 for the γ-optimized scenario.

thumbnail Fig. 4.

Gamma-ray spectra computed within the conventional (Base) and γ-optimized scenarios compared to Tibet ASγ (Amenomori et al. 2021) and LHAASO (Zhao et al. 2021; preliminary) data in the window |b|< 5°, 25° < l <  100°. The Galactic diffusion emission spectrum measured by Fermi-LAT and extracted as discussed in Sect. 2.2, and the ARGO-YBJ data (Bartoli et al. 2015) in the same region, are also shown. The contribution of unresolved sources, which may be significant at the highest energies, is not shown. The models account for the effect of γ-ray absorption onto the CMB photons (see Sect. 3.2).

thumbnail Fig. 5.

Predicted γ-ray spectra for the different scenarios studied in this work and compared to Tibet ASγ (Amenomori et al. 2021) and Fermi-LAT data in the window |b|< 5°, 50° < l <  200°. The experimental error bars show the 1σ statistical uncertainty of the measurement for CASA-MIA and TIBET data and the systematic plus statistical uncertainty (syst.+stat) for Fermi. The Fermi systematic uncertainties dominate along the full energy range shown, while the systematic error associated with TIBET data in this region is estimated to be around 30% (Amenomori et al. 2009). CASA-MIA (Borione et al. 1998) upper limits in the same region are also reported. The contribution of unresolved sources is not included here.

thumbnail Fig. 6.

Gamma-ray spectra computed in the conventional (Base) and γ-optimized CR transport scenarios compared to IceCube (Aartsen et al. 2019b) and CASA-MIA (Borione et al. 1998) upper limits. Since those data refer to different regions of the sky, they are rescaled as described in Aartsen et al. (2019b; see Fig. 12 in that paper). The contribution of unresolved sources is not included here.

thumbnail Fig. 7.

Effect of γ-ray absorption onto the CMB photons (see Sect. 3.2) for the γ-optimized scenario.

Figure 4, in particular, clearly represents the main result of this paper. This plot demonstrates that the diffuse emission models presented in this work, obtained under the assumption that the emission is fully originated by the diffuse Galactic CR “sea”, are able to capture the main features of the observed data over a remarkably wide range of energies, from 10 GeV all the way up to the PeV domain. This is already a major result.

However, since we are willing to go beyond this first level of interpretation and use our results to learn something about Galactic CR properties we face two main problems. First, there is a significant degeneracy between the choice of the CR transport setup and that of the source spectra (which, as we show, also depends on the CR data systematics. Second, there is a significant scatter of the Tibet and LHAASO data above 50 TeV. While this situation is likely to improve with the next data releases, we may already get some valuable hints limiting ourselves to consider only the lowest energy bin of the two experiments that should be affected by lower systematics. Interestingly, we find that the four lowest energy LHAASO points (below 50 TeV) are well aligned among themselves and the Tibet values. We note that these data favor the γ-optimized Max model. Even if we were to disregard the Tibet data, or assume that they are contaminated by the emission of the Cygnus cocoon (see Sect. 2.3), the γ-optimized scenario would still be the preferred one, but in its Min realization (see also Fig. 7). Although the Base–Max model is also in reasonable agreement with the LHAASO data, it is disfavored by the Fermi-LAT and ARGO results. This shows the importance of using data over the widest possible energy range.

We also consider the Tibet ASγ data in the window |b|< 5°, 50° < l <  200° (Fig. 5). We note that in this more external region the predictions of the γ-optimized and Base scenarios are quite similar so that these data may help to remove the degeneracy between the choice of the transport scenario and the shape of the source spectrum. Remarkably, even accounting for a possible contamination due to Cygnus-OB2, the Tibet results seems to clearly favor the Max setup. It will be very interesting, therefore, to see if LHAASO can confirm the Tibet results in that region. This will be also relevant in order to find an alternative interpretation of the Tibet results given in terms of the emission of unresolved pulsar wind nebulae (Vecchiotti et al. 2022).

We also performed a comparison of our models with IceTop and CASA-MIA upper limits which refer to regions different from those probed by Tibet and LHAASO (see Fig. 3). As is evident in Fig. 6, where we also show the ARGO-YBJ data, although these limits do not constrain any of our models yet, the IceTop sensitivity is close to the level required to test the γ-optimized Max model.

5. Conclusions

In this paper we presented a set of gamma-ray diffuse emission models that are able to consistently reproduce the available measurements from the GeV domain all the way up to PeV energies in the Galactic plane region.

In particular, we discussed a reference model based on the assumption of homogeneous transport properties in the whole Galaxy, and an optimized model aimed at capturing the progressive hardening of the proton slope inferred from Fermi-LAT data in the GeV domain. Both scenarios are tuned on local CR data, and are presented in two different versions that correspond to different fitting strategies of local CR data in the very high-energy part of the spectrum, which results in different choices of the injection spectra.

We found a relevant degeneracy between the choice of the CR propagation setup and that of the injection spectrum. In spite of this , we argue that the comparison between our models and the combination of different γ-ray data sets is able to provide valuable hints and may help to shed light on CR transport properties in different regions of the Galaxy.

We highlighted in particular that the Galactic diffuse emission measured by most experiments from 10 GeV to the PeV can almost entirely be explained as truly diffuse emission stemming from the Galactic CR sea. We also note that, if established the LHAASO results in combination with Fermi-LAT and ARGO-YBJ would favor a transport scenario characterized by spatially dependent diffusion. However, the confirmation of the robustness of that hint requires increasing the statistics and extending LHAASO measurements to other sky regions. Moreover, other experimental results at lower energies, such as those by HAWC (Nayerhoda et al. 2020), H.E.S.S. (Abramowski et al. 2014), SWGO (Albert et al. 2019), CTA (Cherenkov Telescope Array Consortium 2019), and ALPACA (ALPACA Collaboration 2017, 2021), will also be crucial to further check the scenario discussed in this work and to probe the CR shape throughout the Galaxy. Our analysis offers a valuable benchmark for the interpretation of these measurements.

In order to facilitate the comparison with these forthcoming data, we provide the scientific community with high-resolution all-sky maps of the diffuse γ-ray emission of the Galaxy from a few GeV to a few PeV computed for our benchmark models4. They can be valuable tools for experimental collaborations and can be used as background models in different contexts, from the generation of Galactic and extra-Galactic source catalogs to indirect dark matter searches.

As a final discussion point, we now return to the potential role of uncertainties. First of all, we note the role of unresolved sources. In general, the relative weight of truly diffuse emission and unresolved source contribution depends on a wide range of parameters that characterize the nature of the sources, the capability of the experiment to identify and resolve individual sources, the transport and/or escape of the high-energy particles that constitute the diffuse CR sea, and the total amount of target gas and photon background that is directly responsible for the truly diffuse signal. In this work, we chose to consider a specific model for the unresolved contribution and took it into account consistently when tuning our prediction for the diffuse emission on the Fermi-LAT data. Due to the uncertainty associated with the modeling of this component, and the impossibility of directly extrapolating the model to the PeV domain (a task that would require an accurate characterization of each PeV-oriented experiment to resolve individual sources), we cannot exclude a degeneracy between our scenario and an alternative model featuring a more prominent role of the unresolved component. We also point out that the leptonic component is expected to significantly fluctuate across the Galactic plane, with potential impact on the fit of Fermi-LAT data. Given the simplified setup proposed here, mainly characterized by a linear change of the δ parameter with galactocentric radius, the agreement with the data sets under consideration appears reasonable. However, a more specific work aimed at improving the Fermi-LAT data fit would require taking into account these uncertainties and is left for future works.

We finally note that in order to safely disentangle different interpretations, having more data will be crucial. In particular, we emphasize the role of neutrino measurements in this context (see also Ahlers et al. 2016; Gaggero et al. 2015a; Fang & Murase 2021; Breuhaus et al. 2022). The truly diffuse component is likely to be entirely hadronic above a few TeV, while the sources that could potentially contribute to the unresolved flux are mostly leptonic (namely, pulsar wind nebulae). Hence, a possible forthcoming discovery of a neutrino diffuse component associated with the Galactic plane, strengthening a 2σ hint of the γ-optimized KRA γ 5 $ _{\gamma}^5 $ model (Gaggero et al. 2015a) (similar to the γ-optimized Min model considered here) found by the IceCube collaboration (Aartsen et al. 2019c), would be a clear signature of the scenario we propose here, given the hadronic nature of the diffusion emission at very high energy considered in this work.

1

https://fermi.gsfc.nasa.gov/ssc/data/analysis/software/; https://github.com/fermi-lat/Fermitools-conda/wiki/Installation-Instructions

3

Often, for simplicity, D0 is assumed to be spatially independent.

Acknowledgments

We thank Quentin Remy for providing us with the interstellar HI and H2 3D distributions (“ring model”) used in this work. We also thank Hershal Pandya for informing us about IceCube collaboration γ-ray measurements and providing us with the corresponding sky window. We thank Paolo Lipari and Silvia Vernetto as well, for reading our manuscript and giving us useful comments. D. Gaggero has received financial support in the early stage of the project through the Postdoctoral Junior Leader Fellowship Programme from la Caixa Banking Foundation (grant n. LCF/BQ/LI18/11630014) during the early stage of the project. D.Gaggero was also supported by the Spanish Agencia Estatal de Investigación through the grants PGC2018-095161-B-I00, IFT Centro de Excelencia Severo Ochoa SEV-2016-0597, and Red Consolider MultiDark FPA2017-90566-REDC during the early stage of the project. D. Gaggero also acknowledges funding from the “Department of Excellence” grant awarded by the Italian Ministry of Education, University and Research (MIUR) for the period October–December 2021. D.Gaggero also acknowledges support from the INFN grant “LINDARK,” and the project “Theoretical Astroparticle Physics (TAsP)” funded by the INFN for the period October–December 2021. D. Grasso is also supported by TAsP. D. Gaggero also acknowledges the support from Generalitat Valenciana through the plan GenT program (CIDEGENT/2021/017) staring from 1/01/2022. D. Gaggero is also supported by Spanish MINECO through the Ramon y Cajal programme RYC2020-029184-I starting from 1/09/2022. C.E. acknowledges the European Commission for support under the H2020-MSCA-IF-2016 action, Grant No. 751311 GRAPES 8211 Galactic cosmic RAy Propagation: An Extensive Study. P. De la Torre is supported by the Swedish National Space Agency under contract 117/19. Infrastructure for Computing (SNIC) under project Nos. 2021/3-42 and 2021/6-326 partially funded by the Swedish Research Council through grant no. 2018-05973. D. Grasso was also supported by the grant ASI/INAF No. 2017-14-H.O.

References

  1. Aartsen, M. G., Ackermann, M., Adams, J., et al. 2017, ApJ, 849, 67 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aartsen, M. G., Ackermann, M., Adams, J., et al. 2019a, ApJ, 891, 9 [Google Scholar]
  3. Aartsen, M. G., Ackermann, M., Adams, J., et al. 2019b, Phys. Rev. D, 100, 082002 [Google Scholar]
  4. Aartsen, M. G., Ackermann, M., Adams, J., et al. 2019c, ApJ, 886, 12 [NASA ADS] [CrossRef] [Google Scholar]
  5. Abdalla, H., Abramowski, A., Aharonian, F., et al. 2018, A&A, 612, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Abdo, A. A., Allen, B., Aune, T., et al. 2008, ApJ, 688, 1078 [NASA ADS] [CrossRef] [Google Scholar]
  7. Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [Google Scholar]
  8. Abeysekara, A. U., Albert, A., Alfaro, R., et al. 2019, JCAP, 07, 022 [CrossRef] [Google Scholar]
  9. Abeysekara, A. U., Albert, A., Alfaro, R., et al. 2020, Phys. Rev. Lett., 124, 021102 [NASA ADS] [CrossRef] [Google Scholar]
  10. Abeysekara, A. U., Albert, A., Alfaro, R., et al. 2021, Nat. Astron., 5, 465 [Erratum: Nature Astron. 5, 724–724 (2021)] [NASA ADS] [CrossRef] [Google Scholar]
  11. Abramowski, A., Aharonian, F., Ait Benkhali, F., et al. 2014, Phys. Rev. D, 90, 122007 [NASA ADS] [CrossRef] [Google Scholar]
  12. Abramowski, A., Acero, F., Aharonian, F., et al. 2016, Nature, 531, 476 [CrossRef] [Google Scholar]
  13. Acero, F., Ackermann, M., Ajello, M., et al. 2016, ApJS, 223, 26 [Google Scholar]
  14. Acharyya, A., Adam, R., Adams, C., et al. 2021, JCAP, 01, 057 [CrossRef] [Google Scholar]
  15. Ackermann, M., Ajello, M., Atwood, W. B., et al. 2012, ApJ, 750, 3 [NASA ADS] [CrossRef] [Google Scholar]
  16. Ackermann, M., Ajello, M., Albert, A., et al. 2015, ApJ, 799, 86 [Google Scholar]
  17. Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2011, Science, 332, 69 [NASA ADS] [CrossRef] [Google Scholar]
  18. Adriani, O., Akaike, Y., Asano, K., et al. 2018, Phys. Rev. Lett., 120, 261102 [NASA ADS] [CrossRef] [Google Scholar]
  19. Adriani, O., Akaike, Y., Asano, K., et al. 2019, Phys. Rev. Lett., 122, 181102 [NASA ADS] [CrossRef] [Google Scholar]
  20. Aguilar, M., Aisa, D., Alpat, B., et al. 2014, Phys. Rev. Lett., 113, 121102 [NASA ADS] [CrossRef] [Google Scholar]
  21. Aguilar, M., Aisa, D., Alpat, B., et al. 2015a, Phys. Rev. Lett., 115, 211101 [NASA ADS] [CrossRef] [Google Scholar]
  22. Aguilar, M., Aisa, D., Alpat, B., et al. 2015b, Phys. Rev. Lett., 114, 171103 [CrossRef] [PubMed] [Google Scholar]
  23. Aguilar, M., Ali Cavasonza, L., Ambrosi, G., et al. 2016, Phys. Rev. Lett., 117, 231102 [NASA ADS] [CrossRef] [Google Scholar]
  24. Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2008, Phys. Rev. Lett., 101, 261104 [NASA ADS] [CrossRef] [Google Scholar]
  25. Aharonian, F., Yang, R., & de Oña Wilhelmi, E. 2019, Nat. Astron., 3, 561 [Google Scholar]
  26. Ahlers, M., Bai, Y., Barger, V., & Lu, R. 2016, Phys. Rev. D, 93, 013009 [CrossRef] [Google Scholar]
  27. Ahn, H. S., Allison, P., Bagliesi, M. G., et al. 2010, ApJ, 714, L89 [NASA ADS] [CrossRef] [Google Scholar]
  28. Albert, A., Alfaro, R., Ashkar, H., et al. 2019, ArXiv e-prints [arXiv:1902.08429] [Google Scholar]
  29. Albert, A., Alfaro, R., Alvarez, C., et al. 2020, ApJ, 905, 76 [NASA ADS] [CrossRef] [Google Scholar]
  30. Alemanno, F., An, Q., Azzarello, P., et al. 2021, Phys. Rev. Lett., 126, 201102 [NASA ADS] [CrossRef] [Google Scholar]
  31. ALPACA Collaboration (Takita, M., et al.) 2017, EPJ Web Conf., 145, 01002 [NASA ADS] [Google Scholar]
  32. ALPACA Collaboration (Sako, T., et al.) 2021, PoS, ICRC2021, 733 [Google Scholar]
  33. Ambrosi, G., An, Q., Asfandiyarov, R., et al. 2017, Nature, 552, 63 [NASA ADS] [CrossRef] [Google Scholar]
  34. Amenomori, M., Bi, X. J., Chen, D., et al. 2009, ApJ, 692, 61 [NASA ADS] [CrossRef] [Google Scholar]
  35. Amenomori, M., Bao, Y. W., Bi, X. J., et al. 2021, Phys. Rev. Lett., 126, 141101 [NASA ADS] [CrossRef] [Google Scholar]
  36. An, Q., Asfandiyarov, R., Azzarello, P., et al. 2019, Sci. Adv., 5, eaax3793 [NASA ADS] [CrossRef] [Google Scholar]
  37. Antoni, T., Apel, W., Badea, A., et al. 2005, Astropart. Phys., 24, 1 [NASA ADS] [CrossRef] [Google Scholar]
  38. Apel, W. D., Arteaga-Vel\’{a}zquez, J. C., Bekk, K., et al. 2013, Astropart. Phys., 47, 54 [NASA ADS] [CrossRef] [Google Scholar]
  39. Atkin, E., Bulatov, V., Dorokhov, V., et al. 2018, JETP Lett., 108, 5 [CrossRef] [Google Scholar]
  40. Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [CrossRef] [Google Scholar]
  41. Bartoli, B., Bernardini, P., Bi, X. J., et al. 2015, ApJ, 806, 20 [NASA ADS] [CrossRef] [Google Scholar]
  42. Blasi, P., Amato, E., & Serpico, P. D. 2012, Phys. Rev. Lett., 109, 061101 [Google Scholar]
  43. Borione, A., Catanese, M. A., Chantell, M. C., et al. 1998, ApJ, 493, 175 [NASA ADS] [CrossRef] [Google Scholar]
  44. Breuhaus, M., Hinton, J. A., Joshi, V., Reville, B., & Schoorlemmer, H. 2022, A&A, 661, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Cao, Z., Aharonian, F. A., An, Q., et al. 2021, Nature, 594, 33 [NASA ADS] [CrossRef] [Google Scholar]
  46. Casanova, S., & Dingus, B. L. 2008, Astropart. Phys., 29, 63 [NASA ADS] [CrossRef] [Google Scholar]
  47. Cerri, S. S., Gaggero, D., Vittino, A., Evoli, C., & Grasso, D. 2017, JCAP, 2017, 019 [Google Scholar]
  48. Cesarsky, C. J., & Montmerle, T. 1983, Space. Sci. Rev., 36, 173 [NASA ADS] [CrossRef] [Google Scholar]
  49. Cherenkov Telescope Array Consortium (Acharya, B. S., et al.) 2019, Science with the Cherenkov Telescope Array (World Scientific Publishing Co. Pte. Ltd.) [Google Scholar]
  50. Dame, T. M., & Thaddeus, P. 2004, ASP Conf. Ser., 317, 66 [Google Scholar]
  51. Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [Google Scholar]
  52. De La Torre Luque, P. 2021, JCAP, 11, 018 [CrossRef] [Google Scholar]
  53. De La Torre Luque, P., Mazziotta, M. N., Loparco, F., Gargano, F., & Serini, D. 2021, JCAP, 03, 099 [CrossRef] [Google Scholar]
  54. Di Bernardo, G., Evoli, C., Gaggero, D., Grasso, D., & Maccione, L. 2010, Astropart. Phys., 34, 274 [NASA ADS] [CrossRef] [Google Scholar]
  55. Dundovic, A., Evoli, C., Gaggero, D., & Grasso, D. 2021, A&A, 653, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Evoli, C., Gaggero, D., Vittino, A., et al. 2017, JCAP, 2017, 015 [Google Scholar]
  57. Evoli, C., Gaggero, D., Vittino, A., et al. 2018, JCAP, 2018, 006 [Google Scholar]
  58. Fang, K., & Murase, K. 2021, ApJ, 919, 93 [CrossRef] [Google Scholar]
  59. Fermi-LAT 2021, Galactic Interstellar Emission Model for the 4FGL Catalog Analysis, https://fermi.gsfc.nasa.gov/ssc/data/analysis/software/aux/4fgl/Galactic_Diffuse_Emission_Model_for_the_4FGL_Catalog_Analysis.pdf [Google Scholar]
  60. Ferriere, K. M. 2001, Rev. Mod. Phys., 73, 1031 [NASA ADS] [CrossRef] [Google Scholar]
  61. Fornieri, O., Gaggero, D., & Grasso, D. 2020, JCAP, 2020, 009 [Google Scholar]
  62. Fornieri, O., Gaggero, D., Guberman, D., et al. 2021, Phys. Rev. D, 104, 103013 [NASA ADS] [CrossRef] [Google Scholar]
  63. Gabici, S., Evoli, C., Gaggero, D., et al. 2019, Int. J. Mod. Phys. D, 28, 1930022 [CrossRef] [Google Scholar]
  64. Gaggero, D., Urbano, A., Valli, M., & Ullio, P. 2015a, Phys. Rev. D, 91, 083012 [Google Scholar]
  65. Gaggero, D., Grasso, D., Marinelli, A., Urbano, A., & Valli, M. 2015b, ApJ, 815, L25 [NASA ADS] [CrossRef] [Google Scholar]
  66. Gaggero, D., Grasso, D., Marinelli, A., Taoso, M., & Urbano, A. 2017, Phys. Rev. Lett., 119, 031101 [NASA ADS] [CrossRef] [Google Scholar]
  67. Génolini, Y., Boudaud, M., Batista, P. -I., et al. 2019, Phys. Rev. D, 99, 123028 [NASA ADS] [CrossRef] [Google Scholar]
  68. Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
  69. HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Jansson, R., & Farrar, G. R. 2012, ApJ, 757, 14 [NASA ADS] [CrossRef] [Google Scholar]
  71. Kafexhiu, E., Aharonian, F., Taylor, A. M., & Vila, G. S. 2014, Phys. Rev. D, 90, 123014 [Google Scholar]
  72. Kelner, S. R., & Aharonian, F. A. 2008, Phys. Rev. D, 78, 034013 [Google Scholar]
  73. Koldobskiy, S., Neronov, A., & Semikoz, D. 2021a, Phys. Rev. D, 104, 043010 [NASA ADS] [CrossRef] [Google Scholar]
  74. Koldobskiy, S., Kachelrieß, M., Lskavyan, A., et al. 2021b, Phys. Rev. D, 104, 123027 [NASA ADS] [CrossRef] [Google Scholar]
  75. Lagage, P. O., & Cesarsky, C. J. 1983a, A&A, 118, 223 [NASA ADS] [Google Scholar]
  76. Lagage, P. O., & Cesarsky, C. J. 1983b, A&A, 125, 249 [NASA ADS] [Google Scholar]
  77. Linden, T., & Buckman, B. J. 2018, Phys. Rev. Lett., 120, 121101 [NASA ADS] [CrossRef] [Google Scholar]
  78. Lipari, P., & Vernetto, S. 2018, Phys. Rev. D, 98, 043003 [CrossRef] [Google Scholar]
  79. Liu, R.-Y., & Wang, X.-Y. 2021, ApJ, 914, L7 [NASA ADS] [CrossRef] [Google Scholar]
  80. Luque, P. D. L. T., Mazziotta, M., Loparco, F., Gargano, F., & Serini, D. 2021, JCAP, 2021, 010 [CrossRef] [Google Scholar]
  81. Morlino, G., Blasi, P., Peretti, E., & Cristofari, P. 2021, MNRAS, 504, 6096 [NASA ADS] [CrossRef] [Google Scholar]
  82. Nayerhoda, A., Salesa Greusa, F., Casanova, S., et al. 2020, PoS, ICRC2019, 750 [Google Scholar]
  83. Panov, A. D., Adams, J. H., Ahn, H. S., et al. 2009, Bull. Russ. Acad. Sci.: Phys., 73, 564 [CrossRef] [Google Scholar]
  84. Parsons, R., Bleve, C., Ostapchenko, S., & Knapp, J. 2011, Astropart. Phys., 34, 832 [NASA ADS] [CrossRef] [Google Scholar]
  85. Pierog, T., Engel, R., & Heck, D. 2006, Czech. J. Phys., 56, A161 [NASA ADS] [CrossRef] [Google Scholar]
  86. Pothast, M., Gaggero, D., Storm, E., & Weniger, C. 2018, JCAP, 2018, 045 [Google Scholar]
  87. Serpico, P. D. 2018, J. Astrophys. Astron., 39, 41 [NASA ADS] [CrossRef] [Google Scholar]
  88. Steppa, C., & Egberts, K. 2020, A&A, 643, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Vecchiotti, V., Zuccarini, F., Villante, F. L., & Pagliaroli, G. 2022, ApJ, 928, 19 [NASA ADS] [CrossRef] [Google Scholar]
  90. Vernetto, S., & Lipari, P. 2016, Phys. Rev. D, 94, 063009 [NASA ADS] [CrossRef] [Google Scholar]
  91. Vernetto, S., & Lipari, P. 2021, PoS, ICRC2021, 923 [Google Scholar]
  92. Yang, R., Aharonian, F., & Evoli, C. 2016, Phys. Rev. D, 93, 123007 [Google Scholar]
  93. Yoon, Y. S., Anderson, T., Barrau, A., et al. 2017, ApJ, 839, 5 [CrossRef] [Google Scholar]
  94. Zhao, S., Zhang, R., Zhang, Y., & Yuan, Q. 2021, PoS, ICRC2021, 859 [Google Scholar]

Appendix A: Detailed comparison to Fermi-LAT data

We present here a detailed comparison between the gamma-ray diffuse emission models presented in this work and the Fermi-LAT data, with particular focus on the Galactic plane. We note that our modeling aims at capturing at first order the large-scale spectral trend inferred from the data and highlighted in several papers (Gaggero et al. 2015b; Pothast et al. 2018; Acero et al. 2016). We do not perform any post-processing or fitting of the templates nor do we include specific models for extended emission, for instance from star-forming regions.

We consider different regions of interest along the Galactic plane, and compare the Fermi-LATPASS8 data to the sum of the following components, for each model setup considered here:

  • A model for the π0 emission obtained with HERMES as described in the text. The rescaling factor XCO is tuned on a ring-by-ring basis in order to match the data normalization in the [1 − 10] GeV interval.

  • A model for the leptonic inverse-Compton scattering onto the diffuse low-energy photon component, obtained with HERMES.

  • A model for the emission due to Bremsstrahlung, obtained with HERMES.

  • The total flux associated with the resolved point sources, taken from the fourth Fermi Large Area Telescope catalog (4FGL) (Abdollahi et al. 2020).

  • A model for the unresolved flux contribution, described in Sec. 3.

We show the comparison in Fig. A.1. The three components of the Galactic diffuse emission (GDE) modeled with HERMES are computed in both the Base (Min) and the Gamma-Optimized (Min) setups. In both cases the total GDE is added to the isotropic spectral template and to the (unresolved plus resolved) source model. The corresponding total contribution is plotted as a dashed (solid) black line for the Base (optimized) model. We find an overall good agreement of the gamma-optimized model with the data. In particular, the region characterized by −10° < l <  10° is better reproduced by this setup, due to the hard spectrum detected by Fermi-LAT, and confirms the previous findings.

thumbnail Fig. A.1.

Comparison between Gamma-optimized models and Fermi-LAT data.

Appendix B: Electron spectrum

In this Appendix, we show in Fig. B.1 the electrons and the all-lepton spectrum computed with our models and fitted to experimental data from AMS-02, also in agreement with CALET (Adriani et al. 2018). We note that the small discrepancy between the AMS-02 data and the data measured by DAMPE does not affect our results since this difference would mean a completely negligible contribution to the total diffuse emission. A broken power law with a break at 60 GeV and spectral indices γ1 = 3.37 and γ1 = 3.20 (where γ1 and γ2 are the spectral indices before and after the break, respectively) was used to reproduce these spectra, with an exponential cutoff at 6 TeV.

thumbnail Fig. B.1.

Electrons and all-lepton spectrum for the models employed in this work, compared to available experimental data.

All Tables

Table 1.

Spectral indexes at injection for the Max and Min models.

In the text

All Figures

thumbnail Fig. 1.

Proton (left panel) and helium (right panel) local spectra computed for the γ-optimized scenario are plotted against a representative set of data. For each species the spectra as predicted using the Max and Min source spectrum setups are shown. The corresponding lines computed for the Base scenario are not shown since they are almost coincident with those reported here above 10 GeV n−1 (at the Solar System position).
In the text
thumbnail Fig. 2.

Average spectrum of the γ-ray diffuse emission along the galactic plane (|b|< 5°) compared with Fermi-LAT data in three longitude intervals. The “Sources” component comprises the sources included in the 4FGL Fermi Catalog as well as unresolved sources and the interstellar galactic background light (IGB) component comprises the extra-galactic background light and Fermi’s instrumental background.
In the text
thumbnail Fig. 3.

Mollweide projection of the all-sky map of Galactic diffuse emission flux above 100 TeV obtained for the Min γ-optimized model. The contours of the regions probed by Tibet/LHAASO and by IceCube (IC-86) are shown. J represents the differential flux of γ-rays per unit of solid angle.
In the text
thumbnail Fig. 4.

Gamma-ray spectra computed within the conventional (Base) and γ-optimized scenarios compared to Tibet ASγ (Amenomori et al. 2021) and LHAASO (Zhao et al. 2021; preliminary) data in the window |b|< 5°, 25° < l <  100°. The Galactic diffusion emission spectrum measured by Fermi-LAT and extracted as discussed in Sect. 2.2, and the ARGO-YBJ data (Bartoli et al. 2015) in the same region, are also shown. The contribution of unresolved sources, which may be significant at the highest energies, is not shown. The models account for the effect of γ-ray absorption onto the CMB photons (see Sect. 3.2).
In the text
thumbnail Fig. 5.

Predicted γ-ray spectra for the different scenarios studied in this work and compared to Tibet ASγ (Amenomori et al. 2021) and Fermi-LAT data in the window |b|< 5°, 50° < l <  200°. The experimental error bars show the 1σ statistical uncertainty of the measurement for CASA-MIA and TIBET data and the systematic plus statistical uncertainty (syst.+stat) for Fermi. The Fermi systematic uncertainties dominate along the full energy range shown, while the systematic error associated with TIBET data in this region is estimated to be around 30% (Amenomori et al. 2009). CASA-MIA (Borione et al. 1998) upper limits in the same region are also reported. The contribution of unresolved sources is not included here.
In the text
thumbnail Fig. 6.

Gamma-ray spectra computed in the conventional (Base) and γ-optimized CR transport scenarios compared to IceCube (Aartsen et al. 2019b) and CASA-MIA (Borione et al. 1998) upper limits. Since those data refer to different regions of the sky, they are rescaled as described in Aartsen et al. (2019b; see Fig. 12 in that paper). The contribution of unresolved sources is not included here.
In the text
thumbnail Fig. 7.

Effect of γ-ray absorption onto the CMB photons (see Sect. 3.2) for the γ-optimized scenario.
In the text
thumbnail Fig. A.1.

Comparison between Gamma-optimized models and Fermi-LAT data.
In the text
thumbnail Fig. B.1.

Electrons and all-lepton spectrum for the models employed in this work, compared to available experimental data.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.