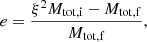| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | L14 | |
| Number of page(s) | 11 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202245796 | |
| Published online | 09 February 2023 | |
Letter to the Editor
A neutron star candidate in the long-period binary 56 UMa
1
European Southern Observatory, Alonso de Córdova 3107, Vitacura, Santiago, Chile
e-mail: ana.escorza@eso.org
2
Department of Physics, University of Calicut, Thenhipalam, Malappuram 673635, India
3
Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles, ULB, Campus Plaine C.P. 226, Boulevard du Triomphe, 1050 Bruxelles, Belgium
4
USRA, 7178 Columbia Gateway Drive, Columbia, 21046 MD, USA
5
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
6
Institute of Astronomy, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
Received:
24
December
2022
Accepted:
16
January
2023
Context. 56 UMa is a wide binary system that contains a chemically peculiar red giant and a faint companion. Due to its surface chemical abundances, the red giant was classified as a barium (Ba) star. This implies that the companion has to be a white dwarf, since Ba stars form when mass is transferred to them from an s-process rich Asymptotic Giant Branch (AGB) star. However, in the case of 56 UMa, the companion might be too massive to be the progeny of an AGB star that efficiently produced s-process elements such as barium.
Aims. In this Letter, we revisit the orbital parameters of the system and perform a full spectral analysis with the goal of investigating the Ba-star classification of the giant and unravelling the nature of its faint companion.
Methods. We combined radial-velocity and astrometric data to refine the orbital parameters of the system, including the orbital inclination and the companion mass. Then, we re-determined the stellar parameters of the giant and its chemical abundances using high-resolution HERMES spectra. Finally, we investigated the morphology of the interstellar gas in the vicinity of the system.
Results. The faint component in 56 UMa has a mass of 1.31 ± 0.12 M⊙, which, together with the mixed s + r abundance profile of the red giant, confirms that the giant is not a standard barium star. Additionally, the clear identification of a cavity surrounding 56 UMa could indicate that a supernova explosion occurred about 105 years ago in the system, suggesting that the faint companion might be a neutron star. However, finding an evolutionary scenario that explains all the observables is not trivial, so we discuss different possible configurations of the system and their respective merits.
Key words: binaries: spectroscopic / astrometry / stars: late-type / white dwarfs / stars: neutron / stars: abundances
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
56 Ursae Majoris (also known as 56 UMa, HD 98839, or HIP 55560) is a binary system that contains a G8-type giant and a faint lower-mass companion (Keenan & McNeil 1989). The giant was identified as a mild barium (Ba) star by Keenan & Wilson (1977). Ba stars are chemically peculiar stars that show an overabundance of carbon and elements formed by the slow-neutron-capture (s-) process of nucleosynthesis (Bidelman & Keenan 1951), which mostly operates in the interiors of Asymptotic Giant Branch (AGB) stars (e.g., Lugaro et al. 2003; Cristallo et al. 2009; Karakas 2010). Ba stars form when an AGB star transfers enriched material to a companion in a binary system (McClure et al. 1980). According to this scenario, the donors in these systems evolved off the AGB long ago and are now dim white dwarfs (WDs).
Even though the Ba-star classification of the giant star in 56 UMa has been debated (e.g., Keenan & McNeil 1989; Lu 1991; Griffin 1996; Karinkuzhi et al. 2018), and its high luminosity and mass made it an outlier among Ba giants (Jorissen et al. 2019), the nature of its companion has not been extensively discussed. Böhm-Vitense et al. (1984) noticed that the International Ultraviolet Explorer (IUE) spectrum of 56 UMa showed two weak emission lines at 147.4 and 166.8 nm, likely due to the N IV] and O III] semi-forbidden lines. They proposed that these lines arise from an extended region of high-temperature, low-density gas coming from a small, hot source in the system, and suggested that this source might be a massive WD. However, it is interesting to note that the same lines arise in the hot gas surrounding accreting neutron stars (NSs; Anderson et al. 1994; Castro Segura et al. 2022).
At the location of 56 UMa, there is also a strong detection in the GALEX (Galaxy Evolution Explorer) far-UV band (153 nm), at the level of 7.66 × 10−5 Jy (GALEX-DR5; Bianchi et al. 2011). This is comparable with the 6.09 × 10−6 Jy measured at 212 nm (XMM-SUSS5.0; Page et al. 2012) for the closest (120 pc) NS to Earth, RX J1856.5−3754 (Walter et al. 2010). 56 UMa is located at 170 pc (Lindegren et al. 2021). Finally, in a study of coronal X-ray emission in late-type giants, Gondoin (1999) reports an X-ray luminosity of LX = 1.07 × 1029 erg s−1 for 56 UMa. This could be ascribed to coronal emission or to X-ray emission associated with a NS. Neutron stars are observed to have masses between 1.2 and 2.35 M⊙ (Romani et al. 2022) and typically emit at radio and X-ray wavelengths when they are young and rapidly rotating. As they age, their rotation slows down and their emission fades, unless they are fuelled by mass transfer from a companion. Neutron stars not powered by accretion are difficult to detect and, therefore, very rarely observed (Mazeh et al. 2022).
Here, we revisit the stellar and orbital parameters of 56 UMa (Sect. 2), the stellar properties of the giant component (Sect. 3), and its heavy-element abundances (Sect. 4). We show possible evidence of a supernova explosion in the system (Sect. 5), and we discuss different evolutionary scenarios compatible with these observations (Sect. 6), including the possibility that the faint component of 56 UMa is a NS.
2. Orbital parameters and companion mass
In order to obtain the orbital parameters of 56 UMa, we fit a Keplerian orbital model to the available radial-velocity (RV) and astrometric data. We used CAMCOR (Coravel at the Cambridge 36-inch telescope; Griffin 2008) and HERMES (High-Efficiency and high-Resolution Mercator Echelle Spectrograph; Raskin et al. 2011; Jorissen et al. 2019) RV data, the positions and proper motions provided by the HIPPARCOS catalogue (ESA 1997; Perryman et al. 1997) and the Gaia Early Data Release 3 (EDR3; Gaia Collaboration 2021; Lindegren et al. 2021), the individual astrometric measurements from the re-reduction of the HIPPARCOS intermediate astrometric data (van Leeuwen 2007) and the HIPPARCOS-Gaia Catalogue of Accelerations (HGCA; Brandt 2018, 2021). We used the code ORVARA, developed by Brandt et al. (2021), to exploit the combinations of these datasets. ORVARA fits a single Keplerian model to the datasets described above, employing a parallel-tempering Markov chain Monte Carlo minimisation routine (PTMCMC; Foreman-Mackey et al. 2013). We fit ten parameters: the six Keplerian orbital elements, the masses of the two components and a RV jitter per instrument to be added to the RV uncertainties. We assumed uninformative priors for the orbital elements and the faint companion mass, but we adopted a Gaussian prior of 4.3 ± 0.6 M⊙ (Jorissen et al. 2019) for the primary mass (we used a 3σ uncertainty to account for systematic errors in the mass determination) and another Gaussian prior for the parallax that corresponded to the EDR3 value. The results are presented in Table 1.
Stellar and orbital parameters of the 56 UMa system.
Figure 1 shows the fit to the RV data and to the HIPPARCOS and Gaia proper motions, and Fig. A.1 shows a corner plot with some derived parameters. The system is in an orbit of about 46 years and has a significant eccentricity of 0.56. Our joint RV and astrometric fit yields orbital parameters that are compatible with the results published by Jorissen et al. (2019). Additionally, for the first time, we constrained the inclination to 67.5 ± 4° and the secondary mass to 1.31 ± 0.12 M⊙. This mass estimate, which is compatible with the value estimated by Kervella et al. (2019) from the proper motion anomaly only, raises three issues: (i) the companion mass is surprisingly high for WDs and close to the Chandrasekhar mass (Chandrasekhar 1939); (ii) in the context of Ba stars, this WD would be significantly more massive than any other Ba-star companion (see Escorza & De Rosa 2023); and (iii) the AGB progenitor of such a WD would be at the upper end of intermediate-mass stars, where the s-process is predicted to be fairly inefficient (Käppeler et al. 2011). Alternatively, this high mass is compatible with the mass of a NS.
 |
Fig. 1. Fits to the RV curve (left) and the HIPPARCOS and Gaia proper motions (middle and right) of 56 UMa. The black line is the orbit with the maximum likelihood, and 40 additional well-fitting solutions are included, colour-coded as a function of companion mass. |
3. Constraining the primary mass
Given the strong correlation between the primary and secondary masses (see Fig. A.1) and the fact that we used a prior for the primary mass, we re-evaluated this value. To do this, we co-added 27 high-resolution (R = 86 000) HERMES (Raskin et al. 2011) spectra to first recalculate the stellar parameters of the giant. The signal-to-noise ratio (S/N) of the co-added spectrum was about 500, and the stellar parameters were derived using the Brussels Automatic Code for Characterizing High accUracy Spectra (BACCHUS) in a semi-automated mode (Masseron et al. 2016). BACCHUS uses interpolated MARCS model atmospheres (Gustafsson et al. 2008) and the 1D local thermodynamical equilibrium (LTE) spectrum-synthesis code TURBOSPECTRUM (Plez 2012). It computes abundances using equivalent widths or spectral synthesis, allowing excitation and ionization equilibria to be checked for, thereby constraining Teff and log g. It also calculates the microturbulence velocity (ξ) by ensuring consistency between the Fe abundances derived from lines of various equivalent widths. We adopted solar abundances from Asplund et al. (2009) and the line lists assembled in the framework of the Gaia-ESO survey (Heiter et al. 2015; Heiter 2020).
Our analysis confirms the stellar parameters derived by Jorissen et al. (2019) and the updated results are listed in Table 1. Our results are also in agreement with those previously derived by other authors (Table B.1). A luminosity of L = 332 L⊙ was also derived by Jorissen et al. (2019) by integrating the spectral energy distribution of the star and using the Gaia Data Release (DR) 2 parallax (5.87 ± 0.19 mas; Gaia Collaboration 2018), following Escorza et al. (2017). The Gaia DR2 parallax is in agreement with its re-evaluation in DR3 (5.88 ± 0.093 mas, Lindegren et al. 2021). With the latter as an input, our Markov chain Monte Carlo (MCMC) optimisation converges to 5.86 ± 0.04 mas (Table 1), so the luminosity quoted above remains valid.
Once Teff and L are confirmed, the evolutionary mass of the giant can be revisited. Jorissen et al. (2019) obtained it by comparing its location in the Hertzsprung–Russell diagram (HRD) with solar-metallicity tracks from STAREVOL (Siess et al. 2000; Siess 2006). However, evolutionary tracks differ from one another depending on the prescriptions used for overshooting, rotation, mass loss, and so on. The right panel of Fig. 2 shows a comparison between STAREVOL, Geneva (Ekström et al. 2012) and Padova (Girardi et al. 2000) models of solar metallicity (Z⊙ = 0.0134, 0.014, and 0.019, respectively) and demonstrates that a range from 4 to 5 M⊙ is suitable for the red giant, independently of the used models. That range for the primary mass implies a range from 1.1 to 1.5 M⊙ for the companion.
 |
Fig. 2. Location of 56 UMa in the HRD. On the left, we included STAREVOL solar-metallicity tracks, and on the right, we compared STAREVOL (solid lines), Geneva (dot-dashed lines) and Padova (dashed lines) tracks for 3, 4 and 5 M⊙ stars. |
4. Chemical abundance profile of the red giant
To investigate the origin of the chemical enrichment of the giant, we derived its chemical abundances, including the abundances for 14 heavy elements, some of which are predominantly produced by the s-process, some by the r-process, and some by both. The atomic lines we used, including hyperfine (HF) splitting when available, are listed in Table C.1.
The abundances of four s-process elements (Y, Zr, La, and Ce) were published by Jorissen et al. (2019), but we present a new analysis that uses the co-added spectrum with a higher S/N. The measured abundances and the non-LTE corrections, when available, are listed in Table D.1. A non-LTE correction of 0.19 dex, corresponding to the atmospheric parameters of the Sr I line, was adopted from Bergemann et al. (2012). Table D.2 lists the sensitivity of the abundances to variations in the atmospheric parameters (determined following Karinkuzhi et al. 2018). Figure D.1 shows the fit to a few heavy-element lines.
56 UMa has a (moderate) enhancement in s-process elements, consistent with its mild Ba-star classification, but also an unexpected r-process enhancement. A small group of carbon-enriched metal-poor (CEMP) stars are known to have such a hybrid (s + r) profile (Karinkuzhi et al. 2021a), but contrarily to these CEMP-rs stars, 56 UMa has a solar metallicity and a solar C/O ratio. The left panel of Fig. 3 shows the location of 56 UMa in the [La/Fe]–[Eu/Fe] plane compared to the CEMP stars studied by Karinkuzhi et al. (2021a). Additionally, we computed an abundance distance, d, from the solar r-process abundance pattern, which is described in Appendix E. The r-process was adopted as reference because, although it shows some variations (Goriely & Arnould 1997; Roederer 2011), it appears less sensitive to its operating conditions (metallicity, radiative or convective environment, mixing of protons into the C-rich intershell, etc.) than the s-process. The abundance distance, d, allowed us to discern whether the star abundance profile is pure r (d < 0.25), predominantly s (d > 0.6), or hybrid s + r (0.25 < d < 0.6) as defined by Karinkuzhi et al. (2021a). 56 UMa, with d = 0.54, falls among the CEMP-rs objects (right panel of Fig. 3). Karinkuzhi et al. (2021a) showed that AGB nucleosynthesis may account for such a mixed s + r profile, but only at low metallicity. To our knowledge, 56 UMa is the first object at solar metallicity that shows an enrichment of both s- and r-process origin.
 |
Fig. 3. 56 UMa compared to the CEMP stars from Karinkuzhi et al. (2021a). Left: [La/Fe]–[Eu/Fe] plane, where the dashed green line corresponds to a pure solar r-process, and the continuous blue line to s-process predictions. Right: histograms of the abundance distance d (Appendix E) of 56 UMa and the reference stars. The vertical dashed line at d = 0.6 marks the threshold adopted between CEMP-s and CEMP-rs stars. |
5. A neutral hydrogen cavity
We also investigated the morphology of the interstellar gas in the vicinity of 56 UMa. Figure 4 shows an integrated λ21 cm map of neutral atomic hydrogen in Galactic coordinates, centred on 56 UMa for H I with velocities between ±25 km s−1 (the center-of-mass velocity of 56 UMa is 0.13 km s−1; Table 1). The data are from the HI4PI survey (HI4PI Collaboration 2016), which has an angular resolution of ΘFWHM = 16′2, a sensitivity of σ = 43 mK, and full spatial sampling of 5′ in both Galactic longitude and latitude.
 |
Fig. 4. Galactic-coordinate map of H I at λ 21 cm integrated between ±25 km s−1 and centred on 56 UMa. The arrow corresponds to the motion of the star over the last 105 yr (Schmelz & Verschuur 2022), and was derived from the orbital solution (Table 1). Colour bar units are kelvins. |
While there is complex structure in the area, the image shows a clear absence of emission, a cavity, surrounding 56 UMa, although the star is not exactly at its centre. Schmelz & Verschuur (2022) propose that this cavity is associated with the remnant of a SN that exploded about 105 years ago. Its rim is steepest in the lower-right quadrant, where we have the clearest view of the material that may have piled up during the snow-plough phase. The minimum column density is found at Galactic coordinates l, b = 170.67, 62.42 is 6.5 × 1018 cm−2, and there is also about 1.2 M⊙ (Schmelz & Verschuur 2022) of low-velocity gas in the cavity that could be associated with mass lost by the giant after the explosion. The clear identification of this cavity is only possible because it is within the Local Chimney (Lallement et al. 2003), a low-density extension of the Local Bubble (Zucker et al. 2022) that stretches from the solar neighbourhood to the Galactic halo.
The unseen companion of 56 UMa has traditionally been identified as a WD, but if it were a NS, it could be the remains of the SN that evacuated the MI cavity and blasted MI itself outwards at 120 km s−1 (Schmelz & Verschuur 2022). Then, one might expect to find evidence for high energy emission, as was indeed found by ROSAT as diffuse 1/4 keV X-rays in the lower-left half of the cavity, the area of the lowest H I emission (Herbstmeier et al. 1995; Schmelz & Verschuur 2022).
6. Summary, discussion and conclusions
We have presented the orbital, stellar, and chemical properties of the wide binary system 56 UMa and determined the mass of the unseen component to be 1.31±0.12 M⊙, which is compatible with both a WD and a NS. In the remainder of this section, we discuss the possible configurations of the system along with their pros and cons.
-
The faint companion could be a 1.3 M⊙ WD, implying an AGB progenitor of a rather high mass, of the order of 6 M⊙ (Marigo et al. 2022). However, massive AGB stars are not expected to be efficient enough s-process producers (Käppeler et al. 2011) to account for the observed barium overabundance. Additionally, the lack of rubidium overabundance, which is considered the major signature of super-AGB nucleosynthesis (García-Hernández et al. 2006; Doherty et al. 2017), is also an argument against this scenario. A new exploration of the nucleosynthesis parameter space could add to this discussion. Finally, this scenario would require the observed H I cavity to have been created by an AGB (super-)wind or by a last-thermal pulse ejection event that produced a shock wave that cleared out the accumulated material around the AGB star. However, we would then need to understand why not all AGB stars are surrounded by interstellar medium cavities. As already mentioned, this cavity was discovered only because it is in a low-density environment, and such favourable conditions probably do not occur for each AGB star. An alternative option is that the cavity is not associated with any of the components of the 56 UMa system, given its off-centre location.
-
The companion could be a close pair formed by two low-mass stars (e.g., van den Heuvel & Tauris 2020). If they were both main-sequence stars, mass transfer could not explain the peculiar abundances of the giant. Therefore, at least one companion must be an evolved star, a WD. Assuming we can extrapolate the stability criterion discussed by Tokovinin (2014) to this more evolved system, the ratio between the two periods must be higher than 4.7. If 56 UMa were a triple system, the inner orbit would have to be shorter than 3600 days. Most Ba stars are in orbits below that threshold (Jorissen et al. 2019; Escorza et al. 2019), so that period should give enough space for an AGB star to evolve. A problem in this scenario is that this WD must still originate from a star more massive than the initial mass of the current primary, so we cannot circumvent the difficulties listed for the previous scenario.
-
The faint companion could be a NS. This scenario can explain the cavity better than the previous ones; however, the SN rate in the Milky Way is estimated to be one to two every 100 yr (e.g., Rozwadowska et al. 2021), so the probability of such an event occurring within 170 pc of Earth and within 105 yr is very low. Even if we spotted such an event, the fact that the system is bound, yet very eccentric, together with the current location of the giant on the HRD require dynamical and evolutionary fine-tuning. We estimate that for this scenario to work, it would require an asymmetric explosion, with a small associated kick opposite to the orbital motion, in order to match the mass budget imposed by the evolutionary timescales (see Appendix F). Schmelz & Verschuur (2022) suggest that the SN exploded about 105 yrs ago, and the Padova isochrones (Bressan et al. 2012) predict that a solar-metallicity 8 M⊙ star would reach carbon ignition at an age of 40 Myr. At that age, a 4.3 M⊙ star (the current mass of the giant) would still be on the main sequence, which is incompatible with its current status. A possible way to solve this tension is to assume that the initial masses of the two components were almost equal, and that the SN blast removed a couple of solar masses from the current red giant envelope. Leigh et al. (2016) show, however, that red giant stars must be nearly completely stripped for their luminosity to change significantly. Hence, 56 UMa should have kept a luminosity typical of a 7–8 M⊙ star, which it did not (Fig. 2). Additionally, numerical simulations of SN explosions in binaries (Hirai et al. 2014) indicate that there is no mixing between the SN ejecta and the companion material, so the SN would leave no chemical imprint on the surviving companion. Thus, the chemical peculiarities detected on the giant remain unexplained in this scenario too.
We conclude that none of the potential scenarios can explain all observables, and we cannot yet pin down the nature of the faint companion in 56 UMa. A crucial ingredient is whether or not the H I cavity is a SN remnant associated with 56 UMa. Even if it is not, the massive chemically peculiar giant in combination with the massive unseen companion is difficult to reconcile with stellar evolution. We stress that the chemistry in 56 UMa, bearing imprints from both the s- and r-process of nucleosynthesis, is the first such star at solar metallicity. This system provides a strong test for binary evolution.
Acknowledgments
We thank N. Chamel, L. Siess and S. Goriely for the useful discussions. The HERMES spectrograph is supported by the Fund for Scientific Research of Flanders (FWO), the Research Council of KU Leuven, Belgium, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), the Royal Observatory of Belgium, the Observatoire de Genève, and the Thüringer Landessternwarte Tautenburg. This work makes use of SIMBAD, operated at CDS, Strasbourg, and of data from the European Space Agency (ESA), processed by the Gaia Data Processing and Analysis Consortium (DPAC).
References
- Anderson, S. F., Wachter, S., Margon, B., et al. 1994, ApJ, 436, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., Hansen, C. J., Bautista, M., & Ruchti, G. 2012, A&A, 546, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, L., Herald, J., Efremova, B., et al. 2011, Ap&SS, 335, 161 [Google Scholar]
- Bidelman, W. P., & Keenan, P. C. 1951, ApJ, 114, 473 [Google Scholar]
- Böhm-Vitense, E., Nemec, J., & Proffitt, C. 1984, ApJ, 278, 726 [CrossRef] [Google Scholar]
- Brandt, T. D. 2018, ApJS, 239, 31 [Google Scholar]
- Brandt, T. D. 2021, ApJS, 254, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., Dupuy, T. J., Li, Y., et al. 2021, AJ, 162, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Castro Segura, N., Knigge, C., Long, K. S., et al. 2022, Nature, 603, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1939, An Introduction to the Study of Stellar Structure (Chicago: University of Chicago Press) [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Doherty, C. L., Gil-Pons, P., Siess, L., & Lattanzio, J. C. 2017, PASA, 34, e056 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues (ESA) [Google Scholar]
- Escorza, A., & De Rosa, R. J. 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202244782 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Escorza, A., Boffin, H. M. J., Jorissen, A., et al. 2017, A&A, 608, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Escorza, A., Karinkuzhi, D., Jorissen, A., et al. 2019, A&A, 626, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feuillet, D. K., Bovy, J., Holtzman, J., et al. 2016, ApJ, 817, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Hernández, D. A., García-Lario, P., Plez, B., et al. 2006, Science, 314, 1751 [Google Scholar]
- Gessner, A., & Janka, H.-T. 2018, ApJ, 865, 61 [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gondoin, P. 1999, A&A, 352, 217 [NASA ADS] [Google Scholar]
- González Hernández, J. I., & Bonifacio, P. 2009, A&A, 497, 497 [Google Scholar]
- Goriely, S., & Arnould, M. 1997, A&A, 322, L29 [Google Scholar]
- Griffin, R. F. 1996, The Observatory, 116, 398 [NASA ADS] [Google Scholar]
- Griffin, R. F. 2008, The Observatory, 128, 176 [NASA ADS] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U. 2020, IAU General Assembly, 458–462 [Google Scholar]
- Heiter, U., Lind, K., Asplund, M., et al. 2015, Phys. Scr., 90, 054010 [Google Scholar]
- Herbstmeier, U., Mebold, U., Snowden, S. L., et al. 1995, A&A, 298, 606 [NASA ADS] [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirai, R., Sawai, H., & Yamada, S. 2014, ApJ, 792, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A. 2002, ApJS, 139, 219 [Google Scholar]
- Jorissen, A., Boffin, H. M. J., Karinkuzhi, D., et al. 2019, A&A, 626, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käppeler, F., Gallino, R., Bisterzo, S., & Aoki, W. 2011, Rev. Mod. Phys., 83, 157 [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Karinkuzhi, D., Van Eck, S., Jorissen, A., et al. 2018, A&A, 618, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karinkuzhi, D., Van Eck, S., Goriely, S., et al. 2021a, A&A, 645, A61 [EDP Sciences] [Google Scholar]
- Karinkuzhi, D., Van Eck, S., Jorissen, A., et al. 2021b, A&A, 654, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keenan, P. C., & McNeil, R. C. 1989, ApJS, 71, 245 [Google Scholar]
- Keenan, P. C., & Wilson, O. C. 1977, ApJ, 214, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019, A&A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Welsh, B. Y., Vergely, J. L., Crifo, F., & Sfeir, D. 2003, A&A, 411, 447 [EDP Sciences] [Google Scholar]
- Lèbre, A., de Laverny, P., Do Nascimento, J. D., Jr., & de Medeiros, J. R. 2006, A&A, 450, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leigh, N. W. C., Antonini, F., Stone, N. C., Shara, M. M., & Merritt, D. 2016, MNRAS, 463, 1605 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Lu, P. K. 1991, AJ, 101, 2229 [CrossRef] [Google Scholar]
- Lugaro, M., Herwig, F., Lattanzio, J. C., Gallino, R., & Straniero, O. 2003, ApJ, 586, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Bossini, D., Trabucchi, M., et al. 2022, ApJS, 258, 43 [NASA ADS] [Google Scholar]
- Masseron, T., Merle, T., & Hawkins, K. 2016, Astrophysics Source Code Library [record ascl: 1605.004] [Google Scholar]
- Mazeh, T., Faigler, S., Bashi, D., et al. 2022, MNRAS, 517, 4005 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, R. D., Fletcher, J. M., & Nemec, J. M. 1980, ApJ, 238, L35 [Google Scholar]
- Page, M. J., Brindle, C., Talavera, A., et al. 2012, MNRAS, 426, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 500, 501 [NASA ADS] [Google Scholar]
- Plez, B. 2012, Astrophysics Source Code Library [record ascl: 1205.004] [Google Scholar]
- Postnov, K. A., & Yungelson, L. R. 2014, Liv. Rev. Relat., 17, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [CrossRef] [EDP Sciences] [Google Scholar]
- Roederer, I. 2011, ApJ, 732, L17 [CrossRef] [Google Scholar]
- Romani, R. W., Kandel, D., Filippenko, A. V., Brink, T. G., & Zheng, W. 2022, ApJ, 934, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Rozwadowska, K., Vissani, F., & Cappellaro, E. 2021, New Astron., 83, 101498 [NASA ADS] [CrossRef] [Google Scholar]
- Schmelz, J. T., & Verschuur, G. L. 2022, ApJ, 938, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L. 2006, A&A, 448, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Takeda, Y., Sato, B., & Murata, D. 2008, PASJ, 60, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. 2014, AJ, 147, 87 [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J., & Tauris, T. M. 2020, Science, 368, eaba3282 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [CrossRef] [EDP Sciences] [Google Scholar]
- Walter, F. M., Eisenbeiß, T., Lattimer, J. M., et al. 2010, ApJ, 724, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, C., Goodman, A. A., Alves, J., et al. 2022, Nature, 601, 334 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: MCMC corner plot
Figure A.1 shows the 1D and 2D projections of the posterior probability distributions of the masses of the two stellar components in 56 UMa (Mprim corresponds to the red giant and Msec, to the faint companion) and a few orbital parameters (semi-major axis, a, eccentricity, e, and inclination, i) from the joint RV and astrometric MCMC fit (Sect. 2). The plot shows that the two masses are correlated, and that the semi-major axis is also correlated with the total mass of the system.
 |
Fig. A.1. MCMC corner plot. |
Appendix B: Literature parameters for 56 UMa
Atmospheric parameters (effective temperature, Teff, surface gravity, log g, metallicity, [Fe/H] and microturbulence, ξ) for 56 UMa collected from the literature.
We collected from the literature the atmospheric parameters derived for the giant star in 56 UMa over the past two decades. We list them in Table B.1 ordered by decreasing Teff.
Appendix C: Spectral line list
Table C.1 presents the lines used in the present abundance analysis.
Spectral lines used in the abundance analysis.
Appendix D: Individual abundances and their uncertainties
Table D.1 lists the measured individual abundances along with non-LTE corrections when available, and Table D.2 lists the sensitivity of these abundances to variations in the atmospheric parameters. Figure D.1 shows the spectral fit for a few heavy-element lines.
The abundance uncertainties were calculated for all elements using the methodology described in Karinkuzhi et al. (2021a,b). Following Eq. 2 from Johnson (2002), the uncertainties on the elemental abundances log ϵ were calculated as:
where σT, σlog g, and σξ are the typical uncertainties on the atmospheric parameters. These values are estimated as σT = 34 K, σlog g = 0.6 dex, and σξ = 0.05 km/s. The uncertainty on metallicity was estimated as σ[Fe/H] = 0.12 dex. The partial derivatives that appear in Eq. D.1 were evaluated by varying the atmospheric parameters Teff, log g, microturbulence (ξ), and [Fe/H] by 100 K, 0.5, 0.5 km/s, and 0.5 dex, respectively. The covariances σT, log g, σlog g, ξ, and σξ, T were derived using the same method as given by Johnson (2002). In order to calculate σT, log g, we varied the temperature while fixing metallicity and microturbulence, and determined the log g value required for ensuring the ionisation balance. Then, using Eq. 3 of Johnson (2002), we derived the covariance, σT, log g, and find a value of 23. Similarly, we find σlog g, ξ = 0.01 and σξ, T = 83.
 |
Fig. D.1. Spectral fitting of La II, Ce II, Nd II and Eu II. Red curves correspond to spectral syntheses with the adopted abundances for these elements, as listed in Table D.1. Blue and green curves correspond to syntheses with abundances deviating by ± 0.3 dex from the adopted abundance. The dashed black line represents the observed spectrum. The magenta line corresponds to the synthesis with a null abundance for the corresponding element. |
Individual abundances of the giant component in 56 UMa
Sensitivity of the abundances (Δlog ϵX) to variations in the atmospheric parameters.
The random error, σran, is the line-to-line scatter. For elements for which we used more than four lines to derive the abundances, we adopted σran = σl/N1/2, where σl is the standard deviation of the abundances derived from all the N lines of the considered element. For the elements for which fewer numbers of lines were used to derive the abundances, we selected a σran value as described in Karinkuzhi et al. (2021a). The final error on [X/Fe] was derived as
where σX, Fe was calculated using Eq. 6 from Johnson (2002) with the additional term ![$ \left(\frac{\partial \log\epsilon}{\partial \mathrm{[Fe/H]}}\right) $](/articles/aa/full_html/2023/02/aa45796-22/aa45796-22-eq13.gif) included.
included.
Appendix E: The abundance distance, d
In order to characterise in more detail the abundance profile of 56 UMa, we computed an abundance distance from the solar r-process abundance pattern following Karinkuzhi et al. (2021a). We used seven chemical elements (Y, Zr, Ba, La, Ce, Nd, and Sm), instead of only two as in Karinkuzhi et al. (2021a), to compute the abundance distance from the solar r-process abundance pattern. We also used Eu as the normalising element between the reference r-process abundance profile and the abundance profile of our target, because it is formed mainly via the r-process and is easily measurable in most stars.
The distance, d, was defined as follows by Karinkuzhi et al. (2021a):
where {x1...xN} is the list of the N considered heavy elements, and we use the usual notation log10ϵxi = log10(nxi/nH)+12, with nxi the number density of element xi. We denote as log10ϵxi, * the abundance of element xi as measured for 56 UMa (Table D.1), and log10 ϵxi,norm(r,*), the standard r-process abundance profile log ϵxi, r normalised to the star abundance profile with respect to europium:
The adopted r-process abundances, log ϵxi, r, are listed in Karinkuzhi et al. (2021a). We find d = 0.54 for 56 UMa.
When adopting instead the RMS distance as defined in Karinkuzhi et al. (2021a),
we find dRMS = 0.63, well within the bulk of the RMS distances of hybrid-profile stars such as CEMP-rs objects.
Appendix F: Exploding stars in binary systems
We followed Postnov & Yungelson (2014) and used the fact that the SN explosion in 56 UMa did not unbind the system to set constraints on the initial masses. We adopt the subscript ‘p’ for the current primary star, the giant, and ‘s’ for the NS and its progenitor. Assuming an initially circular orbit, a product of strong tidal circularisation, and a symmetric explosion (no kick imparted on the NS), the mass ejected by the explosion, ΔMs, must fulfil the following relation for the system to remain bound:
This expression, only valid for a symmetric explosion, is the equivalent to imposing that the post-explosion eccentricity,
is smaller than unity (Eq. 51 in Postnov & Yungelson (2014)).
Schmelz & Verschuur (2022) suggest that the red giant has ejected 1.2 M⊙ since the explosion of its companion via wind mass loss (visible as a hydrogen feature close to 56 UMa in Fig. 4). Hence, plugging Mp, f = 5.5 M⊙ (the currently measured 4.3 M⊙ plus the 1.2 M⊙ ejected via wind mass loss), Ms, f = 1.3 M⊙, and the measured eccentricity of 0.562 (Table 1) into Eq. F.2, we obtain ΔMs = 3.8 M⊙, which is not enough considering that a star needs to have a mass of at least 8 M⊙ to explode as a SN.
Since the discrepancy clearly indicates that the above picture is far too simple, we considered how an asymmetric SN explosion and its associated kick can modify the orbital eccentricity of a system. Again, according to Postnov & Yungelson (2014) (Eqs. 46-47),
with
where χ = (Mp, i + Ms, i)/(Mp, f + Ms, f). The kick velocity imparted to the NS is expressed as (wx, wy, wz) in an instantaneous reference frame centred on the primary star (the companion to the exploding star), with the x-axis directed from the primary to the secondary, the y-axis pointing in the direction of the relative pre-SN orbital velocity, Vi, of the primary around the secondary (the NS star), and the z-axis perpendicular to the orbital plane. In this frame, the pre-SN relative velocity is Vi = (0, Vi, 0), where Vi = (G(Mp, i+Ms, i)/ai)1/2.
It is easy to show that if the kick imparted to the NS by the asymmetric explosion is along the orbital motion, thus of the form (0, wy, 0), the post-explosion eccentricity is
where Mtot, i and Mtot, f are the initial and final total mass in the system, and with ξ = (Vi + wy)/Vi. Thus, a kick with wy < 0 and wx = wz = 0 has the same effect as reducing the effective initial mass by a factor ξ2.
As discussed in Sect. 6, the evolutionary timescales give important constraints. The two stars must have had similar initial masses for the current giant to be a giant. If it ejected 1.2 M⊙ since the explosion, and the stars were initially of almost equal mass, there would be an extra 2 M⊙ that had to have been blown away by the passing SN remnant (Hirai et al. 2014).
In summary, we reach the following picture: Mp, f = 5.5 M⊙ for the giant companion just after the explosion (currently 4.3 M⊙) and Ms, f = 1.3 M⊙ for the NS, or Mtot, f = 6.8 M⊙. Along with the eccentricity of 0.562, this yields ξ2Mtot, i = 1.562 Mtot, f = 10.62 M⊙. If Ms, i = 8 M⊙ and Mp, i = 7.5 M⊙, Mtot, i = 15.5 M⊙, so ξ2 = 0.685 or wy = −0.17 Vi ∼ 6 km/s, a value compatible with simulations of electron-capture SNe (e.g. Gessner & Janka 2018). With these values, Eq. F.4 moreover predicts ai = 10 AU, thus leaving enough room for the NS progenitor to reach the SN stage without filling its Roche lobe.
Finally, we wanted to estimate if the energy of the explosion was enough to unbind 2 M⊙. If at the time of the explosion the core of the giant star had a radius of 58 R⊙, then the energy needed to unbind 2 M⊙ from such a giant star would be ∼7.2 1047 erg, of the order of the energy budget of a typical type II SN (1051 erg, translated to 7.2 1047 erg considering the dilution factor (Rg/ai)2 with Rg ∼ 58 R⊙ and ai ∼ 10 au, according to Eq. F.4).
All Tables
Atmospheric parameters (effective temperature, Teff, surface gravity, log g, metallicity, [Fe/H] and microturbulence, ξ) for 56 UMa collected from the literature.
Sensitivity of the abundances (Δlog ϵX) to variations in the atmospheric parameters.
All Figures
 |
Fig. 1. Fits to the RV curve (left) and the HIPPARCOS and Gaia proper motions (middle and right) of 56 UMa. The black line is the orbit with the maximum likelihood, and 40 additional well-fitting solutions are included, colour-coded as a function of companion mass. |
| In the text | |
 |
Fig. 2. Location of 56 UMa in the HRD. On the left, we included STAREVOL solar-metallicity tracks, and on the right, we compared STAREVOL (solid lines), Geneva (dot-dashed lines) and Padova (dashed lines) tracks for 3, 4 and 5 M⊙ stars. |
| In the text | |
 |
Fig. 3. 56 UMa compared to the CEMP stars from Karinkuzhi et al. (2021a). Left: [La/Fe]–[Eu/Fe] plane, where the dashed green line corresponds to a pure solar r-process, and the continuous blue line to s-process predictions. Right: histograms of the abundance distance d (Appendix E) of 56 UMa and the reference stars. The vertical dashed line at d = 0.6 marks the threshold adopted between CEMP-s and CEMP-rs stars. |
| In the text | |
 |
Fig. 4. Galactic-coordinate map of H I at λ 21 cm integrated between ±25 km s−1 and centred on 56 UMa. The arrow corresponds to the motion of the star over the last 105 yr (Schmelz & Verschuur 2022), and was derived from the orbital solution (Table 1). Colour bar units are kelvins. |
| In the text | |
 |
Fig. A.1. MCMC corner plot. |
| In the text | |
 |
Fig. D.1. Spectral fitting of La II, Ce II, Nd II and Eu II. Red curves correspond to spectral syntheses with the adopted abundances for these elements, as listed in Table D.1. Blue and green curves correspond to syntheses with abundances deviating by ± 0.3 dex from the adopted abundance. The dashed black line represents the observed spectrum. The magenta line corresponds to the synthesis with a null abundance for the corresponding element. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \sigma ^{2}_{\rm tot}&=\sigma ^{2}_{\rm ran} \;+\; \left(\frac{\partial \log \epsilon }{\partial T}\right)^{2}\sigma ^{2}_{T} \;+\; \left(\frac{\partial \log \epsilon }{\partial \log g}\right)^{2}\;\sigma ^{2}_{\log g} \nonumber \\&\;+\; \left(\frac{\partial \log \epsilon }{\partial \xi }\right)^{2}\;\sigma ^{2}_{\xi }\;+\; \left(\frac{\partial \log \epsilon }{\partial \mathrm{[Fe/H]} }\right)^{2}\sigma ^{2}_{\mathrm{[Fe/H]} } \;+\; \nonumber \\&2\bigg [\left(\frac{\partial \log \epsilon }{\partial T}\right) \left(\frac{\partial \log \epsilon }{\partial \log g}\right) \sigma _{T,\log g} \;+\; \left(\frac{\partial \log \epsilon }{\partial \xi }\right) \left(\frac{\partial \log \epsilon }{\partial \log g}\right) \sigma _{\log g, \xi }\nonumber \\&\;+\;\left(\frac{\partial \log \epsilon }{\partial \xi }\right) \left(\frac{\partial \log \epsilon }{\partial T}\right) \sigma _{ \xi , T}\Bigg ], \end{aligned} $$](/articles/aa/full_html/2023/02/aa45796-22/aa45796-22-eq10.gif)
![$$ \begin{aligned} \sigma ^{2}_{\rm [X/Fe]} =\sigma ^{2}_{\rm X} + \sigma ^{2}_{\rm Fe} - 2\;\sigma _{\rm X,Fe}, \end{aligned} $$](/articles/aa/full_html/2023/02/aa45796-22/aa45796-22-eq12.gif)
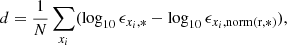
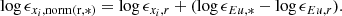
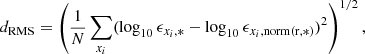
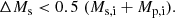
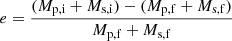
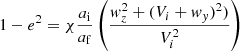
![$$ \begin{aligned} \frac{a_{\rm i}}{a_{\rm f}} = \left[2-\chi \left(\frac{w_x^2+w_z^2+(V_i+w_y)^2)}{V_i^2}\right)\right], \end{aligned} $$](/articles/aa/full_html/2023/02/aa45796-22/aa45796-22-eq20.gif)