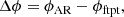| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | L24 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202245312 | |
| Published online | 24 February 2023 | |
Letter to the Editor
Impact of corotation on gradual solar energetic particle event intensity profiles
Jeremiah Horrocks Institute, University of Central Lancashire, Preston PR1 2HE, UK
e-mail: AHutchinson3@uclan.ac.uk
Received:
28
October
2022
Accepted:
30
December
2022
Context. The corotation of particle-filled magnetic flux tubes is generally thought to have a minor influence on the time-intensity profiles of gradual solar energetic particle (SEP) events. For this reason, many SEP models solve the focussed transport equation within the corotating frame, thus neglecting corotation effects.
Aims. We use simulations to study the effects of corotation on gradual SEP intensity profiles at a range of observer longitudinal positions relative to the solar source. We study how corotation affects the duration and decay time constant of SEP events as well as the variation in the peak intensity with the observer’s position.
Methods. We used a 3D full-orbit test particle code with time-extended SEP injection via a shock-like source. In contrast to the case of focussed transport models, the test particle approach enables us to easily switch corotation on and off. While shock acceleration and downstream features are not modelled directly, our methodology allows us to study how corotation and the time-varying observer-shock magnetic connection influence the intensity profiles detected at several observers.
Results. We find that corotation has a strong effect on the SEP intensity profiles for a monoenergetic population of 5 MeV protons, having a dominant influence during the decay phase. Simulations that include corotation display dramatically shortened durations for western events, compared to ones where it is not included. When corotation effects are taken into account, for both eastern and western events, the decay time constant is reduced and its dependence on the value of the scattering mean free path becomes negligible. Corotation reduces the SEP peak intensity for western events and enhances it for eastern ones, thus making the east-west asymmetry in peak intensity stronger, compared to the non-corotation case. Modelling SEP intensity profiles without carefully accounting for the effects of corotation leads to artificially extended decay phases during western events, leading to profiles with a similar shape regardless of the observer’s longitudinal position.
Key words: Sun: particle emission / Sun: coronal mass ejections (CMEs) / Sun: rotation
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Solar energetic particles (SEPs) in the ∼1–10 MeV nuc−1 range in large gradual events are thought to be accelerated at shocks driven by coronal mass ejections (CMEs) as they propagate throughout the corona and interplanetary space. The characteristic long duration decays measured by spacecraft at 1 au are assumed to arise from acceleration at the shock that is extended in time (Cane et al. 1988; Reames et al. 1997; Desai & Giacalone 2016).
Magnetic flux tubes that guide energetic particle propagation corotate with the Sun. Depending on the location of an observing spacecraft, corotation may carry SEP-filled flux tubes either towards or away from the observer. Several authors have pointed out the importance of this effect on SEP intensity profiles for the case of an instantaneous injection at the Sun (Dróge et al. 2010; Giacalone & Jokipii 2012; Marsh et al. 2015; Laitinen et al. 2018). The corotation of steady state and quasi-steady state solar wind structures is the basis of empirical solar wind forecast models (e.g., Owens et al. 2013).
Relatively few studies have commented on the effects of corotation on SEP intensity profiles for the case of time-extended injection at a CME-driven shock. Using an approximate methodology for including corotation within a focussed transport model, Kallenrode & Wibberenz (1997) concluded that it is not very important for events with an injection that is extended in time. Lario et al. (1998) also studied the effect of corotation in a focussed transport model by considering particle injection into a discrete number of flux tubes that sequentially pass over the observer. They noted that for certain periods, corotation could affect their derived injection rate by up to a factor of 1.4. However, they concluded that corotation is not relevant in most situations within 1 au.
Overall, corotation is not thought to play a major role in large gradual SEP events. Possibly as a result, many studies modelling extended SEP shock-like injections solve the relevant equations (usually focussed transport equations) in the corotating frame, neglecting corotation effects (e.g., Wang et al. 2012; He & Wan 2017; Hu et al. 2018).
Although corotation is largely neglected, it is natural to assume it may play a role in the east-west asymmetries found for a number of SEP intensity profile parameters. Several studies of SEP measurements have reported east-west asymmetries. In their study of 35 SEP events, Lario et al. (2013) analysed the longitudinal dependence of peak intensities, finding that the distribution is centred at eastern longitudes. This finding was confirmed by Richardson et al. (2014), who also found east-west asymmetries in proton onset delays and the time to peak intensity.
Ding et al. (2022) investigated the east-west asymmetry in time-averaged fluence and peak intensity by studying multi-spacecraft SEP events and modelling the SEP fluence at ten observer positions using their 2D iPATH model. They concluded that the observed east-west asymmetric distribution can be explained by the combined effect of time-extended shock acceleration and the geometry of interplanetary magnetic field (IMF) lines, as well as determining that slower solar wind speeds and faster CME speeds enhance the east-west asymmetry. Although they stated that corotation is included in their model, its effect on observables was not discussed.
He & Wan (2015) used a 5D focussed transport equation to model SEP propagation from several solar sources separated by 30° longitude. In comparing cases where the separation between the source and the observer’s magnetic footpoint was the same, they found that eastern sources relative to the observer produced systematically larger SEP peak fluxes. They concluded that the east-west azimuthal asymmetry in the IMF and the effects of perpendicular transport lead to the longitudinally asymmetric distribution of SEPs. This conclusion was supported by He & Wan (2017), who investigated 78 solar proton events and found that for the same flare-footpoint separation, the number of solar proton events is greater for eastern solar sources.
An alternative methodology to using focussed transport approaches for describing SEP propagation through interplanetary space consists of using 3D test particle simulations, in which the trajectories of an SEP population of specified initial parameters can be calculated (e.g., Marsh et al. 2013; Dalla et al. 2020; Waterfall et al. 2022). While focussing on different aspects of SEP propagation, the latter studies have all considered instantaneous injections taking place close to the Sun. The results of these simulations (e.g., Marsh et al. 2015; Dalla et al. 2017, 2020) produce time-intensity profiles with a characteristic ordering based on east-west observer longitudes (Cane et al. 1988).
In this paper we study the role of corotation effects in SEP events by means of 3D test particle simulations, with time-extended particle injection, describing continuous acceleration at a CME shock-like source. The test particle approach provides a natural way to describe corotation via the presence of a solar wind electric field, as described below. It is also easy to remove corotation by switching off the electric field.
Rather than a full shock model, we use a concentrically expanding moving shock-like source as an initial approximation. Features of the shock’s downstream region are not modelled. The latter is often characterised by a complicated magnetic configuration, due to the presence of a flux rope (e.g., Zurbuchen & Richardson 2006) and non-Parker magnetic field lines (see e.g., Lario et al. 1998, Fig. 1). A moving shock model similar to ours has previously been used by Kallenrode & Wibberenz (1997) and Wang et al. (2012).
Our simulations show that although the role of corotation is generally ignored in the interpretation of gradual SEP events, it plays a major role in shaping observables and can impact the east-west asymmetries in a variety of parameters. The structure of the paper is as follows. In Sect. 2, we describe our simulations. In Sect. 3, we consider the effect of corotation on intensity profiles. We present the discussion and conclusions in Sect. 4.
2. Simulations
We used a 3D full-orbit test particle code (Marsh et al. 2013) that was modified to describe a temporally extended injection of particles by a shock-like source. We used a model of an outwardly propagating shock, similar to that used by Heras et al. (1994) and Kallenrode & Wibberenz (1997). A full description of the model is given in a companion paper (Hutchinson et al. 2023). We briefly summarise its main features for the purposes of the current work. The shock-like source is a concentrically expanding front of fixed angular width. Shock acceleration and downstream features were not modelled and the front only acts as a particle injector.
Particles are injected at a time, tinj, at a radial distance, rinj = r0 + vshtinj, where r0 is the shock position at t = 0 and vsh is its velocity (assumed to be constant). Particles are injected uniformly across the shock front in both longitude and latitude. The number of particles injected by the shock at a distance, r, with the radial injection profile being R(r), is constant with r for r < rmax, where we assume that the injection stops.
In our simulations, we followed a 5 MeV mono-energetic proton population consisting of Np = 106 particles. The particle crossing times at 1 au were collected to form intensity-time profiles at energy > 1 MeV. The parameters of the shock front are as follows: shock speed: vsh = 1500 km s−1 and the longitudinal and latitudinal width of the shock: wϕ = wδ = 70°. The shock nose is located at heliolongitude: ϕnose = 0° and heliolatitude: δnose = 15°. Injection at the shock ends at t = 48 h, corresponding to rmax = 1.73 au, and we propagated the SEPs until t = 72 h.
Particles propagate in a unipolar Parker spiral IMF, a valid assumption when the SEP source region is far from the heliospheric current sheet, with a constant solar wind speed of vsw = 500 km s−1. The shock does not disturb the Parker spiral and it is not a magnetic enhancement. After injection, the shock is transparent to particles. We considered the influence of IMF magnetic turbulence by including parallel scattering, parameterised by the mean free path, λ (Marsh et al. 2013; Dalla et al. 2020). Unless otherwise stated, we used λ = 0.1 au. The model does not include any perpendicular diffusion associated with turbulence, allowing us to investigate the corotation effects on SEP observables isolated from effects caused by cross-field diffusion (He & Wan 2017).
In the test-particle code, corotation is accounted for by including the solar wind electric field, E, into the equation of motion of the particle (Dalla et al. 2013; Marsh et al. 2013). The resulting electric field drift is a corotation drift (see Eqs. (7)–(9) of Dalla et al. 2013), moving the particle’s guiding centre by ∼14.2° per day (sidereal rotation rate, Ω = 2.86 × 10−6 rad s−1) in the direction of solar rotation. Setting E = 0 in the test particle code switches off the corotation drift and allows for the SEP propagation to be studied when corotation is neglected.
3. Intensity profiles at different observers
We studied time-intensity profiles at six observers (labelled A-F, see Fig. 1). All observers are located at the same latitude as the shock nose (δ = 15°). We define the longitudinal separation, Δϕ, between the source active region (AR) and the observer’s magnetic footpoint as:
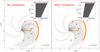 |
Fig. 1. Schematic showing the geometry of the shock, observers, and particle-filled flux tubes for the cases with (right panel) and without (left panel) corotation after 48 h of shock propagation. Here, x and y are heliocentric cartesian coordinates in the heliographic equatorial plane. Observers A-F are denoted by the coloured circles. The shock’s projection onto the plane is displayed here as the orange shaded segments. The grey IMF lines represent the range of particle-filled flux tubes. The inset shows the range of longitudes that are filled with particles. The solid red curved lines show the IMF lines that are currently connected to the edges of shock. The solid green curved lines show the magnetic flux tubes at the edges of the shock at the initial time. In the corotation case, these have rotated with respect to their initial location, shown by the dashed green line. |
where ϕAR is the AR longitudinal position and ϕftpt is the longitude of the observer footpoint. The AR locations and corresponding Δϕ values are given in Table 1. A Parker spiral magnetic connection is assumed when calculating ϕftpt.
Geometry of A-F observers and associated decay time constant of 5 MeV intensity profiles for λ = 0.1 au.
Figure 1 shows a schematic of the shock, observers, and particle-filled magnetic flux tubes when corotation is excluded (left) and included (right) at t = 48 h. The grey lines show the range of particle-filled flux tubes (i.e., IMF lines connected to the shock at t ≤ 48 h). The insets shows the range of longitudes filled with particles versus shock height.
Figure 2 shows intensity profiles for observers A-F, without and with corotation (top and bottom rows, respectively). The intensity profiles are obtained by collecting counts within 10° ×10° tiles on the 1 au sphere. Features of the profiles such as the onset time and peak time relate to the establishment or loss of connection to the shock and its arrival at the spacecraft, as was noted in a number of previous studies (e.g., Heras et al. 1994). Here, the inclusion or non-inclusion of corotation has a very significant effect on intensity profiles, in particular, for observers A-C, which see the source AR as western.
 |
Fig. 2. Intensity profiles for the six observers in Fig. 1 without (top panels) and with (bottom panels) corotation for scattering conditions described by λ = 0.1 au. The dashed lines display the exponential decay fit for observers A-D. The shock reaches the 1 au distance at t ∼ 28 h. |
Comparing the top and bottom rows in Fig. 2, corotation has two main effects on the intensity profiles. Firstly, because the flux tubes are swept westward, the western events are cut short (observers A, B, and C). For example, with corotation, the duration for observer A drops significantly from ∼65 h to ∼12 h. Secondly, corotation increases the intensity during eastern events (observers D, E, and F). For the observers located directly in the path of the shock (C and D), the effects of corotation are mainly seen after the shock passage (t ∼ 28 h). We quantified the effect of corotation on profiles for observers A-D by determining the decay time constant, τ, by fitting an exponential between the peak intensity and a second point near the end of the profile, chosen by eye to avoid regions that fluctuate due to low counts. The decay time constants are given in Table 1 for the simulations in Fig. 2 and are plotted versus Δϕ in Fig. 3, where the data points corresponding to λ = 0.5 and 1.0 au are also shown – for simulations with (dashed lines) and without (dotted lines) corotation. There are no data points for observers E and F as there are no clearly defined decay phases in the intensity profiles. Figure 3 shows a systematic shift to low τ for simulations with corotation, corresponding to faster decay phases for all observers. When corotation is included, there is little dependence on the scattering conditions as corotation dominates the decay phase. When corotation is neglected, τ is a measure of the degree of scattering, with smaller λ leading to extended decay phases.
 |
Fig. 3. Decay time constant (τ) for four of our observers with (dashed lines) and without (dotted lines) corotation and scattering conditions in the range λ = 0.1 au to λ = 1.0 au. |
The peak intensity, Ipeak, is plotted vs. Δϕ in Fig. 4. The value of Ipeak is greatest for observers C and D, which are directly in the path of the shock. We fit both sets of points with a Gaussian centred at Δϕ = ϕ0. Figure 4 shows that ϕ0 is shifted with respect to the well-connected location (Δϕ = 0), with ϕ0 = −36.4° for the corotation fit and ϕ0 = −31.2° for no corotation. The corotation fit has a standard deviation σ = 33.4° and the no-corotation case has σ = 31.3°. This east-west asymmetry has previously been noted by several authors (Ding et al. 2022; Lario et al. 2013; He & Wan 2017). Figure 4 shows that corotation enhances the asymmetry.
 |
Fig. 4. Peak intensity vs. Δϕ for the six observers A-F with (red triangles) and without (blue circles) the effects of corotation for scattering conditions described by λ = 0.1 au. The points are fit with Gaussian functions shown as the dashed lines. |
Figure 5 shows the median longitude, ϕSEP, of all the test particles in our simulation versus time. The geometry of the shock connection to the observer already naturally produces a westward shift of ϕSEP with time, as shown by the blue triangles (Ding et al. 2022). When corotation is taken into account, the latter effect becomes more pronounced (red points), resulting in the larger σ value for the corotation points in Fig. 4. We note that the discontinuity at t = 48 h is due to the shock injection ending at this time.
 |
Fig. 5. Median longitudinal position of the SEP population, ϕSEP, for the shock-like injection with corotation (red circles), without corotation (blue triangles). The grey dashed line shows the corotation of the flux tube connected to the source region at t = 0. |
4. Discussion and conclusions
In this work, we simulate particle injection from a shock-like source using 3D test particle simulations. We compare the intensity profiles over a wide range of observer longitudes with and without corotation. The main conclusions of our work are as follows:
-
The corotation of particle-filled flux tubes has a strong effect on SEP intensity profiles for the case of time-extended acceleration at a propagating CME-shock (Fig. 2). Its main influence is on the decay phase of the event: namely, it reduces the decay time constant compared to the case when corotation is not included. The strongest corotation effects are on observers that see the source AR in the west: both the event duration and decay time constant are significantly reduced (see Table 1 and Fig. 3).
-
Corotation enhances maximum intensities during eastern events and makes the east-west asymmetry in peak intensity vs. Δϕ stronger (see Fig. 4).
-
Deriving the intensity profiles without including the effects of corotation (by solving particle transport equation in the corotating frame or using a 1D approach that models propagation along a single flux tube) artificially extends the decay phase, especially for western events.
-
Varying the scattering mean free path between λ = 0.1 and 1.0 au has very little influence on the decay phase (negligible difference in the value of τ) when corotation is included, indicating that corotation is a dominant process during the decay phase of SEP events.
Our simulations show that, contrary to the conclusions of previous studies (e.g., Kallenrode & Wibberenz 1997; Lario et al. 1998), corotation plays a key role in the decay phase of SEP events. It also affects the peak intensity phase (excluding possible energetic storm particle, ESP, enhancements). Within the broad variability among the properties of SEP events, there is some indication that corotation plays a role. Dalla et al. (2003) analysed the duration of 52 events and showed that there is a tendency for eastern events to have longer durations compared to western ones. The longitudinal dependence of the SEP spectral index, first reported by Van Hollebeke et al. (1975), can be explained by corotation effects: eastern events take a long time to corotate to a near-Earth observer and it is for this reason that their spectral index is larger, as the high-energy particles have escaped the inner heliosphere by the time the flux tube corotates over the observer.
In the work presented here, we have used a uniform rate of injection from the shock with radial distance and longitude/latitude across the shock. Hutchinson et al. (2023) have also considered two other radial injection functions: we verified that corotation plays an important role regardless of the details of the injection function. Similarly, those authors showed that varying the spatial profile of injection along the shock front has a minor effect on the intensity profiles.
Our shock model is intended as only an initial approximation, given that the present work is the first analysis of a moving shock source in the context of 3D test particle simulations. In particular, downstream features, such as a flux rope and non-Parker field lines, are not described. We note that MHD simulations of shock propagation show that the magnetic field lines in the downstream can connect back to the shock. In 3D, the magnetic field lines are known to wrap over/under the ejecta (Lario et al. 1998): we expect that there are many cases where an observer behind the shock would be connected to it and our study applies directly to these cases. With a more accurate model of the downstream region, the intensities may differ from those in Fig. 2 behind the shock; however, they would still be influenced by the corotation of the magnetic flux tubes. We hope to include such a model in future studies.
We note that when constructing time-intensity profiles (as shown in Fig. 2), we used all particles (> 1 MeV), although some of them have an energy lower than the initial 5 MeV, due to adiabatic deceleration. We have determined intensity profiles for particles in the energy range of 4.5–5.0 MeV (not shown), which show a very similar behaviour to those in Fig. 2, displaying even smaller decay time constants in the corotation case. During an SEP event, particles over a range of energies will be injected and those produced with initial energy higher than 5 MeV will decelerate into the latter energy band.
A number of studies have used focussed transport or Fokker-Planck equations to determine intensity profiles after injections from a CME-driven shock-like source (e.g., He & Wan 2015; Wang et al. 2012). In contrast to our results, their intensity profiles look very similar across a range of longitudinal positions for the observer – and we find this may be due to the corotation being neglected.
We have derived other observables such as the onset time and time of peak intensity from our simulations. However, corotation does not have a significant effect on these quantities as they are primarily determined by geometric factors, such as the times of the observer-shock connection and of shock passage at the observer position.
In the present study, the role of corotation has been investigated without including the effect of possible turbulence-induced perpendicular diffusion that is associated with magnetic field line meandering. Traditionally, in the interpretation of gradual SEP events, this effect has not been included (e.g., Reames et al. 1997; Lario et al. 1998; Bain et al. 2016), although other researchers have emphasised its importance (e.g., Wang et al. 2012; He & Wan 2015, 2017) in models that do not include corotation. We aim to include this effect in future works. We would expect perpendicular diffusion to produce earlier SEP onsets for eastern events and to help SEP intensities reach similar values at far away locations faster.
Our study has used a simplified model of injection at a shock to highlight the effects of corotation and geometry of observer-shock connection. In future works, we hope to use a more sophisticated description of shock acceleration in modelling specific SEP events. The SEP intensity profiles may be influenced by complex coronal and interplanetary magnetic field configurations and solar wind structures, which are not considered in the present study. A full analysis of these effects requires detailed modelling on an event-by-event basis.
Acknowledgments
A. Hutchinson, S. Dalla and T. Laitinen acknowledge support from the UK Science and Technology Facilities Council (STFC), through a Doctoral Training grant – ST/T506011/1 and grants ST/R000425/1 and ST/V000934/1. C.O.G. Waterfall and S. Dalla acknowledge support from NERC grant NE/V002864/1. This work was performed using resources provided by the Cambridge Service for Data Driven Discovery (CSD3) operated by the University of Cambridge Research Computing Service (https://www.csd3.cam.ac.uk/), provided by Dell EMC and Intel using Tier-2 funding from the Engineering and Physical Sciences Research Council (capital grant EP/P020259/1), and DiRAC funding from the Science and Technology Facilities Council (www.dirac.ac.uk).
References
- Bain, H. M., Mays, M. L., Luhmann, J. G., et al. 2016, ApJ, 825, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cane, H. V., Reames, D. V., & von Rosenvinge, T. T. 1988, J. Geophys. Res. Space Phys., 93, 9555 [NASA ADS] [CrossRef] [Google Scholar]
- Dalla, S. 2003, in Solar Wind Ten, eds. M. Velli, R. Bruno, F. Malara, & B. Bucci, AIP Conf. Ser., 679, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Dalla, S., Marsh, M., Kelly, J., & Laitinen, T. 2013, J. Geophys. Res. Space Phys., 118, 5979 [NASA ADS] [CrossRef] [Google Scholar]
- Dalla, S., Marsh, M. S., & Battarbee, M. 2017, ApJ, 834, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Dalla, S., de Nolfo, G. A., Bruno, A., et al. 2020, A&A, 639, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desai, M., & Giacalone, J. 2016, Liv. Rev. Sol. Phys., 13 [Google Scholar]
- Ding, Z., Li, G., Ebert, R. W., et al. 2022, J. Geophys. Res. Space Phys., 127, e2022JA030343 [CrossRef] [Google Scholar]
- Dróge, W., Kartavykh, Y. Y., Klecker, B., & Kovaltsov, G. A. 2010, ApJ, 709, 912 [CrossRef] [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 2012, ApJ, 751, L33 [NASA ADS] [CrossRef] [Google Scholar]
- He, H.-Q., & Wan, W. 2015, ApJS, 218, 17 [NASA ADS] [CrossRef] [Google Scholar]
- He, H.-Q., & Wan, W. 2017, MNRAS, 464, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Heras, A. M., Sanahuja, B., Sanderson, T. R., Marsden, R. G., & Wenzel, K. P. 1994, J. Geophys. Res. Space Phys., 99, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, J., Li, G., Fu, S., Zank, G., & Ao, X. 2018, ApJ, 854, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Hutchinson, A., Dalla, S., Laitinen, T., & Waterfall, C. O. G. 2023, A&A, 670, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallenrode, M.-B., & Wibberenz, G. 1997, J. Geophys. Res. Space Phys., 102, 22311 [NASA ADS] [CrossRef] [Google Scholar]
- Laitinen, T., Dalla, S., Battarbee, M., & Marsh, M. S. 2018, in Space Weather of the Heliosphere: Processes and Forecasts, eds. C. Foullon, & O. E. Malandraki, 335, 298 [NASA ADS] [Google Scholar]
- Lario, D., Sanahuja, B., & Heras, A. M. 1998, ApJ, 509, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Lario, D., Aran, A., Gómez-Herrero, R., et al. 2013, ApJ, 767, 41 [CrossRef] [Google Scholar]
- Marsh, M. S., Dalla, S., Kelly, J., & Laitinen, T. 2013, ApJ, 774, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, M. S., Dalla, S., Dierckxsens, M., Laitinen, T., & Crosby, N. B. 2015, Space Weather, 13, 386 [CrossRef] [Google Scholar]
- Owens, M. J., Challen, R., Methven, J., Henley, E., & Jackson, D. R. 2013, Space Weather, 11, 225 [CrossRef] [Google Scholar]
- Reames, D. V., Kahler, S. W., & Ng, C. K. 1997, ApJ, 491, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, I. G., von Rosenvinge, T. T., Cane, H. V., et al. 2014, Sol. Phys., 289, 48 [NASA ADS] [Google Scholar]
- Van Hollebeke, M. A. I., Ma Sung, L. S., & McDonald, F. B. 1975, Sol. Phys., 41, 189 [Google Scholar]
- Wang, Y., Qin, G., & Zhang, M. 2012, ApJ, 752, 37 [CrossRef] [Google Scholar]
- Waterfall, C. O. G., Dalla, S., Laitinen, T., Hutchinson, A., & Marsh, M. 2022, ApJ, 934, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Zurbuchen, T. H., & Richardson, I. G. 2006, In-Situ Solar Wind and Magnetic Field Signatures of Interplanetary Coronal Mass Ejections (New York: Springer), 31 [Google Scholar]
All Tables
Geometry of A-F observers and associated decay time constant of 5 MeV intensity profiles for λ = 0.1 au.
All Figures
 |
Fig. 1. Schematic showing the geometry of the shock, observers, and particle-filled flux tubes for the cases with (right panel) and without (left panel) corotation after 48 h of shock propagation. Here, x and y are heliocentric cartesian coordinates in the heliographic equatorial plane. Observers A-F are denoted by the coloured circles. The shock’s projection onto the plane is displayed here as the orange shaded segments. The grey IMF lines represent the range of particle-filled flux tubes. The inset shows the range of longitudes that are filled with particles. The solid red curved lines show the IMF lines that are currently connected to the edges of shock. The solid green curved lines show the magnetic flux tubes at the edges of the shock at the initial time. In the corotation case, these have rotated with respect to their initial location, shown by the dashed green line. |
| In the text | |
 |
Fig. 2. Intensity profiles for the six observers in Fig. 1 without (top panels) and with (bottom panels) corotation for scattering conditions described by λ = 0.1 au. The dashed lines display the exponential decay fit for observers A-D. The shock reaches the 1 au distance at t ∼ 28 h. |
| In the text | |
 |
Fig. 3. Decay time constant (τ) for four of our observers with (dashed lines) and without (dotted lines) corotation and scattering conditions in the range λ = 0.1 au to λ = 1.0 au. |
| In the text | |
 |
Fig. 4. Peak intensity vs. Δϕ for the six observers A-F with (red triangles) and without (blue circles) the effects of corotation for scattering conditions described by λ = 0.1 au. The points are fit with Gaussian functions shown as the dashed lines. |
| In the text | |
 |
Fig. 5. Median longitudinal position of the SEP population, ϕSEP, for the shock-like injection with corotation (red circles), without corotation (blue triangles). The grey dashed line shows the corotation of the flux tube connected to the source region at t = 0. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.