EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 669 (January 2023) A&A, 669 (2023) A146 Full HTML
Open Access
Issue
A&A
Volume 669, January 2023
Article Number A146
Number of page(s) 11
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202245294
Published online 25 January 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1 Introduction

The origin of the two Martian moons, Phobos and Deimos, remains unknown. The two main hypotheses for the formation of Phobos and Deimos are the accretion of material from Mars, resulting from a collision between Mars and a protoplanet, or the capture of an asteroid from the main asteroid belt. The orbital parameters of the moons are not really consistent with the hypothesis of a captured main-belt asteroid. In particular, the null eccentricity and the null inclination are difficult to explain in the case of a captured asteroid due to the time for tidal dissipation (Burns 1992). In the collision scenario, Phobos would be a mixture of the basaltic martian material and the metallic material of the protoplanet (Craddock 1994, 2011). However, the different observations of Phobos have not shown any spectral features relative to these types of martian material. On the other hand, the red and featureless Phobos spectrum is consistent with a D-type asteroid (Murchie 1999; Rivkin et al. 2002; Fraeman et al. 2014), which is carbonaceous, and usually found in the outer main belt or in the Jupiter Trojans’ swarms and possibly related to comets (Vernazza & Beck 2017). All of these characteristics led to the theory of a captured asteroid to explain the origins of Phobos. Moreover, Phobos is a small body with a major axis of 27 km (Willner et al. 2010). It also has a cratered surface, an irregular shape, and a very low albedo. Results from observations by ground-based observations or space missions such as Mars Express or Mars Reconnaissance Orbiter have considerably increased our knowledge about Phobos (Fraeman et al. 2012, 2014). In 1991, Murchie et al. (1991), using observations of Mariner 9, Viking 1 and 2, and Phobos 2, showed that Phobos’ surface is heterogeneous and that two distinct units are present: a blue and a red unit. The blue unit corresponds to a spectrum with a positive moderate slope and the red unit corresponds to a steeper positive slope in the near-infrared. The red unit dominates the majority of the surface of Phobos, whereas the blue unit is mostly around the Stickney crater rim. It could correspond to an ejecta deposit and hence to younger and fresher areas of the surface. However, Thomas et al. (2011) with the High Resolution Imaging Science Experiment (HiRISE) instrument onboard Mars Reconnaissance Orbiter have shown that the surface is heterogeneous with some spots of red within the blue unit and blue unit areas outside the crater rim.

The Martian Moon eXploration (MMX) mission of the Japanese space agency (JAXA), which will leave Earth towards Phobos in 2024, will have to answer the question of the origins of Phobos, in particular, by sampling its surface and returning more than 10 g of samples to Earth (Kuramoto et al. 2022). MMX will also study Phobos with in situ observations, for example with the MMX InfraRed Spectrometer (MIRS, 0.9–3.6 µm) described in Barucci et al. (2021) and currently under development at the Laboratoire d’Etudes Spatiales et d’Instrumentation en Astrophysique (LESIA).

MIRS will allow one to obtain, for the first time, spectra of Phobos with a high spatial resolution (20 m px−1 and up to 1 m px−1 for investigation of sampling sites) and spectral resolution (<20 nm), and with a signal-to-noise ratio (S/N) > 100 at 3.2 µm. To determine the origin of Phobos, it will be necessary to identify its composition. If Phobos comes from a primitive captured asteroid – such as D-type asteroids – it would be legitimate to expect organic matter to represent a significant mass fraction of the surface material. In particular, measurements on the 67P/Churyumov-Gerasimenko have shown that cometary dust are roughly made of 50 wt.% of organic matter (Bardyn et al. 2017). Such organic compounds can be detected by infrared spectroscopy, especially due to the vibration modes of the C– H bonds near 3.4–3.5 µm (Raponi et al. 2020). The wavelength range of MIRS may permit one to see a spectral signature of organic compounds and also of minerals. For this work, we studied the detectability of organic matter that is we searched the concentration of organics necessary to detect the associated bands in Phobos materials. To answer this question, we produced a Phobos spectral analogue – a mixture of powders of different materials that reproduces Phobos spectral properties – and added a different quantity of organic matter in the mixture.

Several Phobos laboratory analogues have already been explored, but they were more focussed on the mechanical properties of the martian moon (D’Amore et al. 2019; Miyamoto et al. 2021; Landsman et al. 2021). The proposed existing spectral analogues of Phobos in the visible and near-infrared are rare meteoritic samples and include Tagish Lake meteorite – which is a common analogue for ultra-primitive D-type asteroids (Hiroi et al. 2001, 2022; Potin et al. 2021) – heated Murchison meteorite (700K during one week, Fraeman et al. 2012), or other meteorites related to D-type asteroids (Hiroi et al. 2005; Marrocchi et al. 2021). More recently, Poggiali et al. (2022) proposed some developments regarding the search for a spectral analogue of Phobos.

In this study, we first developed a laboratory analogue to reproduce the peculiar spectral signature of Phobos between 1 and 2.5 µm: a very low albedo, a red slope, and with no characteristic absorption bands (Fraeman et al. 2012). This spectral analogue is easy to produce in large quantities and reproducible for other studies. In the context of a captured asteroid, we then investigated the feasibility of detecting organic compounds on the surface of Phobos by MIRS.

Table 1

End members’ characteristics and properties for the analogue research.

2 Methods

2.1 Choice of materials

We produced our Phobos spectral analogue by mixing different components (see Table 1). While we mainly aimed to have a spectral analogue, we tried to make it fairly representative of the composition of a small body, for example with olivine and pyroxenes (Zolensky et al. 1993; Crovisier et al. 1996; Beck et al. 2014). Such mafic minerals are expected on Phobos based on the observations made so far (Poggiali et al. 2022) and they are common on non-differenciated asteroids, or asteroids covered by basaltic materials. For this study, olivine from Brazil and augite from the Czech Republic were used. However, these silicates are relatively bright materials, while Phobos presents an extremely low albedo. An additional absorbing component is thus essential in order to decrease the reflectance as the bi-directional reflectance (incidence =30°, null emission, and azimuth angles) is 2.4% at 550 nm and roughly 5% at 2 µm for the red unit (Fraeman et al. 2012). We therefore added iron sulfide powder and/or anthracite powder to our mixtures for this purpose. Moreover, this absorbent also strongly decreases the absorption band depth (Singer 1981; Cloutis et al. 1990a,b,c, Cloutis et al. 2009). The effects of iron sulfides on the spectral properties are particularly discussed in Quirico et al. (2016) and Rousseau et al. (2018). Iron sulfides or Fe-Ni alloys, which can be found in carbonaceous chondrites and interplanetary dust particles (IDPs), would explain the low reflectance of comets and primitive asteroids from the visible to infrared range. The chemical composition of organic matter on these objects is such that one expects that organics will be dark in the visible, but brighter in the infrared. On the other hand, anthracite is dark in both the visible and the infrared, but its chemical composition is very different from the one of organic matter of carbonaceous chondrites and IDPs (Quirico et al. 2016). Both iron sulfide and anthracite are featureless, but they have a variation in the spectral slope. Iron sulfide (<1 µm) shows a blue spectral slope after 2 µm, whereas anthracite is red at all wavelengths of interest (Figs. 1 and 2). Hence, the spectral behaviour of anthracite is closer to the characteristics of the Phobos spectrum. These two darkening agents were used with a sub-micrometre-sized grain, which allowed for the darkening power of these components to be increased (Rousseau et al. 2018; Sultana 2021). They were provided and grinded at the Institut de Planétologie et d’Astrophysique de Grenoble (IPAG). More details about this preparation process are given in Sect. 2.3.

To study the detectability of organics in the analogue, we added Titan tholins; this was a convenient way to introduce sub-micrometre-sized particles exhibiting absorption bands of organ-ics’ molecules. Titan tholins were produced with the Production d’Aérosols en Microgravité par Plasma REactifs (PAMPRE) experiment at Laboratoire Atmosphère, Milieux, Observations Spatiales (LATMOS), which simulates Titan’s atmosphere by radio-frequency plasma discharge in a gas mixture composed of nitrogen (95%) and methane (5%). The experiment is described in detail in Szopa et al. (2006). In the present work, tholins have quasi-stoechiometric H, C, and N ratios (Sciamma-O’Brien et al. 2011); they present strong mid-infrared absorption bands due to CH and NH functions (Gautier et al. 2012); and they are made of spheres of a few hundred nanometres in diameter (Hadamcik et al. 2009; Perrin et al. 2021). However, the high concentration in organics and the absence of oxygenated compounds in the tholins are not expected to be fully representative to what may be expected on a body similar to Phobos. For example, the insoluble organic matter (IOM) is a polymer based on polyaromatic compound with little nitrogen content, hence detection criteria based on the nitrogen-bearing feature shall not be considered applicable for the detection of the IOM.

2.2 Reflectance measurements

Reflectance spectra were made at room temperatures using the Spectro-photometre with cHanging Angles for Detection Of Weak Signals (SHADOWS) spectrogonio radiometre (fully described in Potin et al. 2018) at IPAG. The instrument allows one to measure reflectance with an absolute photometric accuracy of 1% at various illuminations and observation geometries from 0.4 to 4.75 µm. Two detectors are used for the visible and the near-infrared part of the spectrum, with a silicon detector for wavelength until 1.0 µm and an InSb detector between 1.0 and 4.75 µm. The infrared detector is cooled at 77 K to reduce its thermal noise. We used a spectral resolution of 20 nm in the 1000–2520 nm and 3100–3300 nm wavelength ranges to allow for a comparison with the MIRS instrument. In the region of the absorption bands of interest, a higher resolution was used, with 10 nm in the wavelength range 400–1000 nm, 2520–3100 nm, and 3300–3550 nm. For the extreme part of the spectrum between 3550 and 3750 nm, a spectral resolution of 50 nm was used. To account for instrumental and atmospheric effects, spectral references were measured before the measurement of samples using a Spectralon (Labsphere, 99% reflectance) for the visible part of the spectrum and an Infragold (Labsphere) for the infrared range. The bidirectional reflectance of the sample was then directly computed by taking the spectral references into account with the software developed in Potin et al. (2018). In the following, unless noted otherwise, we chose to use a nominal geometrical configuration with incidence i = 0°, emission e = 30°, and an azimuth ϕ = 0°.

thumbnail Fig. 1

Individual spectra – between 0.4 and 4.7 µm – of the end members used for this work.

2.3 The preparation of samples

The protocol described in this paragraph has only been applied for the silicated end members. Centimetre-sized end members were first crushed with a hammer. Then, to decrease the grain size from a millimetre to roughly 100 µm, the samples were grinded and cooled with pure liquid nitrogen during the process in order to prevent amorphisation of the minerals, which could affect their spectral properties. A Retsch Cryomill cryogenic grinder (in the Laboratoire Génies des Procédés et des Matériaux) with a steel ball of 1 cm in diameter was used for this dry grinding process. For each end member, this process took roughly two hours. The size of the silicate grains was chosen to decrease the absorption band depth (Kiddell et al. 2018; Sultana et al. 2021) because we aim to produce a featureless spectrum, but also to be representative of a small body surface with regolith grain of about 80 µm (Kuehrt et al. 1992; Giuranna et al. 2011; Miyamoto et al. 2021). Finally, a sequential dry sieving was applied to these grains – with 500, 250, and 125 µm sieves. The size of the silicates grains used in this work was confirmed by scanning electron microscopy (SEM) images. Table 1 and Fig. 1 summarise the properties and show the spectra of the different end members used in this work.

In Fig. 1, pertaining to organics, it is interesting to note that overtones of the tholins are visible at shorter wavelengths (1.3–2.7 µm) than the very deep absorption features due to the amines, contrary to the previous transmittance measurement performed on these materials (Gautier et al. 2012). Such N-H bands can be observed on comets, for example on 67P (Raponi et al. 2020). On 67P, the N–H absorption at 3.2 µm, in this case coming from ammonium salts (Poch et al. 2020), is the deepest feature on the near-infrared spectrum, compared to the absorption band due to aromatic or aliphatic carbon. If Phobos is indeed a D-type asteroid related to comets (Vernazza & Beck 2017), it could be possible to find a similar absorption feature. In the tholins spectrum, we also note the presence of weak absorption bands at 3.4 µm, corresponding to the absorption by aliphatic and/or aromatic C-H stretching modes. These bands are very characteristic of the detection of organics, and they have already been observed on small bodies such as Bennu (Kaplan et al. 2021). Regarding the olivine spectrum, we notice a broad band in the 1 µm range due to Fe2+ (Sultana et al. 2021) and the smallest absorption band near 3 µm due to O-H. We observe a similar but deeper band in the augite and small bands at 1 and 2.4 µm due to the presence of iron.

Iron sulfide was purchased from Alfa Aesar (ref. A15569.0B). The purchased powder has a composition made of 55 vol.% troilite (FeS) and 45 vol.% pyrrhotite (Fel−xS with 0 < x < 0.2) according to X-ray diffraction patterns. Anthracite was obtained from the Musée de la Mûre (France). It is a very mature coal, composed of 91.9% carbon, and made of large aromatic units, which are linked and covered by less organised aromatic or aliphatic compounds (Albiniak et al. 1996). The iron sulfide and the anthracite powders were produced by a series of dry and wet grinding (in ethanol) using a planetary ball mill (Planetary Grinder Retsch PM100), followed by sieving, as is detailed in Sultana et al. (2021). This protocol permits the preparation for sub-micrometre-sized grains, as confirmed by SEM images (see Sultana 2021). From Figs. 1 and 2, iron sulfide and anthracite are indeed very dark with a reflectance lower than 5% in the whole wavelength range.

Our olivine presented organic contamination with strong bands at 3.43 µm and 3.51 µm, which required further cleaning processes. First, grains were put in acetone to extract the unexpected organic material and then they were suspended in the acetone using a sonotrode coupled to an ultrasonic generator. Acetone is a volatile solvent that can be easily eliminated. After drying, the process was repeated four times. Organic bands have almost completely disappeared after this cleaning, as is visible in Fig. 1.

Finally, the individual components were weighed and mixed together with different volume fractions (Table 2) by hand in an agate mortar for 10 min in order to obtain the intimate mixtures investigated. Using SEM images, it appears that the fine-grained opaques are sometimes clumped together and generally stuck on the larger silicate grains. Volume percents were chosen based on the fact that volume plays a role in the radiative transfer from the surface. Values of density used in this work and their references are given in Table 1.

Table 2

Composition of the different mixtures prepared.

thumbnail Fig. 2

Spectra of the darkening agents used for this work – anthracite and iron sulfide.

2.4 Spectral analysis

Two spectral parameters are necessary to study the SHADOWS spectra: the band depth and the spectral slope. The band depth is the depth of an absorption band with respect to the continuum. It is computed using the following formula from Clark & Roush (1984): 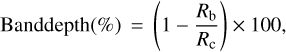Banddepth(%)=(1−RbRc)× 100,${\rm{Banddepth}}\left( \% \right) = \left( {1 - {{{R_{\rm{b}}}} \over {{R_{\rm{c}}}}}} \right) \times \,100,$(1)

where Rb is the reflectance in the absorption band and Rc is the reflectance of the continuum. The spectral slope can be computed using the expression from Delsanti et al. (2001) as follows: 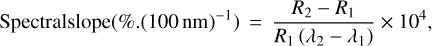Spectralslope(%.(100 nm)−1)=R2−R1R1(λ2−λ1)× 104,${\rm{Spectralslope}}\left( {\% .{{\left( {100\,{\rm{nm}}} \right)}^{ - 1}}} \right) = {{{R_2} - {R_1}} \over {{R_1}\left( {{\lambda _2} - {\lambda _1}} \right)}} \times \,{10^4},$(2)

where R2 and R1 are the reflectance of the spectrum at the wavelength λ2 and λ1, respectively. To allow for comparison with the reprojected (i = 30°, e = 0°, and ϕ = 0°) Phobos CRISM spectrum from Fraeman et al. (2012), the spectral slope was computed between 1.5 and 2.4 µm.

thumbnail Fig. 3

SHADOWS spectra of the mixtures 1 and 2 compared to the Phobos Red Unit CRISM spectra from Fraeman et al. (2012). For these mixtures, two different darkening agents were used in the same volume quantity. Quantities of each end member in the mixtures are given in vol.%.

3 Results and discussion

3.1 Looking for a Phobos spectral analogue

A spectral analogue of the red and featureless Phobos spectrum has been developed after several test mixtures. The mixture that best reproduces the Phobos spectrum was chosen using its match to the spectral slope and the reflectance at 1.8 µm of Phobos as measured by the Compact Reconnaissance Imaging Spectrometer for Mars (CRISM), and it was reprojected in laboratory viewing geometry (Fraeman et al. 2012). In the following parts of this section, we detail the production steps of our analogue.

3.1.1 Choice of darkening agent

As described earlier, we tried two different darkening agents – iron sulfide and anthracite. Choosing a darkening agent is crucial because it affects the reflectance, the decrease in band depth as seen before, in addition to the spectral slope (Figs. 2 and 3). Figure 2 shows the spectra of the two tested darkening agents. Anthracite and iron sulfide generally have a similar value of reflectance. The iron sulfide spectrum (in blue) shows a concave behaviour, which is red-sloped between 0.5 and 2 µm and then blue-sloped until 4 µm. As for anthracite, its spectrum (in orange) is red-sloped from 0.5 to 4 µm.

In the two different mixtures of spectra presented in Fig. 3, no or a very weak absorption band related to the presence of olivine at 1 µm is observed. This is mainly due to the presence of a darkening agent, which tends to almost completely suppress the absorption band in mixtures (Sultana 2021). It can also be noted that mixture 1 and 2 contain the same quantity (in vol.) in olivine and in darkening agents, indicating that iron sulfide powder has a greater effect than anthracite powder on reflectance. The variations of the spectral slope of these darkening agents greatly influence the spectral slope of the mixture (Fig. 3). In particular, mixtures with anthracite show red-sloped spectra. The red slope of the Phobos spectra in the near-infrared is closer to the spectral characteristics of the anthracite powder. Thus, anthracite powder was chosen in the following as a darkening agent of the different mixtures.

thumbnail Fig. 4

SHADOWS spectra of mixtures 2, 3, 5, and 6 to compare the effect of different ratios in an olivine-anthracite mixture. Quantities of each end member in the mixtures are given in vol.%.

3.1.2 The olivine-anthracite mixture

Figure 4 shows the spectra of olivine-anthracite mixtures with different volume percentages of anthracite powder. The mixture 2 spectrum with 5 vol.% of anthracite shows a spectral slope (1.5–2.4 µm) of 2.5%/(100 nm) and a reflectance of 0.1 at 1.8 µm. The mixture 3 spectrum with 10 vol.% presents a similar slope and reflectance as the mixture with 5 vol.% of anthracite. The mixture 6 spectrum with 20 vol.% and the mixture 5 spectrum with 30 vol.% of anthracite appear to be quite different from the two other spectra with a reflectance roughly twice as low and a spectral slope (1.5–2.4 µm) of 2.12%/(100 nm) for 30 vol.% and 2.45%/(100 nm) for 20 vol.%. Furthermore, an observation of spectra with a different ratio of olivine and anthracite (ratio from 19:1 to 2.3:1) shows that a decrease in the olivine quantity in the mixture induces a decrease in the spectral slope. In particular, this effect can be observed between mixtures 5 and 6. Hence, olivine has a significant effect on the spectral slope and was important to reproduce the slope of the Phobos spectrum. In addition, only one grain size for each end member was used in this study. After several tests, olivine-anthracite mixtures with a ratio of 4:1 between the two end members were chosen according to their reflectance and spectral slope, which roughly reproduce the Phobos spectrum as a first approximation.

3.1.3 Effect of pyroxene in the mixture

The effect of adding pyroxene to the mixtures has been explored and the result of this investigation is given in Fig. 5. We compared the spectrum with the same silicate-darkening agent ratio, but with a different composition of silicates in the mixture such as 100% olivine for mixture 6 or 56% olivine and 44% augite for mixture 10. Spectra for a different silicate composition show small differences in terms of the spectral slope, but large effects in terms of the overall reflectance level, which is higher with pyroxene in the mixture. Moreover, the molecular water broad band due to the augite is visible in the spectrum of the mixture containing pyroxene. Since this band has not been detected on Phobos, we decided to retain olivine for our silicate base for the rest of this study.

thumbnail Fig. 5

SHADOWS spectra of mixtures 6 and 10. Comparison with an olivine-antracite spectrum and an olivine-anthracite-augite spectrum. Quantities of each end member in the mixtures are given in vol.%.
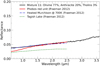thumbnail Fig. 6

Spectra of our laboratory spectral analogue of Phobos compared to the Phobos red unit CRISM spectrum and some meteorites from Fraeman et al. (2012).

3.1.4 Phobos red unit analogue

The analogue that best reproduces the CRISM spectrum of the Phobos red unit in the near-infrared domain is a mixture of olivine (77 vol.%, 50–125 µm), hyperfine anthracite (20 vol.%, <1 µm), and a small quantity of Titan tholins (3 vol.%, ~400 nm). Figure 6 presents the CRISM spectrum, which covers the wavelengths from 0.6 to 2.5 µm with our analogue spectrum and the spectra of meteorites. Our analogue spectrum exhibits a reflectance and a spectral slope similar to the CRISM spectrum between 1.3 and 2.5 µm. The dashed and dash-dotted curves present the spectrum of meteorites generally proposed as a blue unit spectral Phobos analogue, which is subsequently discussed further in the part of the paper concerning the Pho-bos blue unit. We have not found any analogues so far for the red unit in the literature. For our analogue, we found a spectral slope of 2.4%/(100 nm) and a reflectance at 1.8 µm of 0.05, which can be compared to the same parameters (spectral slope of 3.0%/(100 nm) and reflectance at 1.8 µm of 0.05) for the CRISM spectrum of the Phobos red unit, computed for the same phase angle conditions. It should be noted that while our analogue spectral properties match the Phobos spectrum in the near-infrared, the visible part of the Phobos spectrum is not well reproduced by our analogues and further investigations will be needed.

thumbnail Fig. 7

Spectra of mixtures 4, 7, and 11 compared to the Phobos blue unit CRISM spectrum from Fraeman et al. (2012).

3.1.5 The Phobos blue unit analogue

We also observed that the blue unit of Phobos can be reproduced with another analogue composition. Figure 7 shows several mixtures that can be used as a spectral analogue of the blue unit compared to the CRISM Phobos blue unit and heated Murchi-son spectra (Fraeman et al. 2012). Mixture 4, which is composed of 90 vol.% of olivine, 8 vol.% of anthracite, and 2 vol.% of iron sulfide (black dashed curve), presents the most similar spectral slope compared to the Phobos blue unit spectrum. However, the reflectance is a little higher than expected. Mixture 7 (black dotted curve) and 11 (black solid line), which are made of olivine (76 vol.%), anthracite (19 vol.%), and tholins (5 vol.%) and olivine (77 vol.%), anthracite (20 vol.%), and tholins (3 vol.%), respectively, also fit the blue unit spectrum, but mixture 7 presents a small absorption band due to the presence of tholins in the mixture. In Figs. 6 and 7, weak absorption bands can be observed between 2.6 and 2.8 µm. These features are not related to the sample, but they are due to atmospheric H2O due to variation in the atmospheric concentration one day during our measurements.

Figures 6 and 7 also show comparisons with the generally proposed analogue for the Phobos blue unit such as Tagish Lake and heated Murchison (700 K during one week) meteorites (Fraeman et al. 2012; Pajola et al. 2013). It appears that our analogues reproduce the heated Murchison spectrum well in reflectance, but also in spectral slope. However, analogues from this work reproduce the Phobos spectral slope better after 2 µm. Between 2 and 2.5 µm, the Murchison meteorite exhibits a spectral slope of 1.28%.(100 nm)−1, which can be compared to the spectral slope of mixture 11 (solid black line in Fig. 7): 1.78% (100 nm)−1 for the same wavelength range. Furthermore, meteorites such as Tagish Lake or Murchison are rare and should be contaminated as little as possible. In comparison, near-infrared spectral analogues proposed in this work are easy to reproduce, which allow for the use of a large quantity of them for further studies.

thumbnail Fig. 8

SHADOWS spectra of mixtures 6 (olivine 80 vol.%, anthracite 20 vol.%), 7, 8, 11, 13, and 16. Spectra with various volume quantities of tholins are plotted from 3 vol.% to 20 vol.%.
thumbnail Fig. 9

Signal-to-noise ratio (S/N) of the 3 µm band depth due to tholins as a function of the tholin volume percentage in the mixture. Numbers near each point represent the mixture number (see Table 2).

3.2 Detection limit of organic matter

To prepare the future MIRS observations, we studied the limit of detection of primary and secondary amine groups linked to the presence of organics in the regolith analogue (Fig. 8). For this purpose, we added organics in different proportions from 3% to 20% in volume in the mixture (mixture 7, 8, 11, 13, and 16). We first noticed that an aliphatic and/or aromatic C-H feature at 3.4 µm is not clearly visible even in the case of an organic-rich mixture. However, a broad absorption band near 3 µm due to N-H stretching modes in the Titan tholins is clearly visible. Because in all mixtures only the 3 µm band was always visible, it was used as a tracer for the detectability of organics. We computed S/N of the 3 µm band depth for each mixture.

Figure 9 presents the result of this investigation. This figure presents the S/N of the 3 µm band depth as a function of the volume percentage of the organics (tholins) in the mixture. The computation of the S/N and associated error bars was done as follows: after removing the continuum using a spline fit algorithm, the noise was computed by taking the standard deviation of the noise on the baseline before and after the band. Error bars for the x and y axis were estimated from the weighting scales’ uncertainty and from the uncertainties on the band depth measurement, respectively. The different areas represent delimitations given by the limit of detection (LOD, S/N = 3) and the limit of quantification (LOQ, S/N = 10). A clear detection of organics (S/N > 3) is obtained for 5 vol.% of tholins in the mixture. If the band strength is known, a quantification of the content of organics would even be possible for a volume percentage of tholins larger than or equal to 15 vol.%; although, we do not necessarily expect such a high amount of organics on Phobos. A previous study of the Bennu surface (Simon et al. 2020) has shown that observations of 3% depth absorption features would be detectable with an instrumental S/N equal to or larger than 100. MIRS will observe Phobos with a S/N larger than 100 (but depending on phase angle, integration time, and wavelength, see Sect. 1), implying that MIRS will permit such weak organic matter features to be detected (for 5 vol.% and more of organics), if present. However, as has already been discussed in Sect. 2, tholins are rich-nitrogenous organic compounds and may not be representative of highly carbonaceous organic matter. Organic material containing mainly aliphatic and/or aromatic carbons would be more representative for this purpose and further work is needed to assess the detectability of the C-H bending modes in our analogue. The result of this work will be useful for interpretation of the MIRS observations of the Phobos surface.

3.3 Effect of observation geometry

During the MMX mission, the spacecraft will observe Phobos in a different geometry of observation (incidence, emission, and azimuth angles). Previous studies have shown the importance of these parameters and the possible effects on the absorption features detected on small bodies (Shepard & Cloutis 2011; Takir et al. 2015; Potin et al. 2019). In this section, we investigate the variations of the reflectance spectra under different geometrical configurations in terms of absolute reflectance, spectral slope, and studying the detection limit of absorption features in particular.

To study the spectroscopic limit of detection as a function of the phase angle, we observed the effect of the phase angle on the 3 µm absorption band for a mixture composed of olivine (68 vol.%), anthracite (17 vol.%), and a large amount of Titan tholins (15 vol.%). This study will permit a better interpretation of the MIRS data which will observe Phobos at different phase angles. We performed a bidirectional reflectance distribution function (BRDF) using the SHADOWS spectrogonio radiome-tre with an incident angle from 0 to 60° with a step of 20°, and an emission angle from −70 to 70° with a step of 10° for a fixed azimuth of 0°. A set of data with an azimuth of 30°, with a fixed incidence of 20°, and emission from −70 to 70° was also made. This resulted in 81 spectra with a different geometry of observations. Figure 10 shows the phase function of the mixture in polar coordinates. In this figure, we noticed that the SHADOWS configuration does not allow for observations in specular reflection. Moreover, near 3 µm, the reflectance is particularly low due to the N–H absorption bands in the mixture spectrum. The spectrum of the mixture in different geometrical configurations is given in Fig. 11. We plotted five spectra of the mixture under various geometries with a phase angle from 10 to 50°. We remark a decrease in the reflectance until 50° and a variation in the spectral slope, which is particularly visible between 1.5 and 2.4 µm.

The study of the 3 µm absorption band depth as a function of the phase angle (Fig. 12a) shows a constant band depth for phase angles from 0 to 80°. The band depth then decreases for high phase angles larger than 80–90°. Fornasier et al. (2020) also reported this trend for the 2.74 µm absorption band on Bennu. This implies that a comparison of the abundances of organic matter using band depth is possible if phase angles do not exceed 80°, but it would be more uncertain for higher phase angles. Regarding the planned MIRS observation, the band depth of possible organics should not be affected too much by the different phase angles that are to be probed; in addition, low phase angle observations should be favoured when looking for organic compounds.

Others spectral parameters such as the spectral slope and reflectance were also studied to obtain information about surface properties of the studied mixture (mixture 16: olivine 68 vol.%, anthracite 17 vol.%, and tholins 15 vol.%). Spectral slope measurements for different phase angles show a phase reddening (see Fig. 12b). This effect was previously described for other small bodies such as Bennu or 67P (Fornasier et al. 2015, 2020). It is potentially due to an increase in multiple scattering as the phase angle increases, in the case of small grains (Schröder et al. 2014; Fornasier et al. 2015; Pilorget et al. 2016). From a linear fit of these data, a slope of 0.019 ± 0.001 × 10+4 nm−1/° and a value at a zero phase angle of −0.08 ± 0.05%.(100 nm)−1 were estimated. The spectral slope of the sample varies between 0.1 at phase 0° and 2.4% (100 nm)−1 at 120°. These values can be compared to those for other small bodies such as 67P and Bennu (Table 3). 67P has a significant phase reddening compared to Bennu, which is roughly seven times that of Bennu for the same wavelength range (535–882 nm and 550–860 nm), and our investigation shows a phase reddening comparable to 67P between 1 and 2 µm and close to Bennu between 550 and 860 nm. However, due to a lack of data in the literature, here the spectral slope was not computed for the same wavelength domain and phase reddening is known to be generally less efficient at a longer wavelength (Ciarniello et al. 2017, 2020; Fornasier et al. 2020).

It is also interesting to note that phase reddening has been proposed for Phobos to explain differences between Rosetta and Phobos 2 data (Pajola et al. 2012). From the Rosetta measurement, a spectral slope value of 11.4% (100 nm)−1 has been found at 138 degrees of the phase angle. But for a phase of roughly 8 degrees, using Phobos 2 observations a spectral slope of 10.8% (100 nm)−1 was measured. These two values were computed for the wavelength range 360–990 nm. In this hypothesis, the phase reddening of Phobos would be 0.0046 × 10−4 nm−1 /°. Phase reddening on Phobos would then be smaller than the phase reddening of our mixture used for the BRDF. Due to the lack of uncertainties on the Rosetta and Phobos 2 measurements, a comparison with our mixture cannot be realised and differences are difficult to interpret. Moreover, the spectral slope for Pajola et al. (2012) and for this work was also not computed for the same wavelength or for our best analogue of the Phobos red unit (mixture 11). It is however interesting to note that a clear phase reddening could be expected on the surface of Phobos and that this spectral characteristic is present in our mixture. Further investigations may be necessary to measure the BRDF of an analogue with an improved spectral match in the visible range.

Reflectance (Fig. 12c) shows a decrease in phase between 0 and 60° (backscattering) and increases towards higher phase angles (forward scattering). This phase function gives information about the texture and the heterogeneity of the mixture with quite big grains of olivine and submicrometric grains of anthracite and tholins. Indeed, backscattering is more important for such fine grains compared to larger grains where forward scattering dominates. On Phobos, the phase function shows that reflectance decreases with phase angle, and then that backscattering is more significant on the martian moon (Avanesov et al. (1991) and S. Fornasier, priv. comm.). The difference as to this phase behaviour could be due to the grain sizes on Phobos, which are probably different from our grain size distribution.

Even if observations at phase angles larger than 30° will rapidly degrade the MIRS S/N and if the detection of organics will be more efficient for low phase angles, observations at different phase angles will allow for additional information about the surface properties to be inferred. For an interpretation of MIRS data, it will be necessary to take all these geometrical effects into account.

thumbnail Fig. 10

Reflectance of the mixture 16 in polar coordinates with emergence angle variations from −70° to +70° and at different wavelengths. The straight black line represents the incidence angle.
thumbnail Fig. 11

Effect on phase angle on the reflectance on mixture 16: 68% olivine, 17% anthracite, and 15% tholins.
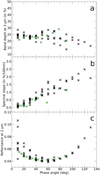thumbnail Fig. 12

Geometry observation effects on the 3 µm band depth (a), on the spectral slope evaluated between 1.5 and 2.4 µm (b), and on the reflectance at 2 µm (c) for mixture 16 composed of olivine 68 vol.%, anthracite 17 vol.%, and tholins 15 vol.%. Black crosses represent points for which the azimuth is 0º and green crosses are for an azimuth of 30º.

4 Conclusions

In this study, we have presented the production of a spectral analogue of the Phobos surface in the near-infrared from the measurement of reflectance spectra using the spectrogonio-radiometre SHADOWS. The mixture of olivine (77 vol.%), anthracite (20 vol.%), and Titan tholins (3 vol.%) reproduced the Phobos CRISM spectra from 1 to 2.4 µm, that is a dark red featureless spectrum. We then used this optical analogue to study the feasibility of organic matter detection. The strong signature at 3 µm attributed to N-H stretching modes does not appear to be detectable for less than 5 vol.% of organic compounds. However, such a high proportion of organic matter could only be expected on Phobos if Phobos is a D-type asteroid and if D-type asteroids are related to comets (Vernazza & Beck 2017). The 67P/Churyumov-Gerasimenko comet would have around 70% of volume content in organics (Isnard et al. 2019), which means that a significant part of the comet nucleus is composed of organics. Carbonaceous chondrites contain less than 10 wt.% of organic compounds (Kerridge 1985). This value depends on the heating of the surface, which tends to decrease the organic signature of the surface (Potiszil et al. 2020). On Phobos, organic matter has not been detected so far by the different in situ or space-ground observations. Organic matter could be present only in the subsurface or strongly processed with a loss of spectral features. Our result will also be useful to interpret future MIRS observations and to provide observation strategies of the surface of Phobos. Our work provides new insight into the detectability of organics for the MIRS near-infrared spectrometer. Such a detection would provide precious clues as to the origins of Phobos since organics are expected in the case of the captured asteroid hypothesis.

Further investigations will be necessary to increase the min-eralogical representativeness of our analogue, to study grain size and porosity effects further, or other effects known to occur on Phobos’ surface. In particular, space weathering is of prime importance on small bodies and has been previously observed on other airless bodies such as Bennu (Lantz et al. 2018), Ryugu (Matsumoto et al. 2022), and the Moon (Hapke 2001). It has a significant effect on their dark colour (Hapke 2001) and absorption bands and it causes spectral reddening (Hapke 2001; Lantz et al. 2017), all of which would strongly influence the Phobos spectrum and affect organic matter detection on its surface.

Table 3

Phase reddening coefficients for different small bodies and for different wavelength ranges.

Acknowledgements

We are grateful to the Centre National d’Etudes Spatiales (CNES) for its financial support. T.G. and A.W. acknowledge financial support from Agence Nationale de la Recherche under the grant ANR-20-CE49-0004-01. We thank the referee, E. A. Cloutis, for his comments and suggestions that contributed to improve the manuscript.

References

  1. Albiniak, A., Furdin, G., Begin, D., et al. 1996, Carbon, 34, 1329 [CrossRef] [Google Scholar]
  2. Avanesov, G., Zhukov, B., Ziman, Y., et al. 1991, Planet. Space Sci., 39, 281 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bardyn, A., Baklouti, D., Cottin, H., et al. 2017, MNRAS, 469, S712 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barucci, M. A., Reess, J.-M., Bernardi, P., et al. 2021, Earth, Planets and Space, 73, 211 [NASA ADS] [CrossRef] [Google Scholar]
  5. Beck, P., Garenne, A., Quirico, E., et al. 2014, Icarus, 229, 263 [Google Scholar]
  6. Burns, J. A. 1992, in Mars, ed. M. George, 1283 [Google Scholar]
  7. Carrasco, N., Schmitz-Afonso, I., Bonnet, J. Y., et al. 2009, J. Phys. Chem. A, 113, 11195 [NASA ADS] [CrossRef] [Google Scholar]
  8. Ciarniello, M., Capaccioni, F., Filacchione, G., et al. 2015, A&A, 583, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Ciarniello, M., De Sanctis, M. C., Ammannito, E., et al. 2017, A&A, 598, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Ciarniello, M., De Sanctis, M. C., Raponi, A., et al. 2020, A&A, 634, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Clark, R. N., & Roush, T. L. 1984, J. Geophys. Res., 89, 6329 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cloutis, E. A., Gaffey, M. J., Smith, D. G. W., & Lambert, R. S. J. 1990a, J. Geophys. Res., 95, 8323 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cloutis, E. A., Gaffey, M. J., Smith, D. G. W., & Lambert, R. S. J. 1990b, J. Geophys. Res., 95, 281 [CrossRef] [Google Scholar]
  14. Cloutis, E. A., Gaffey, M. J., Smith, D. G. W., & Lambert, R. S. J. 1990c, Icarus, 84, 315 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cloutis, E. A., Hardersen, P. S., Reddy, V., et al. 2009, in 40th Annual Lunar and Planetary Science Conference, Lunar and Planetary Science Conference, 1332 [Google Scholar]
  16. Craddock, R. A. 1994, in Lunar and Planetary Science Conference, Lunar and Planetary Science Conference, 293 [Google Scholar]
  17. Craddock, R. A. 2011, Icarus, 211, 1150 [NASA ADS] [CrossRef] [Google Scholar]
  18. Crovisier, J., Brooke, T. Y., Hanner, M. S., et al. 1996, A&A, 315, L385 [NASA ADS] [Google Scholar]
  19. D'Amore, M., Maturilli, A., Miyamoto, H., et al. 2019, in 50th Annual Lunar and Planetary Science Conference, Lunar and Planetary Science Conference, 2383 [Google Scholar]
  20. Delsanti, A. C., Boehnhardt, H., Barrera, L., et al. 2001, A&A, 380, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Deng, L., Yun, F., Jia, R., et al. 2020, Mater. Chem. Phys., 239, 122039 [CrossRef] [Google Scholar]
  22. Flinn, D. 1983, Geol. J., 18, 277 [Google Scholar]
  23. Fornasier, S., Hasselmann, P. H., Barucci, M. A., et al. 2015, A&A, 583, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Fornasier, S., Hasselmann, P. H., Deshapriya, J. D. P., et al. 2020, A&A, 644, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Fraeman, A. A., Arvidson, R. E., Murchie, S. L., et al. 2012, J. Geophys. Res. (Planets), 117, E00J15 [Google Scholar]
  26. Fraeman, A. A., Murchie, S. L., Arvidson, R. E., et al. 2014, Icarus, 229, 196 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gautier, T., Carrasco, N., Mahjoub, A., et al. 2012, Icarus, 221, 320 [NASA ADS] [CrossRef] [Google Scholar]
  28. Giuranna, M., Roush, T. L., Duxbury, T., et al. 2011, Planet. Space Sci., 59, 1308 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hadamcik, E., Renard, J. B., Alcouffe, G., et al. 2009, Planet. Space Sci., 57, 1631 [NASA ADS] [CrossRef] [Google Scholar]
  30. Hapke, B. 2001, J. Geophys. Res., 106, 10039 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hiroi, T., Zolensky, M. E., & Pieters, C. M. 2001, Science, 293, 2234 [CrossRef] [Google Scholar]
  32. Hiroi, T., Tonui, E., Pieters, C. M., et al. 2005, in 36th Annual Lunar and Planetary Science Conference, eds. S. Mackwell, & E. Stansbery, 1564 [Google Scholar]
  33. Hiroi, T., Ohtsuka, K., Zolensky, M. E., Rutherford, M. J., & Milliken, R. E. 2022, in LPI Contributions, 2678, 53rd Lunar and Planetary Science Conference, 1149 [Google Scholar]
  34. Isnard, R., Bardyn, A., Fray, N., et al. 2019, A&A, 630, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Kaplan, H. H., Simon, A. A., Hamilton, V. E., et al. 2021, A&A, 653, A1 [Google Scholar]
  36. Kerridge, J. F. 1985, Geochim. Cosmochim. Acta, 49, 1707 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kiddell, C. B., Cloutis, E. A., Dagdick, B. R., et al. 2018, J. Geophys. Res. (Planets), 123, 2803 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kuehrt, E., Giese, B., Keller, H. U., & Ksanfomality, L. V. 1992, Icarus, 96, 213 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kuramoto, K., Kawakatsu, Y., Fujimoto, M., et al. 2022, Earth, Planets and Space, 74, 12 [NASA ADS] [CrossRef] [Google Scholar]
  40. Landsman, Z. A., Schultz, C. D., Britt, D. T., et al. 2021, Adv. Space Res., 67, 3308 [NASA ADS] [CrossRef] [Google Scholar]
  41. Lantz, C., Brunetto, R., Barucci, M. A., et al. 2017, Icarus, 285, 43 [CrossRef] [Google Scholar]
  42. Lantz, C., Binzel, R. P., & DeMeo, F. E. 2018, Icarus, 302, 10 [CrossRef] [Google Scholar]
  43. Marrocchi, Y., Avice, G., & Barrat, J.-A. 2021, ApJ, 913, L9 [NASA ADS] [CrossRef] [Google Scholar]
  44. Matsumoto, T., Noguchi, T., Miyake, A., et al. 2022, in LPI Contributions, 2678, 1693 [NASA ADS] [Google Scholar]
  45. Miyamoto, H., Niihara, T., Wada, K., et al. 2021, Earth, Planets and Space, 73, 214 [NASA ADS] [CrossRef] [Google Scholar]
  46. Murchie, S. 1999, J. Geophys. Res., 104, 9069 [NASA ADS] [CrossRef] [Google Scholar]
  47. Murchie, S. L., Britt, D. T., Head, J. W., et al. 1991, J. Geophys. Res., 96, 5295 [NASA ADS] [Google Scholar]
  48. Pajola, M., Lazzarin, M., Berini, I., et al. 2012, MNRAS, 427, 3230 [NASA ADS] [CrossRef] [Google Scholar]
  49. Pajola, M., Lazzarin, M., Dalle Ore, C. M., et al. 2013, ApJ, 777, 127 [NASA ADS] [CrossRef] [Google Scholar]
  50. Perrin, Z., Carrasco, N., Chatain, A., et al. 2021, in European Planetary Science Congress, EPSC2021-491 [Google Scholar]
  51. Pilorget, C., Fernando, J., Ehlmann, B. L., Schmidt, F., & Hiroi, T. 2016, Icarus, 267, 296 [NASA ADS] [CrossRef] [Google Scholar]
  52. Poch, O., Istiqomah, I., Quirico, E., et al. 2020, Science, 367, aaw7462 [NASA ADS] [CrossRef] [Google Scholar]
  53. Poggiali, G., Matsuoka, M., Barucci, M. A., et al. 2022, MNRAS, 516, 465 [NASA ADS] [CrossRef] [Google Scholar]
  54. Potin, S., Brissaud, O., Beck, P., et al. 2018, Appl. Opt., 57, 8279 [NASA ADS] [CrossRef] [Google Scholar]
  55. Potin, S., Beck, P., Schmitt, B., & Moynier, F. 2019, Icarus, 333, 415 [Google Scholar]
  56. Potin, S. M., Cloutis, E. A., & Izawa, M. R. M. 2021, in 52nd Lunar and Planetary Science Conference, Lunar and Planetary Science Conference, 1544 [Google Scholar]
  57. Potiszil, C., Tanaka, R., Kobayashi, K., Kunihiro, T., & Nakamura, E. 2020, Astrobiology, 20, 916 [NASA ADS] [CrossRef] [Google Scholar]
  58. Quirico, E., Moroz, L. V., Schmitt, B., et al. 2016, Icarus, 272, 32 [CrossRef] [Google Scholar]
  59. Raponi, A., Ciarniello, M., Capaccioni, F., et al. 2020, Nat. Astron., 4, 500 [NASA ADS] [CrossRef] [Google Scholar]
  60. Rivkin, A. S., Brown, R. H., Trilling, D. E., Bell, J. F., & Plassmann, J. H. 2002, Icarus, 156, 64 [NASA ADS] [CrossRef] [Google Scholar]
  61. Rousseau, B., Érard, S., Beck, P., et al. 2018, Icarus, 306, 306 [CrossRef] [Google Scholar]
  62. Schröder, S. E., Grynko, Y., Pommerol, A., et al. 2014, Icarus, 239, 201 [Google Scholar]
  63. Sciamma-O'Brien, E., Contreras, C. S., Ricketts, C. L., & Salama, F. 2011, in EPSC-DPS Joint Meeting 2011, 1303 [Google Scholar]
  64. Shepard, M. K., & Cloutis, E. 2011, in 42nd Annual Lunar and Planetary Science Conference, Lunar and Planetary Science Conference, 1043 [Google Scholar]
  65. Simon, A. A., Kaplan, H. H., Cloutis, E., et al. 2020, A&A, 644, A148 [EDP Sciences] [Google Scholar]
  66. Singer, R. B. 1981, J. Geophys. Res., 86, 7967 [NASA ADS] [CrossRef] [Google Scholar]
  67. Sultana, R. 2021, PhD thesis, Université de Grenoble Alpes, France [Google Scholar]
  68. Sultana, R., Poch, O., Beck, P., Schmitt, B., & Quirico, E. 2021, Icarus, 357, 114141 [CrossRef] [Google Scholar]
  69. Szopa, C., Cernogora, G., Boufendi, L., Correia, J. J., & Coll, P. 2006, Planet. Space Sci., 54, 394 [NASA ADS] [CrossRef] [Google Scholar]
  70. Takir, D., Reddy, V., Sanchez, J. A., et al. 2015, ApJ, 804, L13 [NASA ADS] [CrossRef] [Google Scholar]
  71. Thomas, N., Stelter, R., Ivanov, A., et al. 2011, Planet. Space Sci., 59, 1281 [NASA ADS] [CrossRef] [Google Scholar]
  72. Vernazza, P., & Beck, P. 2017, in Planetesimals: Early Differentiation and Consequences for Planets, eds. L. T. Elkins-Tanton, & B. P. Weiss, 269 [CrossRef] [Google Scholar]
  73. Willner, K., Oberst, J., Hussmann, H., et al. 2010, Earth Planet. Sci. Lett., 294, 541 [Google Scholar]
  74. Zolensky, M., Barrett, R., & Browning, L. 1993, Geochim. Cosmochim. Acta, 57, 3123 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

End members’ characteristics and properties for the analogue research.

In the text
Table 2

Composition of the different mixtures prepared.

In the text
Table 3

Phase reddening coefficients for different small bodies and for different wavelength ranges.

In the text

All Figures

thumbnail Fig. 1

Individual spectra – between 0.4 and 4.7 µm – of the end members used for this work.
In the text
thumbnail Fig. 2

Spectra of the darkening agents used for this work – anthracite and iron sulfide.
In the text
thumbnail Fig. 3

SHADOWS spectra of the mixtures 1 and 2 compared to the Phobos Red Unit CRISM spectra from Fraeman et al. (2012). For these mixtures, two different darkening agents were used in the same volume quantity. Quantities of each end member in the mixtures are given in vol.%.
In the text
thumbnail Fig. 4

SHADOWS spectra of mixtures 2, 3, 5, and 6 to compare the effect of different ratios in an olivine-anthracite mixture. Quantities of each end member in the mixtures are given in vol.%.
In the text
thumbnail Fig. 5

SHADOWS spectra of mixtures 6 and 10. Comparison with an olivine-antracite spectrum and an olivine-anthracite-augite spectrum. Quantities of each end member in the mixtures are given in vol.%.
In the text
thumbnail Fig. 6

Spectra of our laboratory spectral analogue of Phobos compared to the Phobos red unit CRISM spectrum and some meteorites from Fraeman et al. (2012).
In the text
thumbnail Fig. 7

Spectra of mixtures 4, 7, and 11 compared to the Phobos blue unit CRISM spectrum from Fraeman et al. (2012).
In the text
thumbnail Fig. 8

SHADOWS spectra of mixtures 6 (olivine 80 vol.%, anthracite 20 vol.%), 7, 8, 11, 13, and 16. Spectra with various volume quantities of tholins are plotted from 3 vol.% to 20 vol.%.
In the text
thumbnail Fig. 9

Signal-to-noise ratio (S/N) of the 3 µm band depth due to tholins as a function of the tholin volume percentage in the mixture. Numbers near each point represent the mixture number (see Table 2).
In the text
thumbnail Fig. 10

Reflectance of the mixture 16 in polar coordinates with emergence angle variations from −70° to +70° and at different wavelengths. The straight black line represents the incidence angle.
In the text
thumbnail Fig. 11

Effect on phase angle on the reflectance on mixture 16: 68% olivine, 17% anthracite, and 15% tholins.
In the text
thumbnail Fig. 12

Geometry observation effects on the 3 µm band depth (a), on the spectral slope evaluated between 1.5 and 2.4 µm (b), and on the reflectance at 2 µm (c) for mixture 16 composed of olivine 68 vol.%, anthracite 17 vol.%, and tholins 15 vol.%. Black crosses represent points for which the azimuth is 0º and green crosses are for an azimuth of 30º.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.