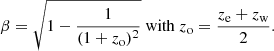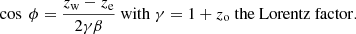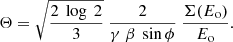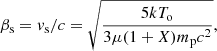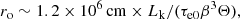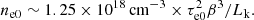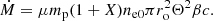EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 669 (January 2023) A&A, 669 (2023) A149 Full HTML
Open Access
Issue
A&A
Volume 669, January 2023
Article Number A149
Number of page(s) 12
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202243951
Published online 26 January 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1. Introduction

SS433 is a Galactic eclipsing X-ray binary (XRB) system which is a member of the microquasar class (Margon 1984; Mirabel & Rodríguez 1998). It is composed of an A-type supergiant star and either an accreting neutron star or a black hole (Kubota et al. 2010; Robinson et al. 2017), with the nature of its compact object still being controversial, on a circular orbit with an orbital period of 13.1 days (Fabrika 2004). It seems to be located at a distance of 5.5 ± 0.2 kpc (Lockman et al. 2007), a value that is consistent with the recent geometric parallax from the Gaia satellite (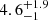 kpc at 1σ; Lindegren et al. 2016).

Jets in SS433 are its more prominent feature. They are the most powerful ones known in the Galaxy with luminosities of Ljet ≳ 1039 erg s−1 (Marshall et al. 2002), and they were discovered first for a compact Galactic source (Abell & Margon 1979; Fabian & Rees 1979). They are ejected at a mildly relativistic velocity of v ∼ 0.26c (Margon & Anderson 1989). It is remarkable that baryons are present in these jets, with SS433, along with 4U 1630–47, being the only two Galactic XRBs in which baryonic jets have been observed (Kotani et al. 1994; Díaz et al. 2013). X-ray emission lines from ionised heavy elements have been detected (Margon & Anderson 1989; Marshall et al. 2002), and they are associated with adiabatic expansion and radiative losses of hot and dense blobs of gas propagating outwards from the compact source and following the jet precessional motion. Multi-wavelength observations of the SS433 outflow reveal a consistent scheme of symmetric jet flow once Doppler boosting and projection effects are taken into account (Roberts et al. 2010; Bell et al. 2011; Martí et al. 2018), with adiabatic losses playing a major role in the jet emission and following a path accurately described by a kinematic model (Hjellming & Johnston 1981; Margon & Anderson 1989). Using archival data from the Atacama Large Millimeter Array (ALMA) observatory, Martí et al. (2018) confirmed that the energy losses of radiating electrons in the jet are dominated by adiabatic expansion instead of synchrotron radiative losses.

Precession of the jet in SS433 has been extensively studied at different wavelengths for decades. Apart from its apparent shape, it was observed in both the Doppler-shifted X-ray with the EXOSAT satellite (Watson et al. 1986) and optical (Margon et al. 1979) emission lines, from which precessional parameters could be determined. The exhaustive monitoring of the source led to the obtention of its power spectrum, thus allowing a time-series analysis which has resulted in SS433 being the only XRB with a measured orbital, precessional, and nutational period thus far (Eikenberry et al. 2001).

Medvedev et al. (2018) studied SS433 on the X-ray domain using data from Chandra to describe the hard component of the spectra by including a hot extension of the jets, which is optically thick to low energy photons (E < 3 keV), but progressively optically thinner to higher energy photons. This serves as a source of high dense absorption to the central source and lower parts of the jets, as well as an up-scattering component of soft photons emitted by the visible part of the jets.

Although SS433 has been extensively studied in the X-ray domain, data from the NuSTAR satellite have not been completely exploited yet. The NuSTAR observatory operates up to very hard X-ray energies (3 to 79 keV) with spectral resolutions of 0.4 keV at 10 keV and 0.9 keV at 68 keV. The combination of emission line spectroscopy with the study of hard X-ray continuum emission should thus provide a more detailed description of SS433.

In this article we present a spectral analysis of a publicly-available dataset consisting of ten NuSTAR observations of SS433, performed between October 2014 and July 2015. The paper is structured as follows: we present the observations and data reduction in Sect. 2. In Sect. 3, we show the results of our X-ray spectral analysis in the context of a kinematic model for the SS433 precessing jet. Finally, in Sects. 4 and 5 we draw and present our main conclusions derived from our results.

In a recent paper, Middleton et al. (2021) have also exploited the same NuSTAR dataset. In their work, they focussed on the analysis of the time-resolved covariant spectrum, as well as the associated frequency- and energy-dependent time lags, which they used to constrain physical properties of the accretion regime, associated with different scenarios for SS433. In our work, we analyse the complete dataset of ten observations, without disregarding any of them, and we focus on the time-averaged, or stationary spectra, which we used to derive geometrical and physical properties of SS433 using detailed jet and disk-reflection models, in the context of their mutual precessional motion.

2. Data analysis

NuSTAR observed SS433 ten times between modified Julian dates (MJD) 56934 and 57207 with typical exposures of 20–30 ks in the 0.2–0.3 orbital phase range, spanning over roughly one and a half precessional periods of the source. Details of the observational dataset are given in Table 1. Observations ID span from 30002041002 to 30002041020. From now on, we shorten their Obs names to the last two digits for simplicity. Due to the triggered read-out mechanism of NuSTAR, the spectra derived for a source as bright as SS433 have a great signal-to-noise ratio and are safe from pileup.

Table 1.

NuSTAR observations of SS433.

We processed the data obtained with the two focal plane modules (FPMA and FPMB; Harrison et al. 2013), using the NuSTAR Data Analysis Software (NUSTARDAS) available via the HEASOFT v6.28 package. The observation files were reduced with the NUPIPELINE tool using CALDB v.20200429. We generated source and background spectra, as well as the ancillary and response matrices for each observation using the NUPRODUCTS script. We extracted photons in circular regions of 50–70 arcsec centred at the centroid of the source and of 70–100 arcsec for the background, using the same chip, in regions that were not contaminated by the source. The X-ray spectral analysis was performed using XSPEC (Arnaud 1996) considering the 3–70 keV energy range, as we did not detect significant emission from the source over the background level at higher energies.

In order to filter the southern Atlantic anomaly (SAA) passages, we applied different criteria depending on the individual observation reports1. We also performed the standard analysis SAAMODE=NONE and TENTACLE=NO and checked the dependence of our results on this filtering. For each observation, we found that the spectral parameters were consistent within the errors. We performed a similar check by considering two different spectral backgrounds, and we obtained consistent results.

For Obs10, the total exposure of Science Mode 01 was about 3 ks. We thus reduced the Spacecraft Mode 06 data by means of the standard splitter task NUSPLITSC. Using the camera head unit CHU12 combination in STRICT mode, we obtained an enhanced exposure of 12.59 ks, and we used this dataset for the spectral analysis.

In Table 1 we show the ten observations and their characteristics including the operating mode; MJD date; final GTI exposure; precessional, nutational, and orbital phases; as well as the SAA parameters used for GTI filtering and the extraction radii for the spectral analysis. Phases were calculated based on the ephemeris of Eikenberry et al. (2001) and include their corresponding intervals according to their exposure time fraction.

3. Results

3.1. Model setup

In order to investigate the spectral X-ray variability of SS433 along the ten NuSTAR observations, we propose the same spectral model for the whole set of averaged spectra, with similar Galactic absorption, jet, and accretion disk components. In particular, we consider a double neutral Galactic absorption model tbabs with abundances from Anders & Grevesse (1989) and Balucinska-Church & McCammon (1992) cross sections. We fixed the Galactic absorption parameter throughout our entire spectral analysis to a value of NH = 0.67 × 1022 cm−2 (Marshall et al. 2002; Namiki et al. 2003), while leaving local absorption free. In XSPEC this double absorption component reads tbabs*tbabs.

To account for cross-calibration uncertainties between both NuSTAR instruments FPMA and FPMB, we included a constant factor between each spectrum (constant model in XSPEC). We checked that this constant remains in the 3% level for all the epochs, which is inside the expected 0–5% range (Madsen et al. 2015). The spectra were grouped to a minimum of 30 counts per bin to properly use χ2 statistics. Throughout this paper, we quote parameter uncertainties to a 90% confidence level, which was computed using the XSPEC CHAIN task with the Goodman–Weare algorithm and 360 walkers (20 times the number of free parameters).

To check for convergence of Markov chain Monte Carlo (MCMC) chains, we visually inspected the chains of each parameter and determined the most appropriate number of burn-in steps in order to obtain uncorrelated series for the parameters of interest. We corroborated this method by computing the integrated autocorrelation time associated with each series, and verified that it remained as close to unity as possible (see documentation2 on the PYTHON-EMCEE package for more details). We found that a total length of 1.2 × 107 with a burn-in phase of 6 × 106 was sufficient for all ten observations to reach convergence.

In Fig. A.1 we show an example of a parameter chain series with the computed, integrated autocorrelation time τ.

To represent the X-ray emission from the jet in SS433, we considered a spectral model developed by Khabibullin et al. (2016). We adopted the SS433 flavour which has the jet opening angle and bulk velocity fixed at Θ = 0.024 rad and β = 0.2615, respectively. This table model depends on the jet kinetic luminosity Lk, the jet base temperature To, and the electron transverse opacity τe0 at the base of the jet. The model also includes iron and nickel abundances. By considering a distance of ds = 5.5 kpc (Blundell & Bowler 2004), the model normalisation can be expressed as 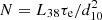, where L38 = Lk/1038 erg s−1 and d10 = ds/10 kpc.

To account for the western jet contribution, we included a second additive table model multiplied by an attenuation factor 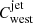(constant in XSPEC). The western jet parameters were linked to that of the eastern jet. Both table models were loaded in the XSPEC environment by means of the atable command. To account for the precessional motion of the jet (Doppler shifting and boosting), we included a convolution model (zashift in XSPEC) to each table model. A Gaussian smoothing component gsmooth (with index α = 1) was also added to take the broadening of the emission lines into account, which was caused by the gas expansion of the ballistic jet. Therefore, both jet X-ray spectra were modelled by zashift*bjet+constant*zashift*bjet, in XSPEC language.

To account for the accretion disk emission, we included a linear combination of direct thermal emission from a black-body spectrum (diskbb), which significantly contributes at energies below 5 keV, and pure-reflected neutral (xillverCp; García et al. 2013) and relativistic-emission spectra (relxilllpCp; Dauser et al. 2014). For both of the latter components, we chose to use the coronal flavours (Cp). In the relativistic case, we chose the lamp post geometry (lp). These reflection components contribute both to the ionised iron clomplex at ∼6.7 keV, and to the hard excess at 20–30 keV through the Compton hump.

In summary, the complete disk emission spectrum was modelled by diskbb+xillverCp+relxilllpCp. The free parameters are the following: the temperature kTdbb and the normalisation of the black-body component Ndbb; the incident photon spectrum index Γ, the ionisation degree ξ, the inclination angle ϕ, and normalisation of the xillverCp component; and the source height h above the disk of the relxilllpCp component. The reflection fraction was set to −1 in order to obtain only the reflected spectrum. The iron abundance and coronal temperature of the xillverCp component were tied to their respective analogues of the bjet components. All identical parameters of both reflection components were tied together. The remaining parameters were left frozen to their default values.

The resulting best-fitting parameters of the entire model are shown in Table A.1. In Fig. A.2 we show a simplified picture of the SS433 jet-disk system, indicating each model contribution to the total X-ray spectra.

3.2. Broadband description

In the left panels of Fig. 1, we show the spectra for observations #14 (ψpre ∼ 0.71) and #08 (ψpre ∼ 0.06) and their best fits along with their residuals. These two examples show two very different instances of precessional motion. Observation #14 has both jets at similar Doppler shifts and thus shows overlapping emission lines (unresolvable by NuSTAR). Observation #08 has the eastern and western jet at opposing Doppler shifts, and thus shows iron and nickel emission lines perfectly resolvable by NuSTAR (dashed and dot-dashed lines). We also clearly see the different disk component contribution (dotted lines) at very soft energies (E < 5 keV; diskbb), the Fe Kα line (∼6.4 keV; xillverCp), and the harder (E>20 keV) reflected component (both xillverCp and relxilllpCp).

thumbnail Fig. 1.

Spectral behaviour of SS433 on two distinct precessional phases. Left column: sample of NuSTAR FPMA/B averaged spectra fitted with a combination of bjet, diskbb, xillverCp, and relxilllpCp. The dashed line corresponds to the eastern jet model component. The dot-dashed line corresponds to the western jet model component. Dotted lines correspond to the different disk model components. Right column: one- and two-dimensional distribution of some continuum model parameters derived from the MCMC simulations. The outward colour gradient indicates the following confidence levels: 90%, 99%, 99.9%, and 99.99%. See Table A.1 for details on parameters units.

The soft energy range of the NuSTAR spectra (E < 10 keV) is dominated by the contribution of one or both jets and the thermal disk component. In highly blue-shifted phases (ψpre < 0.2 and ψpre > 0.8), the western jet contribution to the total flux seems to be ∼0.1–0.3 times that of the eastern jet, as modelled by the attenuation factor. During the in-between phases, when the merging of emission lines starts to occur, the western jet contributes significantly more, with factors ranging from 0.6 to 1.

The absorption column density does not seem to vary significantly among the different precessional phases. It stays somewhat high and constant at an average value of 12 × 1022 cm−2. We must note that the NuSTAR lower energy detection limit of 3 keV does not allow for this parameter to be constrained better. Furthermore, the black-body component also dominates at very low energies, so the absorption column and black-body parameters (temperature and normalisation) are tightly correlated (see the left panel of Fig. 2).

thumbnail Fig. 2.

Precessional evolution of different parameters of the disk components. Left panel, top to bottom: local absorption column, diskbb inner radius temperature, and inner radius. Right panel, top to bottom: incident spectral index, ionisation degree, inclination angle, and source height.

Using the thermal diskbb component, we get an inner temperature that ranges from approximately 0.36–0.42 keV. This model normalisation Ndiskbb can be used to estimate the inner disk radius Ndiskbb = (fcRdiskbb/d10)2 cos ϕ, where fc = 1.7 is the colour–temperature correction factor (Kubota et al. 1998), and ϕ is the angle between the normal to the disk and the line of sight. As shown in the bottom left panel of Fig. 2, we see that this parameter remains very well constrained between 1 and 5 × 107 cm (10–60 rg for MBH = 3 M⊙).

As already mentioned in the previous section, the bjet model normalisation can be expressed in terms of Lk and τe0 by fixing a distance to the source. We constrained the value of Lk * τe0 and used it as a measure of the jet kinetic power (Khabibullin et al. 2016) transverse to the outflow axis. We report the best bjet parameters in the right panel of Fig. 3. The jet kinetic luminosity ranges from between 1 and 10 times the Eddington luminosity (∼1038 erg s−1), with higher values at extreme precessional phases. The temperature at the base of the jet (where it becomes visible in X-rays) ranges from 12 to 18 keV (within errors), averaging ∼15 keV. The base electron optical depth ranges from between ∼0.1 and its maximum accessible value of 0.5.

thumbnail Fig. 3.

Precessional evolution of bjet and system parameters derived from the 3–70 keV fit to NuSTAR spectra. Left panel, top to bottom: Bulk velocity factor β = v/c, jet inclination angle ϕ, jet opening angle Θ, and western jet attenuation factor. Right panel, top to bottom: jet kinetic luminosity weighted by opacity Lk × τe0 (1038 erg s−1), jet base temperature To, and ratio of nickel-to-iron abundances.

We notice the nickel overabundance with respect to iron already reported in Medvedev et al. (2018). The nickel-to-iron abundance ratio varies from between 5 and 15, being highest during the intermediate phases. Although an apparent precessional motion of this ratio can be seen (bottom right panel of Fig. 3), it can be thought to be constant at ∼9 within 1σ.

The disk continuum parameters show a more intricate behaviour. The incident power-law index ranges from between 1.6 and 2, and it has the lowest value of ∼1.4 for observation #02. It becomes harder towards intermediate phases, pointing to a weaker jet-dominated state. It is interesting to note that the spectral index of the pexmon component used by Middleton et al. (2021) to fit the average spectra, which was tied across all eight observations, is considerably harder than the one found in the fits to the covariance spectrum (∼1.4 and ∼2.2, respectively). Our results lie between these two boundaries, which shows that our precessional analysis is compatible with the fits to the time-resolved covariance spectra.

Both ionisation degree ξ and inclination angle ϕ do not seem to follow any particular precessional behaviour, but instead they seem anti-correlated somehow. At lower inclination angles, the ionisation degree increases. This may indicate that at lower (higher) inclinations, we see more (less) of the inner and hotter regions of the accretion disk, and thus this is seen as a higher (lower) ionisation degree of the reflecting material.

Lastly, the illuminating source height h ranges (within errors) from between 0.2 and 9 × 107 cm (3–100 rg for MBH = 3 M⊙), taking lower values (with lower relative errors) towards extreme phases. This effect might be related to the fact that the more edge-on the accretion disk is seen, the weaker the contribution is to the total flux from reflection, and thus, the most important the contribution is of direct emission. This makes the height parameter more difficult to constrain.

In the right column of Fig. 1, we present the triangle plot of observations #14 and #08, where the diagonal subplots represent the one-dimensional distribution (histogram) of each parameter derived from the MCMC chains. The remaining subplots contain the two-dimensional distribution of values of the ith column parameter with the jth row parameter. Colours indicate different confidence levels: 90% (red), 99% (green), and 99.9% (blue). For better display purposes, we show only a subset of the parameters. The top label above each parameter histogram indicates the relevant parameter name and its best fit value with the 90% confidence level error range. We also included a table of units for clarity.

3.3. Flux evolution and hardness

To further investigate the spectral contributions of the jet and the accretion disk along the precessional motion, we calculated each model’s unabsorbed flux (using the cflux convolution model in XSPEC) in two different bands: soft, 3–10 keV; and hard, 10–70 keV. In the left panel of Fig. 4, we show the precessional evolution of both defined bands for each model component. We only show the ‘eastern’ bjet component, as the remaining ‘western’ one would be the same multiplied by the attenuation factor. We also show the total flux for reference.

thumbnail Fig. 4.

Spectral behaviour of the jet and disk model components. Left panel: precessional evolution of the total flux (3–70 keV) of each model component. Right panel: hardness–intensity diagram (soft: 3–10 keV, hard: 10–70 keV). The diskbb (purple) component was only included in the left panel. Error bars appear smaller than the marker size foralmost all data points.

The eastern jet component dominates and contributes from 30% up to 65% of the total observed flux depending on the precessional phase. The thermal disk component contributes ∼2% almost independently of the phase to the total flux.

In intermediate phases, where the total flux is reduced by a third, the contribution of both jet dominates, while the contribution of the disk comes almost equally from xillverCp and relxilllpCp components. In this phase (0.15–0.85), the disk components contribute up to 30% of the total flux.

For extreme phases, the total flux is distributed as follows: 65% is from the disk (considering the three components) and 45% is from both jets (mainly the eastern jet). Moreover, the neutral reflection component almost has the same flux as the eastern jet component. This could be attributed, in part, to the beaming effect produced by the particular orientation of the system on these phases.

Lastly, we note a similar precessional behaviour between the jet and disk measured fluxes, the attenuation factor, and the illuminating source height. The more edge-on the accretion disk is, the less contribution to total flux from reflection there is, and thus, the more important the contribution is of the direct emission. In these precessional phases, the western jet emission becomes significant as well.

When looking at the spectral distribution within energy bands shown in the right panel of Fig. 4, we see a clear difference between systems. By defining the hardness as the ratio between the measured fluxes of 10–70 keV (hard) to 3–10 keV (soft), we see that the jet component is purely soft X-ray dominated, while the disk components (without the thermal diskbb) is purely hard X-ray dominated. We also note that as the total flux increases, every component tends to have a hardness ratio of 1. Inversely, as total flux decreases, the jet becomes softer and the disk harder.

As a final remark, we note that the total bjet unabsorbed luminosity in the 3–70 keV band (assuming a distance of 5.5 kpc), ranges from 0.2 to 2 × 1038 erg s−1. These values are approximately 2–10 times that of the measured kinetic luminosities (see Fig. 3). For the intermediate phases, the ratio between these two kinds of luminosities is the greatest.

4. Discussion

4.1. Precessing lines and kinematic model

From the obtained values of both jet redshifts Z and the broadening factor of the lines Σ, we used the kinematic model equations in order to compute the bulk velocity of matter across the jet, βjet = v/c. This is the angle sustained by the eastern jet with respect to the observer ϕ and the half opening angle Θ of the jet.

We define ze and zw as the respective eastern and western jet redshifts. Then, by assuming perfect alignment between jets and equal velocities, we have the following:

(1)

By application of kinematic equations (see Cherepashchuk et al. 2018 for a full set of equations), we can express the angle between the jet axes and the line of sight in terms of both jet redshifts:

(2)

Lastly, by considering the line profiles to be Gaussians with dispersion Σ (Eo) (with Eo being the line centroid at rest), we can estimate the jet half opening angle (Marshall et al. 2002):

(3)

The application of these three equations can be seen in the left panel of Fig. 3.

Overall, we get an average bulk velocity factor β ∼ 0.29, and with values (and errors) that increase towards extreme phases. This effect comes from the fact that at higher redshift, the western jet redshift becomes harder to constrain, as its flux becomes significantly lower than the eastern jet, and it competes with the thermal diskbb and the reflection components. For comparison, the reference value obtained from decades of optical data is ∼0.26 (Cherepashchuk et al. 2018).

From the inclination angle, we can derive estimates for the mean inclination of the system and the precession angle that the jet sustain with respect to the axis of rotation. By fitting a linear function to the second half of precessional phases (> 0.5), we get an inclination of approximately 82 deg and a precession angle of ∼23 deg, which are in complete agreement with the ephemeris of Eikenberry et al. (2001).

The half opening angle of the jet can range from between 1 up to 6 degrees, with lower values (but greater relative errors) on intermediate phases (0.15–0.85). This comes from the fact that during these phases, the width of the emission lines becomes harder to constrain as they start to overlap, and with NuSTAR’s resolution they cannot be resolved separately.

An interesting result comes from comparing the expansion velocity of the jet perpendicular to the jet axis (β sin Θ), as well as the sound speed in the rest frame of the flowing gas

(4)

where kTo is the measured temperature of the gas at the base of the jet, mp is the proton mass, μ ∼ 0.62 is the mean molecular weight, and X = ni/ne ∼ 0.91 is the ion-to-electron ratio. We show this relationship in Fig. 5. We note that within errors, the relationship between these parameters holds true for small angles where sin Θ ∼ Θ. By looking at Fig. 3, we see that this corresponds to observations in intermediate phases (0.15–0.85), where Θ < 2 deg. As suggested by Marshall et al. (2002), this relationship might be physical, which would be interpreted as the jet expanding sideways at the sound speed of plasma at its base.

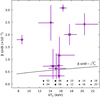thumbnail Fig. 5.

Relationship between the temperature at the base of the jet and the transversal velocity of matter thought the jet. We plot the expected velocity caused by adiabatic expansion of the jet.

4.2. Outflow overview

By following Khabibullin et al. (2016), we can estimate the evolution of some of the initial conditions at the base of the jet, using the derived fit parameters. Namely, the height from the jet cone apex where it becomes visible to an observer,

(5)

and the electron density at this radius,

(6)

As shown in Fig. 6, we see that the jet base (also referred as the truncation radius) is of the order of 1010 cm (∼1.1 × 104 rg for MBH = 3 M⊙), ranging from 0.5 to 5 times this value. By taking averaged values of Θ and ro, we can estimate the size of the jet base roΘ ∼ 5.2 × 108 cm (∼600 rg).

thumbnail Fig. 6.

Precessional evolution of different jet parameters (see text for equations). From top to bottom: jet base height from cone apex, electron density at base height and mass flow rate through the jet.

The electron density at the jet base ne0 ranges from 0.2 to 4 × 1014 cm−3. We note that these two quantities follow a simplified version of the continuity equation, with 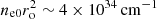remaining constant throughout the jet.

Finally, we can estimate the mass flow through the jet by combining all of the above quantities:

(7)

We show this result in the bottom panel of Fig. 6. We see that the mass flow rate ranges from between 0.4 up to 3 × 10−6 M⊙ yr−1. Assuming a mass of 3 M⊙ for the compact object (Cherepashchuk et al. 2018), we get a maximum of ∼20 times the Eddington mass transfer rate.

For reference, Marshall et al. (2002) obtained a value of ro ∼ 2 × 1010 cm, which lies very well between our estimates. Conversely, they obtained a higher upper limit of 4 × 1015 cm−3 for the electron density at the jet base, which is almost ten times our upper limit. This gives 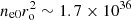cm−1, which is ≲100 times greater than our estimate.

By taking the maximum measured 3–70 keV bjet luminosity (2 × 1038 erg s−1), we can compute the photoionisation degree ξ over the spherical region of size ro and electron density ne0, log ξ = log LX/(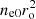)≲4. This means that the illuminating jet power is sufficient to account for the higher ionisation degrees obtained by the reflection components. As already stated by Middleton et al. (2021), the use of more complex reflection models, such as xillverCp and relxilllpCp, provides a more detailed description of the reflecting medium.

The high absorption column obtained in the spectral fits could be associated with a region of the wind around the jets, which separates the visible part from the invisible one. The density of this region provides an appreciable optical depth for photo-absorption, blocking the jet and thermal disk emission at energies below ∼10 keV, but, at the same time, being optically thin for electron scattering, and thus partially scattering photons with higher energies.

This concept has already been developed by Medvedev et al. (2018; cwind model), and they estimate that such a condition would require an absorbing column density NH between 15 and 20 × 1022 cm−2 with an optical depth of the order of 0.1. These estimates are in full agreement with our obtained values for both parameters.

We can estimate the size of this region if we assume that ne0R ∝ NH, in other words a balance of between neutral hydrogen and free electrons. By taking average values of NH and ne0, we get R ∼ 1.5 × 109 cm (∼1700 rg for MBH = 3 M⊙), which is very similar (within errors and approximations) to the accretion disk spherisation radius Rsph ∼ 1.8 × 109 cm ∼ 2000 rg where the accretion regime becomes supercritical (Medvedev et al. 2018). This suggests that the absorbing region originates from the combined effect of the high accretion rate, which generates dense gas structures around the compact object in SS433, as well as the supercritical disk winds which effectively scatter the soft (E < 10 keV) photons.

Middleton et al. (2021) attribute the disk wind cone (Dauser et al. 2017) as being responsible for the lags found at energies up to 9 keV and the hard X-ray excess at 20–30 keV. We framed these results in our scenario by linking the disk wind cone with the combined effect of the reflected spectrum and the central obscuring region.

Specifically, the wind cone model assumes low opening angles (< 10 deg) for velocities β ∼ 0.2–0.4 to show beaming effects, and a cone height of 105 rg ∼ 9 × 1010 cm. Both of these model assumptions are in agreement with the values that we found (β ∼ 0.28–0.32 and ro < 1011 cm).

According to our fitting results, we attribute the reflected spectrum of the accretion disk as being responsible for the hard excess component (see Fig. 4), and make the case for this obscuring region as the wind itself reprocessing Fe XXV and Fe XXVI emission lines (6.7 and 6.97 keV, respectively) and thus shifting them onto higher energies. For this to be possible, we followed calculations by Inoue (2022), who estimated an optical depth of ∼1.6 for a compact object of 10 MBH and a radius of 1012 cm. If we re-scale by the magnitudes used and obtained in our paper, we find that a lower optical depth of τ > 0.02 is sufficient to account for soft-photon scattering. We find optical depths at the jet base τe0 > 0.1 that satisfy the former condition.

5. Conclusions

We have reported on the analysis of ten NuSTAR observations of the Galactic microquasar SS433 that span 1.5 precessional cycles, which were taken from almost the same orbital phase. We modelled the averaged spectra with a combination of two precessing thermal jets (bjet; Khabibullin et al. 2016) and cold (xillverCp; García et al. 2013) and relativistic reflection (xillverCp; Dauser et al. 2014) emission from a black-body-type accretion disk (diskbb). We also included Doppler shifting (zashift) and broadening (gsmooth) components, as well as local and Galactic absorption (tbabs).

Our main results are summarised as follows:

  1. Jet bulk velocity ranges from between 0.28 and 0.32c and the jet half opening angle is ≲6 deg.

  2. The bjet kinetic luminosity ranges from between 2 and 20 × 1038 erg s−1, with an average base temperature of ∼16 keV and a nickel-to-iron ratio of ∼9.

  3. The western jet relative flux with respect to the eastern jet flux ranges from 0.2 for extreme phases up to ∼1 for intermediate phases.

  4. The diskbb component gives an inner disk temperature of ∼0.38 keV with an inner radius of ≲30 rg.

  5. The total 3–70 keV luminosity of both jet and disk reflection components range from between 0.2 and 2 × 1038 erg s−1, with the jet being completely soft X-ray dominated (3–10 keV), and the disk reflection components being hard X-ray dominated (10–70 keV).

  6. We find that at low half opening angles (≲2°), the jet sideways velocity, β sin Θ, can be expressed in terms of the jet base temperature, indicating that it follows an adiabatic expansion regime.

  7. The unabsorbed jet luminosity LX ≲ 2 × 1038 erg s−1 is sufficient to account for the high ionisation degrees (log ξ ≲ 4) obtained from the reflection components.

  8. The central source and lower parts of the jets could be hidden by an optically thick region of τ > 0.1 and size R ∼ NH/ne0 ∼ 1.5 × 109 cm ∼ 1700 rg for MBH = 3 M⊙.

Future works done with observations of higher spectral and temporal resolutions missions, such as NICER, will give a much more detailed description of the geometry and physics of the accretion flow that takes place on the most inner and closest regions to the compact object in SS433. Moreover, it will provide a better understanding of the current picture we have of accretion flows and outflows on ultra luminous X-ray sources (ULX) and X-ray binaries in general.

Acknowledgments

FAF, JAC and FG acknowledge support by PIP 0113 (CONICET). This work received financial support from PICT-2017-2865 (ANPCyT). FAF is fellow of CONICET. JAC and FG are CONICET researchers. JAC is a María Zambrano researcher fellow funded by the European Union -NextGenerationEU- (UJAR02MZ). JAC, JM, FG and PLLE were also supported by Grant PID2019-105510GB-C32/AEI/10.13039/501100011033 from the Agencia Estatal de Investigación of the Spanish Ministerio de Ciencia, Innovación y Universidades, and by Consejería de Economía, Innovación, Ciencia y Empleo of Junta de Andalucía as research group FQM-322, as well as FEDER funds.

References

  1. Abell, G. O., & Margon, B. 1979, Nature, 279, 701 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta., 53, 197 [NASA ADS] [CrossRef] [Google Scholar]
  3. Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
  4. Balucinska-Church, M., & McCammon, D. 1992, ApJ, 400, 699 [Google Scholar]
  5. Bell, M. R., Roberts, D. H., & Wardle, J. F. C. 2011, ApJ, 736, 118 [NASA ADS] [CrossRef] [Google Scholar]
  6. Blundell, K. M., & Bowler, M. G. 2004, ApJ, 616, L159 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cherepashchuk, A. M., Esipov, V. F., Dodin, A. V., et al. 2018, Astron. Rep., 62, 747 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dauser, T., Garcia, J., Parker, M. L., et al. 2014, MNRAS, 444, L100 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dauser, T., Middleton, M., & Wilms, J. 2017, MNRAS, 466, 2236 [Google Scholar]
  10. Díaz, Trigo M., Miller-Jones, J. C. A., Migliari, S., Broderick, J. W., & Tzioumis, T. 2013, Nature, 504, 260 [CrossRef] [Google Scholar]
  11. Eikenberry, S. S., Cameron, P. B., Fierce, B. W., et al. 2001, ApJ, 561, 1027 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fabian, A. C., & Rees, M. J. 1979, MNRAS, 187, 13P [NASA ADS] [CrossRef] [Google Scholar]
  13. Fabrika, S. 2004, AdSpRv, 12, 1 [Google Scholar]
  14. García, J., & Kallman, T. R. 2010, ApJ, 718, 695 [CrossRef] [Google Scholar]
  15. García, J., Kallman, T. R., & Mushotzky, R. F. 2011, ApJ, 731, 131 [CrossRef] [Google Scholar]
  16. García, J., Dauser, T., Reynolds, C. S., et al. 2013, ApJ, 768, 146 [Google Scholar]
  17. García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [Google Scholar]
  18. Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
  19. Hjellming, R. M., & Johnston, K. J. 1981, ApJ, 246, L141 [NASA ADS] [CrossRef] [Google Scholar]
  20. Inoue, H. 2022, PASJ, 74, 991 [NASA ADS] [CrossRef] [Google Scholar]
  21. Khabibullin, I., Medvedev, P., & Sazonov, S. 2016, MNRAS, 455, 1414 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kotani, T., Kawai, N., Aoki, T., et al. 1994, PASJ, 46, L147 [NASA ADS] [Google Scholar]
  23. Kubota, A., Tanaka, Y., Makishima, K., et al. 1998, PASJ, 50, 667 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kubota, K., Ueda, Y., Kawai, N., et al. 2010, PASJ, 62, 323 [NASA ADS] [CrossRef] [Google Scholar]
  25. Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Lockman, F. J., Blundell, K. M., & Goss, W. M. 2007, MNRAS, 381, 881 [NASA ADS] [CrossRef] [Google Scholar]
  27. Madsen, K. K., Harrison, F. A., Markwardt, C. B., et al. 2015, ApJS, 220, 8 [Google Scholar]
  28. Margon, B., Ford, H. C., Grandi, S. A., & Stone, R. P. S. 1979, ApJ, 233, L63 [NASA ADS] [CrossRef] [Google Scholar]
  29. Margon, B. 1984, ARA&A, 22, 507 [NASA ADS] [CrossRef] [Google Scholar]
  30. Margon, B., & Anderson, S. F. 1989, ApJ, 347, 448 [NASA ADS] [CrossRef] [Google Scholar]
  31. Marshall, H. L., Canizares, C. R., & Schulz, N. S. 2002, ApJ, 564, 941 [NASA ADS] [CrossRef] [Google Scholar]
  32. Martí, J., Bujalance-Fernández, I., Luque-Escamilla, P. L., et al. 2018, A&A, 619, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Medvedev, P. S., Khabibullin, I. I., Sazonov, S. Y., Churazov, E. M., & Tsygankov, S. S. 2018, Astron. Lett., 44, 390 [NASA ADS] [CrossRef] [Google Scholar]
  34. Medvedev, P. S., Khabibullin, I. I., & Sazonov, S. Y. 2019, Astron. Lett., 45, 299 [NASA ADS] [CrossRef] [Google Scholar]
  35. Middleton, M. J., Walton, D. J., Alston, W., et al. 2021, MNRAS, 506, 1045 [NASA ADS] [CrossRef] [Google Scholar]
  36. Mirabel, I. F., & Rodríguez, L. F. 1998, Nature, 392, 673 [NASA ADS] [CrossRef] [Google Scholar]
  37. Namiki, M., Kawai, N., Kotani, T., & Makishima, K. 2003, PASJ, 55, 281 [NASA ADS] [CrossRef] [Google Scholar]
  38. Roberts, D. H., Wardle, J. F. C., Bell, M. R., et al. 2010, ApJ, 719, 1918 [NASA ADS] [CrossRef] [Google Scholar]
  39. Robinson, E. L., Froning, C. S., Jaffe, D. T., et al. 2017, Am. Astron. Soc. Meet. Abstr., 229, 344.01 [NASA ADS] [Google Scholar]
  40. Watson, M. G., Stewart, G. C., Brinkmann, W., & King, A. R. 1986, MNRAS, 222, 261 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Complementary Material

In Table A.1 we present the complete best-fit parameters with errors reported to a 90% confidence level, which were extracted from MCMC chains of 7×106 steps (after burning in the same amount) and obtained using 360 walkers (20 times the number of free parameters). To check for MCMC convergence, we visually inspected the chains of each parameter and determined the most appropriate number of burn-in steps in order to obtain uncorrelated series for the parameters of interest. We corroborated this method by computing the integrated autocorrelation time associated with each series, and verified that it remained as close to unity as possible.

Table A.1.

Complete model best fit parameters and fit statistics.

We show an example of a chain ’trace’ plot which converged in Figure A.1. The integrated autocorrelation time τ is very close to unity, which serves as an numerical indicator of the chain convergence.

thumbnail Fig. A.1.

Example of a ’trace’ plot derived from a MCMC chain. The integrated autocorrelation time τ is close to unity, which serves as an indicator of the chain convergence. The colour gradient indicates the density of data points.

In Figure A.2, we present a schematic picture of the microquasar SS433, where the X-ray emission from the jets and the accretion disk components of our scenario are depicted. We also indicate the different geometrical parameters involved, together with specific physical parameters of the model.

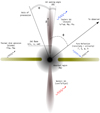thumbnail Fig. A.2.

Schematic view of SS433. Each model component is indicated, with the most relevant parameters of the system.

All Tables

Table 1.

NuSTAR observations of SS433.

In the text
Table A.1.

Complete model best fit parameters and fit statistics.

In the text

All Figures

thumbnail Fig. 1.

Spectral behaviour of SS433 on two distinct precessional phases. Left column: sample of NuSTAR FPMA/B averaged spectra fitted with a combination of bjet, diskbb, xillverCp, and relxilllpCp. The dashed line corresponds to the eastern jet model component. The dot-dashed line corresponds to the western jet model component. Dotted lines correspond to the different disk model components. Right column: one- and two-dimensional distribution of some continuum model parameters derived from the MCMC simulations. The outward colour gradient indicates the following confidence levels: 90%, 99%, 99.9%, and 99.99%. See Table A.1 for details on parameters units.
In the text
thumbnail Fig. 2.

Precessional evolution of different parameters of the disk components. Left panel, top to bottom: local absorption column, diskbb inner radius temperature, and inner radius. Right panel, top to bottom: incident spectral index, ionisation degree, inclination angle, and source height.
In the text
thumbnail Fig. 3.

Precessional evolution of bjet and system parameters derived from the 3–70 keV fit to NuSTAR spectra. Left panel, top to bottom: Bulk velocity factor β = v/c, jet inclination angle ϕ, jet opening angle Θ, and western jet attenuation factor. Right panel, top to bottom: jet kinetic luminosity weighted by opacity Lk × τe0 (1038 erg s−1), jet base temperature To, and ratio of nickel-to-iron abundances.
In the text
thumbnail Fig. 4.

Spectral behaviour of the jet and disk model components. Left panel: precessional evolution of the total flux (3–70 keV) of each model component. Right panel: hardness–intensity diagram (soft: 3–10 keV, hard: 10–70 keV). The diskbb (purple) component was only included in the left panel. Error bars appear smaller than the marker size foralmost all data points.
In the text
thumbnail Fig. 5.

Relationship between the temperature at the base of the jet and the transversal velocity of matter thought the jet. We plot the expected velocity caused by adiabatic expansion of the jet.
In the text
thumbnail Fig. 6.

Precessional evolution of different jet parameters (see text for equations). From top to bottom: jet base height from cone apex, electron density at base height and mass flow rate through the jet.
In the text
thumbnail Fig. A.1.

Example of a ’trace’ plot derived from a MCMC chain. The integrated autocorrelation time τ is close to unity, which serves as an indicator of the chain convergence. The colour gradient indicates the density of data points.
In the text
thumbnail Fig. A.2.

Schematic view of SS433. Each model component is indicated, with the most relevant parameters of the system.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.