| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 11 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202243746 | |
| Published online | 13 September 2022 | |
Dynamical essence of the eccentric von Zeipel-Lidov-Kozai effect in restricted hierarchical planetary systems
1
School of Astronomy and Space Science and Key Laboratory of Modern Astronomy and Astrophysics in Ministry of Education, Nanjing University,
Nanjing
210023, PR China
e-mail: leihl@nju.edu.cn
2
College of Physics and Electronic Engineering, Taishan University,
Taian
271000, PR China
Received:
10
April
2022
Accepted:
23
May
2022
Aims. The eccentric von Zeipel–Lidov–Kozai (ZLK) effect is widely used to explain dynamical phenomena in a variety of astrophysical systems. The purpose of this work is to clarify the dynamical essence of the eccentric ZLK effect by constructing an inherent connection between this effect and the dynamics of secular resonance in restricted hierarchical planetary systems.
Methods. Dynamical structures of apsidal resonance were studied analytically by means of perturbative treatments. The resonant model was formulated by averaging the Hamiltonian (up to octupole order) over rotating ZLK cycles, producing an additional motion integral. The phase portraits under the resonant model can be used to analyse dynamical structures, including resonant centres, dynamical separatrices, and islands of libration.
Results. By analysing phase portraits, five branches of libration centres and eight libration zones are found in eccentricity-inclination space. The analytical results of the libration zone and the numerical distributions of the resonant orbit agree very well, indicating that the resonant model for apsidal resonances is valid and applicable. Additionally, we found that in the test-particle limit, the distributions of flipping orbits are dominated by the apsidal resonances that are centred at an inclination of i = 90°.
Conclusions. The eccentric ZLK effect is dynamically equivalent to the effect of apsidal resonance in restricted hierarchical planetary systems. The dynamical response of the eccentric ZLK effect (or of the effect of apsidal resonance) is to significantly excite the eccentricities and/or inclinations of test particles in the very long-term evolution.
Key words: methods: analytical / planets and satellites: dynamical evolution and stability / celestial mechanics
© H. Lei and Y.-X. Gong 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Hierarchical three-body configurations are common in various astrophysical systems, ranging from satellite and planet scales to supermassive black holes (Naoz 2016). Under the test-particle approximation, this configuration reduces to the so-called restricted hierarchical three-body problem, where the test particle moves around the central body under the gravitational perturbation from the perturber. For a situation in which the perturber moves on a circular orbit, Kozai (1962) and Lidov (1962) studied the long-term dynamics of test particles and found that a resonance occurs between the longitude of pericentre ϖ and the longitude of ascending node Ω when the inclination is greater than 39.2°. In the long-term evolution, coupled oscillations between eccentricity and inclination are called standard Kozai–Lidov oscillations (or Kozai–Lidov effect; Lithwick & Naoz 2011). About the same issue, Ito & Ohtsuka (2019) pointed out that Von Zeipel (1910) performed a similar analysis; thus they suggested to refer to this mechanism as the von Zeipel–Lidov–Kozai (ZLK) effect.
Under the circular assumption (for the orbit of perturber), the vertical angular momentum 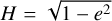 cos i is conserved in the long-term evolution, showing that the orbits of test particle cannot flip between prograde and retrograde. This means that the standard ZLK effect cannot lead to the phenomenon of orbit flips. However, the situation is different when the circular assumption is relaxed. In this context, the Hamiltonian needs to be formulated up to the octupole order in the semi-major axis ratio. Under the octupole-level approximation, the vertical angular momentum is no longer constant (Naoz 2016). In particular, long-timescale modulations of the Kozai–Lidov cycle can force the variation of vertical angular momentum H, leading to striking features including flipping between prograde and retrograde, extremely high eccentricities, and chaotic behaviours (Katz et al. 2011). This mechanism can be referred to as the eccentric ZLK effect (Ito & Ohtsuka 2019). It has been used to interpret various dynamical phenomena in astrophysical systems (Libert & Tsiganis 2009; Shevchenko 2016; Naoz 2016). In the test-particle limit, Antognini (2015) investigated the timescales of ZLK oscillations at quadrupole- and octupole-order dynamical models.
cos i is conserved in the long-term evolution, showing that the orbits of test particle cannot flip between prograde and retrograde. This means that the standard ZLK effect cannot lead to the phenomenon of orbit flips. However, the situation is different when the circular assumption is relaxed. In this context, the Hamiltonian needs to be formulated up to the octupole order in the semi-major axis ratio. Under the octupole-level approximation, the vertical angular momentum is no longer constant (Naoz 2016). In particular, long-timescale modulations of the Kozai–Lidov cycle can force the variation of vertical angular momentum H, leading to striking features including flipping between prograde and retrograde, extremely high eccentricities, and chaotic behaviours (Katz et al. 2011). This mechanism can be referred to as the eccentric ZLK effect (Ito & Ohtsuka 2019). It has been used to interpret various dynamical phenomena in astrophysical systems (Libert & Tsiganis 2009; Shevchenko 2016; Naoz 2016). In the test-particle limit, Antognini (2015) investigated the timescales of ZLK oscillations at quadrupole- and octupole-order dynamical models.
Naoz et al. (2011) found that planetary orbits can flip between prograde and retrograde with respect to the invariant plane of the system due to the eccentric ZLK effect. They proposed a possible clue for forming hot Jupiters on retrograde orbits by combining the eccentric ZLK effect with tidal friction at the late stage. To analytically understand the eccentric ZLK effect, Katz et al. (2011) performed an average for the secular equations of motion over the period of the Kozai–Lidov cycle and found a new constant of motion. In particular, they derived an analytical criterion for orbit flips. At the same time, Lithwick & Naoz (2011) performed a numerical investigation of the eccentric ZLK effect. They numerically mapped the initial conditions for which flipping orbits occur for various values of ϵ (ϵ stands for the contribution of the octupole-order Hamiltonian). By using surfaces of section and Lyapunov exponents, Li et al. (2014a) studied the chaotic and quasi-periodic evolutions caused by the eccentric ZLK effect. For the same topic, Li et al. (2014b) classified flipping orbits into two types: the low-eccentricity, high-inclination (LeHi) case, and the high-eccentricity, low-inclination (HeLi) case. They pointed out that the first type of flipping orbit is governed by the joint effect of quadrupole-order and octupole-order resonances, and the second type of flipping orbit is dominated by octupole-order resonances (Li et al. 2014a,b). Recently, Sidorenko (2018) interpreted the eccentric ZLK effect working in the LeHi space as a resonant phenomenon. In a recent work (Lei 2022), a systematical study was performed for the dynamics of orbit flips caused by eccentric ZLK effect through three approaches: Poincaré surfaces of the section, dynamical system theory (periodic orbit and invariant manifold), and perturbative treatments. Through these studies, the dynamical essence of flipping orbits is very clear: flipping orbits are a kind of quasi-periodic (or resonant) trajectory around stable, polar, periodic orbits (Sidorenko 2018; Lei 2022).
However, the dynamical essence of the eccentric ZLK effect is not clear. We know that the eccentric ZLK effect is the dynamical response under the octupole-level Hamiltonian model. This means that there must be a certain correspondence between the secular dynamics and the eccentric ZLK effect. Based on this consideration, the purpose of this work is twofold. The first purpose is to analytically explore the dynamical structures of secular resonances (apsidal resonances) under the octupole-level approximation by means of the perturbative treatments developed by Henrard & Lemaitre (1986) and Henrard (1990). This theory was adopted by Sidorenko (2018) to study the same topic. The second purpose is to construct the dynamical connection between the eccentric ZLK effect and apsidal resonances at the octupole-level approximation in restricted hierarchical planetary systems. Our results show that (a) the webs of apsidal resonance constitute basic backbones imbedded in phase space that govern the very long-term dynamics of particles, (b) in the test-particle limit, the eccentric ZLK oscillations are attributed to the effect of apsidal resonance, and (c) only apsidal resonances with centres at i = 90° may cause orbit flips.
Throughout this study, the inherent connection between the eccentric ZLK effect and apsidal resonances becomes clear: from the point of view of dynamics, the eccentric ZLK effect is equivalent to the effect of apsidal resonance under the octupolelevel approximation in restricted hierarchial planetary systems. The dynamical consequence of the eccentric ZLK effect (or the effect of apsidal resonance) is to significantly excite eccentricities and/or inclinations of test particles in the long-term evolution. In particular, the behaviour of orbit flip is just one kind of dynamical response due to the eccentric ZLK effect (or the effect of apsidal resonance). In this sense, the present work can be considered as an extension of the resonant interpretation of the eccentric ZLK effect (Sidorenko 2018).
The remaining part of this work is organised as follows. In Sect. 2, the Hamiltonian model is briefly introduced under the test-particle and octupole-order approximation. In Sect. 3, the fundamental frequencies and nominal location of apsidal resonance are identified under the quadrupole-order Hamiltonian flow. Resonant model for apsidal resonances is formulated in Sect. 4 by means of first-order perturbation theory. Results including the dynamical structures, libration zones, and applications are presented in Sect. 5. Finally, the conclusions of this work are summarised in Sect. 6.
2 Hamiltonian model
We investigated secular resonances for an inner test particle moving around a central star under gravitational perturbation from a distant planet. This dynamical model is called a restricted hierarchical planetary system. It is widely adopted as the basic dynamical model for studying secular dynamics in various astro-physical systems (Lithwick & Naoz 2011; Li et al. 2014a,b; Sidorenko 2018; Luo et al. 2016; Lei et al. 2018; Lei 2019, 2021a,b, 2022; Katz et al. 2011; Antognini 2015). The mass of the central star is denoted by m0 and the mass of the perturber is denoted by mp. In the test-particle limit, the orbit of the perturber around the central star is unchanged, while the test particle moves around the central star on a perturbed Keplerian orbit. Under this hierarchical configuration, the invariant plane of the system is coincident with the orbit of the perturber.
For convenience, we introduce a right-handed inertial reference frame, with the origin at the central star, the x-y plane at the invariable plane (i.e. the perturber’s orbit), the x-axis along the eccentricity vector of the perturber’s orbit, and the z-axis parallel to the vector of the total angular momentum. In this coordinate system, the orbits of the test particle (perturber) are described by the semi-major axis a(ap), the eccentricity e(ep), the inclination i(ip), the longitude of the ascending node Ω(Ωp), the argument of pericentre ω(ωp), and the mean anomaly M(Mp). For both prograde and retrograde configurations, the longitude of pericentre and mean anomaly can be defined in a general manner (Shevchenko 2016)
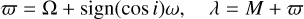
for the perturber. Here, sign(x) is a sign function of x and it is equal to 1.0 when x is greater than zero and it is equal to −1.0 when x is smaller than zero. In the chosen reference frame, ip = 0 and ϖp = 0 (this is due to the setting that the x-axis is along the eccentricity vector of the perturber orbit). If not stated otherwise, we adopt the variables with subscript p for the perturber and variables without subscripts for the test particle.
In the long-term evolution, the short-period terms arising in the Hamiltonian can be filtered out by means of double-averaging techniques over the orbital periods of the test particle and the perturber (Ford et al. 2000; Naoz et al. 2013; Naoz 2016; Luo et al. 2016; Shevchenko 2016; Lei et al. 2018; Lei 2019). This process of phase averaging is called secular approximation (Naoz 2016). Due to the hierarchial configuration, the semi-major axis ratio 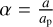 is a small parameter, leading to the fact that the Hamiltonian can be truncated at a certain order in the semi-major axis ratio. The Hamiltonian truncated at the second order corresponds to the quadrupole-level approximation, and the Hamiltonian truncated at the third order corresponds to the octupole-level approximation.
is a small parameter, leading to the fact that the Hamiltonian can be truncated at a certain order in the semi-major axis ratio. The Hamiltonian truncated at the second order corresponds to the quadrupole-level approximation, and the Hamiltonian truncated at the third order corresponds to the octupole-level approximation.
The (normalised) double-averaged Hamiltonian, up to the octupole order in the semi-major axis ratio, can be written as (Lithwick & Naoz 2011; Naoz 2016)
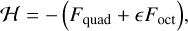 (1)
(1)
where the coefficient ϵ, measuring the significance of the octupole-order contribution, is a small parameter, given by
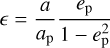
showing that when the semi-major axis ratio 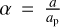 or the eccentricity of the perturber ep is higher, the contribution of the octupole-order term is greater. The quadrupole-order term is given by
or the eccentricity of the perturber ep is higher, the contribution of the octupole-order term is greater. The quadrupole-order term is given by
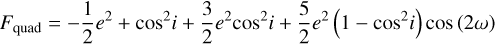
and the octupole-order term is given by
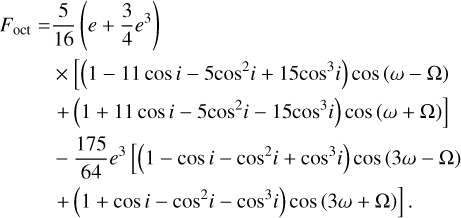
The double-averaged Hamiltonian up to an arbitrary order in α can be found in Laskar & Boué (2010) and Lei (2021a).
In order to formulate the Hamiltonian model, a set of (normalised) Delaunay variables are introduced as follows (Lithwick & Naoz 2011):
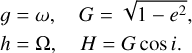
In terms of Delaunay’s variables, the Hamiltonian can be further expressed as follows:
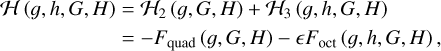 (2)
(2)
which determines a dynamical model with two degrees of freedom. The canonical Hamiltonian relations lead to the equations of motion as follows (Morbidelli 2002):
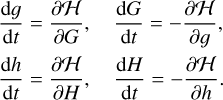 (3)
(3)
The Hamiltonian given by Eq. (2) holds the following symmetries (Sidorenko 2018):
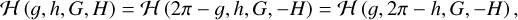
which implies that the solution curves under the Hamiltonian flow are symmetric with respect to H = 0 (i.e. i = 90°). The unique parameter (ϵ) characterizes the dynamical model. The effectiveness of the standard double-averaging process requires that ϵ should be a small parameter (ϵ ≪ l) and the mass of the perturber should be much lower than that of the central star (mp ≪ m0) (Naoz 2016; Luo et al. 2016; Lei et al. 2018; Lei 2019). For all the following simulations, the dynamical model with system parameter ϵ = 0.03 is adopted as an example. Without doubt, the method adopted in this work is applicable to dynamical models specified by other values of ϵ.
 |
Fig. 1 Phase portrait (level curves of Hamiltonian in the phase space) with the motion integral at ∣H∣ = 0.5 (corresponding to the critical inclination at ic = 60° or ic = 120°) under the quadrupole-order Hamiltonian model. The ZLK centre is marked by the black dot, and the dynamical separatrix is shown as a red line. The regions filled with circulating and librating ZLK cycles are divided by the dynamical separatrix expressed by ℋ2 + H2 = 0. For the current example, the phase space with ℋ2 > −0.25 is of ZLK libration and the space with ℋ2 < −0.25 is of ZLK circulation. |
3 Nominal location of the apsidal resonance
In this section, we identify the fundamental frequencies under the quadrupole-order dynamical model. Based on this, we determine the nominal location of secular resonance.
The quadrupole-order Hamiltonian ℋ2 is very simple and can be written as
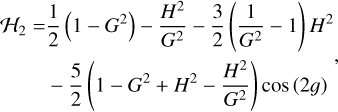 (4)
(4)
where the angular coordinate h is absent from ℋ2, indicating that the z-component of the angular momentum H is conserved under the quadrupole-order model. The conserved quantity H can be specified by the critical inclination ic (when the eccentricity is assumed as zero) of the manner (Kozai 1962)
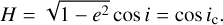
In the following discussions, we often use ic to stand for H. The dynamical model determined by ℋ2 is of one degree of freedom. With given H (or ic), the solution curves under the Hamiltonian flow of ℋ2 are usually called the ZLK cycles, including the librating ZLK cycles and the rotating ZLK cycles. Rotating and librating ZLK cycles are divided by means of a dynamical separatrix in the phase space.
The global structures in the phase space can be explored by analysing phase portraits that correspond to level curves of Hamiltonian with given motion integral. As an example, the case of ∣H∣ = 0.5 (corresponding to the critical inclination at ic = 60° or ic = 120°) is considered, and the associated phase portrait is presented in Fig. 1. In this case, the ZLK resonance may occur. At the ZLK centre, the eccentricity and inclination should satisfy (Kozai 1962)
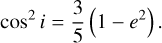
In Fig. 1, the black dot stands for the position of the ZLK centre, at which the Hamiltonian takes its maximum. The dynamical separatrix, shown as a red line, divides the rotating ZLK cycles from the librating ZLK cycles. It is known that the separatrix corresponds to the level curve of a Hamiltonian passing through G = 1 (corresponding to e = 0). Substituting G = 1 into the quadrupole-order Hamiltonian ℋ2 given by Eq. (4), it is not difficult to obtain the expression of the separatrix as (Lei 2021b)
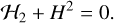
For the current example (the motion integral is taken as ∣H∣ = 0.5), the Hamiltonian of the separatrix is equal to ℋ2 = −0.25. From the phase portrait, we observe that in the phase space, the region with ℋ2 > −0.25 is of ZLK libration and the region with ℋ2 < −0.25 is of ZLK circulation.
Inside the regions filled with ZLK librating cycles, the dynamics is dominated by the quadrupole-order resonance (i.e. ZLK resonance). Only in regions filled with ZLK rotating cycles does the octupole-order resonance play an important role in governing the very long-term behaviours of particles (Li et al. 2014a). Figure 1 further shows that the ZLK cycles starting from 2g = 0 are of circulation. In the following, we focus on the regions that are filled with rotating ZLK cycles, where the octupole-order resonances may appear and dominate the long-term dynamics. Without loss of generality, we fix the initial condition at 2g = 0 for rotating ZLK cycles (Katz et al. 2011; Li et al. 2014a; Sidorenko 2018; Lithwick & Naoz 2011) and then determine the fundamental frequencies in the parameter space spanned by orbit elements (e, i) or conserved quantities (ℋ2, H).
In order to study the dynamics of secular resonance by means of perturbative treatments (Henrard & Lemaitre 1986; Henrard 1990), we introduce the following action–angle variables under the quadrupole-order Hamiltonian flow,
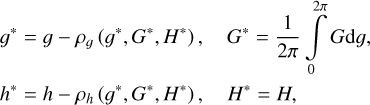 (5)
(5)
which is canonical with the generating function
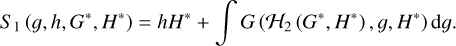
In Eq. (5), ρg and ρh are periodic functions with the same period of the rotating ZLK cycle. The variable G* is called Arnold action, which stands for the phase-space area bounded by the ZLK cycle (divided by 2π).
Under the quadrupole-order dynamical model, we denote the period of g as Tg and the period of h as Th. Thus, the linear functions of g* and h* can be expressed as
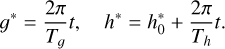
At the initial instant, g* = 0 and 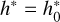 for rotating ZLK cycles.
for rotating ZLK cycles.
In Fig. 2, a rotating ZLK cycle in the phase space (g, G) is shown in the left panel, and the relation between the Arnold action G* and G(0) is plotted in the right panel. In the lef panel, the location of G* for the particular example is marked in red. Evidently, G* is a constant under the quadrupole-order Hamiltonian flow.
In practice, we produce the ZLK cycle as well as the action G* by integrating the following differential equations over one period of ZLK cycle (i.e. Tg) under the quadrupole-order Hamiltonian flow,
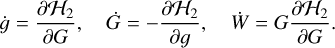
At the initial instant, g0 = 0 and W0 = 0. Here, W(t) stands for the oriented area enclosed by the solution curve G(g) under the quadrupole-level Hamiltonian flow. In particular, when the integration time is equal to one period of the rotating ZLK cycle, it holds
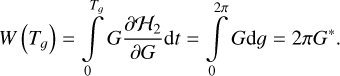
Thus, the Arnold action G* is equal to 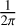 W (Tg). The ZLK cycle G(g) and the Arnold action G* can alternatively be produced by means of elliptic integrals, as presented by Sidorenko (2018).
W (Tg). The ZLK cycle G(g) and the Arnold action G* can alternatively be produced by means of elliptic integrals, as presented by Sidorenko (2018).
According to the generating function, we can obtain an alternative expression for the new set of angles (g*, h*) as follows:
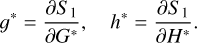
Thus, we can obtain the expressions for computing periodic functions ρg = g − g* and ρh = h − h* as
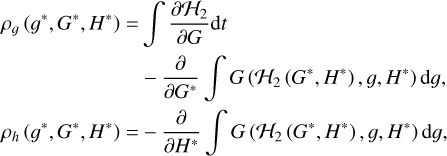
which indicate that ρg = g − g* and ρh = h − h* are equal to zero when g* = 0 or g* = 2π (Henrard 1990). This means that the old and new sets of angles are coincident at the initial instant and at one period of ZLK cycle.
For the example shown in the left panel of Fig. 2, the time histories of (g, h) and (g*, h*) are shown in the left panel of Fig. 3. The differences between the old and new sets of angles ρg and ρh as functions of g* are reported in the right panel of Fig. 3. It is observed that (a) the new angles g* and h* are linear functions of time, and (b) ρg and ρh are periodic functions of g* and are equal to zero when g* is at 0, π/2, π, 3π/2, and 2π.
Under the canonical transformation given by Eq. (5), the quadrupole-level Hamiltonian ℋ2 becomes (Henrard 1990)
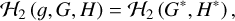 (6)
(6)
which shows that g* and h* are absent from the Hamiltonian ℋ2. This in turn indicates that G* and H* are conserved quantities along the ZLK cycle. The fundamental frequencies under the quadrupole-order dynamical model are identified by
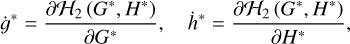 (7)
(7)
which determines the periods of g and h as
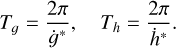
Based on the fundamental frequencies, it is possible for us to determine the nominal location of secular resonance by the following resonant condition:
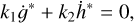 (8)
(8)
where k1; k2 ϵ ℤ.
As for the octupole-order resonance, the critical argument is given by
σ = h* + sign(H*)g*.
In Fig. 4, the solution of 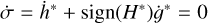 is distributed in (i, e) space in the left panel and in (H, ℋ2) space in the right panel. In the left panel, the eccentricity and inclination are evaluated when the angle g is equal to zero. This is because we fixed 2g = 0 as initial conditions of rotating ZLK cycles. In the right panel, the shaded region shows the ZLK circulation, the upper boundary of circulation region is given by ℋ2 + H2 = 0, and the bottom boundary is given by ℋ2 − H2 + 2 = 0 (Lei 2021b). In both panels, the distribution of the nominal location of the resonant centre is symmetric with respect to i = 90° (or H = 0).
is distributed in (i, e) space in the left panel and in (H, ℋ2) space in the right panel. In the left panel, the eccentricity and inclination are evaluated when the angle g is equal to zero. This is because we fixed 2g = 0 as initial conditions of rotating ZLK cycles. In the right panel, the shaded region shows the ZLK circulation, the upper boundary of circulation region is given by ℋ2 + H2 = 0, and the bottom boundary is given by ℋ2 − H2 + 2 = 0 (Lei 2021b). In both panels, the distribution of the nominal location of the resonant centre is symmetric with respect to i = 90° (or H = 0).
The left panel of Fig. 4 shows that there are three branches of resonant centres in the considered parameter space: one branch corresponds to polar orbits at arbitrary eccentricities, and the other two branches occupy the low-eccentricity space. The latter two branches are called asymmetric families of the resonant centre. The right panel of 4 shows that these two asymmetric branches are close to the upper boundary of the circulation region represented by ℋ2 + H2 = 0 (this boundary corresponds to the ZLK separatrix, as discussed in Fig. 1).
Next, we discuss the essence of the resonance with the critical argument of σ = h* + sign(H*)g*. According to the general definition of the longitude of pericentre ϖ* for prograde and retrograde orbit configurations (Shevchenko 2016),
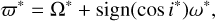
the critical argument σ is equal to the longitude of pericentre ϖ*. Because of the choice of the reference frame, it is known that the longitude of pericentre of the perturber orbit is fixed at zero, that is, ϖp = 0 and 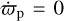 . As a result, we can further write the critical argument as
. As a result, we can further write the critical argument as
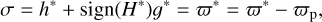 (9)
(9)
which means that in essence, the resonances arising in Fig. 4 are the so-called apsidal resonances with the critical argument of σ = ϖ* − ϖp. For simplicity, we denote the critical argument of the apsidal resonance as σ = h* + sign(H*)g* in the test-particle limit. Based on the set of Delaunay variables (g, h, G, and H), Sidorenko (2018) defined the critical argument as σ = h + sign(H)g, which was also adopted by Lei (2022). Additionally, Katz et al. (2011) introduced the longitude Ωe = Ω + arctan (tan ω cos i) to describe the very long-term behaviours caused by the eccentric ZLK effect. The relation between Ωe and σ = h + sign(H)g is discussed in Lei (2022).
In the next section, we study the dynamics of apsidal resonance from the point of view of perturbative treatments developed by Henrard & Lemaitre (1986) and Henrard (1990). The core concept is to consider the octupole-order term in the Hamiltonian as the perturbation to the quadrupole-order dynamics.
 |
Fig. 2 Rotating ZLK cycle shown in the phase space (left panel) and the Arnold action G* as a function of G(0) (right panel) under the quadrupole-order Hamiltonian flow. See the text for the definition of the Arnold action G*. For the example shown in the left panel, the initial condition is taken as g0 = 0, h0 = 2π, G0 = 0.9950 and H0 = 0.4975. |
 |
Fig. 3 Old and new sets of angular coordinates (g, h) and (g*, h*) as functions of time (left panel) as well as the differences between them ρg = g − g* and ρh = h − h* as functions of g* (right panel). These two plots correspond to the example shown in the left panel of Fig. 2. |
 |
Fig. 4 Nominal location of apsidal resonance with critical argument of σ1 = h* + sign(H*)g*, shown in (i, e) space (left panel) and in (H, ℋ2) space (right panel). The shaded region in the right panel shows the ZLK circulation. |
4 Resonant Hamiltonian of apsidal resonance
In the previous section, we showed that the apsidal resonances with the critical argument of σ = h* + sign(H*)g* can occur in the considered parameter space. The purpose of this section is to formulate the resonant Hamiltonian by means of first-order perturbation theory (Henrard 1990). This theory was also adopted by Sidorenko (2018).
Under the new set of canonical variables (g*, h*, G*, H*), the Hamiltonian up to the octupole order can be expressed as
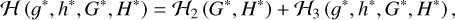 (10)
(10)
where the quadrupole-order Hamiltonian ℋ2 (independent of the angular coordinates) is considered as the unperturbed part, and the octupole-order Hamiltonian ℋ3 plays the role of perturbation to the quadrupole-order dynamics. The magnitude of the perturbation is measured by the small parameter ϵ. In such a perturbed Hamiltonian model, the unperturbed part ℋ2 is also called the kernel function, which yields the fundamental (or proper) frequencies.
In order to study the dynamics of apsidal resonance with the critical argument of σ = h* + sign(H*)g*, the following transformation is introduced:
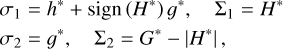 (11)
(11)
which is canonical, with the generating function
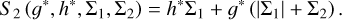
A similar transformation to Eq. (11) was introduced by Sidorenko (2018) and Lei (2022), but based on the set of canonical variables (g, h, G, and H).
Under the new set of canonical variables (σ1, σ2, Σ1, and Σ2), the Hamiltonian can be further written as
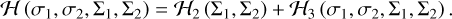 (12)
(12)
It is difficult to obtain the explicit expression of Eq. (12). In practice, we computed the Hamiltonian ℋ numerically when the set of variables (σ1, σ2, Σ1, and Σ2) was given.
At the resonant centre shown in Fig. 4, it holds
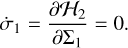
As the octupole-order Hamiltonian ℋ3 is small compared to the quadrupole-order Hamiltonian ℋ2, we can obtain
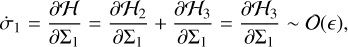
which shows that under the perturbation of the octupole-order interaction, apsidal resonances may also take place.
When the test particle is inside an apsidal resonance, the resonant angle σ1 becomes a long-period variable and the angle σ2 is a short-period variable. This is a separable Hamiltonian system (Henrard 1990). Thus, the terms involving σ2 in the Hamiltonian yield short-period influences. They can therefore be filtered out by means of an averaging technique, which corresponds to the lowest-order perturbation method (Naoz 2016). To this end, we can formulate the resonant Hamiltonian by performing a further average for the Hamiltonian over one period of σ2,
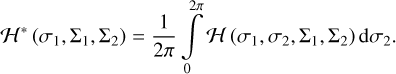 (13)
(13)
Because of the definition σ2 = g*, we can understand that this average is performed over one period of a rotating ZLK cycle under the quadrupole-order Hamiltonian flow (Sidorenko 2018; Katz et al. 2011). Under the dynamical model determined by Eq. (13), the angle σ2 becomes a cyclic coordinate, so that its action Σ2 becomes a constant of motion (or motion integral). The resulting resonant model determined by Eq. (13) has one degree of freedom, depending on the motion integral Σ2.
When the eccentricity is assumed to be zero, the motion integral Σ2 can be specified by a critical inclination i*,
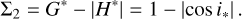 (14)
(14)
The critical inclination i* corresponds to the minimum inclination in prograde space and to the maximum inclination in retrograde space. Clearly, i* and π − i* stand for the same motion integral.
 |
Fig. 5 Phase portraits (level curves of resonant Hamiltonian) of apsidal resonance with critical argument of σ1 = h* + sign(H*)g* at different levels of motion integral specified by i*. Here i* represents the magnitude of motion integral Σ2 (see text for details). i0 shown on the y-axis corresponds to the inclination when the angle g is equal to zero. Dynamical separatrices are marked as red lines. The resonant width, denoted by Δi0, measures the maximum size of the island of libration. |
5 Results
In the previous section, the resonant Hamiltonian for apsidal resonances was formulated as ℋ* Σ1, Σ2), where Σ2 is the motion integral of the resonant model. The global dynamics of apsidal resonance in phase space can be revealed by phase portraits. In this section, we produce phase portraits and then analyse the phase portraits to estimate the resonant width (Lei 2021a, 2022; Lei & Li 2021). We finally construct a connection between the libration zones of the apsidal resonance and the numerical distributions of the resonant orbit (or flipping orbit).
5.1 Dynamical structures of the apsidal resonance
In Fig. 5, the (pseudo-) phase portraits are shown in the i0) space for the motion integral specified by the critical inclination at i* = 30°(150°), 45°(135°), 50°(130°), and 65°(115°). i0 given on the y-axis corresponds to the inclination when the angle g is assumed at zero. This assumption is often used in this work. Dynamical separatrices are marked as red lines, and the resonant width, measuring the maximum size of the island of libration, is denoted by Δi0. Evidently, all the dynamical structures are symmetric with respect to the line of i0 = 90° because of the symmetry of the Hamiltonian function.
When the critical inclination is at i* = 30°(150°) (see the top left panel of Fig. 5), the structure arising in the phase portrait is like a pendulum: there is one resonant centre and one saddle point. The resonant centre is located at (σ1 = 180°, i0 = 90°) and the saddle point is located at (σ1 = 0°, i0 = 90°). The single island of libration is bounded by the dynamical separatrix shown by the red line. As for this low-inclination case, there is another island of libration arising in low-eccentricity space, which is shown in Fig. 6.
When the critical inclination is increased up to i* = 45° (135°) (see the top right panel of Fig. 5), the dynamical structures become complex. In total, there are three islands of libration: one is centred at (σ1 = 0, i0 = 90°), and the other two islands are centred at (σ1 = 180°, i0 ≠ 90°); the latter two islands of libration are symmetric with respect to i0 = 90°. There are three separatrices (shown by the red lines), stemming from three saddle points. These separatrices provide boundaries for three isolated islands of libration in phase space.
When the critical inclination is up to i* = 50°(130°) (see the bottom left panel of Fig. 5), there are also three resonant centres and three saddle points. However, it is different from the case of i* = 45°(135°) because there are only two separatrices: an inner separatrix, and an outer separatrix. The inner separatrix bounds two asymmetric islands of libration, and the outer separatrix bounds the island centred at (σ1 = 0, i0 = 90°) and the island centred at (σ1 = 180°, i0 = 90°). The region bounded by the inner and outer separatrices is also a libration region. The resonant trajectory inside this region holds the maximum variation of the inclination up to ~80°.
When the critical inclination is at i* = 65°(115°) (see the bottom right panel of Fig. 5), the dynamical structure becomes pendulum-like again: there is a single island of libration, centred at (σ1 = 180°, i0 = 90°). Along the resonant trajectory inside this island, the maximum variation of the inclination can reach ~50°.
The phase portraits shown by Fig. 5 indicate that the inclinations of test particles can be effectively excited following the trajectories inside the islands of libration. This significant variation of the orbit orientation is due to the effect of apsidal resonance in the octupole-order Hamiltonian model.
For the low-inclination cases, two examples are presented in Fig. 6 for the cases of i* = 20°(160°) and i* = 30°(150°). Different from Fig. 5, the phase portraits are plotted in(σ1, e0) space. Here e0 corresponds to the eccentricity when the angle g is equal to zero. In addition to the islands shown in Fig. 5 (see the top left panel), a new island arises in low-eccentricity space and is centred at σ1 = 0. The dynamical separatrices are shown as red lines. In these two plots, the resonant width is measured by Δe0. Following the trajectories inside the islands of libration, the eccentricities of the test particles can be excited through the effect of apsidal resonance.
 |
Fig. 6 Phase portraits (level curves of resonant Hamiltonian) for low-inclination cases, shown in (σ1, e0) space. e0 is the eccentricity when the angle g is equal to zero. Dynamical separatrices are marked as red lines. The resonant width, denoted by Δe0, measures the maximum size of the island of libration. |
5.2 Libration zones of the apsidal resonance
By analysing phase portraits at different levels of motion integral Σ2, it is possible for us to identify the location of resonant centre and boundaries of libration zones. The main results of this work are reported in Fig. 7, where the resonant centres are marked as black dots and the libration zones are shown as shaded areas with different colours. The boundaries of each libration zone are provided by the dynamical separatrix evaluated at the angle of the corresponding resonant centre (see Figs. 5 and 6 for representative phase portraits). The level curves of the motion integral Σ2 are plotted as dashed lines as background. The resonant width is measured along the isolines of the motion integral.
Figure 7 shows that the dynamical structures arising in the (e, i) space are symmetric with respect to the line of i = 90°. In total, there are five branches of the libration centres: one branch located on the polar line, two branches occupying the low-eccentricity and low-inclination space, and the remaining twobranches located in the space in which the eccentricities change from ~0 to ~0.4. In addition, there are eight libration zones, denoted by numbers from 1 to 8. The branches of the resonant centres in zones 1 and 2 are absent in the quadrupole-level dynamical model (see Fig. 4 for the nominal location of apsidal resonance). This means that these two branches are present due to the effect of the octupole-order Hamiltonian alone. Except for zones 1 and 2, all the other branches of libration centres are consistent with those shown in Fig. 4.
In libration zone 1 (see Fig. 6 for the representative phase portraits), the bottom boundary is located at e = 0, and the resonant width decreases first and then increases with inclination i. Inside this zone, Funk et al. (2011) found an interesting dynamical region around i ~ 35°, where the low-eccentricity orbits are long-term stable, meaning that an inclined (~35°) quasi-circular Earth-mass companion can survive in the habitable zone of an extrasolar system. Libert & Delsate (2012) explained that the long-term stable dynamics at an inclination of ~35° is due to the secular resonance associated with σ = ω ° Ω. In the low-eccentricity space with i < 39°, Lei (2021a) studied the long-term dynamics by means of Lie series transformation. They reported that the long-term stability inside this zone is governed by the apsidal resonance with an argument of σ = ω + Ω, which is consistent with the result of the present work.
Libration zone 1 has a symmetric zone in the retrograde space, denoted by 2. In this zone, the bottom boundary of the libration is located at e = 0, and the resonant width decreases first and then increases with π − i. Inside zones 1 and 2, the effect of the apsidal resonance is to excite the eccentricities. However, the inclination has little variation during the long-term evolution. The low-eccentricity islands of libration therefore cannot be found in the phase portrait plotted in (σ1, i0) space (see the first panel of Fig. 5).
Libration zone 3 appears when the critical inclination is higher than ~59° and lower than ~121° (see the bottom right panel of Fig. 5 for the representative phase portrait). The eccentricity of this zone ranges from zero to ~0.35. The effect of the apsidal resonance inside this zone is to exchange the eccentricity and inclination of the test particle. The resonant trajectories inside this zone hold resonant centres at i = 90°. Thus all the trajectories inside this zone could flip from prograde to retrograde and back again.
There are two subregions in zone 4: one zone in the prograde space, and the other one in the retrograde space. According to the phase portrait shown in the bottom left panel of Fig. 5, this zone of libration holds centres at i = 90° and is bounded by the inner and outer separatrices. The effect of apsidal resonance inside this zone is to significantly change the eccentricity and inclination of test particles. In addition, all the trajectories inside this zone could realise flips between prograde and retrograde.
Zones 5 and 6 are symmetric with respect to i = 90°. The top-right panel of Fig. 5 shows the representative phase portrait.
For these two zones, the line of i = 90° provides one boundary, so that the resonant trajectories are restrained in either prograde or retrograde space. This means that the trajectories inside these two zones cannot flip from prograde to retrograde or vice versa.
The phase portraits of last two zones 7 and 8 are shown in the top left and top right panels of Fig. 5. Zone 7 is located in the intermediate-eccentricity region, and zone 8 is located in the high-eccentricity region. Both of them hold resonant centres at i = 90°. As a result, all the resonant trajectories inside these two zones can flip from prograde to retrograde and back again.
Figures 8 and 9 provide comparisons between analytical and numerical results for the libration zones of the apsidal resonance. In particular, Fig. 8 corresponds to apsidal resonances centred at σ1,c = π, and Fig. 9 corresponds to those centred at σ1,c = 0. For analytical results, libration zones 3, 4, 5, 6 and 8 are shown in the left panel of Fig. 8 and libration zones 1, 2 and 7 are presented in the left panel of Fig. 9. To be consistent, the initial conditions of numerical results are assumed as g0 = π and h0 = 0 corresponding to the resonant centre at σ1,c = π, and they are assumed as g0 = 0 and h0 = 0, corresponding to the resonant centre at σ1,c = 0. To produce numerical results, the equations of motion represented by Eq. (3) are numerically integrated over 500 units of dimensionless time. The orbit is recorded as a librating trajectory if the maximum variation of critical argument σ = h + sign(H)g is smaller than 2π during the considered integration period. This means that the critical argument is librating during the integration period. The numerical distributions of the apsidal resonance are shown in the right panels of Figs. 8 and 9. As expected, good agreement can be found between analytical and numerical results, indicating that the resonant Hamiltonian formulated in the previous section is valid and can be applied to explore the dynamics of the apsidal resonance under the octupole-level approximation.
 |
Fig. 7 Resonant centres of apsidal resonance distributed in the inclination-eccentricity space (black dots) and libration zones obtained by analysing phase portraits (shaded areas). The level curves of the motion integral Σ2 are shown as background and the resonant width is measured along the isoline of Σ2. There are eight libration zones, denoted by numbers from 1 to 8. Evidently, the distribution of libration zones is symmetric with respect to the line of i = 90°. |
 |
Fig. 8 Analytical results for the resonant regions for apsidal resonances centred at σ1,e = π (left panel) and the associated numerical results for the distribution of the apsidal resonance (right panel). For the numerical results, the initial condition is g0 = 0 and h0 = π (corresponding to σ1,e = π at the initial instant). In the left panel, level curves of the motion integral Σ2 are presented as background. In the right panel, blue dots stand for resonant trajectories inside islands centred at i = 90°, and red dots show resonant trajectories inside asymmetric islands of libration. The difference arising in the top space is due to the fact that the analytical results are restrained by level curves of the motion integral Σ2. |
 |
Fig. 9 Analytical results for the resonant regions for apsidal resonances centred at σ1,c = 0 (left panel) and the associated numerical results for the distribution of apsidal resonance (right panel). For the numerical results, the initial condition is g0 = 0 and h0 = 0 (corresponding to σ1,c = 0 at the initial instant). In the left panel, level curves of the motion integral Σ2 are presented as background. In the right panel, blue dots stand for resonant trajectories inside islands centred at i = 90°, and red dots show resonant trajectories occurring in low-eccentricity, low-inclination spaces. |
 |
Fig. 10 Analytical results of libration zones for apsidal resonances causing orbit flips (left panel) and the numerical results of flipping regions (right panel). The left panel shows four libration zones causing orbit flips (zones 3, 4, 7, and 8). Apsidal resonances with centres at i = 90° cause orbit flips. The right panel shows three distinct regions of orbit flips, located in low-eccentricity, intermediate-eccentricity, and high-eccentricity space. |
5.3 Application to orbit flips
According to the results given in Fig. 7, it is known that the resonant trajectories with resonant centres at i = 90° can flip from prograde to retrograde and back again. In Fig. 10, analytical results of libration zones causing orbit flips are compared with the numerical distribution of flipping orbits under the octupole-level Hamiltonian model. Four libration zones cause orbit flips (zones 3, 4, 7, and 8). Inside zones 3, 4, and 8, the resonant centres are at σ1,c = π, and inside zone 7, the resonant centres are at σ1,c = 0. Analytical results for the libration zones causing orbit flips are presented in the left panel of Fig. 10.
To be consistent with the analytical results, the initial conditions of numerical results are assumed at g0 = 0 and h0 = 0 for the case of σ1,c = 0, and they are assumed at g0 = 0 and h0 = π for the case of σ1,c = π. Similarly, the equations of motion are numerically integrated over 500 units of dimension-less time. The numerically propagated trajectories are recorded as flipping orbits when the orbit inclinations can switch between prograde and retrograde. The numerical distribution of flipping orbits is shown in the right panel of Fig. 10. Similar numerical results of flipping regions can be found in Lei (2022) under the dynamical model specified by ϵ = 0.1. In particular, the flipping region located in the low-eccentricity space corresponds to the LeHi case and the one located in the high-eccentricity space corresponds to the HeLi case shown in Li et al. (2014b).
The right panel of Fig. 10 shows three distinct flipping regions in (i, e) space: one located in low-eccentricity region, one located in intermediate-eccentricity space, and the third one located in high-eccentricity space. The low-eccentricity region of orbit flips corresponds to libration zones 3 and 4. Inside such a low-eccentricity flipping region, the critical argument σ = h + sign(H)g is librating around π. The intermediate-eccentricity region of flipping orbits corresponds to libration zone 7, where the critical argument σ = h + sign(H)g librates around 0. Finally, the high-eccentricity region of flipping orbits corresponds to libration zone 8, where the critical argument σ = h + sign(H)g librates around π.
The comparison made in Fig. 10 shows an excellent agreement between the analytical and numerical results. The results imply that the dynamics of orbit flips can be well understood with the help of dynamical structures of the apsidal resonance.
6 Conclusions
We studied the dynamics of apsidal resonance by means of perturbation treatments under the octupole-level approximation in restricted hierarchial planetary systems. The Hamiltonian function is composed of the quadrupole-order term ℋ2 and the octupole-order term ℋ3. From the point of view of perturbative treatments, the quadrupole-order Hamiltonian is considered as the kernel function, and the octupole-order Hamiltonian plays the role of perturbation to the quadrupole-order dynamics. By introducing the action-angle variables (a kind of canonical transformation), the quadrupole-order Hamiltonian can be converted to be independent of angular coordinates, leading to the fact that the action variables become conserved quantities under the quadrupole-order Hamiltonian flow. The transformed quadrupole-order Hamiltonian gives rise to the fundamental frequencies (or proper frequencies), which can be used to identify the nominal location of secular resonances. Secular resonances with critical argument of σ = h* + sign(H*)g* occur in the considered parameter space. We have demonstrated that in the test-particle limit, the argument σ = h* + sign(H*)g* can be equivalently expressed as σ = ϖ* − ϖp, which corresponds to apsidal resonances.
To study the dynamics of apsidal resonance, a canonical transformation was introduced. After transformation, it becomes a typical separable Hamiltonian model, so that we can apply first-order perturbation theory to formulate the resonant Hamiltonian model by averaging the Hamiltonian over rotating ZLK cycles. Application of first-order perturbation theory gives rise to a new constant of motion, and the resulting resonant Hamiltonian model has one degree of freedom. Phase portraits (level curves of resonant Hamiltonian with a given motion integral) can be used to analyse the global dynamical structures of apsidal resonance. In particular, the location of the resonance centre, the saddle points, the dynamical separatrix between circulating and librating regions, as well as islands of libration can be determined from the resonant model.
Our main results are reported in Fig. 7. We conclude that (a) dynamical structures are symmetric with respect to i = 90°, (b) there are five branches of libration centres, and (c) there are eight libration zones. The comparisons between analytical and numerical results for libration zones of apsidal resonance shows that they agree well.
Islands of libration centred at i = 90° can cause orbit flips. Thus, libration zones with resonant centres at i = 90° correspond to flipping regions in phase space. To validate this point, the analytical results of libration zones were compared with numerical distributions of flipping orbits. A perfect correspondence can be found between the analytical and numerical results.
Through this study, we can conclude that from the point of view of dynamics, the eccentric ZLK effect is equivalent to the effect of apsidal resonance at the octupole-level approximation in restricted hierarchical planetary systems. The dynamical response of the eccentric ZLK effect (or the effect of apsidal resonance) is to significantly excite eccentricities and/or inclinations (even flipping) of test particles in the very long-term evolution.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Nos. 12073011, 12073019).
References
- Antognini, J. M. 2015, MNRAS, 452, 3610 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B., Kozinsky, B., & Rasio, F. A. 2000, ApJ, 535, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Funk, B., Libert, A.-S., Süli, Á., & Pilat-Lohinger, E. 2011, A&A, 526, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henrard, J. 1990, CeMDA, 49, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Henrard, J., & Lemaitre, A. 1986, Celest. Mech., 39, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Ito, T., & Ohtsuka, K. 2019, Monogr. Environ. Earth Planets, 7, 1 [Google Scholar]
- Katz, B., Dong, S., & Malhotra, R. 2011, Phys. Rev. Lett., 107, 181101 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Laskar, J., & Boué, G. 2010, A&A, 522, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lei, H. 2019, MNRAS, 490, 4756 [NASA ADS] [CrossRef] [Google Scholar]
- Lei, H. 2021a, MNRAS, 506, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Lei, H. 2021b, CeMDA, 133, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lei, H. 2022, AJ, 163, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Lei, H., & Li, J. 2021, MNRAS, 504, 1084 [NASA ADS] [CrossRef] [Google Scholar]
- Lei, H., Circi, C., & Ortore, E. 2018, MNRAS, 481, 4602 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G., Naoz, S., Holman, M., & Loeb, A. 2014a, ApJ, 791, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G., Naoz, S., Kocsis, B., & Loeb, A. 2014b, ApJ, 785, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Libert, A.-S., & Delsate, N. 2012, MNRAS, 422, 2725 [CrossRef] [Google Scholar]
- Libert, A.-S., & Tsiganis, K. 2009, A&A, 493, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lidov, M. 1962, P&SS, 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Lithwick, Y., & Naoz, S. 2011, ApJ, 742, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, L., Katz, B., & Dong, S. 2016, MNRAS, 458, 3060 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A. 2002, Modern Celestial Mechanics: Aspects of Solar System Dynamics (London and New York Taylor & Francis) [Google Scholar]
- Naoz, S. 2016, ARA&A, 54, 441 [Google Scholar]
- Naoz, S., Farr, W. M., Lithwick, Y., Rasio, F. A., & Teyssandier, J. 2011, Nature, 473, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Naoz, S., Farr, W. M., Lithwick, Y., Rasio, F. A., & Teyssandier, J. 2013, MNRAS, 431, 2155 [NASA ADS] [CrossRef] [Google Scholar]
- Shevchenko, I. I. 2016, The Lidov-Kozai Effect-Applications in Exoplanet Research and Dynamical Astronomy (Springer), 441 [Google Scholar]
- Sidorenko, V. V. 2018, CeMDA, 130, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Von Zeipel, H. 1910, Astron. Nachr., 183, 345 [Google Scholar]
All Figures
 |
Fig. 1 Phase portrait (level curves of Hamiltonian in the phase space) with the motion integral at ∣H∣ = 0.5 (corresponding to the critical inclination at ic = 60° or ic = 120°) under the quadrupole-order Hamiltonian model. The ZLK centre is marked by the black dot, and the dynamical separatrix is shown as a red line. The regions filled with circulating and librating ZLK cycles are divided by the dynamical separatrix expressed by ℋ2 + H2 = 0. For the current example, the phase space with ℋ2 > −0.25 is of ZLK libration and the space with ℋ2 < −0.25 is of ZLK circulation. |
| In the text | |
 |
Fig. 2 Rotating ZLK cycle shown in the phase space (left panel) and the Arnold action G* as a function of G(0) (right panel) under the quadrupole-order Hamiltonian flow. See the text for the definition of the Arnold action G*. For the example shown in the left panel, the initial condition is taken as g0 = 0, h0 = 2π, G0 = 0.9950 and H0 = 0.4975. |
| In the text | |
 |
Fig. 3 Old and new sets of angular coordinates (g, h) and (g*, h*) as functions of time (left panel) as well as the differences between them ρg = g − g* and ρh = h − h* as functions of g* (right panel). These two plots correspond to the example shown in the left panel of Fig. 2. |
| In the text | |
 |
Fig. 4 Nominal location of apsidal resonance with critical argument of σ1 = h* + sign(H*)g*, shown in (i, e) space (left panel) and in (H, ℋ2) space (right panel). The shaded region in the right panel shows the ZLK circulation. |
| In the text | |
 |
Fig. 5 Phase portraits (level curves of resonant Hamiltonian) of apsidal resonance with critical argument of σ1 = h* + sign(H*)g* at different levels of motion integral specified by i*. Here i* represents the magnitude of motion integral Σ2 (see text for details). i0 shown on the y-axis corresponds to the inclination when the angle g is equal to zero. Dynamical separatrices are marked as red lines. The resonant width, denoted by Δi0, measures the maximum size of the island of libration. |
| In the text | |
 |
Fig. 6 Phase portraits (level curves of resonant Hamiltonian) for low-inclination cases, shown in (σ1, e0) space. e0 is the eccentricity when the angle g is equal to zero. Dynamical separatrices are marked as red lines. The resonant width, denoted by Δe0, measures the maximum size of the island of libration. |
| In the text | |
 |
Fig. 7 Resonant centres of apsidal resonance distributed in the inclination-eccentricity space (black dots) and libration zones obtained by analysing phase portraits (shaded areas). The level curves of the motion integral Σ2 are shown as background and the resonant width is measured along the isoline of Σ2. There are eight libration zones, denoted by numbers from 1 to 8. Evidently, the distribution of libration zones is symmetric with respect to the line of i = 90°. |
| In the text | |
 |
Fig. 8 Analytical results for the resonant regions for apsidal resonances centred at σ1,e = π (left panel) and the associated numerical results for the distribution of the apsidal resonance (right panel). For the numerical results, the initial condition is g0 = 0 and h0 = π (corresponding to σ1,e = π at the initial instant). In the left panel, level curves of the motion integral Σ2 are presented as background. In the right panel, blue dots stand for resonant trajectories inside islands centred at i = 90°, and red dots show resonant trajectories inside asymmetric islands of libration. The difference arising in the top space is due to the fact that the analytical results are restrained by level curves of the motion integral Σ2. |
| In the text | |
 |
Fig. 9 Analytical results for the resonant regions for apsidal resonances centred at σ1,c = 0 (left panel) and the associated numerical results for the distribution of apsidal resonance (right panel). For the numerical results, the initial condition is g0 = 0 and h0 = 0 (corresponding to σ1,c = 0 at the initial instant). In the left panel, level curves of the motion integral Σ2 are presented as background. In the right panel, blue dots stand for resonant trajectories inside islands centred at i = 90°, and red dots show resonant trajectories occurring in low-eccentricity, low-inclination spaces. |
| In the text | |
 |
Fig. 10 Analytical results of libration zones for apsidal resonances causing orbit flips (left panel) and the numerical results of flipping regions (right panel). The left panel shows four libration zones causing orbit flips (zones 3, 4, 7, and 8). Apsidal resonances with centres at i = 90° cause orbit flips. The right panel shows three distinct regions of orbit flips, located in low-eccentricity, intermediate-eccentricity, and high-eccentricity space. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.