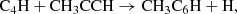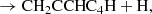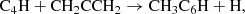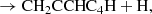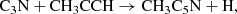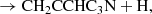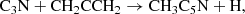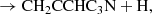| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 12 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202243857 | |
| Published online | 08 July 2022 | |
Letter to the Editor
Discovery of CH2CCHC4H and a rigorous detection of CH2CCHC3N in TMC-1 with the QUIJOTE line survey⋆,⋆⋆
1
Dpt. de Astrofísica Molecular, Instituto de Física Fundamental (IFF-CSIC), C/ Serrano 121, 28006 Madrid, Spain
e-mail: r.fuentetaja@csic.es, jose.cernicharo@csic.es
2
Centro de Desarrollos Tecnológicos, Observatorio de Yebes (IGN), 19141 Yebes, Guadalajara, Spain
3
Observatorio Astronómico Nacional (OAN, IGN), Madrid, Spain
Received:
25
April
2022
Accepted:
6
June
2022
Using the QUIJOTE line survey in the 32.0–50.4 GHz range, we report the discovery of the molecule CH2CCHC4H towards the prestellar cold core TMC-1 in the Taurus region. We also present a rigorous detection of CH2CCHC3N, along with its detailed analysis. We identified a total of twenty rotational transitions for each one of these molecules. The rotational quantum numbers range from Ju = 17 up to 24 and Ka≤ 3. The column density for CH2CCHC4H is N = (2.2 ± 0.2) × 1012 cm−2, while for CH2CCHC3N, we derived N = (1.2 ± 0.15) × 1011 cm−2. The rotational temperature is 9.0 ± 0.5 K for both species. The abundance ratiobetween CH2CCHC4H and CH2CCHC3N is 18 ± 4. We also compared the column densities of these species with those of their isomers CH3C6H and CH3C5N, derived from their J = 20 − 10 up to J = 31 − 30 rotational transitions observed with the QUIJOTE line survey. The observed abundances for all these species are reasonably well explained by state-of-the-art chemical models of TMC-1. The observed astronomical frequencies were merged with laboratory frequencies from the literature to derive improved spectroscopic parameters.
Key words: molecular data / line: identification / ISM: molecules / ISM: individual objects: TMC-1 / astrochemistry
© R. Fuentetaja et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
The recent results obtained towards TMC-1 with the Yebes 40 m radio telescope through the QUIJOTE (Q-band Ultrasensitive Inspection Journey to the Obscure TMC-1 Environment) line survey (Cernicharo et al. 2021a) and those of the Green Bank 100 m telescope with the GOTHAM survey (McGuire et al. 2018) show that this source presents a paramount challenge to our understanding of the chemical processes in cold prestellar cores. Several cyclic molecules have been detected such as cyclopentadiene and indene (Cernicharo et al. 2021b), as well as ortho-benzyne (Cernicharo et al. 2021a), the cyano derivatives of cyclopentadiene, benzene, and naphthalene (McGuire et al. 2018, 2021; McCarthy et al. 2021; Lee et al. 2021), and the ethynyl derivatives of cyclopentadiene (Cernicharo et al. 2021c). Moreover, several extremely abundant hydrocarbons such as propargyl (Agúndez et al. 2021), vinyl acetylene (Cernicharo et al. 2021d), and allenyl acetylene (Cernicharo et al. 2021e) have also been discovered towards TMC-1. Most of these species had not been predicted to exhibit a significant abundance in chemical models prior to their detections. These results indicate that key chemical processes involving hydrocarbons (radical, neutral, ion-neutral, and perhaps dust grain surface reactions) have been neglected in previous chemical networks. Thus, a new chemistry is emerging based on these TMC-1 observations.
The study of ethynyl and cyanide derivatives of hydrocarbons is of paramount importance, as they can allow us to follow the different chemical paths to produce them from a common precursor through reactions involving the CCH and CN radicals (Cernicharo et al. 2021f). In this regard, the discovery in TMC-1 of various isomers with formulae C5H4 and C4H3N allows us to also constrain the chemical schemes behind their formation (Cernicharo et al. 2021e; Marcelino et al. 2021). These schemes involve reactions of CCH and CN with the hydrocarbons CH3CCH and CH2CCH2, allowing for an indirect estimation of the abundance of the non-polar but abundant hydrocarbon allene to be made. The same chemical schemes leading to C5H4 and C4H3N isomers can be extended to longer species by substituting the radicals CCH and CN by their longer equivalents C4H and C3N, which would result in different isomers with formula C7H4 and C6H3N.
In this Letter, we report the discovery of CH2CCHC4H (allenyl diacetylene) using a line survey performed with the Yebes 40 m telescope (QUIJOTE; see Cernicharo et al. 2021a). This species is an isomer of CH3C6H, both with the formula C7H4. We also present a detailed study and a rigorous and robust detection of CH2CCHC3N, an isomer of CH3C5N (both with formula C6H3N) which was recently claimed through stacking techniques by Shingledecker et al. (2021). Each of these large species has small rotational constants. These, together with an unbiased line surveys such as QUIJOTE, allow studying many rotational transitions and, hence, to derive homogeneous and realistic values of their column densities. We investigate the chemistry of these species with the aid of updated gas-phase chemical models.
2. Observations
New receivers built within the Nanocosmos project1 and installed at the Yebes 40 m radiotelescope were used for the observations of TMC-1 (αJ2000 = 4h41m41.9s and 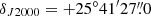 ). A detailed description of the system is given by Tercero et al. (2021). The receiver consists of two cold high electron mobility transistor amplifiers covering the 31.0–50.3 GHz band with horizontal and vertical polarizations. Receiver temperatures in the runs achieved during 2020 vary from 22 K at 32 GHz to 42 K at 50 GHz. Some power adaptation in the down-conversion chains effectively reduced the receiver temperatures during 2021 to 16 K at 32 GHz and 30 K at 50 GHz. The backends are 2 × 8 × 2.5 GHz fast Fourier transform spectrometers with a spectral resolution of 38.15 kHz, providing full coverage of the Q-band in both polarizations.
). A detailed description of the system is given by Tercero et al. (2021). The receiver consists of two cold high electron mobility transistor amplifiers covering the 31.0–50.3 GHz band with horizontal and vertical polarizations. Receiver temperatures in the runs achieved during 2020 vary from 22 K at 32 GHz to 42 K at 50 GHz. Some power adaptation in the down-conversion chains effectively reduced the receiver temperatures during 2021 to 16 K at 32 GHz and 30 K at 50 GHz. The backends are 2 × 8 × 2.5 GHz fast Fourier transform spectrometers with a spectral resolution of 38.15 kHz, providing full coverage of the Q-band in both polarizations.
A detailed description of the QUIJOTE line survey is provided in Cernicharo et al. (2021a). In brief, the present data come from several observing runs between December 2019 and January 2022. All observations were performed in the frequency-switching mode with frequency throws of 8 and 10 MHz. The total on-source observing time for data taken with frequency throws of 8 MHz and 10 MHz is 173.1 and 253.6 h, respectively. Hence, the total observing time on source by December 2021 is 426.7 h. The measured sensitivity varies between 0.12 mK at 32 GHz and 0.25 mK at 49.5 GHz. For each frequency throw, different local oscillator frequencies were used in order to remove possible side band effects in the down conversion chain.
The main beam efficiency varies from 0.6 at 32 GHz to 0.43 at 50 GHz (Tercero et al. 2021). Pointing corrections were derived from nearby quasars and SiO masers and the errors were always within 2–3″. The telescope beam size is 56″ and 31″ at 31 and 50 GHz, respectively. The intensity scale used in this work, antenna temperature (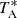 ), was calibrated using two absorbers at different temperatures and the atmospheric transmission model ATM (Cernicharo 1985; Pardo et al. 2001). The adopted calibration uncertainties are at the level of 10% and all the data were analysed using the GILDAS package2.
), was calibrated using two absorbers at different temperatures and the atmospheric transmission model ATM (Cernicharo 1985; Pardo et al. 2001). The adopted calibration uncertainties are at the level of 10% and all the data were analysed using the GILDAS package2.
3. Results
The line identification in this work has been achieved using the MADEX (Cernicharo 2012), CDMS (Müller et al. 2005), and JPL (Pickett et al. 1998) catalogues. By April 2021, the MADEX has featured 6433 spectral entries corresponding to the ground and vibrationally excited states, together with the corresponding isotopologues of 1733 molecules.
3.1. Discovery of CH2CCHC4H
The search for new species in our survey is based on intensity predictions for the molecules for which their rotational spectroscopy is available. The sensitivity of QUIJOTE is a factor ∼50 larger than that of previous TMC-1 Q-band line surveys (Kaifu et al. 2004), which has permitted us to address the search of molecules with a very low dipole moment (Cernicharo et al. 2021a). Taking into account the large abundances derived from QUIJOTE’s data for hydrocarbons such as CH2CHCCH (Cernicharo et al. 2021d), CH2CCH (Agúndez et al. 2021, 2022), CH2CCHCCH (Cernicharo et al. 2021e), H2C5 (Cabezas et al. 2021), c-C6H4 (Cernicharo et al. 2021a), c-C5H6, and c-C9H8 (Cernicharo et al. 2021d), other similar species could be present in the survey, such as allenyl diacetylene (CH2CCHC4H). Rotational spectroscopy for this species has been measured in the laboratory by McCarthy et al. (2020). We fitted these lines and implemented the rotational constants into MADEX (Cernicharo 2012). The derived constants, given in Table B.1, are identical to those of McCarthy et al. (2020). We predicted the intensities for all lines above 0.5 mK, adopting an initial column density of 5 × 1012 cm−2 and a rotational temperature of 10 K. Twenty lines of this species with intensities between 0.4 and 0.7 mK have been found with a signal-to-noise ratio (S/N) between 3 and 6. These are shown on Fig. 1 and the derived line parameters are given in Table A.1. Several lines are partially blended with other features, most of them arising from unknown species. Nevertheless, many lines appear as single features and provide a solid detection of this molecule.
 |
Fig. 1. Observed transitions of CH2CCHC4H in TMC-1. The abscissa corresponds to the rest frequency of the lines. Frequencies and intensities for the observed lines are given in Table A.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in milliKelvin. The quantum numbers of each transition are indicated in the corresponding panel. Red line shows the computed synthetic spectrum for this species for Trot = 9 K and a column density of 2.2 × 1012 cm−2. Blanked channels correspond to negative features produced when folding the frequency-switched data. |
Using the observed frequencies and those measured in the laboratory, we derived a new set of rotational and distortion constants. They are provided in Appendix B and Table B.1. The difference between observed and calculated values are given in Table B.3. The new constants are practically identical to those of McCarthy et al. (2020), but have lower uncertainties, which allow for more precise frequency predictions at higher frequencies.
To derive the column density and rotational temperature we used a model line fitting procedure (see e.g. Cernicharo et al. 2021d), which leads to N(CH2CCHC4H) = (2.2 ± 0.2) × 1012 cm−2 and Trot = 9.0 ± 0.5 K. A rotational temperature lower than 8.5 K results on an underestimation of the observed intensity for transitions with Ka = 2. We assumed a source of uniform brightness with a diameter of 80″ (Fossé et al. 2001; Cernicharo et al., in prep.). The predicted synthetic lines for these parameters are shown on Fig. 1 (red lines). Adopting a H2 column density for TMC-1 of 1022 cm−2 (Cernicharo & Guélin 1987), the abundance of CH2CCHC4H is (2.2 ± 0.2) × 10−10. Using a CH2CCHCCH column density of N = 1.2 × 1013 cm−2 (Cernicharo et al. 2021e), we derive a CH2CCHCCH/CH2CCHC4H abundance ratio of ∼5.5, similar to the CCH/C4H radicals abundance ratio of ∼4 derived by Cernicharo et al. (in prep.).
3.2. A robust detection of CH2CCHC3N
CH2CCHC3N (cyanoacetyleneallene or 4.5-hexadien-2-ynenitrile) was recently reported as having been detected towards TMC-1 by Shingledecker et al. (2021). No individual lines were reported but the stacking of all lines within their line survey. In order to search for the lines of this species with QUIJOTE, we fit the rotational lines of this species kindly provided to us by M. McCarthy. Using these constants, we predicted the frequencies for all the lines of this molecule with Ka ≤ 3 within the Q-band. Twenty eight lines were detected and their line parameters are given in Table A.1. Twenty of these lines are shown on Fig. 2. Although some lines are blended, the detection is now rigorous, as many individual lines are clearly seen in our data. Improved rotational and distortion constants are provided in Appendix B and Table B.2.
 |
Fig. 2. Selected transitions of CH2CCHC3N in TMC-1. The abscissa corresponds to the rest frequency of the lines. Frequencies and intensities for all observed lines are given in Table A.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in milliKelvin. The quantum numbers of each transition are indicated in the corresponding panel. The red line shows the computed synthetic spectrum for this species for Trot = 9 K and a column density of 1.2 × 1011 cm−2. Blanked channels correspond to negative features produced when folding the frequency-switched data. |
We assumed the same source parameters than for CH2CCHC4H. Through a model fitting procedure, we derive a rotational temperature of 9.0 ± 0.5 K and a column density of (1.20 ± 0.15) × 1011 cm−2. Hence, the abundance of CH2CCHC3N is (1.20 ± 0.15) × 10−11. Our column density agrees with the total value derived from the four velocity and source components of model B of Shingledecker et al. (2021) (1.6 × 1011 cm−2, see their Table A.1). The results concerning their models A or C can be fully discarded, as they provide unreasonable rotational temperatures (model A) or extremely large column densities (model C). We consider that our determination based on the observation of many individual lines is more accurate. Hence, the CH2CCHC4H/CH2CCHC3N abundance ratio is 18 ± 4.
It is interesting to compare the column densities of the different ethynyl and cyanide derivatives of species containing the allenyl group CH2CCH. To this purpose, we derived the column density of C4H and C3N from our data, and we found N(C4H) = 1.1 × 1014 cm−2 and N(C3N) = 1.4 × 1013 cm−2 (Cernicharo et al., in prep.). These values result in an abundance ratio C4H/C3N of 8, which is somewhat lower than the CH2CCHC4H/CH2CCHC3N ratio of 18 ± 4 derived in this work.
4. Discussion
For a better understanding of the formation of CH2CCHC4H and CH2CCHC3N, we carried out chemical model calculations. The chemical model is similar to those presented in Marcelino et al. (2021) and Cernicharo et al. (2021e). Briefly, we adopted typical parameters of cold dark clouds, namely, a gas kinetic temperature of 10 K, a volume density of H nuclei of 2 × 104 cm−3, a visual extinction of 30 mag, a cosmic-ray ionization rate of 1.3 × 10−17 s−1, and the set of “low-metal” elemental abundances (Agúndez & Wakelam 2013). We adopted the chemical network RATE12 from the UMIST database (McElroy et al. 2013), updated to include the chemistry of C5H4, C7H4, C4H3N, and C6H3N. The chemistry of C5H4 and C4H3N isomers has been discussed by Cernicharo et al. (2021e) and Marcelino et al. (2021), respectively. In the case of C7H4 isomers, the main formation routes involve the dissociative recombination of C7H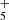 with electrons and the neutral-neutral reactions of the C4H radical with CH3CCH, CH2CCH2, and CH3CHCH2, while C6H3N is formed by the dissociative recombination of C6H4N+ and the neutral-neutral reactions of the radical C3N with CH3CCH and CH2CCH2. The reactions involving C4H have been experimentally studied by Berteloite et al. (2010), while those involving C3N have been studied also experimentally by Fournier (2014). These reactions are found to be rapid at low temperatures, although information on the branching ratios of the different exothermic channels is not available. Therefore, in the chemical model, we do not distinguish between different isomers of C7H4 or C6H3N. The chemistry of these two isomeric families share similarities because an important part of the synthesis relies on the reaction of either C4H or C3N with methyl acetylene and allene. We may summarize these routes as:
with electrons and the neutral-neutral reactions of the C4H radical with CH3CCH, CH2CCH2, and CH3CHCH2, while C6H3N is formed by the dissociative recombination of C6H4N+ and the neutral-neutral reactions of the radical C3N with CH3CCH and CH2CCH2. The reactions involving C4H have been experimentally studied by Berteloite et al. (2010), while those involving C3N have been studied also experimentally by Fournier (2014). These reactions are found to be rapid at low temperatures, although information on the branching ratios of the different exothermic channels is not available. Therefore, in the chemical model, we do not distinguish between different isomers of C7H4 or C6H3N. The chemistry of these two isomeric families share similarities because an important part of the synthesis relies on the reaction of either C4H or C3N with methyl acetylene and allene. We may summarize these routes as:
where we only consider the C7H4 isomers CH3C6H and CH2CCHC4H because they are the only ones detected in TMC-1 although other C7H4 isomers could also be formed (see Berteloite et al. 2010). Similarly, only the C6H3N isomers CH3C5N and CH2CCHC3N are considered, but others can also be formed. We adopt as main destruction routes for C7H4 and C6H3N the reactions with the ions C+, He+, HCO+, and H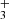 . In Fig. 3 we compare the abundances calculated for C7H4 and C6H3N with the values observed in TMC-1. It is seen that peak calculated abundances, reached between 105 yr and 106 yr, are, within one order of magnitude, in good agreement with the observed values.
. In Fig. 3 we compare the abundances calculated for C7H4 and C6H3N with the values observed in TMC-1. It is seen that peak calculated abundances, reached between 105 yr and 106 yr, are, within one order of magnitude, in good agreement with the observed values.
 |
Fig. 3. Calculated fractional abundances of C5H4, C7H4, C4H3N, and C6H3N (allowing for various isomers) as a function of time. The horizontal dotted lines correspond to the abundances observed in TMC-1, where C5H4 includes CH3C4H and CH2CCHCCH, C7H4 includes CH3C6H and CH2CCHC4H, C4H3N includes CH3C3N, CH2CCHCN, and HCCCH2CN, and C6H3N includes CH3C5N and CH2CCHC3N. |
We note that the peak abundance is reached at different times for C7H4 and C6H3N. This is due to the different contribution of the neutral and ionic routes, both of which contribute to the formation of each species. The neutral route represented by reactions (1)–(4) is most efficient at times around (4–5) × 105 yr and this is the dominant route for C7H4. On the other hand, the ionic route, which involves as final step the dissociative recombination of C7H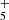 (to yield C7H4) and C6H4N+ (to form C6H3N), is efficient at earlier times, in the range (1–2) × 105 yr, and this pathway becomes dominant over the neutral route when forming C6H3N. Our chemical model is similar to that of Shingledecker et al. (2021) in that both explain the abundance derived for CH2CCHC3N in TMC-1 through gas-phase chemistry. There are however some differences. In our case two gas-phase routes contribute to the formation of CH2CCHC3N: (1) the neutral one based on the reaction of C3N with CH3CCH and CH2CCH2 and (2) the ionic one based on the dissociative recombination of C6H4N+, and the resulting peak abundance of CH2CCHC3N is in the range between 10−11 and 10−10 relative to H2. In the model of Shingledecker et al. (2021), CH2CCHC3N is mainly formed through the gas-phase neutral route and the peak abundance is substantially higher, in the range between 10−9 and 10−8 relative to H2, probably because these authors consider a C/O ratio higher than 1, whereas we adopted a C/O ratio of 0.55.
(to yield C7H4) and C6H4N+ (to form C6H3N), is efficient at earlier times, in the range (1–2) × 105 yr, and this pathway becomes dominant over the neutral route when forming C6H3N. Our chemical model is similar to that of Shingledecker et al. (2021) in that both explain the abundance derived for CH2CCHC3N in TMC-1 through gas-phase chemistry. There are however some differences. In our case two gas-phase routes contribute to the formation of CH2CCHC3N: (1) the neutral one based on the reaction of C3N with CH3CCH and CH2CCH2 and (2) the ionic one based on the dissociative recombination of C6H4N+, and the resulting peak abundance of CH2CCHC3N is in the range between 10−11 and 10−10 relative to H2. In the model of Shingledecker et al. (2021), CH2CCHC3N is mainly formed through the gas-phase neutral route and the peak abundance is substantially higher, in the range between 10−9 and 10−8 relative to H2, probably because these authors consider a C/O ratio higher than 1, whereas we adopted a C/O ratio of 0.55.
The column densities of CH3C6H and CH3C5N in TMC-1 are 7 × 1011 cm−2 and 9.5 × 1010 cm−2, respectively (see Appendix C). This implies that the abundance ratio CH3C6H/CH2CCHC4H is 0.32, which is somewhat lower than that of the smaller analogue system CH3C4H/CH2CCHCCH = 1.1 (Cernicharo et al. 2021e). On the other hand, the abundance ratio CH3C5N/CH2CCHC3N is 0.79, which is similar to the abundance ratio of the smaller analogue system CH3C3N/CH2CCHCN = 0.64 (Marcelino et al. 2021). If most of the synthesis of C7H4 and C6H3N isomers is carried out by reactions (1)–(4), this implies that CH2CCHC4H would be favoured over CH3C6H in reactions (1)–(2), while CH3C5N and CH2CCHC3N would be produced with similar branching ratios in reactions (3)–(4). Moreover, given that in the analogue smaller system C4H3N, three different isomers (CH3C3N, CH2CCHCN, and HCCCH2CN) have been detected in TMC-1 with similar abundances (Marcelino et al. 2021), it would not be surprising to find that the isomer HCCCH2C3N would also be detected in TMC-1.
5. Conclusions
We report the first detection in space of CH2CCHC4H, towards the cold dark cloud TMC-1. The CH2CCHC3N molecule was also detected in a robust way, which allows for its frequencies and rotational constants to be presented for the first time. We observed a total of 20 rotational transitions, from J = 17 to 24 and Ka ≤ 3, using the Yebes 40 m telescope. The frequencies predicted for these two species from laboratory data are rather accurate when compared with those derived from astronomical observations. The rotational temperature for both species is 9.0 ± 0.5 K and the derived column densities are (2.2 ± 0.2) × 1012 cm−2 for CH2CCHC4H and (1.2 ± 0.15) × 1011 cm−2 for CH2CCHC3N. These values give an abundance ratio between CH2CCHC4H and CH2CCHC3N of 18 ± 4. The observed abundances of the C7H4 and C6H3N isomeric families are reasonably well reproduced by a gas-phase chemical model in which the main formation pathways involve dissociative recombination of the precursor ions C7H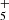 and C6H
and C6H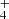 and neutral-neutral reactions involving the C4H and CN reactions with CH3CCH and CH2CCH2.
and neutral-neutral reactions involving the C4H and CN reactions with CH3CCH and CH2CCH2.
Acknowledgments
We thank Ministerio de Ciencia e Innovación of Spain (MICIU) for funding support through projects PID2019-106110GB-I00, PID2019-107115GB-C21/AEI/10.13039/501100011033, and PID2019-106235GB-I00. We also thank ERC for funding through grant ERC-2013-Syg-610256-NANOCOSMOS. M.A. thanks MICIU for grant RyC-2014-16277.
References
- Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]
- Agúndez, M., Cabezas, C., Tercero, B., et al. 2021, A&A, 647, L10 [EDP Sciences] [Google Scholar]
- Agúndez, M., Marcelino, N., Cabezas, C., et al. 2022, A&A, 657, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berteloite, C., Le Picard, S., Balucani, N., et al. 2010, PCCP, 12, 3677 [NASA ADS] [CrossRef] [Google Scholar]
- Cabezas, C., Tercero, B., Agúndez, M., et al. 2021, A&A, 650, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J. 1985, Internal IRAM report (Granada: IRAM) [Google Scholar]
- Cernicharo, J. 2012, in ECLA 2011: Proc. of the European Conference on Laboratory Astrophysics, eds. C. Stehl, C. Joblin, & L. d’Hendecourt (Cambridge: Cambridge Univ. Press), EAS Pub. Ser., 2012, 251 [Google Scholar]
- Cernicharo, J., & Guélin, M. 1987, A&A, 176, 299 [Google Scholar]
- Cernicharo, J., Agúndez, M., Kaiser, R., et al. 2021a, A&A, 652, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021b, A&A, 649, L15 [EDP Sciences] [Google Scholar]
- Cernicharo, J., Agúndez, M., Kaiser, R. I., et al. 2021c, A&A, 655, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021d, A&A, 647, L2 [EDP Sciences] [Google Scholar]
- Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021e, A&A, 647, L3 [EDP Sciences] [Google Scholar]
- Cernicharo, J., Agúndez, M., Kaiser, R. I., et al. 2021f, A&A, 655, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fossé, D., Cernicharo, J., Gerin, M., & Cox, P. 2001, ApJ, 552, 168 [Google Scholar]
- Fournier, M. 2014, Ph.D. Thesis, Université de Rennes, France [Google Scholar]
- Kaifu, N., Ohishi, M., Kawaguchi, K., et al. 2004, PASJ, 56, 69 [Google Scholar]
- Lee, K. L. K., Changala, P. B., Loomis, R. A., et al. 2021, ApJ, 910, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J.-C., Agúndez, M., Wakelam, V., et al. 2017, MNRAS, 470, 4075 [Google Scholar]
- Marcelino, N., Tercero, B., Agúndez, M., & Cernicharo, J. 2021, A&A, 646, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCarthy, M. C., Lee, K. L. K., Porterfield, J. P., et al. 2020, J. Phys. Chem. A, 124, 5170 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, M. C., Lee, K. L. K., Loomis, R. A., et al. 2021, Nat. Astron., 5, 176 [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGuire, B. A., Burkhardt, A. M., Kalenskii, S., et al. 2018, Science, 359, 202 [Google Scholar]
- McGuire, B. A., Loomis, R. A., Burkhardt, A. M., et al. 2021, Science, 371, 1265 [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [Google Scholar]
- Pardo, J. R., Cernicharo, J., & Serabyn, E. 2001, IEEE Trans. Antennas Propag., 49, 12 [Google Scholar]
- Pickett, H. M., & Boyd, T. L. 1978, Chem. Phys. Lett., 58, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectrosc. Radiat. Trans., 60, 883 [Google Scholar]
- Remijan, A. J., Hollis, J. M., Snyder, L. E., et al. 2006, ApJ, 643, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Shingledecker, C. N., Lee, K. L. K., Wandishin, J. T., et al. 2021, A&A, 652, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snyder, L. E., Hollis, J. M., Jewell, P. R., et al. 2006, ApJ, 647, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Tercero, F., López-Pérez, J. A., Gallego, J. D., et al. 2021, A&A, 645, A37 [EDP Sciences] [Google Scholar]
Appendix A: Observed line parameters
The line parameters for the different molecules studied in this work were obtained by fitting a Gaussian line profile to the observed data. A window of ± 15 km s−1 around the vLSR of the source was considered for each transition. The derived line parameters for all the molecular species studied in this work are given in Table A.1. The observed lines of CH2CCHC4H are shown on Fig. 1. Selected lines of CH2CCHC3N are shown on Fig. 2. All lines of both species are weak, with many of them blended with other features. Nevertheless, for most of these blended lines, it is still possible to derive reliable line parameters. It is worth noting that at this level of sensitivity any stacking procedure is not at all recommended due to the forest of weak unknown features. For CH2CCHC3N, we explored lines with Ka=3, but only three of them were detected. These lines involve high energy levels and exhibit intrinsic line strengths weaker than those with Ka=0, 1, and 2. This species also demonstrate a hyperfine structure due to the nitrogen nuclear spin. None of the hyperfine structures are resolved as the splitting is predicted to be of ∼5 kHz for Ka=0 and 1 and around 10 kHz for Ka=2; this is much lower than our spectral resolution of 38.1 kHz. However, the observed linewidths for many of the lines of this species indicate some broadening. For the modelling of the emerging spectrum of this molecule, we used predictions taken into account the hyperfine splitting.
Observed line parameters for the species studied in this work.
Appendix B: Improved rotational constants for CH2CCHC4H and CH2CCHC3N
We merged the laboratory lines of CH2CCHC4H and CH2CCHC3N with those observed in TMC-1 with the QUIJOTE line survey to obtain improved rotational and distortion constants for both species. The results for CH2CCHC4H are given in Table B.1. The predictions from the laboratory data were rather accurate, with deviations between our observed frequencies of a few kHz (see Table B.3). Some lines show differences of up to 25 kHz which is at most 1.5-2 times the accuracy of the observed frequencies in TMC-1 as the signal-to-noise ratio (S/N) of the observations is limited to ∼4-5. As a consequence, the derived constants for this species from the merged fit are practically identical to those obtained from the laboratory data alone. However, the uncertainty of the constants is significantly improved.
Improved rotational and distortion constants for CH2CCHC4H.
The results for CH2CCHC3N are given in Table B.2. The new constants are very similar to the laboratory data, with most of the differences being at frequencies below 3 kHz (see Table B.4) and presenting a maximum deviation of 47 kHz. As in the previous case, the values of the constants obtained are in good agreement with the laboratory data.
Improved rotational and distortion constants for CH2CCHC3N.
Observed frequencies of CH2CCHC4H
Observed frequencies of CH2CCHC3N
Appendix C: Column densities of CH3C6H and CH3C5N
In order to obtain abundance ratios between the different ethynyl and cyanide derivatives of CH2CCH2 in a coherent and comprehensive way, we derived the column densities of CH3C6H (an isomer of CH2CCHC4H) and CH3C5N (an isomer of CH2CCHC3N) using the observed lines of these molecules within the QUIJOTE line survey. Both species have been previously detected towards TMC-1 (Remijan et al. 2006; Snyder et al. 2006). These authors reported a column density of 3.1 × 1012 cm−2 and a rotational temperature of 6K for CH3C6H, and N = 7.4 × 1011 cm−2 and Trot = 4 K for CH3C5N.
In our data, we detected the rotational transitions J=20-19 up to J=31-30 for CH3C6H and CH3C5N ( having very similar rotational constants). The K=0,1 components of all these lines (both species are symmetric rotors) are detected except the K=1 component of the J=30-29 transition of CH3C5N, which we explain as possibly due to an overlap with a negative feature produced in the folding of the frequency switching data. The observed transitions are shown on Fig. C.1 for CH3C6H and Fig. C.2 for CH3C5N. No K=2 lines are detected, which is reasonable taking into account the kinetic temperature of the cloud (10 K) and the high energy of the K=2 levels (from 38.9 for Ju=20 up to 57.3 K for Ju=30).
We derived the column densities and the rotational temperatures of CH3C6H and CH3C5N using a model line fitting procedure (see Section 3 in this work as well as Cernicharo et al. 2021d). We adopt a source of uniform brightness with a diameter of 80″ (Fossé et al. 2001, Cernicharo et al. in prep.) and a linewidth of 0.6 km s−1. The best model for our CH3C6H lines provides N=(7±0.7) × 1011 cm−2 and Trot =9±0.5 K. The computed synthetic line profiles using these values are shown on Fig. C.1 as red lines. The derived rotational temperature and column density are rather different from those derived previously by Remijan et al. (2006). This difference is certainly due to the larger energy range covered by our data, which renders the line intensities very dependent on the rotational temperature. In Fig. C.1, we show in green the expected line profiles if we adopt the rotational temperature and column density derived by Remijan et al. (2006). The low-J transitions overestimate the observed intensities, while a reasonable agreement is found for Ju≥27. Using our derived parameters, we reproduce the intensities of the low-J transitions observed by Remijan et al. (2006) within a factor of 1.5.
For CH3C5N, we derived N=(9.5±0.9) × 1010 cm−2 and Trot = 9±0.5 K. The predicted synthetic lines for this species are shown on red in Fig C.2. These values are also different from those derived by Snyder et al. (2006), Trot = 4 K and N=7.4 × 1011 cm−2. With such a low value for the rotational temperature, it is impossible to reproduce the observed intensities of our lines. We show in green in Fig. C.2 the computed synthetic spectrum of CH3C5N adopting the parameters of Snyder et al. (2006). A good match is obtained for the transitions J=20-19 and J=21-20 but a clear underestimation of the intensity is observed for lines with higher J. Using our Trot and column density for this species, we reproduce the intensities observed for the low-J transitions by Snyder et al. (2006) within a factor of 2.
Adopting a H2 column density for TMC-1 of 1022 cm−2 (Cernicharo & Guélin 1987), we obtain an abundance of (7±0.7) × 10−11 for CH3C6H, and of (9.5±0.9) × 10−12 for CH3C5N.
The relative abundance of the isomers CH2CCHC4H and CH3C6H is, hence, 3.1±0.3. For the pair of isomers CH2CCHC3N and CH3C5N, their abundance ratio is 1.3±0.2.
 |
Fig. C.1. Observed transitions of CH3C6H in TMC-1. The right component corresponds to K = 0 transitions and the left component to K = 1 transitions. The abscissa corresponds to local standard of rest frequencies. Central frequencies and intensities for the observed lines are given in Table A.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in milli Kelvin. The quantum numbers of each transition are indicated in the corresponding panel. The red lines show the computed synthetic spectrum for this species for Trot = 9 K and a column density of 7 × 1011 cm−2. The green line shows the computed synthetic spectrum assuming Trot = 6 K and a N=3.1 × 1012 cm−2(Remijan et al. 2006). Blanked channels correspond to negative features produced when folding the frequency-switched data. |
 |
Fig. C.2. Observed transitions of CH3C5N in TMC-1. The right component corresponds to K = 0 transitions and the left component to K = 1 transitions. The abscissa corresponds to the rest frequency of the lines. Frequencies and intensities for the observed lines are given in Table A.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in milli Kelvin. The quantum numbers of each transition are indicated in the corresponding panel. The red line shows the computed synthetic spectrum for this species for Trot = 9 K and a column density of 9.5 × 1010 cm−2. The green lines show the computed synthetic spectrum adopting Trot = 4 K and N=7.4 × 1011 cm−2(Snyder et al. 2006). Blanked channels correspond to negative features produced when folding the frequency-switched data. |
All Tables
All Figures
 |
Fig. 1. Observed transitions of CH2CCHC4H in TMC-1. The abscissa corresponds to the rest frequency of the lines. Frequencies and intensities for the observed lines are given in Table A.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in milliKelvin. The quantum numbers of each transition are indicated in the corresponding panel. Red line shows the computed synthetic spectrum for this species for Trot = 9 K and a column density of 2.2 × 1012 cm−2. Blanked channels correspond to negative features produced when folding the frequency-switched data. |
| In the text | |
 |
Fig. 2. Selected transitions of CH2CCHC3N in TMC-1. The abscissa corresponds to the rest frequency of the lines. Frequencies and intensities for all observed lines are given in Table A.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in milliKelvin. The quantum numbers of each transition are indicated in the corresponding panel. The red line shows the computed synthetic spectrum for this species for Trot = 9 K and a column density of 1.2 × 1011 cm−2. Blanked channels correspond to negative features produced when folding the frequency-switched data. |
| In the text | |
 |
Fig. 3. Calculated fractional abundances of C5H4, C7H4, C4H3N, and C6H3N (allowing for various isomers) as a function of time. The horizontal dotted lines correspond to the abundances observed in TMC-1, where C5H4 includes CH3C4H and CH2CCHCCH, C7H4 includes CH3C6H and CH2CCHC4H, C4H3N includes CH3C3N, CH2CCHCN, and HCCCH2CN, and C6H3N includes CH3C5N and CH2CCHC3N. |
| In the text | |
 |
Fig. C.1. Observed transitions of CH3C6H in TMC-1. The right component corresponds to K = 0 transitions and the left component to K = 1 transitions. The abscissa corresponds to local standard of rest frequencies. Central frequencies and intensities for the observed lines are given in Table A.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in milli Kelvin. The quantum numbers of each transition are indicated in the corresponding panel. The red lines show the computed synthetic spectrum for this species for Trot = 9 K and a column density of 7 × 1011 cm−2. The green line shows the computed synthetic spectrum assuming Trot = 6 K and a N=3.1 × 1012 cm−2(Remijan et al. 2006). Blanked channels correspond to negative features produced when folding the frequency-switched data. |
| In the text | |
 |
Fig. C.2. Observed transitions of CH3C5N in TMC-1. The right component corresponds to K = 0 transitions and the left component to K = 1 transitions. The abscissa corresponds to the rest frequency of the lines. Frequencies and intensities for the observed lines are given in Table A.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in milli Kelvin. The quantum numbers of each transition are indicated in the corresponding panel. The red line shows the computed synthetic spectrum for this species for Trot = 9 K and a column density of 9.5 × 1010 cm−2. The green lines show the computed synthetic spectrum adopting Trot = 4 K and N=7.4 × 1011 cm−2(Snyder et al. 2006). Blanked channels correspond to negative features produced when folding the frequency-switched data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.