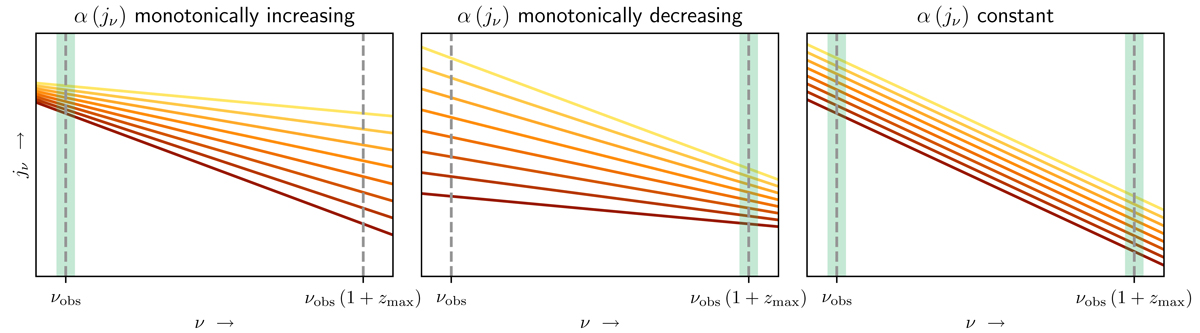
Three scenarios for simple power-law synchrotron spectra of shocks that are consistent with our methodology. Due to cosmological redshifting, the calculation of the specific intensity I_ν at observing frequency ν_obs necessitates knowing the monochromatic emission coefficient (MEC) j_ν at a range of emission frequencies ν (see Eq. 8). In this work, we generate j_ν at emission frequencies ν = ν_obs and ν = ν_obs(1+z_max), where z_max is the maximum cosmological redshift of the large-scale structure reconstructions. We do so using the same Gaussian random field realisation 𝒵 (and thus percentile random field realisation 𝒫), implicitly assuming that shocks retain their MEC percentile rank over the frequency range [ν_obs, ν_obs(1+z_max)]. This assumption holds in the three scenarios sketched above. Each solid line represents a shock with constant percentile rank (over the range shown, at least); the graphs are drawn with logarithmic scaling. Regarding the sign of the spectral index, we use the convention j_ν ∝ ν^α. Left: the integrated spectral index α is a monotonically increasing function of j_ν at ν = ν_obs (‘brighter shocks have flatter spectra’). Middle: the integrated spectral index α is a monotonically decreasing function of j_ν at ν = ν_obs(1+z_max) (‘brighter shocks have steeper spectra’). Right: the integrated spectral index α is a j_ν-independent constant (at all frequencies); this is a limiting case of the previous two.