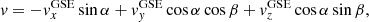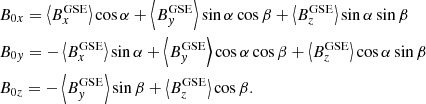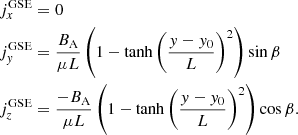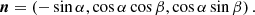| Issue |
A&A
Volume 660, April 2022
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 8 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202142474 | |
| Published online | 30 March 2022 | |
Analysis of the heliospheric current sheet’s local structure based on a magnetic model
University of Alcalá, Spain
e-mail: david.arrazola@uah.es
Received:
18
October
2021
Accepted:
27
December
2021
Context. An approach to the problem of estimating several physical properties of the heliospheric current sheet (HCS) local structure from a single spacecraft observation point of view was published in 2003. This method, HYperbolic TAngent ROtation (HYTARO), is based on the following two main assumptions: (a) that the HCS is locally flat, and (b) that its magnetic topology is described by a modified Harris field.
Aims. A revision of HYTARO by including the spacecraft’s trajectory and developing a more precise procedure able to reduce the number of the required fit parameters is presented in this paper.
Methods. This magnetic topology is proposed for the HCS’s local field at 1 AU, and it was applied as a fit function to a collection of 40 HCS crossings detected by the WIND spacecraft during the solar minimum. The estimated HCS local parameters (i.e., orientation and width) are consistent with previous works, which used the minimum variance analysis or the coplanarity variance analysis, and this is inferred from HYTARO results. One of the points of discussion about HYTARO was determining if it was necessary to apply two or three rotations to characterize the field’s relative orientation with respect to the current sheet (CS) plane. As principal component analysis (PCA) is a method to decompose a set of data into no correlated components by identifying eigenvalues and eigenvectors, it is feasible to analyze the possibility of reducing the dimensionality of the problem.
Results. HYTARO gives a qualitative description of the observed magnetic field during an HCS crossing. The number of free parameters from the original HYTARO method has been reduced including the relative spacecraft trajectory through the CS and adding a background field related to each Cartesian component. Further, PCA has been implemented to justify applying two rotations with the HYTARO model. The dimensionality is another way to explore the number of rotations needed to relate the field in the local system with the field in GSE coordinates.
Key words: Sun: heliosphere / Sun: magnetic fields / solar wind
© ESO 2022
1. Introduction
The heliospheric current sheet (HCS) divides the heliosphere into regions with opposite magnetic polarities. It is observed as a sector boundary in the ecliptic plane, and its orientation and structure have been intensely studied (Smith 2001). Attending to its local structure at 1 AU, the HCS can be studied as a magnetic directional discontinuity supported by a current sheet (CS).
Current sheets are ubiquitous features throughout the heliosphere. They can be found in solar corona, an interplanetary medium, magnetic cloud sheaths, HCSs, or planetary magnetospheres. The magnetic field changes in intensity and direction across a CS; in addition, at the limit of a CS, the width could tend to zero. This is consistent with a magnetic discontinuity where its discontinuity plane and sheet are coincident. Since 1967, the most common tool for analyzing magnetic discontinuities has been minimum variance analysis (MVA; Sonnerup & Cahill 1967). This method is able to estimate the normal vector to the discontinuity plane and it can give us an approximation of its local orientation. Several criteria have been proposed regarding the correct application of MVA, the most widely adopted stating that the discontinuity plane is properly estimated when the ratio between the medium and minimum eigenvalues is equal to or higher than 2, (λ2/λ3 ≥ 2) (Lepping & Behannon 1980). These eigenvalues are obtained by the diagonalization of the covariance matrix of the magnetic field. Nevertheless, several authors (Behannon et al. 1981; Sckopke et al. 2000; Khrabrov & Sonnerup 1998; Blanco et al. 2003; Hausman et al. 2004) have pointed out some problems when MVA is applied to magnetic discontinuities. One of these problems is related to the statistical nature of MVA and how to avoid degenerate eigenvalues, especially between medium and minimum ones. Even when this degeneration is avoided, if there is a direction that is non-coincident with the perpendicular to the discontinuity plane along which the magnetic field is roughly constant, MVA could erroneously identify this direction as being normal in the discontinuity plane. Probably related to the foregoing, another argument suggests that a two-dimensional (or more complex) structure in magnetic field variation could lead to the erroneous estimation of the normal vector to the discontinuity plane. Another problem associated with the MVA method is its great sensitivity to the number of points used in the calculation procedure. It has been observed that even by the addition of one single data point, a different normal vector estimate is obtained. Recently, several authors using multi-spacecraft observations have elevated the MVA validity criterion from 2 to 10 in order to obtain a reliable geometry for a directional discontinuity (DD; Horbury et al. 2001; Knetter et al. 2003).
Scudder (2005) proposed a complementary method to MVA, namely coplanarity variance analysis (CVA), to investigate the nature of DDs. This method uses the same covariance matrix as in the MVA method, but it builds up the natural base of a DD from the maximum variance vector. His results seem to confirm that MVA works poorly for shocks and plane-polarized waves, and that MVA requires higher ratios of eigenvalues if a reliable estimate of the normal vector to the plane of discontinuity wants to be achieved.
A rather different approach to the local structure of the HCS, which is a kind of current sheet in solar wind, was presented by Blanco et al. (2003). This method, HYperbolic TAngent ROtation (HYTARO), assumes a topology for the local magnetic field and can estimate its local orientation, width, and other related physical parameters. Although HYTARO solves some of the MVA problems mentioned above, it has been especially developed for the HCS local structure and cannot replace MVA in a general approach to magnetic discontinuities (Blanco et al. 2003, 2006, 2008). Nevertheless, HYTARO has undergone several changes since 2003. The direction of rotation has been changed in order to adapt to a more intuitive point of view from the Earth. A pure tangential discontinuity, that is HYTARO where the constant term is exactly zero, was employed to analyze multiple HCS crossings (Blanco et al. 2006). Moreover, over the last few years, different discussions and proposals regarding HYTARO have been forthcoming from other researchers at congresses or review processes. The response to these comments and pieces of advise have been included in the present version of HYTARO.
This work presents a revision of the HYTARO model after making several improvements. One of them is the inclusion of relative spacecraft trajectory through the HCS, thus allowing the direct estimation of the HCS width. Another improvement is that the magnetic field has been changed by adding an additional constant component to Bx. This permits the magnetic field to be separated into one constant term and another that follows a hyperbolic tangent along the HCS crossing. Also, a new constraint has been imposed on the constant field term by relating it to the mean magnetic field in the HCS. This allows one to reduce the number of parameters in the model from 8 to 5. Moreover, HYTARO gives a qualitative description of the HCS magnetic structure and it obtains good estimates for the HCS width and its local orientation.
One of the most controversial points of HYTARO is the assumption that two rotations can univocally determine the orientation of the plane defining the HCS. To clarify this, a principal component analysis (PCA) has been implemented to justify the number of rotations needed to fix the field orientation with respect to the CS. PCA is an orthogonal linear transformation allowing a vector space to be transformed to a new coordinate system, reducing the multidimensional data to lower dimensions for analysis, so that the greatest variance by any projection of the data lies on the first coordinate, called the principal component (Pearson 1901; Jolliffe 2011). This reduction implies no significant changes in the local orientation of the CS.
2. HYTARO model
As mentioned in the introduction, CSs are observed in different regions of the heliosphere. Although HYTARO was initially developed for the HCS, we propose that its simple magnetic topology which describes how the magnetic field varies throughout the HCS can also be applied to CSs. HYTARO is based on two main assumptions, the local shape of a CS can be assumed to be a plane, and its magnetic field can be described by a modified Harris field (Harris 1962) with the following components:
where these field components, 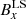 ,
, 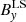 , and
, and 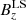 , refer to a Cartesian local system (LS) defined by the YLS axis perpendicular to the CS plane, the XLS axis in the direction where the magnetic field varies and is perpendicular to the YLS axis, and the ZLS axis perpendicular to the other two and in the direction of the electric current, respectively. In this context, the y direction is perpendicular to the CS plane defined by the XLS and ZLS axes, that is to say its normal vector is given by n = (0, 1, 0); B0x, B0y, and B0z are the magnetic field constant terms; and BA is the magnetic amplitude. Furthermore, B0x and B0z lie on the CS plane while B0y is the magnetic constant component perpendicular to it; y0 marks the point of the magnetic field inversion; and L is the HCS local semi width. As can be directly inferred from (1), the magnetic field module is as follows:
, refer to a Cartesian local system (LS) defined by the YLS axis perpendicular to the CS plane, the XLS axis in the direction where the magnetic field varies and is perpendicular to the YLS axis, and the ZLS axis perpendicular to the other two and in the direction of the electric current, respectively. In this context, the y direction is perpendicular to the CS plane defined by the XLS and ZLS axes, that is to say its normal vector is given by n = (0, 1, 0); B0x, B0y, and B0z are the magnetic field constant terms; and BA is the magnetic amplitude. Furthermore, B0x and B0z lie on the CS plane while B0y is the magnetic constant component perpendicular to it; y0 marks the point of the magnetic field inversion; and L is the HCS local semi width. As can be directly inferred from (1), the magnetic field module is as follows:
As is observed in Eq. (2), HYTARO imposes a field intensity which varies throughout the CS, and the way that it changes depends on the BA and B0x relation. If BA > B0x, there is a minimum inside the CS with a magnetic step between both CS sides given by ΔB = |BA + B0x|−|BA − B0x|. Nevertheless, when BA ≤ B0x, only the magnetic step appears. This magnetic field topology drives to a plane of the current (i.e., the current sheet) in the XLS − ZLS plane along to the ZLS direction, is independent of the constant field component, and is given by the following:
where μ0 is the vacuum magnetic permittivity. The current density and the magnetic field variation ΔB vectors define the CS plane, and through the cross product of both the normal vector is obtained.
The comments in the previous paragraph are valid for the CS LS, but the observations normally refer to a common reference system such as the geocentric solar ecliptic (GSE) system and the measurements are time-dependent. In these cases, we have to relate the magnetic structure proposed for the LS to what is actually observed in that system. To achieve this, two consecutive rotations to the magnetic topology in the local frame (Eq. (1)) were performed, the first around the ZLS axis by an angle α and the second one around the X′ axis (i.e., the XLS axis rotated around ZLS) by an angle β. Then the magnetic field components in the GSE system are as follows:
The α and β angles are assumed to be positive in the clockwise direction, t0 marks the time of the magnetic field inversion, and v is the crossing speed given by the following:
with 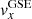 ,
, 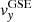 , and
, and 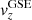 being the averaged solar wind components along the CS crossing. It is assumed that the spacecraft velocity is negligible compared to the solar wind velocity.
being the averaged solar wind components along the CS crossing. It is assumed that the spacecraft velocity is negligible compared to the solar wind velocity.
Although it can seem that three rotations are needed to relate the field in the LS with the field in the GSE system, this is not correct in the HYTARO case because of the field’s relative orientation with respect to the CS plane being fixed by B0x + BA and B0z. Once this is done, two consecutive rotations are enough to relate the CS plane in the LS with those in the GSE system. To confirm this assumption, an estimation analysis of the weights of each of the angular parameters of the model is included in next section using PCA. Of course, the kind and order in the rotations are defined by the choice of the direction perpendicular to the CS plane. In our case, this direction is the Y axis.
In line with the model, the constant term can be related to the mean value of the measured magnetic field in the HCS, that is 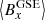 ,
, 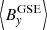 , and
, and 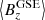 . This relationship was obtained from Eq. (4) after determining the temporal mean value for a symmetric interval around the inversion point (t0). For such an interval, the mean value of the hyperbolic tangent is zero, thus leading to the following expressions for the constant term components:
. This relationship was obtained from Eq. (4) after determining the temporal mean value for a symmetric interval around the inversion point (t0). For such an interval, the mean value of the hyperbolic tangent is zero, thus leading to the following expressions for the constant term components:
This result permits one to reduce the number of free parameters in HYTARO from eight to five. In this final form, HYTARO can directly obtain several physical parameters of the local structure of the CS such as its width, magnetic inversion point, magnetic amplitude, and local orientation.
After applying the rotations, the components of the current density in the GSE system are as follows:
Only currents in the YGSE − ZGSE plane are possible according to HYTARO constrains about magnetic topology, the plane orientation in the LS, and the use of two rotations.
As mentioned above, α and β are the angles which relate the orientation of the CS plane in the LS to its orientation in the GSE system. From these angles, it is possible to determine the CS local orientation in terms of its normal vector n to the HCS plane by applying the two rotations to the normal vector (0, 1, 0) of the CS plane in the LS, obtaining the following expression:
3. Principal component analysis
Principal component analysis was first formulated in statistics by Pearson (1901), who formulated an analysis, from a geometrical point of view, and found “lines and planes of closest fit to systems of points in space”. To study the relationships between n correlated variables, the original set of variables can be transformed into another set of new variables that are not correlated with each other (which does not have redundancy in the information) called a set of principal components. PCA is a linear transformation of the orthogonal coordinate axes to a new orthogonal reference frame that corresponds to the geometry of the data set (Kirschvink 1980). The origin in the new system corresponds to the inversion point of the magnetic field and the new axes are positioned by least squares to best-fit data. Each axis in the new reference frame has, associated with it, a term of the variance about the mean in the particular direction, two in the maximum and minimum direction of variance, and a third in the intermediate direction. As with MVA, PCA works with the covariance matrix; however, PCA allow us to study the contribution of each of the components to the total variance and to approach the problem of dimensionality reduction. One principal component represents the data, and the dimensionality of the total system can be reduced. For example, in the case of two eigenvalues that are zero, the third one is parallel to the line and the other two are at arbitrary right angles to it. When we study a CS, we are analyzing a plane, and the perpendicular direction to the plane has no variance. Applying PCA, we reduced the dimensionality of the problem and that let us avoid working with a third arbitrary angle without including any additional parameter in the model.
A covariance matrix shows the covariance of two vector elements in a data set. If the two elements of the vector vary together, they have a higher covariance. However, if a change in one element is completely independent of another, its covariance is null. The eigenvalues represent the variance of the data along the axes of the principal component. These are ordered based on their variance from largest to smallest, where a large variance indicates that most of the information from the data is in the related component. Eigenvalues associated with each eigenvector represent the variance of the data along the new axes. With eigenvalues, PCA can be used to analyze if a set of points can be adjusted to a line (λmax ≫ λint ≥ λmin ≅ 0), to a plane (λmax ≥ λint ≫ λmin ≅ 0), or to a three-dimensional curve (λmax ≥ λint ≥ λmin ≫ 0) (Kirschvink 1980).
To study the reduction of dimensionality, we removed the smallest main component, just keeping the information along the other two components. A posterior analysis of the new principal components set of data let us evaluate the contribution of the smallest main component. Euler matrices rotate data without changing its shape. In the same way, eigenvectors were used to rotate the data in a new coordinate system, so that the correlated features aligned with the new axes defined by the principal components. With PCA, we identified the principal components and the variance of each of them. When we applied three rotations, a strong correlation appeared between the angles. As a result, it is necessary to analyze each of the variables of the model, eliminating parameters that contribute to high dependencies, or include additional physics parameters to reduce the correlation between angular variables.
A CS example shows the contribution of each of the principal components where the minimum variance is in the perpendicular direction. Results show that a dimensionality reduction can be affordable; after all, we are trying to adjust a plane. Applying the PCA in the event selected (1 April 1997) (Fig. 1), we obtained the following three eigenvalues: the largest one being 10.85, the intermediate one being 0.30, and the minimum one being 0.01. Further, the event selected accomplishes the MVA validity criterion defined by Horbury et al. (2001), Knetter et al. (2003). The variance contribution of each of them is 97.2%, 2.6%, and 0.1%, respectively. Once the principal components are defined, a new set of data is calculated removing the smallest main component contribution. After that, the HYTARO model should be applied over this new base and compared to the results obtained with the analysis for the original data (Table 1).
 |
Fig. 1. HCS crossing of 1 April 1997 including the HYTARO adjustment. The continuous lines are the obtained fit curves and the dots represent the magnetic field. Fit parameters are summarized in Table 2. |
HYTARO angular parameter model results (in degrees), including standard error (SE) for 1 April 1997, obtained using original B data and using reconstructed data with PCA.
As we expected, the results show slight differences between the parameters for both sets of data, that is to say the original data and the principal components’ calculated data. These differences are due to the contribution of the smallest main component. There exists a relation between the variance of each of the main components with the adjust parameters. If a third rotation is included without any other constraint, the dependencies between angles are maxima. Vectors normally calculated by applying HYTARO in both sets of data, that is the original and PCA calculated ones, show a deviation of 14.3° from one another. At this point, it is interesting to mention that a similar analysis working with the original data, between vectors normal for HYTARO versus MVA, show the same deviation. That is because both MVA as PCA use the eigenvalues and eigenvectors obtained via the covariance matrix.
Finally, we checked the variation between the normal vectors calculated by MVA, again, with the original data and with the data calculated by PCA. In this second case, the third eigenvalue is zero since in the dimensionality reduction of the problem we recalculated the data set for the new base defined from the principal components, eliminating the contribution of the smallest component. The eigenvector associated with this third eigenvalue does not change. Since the normal vector in the plane of the CS does not vary, we can interpret that the information that we are eliminating does not imply a substantial change. In fact, it should be remembered that the variance of the minimum eigenvalue represents 0.1% of the total variance.
When the third rotation is implemented in HYTARO, the dependencies that appear between the three angular parameters associated with each of the rotations make it impossible to determine the contribution of each of them. PCA allows us to determine this contribution and eliminate the rotation associated with the main axis whose variance is smaller. In all the cases analyzed, the variance of the lowest eigenvalue is below 1%.
An analysis of the deviation between normal vectors obtained with HYTARO and PCA is summarized in the Fig. 2. A set of 14 CSs were selected from Table 2, and 50% of the crossings analyzed show a deviation under 15°. Only 14% of the HCS crossings show angles between normal vectors greater than 45°. For these cases, a possible explanation is found in the models of the global structure of the solar wind; Peng et al. (2019) conclude that in some cases, the HCS is better described with an Archimedean spiral, superposed by small-scale ripples. Israelevich et al. (2001) carried out numerical simulations with the Alfvén conceptual model including the radial and azimuthal components of the electric current, concluding that current sheet warping exhibits a spiral structure and a high dependency with the solar cycle. The regular structure of the heliospheric current system disappears near the solar maximum. The heliospheric magnetic field behavior during the solar cycle can be described as magnetic flux transport from the equatorial to polar regions of the Sun.
 |
Fig. 2. Deviation between vectors’ normal calculated with HYTARO and PCA. |
40 HCS crossings detected by WIND spacecraft instruments.
4. HCS local structure at 1 AU during the solar minimum between the 22 and 23 maxima
HYTARO can be used to infer information from a CS crossing, such as its width, orientation, and magnetic structure. We selected a group of sector boundary crossings and we applied HYTARO to the HCS to study how it works when it is applied to a real CS. In situ observations show that the HCS local structure is a sharp frontier between magnetic sectors with opposite polarities. The transition between sectors appears as an inversion of the magnetic field direction, which begins by pointing sunward (antisunward) and then pointing antisunward (sunward), with a minimum in the magnetic field strength in between. Additional solar wind signatures observed during an HCS crossing are, for example, the change in the sign of the dot product of the electron heat flux and magnetic field (Qe ⋅ B) (Kahler et al. 1998) or the appearance of a maximum in plasma beta (Winterhalter et al. 1994). With respect to this last signature, Crooker et al. (2004) warn that sometimes HCS crossings are observed without clear plasma beta enhancement. A typical HCS crossing was observed by WIND instruments (Magnetic Field Instrument (MFI) and Solar Wind Experiment (SWE)) on 9 March 1995. The magnetic field showed minimal strength together with a change in the polarity of the magnetic field. At the same time, a plasma beta maximum was detected accompanied by a Qe ⋅ B sign change.
Data from the MFI magnetometer (Lepping et al. 1995) and SWE instrument (Ogilvie et al. 1995), both on board of the WIND spacecraft, have been used. An event was selected as an HCS crossing when the magnetic field showed a change in its direction, from sunward (antisunward) to antisunward (sunward) with a change in the sign of the dot product of the electron heat flux and magnetic field. Because HYTARO needs stable magnetic regions on both HCS crossing sides to be applied, those crossings which fit with the selection criteria, but where the field was not stable enough, were rejected. One of the aims of this research is to test HYTARO as a tool able to infer confident information from a HCS crossing. In fact, we are focusing on the general properties of a HCS crossing.
As stated in the introduction, MVA (Sonnerup & Cahill 1967) can be used to estimate the normal vector to the HCS plane. The eigenvectors obtained define a complete base where the magnetic field exhibits a sign change in its maximum variance component (see Fig. 3).
 |
Fig. 3. HCS crossing detected by WIND spacecraft. From top to bottom: plasma beta, Qe ⋅ B sign, magnetic field components in GSE, and field strength. |
A completely different way to tackle the estimation of the HCS local orientation is to use Eq. (4) as a fit function for the magnetic field data measured during an HCS crossing. The fit parameters are the rotation angles (α and β), the HCS semi width (L), the amplitude BA, and the time of magnetic field inversion t0. The Levenberg–Marquardt algorithm has been used to minimize the chi-square function, building on Eq. (4). As mentioned above, Eq. (6) has been used as constraint, thus reducing the number of free parameters that were needed in the previous version of HYTARO (Blanco et al. 2003). Unfortunately, direct measurements of electric current densities are not available which is what prevents their use in the fit procedure. Nevertheless, this problem has been circumvented thanks to the imposed constrains on the magnetic field as is mentioned in Sect. 2.
Before continuing our analysis, it is necessary to mention errors during the fit procedure. No special weighting has been used for the experimental data. This point is assumed because the MFI magnetometer normally gives similar experimental errors for individual measurements during an HCS crossing. The error associated with each fit parameter is its standard error calculated by 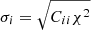 where Cii is the diagonal element of the variance-covariance matrix and χ2 is the reduced chi-square function. The α and β parameters require special attention because they define the HCS local orientation. Typically, the error associated with both parameters is around ±0.03 rad, that is 1.7°. This implies a maximum error of ±0.03 rad in the X component and ±0.06 rad in the other two components of the normal vector for the HCS plane.
where Cii is the diagonal element of the variance-covariance matrix and χ2 is the reduced chi-square function. The α and β parameters require special attention because they define the HCS local orientation. Typically, the error associated with both parameters is around ±0.03 rad, that is 1.7°. This implies a maximum error of ±0.03 rad in the X component and ±0.06 rad in the other two components of the normal vector for the HCS plane.
Another important point consists in establishing the data interval used for the analysis. Because of HYTARO being based on hyperbolic tangents, it needs to include points from stable regions on both sides of the crossing. When comparing HYTARO with MVA and CVA, we used the same data interval for the three methods.
As an example, Fig. 4 shows how HYTARO worked when it is applied to the HCS crossing detected by the WIND spacecraft on 09 March 1995. As can be seen, HYTARO reproduces the measured magnetic field (continuous lines) fine, obtaining the HCS width (132 000 km) and the normal vector to the HCS plane (0.72, 0.66, 0.20). This result is quite similar to those obtained with MVA for the same data interval (0.67, 0.73, −0.16), where the ratio between the mean and minimum eigenvalues is around 3, which is close to the lower limit for applicability established by Lepping & Behannon (1980). Otherwise, CVA gives (0.72, 0.66, 0.20), that is the same normal vector obtained by HYTARO. Finally, the estimated constant term was (−0.51, 0.00, 3.51) nT. It is necessary to comment on the HCS width, as is shown in Fig. 4, where the data interval selected is wide enough to include additional regions out of the HCS. Although, in this case, it is possible to select a shorter data range which fits with the crossing and stability criteria, we have chosen this one to be consistent with the other selected crossings in this work where it is not possible to find magnetic stable conditions so close to the CS. The width obtained must be considered as a sector boundary width more than the proper HCS width.
 |
Fig. 4. Example of HYTARO application. The continuous lines are the obtained fit curves and the dots represent the magnetic field. Fit parameters are given in the box with the chi-square per degree of freedom and the correlation factor. |
As far as its inclination, width, and plasma features are concerned, the HCS local structure shows highly variable characteristics (Blanco et al. 2008). Near solar minimum, the solar magnetic field is well organized and a low number of energetic events such as coronal mass ejections or flares happen. In these calm conditions, a collection of 40 HCS crossings, listed in Table 2 and detected by WIND during the solar minimum between January 1995 and May 1997, was selected under the criteria provided above. In 17 cases, the HCS crossings were detected near or in a stream interaction region, that is the region where fast solar wind is in contact with slow solar wind at 1 AU; in 23 cases, they were detected in a slow solar wind region. After applying HYTARO to this set of crossings, the following results were obtained. The HCS width ranged between 6000 and 1 200 000 km; these values are similar to those presented in Winterhalter et al. (1994) for the HCS and the heliospheric plasma sheet (HPS) that is characterized by enhanced plasma beta and a slightly lower temperature (Liu et al. 2014). It is important to remember that our selection of the range of data which imposes stable magnetic field regions, and, in these conditions, some analyzed crossings could include part of the HPS and so the HCS width could be overestimated especially in the widest crossings. The HPS, embedded in the HCS, is a multiscale structure and cannot be adequately described separately with a semi-empirical model (Kislov et al. 2015). As for the local orientation, the HCS plane mostly lays along the nominal Parker spiral, that is around −45°, and the elevation angle was almost distributed symmetrically around zero degrees and it is the most repeated value in a range of 70° above and below the ecliptic. Histograms of longitude and elevation angles are given in Fig. 5. Although these results are in agreement with those obtained in the previous work on HCS local features by Behannon et al. (1981), Blanco et al. (2008) and Liou & Wu (2021), using the MVA and a previous version of HYTARO, respectively, show that the high elevation values are somewhat surprising considering that the crossings were compiled during the solar minimum. On this point, several authors have proposed the presence of local waviness or irregularities which might explain these elevation values (Villante et al. 1979; Behannon et al. 1981). Nevertheless, 20 HCS crossings gave an elevation lower than 60°.
 |
Fig. 5. Normal vector to HCS plane orientation. The histograms show the longitude angle with respect to the Earth-Sun line (right) and the elevation angle on the ecliptic plane (left) computed. Only events identify which SSW conditions were used. |
5. HCS as magnetic discontinuity
In Fig. 5, a statistical analysis over events associated with slow solar wind (SSW) conditions are used. The elevation angle on the ecliptic plane show angles under 60° for all the events studied with a higher concentration of angles under 20°. For the longitude angles, the results show a Gaussian distribution with a peak around 40°.
The local structure of the HCS may be considered as a magnetic directional discontinuity in the sense established by Burlaga (1969), where a magnetic discontinuity is defined as a change in the magnetic field direction over a relatively short time interval. The kind of magnetic discontinuity is defined by the constant magnetic field term and the magnetic amplitude in HYTARO. The constant term roughly lays on the discontinuity plane in 52% of the crossings, that is in 21 crossings the angle between the normal and the constant term was higher than 60° (Fig. 6). These values were calculated with the dot product between the normal vector to the HCS plane and the constant magnetic term. Moreover, the constant term was different from zero in all the crossings analyzed.
 |
Fig. 6. Histogram of the angle between the magnetic field constant term and the normal vector to the HCS plane. |
6. Conclusions
HYTARO is a model which describes the local magnetic field detected during an HCS crossing. It is a modified Harris field composed of a constant term and a Harris hyperbolic tangent. The model presented in 2003 has been improved upon by reducing the number of free parameters (from eight to five), introducing the relative spacecraft trajectory through the HCS, and adding an X component of the constant term different from zero. HYTARO reproduces several magnetic field topologies observed in HCS crossings thanks to the constant term and in relation to the measured mean field.
HYTARO can obtain different parameters of the local structure of the HCS, such as width, the point of the magnetic inversion, magnetic amplitude, and local orientation. These parameters have been estimated for 40 HCS crossings detected by WIND from January 1995 to May 1997, that is during the solar minimum. HYTARO obtains good correlation values when it is fitted to the magnetic field measured during an HCS crossing and its estimations of the HCS width and local orientation are in agreement with those presented in previous works by different researchers.
In this study, PCA is used to evaluate the contribution of each of the main components and the implications of a reduction of dimensionality removing the smallest component. The results show that it is affordable. In terms of loss of information, less than 1% of the information belong to the smallest principal component, and the HYTARO model adjustment shows slight discrepancies between the original data with respect to the reconstructed data along the principal components. When three rotations were applied to the HYTARO model, a strong correlation between angles was observed and random results in a normal vector and the width of a sheet were obtained in this case.
HYTARO results are consistent with a change in magnetic polarity throughout the crossing due to rotation of the magnetic field accompanied by a variation in field strength. No event was consistent with a strength variation without field rotation. In most of the crossings, the field rotated almost into alignment with the discontinuity plane, while helicoidal rotations were observed in the others.
Although HYTARO obtained similar statistical results as previous works which mainly used MVA in their analysis, this does not replace MVA or CVA; however, it does offer a different approach to local HCS topology by providing an alternative tool.
Acknowledgments
The authors wish to thank the WIND/MFI, WIND/SWE teams for the use of their data. This work has been supported by the Spanish Government project PID2019-107806GB-I00 funded by Ministerio de Economía y Competitividad and by the European Regional Development Fund, FEDER.
References
- Behannon, K. W., Neubauer, F. M., & Barnstorf, H. 1981, J. Geophys. Res.: Space Phys., 86, 3273 [Google Scholar]
- Blanco, J. J., Rodríguez-pacheco, J., & Sequeiros, J. 2003, Sol. Phys., 213, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco, J. J., Rodríguez-Pacheco, J., Hidalgo, M. A., & Sequeiros, J. 2006, J. Atmos. Solar-Terr. Phys., 68, 2173 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco, J. J., Rodriguez-Pacheco, J., Hidalgo, M. A., & Sequeiros, J. 2008, J. Atmos. Solar-Terr. Phys., 70, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F. 1969, Sol. Phys., 7, 54 [Google Scholar]
- Crooker, N. U., Huang, C. L., Lamassa, S. M., et al. 2004, J. Geophys. Res.: Space Phys., 109, A03107 [NASA ADS] [Google Scholar]
- Harris, E. G. 1962, II Nuovo Cimento, 23, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Hausman, B. A., Michel, F. C., Espley, J. R., & Cloutier, P. A. 2004, J. Geophys. Res.: Space Phys., 109 [CrossRef] [Google Scholar]
- Horbury, T. S., Burgess, D., Fränz, M., & Owen, C. J. 2001, Geophys. Res. Lett., 28, 677 [Google Scholar]
- Israelevich, P., Gombosi, T., Ershkovich, A., et al. 2001, A&A, 376, 288 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jolliffe, I. 2011, in Principal Component Analysis, ed. M. Lovric (Berlin, Heidelberg: Springer), 1094 [Google Scholar]
- Kahler, S., Crooker, N. U., & Gosling, J. T. 1998, J. Geophys. Res., 103, 20603 [NASA ADS] [CrossRef] [Google Scholar]
- Khrabrov, A. V., & Sonnerup, B. U. Ö. 1998, J. Geophys. Res., 103, 6641 [NASA ADS] [CrossRef] [Google Scholar]
- Kirschvink, J. L. 1980, Geophys. J. R. Astron. Soc., 62, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Kislov, R. A., Khabarova, O. V., & Malova, H. V. 2015, J. Geophys. Res.: Space Phys., 120, 8210 [NASA ADS] [CrossRef] [Google Scholar]
- Knetter, T., Neubauer, F. M., Horbury, T., & Balogh, A. 2003, Adv. Space Res., 32, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Lepping, R., & Behannon, K. 1980, J. Geophys. Res.: Space Phys., 85, 4695 [NASA ADS] [CrossRef] [Google Scholar]
- Lepping, R. P., Acũna, M. H., Burlaga, L. F., et al. 1995, Space Sci. Rev., 71, 207 [Google Scholar]
- Liou, K., & Wu, C.-C. 2021, ApJ, 920, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y. C.-M., Huang, J., Wang, C., et al. 2014, J. Geophys. Res.: Space Phys., 119, 8721 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, K. W., Chornay, D. J., Fritzenreiter, R. J., et al. 1995, Space Sci. Rev., 71, 55 [Google Scholar]
- Pearson, K. 1901, London Edinb. Dublin Phil. Mag. J. Sci., 2, 559 [CrossRef] [Google Scholar]
- Peng, J., Liu, Y. C.-M., Huang, J., Klecker, B., & Wang, C. 2019, J. Geophys. Res.: Space Phys., 124, 9814 [NASA ADS] [CrossRef] [Google Scholar]
- Sckopke, N., Sonnerup, B. U. O., Bauer, T. M., & Dunlop, M. 2000, in Cluster-II Workshop Multiscale/Multipoint Plasma Measurements, ed. R. A. Harris, ESA SP, 449, 101 [NASA ADS] [Google Scholar]
- Scudder, J. D. 2005, J. Geophys. Res.: Space Phys., 110, A02202 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, E. J. 2001, J. Geophys. Res.: Space Phys., 106, 15819 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnerup, B. U. O., & Cahill, L. J., JR. 1967, J. Geophys. Res., 72, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Villante, U., Bruno, R., Mariani, F., Burlaga, L. F., & Ness, N. F. 1979, J. Geophys. Res., 84, 6641 [NASA ADS] [CrossRef] [Google Scholar]
- Winterhalter, D., Smith, E. J., Burton, M. E., Murphy, N., & McComas, D. J. 1994, J. Geophys. Res., 99, 6667 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
HYTARO angular parameter model results (in degrees), including standard error (SE) for 1 April 1997, obtained using original B data and using reconstructed data with PCA.
All Figures
 |
Fig. 1. HCS crossing of 1 April 1997 including the HYTARO adjustment. The continuous lines are the obtained fit curves and the dots represent the magnetic field. Fit parameters are summarized in Table 2. |
| In the text | |
 |
Fig. 2. Deviation between vectors’ normal calculated with HYTARO and PCA. |
| In the text | |
 |
Fig. 3. HCS crossing detected by WIND spacecraft. From top to bottom: plasma beta, Qe ⋅ B sign, magnetic field components in GSE, and field strength. |
| In the text | |
 |
Fig. 4. Example of HYTARO application. The continuous lines are the obtained fit curves and the dots represent the magnetic field. Fit parameters are given in the box with the chi-square per degree of freedom and the correlation factor. |
| In the text | |
 |
Fig. 5. Normal vector to HCS plane orientation. The histograms show the longitude angle with respect to the Earth-Sun line (right) and the elevation angle on the ecliptic plane (left) computed. Only events identify which SSW conditions were used. |
| In the text | |
 |
Fig. 6. Histogram of the angle between the magnetic field constant term and the normal vector to the HCS plane. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



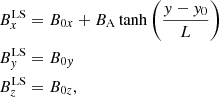
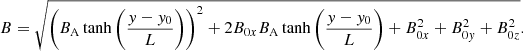

![$$ \begin{aligned} \begin{aligned}&B^\mathrm{GSE}_x = \left[B_{0x} + B_{\rm A} \tanh \left(\frac{(t-t_0){ v}}{L}\right)\right]\cos {\alpha } - B_{0{ y}}\sin {\alpha } \\&B^\mathrm{GSE}_{ y} = \left\{ \left[B_{0x}+ B_{\rm A} \tanh \left(\frac{(t-t_0){ v}}{L}\right)\right]\sin {\alpha }+ B_{0{ y}}\cos {\alpha } \right\} \cos {\beta }-B_{0z}\sin {\beta } \\&B^\mathrm{GSE}_z = \left\{ \left[B_{0x}+ B_{\rm A} \tanh \left(\frac{(t-t_0){ v}}{L}\right)\right]\sin {\alpha }+ B_{0{ y}}\cos {\alpha } \right\} \sin {\beta }+B_{0z}\cos {\beta }. \end{aligned} \end{aligned} $$](/articles/aa/full_html/2022/04/aa42474-21/aa42474-21-eq7.gif)