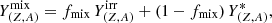| Issue |
A&A
Volume 658, February 2022
|
|
|---|---|---|
| Article Number | A197 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202142319 | |
| Published online | 24 February 2022 | |
Non-thermal nucleosynthesis by accelerated particles to account for the surface composition of P-rich stars
Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles, CP 226, 1050 Brussels, Belgium
e-mail: sgoriely@astro.ulb.ac.be
Received:
28
September
2021
Accepted:
25
November
2021
Context. Fifteen abnormally phosphorus-rich stars were recently discovered. Their peculiar surface abundance distribution is challenging our present stellar nucleosynthesis theories, because none of the standard thermal nucleosynthesis models are found to explain the observed patterns.
Aims. This paper presents an exploration of the extent to which an irradiation process resulting from the interaction of some target material with energetic protons and/or α-particles can by itself be at the origin of the chemical pollution observed at the surface of P-rich stars.
Methods. In light of our lack of knowledge of the characteristics of the accelerated particles that could be held responsible for this nuclear process, a purely parametric site-independent approach is followed, with the proton and α-particle flux amplitude, energy distribution, and fluence taken as free parameters. The irradiated material is assumed to be made either of CNO elements in solar ratio or pure C.
Results. Such an irradiation process with energies of no more than a few MeV per nucleon is shown to give rise to rich nucleosynthesis, including significant production of P, as well as Z > 30 heavy elements in relative abundance similar to what the slow neutron-capture process traditionally produced.
Conclusions. The final composition obtained by mixing such a non-thermal nucleosynthesis by accelerated particles with nuclearly unaffected material is found to reproduce fairly well the global surface composition of P-rich stars, except for a few species like Al, Si, or Ba.
Key words: nuclear reactions, nucleosynthesis. abundances / acceleration of particles / stars: chemically peculiar
© ESO 2022
1. Introduction
Fifteen abnormally phosphorus-rich stars were recently discovered (Masseron et al. 2020a,b). All were found to have a relatively low metallicity with [Fe/H] ≃ −1. In addition to the large P enhancement, such stars also show significant overabundances in other light (O, Mg, Si, and Al) and heavy Z > 30 elements. It is believed that the P-rich stars have been polluted from another stellar source but their peculiar surface abundance distribution is challenging our present stellar nucleosynthesis theories. Detailed comparisons with model predictions by Masseron et al. (2020a), including low- or intermediate-mass asymptotic giant branch (AGB) stars, core-collapse supernovae, Type Ia supernovae, CO or ONe novae, and so on have so far failed to provide a plausible explanation for the origin of the P-rich star enrichment. Two of those P-rich stars have also been observed with high-resolution optical spectra and a large number of elemental abundances from C to Pb determined at their surface (Masseron et al. 2020b). These stars, namely 2M13535604+4437076 and 2M22045404-1148287, have been shown to present heavy-element surface overabundances similar to the one expected from the slow neutron-capture process (or s-process) of nucleosynthesis, with a high enrichment in light-s (Sr, Y, and Zr) and heavy-s (Ba, La, Ce, and Nd) elements and even some Pb overabundance in one of the stars. However, this s-process distribution is found to differ from that expected for low-mass low-metallicity AGB stars with a particularly large Ba/La ratio and low Eu and Pb overabundances found in P-rich stars (Masseron et al. 2020b).
As thermonuclear processes in traditional stellar nucleosynthesis models have so far failed to explain the abundance patterns seen at the surface of P-rich stars, here we explore the possibility that non-thermal reactions due to accelerated charged particles are at its origin. While most nucleosynthesis models are based on thermal processes (for a review, see Arnould & Goriely 2020), it is known that non-thermal processes, such as the interaction of Galactic cosmic rays with the interstellar medium, could also be at the origin of the solar 6Li, 9Be, and 10B, and could provide most of the 11B and at least some of the 7Li (Tatischeff & Gabici 2018). Some non-thermal nucleosynthesis has also been called upon to explain the synthesis of rare neutron-deficient nuclei, and in particular 180Tam (Kusakabe & Mathews 2018).
Stellar energetic particles (SEPs) have also been invoked in order to explain some characteristics of the surface composition of certain stars. This concerns for example the high 6Li abundance observed in metal-poor halo stars, which is very difficult to reconcile with big-bang nucleosynthesis (Tatischeff & Thibaud 2007; Tatischeff & Gabici 2018). Jet-induced nucleosynthesis has also been suggested to explain the large Li enrichment observed in the companions of some black hole or neutron star X-ray binary systems (Butt et al. 2003). Some spectral features of so-called chemically peculiar (CP) stars may be another interesting case. Their abundance patterns have been classically interpreted on the basis of diffusion processes, that is, the diffusive segregation of ionic and isotopic species resulting from the balance between radiative and gravitational forces within the atmosphere and subatmospheric regions (Michaud et al. 2004). However, there have been claims that some short-lived radioactive elements, such as Tc and Pm, and 84 ≤ Z ≤ 99 elements may be present at the surface of the CP roAp star HD 101065, also known as Przybylski’s star (Cowley et al. 2000, 2004; Gopka et al. 2004; Bidelman 2005). Such a remarkable observation of short-lived radioactive elements certainly needs to be confirmed, considering the complexity of identifying the spectral lines of ionised radio elements in warm, abnormal, stratified, and non-local thermodynamic-equilibrium atmospheres. If firmly established, the origins of these radionuclides (in particular Pm with a 17.7 y half-life for its longest-lived isotope) cannot be found in diffusion processes, but in nuclear processes instead. Another feature of HD 101065 abundances is that they exhibit 35 < Z < 82 elements exceeding the Solar System values by three to four orders of magnitude and unusual Co/Fe and 6Li/7Li abundance ratios. Again, this rather spectacular feature can hardly be accounted for by diffusion processes, while it can be explained by the action of SEPs. This has been shown by Goriely (2007) on grounds of a simple approach taking as free parameters the observationally unknown proton and α-particle spectra, the time of irradiation, and the possible mixing with nuclearly unprocessed material. High fluences of the order of 1027cm−2 were needed to account for such observations.
The purpose of the present work is to study the irradiation process by energetic particles and to analyse if it can alone explain the abundances observed at the surface of the P-rich stars 2M13535604+4437076 and 2M22045404-1148287, as determined by Masseron et al. (2020a,b). This includes the particularly large overabundances of Al, Si, and P, the significant overproduction of the heavy elements with 37 ≤ Z ≤ 82 by typically 1 dex with respect to the solar composition, and the relatively low enhancement of S and elements between K (Z = 19) and Zn (Z = 30). In Sect. 2, we outline the model used to describe the nucleosynthesis resulting from the interaction of energetic protons and α-particles with some target material, including the input physics and the approximation and parametrisation adopted. Section 3 describes the specific SEP events chosen to describe the potential enrichment of P-rich stars with a detailed analysis of the chemical transmutation taking place during the irradiation process. In Sect. 4, assuming the irradiated material is mixed with stellar material, the SEP event outcomes are quantitatively compared with the spectroscopically determined abundance distribution in both P-rich stars 2M13535604+4437076 and 2M22045404-1148287 (Masseron et al. 2020a,b). Conclusions are drawn in Sect. 5.
2. SEP modelling
The modelling of the interaction of SEPs with some target material is similar to that detailed in Goriely (2007). Some of its main features are repeated here. To describe changes in the abundances of the nuclei as a result of the interaction of the energetic incident particles with the low-density stellar atmosphere, a nuclear reaction network including all relevant reactions is used. All nuclei with 0 ≤ Z ≤ 102 and located between the proton drip line and the neutron-rich side of the valley of stability are included in the network. The chosen set of nuclear species are then coupled by a system of differential equations corresponding to all the reactions affecting each nucleus, i.e. mainly proton, α and neutron captures, β- and α-decays, as well as spontaneous fission decays. The rate of change of the molar fraction Y(Z, A) of a nucleus (Z, A) with charge number Z and mass number A can be written as
where λβ±, λα, and λsf are the β±, α, and spontaneous fission decay rate, respectively, Na is the Avogadro number, ρ the local density, and Yn the neutron abundance. In Eq. (1), ⟨σ⟩p and ⟨σ⟩α are the total effective cross sections for proton and α-captures averaged over their energy distribution ϕ(E); i.e. for the proton case,
where σp(E) is the E-dependent total proton capture cross section and 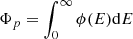 is the proton flux amplitude. Similarly,
is the proton flux amplitude. Similarly,  is the partial effective cross section for proton capture on a nucleus k leading to the residual (Z, A) nucleus. The proton and α-particle capture cross sections σ(E) are either taken from experiments (essentially for light species; Meyer 1972; Ramaty et al. 1997) or estimated with the TALYS nuclear reaction code (Koning & Rochman 2012) which takes into account all types of direct, pre-equilibrium, and compound mechanisms to estimate the total reaction probability, as well as the competition between the various open channels. The cross sections have been estimated at energies up to 200 MeV, though only energies up to a few MeV per nucleon are considered in the present irradiation models (see Sect. 3). The calculation includes single particles (nucleons and α-particles), as well as multi-particle emissions and fission. All the experimental information on nuclear masses, deformation, and the spectra of low-lying states is considered whenever available. Where these are unavailable, global nuclear level formulas, γ-ray strength functions, and nucleon and α-particle optical model potentials are considered to determine the excitation level scheme and the photon and particle transmission coefficients. Due to the large number of open channels at high energies, typically about 30 different (p or α,xn yp zα) reaction types corresponding to the emission of x neutrons, y protons, and zα-particles need to be taken into account per target nucleus. The reaction network (Eq. (1)) includes about 5600 different species with 0 ≤ Z ≤ 102 and some 142 000 capture reactions for the incident energies considered here (see Sect. 3).
is the partial effective cross section for proton capture on a nucleus k leading to the residual (Z, A) nucleus. The proton and α-particle capture cross sections σ(E) are either taken from experiments (essentially for light species; Meyer 1972; Ramaty et al. 1997) or estimated with the TALYS nuclear reaction code (Koning & Rochman 2012) which takes into account all types of direct, pre-equilibrium, and compound mechanisms to estimate the total reaction probability, as well as the competition between the various open channels. The cross sections have been estimated at energies up to 200 MeV, though only energies up to a few MeV per nucleon are considered in the present irradiation models (see Sect. 3). The calculation includes single particles (nucleons and α-particles), as well as multi-particle emissions and fission. All the experimental information on nuclear masses, deformation, and the spectra of low-lying states is considered whenever available. Where these are unavailable, global nuclear level formulas, γ-ray strength functions, and nucleon and α-particle optical model potentials are considered to determine the excitation level scheme and the photon and particle transmission coefficients. Due to the large number of open channels at high energies, typically about 30 different (p or α,xn yp zα) reaction types corresponding to the emission of x neutrons, y protons, and zα-particles need to be taken into account per target nucleus. The reaction network (Eq. (1)) includes about 5600 different species with 0 ≤ Z ≤ 102 and some 142 000 capture reactions for the incident energies considered here (see Sect. 3).
The proton and α-particle fluxes are assumed to remain constant over time during the irradiation period τirr. Many different energy distributions could be studied, but we restrict ourselves to energy spectra with a constant distribution in a restricted Emin ≤ E/A ≤ Emax energy range. We note that, in the present exploratory site-independent parametric approach, energy loss by the incoming accelerated particles in the target is not taken into account in Eq. (2).
Special attention needs to be paid to the role played by the neutrons emitted during the spallation process. The neutron abundance is followed with the same time-dependent equation as in Eq. (1). We assume that the neutrons produced by spallation processes are thermalised on much shorter timescales than the typical capture timescales. An average thermalisation time needed to bring the MeV neutrons down to a thermal energy Eth after n collisions can be approximated (see e.g. Rinard et al. 1991) by
where vi is the mean neutron velocity after the ith collision. At each collision, the neutron energy is assumed to change energy from Ei to Ei + 1 = Ei × (A2 + 1)/(A + 1)2, where A is the atomic weight of the moderating material. Assuming the matter to be essentially made of C or O (see below), σ corresponds to the C- or O-neutron collision cross section, which amounts to about 1-3 b for neutrons in the eV-MeV range, meaning that for an average temperature of T ≃ 7000 K (corresponding to a thermal energy of about Eth ≃ 0.6 eV) and density ρ = 1 g cm−3, τ ≃ 10 μs (or 1 s for a density ρ = 10−5 g cm−3), which justifies the fast thermalisation of the neutrons for irradiation processes taking place on timescales τirr ≫ τ. In this case, the neutron energy spectrum follows a traditional Maxwell-Boltzmann distribution at a temperature T. The Maxwellian-averaged neutron capture rates ⟨σv⟩n are also estimated by the Hauser-Feshbach reaction code TALYS (Goriely et al. 2008; Koning & Rochman 2012) when not available experimentally. In Eq. (1),  corresponds to either the (n, γ), (n, p), or (n, α) reaction rate leading to the formation of the (Z, A) nucleus. We also note that, here in our one-zone model, the emitted neutrons are assumed to be captured where they are produced, which may not be the case in some more realistic astrophysical scenarios.
corresponds to either the (n, γ), (n, p), or (n, α) reaction rate leading to the formation of the (Z, A) nucleus. We also note that, here in our one-zone model, the emitted neutrons are assumed to be captured where they are produced, which may not be the case in some more realistic astrophysical scenarios.
Due to the exploratory nature of the present study, no effort is made to understand the possible mechanisms that could be held responsible for accelerating the energetic particles. A purely parametric approach is followed by taking the properties of the accelerated proton (Φp) and α-particle (Φα) flux amplitudes as free parameters. Orders of magnitude should nevertheless be kept in mind: in the specific case of solar flares, typical proton fluences Ψ = ∫Φp dt are roughly 1017 − 18 cm−2, while early Solar System models call for fluences of about 1023 cm−2 to explain the origin of the now-extinct short-lived radionuclides known to have been present in the early Solar System (Leya et al. 2003; Liu et al. 2012). As mentioned above, fluences of the order of 1027 cm−2 were called for to explain the CP distribution observed at the surface of HD 101065. The energetic jet particles from supernova explosions represent another possible extreme scenario in which fluences can be achieved that are higher by orders of magnitude. For example, in bipolar supernova explosions (Maeda & Nomoto 2003; Fujimoto et al. 2006), and at a radius of 1000 km from the supernova centre, we deal with fluxes of relativistic jet particles (initially protons that recombine into α-particles at a later time during the expansion) that can reach fluences of about 1037 − 40 cm−2 at a speed of about c/6, i.e. kinetic energy of some 10 MeV per nucleon. The composition of the accelerated particles also depends on the astrophysical site. Protons and α-particles with a typical solar ratio of α/p = 0.1 seems to be an appropriate guess. However, the absence of accelerated protons could also be expected in some cases, for example in supernova explosion jets where neutrons and protons have recombined into α-particles or in a post-accelerated Wolf-Rayet wind.
3. SEP events
As already discussed in Sect. 2, no effort is made in the present work to explain the possible mechanisms responsible for accelerating the energetic particles. The energy spectrum, the proton and α-particle fluxes, the irradiation time, and the nature of the irradiated material are therefore taken as free parameters. In the present study, we consider essentially four different types of SEP events, corresponding to (i) accelerated particles made of α-particles only or a combination of protons and α-particles with the usual 0.1 ratio and (ii) irradiated material made either of CNO elements in solar ratio or pure carbon. In addition, we restrict ourselves to low-energy fluxes with a constant energy spectrum. These conditions have been found to be of relevance to explain the P-rich stars, as discussed in Sect. 4.
The details of the properties of the SEP events considered in the present work are given in Table 1. For each of these four SEP events, the irradiation times and some dilution factors (see below) are adjusted separately to optimise the description of the abundances observed at the surface of our two P-rich stars. Such events cannot be demonstrated to exist but could correspond to events that are relatively similar (though at much lower energies) to those called upon to explain the origin of Li, Be, and B in the Galaxy, namely accelerated CNO elements bombarding interstellar medium H and He nuclei (Reeves et al. 1970; Prantzos 2012; Tatischeff & Gabici 2018). All events considered in Table 1 are characterised by a total fluence Ψ = (Φp + Φα)×τirr of about 0.7 − 14 × 1025 cm−2, i.e. about 60 to 1000 times larger than the fluence invoked for young stellar objects (Leya et al. 2003), but about 10 to 100 times less than those needed to explain the CP distribution observed at the surface of HD 101065 (Goriely 2007).
Summary of the four SEP models considered in the present work.
In Fig. 1, we illustrate the evolution of the abundances of the light nuclides up to F (including P) resulting from the specific SEP events obtained with the irradiation of α-particles only, more specifically model C_a_03, i.e. of a C target irradiated by α-particles with Φα = 10−11 mb−1 s−1 and a constant-energy spectrum with E/A ≤ 3 MeV, and model CNO_a_07, i.e. a CNO target irradiated by α-particles with Φα = 10−11 mb−1 s−1 and a constant-energy spectrum with 0 ≤ E/A ≤ 7 MeV. The interaction of low-energy α-particles with C or CNO nuclei is able to transmute the initial material into heavier species on timescales of the order of years. The transmutation of pure C first gives rise to a significant production of 13C and 15N, and then to production of 16, 18O and 19F. The secondary production of P comes later after a few years or so. For the CNO irradiation, most of the light nuclides up to F are found to be rapidly synthesised. Li, Be, and B elements may also be produced by spallation reactions, except in the C_a_03 models where the α-particles with low energies per nucleon of maximum 3 MeV on a C target cannot open their production channel (as confirmed by Fig. 4 of Tatischeff & Gabici 2018). For higher energies up to 7 MeV per nucleon, the α irradiation could be at the origin of significant Li, Be, and B production, as seen in the lower panels of Fig. 1. In both models, deuterium and 3He are also enriched in significant amounts after a few years. Similarly, Fig. 2 gives the time evolution of the abundances of light nuclides when either C or CNO nuclei are bombarded by both accelerated protons and α-particles. Similar patterns are found. For energies up to 4 MeV, as in the C_pa_04 model, 11B can be produced by secondary reactions, but only a negligible amount of Li, Be, and 10B isotopes are synthesised.
 |
Fig. 1. Upper panel: evolution of the mass fractions of light nuclides up to F (including also P) resulting from the specific SEP event of model C_a_03, i.e. of a C target irradiated by α-particles only with Φα = 10−11 mb−1 s−1 and a constant-energy spectrum with E/A ≤ 3 MeV. Lower panel: same for model CNO_a_07, i.e. a CNO target irradiated by α-particles only with Φα = 10−11 mb−1 s−1 and a constant-energy spectrum with 0 ≤ E/A ≤ 7 MeV. The hashed area corresponds to the irradiation time ranges considered to explain the P-rich abundances of both stars. |
 |
Fig. 2. Same as Fig. 1 but for the specific SEP events of model C_pa_04 (upper panel) and CNO_pa_06 (lower panel). |
Even in such low-energy conditions, the spallation reactions can induce significant production of neutrons. For a C target, the main initial neutron source, namely the 12C(α,n)15O reaction, is followed after ∼4 years by 15N(α,n)18F and after ∼35 years by 18O(α,n)21Ne. These reactions lead to a neutron density Nn of about 1010 cm−3, as shown in Fig. 3. After a few tens of years the neutron exposure is high enough to transmute the light nuclides into elements heavier than iron by a series of neutron captures and β− decays (but also α-captures) in a way similar to what is found in the s-process (Fig. 4). For CNO targets, the neutron source is at first dominated by α-particle irradiation on 14N and 16O, and then also 14C after about a year. The evolution of the neutron density in the four models considered is shown in Fig. 3 and seen to range between 109 and 2 × 1010 cm−3 which are characteristic densities found during the s-process in AGB stars (Käppeler et al. 1989; Goriely & Mowlavi 2000; Karakas 2010). We note that the neutron density resulting from transfer reactions is rather independent of the value adopted for the local density ρ. Test calculations were performed for densities ranging between ρ = 10−5 and 100 g cm−3, which indifferently lead to a constant product ρYn, that, to first approximation, can be expressed as
 |
Fig. 4. Abundance distribution of all stable nuclei as a function of the mass number A resulting from the specific spallation event of a C target irradiated by α-particles only with Φα = 10−11 mb−1 s−1 and a constant-energy spectrum with 0 ≤ E/A ≤ 3 MeV after four irradiation times of 1, 20, 40, and 60 years. |
The resulting abundance distributions are therefore unaffected by changes to the local density. All calculations shown here were obtained for a local density of ρ = 1 g cm−3. The production of heavier and heavier elements is not only triggered by β− decay, as in the s-process nucleosynthesis, but also for the present events by α-captures on heavy elements which efficiently enable synthesis of higher-Z elements at late times, in particular in the CNO_a_07 model after typically 100 years. Also, we note that considering proton or α-particle flux amplitudes that are lower or higher by one or two orders of magnitude essentially gives rise to similar nucleosynthesis as long as the irradiation time is chosen to match a similar total fluence.
Figure 5 illustrates the overabundances for all stable nuclei with A ≥ 69 resulting from our four models for the irradiation times τirr given in Table 1 and adjusted to the composition of 2M22045404-1148287 (see Sect. 4). In Fig. 5, nuclei are distinguished according to their dominant nucleosynthesis process, assuming each has been dominantly produced by the s-, r-, or p-process following the splitting of the Solar System abundances (Goriely 1999; Arnould & Goriely 2020). While for the irradiation times shown in Fig. 5, none of the p-elements are significantly produced, s-dominated nuclei are clearly produced with a ratio that is globally compatible with the solar distribution. Some of the r-dominated nuclides can also be produced, though the r-abundance peak nuclei remain under-abundant. These plots highlight the relevance of non-thermal nucleosynthesis and its possible contribution to the s-process enrichment of the stellar or interstellar environments.
 |
Fig. 5. Upper panel: mass fractions with respect to the solar value for all stable nuclei with A ≥ 69 resulting from the CNO_a_07_2 (full symbols) and CNO_a_03_2 (open symbols) models. Light blue circles, dark blue circles, red squares, and green diamonds correspond to s-only, s-, r-, or p-dominated nuclides, respectively. Lower panel: same for the CNO_pa_06_2 (full symbols) and CNO_pa_04_2 (open symbols) models. |
To illustrate how rich this non-thermal nucleosynthesis can be, we also show in Fig. 6 the overabundances of all stable nuclei resulting from the irradiation of α-particles on CNO elements with a flux Φα = 10−11 mb−1s−1 with constant energy in the 0 ≤ E/A ≤ 7 MeV range during about 100 years, i.e. the same model as CNO_a_07 but with an irradiation that is about three times longer than the event called upon to explain the P-rich stars (see Sect. 4). In this case, neutron-capture nucleosynthesis is supplemented with an efficient α-capture on the freshly produced heavy nuclei with the possible co-production of neutron-deficient p-nuclei, including the puzzling 92, 94Mo and 96, 98Ru as well as 138La (Arnould & Goriely 2003). Additionally, rare light elements such as 9Be or 50V are also produced in significant quantities. Such α-captures are only possible if their energies are sufficiently high. For energies limited to maximum 3–4 MeV per nucleon, as in models C_a_03 and C_pa_04, no significant enrichment of p-nuclei is found, as already visible in Fig. 5. However, for α-captures to become effective in transmuting light elements up to the heaviest nuclei, long irradiation times, and therefore large fluences, need to be envisioned.
 |
Fig. 6. Mass fractions with respect to the solar value for all stable nuclei resulting from the CNO_a_07 model with an irradiation time of 100 years. Black triangles correspond to light A < 69 nuclei; light blue circles, dark blue circles, red squares, and green diamonds correspond to s-only, s-, r-, or p-dominated nuclides, respectively. |
As shown above, the non-thermal nucleosynthesis associated with stellar energetic particles turns out to be of particular interest in many respects for studying the abundance patterns found at the surface of P-rich stars. It can be held responsible for a significant production of odd-Z elements, including in particular P, and of elements heavier than iron through neutron captures. This nucleosynthesis can be accompanied by a significant production of radio elements, such as Tc or Pm, though these will most certainly have disappeared at the time of observation if the nucleosynthesis does not take place in the stellar atmosphere.
4. Comparison with surface abundances of P-rich stars
In the present scenario, we do not make any assumption as to whether the atmosphere of P-rich stars has been directly irradiated by energetic particles or was rather initially polluted by the outcomes of SEP events. We also do not study the possible superposition of different events at this stage because of the already large parameter space being explored. In turn, we can reasonably assume that the material irradiated for a given time τirr is mixed (in one way or another) with unaffected material of solar-type composition characterising the stellar metallicity of our two P-rich stars, i.e. [Fe/H] ≃ −1. This means that the final abundance of a given nucleus (Z, A) can be estimated by
where fmix is an arbitrary dilution factor between the unaffected stellar molar fraction Y* and the fraction of irradiated material Yirr. For a given SEP event, the dilution factor, as given in Table 1, is chosen to reproduce the specific P enrichment observed in each of the two P-rich stars studied here.
Finally, adjusting the irradiation times τirr and the dilution factors fmix, we see in Figs. 7 and 8 that the SEP events mentioned in Table 1 can globally explain the observed abundances of both P-rich stars 2M13535604+4437076 and 2M22045404-11482871 relatively well. The eight models considered here, corresponding to the four SEP events with different irradiation times and dilution factors, show rather similar characteristics. In particular, the large overproduction of P is accompanied with a small enhancement of S and elements in the 19 ≤ Z ≤ 30 range. The elements in the Sr-Zr and Ba-Eu regions are found to be overproduced by typically 1 dex in proportions similar to what is observed. Similar agreement between observation and prediction is found for the Hf-Os elements in 2M22045404-1148287 and Pb in 2M13535604+4437076. In addition, it can be seen that the [Rb/Sr], [La/Eu], and [Pb/La] ratios resulting from the SEP enrichment are, globally, in rather good agreement with observations. As the reactions relevant to nucleosynthesis here include incident α-particles, longer irradiation times need to be adopted when considering irradiations by protons plus α-particles. The enrichment resulting from incident α-particles only is also found to be about ten times larger than that obtained with protons plus α-particles (Fig. 5), meaning that lower dilution factors fmix are required when considering irradiations by α-particles only.
 |
Fig. 7. Comparison of observed and calculated abundances for 2M13535604+4437076 (upper panel) and 2M22045404-1148287 (lower panel). Observed overabundances (full squares) are taken from Masseron et al. (2020b). Calculated abundances are obtained with the models CNO_a_07_1(2) and CNO_a_03_1(2), i.e. with SEP events including only accelerated α particles (see Table 1). |
 |
Fig. 8. Same as Fig. 7 but for SEP events including both proton and α accelerated particles. The corresponding SEP models, as given in Table 1, correspond to models CNO_pa_06_1(2) and CNO_pa_04_1(2). |
However, some features of the observed distributions are not properly described. More specifically, the CNO abundances may in some cases be overestimated (model CNO_pa_06_1) or underestimated (model CNO_a_07_2). The large observed Ba overabundance with respect to its neighbour La cannot be explained, and will probably not be explained by any nucleosynthesis model because it remains difficult to find a neutron-induced process that can give rise to a [Ba/La] = 0.8 ratio. Another major deficiency of the present SEP models is the systematic underestimate of Al and Si overabundances. While production of the odd-Z Al can potentially be corrected by adding an extra SEP component, the large Si enrichment remains more difficult to apprehend in this framework, unless considering a case where the stars were originally already enriched in Si or the irradiated material is also assumed to be Si-rich.
In addition, we note that the present SEP events are also expected to produce F and Cl in significant amounts. Extremely large overproduction of Li, Be, and B elements is also predicted, except by the low-energy model C_a_03, as already mentioned in Sect. 3. Nevertheless, even if our stars were polluted before formation, their initial surface Li, Be, and B content may also have been altered. Indeed, 2M13535604+4437076, with a luminosity of L = 55 ± 5 L⊙ and surface temperature Teff = 5043 ± 100 K (Masseron et al. 2020b), and 2M22045404-1148287, with L = 220 ± 15 L⊙ and Teff = 4630 ± 100 K (Andrae et al. 2018), are found to be compatible with a M = 1.25 ± 0.25 M⊙ star at the beginning of its red giant phase where the envelope has become deeply convective and reaches a few million degrees at its lower boundary. As Li, Be, and B are significantly destroyed in the inner part of the star, the surface content of Li, Be, and B is strongly reduced by the first dredge-up (Iben 1967; Siess et al. 2000). CNO elements may also be affected, leading in particular to a small decrease in the surface C enrichment and a small enhancement of N.
5. Conclusions
The 15 abnormally phosphorus-rich stars discovered by Masseron et al. (2020a,b) are challenging our present stellar nucleosynthesis theories, because none of the standard thermal nucleosynthesis models are able to explain their observed abundance patterns. For this reason, we explored non-thermal processes resulting from the interaction of C-rich or CNO-rich material with energetic protons and/or α-particles to estimate if such irradiation events could be at the origin of the surface enrichment. We took a purely parametric site-independent approach, where the amplitude, the energy distribution of the proton and α-particle fluxes, and the irradiation time are taken as free parameters. It is also assumed that such an irradiation process is not taking place in the stellar atmosphere, but rather that the present stars have been polluted by such nucleosynthesis events prior to their formation. In such an approach, it remains difficult to take complex physical effects into account such as the stopping power of the accelerated particles in the hot low-density plasma target or the hydrodynamical effects resulting from the interaction of the projectile with the irradiated material. The relevance and efficiency of such non-thermal nucleosynthesis processes will need to be confirmed by future realistic models. The irradiation of C-rich or CNO-rich material by α-particles and possibly protons with energies of no more than a few MeV per nucleon has been shown to lead to rich nucleosynthesis, including a significant production of P, and to the production of neutrons that can explain the synthesis of Z > 30 heavy elements in relative abundances similar to those traditionally produced by the slow neutron-capture process. Longer irradiation times with a series of secondary α-captures on the freshly synthesised heavy nuclei could even be at the origin of the puzzling p-nuclei 92, 94Mo, 96, 98Ru, and 138La. If mixed with nuclearly unprocessed stellar material, the resulting enrichment could match most of the abundance patterns observed at the surface of P-rich stars, except for a few species like Al, Si, or Ba. Superposition of events with rather different properties, including target material with other compositions, could help to improve the agreement with the observed overabundances of Al and Si. The contribution of such non-thermal nuclear processes would be strengthened if spectroscopic observations were to confirm the enrichment of additional light elements like F or Cl in the near future.
We note that corrections have been made to Table 1 of Masseron et al. (2020b) in the incorrect attribution of the stellar name and the Pb abundances (Masseron 2021, priv. comm.)
Acknowledgments
S.G. is F.R.S-FNRS. research associate. The author is grateful to M. Arnould, S. Van Eck, L. Siess and T. Masseron for fruitful discussions.
References
- Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnould, M., & Goriely, S. 2003, Phys. Rep., 384, 1 [Google Scholar]
- Arnould, M., & Goriely, S. 2020, Prog. Part. Nucl. Phys., 112, 103766 [NASA ADS] [CrossRef] [Google Scholar]
- Bidelman, W. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, & F. N. Bash (Astronomical Society of the Pacific), ASP Conf. Ser., 336, 309 [NASA ADS] [Google Scholar]
- Butt, Y. M., Maccarone, T. J., & Prantzos, N. 2003, ApJ, 587, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Cowley, C., Ryabchikova, T., Kupka, F., et al. 2000, MNRAS, 317, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Cowley, C., Bidelman, W., Hubrig, S., Mathys, G., & Bord, D. 2004, A&A, 419, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fujimoto, S., Kotake, K., Yamada, S., Hashimoto, M., & Sato, K. 2006, ApJ, 644, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Gopka, V., Yushchenko, A., Shavrina, A., et al. 2004, in The A-Star Puzzle, ed. J. Zverko (Cambridge University Press), IAU symp., 224, 734 [NASA ADS] [Google Scholar]
- Goriely, S. 1999, A&A, 342, 881 [NASA ADS] [Google Scholar]
- Goriely, S. 2007, A&A, 466, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goriely, S., & Mowlavi, N. 2000, A&A, 362, 599 [NASA ADS] [Google Scholar]
- Goriely, S., Hilaire, S., & Koning, A. J. 2008, A&A, 487, 767 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, I. J. 1967, ApJ, 147, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Käppeler, F., Beer, H., & Wisshak, K. 1989, Rep. Prog. Phys., 52, 945 [CrossRef] [Google Scholar]
- Karakas, A. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Koning, A. J., & Rochman, D. 2012, Nuclear Data Sheets, 113, 2841 [NASA ADS] [CrossRef] [Google Scholar]
- Kusakabe, M., & Mathews, G. 2018, ApJ, 854, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Leya, I., Halliday, A., & Wieler, R. 2003, ApJ, 594, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M.-C., Chaussidon, M., Srinivasan, G., & McKeegan, K. D. 2012, ApJ, 761, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., & Nomoto, K. 2003, ApJ, 598, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Masseron, T., Garica-Hernandez, D., Santoveña, R., et al. 2020a, Nat. Commun., 11, 3759 [NASA ADS] [CrossRef] [Google Scholar]
- Masseron, T., Garica-Hernandez, D., Zamora, O., & Manchado, A. 2020b, ApJ, 904, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, J. 1972, ApJS, 7, 417 [Google Scholar]
- Michaud, G. 2004, in The A-Star Puzzle, ed. J. Zverko (Cambridge University Press), IAU symp., 224, 173 [NASA ADS] [Google Scholar]
- Prantzos, N. 2012, A&A, 542, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramaty, R., Kozlovsky, B., Lingenfelter, R., & Reeves, H. 1997, ApJ, 488, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, H., Fowler, W., & Hoyle, F. 1970, Nature, 226, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Rinard, P. 1991, in Passive Nondestructive Assay of Nuclear Materials, ed. D. Reilly, U.S. Nuclear Regulatory Commission, NUREG/CR-5550, 357 [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Tatischeff, V., & Gabici, S. 2018, An. Rev. Nuc. Particle Sci., 68, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Tatischeff, V., & Thibaud, J. 2007, A&A, 469, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Upper panel: evolution of the mass fractions of light nuclides up to F (including also P) resulting from the specific SEP event of model C_a_03, i.e. of a C target irradiated by α-particles only with Φα = 10−11 mb−1 s−1 and a constant-energy spectrum with E/A ≤ 3 MeV. Lower panel: same for model CNO_a_07, i.e. a CNO target irradiated by α-particles only with Φα = 10−11 mb−1 s−1 and a constant-energy spectrum with 0 ≤ E/A ≤ 7 MeV. The hashed area corresponds to the irradiation time ranges considered to explain the P-rich abundances of both stars. |
| In the text | |
 |
Fig. 2. Same as Fig. 1 but for the specific SEP events of model C_pa_04 (upper panel) and CNO_pa_06 (lower panel). |
| In the text | |
 |
Fig. 3. Time evolution of the neutron density for the four SEP events considered in Table 1. |
| In the text | |
 |
Fig. 4. Abundance distribution of all stable nuclei as a function of the mass number A resulting from the specific spallation event of a C target irradiated by α-particles only with Φα = 10−11 mb−1 s−1 and a constant-energy spectrum with 0 ≤ E/A ≤ 3 MeV after four irradiation times of 1, 20, 40, and 60 years. |
| In the text | |
 |
Fig. 5. Upper panel: mass fractions with respect to the solar value for all stable nuclei with A ≥ 69 resulting from the CNO_a_07_2 (full symbols) and CNO_a_03_2 (open symbols) models. Light blue circles, dark blue circles, red squares, and green diamonds correspond to s-only, s-, r-, or p-dominated nuclides, respectively. Lower panel: same for the CNO_pa_06_2 (full symbols) and CNO_pa_04_2 (open symbols) models. |
| In the text | |
 |
Fig. 6. Mass fractions with respect to the solar value for all stable nuclei resulting from the CNO_a_07 model with an irradiation time of 100 years. Black triangles correspond to light A < 69 nuclei; light blue circles, dark blue circles, red squares, and green diamonds correspond to s-only, s-, r-, or p-dominated nuclides, respectively. |
| In the text | |
 |
Fig. 7. Comparison of observed and calculated abundances for 2M13535604+4437076 (upper panel) and 2M22045404-1148287 (lower panel). Observed overabundances (full squares) are taken from Masseron et al. (2020b). Calculated abundances are obtained with the models CNO_a_07_1(2) and CNO_a_03_1(2), i.e. with SEP events including only accelerated α particles (see Table 1). |
| In the text | |
 |
Fig. 8. Same as Fig. 7 but for SEP events including both proton and α accelerated particles. The corresponding SEP models, as given in Table 1, correspond to models CNO_pa_06_1(2) and CNO_pa_04_1(2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



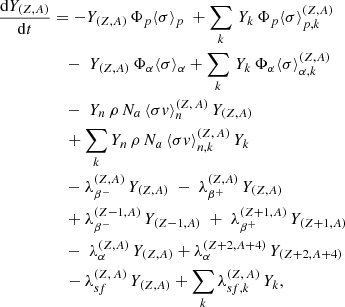
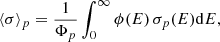
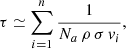
![$$ \begin{aligned} \rho \,Y_n = \frac{\sum _{k,x} x \,Y_{k}\, [\Phi _p \langle \sigma \rangle _{p,k}^x +\Phi _{\alpha } \langle \sigma \rangle _{\alpha ,k}^x]}{\sum _{k} \,Y_{k} \,N_{a} \langle \sigma { v}\rangle _{n}} \quad . \end{aligned} $$](/articles/aa/full_html/2022/02/aa42319-21/aa42319-21-eq7.gif)