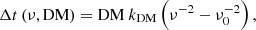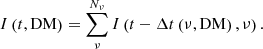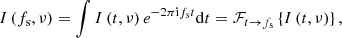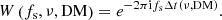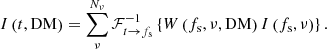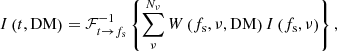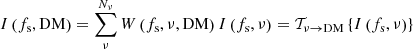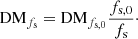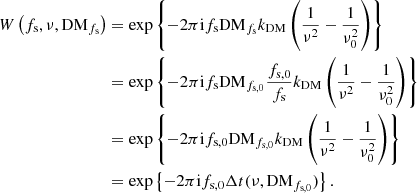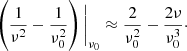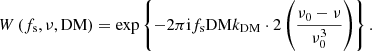| Issue |
A&A
Volume 657, January 2022
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 7 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202142099 | |
| Published online | 04 January 2022 | |
Fourier-domain dedispersion
ASTRON, Netherlands Institute for Radio Astronomy, Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
e-mail: bassa@astron.nl
Received:
27
August
2021
Accepted:
7
October
2021
We present and implement the concept of the Fourier-domain dedispersion (FDD) algorithm, a brute-force incoherent dedispersion algorithm. This algorithm corrects the frequency-dependent dispersion delays in the arrival time of radio emission from sources such as radio pulsars and fast radio bursts. Where traditional time-domain dedispersion algorithms correct time delays using time shifts, the FDD algorithm performs these shifts by applying phase rotations to the Fourier-transformed time-series data. Incoherent dedispersion to many trial dispersion measures (DMs) is compute-, memory-bandwidth-, and input-output-intensive, and dedispersion algorithms have been implemented on graphics processing units (GPUs) to achieve high computational performance. However, time-domain dedispersion algorithms have low arithmetic intensity and are therefore often memory-bandwidth-limited. The FDD algorithm avoids this limitation and is compute-limited, providing a path to exploit the potential of current and upcoming generations of GPUs. We implement the FDD algorithm as an extension of the DEDISP time-domain dedispersion software. We compare the performance and energy-to-completion of the FDD implementation using an NVIDIA Titan RTX GPU against both the standard version and an optimized version of DEDISP. The optimized implementation already provides a factor of 1.5 to 2 speedup at only 66% of the energy utilization compared to the original algorithm. We find that the FDD algorithm outperforms the optimized time-domain dedispersion algorithm by another 20% in performance and 5% in energy-to-completion when a large number of DMs (≳512) are required. The FDD algorithm provides additional performance improvements for fast-Fourier-transform-based periodicity surveys of radio pulsars, as the Fourier transform back to the time domain can be omitted. We expect that this computational performance gain will further improve in the future since the Fourier-domain dedispersion algorithm better matches the trends in technological advancements of GPU development.
Key words: methods: data analysis / pulsars: general
© ESO 2022
1. Introduction
Radio waves propagating through the ionized intergalactic, interstellar, and/or interplanetary medium undergo dispersion, which introduces a frequency-dependent time delay between emission at the source and reception at the telescope (e.g., Lorimer & Kramer 2012). Hence, pulsed radio signals from astrophysical sources such as radio pulsars and fast radio bursts (see Kaspi & Kramer 2016; Petroff et al. 2019, for reviews) have a distinctive dispersion measure (DM), which is directly related to the electron column density between the source and the observer. If not properly corrected for, the dispersion delays lead to smearing and hence a loss in the signal-to-noise of the received radio pulses.
Correcting for the dispersion is called “dedispersion”, and it can be performed using two techniques, depending on the state of the radio observation. For Nyquist-sampled time-series data of orthogonal polarizations (voltage data hereafter), the phase information can be used to “coherently dedisperse” the signals through a convolution with the inverse of the response function of dispersion (Hankins 1971; Hankins & Rickett 1975). This technique completely removes the effects of dispersion. With coherent dedispersion, dedispersion is performed before squaring the orthogonal polarization signals to form the Stokes parameters. For signals that have already been squared to form the Stokes parameters, the “incoherent dedispersion” method is used. The time-series data of finite channels are shifted in time to correct for the dispersion delay between channels, while dispersive smearing within channels remains uncorrected. Hence, the size of frequency channels and time samples is typically optimized to minimize dispersive smearing within channels.
In surveys for new radio pulsars or fast radio bursts, the DM of a new source is a priori unknown, and the input data need to be dedispersed to many, usually thousands of, trial DMs. The majority of current surveys perform incoherent dedispersion on Stokes I time series, typically with sample times between 50 and 100 μs and channel sizes of 0.1 to 0.5 MHz (Keith et al. 2010; Stovall et al. 2014; Lazarus et al. 2015; Bhattacharyya et al. 2016, see also Lyon et al. 2016), as this requires lower data rates and less storage compared to voltage data. Only at the lowest observing frequencies (ν ≲ 300 MHz) are voltage data recorded to perform a combination of coherent and incoherent dedispersion (Bassa et al. 2017a,b; Pleunis et al. 2017).
The computational cost to incoherently dedisperse is significant as the input data typically consist of Nν ∼ 103 frequency channels for Nt ∼ 106 time samples and need to be dedispersed to NDM ∼ 104 DMs. Hence, algorithms have been developed to reduce the computational cost by reducing the complexity – for example, via the use of a tree algorithm (Taylor 1974), a piece-wise linear approximation of the dispersion delay (Ransom 2001), or a transformation algorithm (Zackay & Ofek 2017) – and/or by using hardware acceleration of the direct, brute-force dedispersion approach. A review of these algorithms, and an implementation of the direct dedispersion algorithm on graphics processing units (GPUs), is presented by Barsdell et al. (2012).
Sclocco et al. (2016) found that the direct, brute-force dedispersion algorithm on many-core accelerators is inherently memory-bandwidth-bound due to the low arithmetic intensity of the required calculations. Hence, the direct dedispersion algorithm does not optimally benefit from advances in the computing performance of many-core accelerators. In this paper we investigate the feasibility of the direct dedispersion approach through what we call Fourier-domain dedispersion (FDD), where the time delays due to dispersion are performed as phase rotations in the Fourier transform of the time-series data of each channel1.
We present the description of the FDD algorithm in Sect. 2 and compare it to the time-domain variant. Section 3 provides a GPU implementation of the FDD algorithm along with an optimization of the GPU accelerated time-domain direct dedispersion algorithm by Barsdell et al. (2012), and the results for the different implementations are compared in Sect. 4. We discuss and conclude our feasibility study in Sect. 5.
2. Algorithm description
2.1. Time-domain dedispersion
Dispersion in the ionized intergalactic, interstellar, and interplanetary media leads to delays in the arrival time of radio signals, The magnitude of this delay depends on the frequency of the radio signal observed. For a given dispersion measure DM = ∫nedl (the path integral over the electron density, ne, along the line of sight), signals arrive with a time delay
where ν is the observing frequency and ν0 is the reference frequency. The proportionality constant is kDM = (2.41 × 10−4)−1 MHz2 cm3 pc−1 s (Manchester & Taylor 1972; Kulkarni 2020).
The standard incoherent dedispersion method takes an input dynamic spectrum, I(t, ν), with Stokes I values as a function of observing time, t, and observing frequency, ν, and shifts the time series at the individual observing frequencies to the nearest time sample given the delays described in Eq. (1) based on an assumed DM. This results in a new dynamic spectrum in which all time series are aligned for the assumed DM. The shifted time series are then summed over observing frequency to give the intensity as a function of time observed at the assumed DM,
When the DM of the source is not known, this procedure needs to be repeated for many trial DMs.
The brute-force time-domain dedispersion algorithm requires significant memory bandwidth but requires only minimal computations once the data are properly aligned. This led us to explore the benefits of analyzing the Fourier transform of the time series, where the time shifts can be replaced by phase rotations through the Fourier shift theorem (e.g., Bracewell 1986); this results in dense matrix multiplications, which can be computed efficiently. We describe this FDD method in the next subsection.
2.2. Fourier-domain dedispersion
In FDD, the time series for each observing frequency is Fourier-transformed to the Fourier domain of time, frequency. To distinguish these frequencies from the observing frequencies of the data, ν, we refer to the Fourier transform of the time series as the spin frequencies, fs, that would be associated with a periodic signal from a radio pulsar. The Fourier transform results in a new dynamic spectrum, I(fs, ν), in which the data are represented as a function of spin frequency, fs, and observing frequency, ν. We describe this as
where the Fourier transform operator, ℱ, has the subscript t → fs to emphasize that this is a mapping from the time domain to the spin-frequency domain instead of the regular 2D Fourier transform. This notation also allows us to use the Fourier transform for other mappings later on without causing confusion.
In (spin) frequency space, the time shifts from Eq. (1) can be represented by complex phase rotations, which we refer to as phasors, of the form
The dedispersed time series can now be recovered through the inverse Fourier transform, 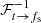 , and a summation over observing frequency,
, and a summation over observing frequency,
Due to the linearity of the Fourier transform, the summation and inverse Fourier transform can be interchanged, yielding
which reduces the number of inverse Fourier transforms from NDM × Nν to NDM.
Furthermore, it is instructive to define
since phase rotations provide a mapping from observing frequencies to DMs. As the phase rotations depend on spin frequency, the data for each spin frequency need to be processed independently. For a given spin frequency, this mapping resembles a direct Fourier transform. However, it cannot be implemented as a fast Fourier transform (FFT) due to the nonlinear dependence of Δt on observing frequency. Despite these two issues that complicate the implementation, we note that Eq. (7) can be viewed as a transformation that maps the space of observing frequencies to the space of DM values; we denote this transformation as 𝒯ν → DM.
Figure 1 shows a cartoon of the traditional time-domain dedispersion algorithm and the Fourier-domain algorithm. The panels in the top row show the traditional algorithm, where time series at individual observing frequencies are shifted in time for a given DM. The steps presented in Eqs. (3), (6), and (7) are illustrated in the bottom row of Fig. 1. After Fourier-transforming the input time series for each frequency, shown in Fig. 1c, a spectrum as a function of spin frequency is obtained, shown in Fig. 1d, that indicates the amplitude and phase of the complex values. The phase of the Fourier-transformed time series encodes the arrival time of the pulse. The phase slope of the W(fs, ν, DM) phasor is shown by the green curves in Fig. 1d and depends on the dispersion delay as given in Eq. (4). The transformation 𝒯ν → DM corrects the measured phases with the appropriate phase slope. In our example, this results in the phases shown in Fig. 1e. As this is a pure phase rotation, the amplitudes are unaltered. After applying the inverse Fourier transform to each of the spectra, we obtain a shifted time series at each frequency. When the correct phasors are applied, this results in the peaks being aligned, as shown in Fig. 1f, and we obtain the same results as with time-domain dedispersion, as shown in Fig. 1b for comparison.
 |
Fig. 1. Comparison between time-domain dedispersion (top row) and FDD (bottom row), with (a) and (c) representing the input dynamic spectrum, (b) showing the dynamic spectrum after applying the appropriate delays for each frequency, (d) showing the Fourier transform of the time series (amplitude and phase) along with the phasors applied in 𝒯ν → DM, (e) showing the result after applying the phasors, and (f) showing the dynamic spectrum after the inverse Fourier transform, |
The use of the Fourier shift theorem and the cyclic nature of the Fourier transform contaminate the end of each time series with samples from the start. Hence, given a maximum DM (DMmax) and the extrema of the observing band (νmin and νmax), at least 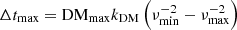 at the end of each time series should be discarded when dedispersing against the highest observing frequency channel (see Fig. 1f). In the time-domain dedispersion algorithm, the same amount of data should be discarded (see Fig. 1b).
at the end of each time series should be discarded when dedispersing against the highest observing frequency channel (see Fig. 1f). In the time-domain dedispersion algorithm, the same amount of data should be discarded (see Fig. 1b).
As dispersive smearing increases with increasing DM, time-domain dedispersion algorithms down-sample the input time series when the smearing exceeds one or more native time samples. In the Fourier-domain algorithm, this down-sampling can be efficiently implemented by reducing the length of the inverse Fourier transform, 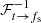 .
.
2.3. Algorithm optimization
The transformation 𝒯ν → DM poses two implementation challenges: The phasors described by Eq. (4) depend on the spin frequency, and the nonlinear dependence of Δt on observing frequency precludes the use of the FFT. In this section we present three approximations to reduce the computational burden incurred by these two challenges.
Calculation of the phasors for each trial DM, observing frequency, and spin frequency consumes a significant amount of computing resources. Also, the implementation of Eq. (7) leads to a matrix-vector product of a matrix of phasors for constant fs extracted from the phasor tensor, W(fs, ν, DM), and a vector with data values for constant fs extracted from the data matrix, I(fs, DM). As GPUs can perform matrix multiplications efficiently, it is expected to be beneficial to process data for multiple spin frequencies simultaneously. Therefore, it may be worthwhile to accept a spin-frequency-dependent set of DM values and resample those afterward to the desired set of trial DMs. To this end, we considered the following spin-frequency-dependent DM,
Substitution in Eq. (4) gives
Note that these phasors are independent of spin frequency, which implies that these phasors can be applied over a range of spin frequencies reasonably close to the reference spin frequency, fs, 0. The extent of this range is limited by the tolerable amount of contraction or expansion of the set of DM values for spin frequencies other than fs, 0 as given by Eq. (8).
Although the structure of the phasors describing the mapping to DM space, 𝒯ν → DM, appears to resemble the Fourier transform very closely, the exact transformation from observing frequencies to DM values cannot be represented by a discrete Fourier transform (DFT) matrix, let alone an FFT, due to the nonlinear dependence of the phases of the phasors on observing frequencies. This can be remedied by using a first-order Taylor approximation for the frequency dependence, namely,
Substitution of this approximation in Eq. (4) gives
This approximation can be exploited to implement 𝒯ν → DM by an FFT per spin frequency or even multiple spin frequencies when combined with the optimization from the previous subsection. The observing frequency range over which this gives acceptable results depends on the DM and spin frequency.
To be able to treat the 𝒯ν → DM transformation as a DFT, and be able to use the advantages of an FFT for precision and performance over a DFT, the observing frequencies, ν, would have to be remapped to a linear scale following ν−2. Such a remapping has been used by Manchester et al. (2001). This mapping could be obtained through either interpolation or inserting empty channels in the linearized scale at ν−2 values that do not map to integer observing channels. It is likely that such a remapping would increase GPU memory usage, as well as introduce some smearing in the dedispersed time series. The analysis of this optimization and assessment of its performance and accuracy over the direct computation of the transform goes beyond the scope of this paper.
3. Implementation
We have implemented FDD as an extension of the DEDISP library2 by Barsdell et al. (2012). This library implements the brute-force, direct incoherent dedispersion algorithm on NVIDIA GPUs and is widely used (e.g., Jameson & Barsdell 2019; Sclocco et al. 2015). To make a fair comparison, we updated the DEDISP library by Barsdell et al. (2012) to make use of newer hardware and software features. In the following, we refer to the original implementation as DEDISP and to the updated implementation as TDD (time-domain dedispersion). We refer to our implementation of Fourier-domain dedispersion as FDD.
For this work we implemented the algorithm as described in Sect. 2.2. Additional optimizations, as proposed in Sect. 2.3, and the use of new GPU tensor-core technology are left to future work.
Sclocco et al. (2016) found that brute-force dedispersion in the time domain has a low arithmetic intensity and is inherently memory-bandwidth-bound. They show that auto-tuning of kernel parameters significantly improves performance on various accelerators. For this work we explore the feasibility of dedispersion in the Fourier domain and compare performance for a representative parameter space according to the use cases outlined in the introduction. The performance of time-domain dedispersion is predominantly determined by the amount of data reuse and memory bandwidth.
The work of Barsdell et al. (2012) already shows that major performance improvements are achieved when moving the implementation from a central processing unit (CPU) to a GPU. Performance improvements are mainly attributed to the higher memory bandwidth of the GPU. We compare DEDISP, TDD, and FDD on the NVIDIA Titan RTX GPU. The full measurement setup is listed in Table 1. We refer, in NVIDIA CUDA terminology, to the CPU as “host” and to the GPU as “device”. The main application runs on the host and launches computational kernels on the device. Input and output data are copied between the host and device over a PCIe interface.
Setup used for the evaluation of the different implementations.
Dedispersion is usually part of a pipeline running on a GPU where the initialization of and input-output (I/O) to the GPU kernels are part of the pipeline. The input to dedispersion is a matrix of size Nν × Nt of packed 8-bit data, with Nν frequency channels and Nt time samples. For time-domain dedispersion, these data have to be transposed, unpacked, and dedispersed. The resulting output is a matrix of NDM × Nt 32-bit floating point data, with NDM trial DMs.
For time-domain dedispersion, the input data, I(t, ν), can be segmented in the time dimension, taking a segment of Mt(< Nt) of time samples, for all frequency channels. DEDISP implements the above-described pipeline with batch processing, where a segment of input data is copied from host to device, the GPU applies the kernel pipelines, parallelizing over DMs, and the resulting output data, I(t, DM), for the segment is copied back to the host before copying a new segment of data to the device.
We extended the DEDISP framework with an optional TDD implementation that contains several improvements over DEDISP. First, the transfers of input and output data were overlapped with computations on the GPU, moving the copying of input and output out of the critical path. Transfer speeds were increased by a factor of two to three by changing the memory transfers from paged to pinned memory. Furthermore, the unpacking and transpose operations were combined into one kernel, thus requiring only a single pass over the data. Finally, the use of texture memory is optionally disabled, as this optimization for old GPUs reduces performance on recent GPUs. These improvements are currently available as a fork3 of the DEDISP library by Barsdell et al. (2012) and are being integrated with the original library.
For the implementation of FDD, the input data cannot straightforwardly be segmented in time. It follows from Eq. (3) that splitting in the time dimension affects the outcome of the FFT. Instead, we split input data along the frequency-channel dimension (shown as channel job on line 7 of Algorithm listing 1). Such an input data segment is copied to the GPU, where the data are transposed and unpacked, as in the preprocessing step in TDD. Next, the data are zero-padded such that the number of samples becomes a power of two. The last step of preprocessing is the Fourier transformation (Eq. (3)) of the input samples. Dedispersion is performed as phase rotations (Eq. (7)) in the Fourier domain, followed by a summation over frequency channels. The result is transformed back to the time domain (Eq. (6)) before it is scaled and transferred back from device to host. Both forward and backward Fourier transformations are implemented with the NVIDIA cuFFT library. Continuing on Algorithm listing 1, we show that within batches of channels the work is split into batches of DMs (DM job starting at line 14) to efficiently parallelize the workload on the GPU. The backward FFT is implemented as a batched series of 1D FFTs for each DM. To allow for efficient batching of the backward FFTs, the output of the dedispersion kernel is buffered on the GPU for all batches of channels before it is transformed back to the time domain (starting at line 19). Due to GPU memory size constraints, we cannot process all the DMs at once when there is a large number of them. We solve this by processing the DMs in batches with an additional DM_outer dimension (line 6). This approach has the advantage that the output data are only copied once, after all input for the current batch of DMs is processed and postprocessing has taken place. The input data, on the other hand, have to be copied and preprocessed multiple times for different batches of DMs. We minimize the cost of these repeated operations by overlapping them with the copy of output data. Batching of channels and DMs also allows for data reuse in the other GPU kernels.

Algorithm 1. This listing shows batch processing for the FDD implementation. This process starts with a number of initialization steps on the host (highlighted in blue). Next, DMs are processed in batches (idmouter). For every batch of DMs, frequency channels are also processed in batches. This enables overlapping of data transfers (highlighted in red) with computation on the GPU (highlighted in green). After dedispersion has finished, the output is again processed in batches such that postprocessing is overlapped with data transfers.
4. Results
4.1. Performance comparison
To allow benchmarking of performance, we generated data sets containing simulated astrophysical signals. The data sets cover a range of trial DMs that number from NDM = 128 to 4096. Each data set consists of 5 min of data with a sampling resolution of 64 μs, 1024 channels, 400 MHz bandwidth, and a maximum frequency of 1581 MHz, similar to the observational setup used by the ongoing SUPERB survey (Keane et al. 2018), which uses the DEDISP library. Trial DMs start at 0 pc cm−3 and increment by 2 pc cm−3 up to the maximum specified DM. These data sets are sufficiently large such that any inaccuracies in CPU or GPU timers can be neglected. Furthermore, for TDD and FDD, the size of the data set requires it to be split into smaller batches, where the input and output for one batch is overlapped with the computation of another batch. Measurements were performed on a GPU node of the DAS-5 cluster (Bal et al. 2016), and the hardware and software setup of the GPU node are listed in Table 1.
Dedispersion is usually a step in a processing pipeline, but for this work we isolated the dedispersion implementation. We define the “runtime” of an implementation as the recurring time of the implementation, which is taken as the summation of individual timings of components in the critical path. The critical path for the runtime differs per implementation.
In Fig. 2 we show the distribution of runtimes for DEDISP, TDD, and FDD. We find that in DEDISP all components (input, preprocessing, dedispersion, and output) are executed serially. The time required for the input and output of data is not addressed in the work by Barsdell et al. (2012) or Sclocco et al. (2016). We argue, however, that the time spent on I/O cannot be ignored for DEDISP, as the GPU is idle while the memory transfers between host and device take place.
 |
Fig. 2. Runtime distribution for DEDISP, TDD, and FDD for 1024 trial DMs. Postprocessing for FDD is optional and depends on the processing pipeline. |
Our implementation of TDD, on the other hand, overlaps computation on the GPU with I/O, which is reflected by an overall runtime that is lower by a factor of 1.5 to 2, depending on the amount of trial DMs. Furthermore, the preprocessing time (transpose and unpack) has been reduced, while the timing for the dedispersion kernel itself is almost the same as in DEDISP.
In FDD, the input and output are overlapped as well. The dedispersion time has been reduced significantly, but at the cost of longer preprocessing times (transpose, unpack, and FFT) and additional postprocessing time (FFT and scaling). We note that most of the preprocessing time is spent performing the FFT. We observe a similar runtime distribution for other numbers of trial DMs. Figure 3 shows a comparison of runtimes for a range of trial DMs, from 128 to 4096. For a low number of trial DMs, TDD is faster than FDD. Looking at the runtime distribution for 128 to 512 DMs, we observe that the preprocessing time is almost equal from 128 until 512 DMs and then increases linearly with the amount of DMs. From 512 DMs onward, the runtime for FDD is up to 20% faster than TDD. The performance for a low number of trial DMs might be improved by tuning batch size parameters. However, performance is mostly of interest for larger numbers of trial DMs. Furthermore, when profiling the GPU implementations, we observe that, despite part of the runtime of the FDD implementation being limited by the available GPU memory4, the dedispersion algorithm itself is compute-bound, except for the FFT.
 |
Fig. 3. Comparison of runtime for DEDISP, TDD, and FDD for a range of trial DMs that number from 128 to 4096. The runtime for FDD includes postprocessing to transform the output data to the time domain. |
4.2. Energy-to-completion
In many applications the total energy consumption of the system is also an important factor. A reduction in the runtime of the implementation might lead to a reduction in energy as well, but it does not necessarily scale linearly since compute utilization of the device and I/O operations also contribute to the total energy utilization. We measured the energy-to-completion for our three implementations with the same setup used for the runtime measurements. Energy usage on the CPU was measured with the LIKWID analysis tool (Gruber et al. 2021) and on the GPU with the NVIDIA Management Library (NVML). Figure 4 shows the obtained energy measurements per implementation. We find that, as one might expect, the energy-to-completion was reduced significantly for both the CPU and GPU from DEDISP to TDD. The implementation of TDD leads to the same result as DEDISP at only 66% of the energy utilization. Also, the FDD implementation leads to a reduction in energy-to-completion by another 5%. We observe that the GPU energy utilization was reduced compared to TDD, with a slightly increased CPU energy utilization.
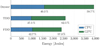 |
Fig. 4. Energy utilization per implementation for 1024 trial DMs, measured as energy-to-completion. Percentages shown are the percentages of either the CPU or GPU energy utilization compared to the total per implementation. |
5. Discussion and conclusions
We have presented the concept of FDD and shown that this direct incoherent dedispersion algorithm is a viable alternative to the traditional time-domain dedispersion. We implemented the Fourier-domain dedispersion algorithm (FDD) in the DEDISP library by Barsdell et al. (2012). An improved version of the DEDISP time-domain dedispersion algorithm (TDD) was also added to allow for a fair comparison.
We find that for a small number of DMs, the TDD is faster than FDD. However, for typical use cases with a large number (hundreds) of DMs, FDD is the fastest dedispersion implementation, outperforming TDD by about 20%. We also show that the energy-to-completion is lower for TDD and FDD than for DEDISP. The energy-to-completion for 1024 trial DMs with FDD is only 61% of the energy utilization of DEDISP on the system used. Furthermore, where DEDISP is largely I/O-bound (Sclocco et al. 2016), we were able to alleviate some of the I/O bottlenecks in TDD: We optimized the memory transfers and re-implemented the kernels that preprocess input data. While some parts of FDD (such as the FFTs) are also I/O-bound, the most dominant FDD dedispersion kernel is compute-bound. We therefore expect FDD to scale better with advances in GPU technology, where compute performance typically increases much faster than memory bandwidth.
For pulsar surveys using FFT-based periodicity searches, the FDD algorithm provides even higher performance compared to the DEDISP and TDD algorithms. For the time-domain dedispersion algorithms, the FFT-based periodicity searches would perform an FFT of the dedispersed time series to produce power spectra to search for periodic signals. By using the FDD algorithm, this FFT of the periodicity search, as well as the FDD postprocessing step in which the data are Fourier-transformed back to the time domain, can be omitted. Instead, the amplitudes and phases of the dedispersed spectra from FDD can be directly used for the subsequent processing steps of periodicity searches, such as Fourier-domain acceleration searches (Ransom 2001). In any situation where the number of DMs exceeds the number of (observing) frequency channels, FDD will require fewer FFTs for dedispersion compared to time-domain dedispersion.
In addition to the algorithmic optimizations proposed in Sect. 2.3, we consider some optimizations that may further improve performance. First, the throughput of the current implementation of FDD depends on parameters such as the data size (e.g., number of channels and number of DMs) as well as the amount of available GPU memory and the PCIe bandwidth. Auto-tuning (Sclocco et al. 2016) may be useful for finding the best performing set of tuning parameters, such as the optimal batch dimensions.
Second, the current implementation performs all operations in 32-bit floating point. The use of 16-bit half precision or even 8-bit integers would not only double or quadruple the amount of samples that can be processed in one batch, it would also allow the use of tensor cores to perform the dedispersion (tensor cores are special-function units in modern GPUs that perform mixed-precision matrix multiplications much faster than regular GPU cores). Unfortunately, neither 8-bit FFTs nor tensor-core dedispersion are simple to implement. In another signal-processing application (a correlator), tensor cores are five to ten times more (energy) efficient compared to regular GPU cores (Romein 2021).
Furthermore, the performance of the Fourier-domain algorithm can be improved by reusing phase rotations (Eq. (4)) when multiple observations with the same observational setup are available. This is the case for telescopes where signals from multiple beams are obtained simultaneously or for survey observations with many similar observations. We note that this approach reduces the number of DMs or time samples that can be processed in one batch as the amount of available GPU memory is limited and requires careful tuning.
Acknowledgments
We thank Scott Ransom for very constructive comments on the manuscript and are indebted to Andrew Jameson for help incorporating FDD into the DEDISP library. This project received funding from the Netherlands Organization for Scientific Research (NWO) through the Fourier-Domain Dedispersion (OCENW.XS.083) and the DAS-5 (621.018.201) grants.
References
- Bal, H., Epema, D., de Laat, C., et al. 2016, IEEE Comput., 49, 54 [CrossRef] [Google Scholar]
- Barsdell, B. R., Bailes, M., Barnes, D. G., & Fluke, C. J. 2012, MNRAS, 422, 379 [CrossRef] [Google Scholar]
- Bassa, C. G., Pleunis, Z., & Hessels, J. W. T. 2017a, Astron. Comput., 18, 40 [Google Scholar]
- Bassa, C. G., Pleunis, Z., Hessels, J. W. T., et al. 2017b, ApJ, 846, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharyya, B., Cooper, S., Malenta, M., et al. 2016, ApJ, 817, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Bracewell, R. N. 1986, The Fourier Transform and its Applications (New York: McGraw Hill) [Google Scholar]
- Gruber, T., Eitzinger, J., Hager, G., & Wellein, G. 2021, RRZE-HPC/likwid: likwid-4.2.1 [Google Scholar]
- Hankins, T. H. 1971, ApJ, 169, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Hankins, T. H., & Rickett, B. J. 1975, Meth. Comput. Phys., 14, 55 [Google Scholar]
- Jameson, A., & Barsdell, B. R. 2019, Heimdall Transient Detection Pipeline [Google Scholar]
- Kaspi, V. M., & Kramer, M. 2016, ArXiv e-prints [arXiv:1602.07738] [Google Scholar]
- Keane, E. F., Barr, E. D., Jameson, A., et al. 2018, MNRAS, 473, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Keith, M. J., Jameson, A., van Straten, W., et al. 2010, MNRAS, 409, 619 [Google Scholar]
- Kulkarni, S. R. 2020, ArXiv e-prints [arXiv:2007.02886] [Google Scholar]
- Lazarus, P., Brazier, A., Hessels, J. W. T., et al. 2015, ApJ, 812, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R., & Kramer, M. 2012, Handbook of Pulsar Astronomy (Cambridge: Cambridge University Press) [Google Scholar]
- Lyon, R. J., Stappers, B. W., Cooper, S., Brooke, J. M., & Knowles, J. D. 2016, MNRAS, 459, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., & Taylor, J. H. 1972, Astrophys. Lett., 10, 67 [NASA ADS] [Google Scholar]
- Manchester, R. N., Lyne, A. G., Camilo, F., et al. 2001, MNRAS, 328, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Petroff, E., Hessels, J. W. T., & Lorimer, D. R. 2019, A&ARv, 27, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Pleunis, Z., Bassa, C. G., Hessels, J. W. T., et al. 2017, ApJ, 846, L19 [Google Scholar]
- Ransom, S. M. 2001, PhD Thesis, Harvard University, USA [Google Scholar]
- Romein, J. W. 2021, A&A, 656, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sclocco, A., van Leeuwen, J., Bal, H. E., & van Nieuwpoort, R. V. 2015, 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP), 468 [CrossRef] [Google Scholar]
- Sclocco, A., van Leeuwen, J., Bal, H., & van Nieuwpoort, R. 2016, Astron. Comput., 14, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Stovall, K., Lynch, R. S., Ransom, S. M., et al. 2014, ApJ, 791, 67 [CrossRef] [Google Scholar]
- Taylor, J. H. 1974, A&AS, 15, 367 [NASA ADS] [Google Scholar]
- Zackay, B., & Ofek, E. O. 2017, ApJ, 835, 11 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Comparison between time-domain dedispersion (top row) and FDD (bottom row), with (a) and (c) representing the input dynamic spectrum, (b) showing the dynamic spectrum after applying the appropriate delays for each frequency, (d) showing the Fourier transform of the time series (amplitude and phase) along with the phasors applied in 𝒯ν → DM, (e) showing the result after applying the phasors, and (f) showing the dynamic spectrum after the inverse Fourier transform, |
| In the text | |
 |
Fig. 2. Runtime distribution for DEDISP, TDD, and FDD for 1024 trial DMs. Postprocessing for FDD is optional and depends on the processing pipeline. |
| In the text | |
 |
Fig. 3. Comparison of runtime for DEDISP, TDD, and FDD for a range of trial DMs that number from 128 to 4096. The runtime for FDD includes postprocessing to transform the output data to the time domain. |
| In the text | |
 |
Fig. 4. Energy utilization per implementation for 1024 trial DMs, measured as energy-to-completion. Percentages shown are the percentages of either the CPU or GPU energy utilization compared to the total per implementation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.