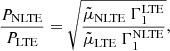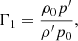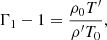| Issue |
A&A
Volume 656, December 2021
|
|
|---|---|---|
| Article Number | A159 | |
| Number of page(s) | 10 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202141851 | |
| Published online | 16 December 2021 | |
The first adiabatic exponent in a partially ionized prominence plasma: Effect on the period of slow waves
1
Departament de Física, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
e-mail: joseluis.ballester@uib.es
2
Departament de Ciències Matemàtiques i Informàtica, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
3
Institute of Applied Computing & Community Code (IAC3), Universitat de les Illes Balears, Spain
Received:
23
July
2021
Accepted:
4
October
2021
Partially ionized plasmas are found in many different astrophysical environments. The study of partially ionized plasmas is of great interest for solar physics because some layers of the solar atmosphere (photosphere and chromosphere) as well as solar structures, such as spicules and prominences, are made of these kinds of plasmas. To our knowledge, despite it being known that the adiabatic coefficient, γ, or the first adiabatic exponent, Γ1, depend on the ionization degree, this fact has been disregarded in all the studies related to magnetohydrodynamic waves in solar partially ionized plasmas. However, in other astrophysical areas, the dependence of γ or Γ1 on the plasma ionization degree has been taken into account. Therefore, our aim here is to study how, in a plasma with prominence physical properties, the joint action of the temperature, density, and ionization degree modifies the numerical values of the first adiabatic exponent Γ1 which affects the adiabatic sound speed and the period of slow waves. In our computations, we have used two different approaches; first of all, we assume local thermodynamic equilibrium (LTE) and, later, we consider a non-local thermodynamic equilibrium (non-LTE) model. When comparing the results in the LTE and non-LTE cases, the numerical values of Γ1 are clearly different for both and they are probably strongly dependent on the assumed model which determines how the ionization degree evolves with temperature. Finally, the effect of the ionization degree dependence of Γ1 on the period of slow waves has been determined showing that it can be of great importance for seismological studies of partially ionized solar structures.
Key words: magnetohydrodynamics (MHD) / Sun: filaments / prominences / Sun: oscillations
© J. L. Ballester et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The thermodynamics of partially ionized gas (Ballester et al. 2018a) differs from that of fully ionized or fully neutral gas. The differences are due to the number of free particles as well as to the fact that the energy associated with ionization and recombination becomes an extra energy source or sink for the gas. Then, in the most general case, in the expression of the specific internal energy, apart from kinetic energy, the energies stored (or released) from ionization (recombination), excitation (de-excitation), dissociation, etc. should also be taken into account. The adiabatic coefficient, γ, depends on the state of the plasma through the internal energy; therefore, it depends on the ionization fraction and its ionization is due to the fact that part of the energy input is invested in ionization, instead of an increasing gas temperature. Therefore, the consideration of a constant value for γ would overestimate the gas temperature and it is very relevant to determine how the numerical value of the adiabatic coefficient changes, for instance, with the ionization degree (Clayton 1984; Prialnik 2000; Hansen et al. 2004; Leake & Arber 2006; Priest 2014; Ballester et al. 2018b). Then, under some assumptions, a general expression for the adiabatic coefficient, γ, as a function of the ionization degree can be obtained (Prialnik 2000).
This approach has been taken into account in studies related with different astrophysical topics using, mostly, the adiabatic exponents, Γ1, Γ2, and Γ3, introduced by Eddington (1918, 1919, 1926) and Chandrasekhar (1939). The expressions for quantities, such as the specific heats of the gas, needed to compute these adiabatic exponents were derived under different assumptions such as radiation included, different stages of ionization, mixtures of different gases, etc., by Fowler & Guggenheim (1925), Möglich et al. (1939), Biermann (1942), Rosa & Unsöld (1948), Krishna Swamy (1961), Bhatnagar et al. (1963), Mihalas (1965), Cox & Giuli (1968), Mihalas & Mihalas (1984), and Weiss et al. (2004) (see Lobel 2001 for a more extense information).
For instance, Black & Bodenheimer (1975) studied the hydrodynamic evolution of rotating interstellar clouds and, since the energy equation involves the internal energy, they considered a specific internal energy which included contributions from translational kinetic energies of hydrogen and helium, dissociation and ionization energies of hydrogen, ionization energies for helium, the contribution to radiation, and the contribution from molecular hydrogen. They used the Saha equation to compute the ionization degrees, and the final expression for the internal energy was used to compute the total specific heat as a function of temperature and to solve the hydrodynamic equations numerically. Decampli et al. (1978) discussed the ortho-para hydrogen ratio in dense clouds. They used the partition function of the hydrogen molecule to compute the specific heat, cv, and the first adiabatic exponent Γ1, and they obtained the temperature dependence of Γ1 for different mixes of ortho- and para-hydrogen. Lobel et al. (1992) discussed the significance of the adiabatic exponents and obtained expressions to calculate these exponents in a stellar atmosphere including simultaneous single-ionization of different elements and a radiation field. Later, Lobel (2001) included photoionization due to radiation in a new formalism developed to compute the adiabatic exponent Γ1, when studying the dynamic stability of stellar atmospheres. Furthermore, they also considered the departures from LTE by using a non-LTE Saha equation which allows one to compute the ionization fractions through a departure coefficient bj included in the Saha equation which becomes the Elwert equation (Elwert 1952; Lobel 2001). Vandenbroucke et al. (2013) focused on the connection between micro- and macroscopic physics in hydrodynamical simulations of an ionizing gas related to the study of the low-density interstellar medium of galaxies. They used an internal energy made of kinetic and ionization energies, a temperature-dependent mean mass per particle, μ(T), and the Chianti database to compute the temperature-dependent specific internal energy, u(T), and the adiabatic index, γ(T), for a mixture of 92% hydrogen and 2% helium. Prialnik (2000) considered a specific internal energy made of kinetic and ionization energy terms and, assuming LTE, used the Saha equation to compute the ionization degree, i. Then, a general expression for the adiabatic coefficient, γ, could be obtained once the adiabatic condition dQ = 0 was imposed. This expression displays the dependence of γ on the ionization potential, χ, the temperature, T, and the ionization degree, i, and shows that γ goes from 5/3 at i = 0 (neutral gas) to 5/3 at i = 1 (fully ionized gas) through a minimum which can have a value close to 1. A different approach was followed by D’Angelo & Bodenheimer (2013) who made 3D radiation hydrodynamics calculations of the envelopes surrounding young planets. They assumed LTE as well, and considered a more complex expression for the specific internal energy involving translational, rotational, and vibrational states of molecular hydrogen, translational energies for hydrogen and helium atoms, dissociation energy of molecular hydrogen, and ionization energies of hydrogen and helium atoms. Using this specific internal energy, they computed the temperature dependence of the first adiabatic exponent Γ1. Vaidya et al. (2015) performed astrophysical fluid simulations of thermally ideal gases not having a constant adiabatic index and considered translational, rotational, vibrational, ionization, and dissociation energy terms in the specific internal energy. They assumed LTE conditions to compute the ionization degree and the temperature-dependent adiabatic exponent Γ1. Finally, de Avillez et al. (2018) followed a similar approach in simulations of the thermal evolution of plasmas in order to determine the temperature dependence of the total internal energy and of the adiabatic index. All of the abovementioned cases are adiabatic, except D’Angelo & Bodenheimer (2013), who considered a viscous term in the energy magnetohydrodynamic (MHD) equation.
However, and to our knowledge, the dependence of the adiabatic coefficient or the adiabatic exponents with the ionization degree has received almost no attention in studies of MHD waves in partially ionized plasmas of the solar atmosphere. Only Settele et al. (1999a,b) considered the effect on magneto-acoustic-gravity waves of the depth variation of the adiabatic coefficient, γ, depending on the depth-dependent ionization. The consideration of the adiabatic coefficient or the adiabatic exponents dependence on the ionization degree and its effects on slow waves is an important issue since the observed prominence oscillations have mostly been interpreted in terms of MHD waves.
Therefore, our main aim here is to point out how the numerical value of the adiabatic coefficient or the first adiabatic exponent are modified in a partially ionized plasma with solar prominence physical properties, as well as to study its effects on the period of slow waves. To this end, we consider a mixture made of hydrogen and helium, adiabatic processes, and we also consider the cases of LTE and non-LTE which allow us to make comparisons between the obtained results. However, we would like to point out that the LTE assumption is not adequate for a prominence plasma which, in general, is far from LTE. The non-LTE ionization in prominences is dominated by the hydrogen Lyman and Balmer continuum photoionization where the continuum radiation fields strongly depend on the solar-disk radiation illuminating the prominence, which is quite different from LTE conditions. In spite of this, the consideration of these two extreme cases is useful to understand how these two completely different physical descriptions of a prominence plasma affect the behavior of the first adiabatic exponent and the period of slow waves.
The layout of the paper is as follows: first of all, we consider the case of a constant adiabatic coefficient γ in the LTE case using a Saha equation adapted to the considered mixture; secondly, assuming again LTE, we consider the case in which Γ1 depends on the ionization degre and we compare the results of this case with the previous one; and subsequently, we consider the non-LTE case and we compare the results obtained for the LTE Γ1 with those obtained for Γ1 in the non-LTE case. In all the cases, we have studied the behavior of the different parameters considered with the temperature and, also, we point out how the period of slow waves was modified in the different cases considered. Finally, we draw our conclusions.
2. Equilibrium and basic equations
For our study, we consider an equilibrium configuration made of an unbounded homogeneous prominence plasma composed of hydrogen and helium, with a helium abundance of 10% which is fully neutral. The ionization degree, i, is defined as 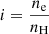 , where ne is the electron density number and nH is the total hydrogen density number (nH I + np), while for pure hydrogen this ionization degree is equivalent to
, where ne is the electron density number and nH is the total hydrogen density number (nH I + np), while for pure hydrogen this ionization degree is equivalent to 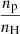 . The reason to consider this mixture is that it has been used by Heinzel et al. (2015) to infer the ionization degree, i, for a broad range of temperatures and pressures using 1D non-LTE radiative transfer models (Heinzel et al. 2014), and we take advantage of this information when considering the non-LTE case later.
. The reason to consider this mixture is that it has been used by Heinzel et al. (2015) to infer the ionization degree, i, for a broad range of temperatures and pressures using 1D non-LTE radiative transfer models (Heinzel et al. 2014), and we take advantage of this information when considering the non-LTE case later.
Following Guidry (2019), the mean mass per particle for this mixture can be computed from
where ij is the ionization degree of the species j, Zj is the atomic number for species j, and 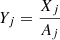 is the abundance of species j divided by the atomic mass Aj. In our case, the abundances of hydrogen and helium are X = 0.9 and Y = 0.1, respectively; therefore, our mean mass per particle is
is the abundance of species j divided by the atomic mass Aj. In our case, the abundances of hydrogen and helium are X = 0.9 and Y = 0.1, respectively; therefore, our mean mass per particle is
where i is the ionization degree for hydrogen because in cool prominence plasmas the helium is weakly ionized mostly due to photoionizations and this can be neglected in comparison to electron density due to hydrogen ionization.
When hydrogen is fully ionized, i = 1 and 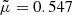 , while when hydrogen is fully neutral, i = 0 and
, while when hydrogen is fully neutral, i = 0 and 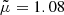 . The mean mass per particle can also be computed following Kippenhahn et al. (2012), and it is
. The mean mass per particle can also be computed following Kippenhahn et al. (2012), and it is
where 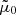 is the mean mass per particle of the neutral mixture, in our case
is the mean mass per particle of the neutral mixture, in our case 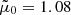 , and E is the number of free electrons per atom which is given by
, and E is the number of free electrons per atom which is given by 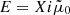 in our case (Kippenhahn et al. 2012), where X is the hydrogen abundance and i is the hydrogen ionization degree, and we obtain
in our case (Kippenhahn et al. 2012), where X is the hydrogen abundance and i is the hydrogen ionization degree, and we obtain
as before, which shows that both expressions are completely equivalent. Once the expression for the mean mass per particle has been obtained, we can write the expression for the equation of state corresponding to our mixture
where p0 is the equilibrium pressure, ρ0 is the equilibrium density, k is the Boltzmann constant, T0 is the equilibrium temperature, and H is the atomic mass unit.
On the other hand, when considering the LTE case, the ionization degree for our mixture is computed using a modified version of Saha’s equation which, following Kippenhahn et al. (2012), is
where χ is the hydrogen ionization potential, me is the electron mass, and h is Planck’s constant. Equation (5) can be substituted in Eq. (6) to obtain
which is a second order polynomial in the ionization degree, i. Figure 1 (left panel) compares the ionization degree for a gas of pure hydrogen and our mixture and it can be seen that there is a negligible difference in the ionization degree for both plasmas; this slight difference is due to the fact that for a pure hydrogen gas, X = 1 and 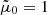 , and we recover the standard Saha equation. Figure 1 (right panel) compares the mean mass per particle for the same plasmas showing a difference between both
, and we recover the standard Saha equation. Figure 1 (right panel) compares the mean mass per particle for the same plasmas showing a difference between both 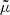 due to the fact that for pure hydrogen
due to the fact that for pure hydrogen 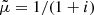 , which is also slightly different from the mean mass per particle for our mixture shown in Eq. (4).
, which is also slightly different from the mean mass per particle for our mixture shown in Eq. (4).
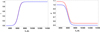 |
Fig. 1. Left panel: comparison of ionization degrees, i, computed from the Saha equation for our mixture (red) and for a gas of pure hydrogen (blue). Right panel: comparison of the mean mass per particle, |
Our plasma, with constant pressure, p0, density, ρ0, and temperature, T0, is threaded by a uniform magnetic field along the x direction, and 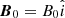 with a B0 constant. Next, we start from the single-fluid equations for a partially ionized plasma, ignoring the effect of gravity and including ambipolar diffusion (Forteza et al. 2007; Soler et al. 2009; Soler 2010; Ballester et al. 2018a). The single-fluid approximation assumes a strong coupling between ions, electrons, and neutrals so that all the species effectively behave as one fluid. In this approximation, the basic MHD equations are written in terms of total quantities, while the effect of the interactions between the various species remains in the form of several nonideal terms. For instance, the influence of ion-neutral collisions is present through the so-called ambipolar diffusion effect, which acts as a diffusive mechanism for the magnetic field. The single-fluid approximation is appropriate when studying MHD waves in partially ionized plasmas as long as the wave frequency remains lower than the ion-neutral collision frequency. The basic single-fluid equations are as follows:
with a B0 constant. Next, we start from the single-fluid equations for a partially ionized plasma, ignoring the effect of gravity and including ambipolar diffusion (Forteza et al. 2007; Soler et al. 2009; Soler 2010; Ballester et al. 2018a). The single-fluid approximation assumes a strong coupling between ions, electrons, and neutrals so that all the species effectively behave as one fluid. In this approximation, the basic MHD equations are written in terms of total quantities, while the effect of the interactions between the various species remains in the form of several nonideal terms. For instance, the influence of ion-neutral collisions is present through the so-called ambipolar diffusion effect, which acts as a diffusive mechanism for the magnetic field. The single-fluid approximation is appropriate when studying MHD waves in partially ionized plasmas as long as the wave frequency remains lower than the ion-neutral collision frequency. The basic single-fluid equations are as follows:
where 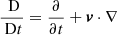 denotes the material or total derivative, ρ is the mass density, p is the thermal pressure, T is the temperature, v is the velocity vector, B is the magnetic field vector, γ is the adiabatic index, μ is the magnetic permeability, η and ηA are the coefficients of Ohmic and ambipolar diffusion, respectively, R is the gas constant, and
denotes the material or total derivative, ρ is the mass density, p is the thermal pressure, T is the temperature, v is the velocity vector, B is the magnetic field vector, γ is the adiabatic index, μ is the magnetic permeability, η and ηA are the coefficients of Ohmic and ambipolar diffusion, respectively, R is the gas constant, and 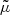 is the mean mass per particle. Equations (8)–(12) are the continuity, momentum, induction, energy, and state equations, respectively. In Eq. (11), ℒ represents the net effect of all the sources and sinks of energy which in our case only includes the generalized Joule heating and is given by
is the mean mass per particle. Equations (8)–(12) are the continuity, momentum, induction, energy, and state equations, respectively. In Eq. (11), ℒ represents the net effect of all the sources and sinks of energy which in our case only includes the generalized Joule heating and is given by
The generalized Joule heating j ⋅ E* takes plasma heating into account due to the dissipation of electric currents by both Ohmic and ambipolar diffusion. The expression of j ⋅ E* is
where ηC is the so-called Cowling’s (or total) diffusivity given by
and j∥ and j⊥ are the components of the current density parallel and perpendicular to the magnetic field, respectively, that can be computed as follows:
Thus, Ohmic diffusion is responsible for the dissipation of parallel currents, while Cowling’s diffusion, that is to say the joint effect of Ohmic and ambipolar diffusion, is responsible for the dissipation of perpendicular currents.
Once Eqs. (8)–(12) were linearized and, considering only propagation along the magnetic field, we Fourier-analyzed our perturbations. Also, combining the resulting equations, we obtained the dispersion relation for slow waves propagating along the magnetic field, which is (Barceló et al. 2011)
with kx, the longitudinal wavenumber characterizing propagation along the magnetic field, and cs, the sound speed given by
where R is the gas constant, then, from Eq. (18) the period for slow waves, P, is given by
where once a numerical value for the longitudinal wavenumber, kx, has been assumed, the first factor is a constant. Equations (18) and (20) are the same as for the case of a fully ionized plasma; however, for a partially ionized plasma, the difference is in the numerical values of the mean mass per particle and the adiabatic coefficient due to the variation of both with the ionization degree. In the following, in all our computations, related with partially ionized plasmas, we consider a constant density, ρ0 = 4 × 10−11 kg m−3, typical of quiescent prominences.
2.1. Constant γ
In many studies related to partially ionized plasmas, the value of the adiabatic coefficient, γ, is assumed to be constant, independent of the plasma ionization degree, and equal to 5/3. To compute the ionization degree, we assumed LTE although this assumption, which implies a strong interaction between matter and radiation as in stellar interiors, is not fully realistic for prominence conditions, as has been stated in the Introduction. In solving Eq. (7), we can obtain the ionization degree as well as the mean mass per particle, 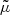 , as functions of temperature, and from Eq. (20), the period behaves as
, as functions of temperature, and from Eq. (20), the period behaves as
then wavelengths which are typically observed in prominence oscillations correspond to wavenumbers, which are in the range 10−8 − 10−6 m−1 (Terradas et al. 2002; Forteza et al. 2007; Soler et al. 2007). Therefore, for our calculations, we have chosen kx = 10−6 m−1, and from Eq. (21) we obtain the behavior of the period of slow waves with the temperature in the case of constant γ. This behavior is shown in Fig. 2 where we can see that the period decreases when the temperature increases, which is due to the fact that the plasma is becoming more ionized, the mean mass per particle decreases, and the factor 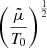 decreases.
decreases.
 |
Fig. 2. Period of slow waves as a function of the temperature for a constant γ = 5/3. Also, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3. |
2.2. The first adiabatic exponent Γ1 in the LTE case
The adiabatic exponents, Γ1, Γ2, and Γ3, were introduced by Eddington (1918, 1919, 1926) and Chandrasekhar (1939), and they are useful for the study of adiabatic processes in an ionizing gas. They are related to the behavior of thermodynamic systems undergoing infinitesimal adiabatic changes. For instance, the adiabatic exponent Γ1 is given by
where the derivative is considered at constant entropy denoted by s, while the adiabatic sound speed, cs, is defined as
with the derivative also being computed at constant entropy. Then, using Eq. (22), we obtained
Our interest here is to obtain, for our considered mixture, an expression for Γ1 as a function of the ionization degree which would allow us to compute the sound speed and the period of slow waves. The expression for Γ1 in the case of a gas of pure hydrogen can be found, for instance, in Bhatnagar et al. (1963), Mihalas (1965), Cox & Giuli (1968), Mihalas & Mihalas (1984), Hansen et al. (2004), and Weiss et al. (2004). However, since we wanted to find an expression for Γ1 that was appropiate for our mixture, we needed to derive it, which involved a long calculation. To this end, we closely followed Hansen et al. (2004), but adapted it to our case. The procedure started from the specific internal energy, U, for a partially ionized plasma containing ions, neutrals, and electrons, considering two terms; the first term is the standard internal energy, while the second term represents the available ionization potential energy which, in this case, corresponds to hydrogen since helium remains neutral and the helium excitation at prominence temperatures is also negligible (Clayton 1984; Prialnik 2000; Hansen et al. 2004; Leake & Arber 2006; Ballester et al. 2018b). Furthermore, we made use of the equation of state (Eq. (5)) and, since we assumed LTE, we also made use of the Saha equation (Eq. (7)) in which the derivatives of the partition functions are usually neglected in the case of hydrogen (Bhatnagar et al. 1963). First of all, we computed the specific heat at constant volume, cv,
and the quantities χρ and χT, which are
and for a perfect gas not undergoing ionization, they are χρ = χρ = 1. Once all of these quantities were computed from the general expression Γ3 − 1 for the third adiabatic exponent,
we obtained
where D is given by
and a = 0.972 is the coefficient of the ionization degree in the equation of state (Eq. (5)). Next, we computed the quantity 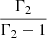 from
from
obtaining
Now, our expression for the first adiabatic exponent can be computed from
and it is as follows:
The obtained expression of Γ1 for our mixture differs from the one corresponding to a gas of pure hydrogen because of coefficient a; however, in the case of pure hydrogen for i = 0 (fully neutral gas) or i = 1 (fully ionized gas), D = 0 and Γ1 = Γ2 = Γ3 = γ = 5/3.
Keeping the density constant as before, we varied the temperature, T0, and from Eq. (7)) we obtained the ionization degree and, with the help of Eq. (34), we computed the temperature behavior of Γ1 for our mixture. Figure 3 makes a comparison of the behavior versus temperature of γ = 5/3, Γ1 for our mixture, and Γ1 for the case of a pure hydrogen gas. In the last two cases, the behavior is almost fully coincident, which is due to the fact that in the case of pure hydrogen, a = 1 instead of 0.972. It can be observed that both parameters γ and Γ1 start at a value of 5/3 and decrease with the temperature reaching a minimum at T0 = 6000 K; later, for lower temperatures, they increase again up to 5/3. The variation of the first adiabatic exponent also depends on the quantity χ/kT; when this quantity is large, the value of Γ1 drops to around 1. This fact can be easily understood since when χ/kT is small, ionizing an atom does not need much energy compared to thermal energy, then, this additional source or sink of energy does not substantially affect the value of Γ1. On the contrary, when χ/kT is large, the ionization energy is not negligible compared to thermal energy and it modifies the value of Γ1 in a substantial way. Next, Fig. 4 displays a comparison of the behavior of sound speeds versus temperature for the three considered cases: constant γ, Γ1 for hydrogen gas, and Γ1 for our mixture. Important differences are seen between sound speeds for constant γ and Γ1 for our mixture for temperatures below 8000 K, which should be reflected in the temperature behavior of the periods of slow waves. Furthermore, a non-negligible difference in the temperature behavior of the sound speeds for the hydrogen gas and our mixture can also be observed, which is due to the small differences in the equation of state and Saha equation between both chemical compositions.
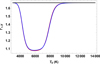 |
Fig. 3. Comparison between a constant γ = 5/3 (black line), Γ1 for our mixture (red line), and Γ1 for pure hydrogen gas (blue line). Also, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
 |
Fig. 4. Comparison between sound speeds for the following: a fully ionized hydrogen gas with constant γ = 5/3 (black line); Γ1 for our mixture (red line); and Γ1 for a pure hydrogen gas (blue line). Also, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
In this case, from Eqs. (18) and (24), the period is given by
and Fig. 5 (left panel) displays a comparison between the periods of slow waves for constant γ and Γ1 in the LTE case as a function of the temperature. It can be seen that for temperatures between 3000−4000 K and 9000−14 000 K, the periods fully agree, while for intermediate temperatures, the period corresponding to the case of Γ1 becomes greater than the period for a constant γ. In the case of Γ1, the behavior of the period given by Eq. (35) was determined by the interplay between the temperature and the behaviors of 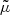 , Γ1 with temperature. Of course, the difference in the period found at temperatures between 4000 and 9000 K comes from the difference between γ and Γ1 at these temperatures since, in both cases, we assumed that LTE and the ionization degree as well as the mean mass per particle were the same. Figure 5 (right panel) shows the temperature dependence of the ratio of the periods for slow waves obtained from the constant γ and Γ1. The temperature behavior of this ratio can be easily understood by combining Eqs. (21) and (35) to obtain
, Γ1 with temperature. Of course, the difference in the period found at temperatures between 4000 and 9000 K comes from the difference between γ and Γ1 at these temperatures since, in both cases, we assumed that LTE and the ionization degree as well as the mean mass per particle were the same. Figure 5 (right panel) shows the temperature dependence of the ratio of the periods for slow waves obtained from the constant γ and Γ1. The temperature behavior of this ratio can be easily understood by combining Eqs. (21) and (35) to obtain
 |
Fig. 5. Left panel: period of slow waves versus temperature for a constant γ = 5/3 (red line) and Γ1 (blue line) for our mixture. Right panel: ratio between the periods of slow waves, Pγ corresponding to a constant γ, and PΓ1 corresponding to Γ1 for our mixture. Furthermore, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
where Pγ and PΓ1 are the periods corresponding to a constant γ and Γ1 for our mixture, respectively. For high and low temperatures, both adiabatic coefficients tend to be 5/3, then the ratio is 1; for intermediate temperatures, Γ1 decreases until reaching a minimum, then the ratio is smaller than 1; while for lower temperatures, the ratio increases again up to 1 following the increase in Γ1 up to 5/3. In summary, our results show that in the considered LTE case for a partially ionized plasma, the numerical values of the periods for slow waves can differ up to a 20%, which can substantially affect other computations based on the numerical values of these periods.
2.3. The first adiabatic exponent Γ1 in the non-LTE case
In previous sections, and despite LTE conditions not being adequate for physical conditions in prominence plasmas, we used a Saha equation appropiate for our mixture, which is a modification of the Saha equation for hydrogen, to compute the ionization degree and to obtain an expression for the first adiabatic exponent Γ1.
Here, we consider a non-LTE model in order to compare it with LTE results. Then, to estimate the ionization degree, we followed Heinzel et al. (2015) who used the 1D non-LTE radiative transfer model (Heinzel et al. 2014) to determine the ionization degree in prominence slabs. In particular, these authors provide tables for the ionization degree for a range of temperatures (6000−14 000 K) and pressures (10−3 − 2 × 10−2 Pa) in prominence plasmas having the composition already introduced in Sect. 2. Using Table 1 in Heinzel et al. (2015) and the Fit function from the Mathematica symbolic package, we performed a polynomial fit up to third order in pressure, p, and temperature, T, plus product terms or interactions of the ionization degree such as,
where a, b, c, d, e, f, g, h, j, k are the coefficients of the fitted function which has R2 = 0.98 (Ballester et al. 2020).
Since in this case we consider a non-LTE model, it is not appropriate to use the Saha equation to determine the ionization degree dependence of Γ1, therefore, we must use a different approach. To this end, we closely followed the procedure of Clayton (1984) adapted to our mixture. First of all, we describe this procedure; next, we show that in the LTE case the behavior of Γ1 obtained with this procedure fully agrees with that of Γ1 obtained in Sect. 2.2; and, finally, we compute Γ1 for our non-LTE case.
In general, the first adiabatic exponent, Γ1, has a functional dependence on the temperature and density (Weiss et al. 2004) such that
where cv is the specific heat at a constant volume given by Eq. (25). It is important to notice that for a perfect gas without ionization processes, 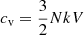 , with V = 1/ρ, a specific volume, and N, the density number of free particles from Eq. (38) then becomes
, with V = 1/ρ, a specific volume, and N, the density number of free particles from Eq. (38) then becomes
which is the constant adiabatic coefficient used in Sect. 2.1.
Now, for the computation of Γ1 in the non-LTE case, we write the specific internal energy as in Clayton (1984),
where the second term is the energy associated with ionization which becomes an extra energy source or sink for the gas. Also, H+ is the density number of hydrogen ions (equivalent to np used elsewhere in the paper) and χ is the ionization potential; then, at constant volume
and the specific heat is
The temperature dependence of the density number of free particles, N, is
then, substituting in Eq. (42),
We first considered the LTE case and the total particle density number is 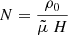 . Then, since we assumed a constant density, once the ionization degree was obtained from Eq. (7), the numerical values of
. Then, since we assumed a constant density, once the ionization degree was obtained from Eq. (7), the numerical values of 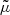 as a function of temperature could also be determined and the density number of free particles, N, could be computed for each temperature considered. Furthermore,
as a function of temperature could also be determined and the density number of free particles, N, could be computed for each temperature considered. Furthermore, 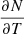 could also be computed, and the variation in the number of free particles comes from hydrogen since helium is always considered as neutral; therefore,
could also be computed, and the variation in the number of free particles comes from hydrogen since helium is always considered as neutral; therefore, 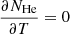 . Then, Eq. (44), together with Eqs. (26) and (27), could be used to compute the first adiabatic exponent from Eq. (38). Figure 6 displays a comparison between the temperature behaviors of Γ1 obtained in Sect. 2.2 and Γ1 obtained from the above computations assuming LTE. This figure shows that, as could be expected, the temperature behavior of both adiabatic exponents fully agree when both are computed under the assumption of LTE. As a consequence, in both cases, the period of slow waves, computed from Eq. (35), is the same.
. Then, Eq. (44), together with Eqs. (26) and (27), could be used to compute the first adiabatic exponent from Eq. (38). Figure 6 displays a comparison between the temperature behaviors of Γ1 obtained in Sect. 2.2 and Γ1 obtained from the above computations assuming LTE. This figure shows that, as could be expected, the temperature behavior of both adiabatic exponents fully agree when both are computed under the assumption of LTE. As a consequence, in both cases, the period of slow waves, computed from Eq. (35), is the same.
 |
Fig. 6. Comparison between Γ1 (red line) computed in Sect. 2.2 and Γ1 (blue line) computed in Sect. 2.3. In both cases, the ionization degree was computed assuming LTE. Furthermore, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
Now, we can consider the non-LTE case. Using Eq. (37), together with the temperature and pressure values in Heinzel et al. (2015), we could compute the fitted ionization degree. In order to follow the same approach of constant density as in Sects. 2.1 and 2.2, we substituted the equation of state (Eq. (5)) in the fitted function for the ionization degree which, in this way, becomes dependent on the density and temperature. Furthermore, the total number of free particles, N, can also be computed as well as 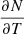 and the needed derivatives in Eqs. (26) and (27). Using Eqs. (38) and (42), the temperature behavior of Γ1 for this non-LTE model could be obtained.
and the needed derivatives in Eqs. (26) and (27). Using Eqs. (38) and (42), the temperature behavior of Γ1 for this non-LTE model could be obtained.
First of all, Fig. 7 (left panel) compares the ionization degrees obtained from the LTE approach described by Eq. (7) and the non-LTE approach described by the fitted function in Eq. (37). As can be observed, the behavior of the ionization degree with the temperature is quite different for LTE and non-LTE approaches. For LTE and temperatures between 14 000 K and 8000 K, the plasma is almost fully ionized; whereas, in the non-LTE case, the plasma ionization degree for high temperatures is still smaller than 1. This plot also shows that in the considered non-LTE model, ionization proceeds more slowly than in the LTE case in which ionization takes place very rapidly. Furthermore, it can also be observed that in the case of non-LTE and around 6000 K, the ionization degree seems to increase which could be a drawback of the fitting, although this behavior could also be due to the fact that non-LTE i is only weakly dependent on the temperature because it is mainly dominated by photoionization. In the following plots, we consider a temperature interval between 7000 and 14 000 K.
 |
Fig. 7. Left panel: comparison of the ionization degree for the LTE (blue line) and non-LTE (red line) cases versus temperature. Right panel: comparison between mean mass per particle for the LTE (blue line) and non-LTE (red line) cases versus temperature. Also, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
Figure 7 (right panel) shows a comparison between the mean mass per particle in the LTE and non-LTE cases, which, again, points out a strong difference between both cases of the temperature behavior of this parameter. Next, Fig. 8 shows a comparison between the temperature behavior of Γ1, computed using Eq. (34) and Γ1 computed from the assumed non-LTE model in this Sect. 2.3. We can observe that the temperature behavior of both coefficients is very different. At 14 000 K, in the LTE case, Γ1 starts from the value 5/3 and remains almost constant up to 9000 K, which later decreases rapidly, reaching a minimum around 6000 K; whereas, in the non-LTE case, Γ1 starts around 1.5 and decreases up to around 8500 K, while later it starts to increase. The reason why at high temperature Γ1 is not equal to 5/3 is that at this temperature in the non-LTE case, the plasma is not fully ionized as in the LTE case. Moreover, we can also observe that for temperatures around 7000 K, Γ1 in the LTE case becomes smaller than Γ1 for the non-LTE case.
 |
Fig. 8. Comparison of Γ1 for the LTE (blue line) case with Γ1 for the non-LTE (red line) case versus temperature. Furthermore, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
Finally, as in Sect. 2.2, the period of slow waves can be computed using Eq. (35) applied to the non-LTE case. Figure 9 (left panel) shows the periods computed for LTE and non-LTE approaches and points out that for the interval of temperatures considered, the period computed in the LTE case is smaller than that of the non-LTE case; however, for the higher and lower temperatures, both periods tend to become equal. On the other hand, from Eq. (35), an analytical relationship between the periods for the non-LTE and LTE cases can be obtained, which is given by
 |
Fig. 9. Left panel: comparison between periods for slow waves in the LTE case (blue line) and in the non-LTE case (red line) versus temperature. Right panel: theoretical (blue line), following Eq. (45), and numerical (red line) ratios of the periods of slow waves versus temperature, computed for the LTE and non-LTE cases. Also, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
and Fig. 9 (right panel) shows the computed ratio between the obtained periods for non-LTE and LTE as well as the theoretical ratio obtained from Eq. (45), indicating an excellent agreement between both ratios. However, an important conclusion can be drawn from this figure which is that within this interval of temperatures, the period of slow waves in the LTE and non-LTE cases are, in general, different and able to reach differences of up to 30%. It is important to notice that from Eq. (45), it is easy to check that if instead of non-LTE we consider LTE, the mean masses per particle are equal as well as both Γ1, as we have shown before, and, then, the periods become equal. It is worth highlighting that we used a particular non-LTE model (Heinzel et al. 2014, 2015) developed to be applied to prominence physical conditions. The Heinzel et al. (2015) model provides a 1D prominence slab with ionization in the center of it, which is a good representation of the ionization degree, although some differences will occur at surface layers. Furthermore, variations in the electron density, for example in 2D models, have also been reported (Jejčič et al. 2014). Therefore, different non-LTE models would probably provide different results for the first adiabatic exponent as well as for the slow waves period. The strong differences shown between LTE and non-LTE periods for slow waves are of great importance for seismological studies of prominences using MHD waves.
Finally, using Eq. (24), Fig. 10 shows a comparison between the temperature behavior of the adiabatic sound speeds in the LTE and non-LTE cases. It shows that the sound speed is greater in the non-LTE case, which agrees with Fig. 9 (left panel) about the behavior of periods in both cases.
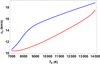 |
Fig. 10. Comparison between sound speeds for Γ1 in the LTE case (blue line) and for Γ1 in the non-LTE case (red line) versus temperature. Furthermore, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
3. Conclusions
The adiabatic coefficient, γ, and the first adiabatic exponent, Γ1, are quantities of great importance in different fields of astrophysics in which partially ionized plasmas play a significant role. Therefore, it is of interest to know the numerical value of these coefficients with accuracy in these types of plasmas oncethe density, temperature, and ionization degree are known. To this end, we have considered a partially ionized plasma composed by neutral and ionized hydrogen as well as neutral helium and, assuming constant density, we have studied the following three different cases: a constant adiabatic coefficient, γ, in the LTE case, the first adiabatic exponent, Γ1, in the LTE case, and the first adiabatic exponent, Γ1, in the non-LTE case. These studies have been focused on determining the dependence of these parameters on the ionization degree and the effect produced by its temperature behavior for our mixture; the latter helped to determine the ionization degree on the period of slow waves. However, as stated in Sect. 2.3, we must keep in mind that in the non-LTE model, i is weakly dependent on the temperature, while in the LTE case, i is determined by the temperature.
First of all, we introduced an equation of state for our mixture and, in order to compute the ionization degree i and the mean mass per particle in the LTE case, we used a modification of the Saha equation for hydrogen. Next, we considered the case in which the adiabatic coefficient γ is constant and equal to 5/3, which has been compared with the case in which the first adiabatic exponent, Γ1, depends on the ionization degree and whose expression, assuming LTE, was computed using our Saha equation. For this computation, we considered a specific energy equation including the internal energy plus a term corresponding to the ionization energy. The comparison shows that, under the assumption of LTE, the numerical value of Γ1 starts from 5/3 at a high temperature, goes through a minimum value around 1.1 at 6000 K, and increases again up to 5/3 for low temperatures, indicating a truly different behavior with respect to a constant γ.
Once the expression for Γ1 was determined, we made a comparison between the sound speeds corresponding to a constant γ and Γ1, which shows that the sound speed associated to Γ1 displays a rather different behavior, in particular for temperatures between 3000 and 9000 K, being always smaller than the sound speed corresponding to a constant γ. This behavior of the sound speed with the temperature must be reflected in the behavior of the period of slow waves and the results show that the period corresponding to the case of Γ1 is equal to that of constant γ in the temperature intervals 9000−14 000 K and 3000−4000 K, while it is greater for intermediate temperatures. When the ratio between the periods corresponding to both cases is plotted, the difference between both periods can reach up to 20%.
Next, we have compared the behavior of Γ1 when the LTE and non-LTE cases are considered. First of all, we have compared the temperature behavior of the ionization degree and mean mass per particle for both cases, and the results show important differences between the behavior and numerical values. As a consequence, these differences should be reflected in the temperature behavior of Γ1. When comparing Γ1 in the LTE case with Γ1 in the non-LTE case, our results clearly show that they do not agree with Γ1 non-LTE having values smaller than those of Γ1 LTE, except for low temperatures. The comparison between the period of slow waves in the LTE and non-LTE cases shows that in the LTE case, the period is smaller than for the non-LTE case, except for low temperatures, and the computed ratio between the periods in both cases reflects this behavior. The ratio is smaller than one for low temperatures and becomes greater than one, and up to 1.3, for temperatures over 7000 K decreasing again for higher temperatures. This result means that there are important differences between both periods which can reach up to 30%. Next, we computed and compared the behavior of sound speeds versus the temperature for two cases and the results show that in the LTE case, the sound speed is much greater than for the non-LTE case, except for the lower and higher temperatures.
These are interesting results since they mean that the physical conditions of a prominence plasma as well as the thermodynamic model used to describe it are of crucial importance for seismological studies related to prominences or with other partially ionized structures of the solar atmosphere. On the other hand, it is important to point out that the non-LTE model we used has some constraints because the range of temperatures is limited to 6000 − 14 000 K and, also, we used a fit for the ionization degree which is not perfect around 6000 K. Furthermore, a different non-LTE model could produce different results, although the general behavior would probably be similar.
When linear and adiabatic MHD waves are considered, the perturbed pressure and density are related in the perturbed energy equation through the adiabatic sound speed, which depends on the adiabatic coefficient or the first adiabatic exponent. Therefore, using Eq. (24), we could write,
where p′ and ρ′ correspond to pressure and density perturbations, respectively. Using the linearized equation of state from the previous equation, we can also obtain
where T′ is the perturbed temperature. Spectroscopic data obtained in different spectral windows could provide us with information about density and temperature perturbations using line ratios, then, once these perturbations are known, we could estimate the value of Γ1. Knowing this value, and in the LTE case, we could take advantage of Eq. (34) to estimate the ionization degree. Then, using prominence oscillations and the above described procedure, we have a seismological tool which could provide us with indirect information about the thermodynamic state of the prominence plasma. However, despite the fact that the physical conditions of the oscillating prominence plasma determine the behavior of the perturbations, it is important to point out that the model, LTE, or non-LTE considered to describe the state of prominence plasma, as well as nonadiabatic effects can substantially affect the interpretation of the spectral indicators, which are of great importance for seismological studies of partially ionized layers or structures of the solar atmosphere.
Furthermore, here we have considered a plasma with physical conditions akin to those of quiescent prominences and, under these conditions, the sound speed, cs, which characterizes slow waves, is smaller than the Alfvén speed, ca, characterizing fast waves, which are not significantly affected by the adiabatic coefficient or the first adiabatic exponent. Therefore, for uncoupled waves, and with these physical conditions, only slow waves are affected for variations of the adiabatic coefficient or the first adiabatic exponent.
Also, it is interesting to point out that from the principle of energy equipartition for perfect gases without radiation, the adiabatic exponent Γ1 is equal to 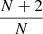 where, in this case, N is the number of degrees of freedom, then, for a 3D nonrelativistic gas, N = 3 and Γ1 = 5/3, which is the constant value that is currently used in most studies. However, when hydrogen is ionized, Γ1 drops to a value close to 1, which means that the number of degrees of freedom, N, is very large. From a physical point of view, this large number of degrees of freedom corresponds to the case in which all the energy added to the system is invested in “internal” forms of energy (ionization, rotation, vibration, etc.) only, instead of kinetic energy (Lobel et al. 1992; Weiss et al. 2004).
where, in this case, N is the number of degrees of freedom, then, for a 3D nonrelativistic gas, N = 3 and Γ1 = 5/3, which is the constant value that is currently used in most studies. However, when hydrogen is ionized, Γ1 drops to a value close to 1, which means that the number of degrees of freedom, N, is very large. From a physical point of view, this large number of degrees of freedom corresponds to the case in which all the energy added to the system is invested in “internal” forms of energy (ionization, rotation, vibration, etc.) only, instead of kinetic energy (Lobel et al. 1992; Weiss et al. 2004).
In summary, the chemical composition of partially ionized gases in different astrophysical enviroments is not uniform. Therefore, in order to know the behavior of the first adiabatic exponent in such different chemical compositions, it is needed to establish the following: (a) the appropriate equation of state; (b) a modified Saha equation for hydrogen in the LTE case; (c) or a non-LTE model, before starting to determine the behavior of the first adiabatic exponent.
Finally, taking the above results into account, we can conclude that this study illustrates how important a correct estimation of the numerical value of Γ1 is in order to determine the right period of slow waves which is of great importance for seismological studies based on prominence oscillations interpreted in terms of MHD waves. Also, with the help of the observed prominence oscillations, we propose a seismological tool to estimate Γ1 and the ionization degree of the prominence plasma. A further extension of this work would be to study the time evolution of the first adiabatic exponent and its impact on the period of slow waves, when a time-dependent ionization degree is considered.
Acknowledgments
We would like to thank the referee for his/her constructive comments. JLB, RS, MC and JT acknowledge support from grant AYA2017-85465-P (MINECO/AEI/FEDER, UE). This publication is part of the R+D+i project PID2020-112791GB-I00, financed by MCIN/AEI/10.13039/501100011033.
References
- Ballester, J. L., Alexeev, I., Collados, M., et al. 2018a, Space Sci. Rev., 214, 58 [Google Scholar]
- Ballester, J. L., Carbonell, M., Soler, R., & Terradas, J. 2018b, A&A, 609, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballester, J. L., Soler, R., Terradas, J., & Carbonell, M. 2020, A&A, 641, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barceló, S., Carbonell, M., & Ballester, J. L. 2011, A&A, 525, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhatnagar, P. L., Menzel, D. H., & Sen, H. K. 1963, Stellar Interiors (London: Chapman and Hall) [Google Scholar]
- Biermann, L. 1942, ZAp, 21, 320 [NASA ADS] [Google Scholar]
- Black, D. C., & Bodenheimer, P. 1975, ApJ, 199, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1939, An Introduction to the Study of Stellar Structure (New York: Dover Publications Inc.) [Google Scholar]
- Clayton, D. D. 1984, Principles of Stellar Evolution and Nucleosynthesis (Chicago: The University of Chicago Press) [Google Scholar]
- Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure (New York: Gordon and Breach) [Google Scholar]
- D’Angelo, G., & Bodenheimer, P. 2013, ApJ, 778, 77 [Google Scholar]
- de Avillez, M. A., Anela, G. J., & Breitschwerdt, D. 2018, A&A, 616, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decampli, W. M., Cameron, A. G. W., Bodenheimer, P., & Black, D. C. 1978, ApJ, 223, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Eddington, A. S. 1918, MNRAS, 79, 2 [NASA ADS] [Google Scholar]
- Eddington, A. S. 1919, MNRAS, 79, 177 [NASA ADS] [Google Scholar]
- Eddington, A. S. 1926, The Internal Constitution of the Stars (New York: Dover Books) [Google Scholar]
- Elwert, G. 1952, Z. Naturforschung Teil A, 7, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Forteza, P., Oliver, R., Ballester, J. L., & Khodachenko, M. L. 2007, A&A, 461, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fowler, R. H., & Guggenheim, E. A. 1925, MNRAS, 85, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Guidry, M. 2019, Stars and Stellar Processes (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Hansen, C. J., Kawaler, S. D., & Trimble, V. 2004, Stellar Interiors: Physical Principles, Structure, and Evolution (New York: Springer-Verlag) [Google Scholar]
- Heinzel, P., Vial, J. C., & Anzer, U. 2014, A&A, 564, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Gunár, S., & Anzer, U. 2015, A&A, 579, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jejčič, S., Heinzel, P., Zapiór, M., et al. 2014, Sol. Phys., 289, 2487 [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2012, Stellar Structure and Evolution (New York: Springer-Verlag) [Google Scholar]
- Krishna Swamy, K. S. 1961, ApJ, 134, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Leake, J. E., & Arber, T. D. 2006, A&A, 450, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lobel, A. 2001, ApJ, 558, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Lobel, A., Achmad, L., de Jager, C., & Nieuwenhuijzen, H. 1992, A&A, 264, 147 [NASA ADS] [Google Scholar]
- Mihalas, D. 1965, ApJ, 141, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., & Mihalas, B. W. 1984, Foundations of Radiation Hydrodynamics (Oxford: Oxford University Press) [Google Scholar]
- Möglich, F., Riewe, K.-H., & Rompe, R. 1939, Ann. Phys., 427, 735 [CrossRef] [Google Scholar]
- Prialnik, D. 2000, An Introduction to the Theory of Stellar Structure and Evolution (Cambridge: Cambridge University Press) [Google Scholar]
- Priest, E. 2014, Magnetohydrodynamics of the Sun (Cambridge: Cambridge University Press) [Google Scholar]
- Rosa, A., & Unsöld, A. 1948, ZAp, 25, 20 [NASA ADS] [Google Scholar]
- Settele, A., Zhugzhda, Y. D., & Staude, J. 1999a, in Magnetic Fields and Solar Processes, ed. A. Wilson, et al., ESA SP, 9, 367 [NASA ADS] [Google Scholar]
- Settele, A., Zhugzhda, Y. D., & Staude, J. 1999b, Astron. Nachr., 320, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R. 2010, PhD Thesis, Departament de Fisica, Universitat de les Illes Balears [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2007, A&A, 471, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2009, ApJ, 699, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Molowny-Horas, R., Wiehr, E., et al. 2002, A&A, 393, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaidya, B., Mignone, A., Bodo, G., & Massaglia, S. 2015, A&A, 580, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vandenbroucke, B., De Rijcke, S., Schroyen, J., & Jachowicz, N. 2013, ApJ, 771, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., Hillebrandt, W., Thomas, H. C., & Ritter, H. 2004, Principles of Stellar Structure (Cambridge: Cambridge Scientific Publishers) [Google Scholar]
All Figures
 |
Fig. 1. Left panel: comparison of ionization degrees, i, computed from the Saha equation for our mixture (red) and for a gas of pure hydrogen (blue). Right panel: comparison of the mean mass per particle, |
| In the text | |
 |
Fig. 2. Period of slow waves as a function of the temperature for a constant γ = 5/3. Also, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3. |
| In the text | |
 |
Fig. 3. Comparison between a constant γ = 5/3 (black line), Γ1 for our mixture (red line), and Γ1 for pure hydrogen gas (blue line). Also, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
| In the text | |
 |
Fig. 4. Comparison between sound speeds for the following: a fully ionized hydrogen gas with constant γ = 5/3 (black line); Γ1 for our mixture (red line); and Γ1 for a pure hydrogen gas (blue line). Also, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
| In the text | |
 |
Fig. 5. Left panel: period of slow waves versus temperature for a constant γ = 5/3 (red line) and Γ1 (blue line) for our mixture. Right panel: ratio between the periods of slow waves, Pγ corresponding to a constant γ, and PΓ1 corresponding to Γ1 for our mixture. Furthermore, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
| In the text | |
 |
Fig. 6. Comparison between Γ1 (red line) computed in Sect. 2.2 and Γ1 (blue line) computed in Sect. 2.3. In both cases, the ionization degree was computed assuming LTE. Furthermore, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
| In the text | |
 |
Fig. 7. Left panel: comparison of the ionization degree for the LTE (blue line) and non-LTE (red line) cases versus temperature. Right panel: comparison between mean mass per particle for the LTE (blue line) and non-LTE (red line) cases versus temperature. Also, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
| In the text | |
 |
Fig. 8. Comparison of Γ1 for the LTE (blue line) case with Γ1 for the non-LTE (red line) case versus temperature. Furthermore, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
| In the text | |
 |
Fig. 9. Left panel: comparison between periods for slow waves in the LTE case (blue line) and in the non-LTE case (red line) versus temperature. Right panel: theoretical (blue line), following Eq. (45), and numerical (red line) ratios of the periods of slow waves versus temperature, computed for the LTE and non-LTE cases. Also, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
| In the text | |
 |
Fig. 10. Comparison between sound speeds for Γ1 in the LTE case (blue line) and for Γ1 in the non-LTE case (red line) versus temperature. Furthermore, kx = 10−6 m−1, ρ0 = 4 × 10−11 kg m−3, and χ = 13.6 eV. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



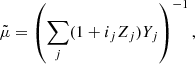
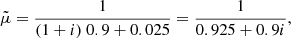
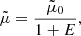
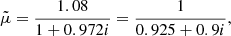
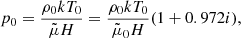
![$$ \begin{aligned} \frac{i}{1-i} \ \frac{\tilde{\mu }_0 X i}{\tilde{\mu }_0 X i+1} = \frac{1}{p_0} \frac{(2 \pi m_{\rm e})^{1.5} (k T)^{2.5}}{h^3} \exp \left[-\frac{\chi }{k T}\right], \end{aligned} $$](/articles/aa/full_html/2021/12/aa41851-21/aa41851-21-eq14.gif)
![$$ \begin{aligned} \frac{X i^2}{1-i} = \frac{H}{\rho _0} \frac{(2 \pi m_{\rm e})^{1.5} (k T)^{1.5}}{h^3} \exp \left[-\frac{\chi }{k T}\right], \end{aligned} $$](/articles/aa/full_html/2021/12/aa41851-21/aa41851-21-eq15.gif)
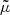
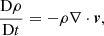
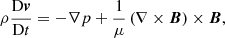
![$$ \begin{aligned}&\frac{\partial {\boldsymbol{B}}}{\partial t} = \nabla \times \left({\boldsymbol{v}} \times {\boldsymbol{B}}\right) - \nabla \times \left(\eta \nabla \times {\boldsymbol{B}}\right)\nonumber \\&\qquad \quad + \nabla \times \left\{ \eta _{\rm A}\left[\left(\nabla \times {\boldsymbol{B}}\right) \times {\boldsymbol{B}}\right] \times {\boldsymbol{B}}\right\} , \end{aligned} $$](/articles/aa/full_html/2021/12/aa41851-21/aa41851-21-eq23.gif)
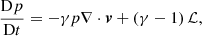
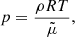
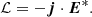
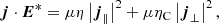
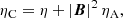
![$$ \begin{aligned}&{\boldsymbol{j}}_\parallel = \frac{1}{\mu } \frac{\left[\left(\nabla \times {\boldsymbol{B}} \right) \cdot {\boldsymbol{B}}\right] {\boldsymbol{B}}}{\left| {\boldsymbol{B}} \right|^2}\end{aligned} $$](/articles/aa/full_html/2021/12/aa41851-21/aa41851-21-eq31.gif)
![$$ \begin{aligned}&{\boldsymbol{j}}_\perp = \frac{1}{\mu } \frac{{\boldsymbol{B}} \times \left[\left(\nabla \times {\boldsymbol{B}}\right) \times {\boldsymbol{B}} \right]}{\left| {\boldsymbol{B}} \right|^2}\cdot \end{aligned} $$](/articles/aa/full_html/2021/12/aa41851-21/aa41851-21-eq32.gif)
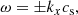
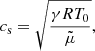
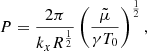
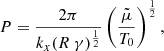
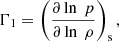
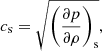
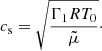
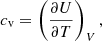
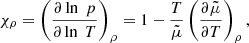
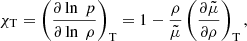
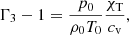
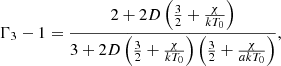
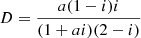
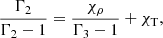
![$$ \begin{aligned} \frac{\Gamma _2}{\Gamma _2 -1} = \frac{1 - D}{\Gamma _3 -1}+\left[1 + D \left(\frac{3}{2} + \frac{\chi }{k T_{0}}\right)\right]. \end{aligned} $$](/articles/aa/full_html/2021/12/aa41851-21/aa41851-21-eq50.gif)
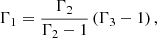
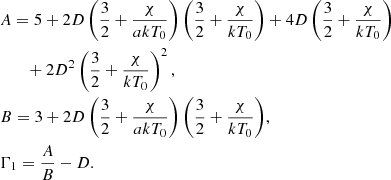
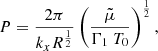
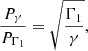
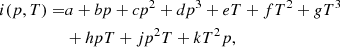
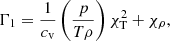
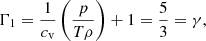
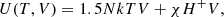
![$$ \begin{aligned} \mathrm{d}U = \left[1.5 N k V + 1.5 k T V \left(\frac{\partial N}{\partial T}\right)_{V} + \chi V \left(\frac{\partial H^+}{\partial T}\right)_{V} \right]\mathrm{d}T \end{aligned} $$](/articles/aa/full_html/2021/12/aa41851-21/aa41851-21-eq61.gif)
![$$ \begin{aligned} c_{\rm v} = \left[1.5 N k V + 1.5 k T V \left(\frac{\partial N}{\partial T}\right)_{V} + \chi V \left(\frac{\partial H^+}{\partial T}\right)_{V} \right]\cdot \end{aligned} $$](/articles/aa/full_html/2021/12/aa41851-21/aa41851-21-eq62.gif)
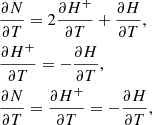
![$$ \begin{aligned} c_V = 1.5 N k V \left[1+\left(\frac{\partial N}{\partial T}\right)_V \frac{2}{3}\frac{T}{N}\left[\frac{3}{2} + \frac{\chi }{k T}\right]\right]\cdot \end{aligned} $$](/articles/aa/full_html/2021/12/aa41851-21/aa41851-21-eq64.gif)