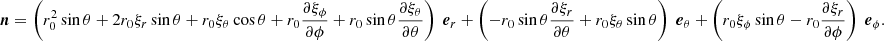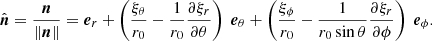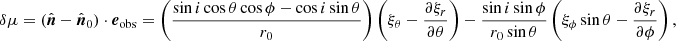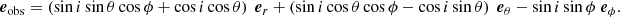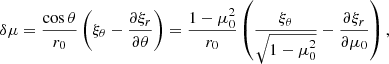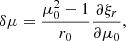| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 11 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202040264 | |
| Published online | 01 October 2021 | |
Modelling continuum intensity perturbations caused by solar acoustic oscillations
1
Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: kostogryz@mps.mpg.de
2
Institut für Astrophysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
3
Center for Space Science, NYUAD Institute, New York University Abu Dhabi, 129188 Abu Dhabi, UAE
Received:
30
December
2020
Accepted:
8
July
2021
Context. Helioseismology is the study of the Sun’s interior using observations of oscillations at the surface. It suffers from systematic errors, for instance a center-to-limb error in travel-time measurements. Understanding these errors requires an adequate understanding of the nontrivial relationship between wave displacement and helioseismic observables (intensity or velocity).
Aims. The wave displacement causes perturbations in the atmospheric thermodynamical quantities which, in turn, perturb the opacity, the optical depth, the source function, and the local ray geometry, thus affecting the emergent intensity. We aim to establish the most complete relationship achieved to date between the wave displacement and the emergent intensity perturbation by solving the radiative transfer problem in the perturbed atmosphere.
Methods. We derived an expression for the emergent intensity perturbation caused by acoustic oscillations at any point on the solar disk by applying a first-order perturbation theory. As input perturbations, we considerd adiabatic modes of oscillation of different degrees in a spherically-symmetric solar model. The background and the perturbed intensities are computed by solving the radiative transfer equation considering the main sources of opacity in the continuum (absorption and scattering).
Results. We find that for all modes, the perturbations to the thermodynamical quantities are not sufficient to model the intensity perturbations: the geometrical effects due to the wave displacement must always be taken into account as they lead to a difference in amplitude and a phase shift between temperature perturbations at the surface and emergent intensity perturbations. The closer to the limb, the greater the differences. For modes with eigenfrequencies around 3 mHz, we found that the radial and horizontal components of the wave displacement are important, in particular, for high-degree modes.
Conclusions. This work presents improvements for the computation of the intensity perturbations, in particular, for high-degree modes. Here, we explain the differences in intensity computations seen in earlier works. The phase shifts and amplitude differences between the temperature and intensity perturbations increase toward the limb. This should prove helpful when interpreting some of the systematic centre-to-limb effects observed in local helioseismology. The computations are fast (3 s for 2000 positions and one frequency for one core) and can be parallelised. This work can be extended to models of the line-of-sight velocity observable.
Key words: radiative transfer / Sun: helioseismology / Sun: oscillations / methods: numerical
© N. M. Kostogryz et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
Studies of local helioseismology are aimed at probing the subsurface structure and the dynamics of the solar convection zone. There are a variety of helioseismology techniques, such as ring diagram analysis, time-distance analysis, and helioseismic holography (see, e.g., the review by Gizon & Birch 2005). All of these techniques suffer from substantial, unexplained systematic effects. One such effect, namely, a systematic center-to-limb variation, was shown in helioseismic travel time measurements by Zhao et al. (2012). They applied time-distance analysis to different observables from the Helioseismic and Magnetic Imager (HMI, Scherrer et al. 2012) instrument: continuum intensity, line-core, and line-depth intensities, as well as Doppler velocity. For each observable, the authors observed strong variations of the travel times in the east-west direction as a function of longitude which cannot be caused by any physical flow. This centre-to-limb effect in travel time manifests itself differently across the range of HMI observables; for instance it is significantly larger in continuum intensity (∼10 s) than in the line-core intensity and Doppler velocity (∼2 s). Moreover, some observables, namely, line-core and line-depth intensities, show opposite trends. As this effect is not fully understood, Zhao et al. (2012) proposed to apply a simple correction to the north-south travel time differences by subtracting the component of the east-west travel time differences that is antisymmetric across the central meridian. This simple procedure has been used to infer the meridional flow from the corrected north-south travel times (Zhao et al. 2012; Gizon et al. 2020). In order to ascertain whether this procedure is valid, it is important to understand the physical and instrumental reasons behind this center-to-limb effect. In the present paper, we focus on the geometrical and radiative transfer effects that may affect the continuum intensity. Liang et al. (2018) and Gizon et al. (2020) noted, however, that the center-to-limb effect seen in HMI travel times varies strongly with time over the course of the mission; thus, an instrumental component (which we do not address here) is expected to play a part as well.
A better understanding of the physical reason for the center-to-limb effect requires a determination of the relationship between solar oscillations and helioseismic observables. In helioseismology, observables are often assumed to be directly proportional to temperature fluctuations or to the line-of-sight projection of the wave displacement at a fixed radius. A step forward in understanding the centre-to-limb effect is to compute the wave perturbations at different heights in the photosphere, where the maximum of solar intensity forms, depending on the position on the solar disk. Woodard et al. (2013) proposed that the phase of the p-mode eigenfunctions combined with the dependence of formation height of solar intensity with heliocentric angle may lead to a centre-to-limb effect in helioseismic observables. Baldner & Schou (2012) proposed that another contribution may be due to the interaction of p-modes with granulation, viewed from different lines of sight. However both authors stress that a full quantitative prediction of the centre-to-limb effect requires solving the radiative transfer problem in the atmosphere perturbed by p-modes.
Various approximations have been considered to compute the disk-integrated intensity perturbations caused by acoustic and gravity modes. The pioneering study from Dziembowski (1977) derived the expression of emergent flux perturbation and surface distortion while assuming that the emergent intensity perturbation caused by the oscillations is known. Further developments have been carried out to consider non-adiabatic and non-radial oscillations (e.g., Provost et al. 1988; Berthomieu & Provost 1990) but the emergent intensity was computed using the black-body or Eddington approximation, so neglecting the perturbations of the opacity induced by the oscillations. The assumption that the brightness fluctuations have the same phase and amplitudes as the temperature perturbation was commonly applied. However, further studies showed that this approximation is not correct. An important improvement in this direction was undertaken by Toutain & Gouttebroze (1993, hereafter TG93) who derived a more complete expression for emergent intensity that takes into account the opacity perturbations caused by solar oscillations of low-degree modes in a non-grey atmosphere. It was shown that the emergent intensity fluctuations are proportional not only to the temperature but also to density perturbations, and that both contributions are equally important. However, the opacity was computed only with the bound-free transitions of H−, which is the main source of opacity in the visible wavelength range – but not the only one, however.
Subsequently, Staude et al. (1995) and Zhugzhda et al. (1996, hereafter ZSB96) took into account various sources of opacity in the continuum, but neglected the geometrical term due to a compression or an expansion of the atmospheric layers due to the solar oscillations. They obtained a slightly different emergent intensity than TG93 and explained this difference by the sources of opacity neglected by TG93. We discuss this point further in Sect. 4.2. Table 1 shows a summary of the main differences between previous studies and our work.
Computation of intensity perturbation by different authors.
All the previous efforts concerning the computation of emergent intensity perturbations were done for the oscillations of the modes with harmonic degree, 0 ≤ l ≤ 2, as only these modes are visible in integrated light. However, the techniques of helioseismology applied to resolved images of the Sun take all modes into consideration, namely, from the pure radial (l = 0) mode for which the horizontal component of wave displacement (ξh) is zero, up to l = 1500 modes for which ξh and ξr are both important at a frequency of 3 mHz. Up to now, ξh was not considered at all in any of the previous studies (Table 1). In this paper, we establish the connection between the observables, namely, the continuum intensity and oscillations, by solving the radiative transfer equation in the perturbed solar atmosphere. We take into account the fact that the perturbation is caused by both the radial and the horizontal components of the wave displacement vector. This study will be extended to the modeling of the spectral line and Doppler velocity, and finally, to the interpretation of the travel time measurements in future works.
The structure of this paper is as follows. In the next section, we derive the expression for emergent intensity perturbations induced by oscillations of different modes taking into account the radial and horizontal components of the wave displacement. Section 3 describes the numerical methods used to compute the adiabatic oscillations and the opacity in the atmosphere. Section 4 validates numerically the theoretical derivation of emergent intensity perturbations and presents the results for the intensity fluctuations due to p-modes oscillations. Finally, we summarise our study and discuss the possible extensions.
2. Intensity perturbation
2.1. Coordinate systems
As the main purpose of our paper is to establish the link between the wave displacement of different oscillation modes and the emergent intensity perturbations, which are performed in different frames (i.e., inertial and observer), respectively, we first describe these frames and the connection between them. Figure 1 presents the coordinate systems. The Cartesian reference (inertial) frame is denoted by (ex, ey, ez) where ez is the rotation axis of the Sun. As the Sun rotates slowly, in this paper, we neglect its rotation. The spherical unit vectors in the reference frame are denoted by (er, eθ, eϕ) with polar and azimuthal angles θ and ϕ. The vector eobs points in the direction of the observer:
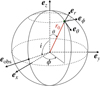 |
Fig. 1. Sketch showing the coordinate systems as well as the different angles used in this study. The reference Cartesian frame is denoted by (ex, ey, ez) and the spherical reference frame by (er, eθ, eϕ). The vector eobs is pointing towards the observer. |
where i is the inclination angle. For the Sun, the inclination angle varying from 83° to 97° during the year. These variations can be responsible for some systematic errors in the data analysis and must be taken into account (Liang et al. 2018). It is thus important to keep the inclination angle in the theoretical derivation of intensity perturbations. However, for the numerical tests in this paper, we use i = 90°.
2.2. Radiative transfer equation
The emergent intensity I(ν) at light frequency ν is computed at each point with coordinates (θ, ϕ) on the visible hemisphere. To solve the radiative transfer problem, we use a plane-parallel approximation, which is valid for most of the positions on the solar disk except very close to the limb. A comparison of intensity perturbations in plane-parallel and spherical geometry was done by Toutain et al. (1999) for low-degree modes. They showed that the differences between the two geometries become significant only very close to the limb (μ = 0.1 corresponding to latitudes higher than 84°). Therefore, we can assume that our computations are also valid for 0.1 ≤ μ ≤ 1.0.
The centre-to-limb distance on the disk, μ, is defined as:
where 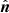 is the normal to the solar surface at centre-to-limb distance (r, θ, ϕ) and γ is the angle between
is the normal to the solar surface at centre-to-limb distance (r, θ, ϕ) and γ is the angle between 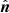 and eobs as shown on the sketch of Fig. 2. Here, we assume that the observer is far enough from the Sun, so that the emergent rays at different positions on the disk are always parallel to the direction to the observer.
and eobs as shown on the sketch of Fig. 2. Here, we assume that the observer is far enough from the Sun, so that the emergent rays at different positions on the disk are always parallel to the direction to the observer.
 |
Fig. 2. Sketch showing the geometrical quantities involved in solving the radiative transfer equation in the initial and perturbed atmospheres. We zoomed around the atmospheric layers located between rmin and rmax where the plane-parallel approximation is justified. Red lines and symbols show the quantities in the background model while the perturbed quantities are presented in blue. |
The computation of emergent intensity requires integrating the formal solution of the radiative transfer equation (RTE) at frequency ν along a ray in the direction of the observer over all the atmospheric layers:
Here, the differential of optical depth is defined as:
with τ = 0 at the top of atmosphere (see Fig. 2). The extinction coefficient α(ν, s) describes the total opacity along the ray and s is the length of the integration path.
The last term defined in Eq. (3) is the source function S(ν, s). Assuming local thermodynamic equilibrium which is an adequate approximation in the lower solar photosphere, S(ν, s) can be expressed as a Planck function:
where c is the speed of light and h and k are the Planck and Boltzmann constants.
To avoid solving the complete set of hydrodynamics equations at each point on the solar disk, we linearise all perturbed quantities around a background state, which is described by radial coordinate r0, background temperature T0, and pressure p0. The background intensity I0 is computed at μ0 defined as cosine of the angle between the observer and the reference normal vector 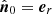 (Fig. 2),
(Fig. 2),
2.3. Perturbations of the path and of thermodynamical quantities of the atmospheric layers due to solar oscillations
In this subsection, we present the perturbed quantities of the model atmosphere. As the surface oscillates, the displacement, r, fluctuates not only in the radial but in all directions and it is written in term of the Lagrangian wave displacement vector ξ:
An equivalent decomposition can be written with an Eulerian displacement vector instead of its Lagrangian description. However, Toutain et al. (1999) found that the final expression of the emergent intensity in this framework is computationally challenging since two terms (the emission and the absorption) nearly cancel each out when their difference is actually a significant quantity. Therefore, we opted to use a Lagrangian formalism where an expression for the difference is directly obtained.
The wave displacement ξ changes the length of the integration path across the atmospheric layers s such that:
where the perturbation δs is:
We used the expression of eobs in the spherical basis given by Eq. (A.12) to compute the scalar product between ξ and eobs.
The oscillations also modify the thermodynamical quantities, T and p. We linearise them around the equilibrium state such that:
where δ indicates the Lagrangian perturbations of the different quantities. Using the adiabatic approximation, the Lagrangian perturbations of temperature δT and pressure δp are:
where Γ1 and Γ3 are the first and third adiabatic exponents (Eq. (3.18) in Christensen-Dalsgaard 2003). For a neutral and fully ionised hydrogen gas, Γ3 approaches 5/3 and decreases in partially ionised regions, such as those located below the optical surface where the continuum forms, or in the lower chromosphere. In this paper, we focus on the continuum formation region, thus, the constant Γ3 is not a good approximation, and we must take a depth-dependent adiabatic exponent from the background model (Sect. 3.1). We note, that in this paper, in presenting the results, we assume adiabaticity for simplicity, such that ξ is the input parameter, but the perturbations of all the thermodynamical quantities could also be obtained without this hypothesis by solving the linear nonadiabatic oscillation equations (e.g., Sect. 13.3 in Unno et al. 1989). In order to make a comparison with the observations, it is required for us to take non-adiabaticity into account.
2.4. Perturbations of the source function, optical depth, and centre-to-limb distance
The perturbations of the length of the integration path and of the thermodynamical quantities modify the source function, the opacity, and, thus, the optical depth and the centre-to-limb distance from their equilibrium values:
By perturbing Eq. (5) around the temperature, T0, we find that the perturbation to the source function is:
The opacity perturbation is caused by fluctuations in temperature and pressure
A similar expression could be written in terms of perturbations in temperature and density, as in TG93 and in ZSB96; however, Eq. (16) is more convenient here since the code we use for opacity calculation returns opacity as a function of temperature and pressure.
The perturbation to the optical depth is:
where the opacity perturbation is given by Eq. (16) and d(δs)/ds0 is obtained by taking the derivative of Eq. (10).
The fluctuation of the centre-to-limb distance, δμ, is given in Appendix A:
This expression is consistent with that derived by Reese et al. (2013) for rapidly rotating stars.
2.5. Radiative transfer in perturbed atmosphere
Using Eq. (14) in the definition of the emergent intensity (Eq. 3), we obtain the Lagrangian perturbation of the emergent intensity:
where
The perturbations of the source function, δS, optical depth, δτ, and incident angle δμ are given by Eqs. (15), (17), and (18), respectively. We note, that in this decomposition of the intensity perturbation, the terms δIτ and δIμ both contain contributions from ξ.
2.6. Comparison of intensity perturbation derivation with previous studies
In order to compare the intensity perturbation to other studies, namely, TG93 and ZSB96, it is more convenient to decompose δI into a thermodynamical term (δIth), which contains all the components with temperature and pressure perturbations along with a geometrical term with a wave displacement contribution (δIξ):
where
The term δIS (Eq. (20)) is the same for all three studies, namely: this paper, TG93, and ZSB96. The contribution of opacity to the emergent intensity perturbation, δIτ, α, is:
with δα/α0 defined in Eq (16).
The contribution from the geometrical term is:
As mentioned in the introduction, ZSB96 neglected the geometrical effect and took only perturbations of thermodynamical quantities as a source of intensity fluctuations. Applying an integration by part to Eq. (25), the value of δIth is then identical to that of Eq. (1) in ZSB96.
The last term in Eq. (23), δIξ, contains all the contributions attributed to ξ and describes purely geometrical effects that are induced by the deformations of the atmospheric layers as well as the centre-to-limb distances that are due to acoustic oscillations. Keeping only the radial displacement ξr in Eq. (26), while neglecting ξθ (ξθ ≪ ξr) leads to the definition of emergent intensity δIξr as in TG93. We note that, additionally, TG93 assumed that ξr/r does not vary with height, while we take the height dependence of ξr/r into account. Therefore, our expression of δIth + δIξr slightly differs from Eq. (4) in TG93, however, it agrees with the plane-parallel expression ΔI// derived later by Toutain et al. (1999), where the height-dependence of ξr/r has been taken into account.
3. Numerical inputs for intensity calculations
The acoustic oscillations of the Sun modify its stratification and, thus, the emergent intensity. The reference intensity is computed in a background model given in Sect. 3.1. We calculate the perturbations caused by a single acoustic mode whose computation is explained in Sect. 3.2. In order to determine equilibrium and perturbed intensities, we explain the computation of opacity and its derivatives in Sect. 3.3.
3.1. Background model
For the background quantities, we use the model S (Christensen-Dalsgaard et al. 1996) which uses the OPAL equation of state (Rogers et al. 1996) and OPAL opacities in the deep layers (Iglesias et al. 1992), and Kurucz et al. (1991) opacities in the atmosphere. This model is accurate in the solar interior, however, it is too simplified in the superadiabatic layer close to the surface. The model of convection is based on the mixing-length theory (Böhm-Vitense 1958), therefore simplifying the computation of the turbulent pressure which contributes significantly to the emitted radiation in this layer. Due to this simplification, the eigenfrequencies of the solar spectrum do not match the observed ones (surface effect, Rosenthal et al. 1999). A better agreement with observations can be obtained by replacing the background in the atmosphere by averaged quantities coming from numerical simulations (Ball et al. 2016) or by patching the eigenfunctions directly calculated from a 3D hydrodynamical simulations onto the one from a 1D model (Schou & Birch 2020). In order to avoid the difficulties due to the matching of all background quantities between model S and the atmospheric model, we used only the model S up to 500 km above the solar surface. This height is sufficient to model continuum intensity. However, the influence of the background model on the intensity should be studied before interpreting the observations.
3.2. p-mode eigenfunctions
The normal modes of acoustic oscillations are computed using the ADIPLS code (Christensen-Dalsgaard 2008). The displacement vector of non-radial modes in the reference frame is written as (see e.g., Christensen-Dalsgaard 2003):
where
Here, 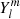 are the spherical harmonics of degree l and azimuthal order m. The code solves an eigenvalue problem in a 1D standard solar model (in this paper, model S, Christensen-Dalsgaard 2003) to determine the radial
are the spherical harmonics of degree l and azimuthal order m. The code solves an eigenvalue problem in a 1D standard solar model (in this paper, model S, Christensen-Dalsgaard 2003) to determine the radial 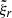 and horizontal
and horizontal 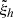 eigenfunctions associated to the eigenvalue ωnlm. The surface boundary condition is applied 500 km above the solar surface by supposing an isothermal atmosphere (Christensen-Dalsgaard 2008). For adiabatic oscillations without attenuation, the frequency and the eigenfunctions
eigenfunctions associated to the eigenvalue ωnlm. The surface boundary condition is applied 500 km above the solar surface by supposing an isothermal atmosphere (Christensen-Dalsgaard 2008). For adiabatic oscillations without attenuation, the frequency and the eigenfunctions 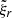 ,
, 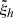 are real. The variations of a radial and a non-radial mode with height are shown on Fig. 3. For high-degree modes with eigenfrequency around 3 mHz, the horizontal part
are real. The variations of a radial and a non-radial mode with height are shown on Fig. 3. For high-degree modes with eigenfrequency around 3 mHz, the horizontal part 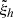 becomes comparable in amplitude to the radial part
becomes comparable in amplitude to the radial part 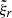 and justifies that we have kept the horizontal displacements ξθ and ξϕ in our derivation of intensity perturbations. Table 2 lists the exact values of eigenfrequencies (ωlmn/2π) considered in this paper which have been chosen around 3 mHz corresponding to the 5 min solar oscillations. For each mode, we give the ratio between the horizontal and radial displacements (
and justifies that we have kept the horizontal displacements ξθ and ξϕ in our derivation of intensity perturbations. Table 2 lists the exact values of eigenfrequencies (ωlmn/2π) considered in this paper which have been chosen around 3 mHz corresponding to the 5 min solar oscillations. For each mode, we give the ratio between the horizontal and radial displacements (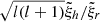 ) at the surface, showing the importance of the horizontal displacement for each of the modes (l, m, n) with frequency ωlmn/2π.
) at the surface, showing the importance of the horizontal displacement for each of the modes (l, m, n) with frequency ωlmn/2π.
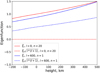 |
Fig. 3. Radial and horizontal eigenfunctions calculated for two normal modes, radial (l = 0, m = 0, n = 20) and non-radial (l = 600, m = 0, n = 1), normalised to the norm of the displacement |
Acoustic modes with their eigenfrequencies and ratio of horizontal-to-radial components at the surface (at solar radius of displacement computed using ADIPLS; Christensen-Dalsgaard 2008).
3.3. Opacity
To compute the optical depth along which the RTE is solved, the opacity as a function of depth should be known. We compute absorption and scattering coefficients using the Merged Parallelized Simplified ATLAS code (MPS-ATLAS, Witzke et al. 2021) developed from the original ATLAS code (Kurucz 1970). To compute continuum opacity we take into account the contributions from the bound-free and free-free transitions of H−, HI, 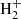 , the free-free transitions of He−, metal photoionisation, Rayleigh scattering on HI and HeI, and Thomson scattering on free electrons. Those are the main sources of opacity in the continuum.
, the free-free transitions of He−, metal photoionisation, Rayleigh scattering on HI and HeI, and Thomson scattering on free electrons. Those are the main sources of opacity in the continuum.
In addition to the opacity in the background model, we also need the derivatives (∂lnα0/∂lnp)|T0 and (∂lnα0/∂lnT)|p0 in order to compute the perturbation of opacity (Eq. (16)). Taking into account only the bound-free transition of H−, which is the main source of continuum opacity in the visible wavelength range, TG93 presented the analytic equation of the opacity derivative. However, as it shown in Kostogryz & Berdyugina (2015), the bound-free transition of H− is not the only contributor to the total opacity and the contribution from other sources of opacity can be larger than H− at some heights in the solar atmosphere. Adding other contributors to the continuum opacity makes the derivation of analytical expression intractable. Another approach is to compute the derivatives of opacity taking all possible contributors into account using the pre-computed opacity table on some temperature-pressure (or density) grid. However, this requires an interpolation in order to evaluate the derivatives at the temperature and pressure (density) of the model atmosphere. This approach was first applied by Staude et al. (1995) in the VALC3 model of atmosphere from (Vernazza et al. 1981). Later, ZSB96 showed that this approach leads to non-smooth derivatives and additionally applied the fitting and smoothing procedure as in OPFIT (Seaton et al. 1994). They showed that the intensity fluctuations caused by the same oscillation mode and at the same wavelength are slightly different from Staude et al. (1995), who did not use any smoothing. In order to avoid any interpolation, fitting, and smoothing schemes that may introduce additional uncertainties to the intensity perturbations, we computed our opacity table for the Model S grid of temperature and pressure using the MPS-ATLAS code. From the table, we numerically calculated the partial derivatives of the opacity.
4. Computation of intensity perturbation due to acoustic oscillations
In this section, in order to validate our algorithm, we compare the perturbed intensity computed using the algorithm described in Sect. 2 with the intensity computed in a perturbed atmosphere directly. Then we present the computation of intensity perturbation caused by p-mode oscillations of different harmonic degrees in the stratified model atmosphere. As we do not study the spectral dependence of intensity perturbation in this paper, all calculations were done at 500 nm. The radial orders of the considered oscillation modes are chosen such that the frequency of the oscillations is around 3 mHz (Table 2).
4.1. Comparison with direct computation
As mentioned in Sect. 2, we derive an emergent intensity in the oscillating atmosphere assuming first-order approximation for the perturbations caused by these oscillations. To validate this approximation, we compare the intensity in a perturbed model I(μ) to the sum of the intensity in an initial model plus a perturbation I0(μ0)+δI. For the test calculation, we assume that the perturbation is caused by the radial mode (l = 0, m = 0, n = 20).
We compute I0(μ0) with T0 and p0 at s0 coming from model S. We then perturb the model by adding δT, δp and δs coming from the eigenfunction of a radial mode multiplied by a factor of 104 and follow the same procedure to compute I(μ) in a model characterised by T = T0 + δT, p = p0 + δp, and s = s0 + δs. The last step is to compute the intensity perturbation δI due to δT, δp and δs by applying the first-order perturbation theory described in Sect. 2.5. We note that the factor we multiplied of the mode is only important for the direct computation as we need to detect the response of intensity on the ensuing perturbations. The factor should be large enough to be visible in the direct computation of intensity but not too large to make that of the first order invalid. Figure 4 shows that the perturbed intensity δI coincides with the difference of direct computations of intensity I(μ) in the perturbed atmosphere and the intensity I0(μ0) in the reference background model. Thus, this agreement between both approaches allows us to conclude that the first-order perturbation theory is applicable (even for the large perturbation used in this test) and the considered algorithm is correctly implemented.
 |
Fig. 4. Comparison of δI computed from the first-order perturbation theory to the difference of direct computation of emergent intensity in the initial and perturbed model atmospheres I0(μ0)−I(μ). Intensities are calculated from the centre to the limb for the radial mode l = 0, m = 0, n = 20. The red line on the panel in the left corner shows the positions on the solar disk in the observer frame where intensity perturbations are computed and which corresponds to i = 90°, ϕ = 0 and 0 ≤ θ < 90°. The intensity perturbation is measured in [erg cm−2 s−1 cm−1 sr−1]. |
4.2. Comparison of intensity computation in other studies
The intensity perturbations caused by radial p-modes were studied by TG93 and ZSB96 but showed slightly different results. On the one hand, ZSB96 claimed that the inconsistency happened because TG93 considered only absorption by H− as source of opacity. On the other hand, ZSB96 considered only perturbations of the thermodynamical quantities and neglected the geometrical effect. Here, we investigate these differences and we thus compute the intensity perturbations (δIth + δIξr) by taking the main sources of opacities in the continuum into account (Sect. 3.3), δIth as in ZSB96, and δIH−, with only H− contribution to the opacity as in TG93. In all cases, we compute opacity tables and their derivatives numerically and do not use the analytic expressions from TG93. We select the same radial mode as in TG93 and ZSB96 and solve RTE at the same wavelength, however, our models of atmosphere are different so we cannot compare directly our results with these papers. Nevertheless, our analysis will help us to understand the differences between the different simplifications and which terms are important when evaluating intensity perturbations.
Figure 5 shows the perturbed emergent intensity divided by the reference intensity (δI/I0) at different value of μ, normalised by the temperature variations (δT/T0) at the optical surface where τ = 1. The first-order approach is linear, so the amplitude of the mode is cancelled out by such a normalisation. As it is not trivial to get the amplitude of each mode, such a normalisation allows us to avoid this difficulty. Thus, all the figures below present the normalised emergent intensity.
 |
Fig. 5. Normalised emergent intensity perturbation caused by the radial mode (l = 0, m = 0, n = 20). The normalisation factor δT/T0 is taken at τ0 = 1. The intensity perturbations are computed at the same points on the solar disk as in Fig. 4, i.e., i = 90°, ϕ = 0 and 0 ≤ θ < 90° (see observer view in the lower left corner). |
Moreover, this normalisation allows us to understand whether approximating the continuum intensity observable by the temperature perturbation at the optical surface is good enough. If δT/T0 is a good approximation of δI/I0, then we should see all three normalised intensity curves as a horizontal line at, for instance, [δI/I0]/[δT/T0] = 4 for the black-body approximation with no variation on μ; however, this is clearly not the case (Fig. 5). The largest difference is between δI and δIth which comes from neglecting the geometrical terms in the latter. This is in contradiction with the intuition of ZSB96 who assumed that the surface distortion was not significantly affecting the emergent intensity for low-degree modes. To further analyse the contribution of different opacity sources to the emergent intensity calculation, we compare the intensity δIH− with δI, as both of them contain the geometrical terms. The two curves are very similar with minor deviations along the disk showing that bound-free and free-free transitions of H− are the main but not the only sources of opacity that contribute to the emergent intensity computation. Therefore, neglecting other sources of continuum opacity at 500 nm have little influence of the continuum intensity and could not explain the divergence between TG93 and ZSB96, which arises due to the geometrical effects.
4.3. Comparison of the different contributions to the perturbation of emergent intensity.
Perturbations of emergent intensity caused by oscillation modes are coming from three contributors describing the radiative transfer in the solar atmosphere (Eqs. (20)–(22)). In this subsection, we study how each of these components affects the emergent intensity perturbation caused by a radial mode as well as an intermediate degree mode (l = 100) which is observed with spatially resolved instruments (Table 2). In Fig. 6, we show that the emergent intensity δI is a balance between δIS and δIτ for the l = 0 mode, while for the l = 100 mode in addition to the δIS and the δIτ components, the contribution from δIμ becomes significant especially close to the limb. The amplitudes of δIS and δIτ are similar at the disk centre (μ = 1), with opposite sign, and decrease towards the limb (μ = 0), where most of the radiation comes from the higher layers with lower temperature and pressure. Both components thus decrease and, as the optical depth drops exponentially, the value of δIτ decreases faster than δIS. The negative sign of δIτ is because 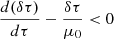 in Eq. (21). For the l = 100 mode the horizontal displacement contributes to a phase shift of δIτ (Eq. (10)) with respect to δIS, especially close to the limb. Thus, the intensity perturbation due to the opacity and source function perturbations almost fully compensate for each other with regard to the radial mode and close to the disc centre for the moderate degree modes; however, these two components are phase-shifted for observation close to the limb.
in Eq. (21). For the l = 100 mode the horizontal displacement contributes to a phase shift of δIτ (Eq. (10)) with respect to δIS, especially close to the limb. Thus, the intensity perturbation due to the opacity and source function perturbations almost fully compensate for each other with regard to the radial mode and close to the disc centre for the moderate degree modes; however, these two components are phase-shifted for observation close to the limb.
 |
Fig. 6. Normalised intensity perturbation and its contributions caused by the radial (l = 0, m = 0, n = 20) and moderate degree (l = 100, m = 0, n = 6) modes. The normalisation factor δT/T0 is taken at τ0 = 1. The intensity perturbations are computed at the same points on the solar disk as in Fig. 4, i.e., i = 90°, ϕ = 0 and 0 ≤ θ < 90° (see observer view on the upper, or lower left corner). |
An additional phase shift comes from δIμ, which becomes more and more important as the degree of the mode increases and is zero for the radial modes. As the emergent intensity combine all the terms, δI is shifted with respect to δIS, and thus δT. Therefore, this effect can lead to certain systematic errors in intensity maps analysis in helioseismology when the radiative transfer is neglected.
4.4. Importance of the geometrical terms with horizontal displacement contribution for intensity computation
In Sect. 4.2, we show the importance of the geometrical term to compute the emergent intensity for a radial mode. Here, we analyse this effect for the modes where an extra contribution comes from the horizontal displacement. We selected two modes, one at l = 100 and one at l = 600 for which both radial and horizontal displacements are significant (see the ratio of the horizontal-to-radial displacements in Table 2). Figure 7 shows the normalised intensity perturbations with different contributors included (i.e., δI, δIth + δIξr, and δIth) for different centre-to-limb distances centered around θ = 30o and θ = 60o (corresponding to μ0 = 0.86 and μ0 = 0.5, respectively).
 |
Fig. 7. Normalised intensity perturbations caused by l = 100 (top) and l = 600 (bottom) modes at frequencies around 3 mHz at different centre-to-limb distances: μ0 around 0.85 (right panels) and around 0.5 (left panels). The observer frame showing where intensity perturbations are calculated is shown at the bottom left corners of the upper panels. |
As for the radial mode, the differences between δI and δIth are important in terms of phase and amplitude, thus the thermodynamical quantities are not sufficient to describe the emergent intensity accurately.
Moreover, we compare δI to δIth + δIξr to see the importance of the horizontal displacement ξθ which was not taken into account in previous studies. As ξr and ξθ are not in phase, it creates an additional phase shift and modifies the amplitude of the observed emergent intensity. The differences increase towards the limb but the importance of the horizontal term is already visible at a latitude of 30° (μ = 0.86). From those examples, we can ascertain that the higher the degree of the mode, the higher the differences between δI and δIth + δIξr.
5. Summary and discussion
Here, we provided a detailed computation of the relationship between the eigenfunctions of solar p modes and continuum intensity, which is one of the helioseismic observables. We derived an analytic expression for the emergent intensity perturbations caused by p-mode oscillations. These oscillations perturb the thermodynamical quantities in the solar atmosphere, as well as the integration path across the atmospheric layers and the position on the disk from which the radiation reaches the observer.
The thermodynamical component contains only the perturbations in temperature and pressure in the atmosphere caused by the oscillations. It leads to perturbations of the source function and opacity in the radiative transfer equation. For the opacity, we considered absorption coefficients caused by bound-free and free-free transitions of different species, metal photoionisation, Rayleigh scattering on HI and HeI, and Thomson scattering on free electrons. We showed that to accurately compute emergent intensity, all sources of opacity should be taken into account and not only the bound-free transition of H− that is the main contributor to the continuum opacity in the visible spectral range.
The geometrical component includes the perturbation to the geometrical ray path (including its direction) and the resulting perturbation to the optical depth. In doing so, we took into account both the radial and the horizontal displacements of the modes. The horizontal displacement has a negligible effect for the low degree modes around 3 mHz, however, it cannot be neglected for low-frequency modes and high-degree modes for which the ratio between horizontal and radial displacements is significant. This may lead to amplitude changes and phase shifts between the temperature and intensity perturbations, which increase toward the limb.
The computation of the continuum intensity at one wavelength takes only 3 s for 2000 points along centre-to-limb distance, which is not an obstacle for global and local helioseismology applications. We presented computations in the continuum at 500 nm, however, there is no limitation on the choice of wavelength. In future works, we will study the emergent intensity perturbations along a spectral line in order to synthesis Doppler velocity observations.
Acknowledgments
We are thankful to Veronika Witzke for providing us with the MPS-ATLAS code for opacity calculation, Vincent Böning for providing us with the ADIPLS eigenfunctions, as well as Aaron Birch, Jesper Schou and Alexander Shapiro for useful discussions. This work was supported in part by a Max Planck Society grant “Preparations for PLATO Science” and German Aerospace Center (DLR) grants “PLATO Data Center” 50OO1501 and 50OP1902. LG and DF acknowledge partial support from ERC Synergy Grant WHOLE SUN 810218 and Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through SFB 1456/432680300 Mathematics of Experiment, project C04.
References
- Baldner, C. S., & Schou, J. 2012, ApJ, 760, L1 [Google Scholar]
- Ball, W. H., Beeck, B., Cameron, R. H., & Gizon, L. 2016, A&A, 592, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berthomieu, G., & Provost, J. 1990, A&A, 227, 563 [NASA ADS] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Christensen-Dalsgaard, J. 2003, Lecture Notes on Stellar Oscillations (Denmark: University of Aarhus) [Google Scholar]
- Christensen-Dalsgaard, J. 2008, Astrophys. Space Sci., 316, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Däppen, W., Ajukov, S. V., et al. 1996, Science, 272, 1286 [CrossRef] [Google Scholar]
- Dziembowski, W. 1977, Acta Actron., 27, 203 [NASA ADS] [Google Scholar]
- Gizon, L., & Birch, A. C. 2005, Living Rev. Sol. Phys., 2, 6 [NASA ADS] [Google Scholar]
- Gizon, L., Cameron, R. H., Pourabdian, M., et al. 2020, Science, 368, 1469 [Google Scholar]
- Heynderickx, D., Waelkens, C., & Smeyers, P. 1994, A&AS, 105, 447 [NASA ADS] [Google Scholar]
- Iglesias, C. A., Rogers, F. J., & Wilson, B. G. 1992, ApJ, 397, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Kostogryz, N. M., & Berdyugina, S. V. 2015, A&A, 575, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 1970, SAO Spec. Rep., 309, 291 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1991, in NATO ASI Ser. C, eds. L. Crivellari, I. Hubeny, & D. G. Hummer, 341, 441 [Google Scholar]
- Liang, Z.-C., Gizon, L., Birch, A. C., Duvall, T. L., & Rajaguru, S. P. 2018, A&A, 619, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Provost, J., & Berthomieu, G. 1988, in Seismology of the Sun and Sun-Like Stars, ed. E. J. Rolfe, ESA SP, 286, 387 [NASA ADS] [Google Scholar]
- Reese, D. R., Prat, V., Barban, C., van ’t Veer-Menneret, C., & MacGregor, K. B. 2013, A&A, 550, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenthal, C. S., Christensen-Dalsgaard, J., Nordlund, Å., Stein, R. F., & Trampedach, R. 1999, A&A, 351, 689 [NASA ADS] [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schou, J., & Birch, A. C. 2020, A&A, 638, A51 [CrossRef] [EDP Sciences] [Google Scholar]
- Seaton, M. J., Yan, Y., Mihalas, D., & Pradhan, A. K. 1994, MNRAS, 266, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Staude, J., Zhugzhda, Y. D., & Dzhalilov, N. S. 1995, in Helio- and Astero-Seismology from the Earth andSpace, eds. R. K. Ulrich, E. J. Rhodes, & W. Dappen, ASP Conf. Ser., 76, 338 [NASA ADS] [Google Scholar]
- Toutain, T., & Gouttebroze, P. 1993, A&A, 268, 309 [NASA ADS] [Google Scholar]
- Toutain, T., Berthomieu, G., & Provost, J. 1999, A&A, 344, 188 [NASA ADS] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (Japan: University of Tokyo Press) [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [Google Scholar]
- Witzke, V., Shapiro, A. I., Cernetic, M., et al. 2021, A&A, 653, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woodard, M., Schou, J., Birch, A. C., & Larson, T. P. 2013, Sol. Phys., 287, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J., Nagashima, K., Bogart, R. S., Kosovichev, A. G., & Duvall, T. L. 2012, ApJ, 749, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Zhugzhda, Y. D., Staude, J., & Bartling, G. 1996, A&A, 305, L33 [Google Scholar]
Appendix A: Derivation of δμ
In this appendix, we derive the analytic expression for the perturbation of the angle of incidence δμ = μ − μ0.
The position vector of a point in the perturbed model is;
where r0 is the unperturbed position vector and r0 is the solar radius in the background model. The perturbation δμ is then given by;
where 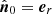 and
and 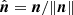 where n is the normal to the perturbed surface element defined as;
where n is the normal to the perturbed surface element defined as;
The term ∂r/∂θ can be computed as follows;
where we use the derivative of the unit vectors in spherical coordinates:
Similarly, we can derive the expression for 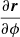 :
:
where we apply the following:
Using Eq. (A.4), Eq. (A.6), and Eq. (A.3), we obtain:
Neglecting the second-order terms in Eq. (A.8) the expression for the normal vector becomes
We normalise the normal vector and take only the first-order terms into account:
Thus, it follows that:
where we used
This expression for δμ can be evaluated for special cases found in the literature. For example, in choosing i = 90° and ϕ = 0, we have μ0 = sin θ and
which is the expression derived by Heynderickx et al. (1994). If we further assume ξθ ≪ ξr, then δμ becomes
as in TG93.
All Tables
Acoustic modes with their eigenfrequencies and ratio of horizontal-to-radial components at the surface (at solar radius of displacement computed using ADIPLS; Christensen-Dalsgaard 2008).
All Figures
 |
Fig. 1. Sketch showing the coordinate systems as well as the different angles used in this study. The reference Cartesian frame is denoted by (ex, ey, ez) and the spherical reference frame by (er, eθ, eϕ). The vector eobs is pointing towards the observer. |
| In the text | |
 |
Fig. 2. Sketch showing the geometrical quantities involved in solving the radiative transfer equation in the initial and perturbed atmospheres. We zoomed around the atmospheric layers located between rmin and rmax where the plane-parallel approximation is justified. Red lines and symbols show the quantities in the background model while the perturbed quantities are presented in blue. |
| In the text | |
 |
Fig. 3. Radial and horizontal eigenfunctions calculated for two normal modes, radial (l = 0, m = 0, n = 20) and non-radial (l = 600, m = 0, n = 1), normalised to the norm of the displacement |
| In the text | |
 |
Fig. 4. Comparison of δI computed from the first-order perturbation theory to the difference of direct computation of emergent intensity in the initial and perturbed model atmospheres I0(μ0)−I(μ). Intensities are calculated from the centre to the limb for the radial mode l = 0, m = 0, n = 20. The red line on the panel in the left corner shows the positions on the solar disk in the observer frame where intensity perturbations are computed and which corresponds to i = 90°, ϕ = 0 and 0 ≤ θ < 90°. The intensity perturbation is measured in [erg cm−2 s−1 cm−1 sr−1]. |
| In the text | |
 |
Fig. 5. Normalised emergent intensity perturbation caused by the radial mode (l = 0, m = 0, n = 20). The normalisation factor δT/T0 is taken at τ0 = 1. The intensity perturbations are computed at the same points on the solar disk as in Fig. 4, i.e., i = 90°, ϕ = 0 and 0 ≤ θ < 90° (see observer view in the lower left corner). |
| In the text | |
 |
Fig. 6. Normalised intensity perturbation and its contributions caused by the radial (l = 0, m = 0, n = 20) and moderate degree (l = 100, m = 0, n = 6) modes. The normalisation factor δT/T0 is taken at τ0 = 1. The intensity perturbations are computed at the same points on the solar disk as in Fig. 4, i.e., i = 90°, ϕ = 0 and 0 ≤ θ < 90° (see observer view on the upper, or lower left corner). |
| In the text | |
 |
Fig. 7. Normalised intensity perturbations caused by l = 100 (top) and l = 600 (bottom) modes at frequencies around 3 mHz at different centre-to-limb distances: μ0 around 0.85 (right panels) and around 0.5 (left panels). The observer frame showing where intensity perturbations are calculated is shown at the bottom left corners of the upper panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



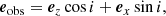
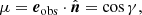
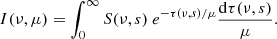
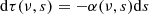
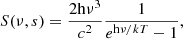
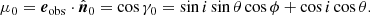
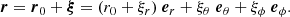
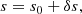
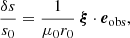
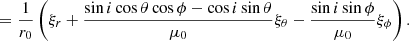
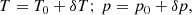
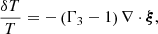
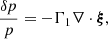
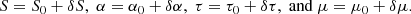
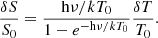
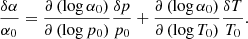
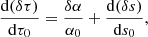
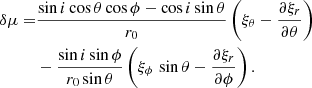
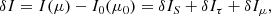
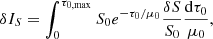
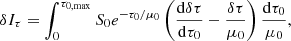
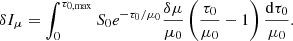
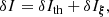
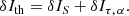
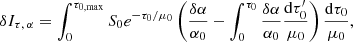
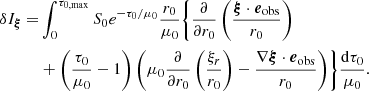
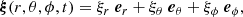
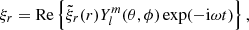
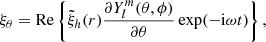
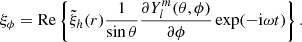
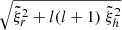
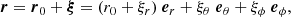
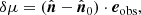
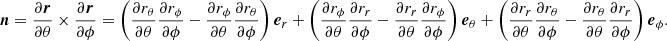
![$$ \begin{aligned} \frac{\partial \boldsymbol{r}}{\partial \theta }&= \frac{\partial }{\partial \theta } \left[ (r_0 + \xi _r) \ \boldsymbol{e}_r \right] + \frac{\partial }{\partial \theta } ( \xi _\theta \ \boldsymbol{e}_\theta ) + \frac{\partial }{\partial \theta } ( \xi _\phi \ \boldsymbol{e}_\phi ) \nonumber \\&= (r_0 + \xi _r) \ \frac{\partial \boldsymbol{e}_r}{\partial \theta } + \frac{\partial \xi _r}{\partial \theta } \ \boldsymbol{e}_r + \xi _\theta \ \frac{\partial \boldsymbol{e}_\theta }{\partial \theta } + \frac{\partial \xi _\theta }{\partial \theta } \ \boldsymbol{e}_\theta + \xi _\phi \ \frac{\partial \boldsymbol{e}_\phi }{\partial \theta } + \frac{\partial \xi _\phi }{\partial \theta } \ \boldsymbol{e}_\phi \nonumber \\&= \left(\frac{\partial \xi _r}{\partial \theta } - \xi _\theta \right) \ \boldsymbol{e}_r + \left(r_0 + \xi _r+\frac{\partial \xi _\theta }{\partial \theta }\right) \ \boldsymbol{e}_\theta + \frac{\partial \xi _\phi }{\partial \theta } \ \boldsymbol{e}_\phi , \end{aligned} $$](/articles/aa/full_html/2021/10/aa40264-20/aa40264-20-eq51.gif)
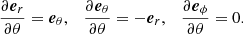
![$$ \begin{aligned} \frac{\partial \boldsymbol{r}}{\partial \phi }&= \frac{\partial }{\partial \phi } \left[ (r_0 + \xi _r) \ \boldsymbol{e}_r \right] + \frac{\partial }{\partial \phi } ( \xi _\theta \ \boldsymbol{e}_\theta ) + \frac{\partial }{\partial \phi } ( \xi _\phi \ \boldsymbol{e}_\phi ) \nonumber \\&= (r_0 + \xi _r)\frac{\partial \boldsymbol{e}_r}{\partial \phi } + \boldsymbol{e}_r \frac{\partial \xi _r}{\partial \phi } + \xi _\theta \frac{\partial \boldsymbol{e}_\theta }{\partial \phi } + \boldsymbol{e}_\theta \frac{\partial \xi _\theta }{\partial \phi } + \xi _\phi \frac{\partial \boldsymbol{e}_\phi }{\partial \phi } + \boldsymbol{e}_\phi \frac{\partial \xi _\phi }{\partial \phi } \nonumber \\&= \left(\frac{\partial \xi _r}{\partial \phi } - \xi _\phi \sin \theta \right) \ \boldsymbol{e}_r + \left(\frac{\partial \xi _\theta }{\partial \phi } - \xi _\phi \cos \theta \right) \ \boldsymbol{e}_\theta + \left((r_0 +\xi _r) \sin \theta + \xi _\theta \cos \theta +\frac{\partial \xi _\phi }{\partial \phi }\right) \ \boldsymbol{e}_\phi , \end{aligned} $$](/articles/aa/full_html/2021/10/aa40264-20/aa40264-20-eq54.gif)
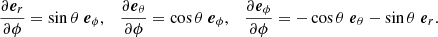
![$$ \begin{aligned} \boldsymbol{n} =&\left(r_0+\xi _r+\frac{\partial \xi _\theta }{\partial \theta } \right) \left( (r_0 +\xi _r)\sin \theta + \xi _\theta \cos \theta + \frac{\partial \xi _\phi }{\partial \phi } \right)\ \boldsymbol{e}_r \nonumber \\&+ \left[\frac{\partial \xi _\phi }{\partial \theta } \left( \frac{\partial \xi _r}{\partial \phi } - \xi _\phi \sin \theta \right) - \left(\frac{\partial \xi _r}{\partial \theta }-\xi _\theta \right) \left( (r_0+\xi _r)\sin \theta +\xi _\theta \cos \theta +\frac{\partial \xi _\phi }{\partial \phi } \right) \right] \ \boldsymbol{e}_\theta \nonumber \\&+ \left[ \left( \frac{\partial \xi _r}{\partial \theta }-\xi _\theta \right) \left( \frac{\partial \xi _\theta }{\partial \phi }-\xi _\phi \cos \theta \right) - \left(r_0+\xi _r+\frac{\partial \xi _\theta }{\partial \theta }\right) \left(\frac{\partial \xi _r}{\partial \phi } - \xi _\phi \sin \theta \right)\right] \ \boldsymbol{e}_\phi . \end{aligned} $$](/articles/aa/full_html/2021/10/aa40264-20/aa40264-20-eq56.gif)