| Issue |
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202140944 | |
| Published online | 14 December 2021 | |
Letter to the Editor
Solar Orbiter observations of the structure of reconnection outflow layers in the solar wind
1
Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
e-mail: c.owen@ucl.ac.uk
2
Now at BBC Research & Development, Wood Lane, London W12 7TQ, UK
3
INAF-Istituto di Astrofisica e Planetologia Spaziali, Via Fosso del Cavaliere 100, 00133 Roma, Italy
4
Southwest Research Institute, 6220 Culebra Road, San Antonio, TX 78238, USA
5
Institut de Recherche en Astrophysique et Planétologie, 9, Avenue du Colonel Roche, B.P. 4346, 31028 Toulouse Cedex 4, France
6
Laboratoire de Physique des Plasmas, Ecole Polytechnique, Palaiseau, France
7
Space Science Center, University of New Hampshire, Morse Hall, Durham, NH 03824, USA
8
Planetek Italia S.r.l., Via Massaua, 12, 70132 Bari, BA, Italy
9
Northumbria University, Department of Mathematics, Physics and Electrical Engineering, Newcastle upon Tyne NE1 8QH, UK
10
Space and Atmospheric Physics, The Blackett Laboratory, Imperial College London, London SW7 2AZ, UK
Received:
30
March
2021
Accepted:
26
September
2021
We briefly review an existing model of the structure of reconnection layers which predicts that several more distinct layers, in the form of contact discontinuities, rotational Alfvèn waves, or slow shocks, should be identifiable in solar wind reconnection events than are typically reported in studies of reconnection outflows associated with bifurcated current sheets. We re-examine this notion and recast the identification of such layers in terms of the changes associated with the boundaries of both the ion and electron outflows from the reconnection current layers. We then present a case study using Solar Orbiter MAG and SWA data, which provides evidence consistent with this picture of extended multiple layers around the bifurcated current sheet. A full confirmation of this picture requires more detailed examination of the particle distributions in this and other events. However, we believe this concept is a valuable framework for considering the nature of reconnection layers in the solar wind.
Key words: magnetic reconnection / solar wind / Sun: heliosphere / plasmas / magnetic fields
© ESO 2021
1. Introduction
The current prevailing framework for interpretation of signatures of reconnection in the solar wind is largely based on the observations reported by Gosling et al. (2005), in which a bifurcated current sheet bounds the reconnection exhaust. This framework has been examined and amplified by a number of studies since it was first published, including the works of Phan et al. (2006, 2009, 2010, 2020), Eriksson et al. (2009), Gosling et al. (2006, 2007a,b), Huttunen et al. (2007), Mistry et al. (2015, 2017), Lavraud et al. (2009).
However, there are other models of reconnection outflow structure that suggest that the outflow region may be more complex than this simple bifurcated current sheet model assumes. In particular, the original Petschek (1964) model of reconnection has been generalised over time to include situations where the inflow conditions are asymmetric. For example, Semenov et al. (1983) presented a two-dimensional model of reconnection in which the inflow magnetic field strength or plasma density (or both) are asymmetric. This concept is further developed in Heyn et al. (1985), who devised a generalised structure for the reconnection outflow region that is dependent on the ratios of the inflow parameters on either side of the structure. In this model, there are four possible discontinuity types that can form within the overall reconnection outflow structure: (1) the contact discontinuity, C, inside the boundary layers separates plasma flow from one side of the structure from the other; (2) two large amplitude Alfvèn rotational waves, A and 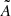 , may then form on either side, which act to deflect and accelerate the inflow plasma; and (3) a pair of slow shocks (S− and
, may then form on either side, which act to deflect and accelerate the inflow plasma; and (3) a pair of slow shocks (S− and 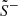 ) or (4) rarefaction waves (R− and
) or (4) rarefaction waves (R− and 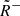 ) may also form on either side of the structure, depending on the respective inflow conditions. The general configuration seen along a cut through these layers can then be represented by a shorthand: AS−(R−)
) may also form on either side of the structure, depending on the respective inflow conditions. The general configuration seen along a cut through these layers can then be represented by a shorthand: AS−(R−)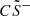 (
(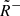 )
)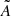 . In this notation, the brackets indicate that the slow shock wave can be replaced by the slow expansion fan in the very asymmetric case. For the Petschek (1964) case, which has symmetrical inflow conditions, the Alfvèn wave and the slow shock on each side of the reconnection event merge into a single, switch-off slow shock. However, in the non-symmetrical inflow case, the model suggests these two waves separate into distinct parts. For the strictly 2D case, with no transverse guide field or transverse plasma flows, one of the Alfvèn discontinuities also disappears. In this case, the side on which the remaining rotation Alfvèn wave forms depends on the ratio of the inflow Alfvèn speeds from either side. The presence of multiple sub-layers in the magnetohydrodynamic models and the existence of numerous possible configurations has also been noted by Lin & Lee (1993), and the merging of layers by Teh et al. (2009).
. In this notation, the brackets indicate that the slow shock wave can be replaced by the slow expansion fan in the very asymmetric case. For the Petschek (1964) case, which has symmetrical inflow conditions, the Alfvèn wave and the slow shock on each side of the reconnection event merge into a single, switch-off slow shock. However, in the non-symmetrical inflow case, the model suggests these two waves separate into distinct parts. For the strictly 2D case, with no transverse guide field or transverse plasma flows, one of the Alfvèn discontinuities also disappears. In this case, the side on which the remaining rotation Alfvèn wave forms depends on the ratio of the inflow Alfvèn speeds from either side. The presence of multiple sub-layers in the magnetohydrodynamic models and the existence of numerous possible configurations has also been noted by Lin & Lee (1993), and the merging of layers by Teh et al. (2009).
Overall, models of this type suggest that there is potentially much more complexity to the structure of the reconnection outflow layers than is seen in the classic Petschek (1964) and Levy et al. (1964) models of reconnection that predict the presence of exhaust regions bounded by rotational discontinuities (RD) and slow shocks, and are characterised by bifurcated current sheets, as summarised by Gosling et al. (2005). It may thus be productive to seek to test this and related hypotheses with new data sets that may be better able to identify these layers. In this Letter, we revisit this general concept for multi-layered outflow regions. In Sect. 2, we first present a revised concept for the structure of a reconnection exhaust region based on results from current sheet acceleration models (e.g. Owen & Cowley 1987a,b, and references therein), which more readily capture the expected field and particle signatures and their interdependence. In Sect. 3, we present a case study of Solar Orbiter MAG and SWA data that illustrates how these structures may manifest themselves in observations. Finally, in Sect. 4, we discuss our results and present our conclusions.
2. Revised concept for the exhaust region
In Fig. 1, we present a sketch which illustrates our alternate concept for the possible boundaries that in this framework would be present within a generalised reconnection event. Figure 1 also shows a graphical representation of some parameters that are relevant to the analysis of candidate events. In this figure, the original current sheet is shown by the horizontal green dashed line. The blue shaded areas on either side of the original current sheet represent the regions that would contain the outflow ions (travelling at speeds VO1 and VO2 on either side of the current sheet) and the red shaded areas represent regions into which the outflow electrons expand. This region extends further from the original current sheet than the region occupied by ions as the electrons are able to stream away from the current sheet along reconnected field lines much faster than the ions. In principle, the fastest moving electrons may form a layer which extends out as far as the most recently reconnected field line, or the magnetic separatrix, which in this figure are represented by the thick red arrowed lines. The angles between the separatrix and the original current sheet are defined as θ1 and θ2 and between the ion outflow boundary and the original current sheet ϕ1 and ϕ2 and will depend on the exterior ion flows on either side of the event, defined as Vin1 and Vin2 with densities of n1 and n2 as well as the exterior magnetic field strength and direction.
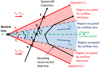 |
Fig. 1. Sketch of possible boundaries associated with a magnetic reconnection exhaust outflow in the solar wind. Here, the upstream magnetic field strengths define the relative angles angle, θ1 and θ2, between the original current sheet and the separatrices (the thick red arrows bounding the red shaded area – the region occupied by the outflow electrons). The blue shaded area shows the region occupied by the outflow ions. These regions on either side of the original current sheet (green dashed line) contain the reconnection outflows (VO1 and VO2). The boundaries of these regions (indicated by the blue dashed lines) form different angles with the original current sheet (ϕ1 ≠ ϕ2). The magnetic field can potentially rotate across each of the boundaries (as represented by the black arrowed line) due to the gradient in plasma properties across the boundary leading to a diamagnetic depression of the field strength. If a spacecraft were to pass through the region, for example along a trajectory represented by the black arrow, it could encounter up to five distinct boundaries (at A, B, C, D, and E), which encompass the four layers. The relative time spent in each of these regions is dependent on the angle between the spacecraft trajectory and the original current sheet, γ, as well as the angles subtended by the separatrices and plasma boundaries. On either side of the event, we have undisturbed external ion inflow velocity, Vin1 and Vin2, with densities of n1 and n2. |
In principle, the confinement of the outflow particles implies there will be a gradient in the plasma properties at each of the boundaries between the regions defined above. If the outflow plasma is heated with respect to the inflow by the reconnection process, then these gradients create a diamagnetic current sheet co-located at the boundary, across which the magnetic field changes strength or rotates, as illustrated by the rotation of the black arrowed line representing the recoiling B-field in the figure. An example spacecraft trajectory through such a reconnection-associated structure is represented by the straight black arrow (in the solar wind context this direction should be approximately similar to the -R direction in RTN co-ordinates as the structure should be carried past the spacecraft with the solar wind velocity). The angle between the spacecraft trajectory and the plane of the original current sheet is given by the parameter γ. Given the above arguments, a spacecraft travelling along such a trajectory could potentially see current sheets at locations A, B, C, D, and E, depending on the field and plasma conditions within and around the structure and/or the nature of the gradients in the plasma properties. A current sheet at location C may be detected if the original current sheet is not completely eliminated by the diamagnetic effects of the heated outflow ions in the reconnection process and a weak gradient persists. We expect that there will be current sheets at locations B and D if the heated ion outflows do have a diamagnetic effect, which may be the cause of the bifurcation of the reconnected current sheet particularly if these act to also reduce any rotation around location C. Current sheets may also appear at locations A and E if the electron outflows also drive a diamagnetic effect.
Figure 2 shows some idealised examples of field and plasma flow variations observed during crossings of possible reconnection structures consistent with some or all of the current sheets identified in Fig. 1. Panel i shows the example where all five boundaries form current sheets and, thus, magnetic field rotations are visible at all, and there are differences between the two outflows. In this scenario, both the ion outflow and the electron outflow show a diamagnetic effect and the original current sheet is still detectable. Panel ii shows the case which is consistent with the typical Gosling sketch of reconnection in the solar wind. In this panel, we show the case in which the original current sheet has been completely destroyed (hence, no rotation at location C) and the electrons are considered to have little or no diamagnetic effect on the magnetic field (at A or E). Also, in this case, there is a single outflow speed, VO1 = VO2.
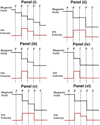 |
Fig. 2. Representative examples of reconnection outflows and current sheet structure. In each panel, the black trace represents the variation of the transverse component of the magnetic field to the current sheet, while the red trace represents the variation in ion flow velocity. Panel i: result if all possible transitions (current sheets and gradients in ion flows) in the model occur. Panel ii: result which is in keeping with the Gosling model (only rotations at B and C and equal outflows). Panel iii: example where there are rotations are seen at locations B, C, and D but only an outflow between locations B and C is large enough to be detected. Panel iv: similar situation but in this case there is also no detectable field rotation at D. Panel v: situation where there are rotations at B, C, and D but the outflows are similar in strength. Panel vi: example where the magnetic field is the same as in the Gosling model but the outflows vary across the region occupied by the ions. We note that in all cases, the region between A and C has undergone a magnetic topology change and may show variations in the electron population in comparison to the undisturbed regions outside. This is not an exhaustive set, as many variations on these themes are possible. |
Panels iii and iv show examples where there is a detectable outflow on only one side of the original current sheet. This situation may arise if the differences in inflow conditions on either side of the current sheets mean that the plasma from one side dominates the interaction and provides the majority of the stress balance across the structure. If this plasma is largely transmitted though the current sheet, it will appear as an accelerated outflow on the other side, but there may be an absence of a counterflow through the current sheet in the other direction, such that there is no outflow jet on that side. Panel iii shows the example with visible current sheets at B, C, and D. This will thus appear as though there is a Gosling-type reconnection event with another current sheet nearby. In contrast, panel iv shows no rotation at point D, in which case it would appear in data to look similar to that of panel ii but perhaps of a relatively shorter duration. If there were a small reconnection outflow between C and D, but there were no ion diamagnetic effect at D, then the structure may appear as though the changes in the ion properties occur somewhat outside the major current sheet boundaries.
Panels v and vi demonstrate scenarios in which a change may be seen in one of the ion or B-field variables but not in the other. Panel v shows a situation where the rotation at C is apparent but the outflow speeds are the same on both sides of the current sheet whereas Panel vi shows a scenario where there is no apparent change in the magnetic field over the current sheet at C but there are two different outflow speeds.
Finally, we note in all cases presented here, the region between A and E has undergone a magnetic topology change, due to reconnection, when compared to the regions outside these boundaries. Since electrons are relatively fast-moving, we would expect to see some disturbances in the electron population throughout these regions. Moreover, if a gradient in electron parameters exists across any of the boundaries A–E then we expect observational signatures mapping to them. In particular, if changes in the electron population at a boundary also support a diamagnetic current, then there should be an additional small gradient in the magnetic field across that boundary. We note that in general the sense of the magnetic field gradient might be expected to be in the same sense at all the boundaries in such a nested set. However, it is possible that for the boundaries at A and E, the discontinuation of the electron source beyond the neutral line for side A and its replacement by electrons streaming through the layers from side B could result in a magnetic field gradient that is in the opposite sense to the overall gradient across the entire structure. This possibility is dependent on the nature of any asymmetry in the electron properties on either side, as well as any physics controlling the mixing and energisation of the electrons as they cross these layers.
The above examples illustrate that there may be a large variety of reconnection-associated structures possible that are dependent on the individual reconnection event characteristics. In the next section, we present a case study demonstrating that such layers can exist in solar wind reconnection events.
3. Solar Orbiter SWA and MAG observations
In this section we present an example of a layered reconnection structure which passed the Solar Orbiter spacecraft on 16 July 2020. On this day the spacecraft was located at a radial distance of 0.64 AU and 46.5° from the Earth-Sun line. We show the contemporaneous variations in the magnetic field vector, the ion parameter and the electron data, and argue that when taken as a whole they are consistent with the multi-layered reconnection outflow region set out in the previous section. Further detailed work on this and similar events will be needed to confirm the detailed correspondences between the observations and the postulated scenario, but the purpose here is to establish that this framework has some validity and should be considered more widely when interpreting such events, and may also lead to a greater understanding of the reconnection process itself.
Figure 3 shows a period of 1 h of observations from the MAG (Horbury et al. 2020) and SWA-PAS and SWA-EAS (Owen et al. 2020) sensors on Solar Orbiter. The top four panels show the magnetic field strength and the LMN vector components of the field, BL, BM, and BN, respectively. The ion density, the three LMN components of the ion bulk velocity and the average ion temperature, are presented as a function of time in panels 5–9 respectively. The current sheet LMN coordinate system used here is established by performing minimum variance analysis on the period of magnetic field data highlighted in red. Finally, the bottom panel in the figure shows the pitch-angle distribution (PAD) spectrogram for the electrons detected by SWA-EAS, averaged over the phase space density of electrons with energy greater than 70 eV, broadly representative of the expected strahl energy range (Feldman et al. 1975). We note that the SWA instrument entered a brief burst mode period from 1235 to 1240 UT, during which the data were recorded at a higher time cadence. Normal mode and burst mode data products (Owen et al. 2020) have been combined in this presentation and are distinguishable in this figure as a change in cadence of the data, which is most obvious in the SWA-PAS data panels.
 |
Fig. 3. Solar Orbiter MAG, SWA-PAS, and SWA-EAS data recorded during a reconnection event that passed the spacecraft on 16th July 2020. The data is presented in a current sheet LMN coordinate system based on results of minimum variance analysis of the MAG data highlighted in red in the top four panels, which show the total field strength, and BL, BM, and BN components respectively. Panels 5–9 show ground-derived moments from these data, showing the ion density, the three LMN components of the ion bulk flow velocity and the average ion temperature. The final panel shows a pitch-angle versus time spectrogram for electrons measured by the SWA-EAS. This panel presents the phase space density of electrons in the solar wind strahl energy range (measurements summed for all electrons with energy > 70 eV). |
Across the period shown in Fig. 3, the magnetic field showed a clear rotation, with a reversal in the BL component, from ∼5 nT at the start of the period shown to around ∼ − 6 nT by the end. The majority of the rotation occurs between 1235 and 1238 UT, and shows a two-step variation bounding a period when the magnetic field strength drops almost to zero. However, we note the presence of other small but relatively sharp rotations at other times throughout this period. During the interval shown there are also characteristic changes in the ion parameters. Across the period overall, the density drops slightly from ∼14 cm−3 to 11 cm−3, while the ion speed drops from 430 km s−1 to 410 km s−1. Across the event the average temperature rises from ∼8 eV to ∼10 eV. Focusing on the period between 1235 and 1238 UT, across which the main B-field rotation occurs, we note a clear deflection of the solar wind velocity vector associated with a concurrent increase in the average temperature, which peaks at ∼12 eV. A step down in ion density also occurs at the end of this period. The velocity change, compared to that immediately prior to 1235 UT is ∼35 km s−1 and is almost entirely in the VL component. We note again that there are a number of other smaller changes in the ion parameters on either side of the main field rotation region.
Finally, turning to the SWA-EAS electron observations in the bottom panel of Fig. 3, we note that the strahl electrons consistently show the highest fluxes in the lower half of the panel, corresponding to pitch angles < 90°. This is despite the rotation of the B-field from a vector direction pointing generally sunwards to antisunwards. A notable exception to this is the period containing the main B-field rotation, 1235−1238 UT, in which there is evidence of a more isotropic PAD. Despite the presence of highest strahl fluxes at pitch angles < 90°, it is clear that there are various sub-intervals, which we have marked with the dashed vertical lines, labelled a–h, in which the PAD shows significant variations, generally in pitch-angle width of the strahl. We note that the extension of these lines, defined through the major changes in the electron PAD, to the upper panels containing ion and B-field data, generally line up with an identifiable variation within a number of the parameters shown.
4. Discussion and conclusions
The case study presented above appears consistent with the broad description of reconnection in the solar wind presented by Gosling et al. (2005), in that the major field rotation in the period 1235−1238 UT (between lines marked b and c) is consistent with a bifurcated current sheet. The deflection of the solar wind bulk velocity vector within this interval is also consistent with this interpretation. The magnitude of the defection of the velocity vector is ∼40 km s−1, which is comparable to the exterior Alfvèn speeds of ∼35 km s−1 (upstream) and ∼40 km s−1 (downstream), which would be expected for a reconnection exhaust jet based on RD jump conditions (Hudson 1970). However, it is clear that the ions within this jet are also significantly heated, which, firstly, supports the observed diamagnetic suppression of the field strength within the jet, and, secondly, implies that the energy liberated from the field is transferred to both the thermal energy of this outflow plasma as well as its bulk flow energy (Phan et al. 2014). These authors also pointed out that when the jet is exactly Alfvènic, as is almost the case here, this accounts for only 50% of the available magnetic energy per particle, and that the remaining energy would be available to heat the plasma. Indeed, the ∼2 eV increase in ion temperature seen here is close to the empirical prediction for reconnection heating of 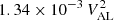 for VAL ∼ 35 − 40 km s−1 established by Phan et al. (2014). Overall, these field and ion observations are such that the period 1235−1238 UT (dashed lines b to c) is likely to be included in any survey looking to select Gosling et al. (2005) type reconnection events.
for VAL ∼ 35 − 40 km s−1 established by Phan et al. (2014). Overall, these field and ion observations are such that the period 1235−1238 UT (dashed lines b to c) is likely to be included in any survey looking to select Gosling et al. (2005) type reconnection events.
Nevertheless, we contend that there are other signatures around this event that are consistent with the more complex layered structure of the reconnected field region set out in Sect. 2. In particular, distinct variations in the electron strahl allow for the identification of small, but significant variations in the ion and B-field parameters. For example, a transition in the angular width of the strahl electrons occurs across the dashed line marked d at 1240 UT, although this is also marked by a short data gap in the electron measurements as the sensor switches back from burst to normal mode. This transition also coincides with rotations in BL and BM, which appear to be in the opposite sense to the main field rotation and end a period of low density and transitional velocity deflection when compared to the flow observed both before 1235 UT and in the period of main field rotation (b–c). The periods 1235−1238 UT (b–c) and 1238−1240 UT (c–d) thus appear to be 2 regions with distinct ion population characteristics compared to those observed outside the combined period. We contend that this ion profile is not unlike that generally represented in panels i and vi of Fig. 2.
Moreover, we note also that there is a transition in the nature of the electron PAD marked by the vertical dashed line at 1245 UT (line f) in which the electron PAD sharply narrows in pitch angle width. This relates to a small rotation in the field components and a small deflection of the ion flow. In this case, rotation in the BL and BN components are in the opposite sense to the directions of rotation between 1235 and 1238 UT. A similar small field rotation occurs at ∼1225 UT (line a) prior to the main field rotation, although a transition in the nature of the electron strahl is not so clear in this presentation. These variations in the B-field and nature of the electron distribution are consistent with the spacecraft crossing reconnected field lines in the separatrix layers outside of the ion outflow region. These correspond to the region between the boundaries labelled A–B and D–E in any of the panels of Fig. 2, in which the nature of the electron population may change due to the changes in topology of the field lines, but where the dynamical changes driving the major variations in the field direction and ion parameters have not had time to propagate this far away from the bifurcated current sheet itself. If these are indeed part of the separatrix layer structure, then variations of the electron fluxes could also be due to variable reconnection rates (e.g. Lavraud et al. 2009). In this case, we argue that there is evidence of small field variations, consistent with the case represented in panel i of Fig. 2. As noted at the end of Sect. 2, the fact that some of these field rotations are in the opposite sense to that seen across the main bifurcated current sheet can be accommodated by noting that the gradient in electron parameters could support a small diamagnetic current, which could be flowing in either direction, depending on the mixing of populations travelling through the reconnected current sheet or the nature of the electrons lost by the topological disconnection from the region on the other side of the neutral line.
Finally, we note that there are other changes in the electron PADs at further distances from the bifurcated current sheet (e.g. as delineated by vertical dashed lines at 1253, 1302 UT in Fig. 3), which are also associated with B-field or ion parameter changes. It is possible that these are also related to an extended multi-layer reconnection separatrix region, but for balance it should probably be noted that further work is needed to confirm or otherwise the association of all these layers with the reconnecting bifurcated current sheet. This requires more detailed examination of the 3D velocity distributions of the quality that is now available from Solar Orbiter and Parker Solar Probe.
In summary, in this Letter we have noted that there exist models of the structure of reconnection outflow layers predicting that more layers may be identifiable in data than are typically reported in studies of ‘Gosling-type’ reconnection events in the solar wind. We have re-examined this concept and recast the identification of these layers on terms of the changes associated with the boundaries of both the ion and electron outflows from the reconnection current layers. Finally, we have presented a case study that illustrates that there may indeed be evidence for this picture of extended multiple layers around the main bifurcated current sheet. It is clear that a more detailed examination of the particle distributions in this and other events is required to confirm whether this interpretation holds more generally, but we believe this could be a fruitful framework for considering the nature of reconnection layers in the solar wind.
Acknowledgments
Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. Solar Orbiter Solar Wind Analyser (SWA) data are derived from scientific sensors which have been designed and created, and are operated under funding provided in numerous contracts from the UK Space Agency (UKSA), the UK Science and Technology Facilities Council (STFC), the Agenzia Spaziale Italiana (ASI), the Centre National d’Etudes Spatiales (CNES, France), the Centre National de la Recherche Scientifique (CNRS, France), the Czech contribution to the ESA PRODEX programme and NASA. Solar Orbiter SWA work at UCL/MSSL is currently funded under STFC grants ST/T001356/1 and ST/S000240/1. The Solar Orbiter Magnetometer was funded by the UK Space Agency (grant ST/T001062/1). D. V. is supported by STFC Ernest Rutherford Fellowship ST/P003826/1. T. H. is supported by STFC grant ST/S000364/1.
References
- Eriksson, S., Gosling, J. T., Phan, T. D., et al. 2009, J. Geophys. Res.: Space Phys., 114, A07103 [NASA ADS] [Google Scholar]
- Feldman, W., Asbridge, J., Bame, S., Montgomery, M., & Gary, S. 1975, J. Geophys. Res., 80, 4181 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J., Skoug, R., McComas, D., & Smith, C. 2005, J. Geophys. Res.: Space Phys., 110, A01107 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J. T., Eriksson, S., & Schwenn, R. 2006, J. Geophys. Res.: Space Phys., 111, A10102 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J. T., Eriksson, S., Blush, L. M., et al. 2007a, Geophys. Res. Lett., 34, L20108 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J. T., Phan, T. D., Lin, R. P., & Szabo, A. 2007b, Geophys. Res. Lett., 34, L15110 [Google Scholar]
- Heyn, M., Biernat, H., Semenov, V., & Kubyshkin, I. 1985, J. Geophys. Res.: Space Phys., 90, 1781 [NASA ADS] [CrossRef] [Google Scholar]
- Horbury, T. S., O’Brien, H., Carrasco Blazquez, I., et al. 2020, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hudson, P. D. 1970, Planet. Space Sci., 18, 1611 [Google Scholar]
- Huttunen, K. E. J., Bale, S. D., Phan, T. D., Davis, M., & Gosling, J. T. 2007, J. Geophys. Res.: Space Phys., 112, A01102 [Google Scholar]
- Lavraud, B., Gosling, J. T., Rouillard, A. P., et al. 2009, Sol. Phys., 256, 379 [Google Scholar]
- Levy, R. H., Petschek, H. E., & Siscoe, G. L. 1964, AIAA J., 2, 2065 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., & Lee, L. 1993, Space Sci. Rev., 65, 59 [Google Scholar]
- Mistry, R., Eastwood, J. P., Phan, T. D., & Hietala, H. 2015, Geophys. Res. Lett., 42, 10,513 [CrossRef] [Google Scholar]
- Mistry, R., Eastwood, J. P., Phan, T. D., & Hietala, H. 2017, J. Geophys. Res.: Space Phys., 122, 5895 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, C. J., & Cowley, S. W. H. 1987a, Planet. Space Sci., 35, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, C. J., & Cowley, S. W. H. 1987b, Planet. Space Sci., 35, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, C. J., Bruno, R., Livi, S., et al. 2020, A&A, 642, A16 [EDP Sciences] [Google Scholar]
- Petschek, H. E. 1964, Magnetic Field Annihilation (NASA Special Publication), 50, 425 [Google Scholar]
- Phan, T., Gosling, J., Davis, M., et al. 2006, Nature, 439, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Phan, T. D., Gosling, J. T., & Davis, M. S. 2009, Geophys. Res. Lett., 36, L09108 [Google Scholar]
- Phan, T. D., Gosling, J. T., Paschmann, G., et al. 2010, ApJ, 719, L199 [Google Scholar]
- Phan, T. D., Drake, J. F., Shay, M. A., et al. 2014, Geophys. Res. Lett., 41, 7002 [Google Scholar]
- Phan, T. D., Bale, S. D., Eastwood, J. P., et al. 2020, ApJS, 246, 34 [Google Scholar]
- Semenov, V., Heyn, M., & Kubyshkin, I. 1983, Astron. Zh., 60, 1138 [NASA ADS] [Google Scholar]
- Teh, W.-L., Sonnerup, B. U. O., Hu, Q., & Farrugia, C. J. 2009, Ann. Geophys., 27, 807 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Sketch of possible boundaries associated with a magnetic reconnection exhaust outflow in the solar wind. Here, the upstream magnetic field strengths define the relative angles angle, θ1 and θ2, between the original current sheet and the separatrices (the thick red arrows bounding the red shaded area – the region occupied by the outflow electrons). The blue shaded area shows the region occupied by the outflow ions. These regions on either side of the original current sheet (green dashed line) contain the reconnection outflows (VO1 and VO2). The boundaries of these regions (indicated by the blue dashed lines) form different angles with the original current sheet (ϕ1 ≠ ϕ2). The magnetic field can potentially rotate across each of the boundaries (as represented by the black arrowed line) due to the gradient in plasma properties across the boundary leading to a diamagnetic depression of the field strength. If a spacecraft were to pass through the region, for example along a trajectory represented by the black arrow, it could encounter up to five distinct boundaries (at A, B, C, D, and E), which encompass the four layers. The relative time spent in each of these regions is dependent on the angle between the spacecraft trajectory and the original current sheet, γ, as well as the angles subtended by the separatrices and plasma boundaries. On either side of the event, we have undisturbed external ion inflow velocity, Vin1 and Vin2, with densities of n1 and n2. |
| In the text | |
 |
Fig. 2. Representative examples of reconnection outflows and current sheet structure. In each panel, the black trace represents the variation of the transverse component of the magnetic field to the current sheet, while the red trace represents the variation in ion flow velocity. Panel i: result if all possible transitions (current sheets and gradients in ion flows) in the model occur. Panel ii: result which is in keeping with the Gosling model (only rotations at B and C and equal outflows). Panel iii: example where there are rotations are seen at locations B, C, and D but only an outflow between locations B and C is large enough to be detected. Panel iv: similar situation but in this case there is also no detectable field rotation at D. Panel v: situation where there are rotations at B, C, and D but the outflows are similar in strength. Panel vi: example where the magnetic field is the same as in the Gosling model but the outflows vary across the region occupied by the ions. We note that in all cases, the region between A and C has undergone a magnetic topology change and may show variations in the electron population in comparison to the undisturbed regions outside. This is not an exhaustive set, as many variations on these themes are possible. |
| In the text | |
 |
Fig. 3. Solar Orbiter MAG, SWA-PAS, and SWA-EAS data recorded during a reconnection event that passed the spacecraft on 16th July 2020. The data is presented in a current sheet LMN coordinate system based on results of minimum variance analysis of the MAG data highlighted in red in the top four panels, which show the total field strength, and BL, BM, and BN components respectively. Panels 5–9 show ground-derived moments from these data, showing the ion density, the three LMN components of the ion bulk flow velocity and the average ion temperature. The final panel shows a pitch-angle versus time spectrogram for electrons measured by the SWA-EAS. This panel presents the phase space density of electrons in the solar wind strahl energy range (measurements summed for all electrons with energy > 70 eV). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


