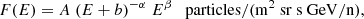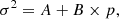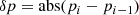| Issue |
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 9 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202140930 | |
| Published online | 14 December 2021 | |
Cosmic-ray flux predictions and observations for and with Metis on board Solar Orbiter
1
DiSPeA, University of Urbino Carlo Bo, Urbino (PU), Italy
e-mail: catia.grimani@uniurb.it
2
INFN, Florence, Italy
3
INAF – Astronomical Observatory of Capodimonte, Naples, Italy
4
CNR – IFN, Via Trasea 7, 35131 Padua, Italy
5
CISAS, Centro di Ateneo di Studi e Attività Spaziali “Giuseppe Colombo”, via Venezia 15, 35131 Padua, Italy
6
Solar-Terrestrial Centre of Excellence – SIDC, Royal Observatory of Belgium, Ringlaan -3- Av. Circulaire, 1180 Brussels, Belgium
7
Dip. di Fisica e Astronomia “Galileo Galilei”, Università di Padova, Via G. Marzolo, 8, 35131 Padua, Italy
8
ASI – Italian Space Agency, Via del Politecnico snc, 00133 Rome, Italy
9
University of Florence, Physics and Astronomy Department, Largo E. Fermi 2, 50125 Florence, Italy
10
INAF Associated Scientist, Florence, Italy
11
Alma Mater University, Bologna, Italy
12
INAF – Astrophysical Observatory of Catania, Catania, Italy
13
INAF – Astrophysical Observatory of Torino, Turin, Italy
14
INAF – Institute for Space Astrophysics and Cosmic Physics, Milan, Italy
15
University of Catania, Physics and Astronomy Department “Ettore Majorana”, via S. Sofia 78, 95123 Catania, Italy
16
Catholic University @ NASA – GSFC, Maryland, USA
17
MPS, Göttingen, Germany
18
Astronomical Institute of the Czech Academy of Sciences, Ondřejov, Czech Republic
19
INAF – Astrophysical Observatory of Trieste, Trieste, Italy
20
Politecnico di Torino, Turin, Italy
21
NASA HQ, Washington, DC, USA
22
National Research Council of Italy and Institute for Electronics, Information Engineering and Telecommunications, University of Padua, Department of Information Engineering via Gradenigo, 6B, 35131 Padua, Italy
23
Institute of Experimental and Applied Physics, Kiel University, 24118 Kiel, Germany
Received:
30
March
2021
Accepted:
8
June
2021
Context. The Metis coronagraph is one of the remote sensing instruments hosted on board the ESA/NASA Solar Orbiter mission. Metis is devoted to carry out the first simultaneous imaging of the solar corona in both visible light (VL) and ultraviolet (UV). High-energy particles can penetrate spacecraft materials and may limit the performance of the on-board instruments. A study of the galactic cosmic-ray (GCR) tracks observed in the first VL images gathered by Metis during the commissioning phase is presented here. A similar analysis is planned for the UV channel.
Aims. We aim to formulate a prediction of the GCR flux up to hundreds of GeV for the first part of the Solar Orbiter mission to study the performance of the Metis coronagraph.
Methods. The GCR model predictions are compared to observations gathered on board Solar Orbiter by the High-Energy Telescope in the range between 10 MeV and 100 MeV in the summer of 2020 as well as with the previous measurements. Estimated cosmic-ray fluxes above 70 MeV n−1 have been also parameterized and used for Monte Carlo simulations aimed at reproducing the cosmic-ray track observations in the Metis coronagraph VL images. The same parameterizations can also be used to study the performance of other detectors.
Results. By comparing observations of cosmic-ray tracks in the Metis VL images with FLUKA Monte Carlo simulations of cosmic-ray interactions in the VL detector, we find that cosmic rays fire only a fraction, on the order of 10−4, of the whole image pixel sample. We also find that the overall efficiency for cosmic-ray identification in the Metis VL images is approximately equal to the contribution of Z ≥ 2 GCR particles. A similar study will be carried out during the whole of the Solar Orbiter’s mission duration for the purposes of instrument diagnostics and to verify whether the Metis data and Monte Carlo simulations would allow for a long-term monitoring of the GCR proton flux.
Key words: cosmic rays / solar-terrestrial relations / instrumentation: detectors
© ESO 2021
1. Introduction
The ESA/NASA Solar Orbiter mission (Müller et al. 2020; García Marirrodriga et al. 2021) was launched on February 10, 2020, at 5:03 AM CET from Cape Canaveral (Florida, USA) during the solar minimum period between the solar cycle 24 and solar cycle 25, characterized by a positive polarity period of the global solar magnetic field (GSMF). Four in situ and six remote sensing instruments were placed on board the spacecraft (S/C) to study how the Sun generates and controls the heliosphere (Müller et al. 2020). The S/C will reach a minimum distance from the Sun of 0.28 AU and a maximum inclination about the solar equator of 33 degrees during the mission lifetime. Galactic cosmic-ray (GCR) and solar energetic particle (SEP) interactions in the material surrounding the sensitive part of the instruments generate secondary particles that limit the performance of the detectors on board space missions (see for instance Telloni et al. 2016; Armano et al. 2018a, 2019; Grimani et al. 2020). In particular, GCRs and SEPs affect the quality of visible light (VL, in the range 580–640 nm) and ultraviolet (UV, in a ≃10 nm band around the 121.6 nm H I Lyman-α line) images of the Metis coronagraph (Antonucci et al. 2020; Andretta et al. 2014). Metis, mounted on an external panel of the Solar Orbiter S/C, is shielded by a minimum of 1.2 g cm−2 of material and consequently is traversed by protons and nucleons with energies > 10 MeV n−1. We present an analysis of cosmic-ray signatures in the VL images in this work. Cosmic-ray observations gathered on board Solar Orbiter between 10 MeV and 100 MeV with the High-Energy Telescope (HET) of the Energetic Particle Detector (EPD) instrument (Rodríguez-Pacheco et al. 2020; Freiherr von Forstner et al. 2021; Mason et al. 2021; Wimmer-Schweingruber et al. 2021) and model predictions of GCR energy spectra above 70 MeV n−1 are also considered in the following for Monte Carlo simulations (Battistoni et al. 2014; Böhlen et al. 2014); flair aimed at reproducing and validating the tracks of cosmic rays observed in the Metis VL images. A similar analysis will be carried out for the UV channel in the future.
The GCRs consist approximately of 98% of protons and helium nuclei, 1% electrons, and 1% nuclei with Z ≥ 3, where percentages are in particle numbers to the total number (Papini et al. 1996). This work is focused on protons and 4He nuclei since these particles constitute the majority of the cosmic-ray bulk and the measurements carried out on board Solar Orbiter allow us to optimize the Monte Carlo simulations by selecting proper input fluxes within the range of predictions. Rare particles such as heavy nuclei and electrons will be considered in the future when data from magnetic spectrometer experiments becomes available (Aguilar et al. 2018) up to high energies for the period under study. At the present time, uncertainties on the predictions of the energy spectra of rare particles would be higher than their contribution to the observations carried out with the Metis coronagraph. The overall GCR flux shows time, energy, charge, and space modulation in the inner heliosphere (Grimani et al. 2020), an aspect of particular importance also in the context of planetary Space Weather and Solar System exploration (Plainaki et al. 2016, 2020). In particular, the GCR flux shows modulations associated with the 11-year solar cycle and the 22-year polarity reversal of the GSMF. These long-term modulations are ascribable to the particle propagation against the outward motion of the solar wind and embedded magnetic field (Balogh 1998). Particles that at the interstellar medium have energies below tens of MeV are convected outward before reaching the inner heliosphere, while interplanetary and interstellar GCR energy spectra do not show any significant difference above tens of GeV (Florinski & Pogorelov 2009).
Adiabatic cooling represents the dominant energy loss of cosmic rays observed in the inner heliosphere in the energy range 10–100 MeV. At these energies cosmic rays can be considered an expanding adiabatically isolated gas of particles that does work on the surrounding medium thus reducing its internal energy. Above tens of MeV cosmic rays diffuse, scatter and drift through the solar wind and across inhomogeneities of the interplanetary magnetic field (Jokipii et al. 1977). The total residence time of cosmic rays in the heliosphere is strongly energy-dependent and varies from hundreds of days at 100 MeV n−1 to tens of days above 1 GeV (Florinski & Pogorelov 2009). Positively charged GCRs undergo a drift process (see for instance Grimani et al. 2004, 2008) during negative polarity periods of the GSMF (when the Sun magnetic field lines exit from the Sun South Pole) propagating mainly sunward from the equator along the heliospheric current sheet. Negatively charged particles would suffer the same drift process during positive polarity periods (epochs during which the Sun magnetic field lines exit from the Sun North Pole). As a result, during negative (positive) polarity periods, the positively (negatively) charged cosmic rays are more modulated than during positive (negative) polarity epochs.
The spatial dependence of the GCR proton flux was studied with different S/C gathering data simultaneously between tens of MeV and GeV energies. The intensity of these particles was observed to decrease by a few percent with decreasing radial distance from the Sun and to vary ≪1% with increasing heliolatitude with gradients depending on the GSMF polarity epoch (De Simone et al. 2011).
Solar Orbiter was launched during a positive polarity period of the Sun, therefore, the drift process played no role in modulating the overall GCR flux in 2020. The same condition will apply until the next polarity change expected at the maximum of solar cycle 25 between 2024 and 2025 (Singh & Bhargawa 2019).
This manuscript is arranged as follows. In Sect. 2, the radial and latitudinal gradients of the cosmic-ray flux in the inner heliosphere along the Solar Orbiter orbit are discussed. In Sect. 3, the GCR flux predictions and observations are presented for the summer of 2020. In Sect. 4, the Metis coronagraph is briefly described. In Sect. 5, the S/C on-board algorithm for cosmic-ray track selection in the Metis VL images is illustrated. In Sect. 6, we present a viewer developed for the Metis cosmic-ray matrices. In Sect. 7, we report the GCR observations with Metis. Finally, in Sect. 8, simulations of the Metis VL detector carried out with the FLUKA Monte Carlo program are discussed and compared to the observations, along with an evaluation of the capability of the Metis VL detector to serve as a cosmic-ray monitor.
2. Galactic cosmic-ray flux radial and latitudinal gradients in the inner heliosphere
The GCR proton flux gradients with radial distance from the Sun and heliolatitude were studied with simultaneous observations gathered by S/C moving along different orbits in order to disentangle the role of space and time variations. The majority of space instruments are flown near Earth. In particular, those missions sent to space during the first part of the solar cycle 23 and the second part of the solar cycle 24 experienced the same polarity of the GSMF as Solar Orbiter. Ulysses, launched on October 6, 1990, was placed in an elliptical orbit around the Sun inclined at 80.2 degrees to the solar equator (Wenzel et al. 1992). The mission was switched off in June 2009. The Kiel Electron Telescope (Wibberenz et al. 1992) on board Ulysses measured electrons, protons, and helium nuclei from MeV to GeV energies. On June 15, 2006, the Pamela (Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics; Picozza et al. 2007) satellite was launched to collect proton, nucleus and electron data near Earth above 70 MeV n−1 during a period characterized by negative polarity of the GSMF and a minimum solar modulation. In that same time, Ulysses covered a distance from the Sun that was between 2.3 and 5.3 AU.
The comparison between Ulysses and Pamela overlapping measurements revealed that the proton flux in the rigidity interval 1.6–1.8 GV (0.92–1.09 GeV, corresponding approximately to the median energy of the GCR spectrum at solar minimum) has a radial intensity variation of 2.7 ± 0.2% AU−1, and a latitudinal gradient of −0.024 ± 0.005% degree−1 (De Simone et al. 2011). Positive (negative) latitudinal gradients are observed during positive (negative) polarity periods. In addition, Experiment 6 (E6) on board Helios-A and Helios-B provided ion data from four to several hundreds of MeV n−1 (Winkler 1976; Marquardt & Heber 2019). The Helios-A and Helios-B S/C were launched on December 10, 1974 and January 15, 1976 during a positive polarity epoch and were sent into ecliptic orbits of 190-day and 185-day periods around the Sun. The orbits perihelia were 0.3095 AU and 0.290 AU, respectively. The aphelia were approximately 1 AU. As a result, the Helios data are representative of the cosmic-ray bulk variations that are to be experienced by Solar Orbiter, which will also reach maximum distances from the Sun of about 1 AU. In the recent paper by Marquardt & Heber (2019), the Helios proton data radial gradients of the GCR flux were found to be 6.6 ± 4% above 50 MeV and 2 ± 2.5% between 250 and 700 MeV between 0.4 and 1 AU. These results are in agreement with those from Pamela/Ulysses (within the statistical and systematic errors). In conclusion, variations in the GCR proton-dominated flux along the Solar Orbiter orbit are expected to be of a few % at most; consequently, it is plausible to assume that models for cosmic-ray modulation developed on the basis of observations gathered near Earth will also apply to Solar Orbiter. On the other hand, the Metis data will allow us to verify this assumption in the unexplored region of tens of degrees above the solar equator. Analogously, even though no SEP data were gathered up to present time, it is likely that a study of the evolution of SEP events near the Sun above the solar equator will be possible for the first time also with Metis, in addition to the dedicated instruments flown on board Solar Orbiter.
3. Galactic cosmic-ray energy spectra in the summer 2020 for Solar Orbiter
Solar activity was observed to modulate the near-Earth cosmic-ray integral flux during the last three solar cycles from solar minimum (e.g., years 2009 and 2019) through solar maximum (years 1989–1991) above 70 MeV n−1 by approximately a factor of four. We consider this particular period of time since solar modulation has been studied in the majority of cases with data gathered in space1. The above estimate was carried out with the Gleeson and Axford model (G&A; Gleeson & Axford 1968). The same model is also adopted here to estimate the GCR flux modulation by considering the observed average monthly sunspot number as a proxy of the solar activity2 (Clette et al. 2014). This model allows us to estimate the cosmic-ray intensity in the inner heliosphere by assuming an interstellar energy spectrum and a solar modulation parameter (ϕ) that basically represents the energy loss of cosmic rays propagating from the interstellar medium to the point of observations.
During GSMF positive polarity epochs, the G&A model is found to reproduce the GCR measurements well at 1 AU in the energy range from tens of MeV to hundreds of GeV (Grimani et al. 2008). It has been pointed out that different values of the solar modulation parameter are estimated if different GCR energy spectra at the interstellar medium are considered in the model. Voyager 1 measured the interstellar spectra of ions and electrons below 1 GeV (Stone et al. 2013). However, the solar modulation parameter3 adopted in this work (Usoskin et al. 2011, 2017 was estimated according to the Burger et al. (2000) interstellar proton spectrum. Since the solar modulation parameter and the interstellar particle spectra must be adequately associated with one another, the interstellar proton spectrum by Burger et al. (2000) is also considered here. Unfortunately, no 4He interstellar spectrum is reported in this last paper and, consequently, here we adopt the estimate by Shikaze et al. (2007) that was inferred from the balloon-borne BESS experiment data (Abe et al. 2014), which were gathered during different solar modulation and solar polarity periods. This choice is not expected to affect the overall simulation outcomes by more than a few % since the cosmic-ray bulk is dominated by protons. A similar approach was considered for the LISA Pathfinder mission orbiting around the first Lagrange point during the years 2016-2017 (Armano et al. 2016, 2018b). It was shown in Villani et al. (2020) that the integral proton flux predictions carried out with the G&A model for LISA Pathfinder differ by less than 10% from the Alpha Magnetic Spectrometer (AMS-02) experiment data (AMS Collaboration 2002); aguilar18 gathered on the Space Station during the Bartels Rotation 2491 (Grimani et al. 2019). For the present work, it is also possible to benefit of the proton and helium differential flux measurements of the EPD/HET instrument flying on board Solar Orbiter and gathering data in the energy range below 100 MeV in order to further reduce the uncertainty on the GCR flux predictions, while we await the publication of the AMS-02 data for the years after 2017, up to TeV energies.
In Fig. 1, we show the average monthly sunspot number observed during the solar cycles 23 and 24. Minimum, average, and maximum predictions of the sunspot number are inferred from the Marshall Space Flight Center website4 and appear as dotted and dashed lines in the same figure. The launch of the Solar Orbiter S/C is also indicated. For the first two to three years of the Solar Orbiter mission, it is reasonable to expect a minimum to low solar modulation, analogously to the years 1996–1997 at the beginning of the solar cycle 23 during a positive polarity epoch.
 |
Fig. 1. Average monthly sunspot number observed since 1994 (Clette et al. 2014). |
Solar activity has been very low since 2019, when the annual sunspot number of 3.6 was observed and it slightly increased in 2020. The average monthly sunspot number observed after the Solar Orbiter launch is also reported in Table 1. It is focused in particular on the period June–July 2020, when the EPD/HET data were released for the first time and the average sunspot number was 6.0. The solar modulation parameter for this period is reasonably assumed to range between 300 MV c−1 and 340 MV c−1. In particular, a solar modulation of 340 MV c−1 corresponds to the average solar modulation parameter observed during periods of a similar solar activity observed in the past years, while 300 MV c−1 is considered a lower limit for ϕ corresponding to the GCR flux modulation that seems to better agree with the EPD/HET data below 100 MeV reported as black stars in Fig. 2 after rebinning. The uncertainty on the integral flux predictions is 16%, only because of the small solar modulation variation between June and July 2020. The EPD/HET data are compared below 100 MeV with measurements carried out by other experiments during similar conditions of solar modulation and GSMF polarity (see Table 2). The estimated proton and 4He energy spectra also appear in Fig. 2, with continuous lines for protons and with dashed lines for 4He.
 |
Fig. 2. Predictions of proton and 4He nucleus fluxes during the summer 2020 for the Solar Orbiter mission. The top and bottom continuous (protons) and dashed (4He nuclei) curves are obtained with the G&A model above 70 MeV(/n) for a solar modulation parameter of 300 and 340 MV c−1, respectively. The dotted curve represents the lower limit to the predictions of the proton spectrum for the same period, representing the Pamela experiment data gathered in 2008 during a period of solar activity similar to that of Solar Orbiter but during a negative GSMF epoch. Data are reported in Stone (1964, solid dots), Logachev et al. (2003, open triangles), and Marquardt & Heber (2019, solid triangles). The solid stars and the open squares indicate the EPD/HET measurements gathered in the summer 2020 on board Solar Orbiter for protons and helium nuclei, respectively. |
Average monthly sunspot number observed after the Solar Orbiter launch.
We are aware that the in-flight calibration of the EPD/HET instrument is still ongoing and, in particular, the proton fluxes above 10 MeV are overestimated by a factor of up to two, as discussed by Wimmer-Schweingruber et al. (2021). However, in the following, we consider ϕ = 300 MV c−1 because this parameter modulation value allows us to reconcile our galactic cosmic-ray flux predictions with HET measurements within the normalization uncertainty and because it appears reasonable with respect to 320 MV c−1 observed at the time of the LISA Pathfinder mission in mid-2017 when the solar modulation was higher than in 2020 (Armano et al. 2018a).
The particle energy spectra above 70 MeV have been parameterized as follows (see for details Grimani et al. 2020):
where E is the particle kinetic energy per nucleon in GeV/n. The parameters A, b, α, and β for minimum (m) and maximum (M) predictions are shown in Table 3, along with the lower limit (ll) for the estimated proton flux in 2020 set by the Pamela experiment observations carried out in 2008 during a period of low solar modulation and negative GSMF polarity (Adriani et al. 2011).
Parameterizations of proton and helium energy spectra in June–July 2020 above 70 MeV n−1.
4. Metis coronagraph and visible light image characteristics
Metis is a solar coronagraph that has been performing the first simultaneous imaging of the off-limb solar corona in both visible light and ultraviolet (Antonucci et al. 2020). The main design constraints for the Metis coronagraph were associated with the aim of obtaining the major scientific return with VL and UV observations of the corona while suffering large thermal variations (up to about 400 °C in the region of the inverted external occulter) along the Solar Orbiter orbit. Total mass (< 24.55 kg) and power consumption (< 28 W) were also limited as imposed to interplanetary missions. Moreover, the Metis design was optimized to achieve a sensitivity to observe the weak corona from 1.7 R⊙ through 9 R⊙ by maintaining a contrast ratio lower than 10−9 and pointing the Sun center within one arcmin. With an innovative occultation design and a unique combination of mirrors and filters, Metis images the VL corona in the range 580–640 nm (corresponding to yellow-orange light) and the UV H I Lyman-α line at 121.6 nm. The VL channel includes a polarimeter that allows us to observe the linearly polarized component of the K corona. The minimum spatial resolution at perihelion is 2000 km for VL images and the temporal resolution is up to 1 s. The VL detector consists of a VL camera with an active CMOS (CMOSIS ISPHI Rev. B developed by CMOSIS Imaging Sensors, now AMS, Belgium) sensor segmented into 4.1943 × 106 pixels. Each pixel has dimensions of 10 μm × 10 μm × 4.5 μm (Antonucci et al. 2020), accounting for a pixel and detector geometrical factors of 401 μm2 sr and 17 cm2 sr, respectively (Sullivan 1971).
5. Metis algorithm for cosmic-ray detection
When the VL and UV detectors work in analog mode, several frames are co-added to obtain a single image to improve the signal-to-noise (S/N) ratio (Andretta et al. 2014). The detection and removal of GCRs, as well as (eventually) solar energetic particles, is carried out on board by the Metis processing unit. The primary goal of the particle track removal process is to improve the quality of the images. As a byproduct, the algorithm also provides the location and number of particle tracks in each image which, in principle, can be correlated with the GCR integral flux over the image integration time. No particle identification is allowed. Other instruments such as the extreme UV imager SOHO-EIT (Delaboudinière et al. 1995) and the coronagraph STEREO-SECCHI (Wuelser et al. 2004) reported a number of pixels fired by GCRs per second per square centimeter differing by almost two orders of magnitude (Andretta et al. 2014). As recalled above, this evidence cannot be ascribable to variations in solar activity. The above-mentioned results must have resulted from particle interactions in the S/C material surrounding the instruments. Therefore, Monte Carlo simulations are needed to correlate the particle tracks observed in the Metis coronagraph images to the incident flux of GCRs.
The temporal noise observed in the CMOS pixel signals includes both the readout noise and the statistical noise associated with photons and dark current fluctuations. In principle, this temporal noise can be expressed as follows:
where p is the pixel value and A and B are coefficients that can be fine-tuned on the basis of the characterization of the VL detector. For each series of N images with exposure times of T seconds each, for each image i of the sequence, starting from i = 2, and for each pixel value p, the difference
is calculated. By defining pm = min(pi, pi − 1), the related noise is then estimated, as indicated in Eq. (2), with p = pm.
In the case δp2 > kthσ2, both pixel values are replaced with pm. This process is repeated for each pixel of each image for i = 2, …, N. The parameter kth is also user defined and determines the detection threshold.
As an example, the STEREO-B COR1 data are shown in Fig. 3 (see Andretta et al. 2014, and references therein). Figure 3 displays the approximate Gaussian distributions of pixel signals generated by photons and noise represented by the dark area, while the cosmic-ray signals are associated with the white area. The threshold is set at 5σ from median.
 |
Fig. 3. STEREO-B COR 1 data gathered in 2007 and reported in Andretta et al. (2014). The dark area is associated with VL photon signals and dark current, while the white area is ascribable to the passage of high-energy particles in the VL detector. |
During the commissioning phase of the Solar Orbiter mission, the parameters A and B for Metis were set to 40 000 and 0, respectively. Despite the possibility of further improvements to the algorithm performance for cosmic-ray searches in the future, very encouraging results have already been obtained in the analysis presented here.
6. APViewer for cosmic-ray track analysis in the Metis VL images
Figure 4 displays a Metis VL image of the solar corona. After removing the cosmic-ray tracks, the on-board algorithm described in the previous section allows us to report the fired pixels in 2048 × 2048 matrices called cosmic-ray matrices. The algorithm cannot discriminate between intense signals generated by cosmic rays from noisy pixels and bright sources that lie in the detector’s field of view. However, external bright sources and noisy pixels would be possibly found in the same matrix cells in more than one image of each set of images, while cosmic rays would hit different pixels in each image. As a result, the superposition of several images allows to increase the statistics for GCR analysis and to improve the S/N ratio. In the cosmic-ray matrices the pixel contents correspond to the number of times that, from the pixel-to-pixel comparison among each image of each set of images, the pixel content was changed to pm. For instance, in this work, where a case study of four sets of four images (N = 4) is presented, the pixel contents are 0, 1, 2, or 3. The format of the images is FITS. A dedicated viewer, APviewer, was developed for Metis in Python programming language for the visual analysis of the particle tracks in the cosmic-ray matrices (Persici 2021). The APViewer allows for a more simplified visualization and search of the cosmic-ray tracks. Furthermore, it provides an efficient solution to a series of problems that other tools present. In particular, the widely used viewer FV5 for images in FITS format does not visually differentiate among pixels with distinct values and does not provide a zoomed-in view of the region surrounding an identified pattern of fired pixels. To this purpose, the APViewer performs a coloring of the pixels according to their values (> 0) and allows the user to choose the window size when looking for a specific cosmic-ray track in order to guarantee an accurate view of the surrounding context.
 |
Fig. 4. Polarized brightness image of the solar corona in VL (June 21, 2020). The vertical orientation is north-south, according to the Solar axis. The image was obtained with an exposure time of 30 s at a distance of 0.5 AU from the Sun. |
In the specific case of VL images, the main window of the APViewer presents a 256 × 256 matrix that constitutes the central inner portion of the original 2048 × 2048 matrix. This reduced matrix provides an overview of the location of the pixels traversed by cosmic rays. The contents of the border cells of the reduced matrix are displayed as: a#b, where a corresponds to the sum of all the fired pixels (i.e., those with values greater than 0) in the row or column portion of the corresponding side of the matrix, whereas b represents the sum of the pixels with value equal to 1, thus returning the number of pixels traversed by cosmic rays in the same undisclosed part of the matrix. In order to guarantee a straightforward search of cosmic-ray tracks, the main window includes two text boxes where the users can type the row and column number of the pixel they wish to see in greater detail. It is worthwhile pointing out that fired pixels can also be analyzed through sub-windows that can be opened starting from the reduced matrix by means of a left or right click on the border cells. These windows vary in size, according to the specific side of the matrix, and in number, depending on whether it is a corner cell or a border one. As an example, in Fig. 5, it is shown how it is possible to open one of the hidden parts of a cosmic-ray matrix starting from the corner of the central inner matrix.
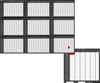 |
Fig. 5. Example of cosmic-ray matrix corner window opening with the APViewer. |
7. Analysis of cosmic-ray tracks in the Metis visible light images
A sample of cosmic-ray tracks observed in the Metis VL images is shown in Fig. 6. GCR tracks are classified as single hits (top left panel), slant tracks (top right panel), and multiple tracks (bottom left panel). Slant tracks are associated with single particles firing more than one pixel. We recall here that GCRs show a spatial isotropic distribution and that each single fired pixel has a geometrical factor and geometrical field of view of 401 μm2 sr and 132 degrees, respectively. Multiple tracks are associated with patterns of fired pixels characterized by a distance from track centroid smaller than 12 pixels. The image shown in the bottom right panel of Fig. 6 is not ascribable to the passage of cosmic rays and, rather, it represents the effects of a bright external source such as a star. The number of pixels with contents associated with external sources moving through the instrument field of view during the acquisition of images was on the order of 10−5 of the total pixel sample.
 |
Fig. 6. Examples of cosmic-ray tracks observations in the Metis VL images (top panels and bottom-left panel). A spurious pattern of hit pixels ascribable to a bright external source, such as a star, appears in the bottom right panel. |
As recalled above, four sets of four co-added cosmic-ray matrices characterized by 15 s (T) of exposure each, for a total of a 60 s exposure time for each set of images, were considered here as a case study. These images were taken on May 29, 2020. The presence of noisy isolated pixels in the four images was studied by searching for fired pixels appearing in more than one image – and none were found. Conversely, noisy columns were found in two cosmic-ray matrices. These pixels were not considered for the analysis as they turned out to be just a fraction of approximately 3 × 10−5 and 5 × 10−5, respectively, of the total number of pixels. The efficiency for single pixels being fired was set with a study of a sample of 23 slant tracks: only 6 pixels out of 106 counted along the particle tracks were not fired and, consequently, the efficiency was set to 0.94 ± 0.02. This estimate represents a lower limit to the actual efficiency applying to the total bulk of incident particles. The pixel inefficiency depends on particle energy losses in the sensitive part of the detector and, consequently, on the particle species and path length. Straight tracks impacting the central part of the pixels are certainly characterized by a higher efficiency than slant tracks. Unfortunately, a dedicated beam test to estimate the efficiency of the detector with different particle species and incident directions was not carried out before the mission launch. Single pixel and Metis on-board algorithm efficiencies for cosmic-ray selection must properly be taken into account to reconcile cosmic-ray observations carried out with Metis and the integral flux of GCRs. Single-pixel, slant, and multiple tracks have been counted in each studied VL image. The results are reported in Table 4 where the tracks have been listed in categories according to their topology. The average number of GCR tracks per set of images corresponding to a total of 60 s exposure time was 271 ± 22.
Cosmic-ray tracks in the studied sets of Metis VL images.
The visual analysis of the Metis VL images did not allow us to distinguish between primary and secondary particles generated by incident cosmic rays interacting in the material surrounding the coronagraph. Monte Carlo simulations of the VL detector were carried out to this end.
8. Comparison of simulations and cosmic-ray observations in the Metis visible light images
While single pixels and slant tracks observed in the Metis VL images are certainly associated with single particles, the multiple tracks could have been generated by incident particle interactions. A toy Monte Carlo allowed us to study the random incidence of 300 particles (roughly equivalent to the number of tracks observed in each set of VL images) on the active part of the detector. Ten different runs were carried out and the average minimum distance observed between different particle tracks was of 5 pixels (≃50 μm), which is consistent with multiple-track observations.
In Fig. 7, the geometry of the Solar Orbiter S/C and instruments adopted for the Metis VL detector simulations carried out with the FLUKA Monte Carlo program (version 4.0.1) is shown. The geometry includes the S/C structure, thrusters fuel tanks and the SPICE, EUI, PHI, and STIX instruments (García Marirrodriga et al. 2021, and references therein). Interplanetary and galactic particles traverse from about 1 g cm−2 to more than 10 g cm−2 of material depending on the particle incidence direction before reaching the Metis VL detector. Proton and helium fluxes, reported in Fig. 2 as the upper continuous and dashed lines, were considered as input GCR energy differential fluxes for the summer 2020 above 70 MeV in the simulations. Particles with energies below 70 MeV n−1 were found not to give any relevant contribution to cosmic-ray tracks in the VL images. The number of incident particles was set in order to reproduce the 60 s exposure time of the VL detector images. Longer simulations would have been unfeasible because of limited available computational power. The simulations returned 276 ± 17 charged particles crossing the VL detector for incident proton flux only. This number of tracks is similar to the observations within statistical uncertainties. It is worthwhile pointing out that the statistical error is smaller than the combination of the uncertainties on input fluxes on the order of 10% on the basis of our previous experience with LISA Pathfinder (Grimani et al. 2019) and the intrinsic Monte Carlo resolution also on the order of 10% (Lechner et al. 2019). While the detector does not allow us to distinguish different particle species, the simulations indicate that for primary protons the particles traversing the sensitive part of the detector in particle numbers to the total number down to 1% in composition are: 80% protons, 17% electrons and positrons, and 3% pions. For the helium run, particles crossing the sensitive part of the VL detector were ascribable to 30% of the total bulk of tracks to He4 nuclei, 34% to electrons and positrons, 25% to protons, 10% to pions, and 1% to deuterium. It is also found that the number of tracks generated by He4 amounts to 30% of the total sample generated by primary protons. The contribution of nuclei with Z > 2 was estimated to be 5% of the total. This last estimate was carried out with a separate set of Monte Carlo simulations with which the relative role of protons, helium and heavy nuclei was set at solar minimum according to Grimani et al. (2005), since no heavy nucleus measurements were available for the summer of 2020. The total number of cosmic-ray tracks in the Metis images is dominated by primary and secondary particles associated with incident protons. It is also noted that the algorithm and detector efficiencies remove 35% of the tracks from the images, which is the same percentage of pixels fired by helium and other nuclei. Finally, the minimum distance between secondary particles generated by the same incident primary on the S/C ranged between 2 cm and 500 μm. As a result, the FLUKA simulations confirmed the toy Monte Carlo results indicating that multiple tracks in the VL images are produced by different incident particles. According to these results – if confirmed during the rest of the mission when the solar modulation is expected to increase and after the next polarity change in 2024-2025 – by assuming that no significant variation of the VL instrument sensitivity for GCR detection is observed, the Metis proton-dominated data joined with the Monte Carlo simulations may allow for the monitoring of long-term variations of GCRs above 70 MeV. When the magnetic spectrometer experiment AMS-02 eventually provides absolute GCR flux measurements in 2020 for model prediction normalization (along with the implementation of the full Solar Orbiter S/C geometry), it should be possible to reduce the uncertainties on the simulations and, consequently, on analyses of the Metis cosmic-ray matrices. Finally, a comparison of the Metis observations with those of other instruments flown on board Solar Orbiter, such as EUI-FSI (Rochus et al. 2020), will allow us to further test the results of this work.
 |
Fig. 7. Solar Orbiter geometrical model. Remote sensing instruments and electronic boxes are visible. |
9. Conclusions
High-energy particles traverse and interact in the S/C materials of space missions, thus limiting the efficiency of on-board instruments. A dedicated Python viewer was developed to study the cosmic-ray tracks observed in the Metis VL images of the solar corona. It was found that in 60 s of exposure time, the number of pixels traversed by cosmic rays is a minor fraction (about 10−4) of the total number of pixels and, therefore, the quality of the images is not significantly affected by cosmic ray tracks. Monte Carlo simulations of the VL detector are consistent with the number of observed tracks when only primary protons are considered. The signatures of the passage of particles with charge > 1 approximately account for the single-pixel and on-board algorithm overall efficiencies. Consequently, Metis data and Monte Carlo simulations may allow for the monitoring of long-term variations of the proton flux. Future analyses of Metis VL and UV cosmic-ray matrices and comparisons with measurements of other instruments such as EUI-FSI will allow us to further test the results of this work.
Data used here are publicly available at http://www.sidc.be/silso/datafiles
Acknowledgments
Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. The Metis programme is supported by the Italian Space Agency (ASI) under the contracts to the co-financing National Institute of Astrophysics (INAF): Accordi ASI-INAF N. I-043-10-0 and Addendum N. I-013-12-0/1, Accordo ASI-INAF N.2018-30-HH.0 and under the contracts to the industrial partners OHB Italia SpA, Thales Alenia Space Italia SpA and ALTEC: ASI-TASI N. I-037-11-0 and ASI-ATI N. 2013-057-I.0. Metis was built with hardware contributions from Germany (Bundesministerium für Wirtschaft und Energie (BMWi) through the Deutsches Zentrum für Luft- und Raumfahrt e.V. (DLR)), from the Academy of Science of the Czech Republic (PRODEX) and from ESA. We thank J. Pacheco and J. Von Forstner of the EPD/HET collaboration for useful discussions about cosmic-ray data observations gathered on board Solar Orbiter. We thank also the PHI and EUI Collaborations for providing useful details about instrument geometries for S/C simulations.
References
- Abe, K., Fuke, H., Haino, S., et al. 2014, Adv. Space Res., 53, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2011, Science, 332, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Ali Cavasonza, L., Alpat, B., et al. 2018, Phys. Rev. Lett., 121, 051101 [Google Scholar]
- AMS Collaboration (Aguilar, M., et al.) 2002, Phys. Rep., 366, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Andretta, V., Bemporad, A., Focardi, M., et al. 2014, in Software and Cyberinfrastructure for Astronomy III, SPIE Conf. Ser., 9152, 91522Q [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, E., Romoli, M., Andretta, V., et al. 2020, A&A, 642, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armano, M., Audley, H., Auger, G., et al. 2016, Phys. Rev. Lett., 116, 231101 [NASA ADS] [CrossRef] [Google Scholar]
- Armano, M., Audley, H., Baird, J., et al. 2018a, ApJ, 854, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Armano, M., Audley, H., Baird, J., et al. 2018b, Phys. Rev. Lett., 120, 061101 [NASA ADS] [CrossRef] [Google Scholar]
- Armano, M., Audley, H., Baird, J., et al. 2019, ApJ, 874, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, A. 1998, Space Sci. Rev., 83, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Battistoni, G., Boehlen, T., Cerutti, F., et al. 2014, in Joint International Conference on Supercomputing in Nuclear Applications + Monte Carlo, 06005 [Google Scholar]
- Böhlen, T. T., Cerutti, F., Chin, M. P. W., et al. 2014, Nucl. Data Sheets, 120, 211 [CrossRef] [Google Scholar]
- Burger, R. A., Potgieter, M. S., & Heber, B. 2000, J. Geophys. Res.: Space Phys., 105, 27447 [NASA ADS] [CrossRef] [Google Scholar]
- Clette, F., Svalgaard, L., Vaquero, J. M., & Cliver, E. W. 2014, Space Sci. Rev., 186, 35 [CrossRef] [Google Scholar]
- De Simone, N., Di Felice, V., Gieseler, J., et al. 2011, Astrophys. Space Sci. Trans., 7, 425 [Google Scholar]
- Delaboudinière, J. P., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [Google Scholar]
- Florinski, V., & Pogorelov, N. V. 2009, ApJ, 701, 642 [CrossRef] [Google Scholar]
- Freiherr von Forstner, J. L., Dumbović, M., Möstl, C., et al. 2021, A&A, 656, A1 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García Marirrodriga, C., Pacros, A., Strandmoe, S., et al. 2021, A&A, 646, A121 [CrossRef] [EDP Sciences] [Google Scholar]
- Gleeson, L. J., & Axford, W. I. 1968, ApJ, 154, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Grimani, C., Vocca, H., Barone, M., et al. 2004, CQG, 21, S629 [NASA ADS] [CrossRef] [Google Scholar]
- Grimani, C., Vocca, H., Bagni, G., et al. 2005, CQG, 22, S327 [NASA ADS] [CrossRef] [Google Scholar]
- Grimani, C., Fabi, M., Finetti, N., & Tombolato, D. 2008, Int. Cosmic Ray Conf., 1, 485 [NASA ADS] [Google Scholar]
- Grimani, C., Telloni, D., Benella, S., et al. 2019, Atmosphere, 10, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Grimani, C., Cesarini, A., Fabi, M., et al. 2020, ApJ, 904, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Jokipii, J. R., Levy, E. H., & Hubbard, W. B. 1977, ApJ, 213, 861 [CrossRef] [Google Scholar]
- Lechner, A., Auchmann, B., Baer, T., et al. 2019, Phys. Rev. Accel. Beams, 22 [CrossRef] [Google Scholar]
- Logachev, Y. I., Zeldovich, M. A., Surova, G. M., & Kecskemety, K. 2003, Cosmic Res., 41, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Marquardt, J., & Heber, B. 2019, A&A, 625, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, G. M., Ho, G. C., Allen, R. C., et al. 2021, A&A, 656, L5 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Papini, P., Grimani, C., & Stephens, S. 1996, Nuovo Cim. C, 19, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Persici, A. 2021, Thesis, University of Urbino Carlo Bo [Google Scholar]
- Picozza, P., Galper, A., Castellini, G., et al. 2007, Astropart. Phys., 27, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Plainaki, C., Lilensten, J., Radioti, A., et al. 2016, J. Space Weather Space Clim., 6, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plainaki, C., Antonucci, M., Bemporad, A., et al. 2020, J. Space Weather Space Clim., 10, 6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rochus, P., Auchère, F., Berghmans, D., et al. 2020, A&A, 642, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-Pacheco, J., Wimmer-Schweingruber, R. F., Mason, G. M., et al. 2020, A&A, 642, A7 [Google Scholar]
- Shikaze, Y., Haino, S., Abe, K., et al. 2007, Astropart. Phys., 28, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, A. K., & Bhargawa, A. 2019, Ap&SS, 364, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, E. C. 1964, J. Geophys. Res., 69, 3939 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2013, Science, 341, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, J. 1971, Nucl. Instrum. Methods, 95, 5 [Google Scholar]
- Telloni, D., Fabi, M., Grimani, C., & Antonucci, E. 2016, AIP Conf. Proc., 1720 [Google Scholar]
- Usoskin, I. G., Bazilevskaya, G. A., & Kovaltsov, G. A. 2011, J. Geophys. Res. (Space Phys.), 116, A02104 [Google Scholar]
- Usoskin, I. G., Gil, A., Kovaltsov, G. A., Mishev, A. L., & Mikhailov, V. V. 2017, J. Geophys. Res. (Space Phys.), 122, 3875 [NASA ADS] [CrossRef] [Google Scholar]
- Villani, M., Benella, S., Fabi, M., & Grimani, C. 2020, Appl. Surface Sci., 512 [Google Scholar]
- Vlachoudis, V. 2009, in International Conference on Mathematics, Computational Methods& Reactor Physics (M&C 2009), Saratoga Springs, New York, 790 [Google Scholar]
- Wenzel, K. P., Marsden, R. G., Page, D. E., & Smith, E. J. 1992, A&AS, 92, 207 [Google Scholar]
- Wibberenz, G., Kunow, H., Müller-Mellin, R., et al. 1992, Geophys. Res. Lett., 19, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Wimmer-Schweingruber, R. F., Janitzek, N. P., Pacheco, D., et al. 2021, A&A, 656, A22 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winkler, W. 1976, Acta Astron., 3, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Wuelser, J. P., Lemen, J. R., Tarbell, T. D., et al. 2004, in Telescopes and Instrumentation for Solar Astrophysics, eds. S. Fineschi, M. A. Gummin, et al., Int. Soc. Opt. Photonics (SPIE), 5171, 111 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameterizations of proton and helium energy spectra in June–July 2020 above 70 MeV n−1.
All Figures
 |
Fig. 1. Average monthly sunspot number observed since 1994 (Clette et al. 2014). |
| In the text | |
 |
Fig. 2. Predictions of proton and 4He nucleus fluxes during the summer 2020 for the Solar Orbiter mission. The top and bottom continuous (protons) and dashed (4He nuclei) curves are obtained with the G&A model above 70 MeV(/n) for a solar modulation parameter of 300 and 340 MV c−1, respectively. The dotted curve represents the lower limit to the predictions of the proton spectrum for the same period, representing the Pamela experiment data gathered in 2008 during a period of solar activity similar to that of Solar Orbiter but during a negative GSMF epoch. Data are reported in Stone (1964, solid dots), Logachev et al. (2003, open triangles), and Marquardt & Heber (2019, solid triangles). The solid stars and the open squares indicate the EPD/HET measurements gathered in the summer 2020 on board Solar Orbiter for protons and helium nuclei, respectively. |
| In the text | |
 |
Fig. 3. STEREO-B COR 1 data gathered in 2007 and reported in Andretta et al. (2014). The dark area is associated with VL photon signals and dark current, while the white area is ascribable to the passage of high-energy particles in the VL detector. |
| In the text | |
 |
Fig. 4. Polarized brightness image of the solar corona in VL (June 21, 2020). The vertical orientation is north-south, according to the Solar axis. The image was obtained with an exposure time of 30 s at a distance of 0.5 AU from the Sun. |
| In the text | |
 |
Fig. 5. Example of cosmic-ray matrix corner window opening with the APViewer. |
| In the text | |
 |
Fig. 6. Examples of cosmic-ray tracks observations in the Metis VL images (top panels and bottom-left panel). A spurious pattern of hit pixels ascribable to a bright external source, such as a star, appears in the bottom right panel. |
| In the text | |
 |
Fig. 7. Solar Orbiter geometrical model. Remote sensing instruments and electronic boxes are visible. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.