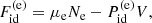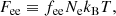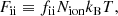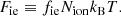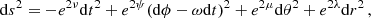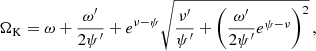| Issue |
A&A
Volume 656, December 2021
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202039749 | |
| Published online | 03 December 2021 | |
Mass limits of the extremely fast-spinning white dwarf CTCV J2056–3014
1
Instituto de Formação de Educadores, Universidade Federal do Cariri, R. Olegário Emidio de Araujo, s/n – Aldeota, 63260-000 Brejo Santo, CE, Brazil
e-mail: edson.otoniel@ufca.edu.br
2
Departamento de Física, Universidade Tecnológica Federal do Paraná, 85884-000 Medianeira, PR, Brazil
3
Divisão de Astrofísica, Instituto Nacional de Pesquisas Espaciais, Avenida dos Astronautas 1758, 12227–010 São José dos Campos, SP, Brazil
e-mail: jazielcoelho@utfpr.edu.br
4
Departamento de Física, Instituto Tecnológico de Aeronáutica, Praça Marechal Eduardo Gomes, 50 – Vila das Acacias, 12228–900 São José dos Campos, SP, Brazil
5
Department of Physics, San Diego State University, 5500 Campanile Drive, San Diego, CA 92182, USA
6
Center for Astrophysics and Space Sciences, University of California at San Diego, La Jolla, CA 92093, USA
e-mail: fweber@sdsu.edu
Received:
23
October
2020
Accepted:
11
October
2021
CTCV J2056–3014 is a nearby cataclysmic variable with an orbital period of approximately 1.76 h at a distance of about 853 light-years from the Earth. Its recently reported X-ray properties suggest that J2056–3014 is an unusual accretion-powered intermediate polar that harbors a fast-spinning white dwarf (WD) with a spin period of 29.6 s. The low X-ray luminosity and the relatively modest accretion rate per unit area suggest that the shock is not occurring near the WD surface. It has been argued that, under these conditions, the maximum temperature of the shock cannot be directly used to determine the mass of the WD (which, under the abovementioned assumptions, would be around 0.46 M⊙). Here, we explore the stability of this rapidly rotating WD using a modern equation of state (EoS) that accounts for electron–ion, electron–electron, and ion–ion interactions. For this EoS, we determine the mass density thresholds for the onset of pycnonuclear fusion reactions and study the impact of microscopic stability and rapid rotation on the structure and stability of WDs, considering them with helium, carbon, oxygen, and neon. From this analysis, we obtain a minimum mass for CTCV J2056–3014 of 0.56 M⊙ and a maximum mass of around 1.38 M⊙. If the mass of CTCV J2056–3014 is close to the lower mass limit, its equatorial radius would be on the order of 104 km due to rapid rotation. Such a radius is significantly larger than that of a nonrotating WD of average mass (0.6 M⊙), which is on the order of 7 × 103 km. The effects on the minimum mass of J2056–3014 due to changes in the temperature and composition of the stellar matter were found to be negligibly small.
Key words: dense matter / stars: rotation / instabilities / nuclear reactions, nucleosynthesis, abundances / stars: fundamental parameters / white dwarfs
© ESO 2021
1. Introduction
Lopes de Oliveira et al. (2020) report on X-ray Multi-Mirror Mission (XMM-Newton) observations that reveal CTCV J2056–3014 to be an X-ray-faint intermediate polar harboring an extremely fast-spinning white dwarf (WD) with a coherent 29.6 s pulsation. This modulation seen in X-rays is also identified in all optical light curves. Over the last decade, there has been increasing interest from the astrophysics community in fast-spinning WDs, both from the theoretical and observational points of view. Typically, WDs rotate with periods of days or even years. A pulsating WD named AR Scorpii was recently discovered (see Marsh et al. 2016; Geng et al. 2016; Buckley et al. 2017). It emits electromagnetic radiation ranging from ultraviolet wavelengths into the radio regime, pulsing in brightness with a spin period of 1.97 min. Other sources have also been observed with similar spin frequencies. A specific example is AE Aquarii, with a short rotation period of P = 33.08 s (see, e.g., Ikhsanov & Biermann 2006; Terada et al. 2008; Kitaguchi et al. 2014). The pulsations were originally discovered in the optical (Patterson 1979), then confirmed in soft X-rays (Patterson et al. 1980) and the ultraviolet (Eracleous et al. 1994). Furthermore, the XMM-Newton observatory has observed a WD rotating faster than AE Aquarii. It was shown by Mereghetti et al. (2009) that the X-ray pulsator RX J0648.0–4418, which belongs to the binary system HD 49798/RXJ0648.0–4418, is a massive (M = 1.28 M⊙) WD with a very small spin period of P = 13.2 s (see Israel et al. 1997), but its nature is not clear (see Mereghetti et al. 2016 and Popov et al. 2018 for details). More recently, Ashley et al. (2020) reported that, based on Hubble Space Telescope ultraviolet data, V1460 Her exhibits strong pulsations with a period of 38.9 s.
In addition, it is important to mention the newly discovered, highly magnetized, isolated, and rapidly rotating WD, designated ZTF J190132.9+145808.7, which, with a mass of 1.35 M⊙ and a radius of 2140 km (see Caiazzo et al. 2021), is as small as the Moon. Such a small radius implies that the star’s mass is close to the Chandrasekhar mass limit. Furthermore, since this WD is isolated, we are observing, for the first time, a very fast, nearby (∼40 pc) WD that is not in a binary system but seems to have been originated by a merger of two WDs. In fact, this source may be the missing link to support a recent claim made in Malheiro et al. (2012) and Coelho & Malheiro (2012, 2014) that some of the anomalous X-ray pulsars (AXPs; see Olausen & Kaspi 2014; Kaspi & Beloborodov 2017) that spin with period of ∼10 s could be isolated, very massive, magnetic, and fast WDs that resulted from WDs mergers (Rueda et al. 2013). Recently, the quiescent spectral energy distribution of (AXP) 4U 0142+61 was reproduced with great success from mid-infrared up to hard X-rays using plausible physical components and parameters (see Cáceres et al. 2017; Borges et al. 2020, for details).
Several theoretical works regarding very magnetic, massive, and fast WDs have been published in the last few years (Belyaev et al. 2015; Lobato et al. 2016; Mukhopadhyay & Rao 2016; Sousa et al. 2020a,b). More recently, Kalita & Mukhopadhyay (2019) showed that continuous gravitational waves can be emitted from rotating magnetized WDs and could possibly be detected in the near future by instruments such as Laser Interferometer Space Antenna (LISA), Big Bang Observer (BBO), and Deci-hertz Interferometer Gravitational wave Observatory (DECIGO), and the Einstein Telescope (see also Sousa et al. 2020a,b).
From a theoretical point of view, WDs can rotate at periods as short as P ≈ 0.5 s (see Boshkayev et al. 2013a), and they can be formed, as we pointed out above, in double WD mergers (see García-Berro et al. 2012; Rueda et al. 2013; Ilkov & Soker 2013; Becerra et al. 2018, and references therein). Livio & Pringle (1998) and Livio (1999) investigated the role of rotation for the maximum mass of a WD (see also Ostriker & Mark 1968; Ostriker & Bodenheimer 1968). General relativistic effects on uniformly rotating WDs have been studied more recently by Boshkayev et al. (2013b). Also, a general relativistic magnetohydrodynamic framework that describes rotating and magnetized axisymmetric WDs was explored sequentially by Subramanian & Mukhopadhyay (2015) and Bera & Bhattacharya (2016).
On the other hand, the two main observables of a WD, its mass and radius, both depend crucially on the equation of state (EoS). It is worth mentioning that the mass presented by Lopes de Oliveira et al. (2020) was poorly determined in the sense that it is based on a fit that uses an X-ray spectrum model that may not be the most appropriate for the source, in addition to other approaches used to calculate the WD mass from the maximum temperature in the post-shock region. According to the authors, under such assumptions the mass would be around 0.46 M⊙. In addition, some arguments strongly suggest that the magnetic field of J2056 is very low (for details, see Lopes de Oliveira et al. 2020).
In this paper we describe WD matter in terms of helium, carbon, oxygen, or a mixture of oxygen (64%) and neon (36%), taking not only the electron Fermi gas contribution into account, but also the contributions from electron–ion, electron–electron, and ion–ion interactions. Recently, we performed a stability analysis of the matter in the cores of WDs against pycnonuclear fusion reactions (see Otoniel et al. 2019; Malheiro et al. 2021). In the present paper, we determine theoretical bounds on the mass of CTCV J2056–3014 that follow from mass shedding caused by rotation at the Kepler frequency and pycnonuclear fusion reactions among carbon nuclei in the core of WD matter.
This paper is organized as follows. In Sect. 2 we present the theoretical framework and methodology used to determined the WD composition and structure, as well as details about Hartle’s stellar rotation formalism and pycnonuclear fusion reactions. In Sect. 3 we present our main results. Concluding remarks are presented in Sect. 4.
2. The model
The increase in more sensitive techniques of observation and detection of WDs (see Eisenstein et al. 2006; Kepler et al. 2013, 2015; Córsico et al. 2019), coupled with advanced calculations of the properties of Fermionic matter under extreme physical conditions, has led to considerable interest in theoretical studies of the structure and evolution of WDs (see, e.g., Chamel et al. 2013, 2014; Boshkayev et al. 2013a; Coelho et al. 2014; Becerra et al. 2018; Otoniel et al. 2019). The EoS of relativistic and degenerate WD matter, which accounts for the excess free energy of a one-component plasma (OCP) made of ions derived from Monte Carlo simulations, is computed from the Helmholtz free energy,
where 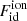 denotes the free energy of a nonrelativistic classical gas given by
denotes the free energy of a nonrelativistic classical gas given by
Here, Nj = njV, kB is the Boltzmann constant, T the temperature of the gas, nj the total number density of ions, and 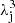 the thermal de Broglie wavelength, λj = (2πℏ2/mjkBT)1/2, where mj is the ion mass and gj the spin multiplicity. The free energy of electrons (
the thermal de Broglie wavelength, λj = (2πℏ2/mjkBT)1/2, where mj is the ion mass and gj the spin multiplicity. The free energy of electrons (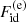 ) is given by (see Chabrier & Potekhin 1998)
) is given by (see Chabrier & Potekhin 1998)
where μe is the electron chemical potential. The pressure (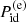 ) and the electron number density (ne = Ne/V) are functions of μe and T and can be written in terms of the Fermi-Dirac integrals Iν(χe,τ), where χe = μe/kBT and ν = 1/2, 3/2, and 5/2. The chemical potential can be obtained by inverting the function ne(χe,T) numerically. The last three terms on the right-hand side of Eq. (1) represent the free energies arising from electron–electron, ion–ion, and ion–electron interactions given by (Chabrier & Potekhin 1998; Potekhin & Chabrier 2000)
) and the electron number density (ne = Ne/V) are functions of μe and T and can be written in terms of the Fermi-Dirac integrals Iν(χe,τ), where χe = μe/kBT and ν = 1/2, 3/2, and 5/2. The chemical potential can be obtained by inverting the function ne(χe,T) numerically. The last three terms on the right-hand side of Eq. (1) represent the free energies arising from electron–electron, ion–ion, and ion–electron interactions given by (Chabrier & Potekhin 1998; Potekhin & Chabrier 2000)
The pressure (P) and the entropy (S) of a plasma with a fixed number of particles in a given volume (V) are obtained from the thermodynamic relations P = − (∂F/∂V)T, N and S = − (∂F/∂T)V, N, with the internal energy of the system given by U = F + TS (see Chabrier & Potekhin 1998; Potekhin & Chabrier 2000).
We computed the EoS for a system of carbon ions at temperatures of T = 104 K and 107 K. Although there are no observational restrictions on what type of WD exists in the CTCV J2056–3014 system, it is worth mentioning that we did the calculations for different WD constitutions. The results are very similar if heavier elements are considered, as shown in this paper. To be specific, we described WD matter in terms of helium, carbon, oxygen, or a mixture of oxygen (64%) and neon (36%), taking the contributions from electron–ion, electron–electron, and ion–ion interactions into account. Here, we used an EoS for the free energy of an ideal relativistic electron gas with an arbitrary degeneracy as well as for the free energy excess of the OCP. We used the Chabrier & Potekhin EoS mainly because of the temperature dependence and electron interactions, which allowed us to create more realistic models to be compared with observed data. In Fig. 1 we show the mass as a function of radius for WDs considering Chandrasekhar’s EoS and the Chabrier & Potekhin EoS for carbon and oxygen. It is important to mention that the Chabrier & Potekhin EoS enables us to obtain different minimum masses according to the composition and temperature, in contrast to Chandrasekhar’s EoS. Additionally, although the difference between the curves is quite small, the precision of the Chabrier & Potekhin EoS is crucial since we are searching for minimum masses. An upper bound on the WD mass follows from the occurrence of electron capture and from the pycnonuclear fusion reaction instability (see Sect. 2.2). These are marked with a solid square and a solid circle in Fig. 1. We thus conclude that the upper limit on the gravitational mass of J2056–3014 is around 1.38 M⊙, provided it is a carbon or oxygen WD rotating near its mass-shedding limit.
 |
Fig. 1. Mass-radius relationships of WDs computed for the EoSs of Chabrier & Potekhin (black and blue curves) and Chandrasekhar (dashed red curve). |
2.1. Hartle’s stellar rotation formalism
The structure of WDs is governed by hydrostatic equilibrium, where gravity is balanced by the outward pressure generated by a relativistic electron gas. Recently, it has been noted that contributions from general relativity ought to be taken into account when modeling the structure of WDs (see Boshkayev et al. 2013b). The Tolman-Oppenheimer-Volkoff equation describes the structure of nonrotating stellar objects and, in particular, determines the radii and masses of such objects. However, in order to account for rotational effects, Einstein’s field equations need to be solved for a metric that accounts for rotational deformation and the dragging of local inertial frames (see Hartle 1967; Hartle & Thorne 1968; Friedman et al. 1986). Such a metric is given by
where the metric functions ν, ψ, μ, and λ and the frame dragging frequency (ω) depend on the radial coordinate (r), the polar angle (θ), and, implicitly, the star’s rotational frequency (Ω; see Friedman et al. 1986; Weber 1999 for details). Thus, we performed a 2D calculation where the rotational star deformation is described by the polar angle (θ), and the compact objects are symmetric around the axis of rotation. The Ω is taken to be in the range of 0 ≤ Ω ≤ ΩK, where ΩK ( = 2π/PK) denotes the Kepler (mass-shedding) frequency, which terminates stable rotation. The ΩK sets an absolute upper limit on rapid rotation. The Kepler frequency must be computed self-consistently, together with Einstein’s field equations for the metric functions, from
where the primes denote partial derivatives of the metric functions with respect to the radial coordinate (Weber & Glendenning 1992; Glendenning & Weber 1994). Hartle’s perturbative treatment of compact objects leads to results that are in good agreement with those obtained by a numerically exact treatment of Einstein’s field equations. This is particularly the case for the mass increase due to rapid rotation at the Kepler frequency Weber & Glendenning (1992).
2.2. Pycnonuclear fusion reactions
We recently performed a stability analysis of the matter in the cores of WDs against pycnonuclear fusion reactions and electron capture reactions (see Otoniel et al. 2019; Malheiro et al. 2021, for details). In the current paper we investigate the stability of carbon WD matter to pycnonuclear fusion reactions using up-to-date theoretical models (see Gasques et al. 2005; Golf et al. 2009). We assumed a uniform nuclear composition throughout the star and focused on nuclear fusion reactions only1 among heavy atomic nuclei, schematically expressed as 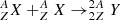 . Examples of such a reaction are carbon on carbon (12C+12C) and oxygen on oxygen (16O+16O). Pycnonuclear reactions have been theoretically calculated over a significant range of stellar densities (see Gasques et al. 2005), including the density ranges that exist in the interiors of WDs (see Chamel et al. 2013, 2014; Chatterjee et al. 2017). The nuclear fusion rates at which pycnonuclear reactions may actually proceed are highly uncertain because of some poorly constrained parameters (see Gasques et al. 2005; Yakovlev et al. 2006, and references therein).
. Examples of such a reaction are carbon on carbon (12C+12C) and oxygen on oxygen (16O+16O). Pycnonuclear reactions have been theoretically calculated over a significant range of stellar densities (see Gasques et al. 2005), including the density ranges that exist in the interiors of WDs (see Chamel et al. 2013, 2014; Chatterjee et al. 2017). The nuclear fusion rates at which pycnonuclear reactions may actually proceed are highly uncertain because of some poorly constrained parameters (see Gasques et al. 2005; Yakovlev et al. 2006, and references therein).
3. Stability boundaries
In this section we establish constraints on the mass and radius of the rapidly rotating WD CTCV J2056–3014 that follow from stable rapid stellar rotation and the microscopic stability of matter, as described in Sects. 2.1 and 2.2. Figure 2 shows the rotational periods of carbon WDs spinning at their respective mass-shedding periods (PK). The solid square in this figure corresponds to a WD whose Kepler period is equal to the rotation period observed for CTCV J2056–3014 of P = 29.6 s. If this period is close to the mass-shedding period, the lower bound on the gravitational mass of J2056–3014 would be 0.56 M⊙ and the central mass density of this object would be 1.70 × 106 g cm−3 (see Table 1). An upper bound on the mass follows from the occurrence of pycnonuclear reactions in WDs. This is the case for the WD model marked with a solid triangle on the dashed line. We thus conclude that the upper limit on the gravitational mass of J2056–3014 is around 1.5 M⊙, provided it is a carbon WD rotating near its mass-shedding limit. The green shaded area in Fig. 2 shows the location of WDs spinning below that limit.
 |
Fig. 2. Mass limits on CTCV J2056–3014 determined by rotation at the Kepler period (PK) and the onset of pycnonuclear reactions (for carbon WD). A minimum mass (solid square) of 0.56 M⊙ is obtained if CTCV J2056–3014’s rotational period of 29.6 s is close to the mass-shedding limit. The upper mass limit (solid triangle) of around 1.5 M⊙ results from the onset of pycnonuclear reactions if CTCV is a carbon WD. |
Theoretically established mass (M), radius (R), and central mass density (ρc) of J2056–3014 set by mass shedding (rotation at the Kepler period of 29.6 s) and pycnonuclear fusion reactions among carbon nuclei in the core of a WD.
When heavier elements, such as oxygen and a mixture of oxygen (64%) and neon (36%), are considered, our calculations indicate that the minimum WD mass for CTCV J2056–3014 decreases only slightly. Temperature effects were also considered on the minimum mass star, and we obtain a small increase in the equatorial radius with an increase in temperature. In our calculations, the difference between the equatorial and polar radius of rapidly spinning WDs was found to be as large as around 10% (for the star with 0.56 M⊙ and P = 29.6 s). In addition, the temperature effect in the minimum mass is also negligible (see Table 2).
Minimum mass (M), equatorial radius (R), and central mass density (ρc) predicted for CTCV J2056–3014 for different matter compositions and temperatures if the star’s rotational period of 29.6 s is the Kepler period.
In Fig. 3 we show the gravitational WD mass as a function of central mass density. In contrast to Fig. 2, where all stars along the dashed line rotate at their respective mass-shedding limits, the stars along the dashed line shown in this figure all rotate at 29.6 s, the spin period of CTCV J2056–3014. This lies well above the respective Kepler periods for most stars along the sequence. The most massive WD on the sequence, marked with a solid triangle, has a central density of 9.26 × 109 g cm−3 (see Table 1). At this density, pycnonuclear reactions set in and terminate the microscopic stability of WDs. The area highlighted in green shows the mass-central density region predicted to exist in a WD with a rotation period of P ≥ 29.6 s. We stress that this is an important theoretical limit that will be useful for the interpretation of WDs discovered in the future.
 |
Fig. 3. Carbon WD mass vs. central mass density. All stars along the dashed curve rotate at P = 29.6 s, as observed for J2056–3014. The solid square marks the least massive WD, whose Kepler period is 29.6 s. For all other stars along the dashed line, the rotation period of 29.6 s is greater than the Kepler period. The most massive WD on the sequence, marked with a solid triangle, has a central density of 9.26 × 109 g cm−3. At this density, pycnonuclear reactions set in and microscopic stability ends. |
The reaction rates used to study the pycnonuclear reactions were calculated with an astrophysical S factor computed for the NL2 nuclear model parametrization (for details, see Otoniel et al. 2019). The threshold density at which pycnonuclear reactions are triggered in a carbon WD is shown in Table 1. We also adopted the pycnonuclear reaction timescale of 10 Gyr to obtain the threshold density. It is worth mentioning that the reaction rates are rather uncertain and that the analytic astrophysical S factor has an uncertainly of about 3.5, which affects the density thresholds of pycnonuclear reactions and their reaction times considerably.
It is important to mention what happens with the allowed mass region in Fig. 3 if different constitutions of matter are considered. As reported by Salpeter (1961), the threshold density for pycnonuclear reactions is smaller for helium than for carbon. Indeed, the threshold density for helium is around 87% smaller than for carbon. This would make the allowed mass regions for He WDs smaller than those of the carbon WDs shown in Fig. 3. Besides, as can be observed in Table 2, the allowed region of helium WDs decreases even more at the minimum mass. Therefore, for oxygen and even a mixture of oxygen (64%) and neon (36%), the stability region would be greater than for a pure carbon WD.
4. Concluding remarks
In this paper we stress that some macro and micro physical aspects, such as rotation and pycnonuclear fusion reactions, are of great relevance for the self-consistent description of the structure and the assessment of the stability of CTCV J2056–3014. As argued by Lopes de Oliveira et al. (2020), the mass inferred for this object was poorly estimated in the sense that it is based on the assumptions often made when solving the structure equations in the X-ray-emitting region that is produced by a shock near the WD. These assumptions include radial accretion, free-fall from infinity, and a shock near the WD surface such that the maximum temperature of the shock cannot be directly used to calculate the mass of the WD. Here, we used the EoS of helium, carbon, oxygen, and neon WDs that accounts for electron–ion, electron–electron, and ion–ion interactions. For this EoS, we determined the mass density thresholds for the onset of pycnonuclear fusion reactions and studied the impact of microscopic stability and of rapid rotation on the structure and stability of WDs. Our analysis predicts a minimum mass for CTCV J2056–3014 of 0.53 M⊙ for a mixture of oxygen (64%) and neon (36%). We estimate the theoretical limit of the mass-central density region for future observations of WDs with rotation periods P ≥ 29.6 s. Should the mass of CTCV J2056–3014 be close to the lower mass limit at T = 104 K, its equatorial radius would be on the order of 104 km due to rapid rotation. Such a radius is significantly greater than the radius of a nonrotating WD of average mass (0.6 M⊙), which is on the order of 7 × 103 km.
Also, we stress an important point of our analysis. Very fast WDs with periods in the range of tens of seconds, and even a WD pulsar, have been detected in recent years. In order to spin so fast, such WDs need to be massive, with the minimum mass limit determined by the Kepler frequency. The Zwicky Transient Facility is currently discovering large numbers of very massive and fast-spinning WDs (see Caiazzo et al. 2021). These and future observations will help us to better understand such objects.
It is known that, at sufficiently high densities in the interior of WDs, the inverse β-decay, or electron capture, process becomes energetically favorable. Such a process destabilizes the star because the electrons provide all the pressure required to balance gravity. However, as pointed out by Otoniel et al. (2019), these densities are higher than the density at which pycnonuclear fusion reactions in a 12C WD set in.
Acknowledgments
The authors thank the referee for comments which helped to improve the quality of the manuscript. We are deeply grateful to Claudia V. Rodrigues for useful discussions. E.0. is grateful for the support of Pró-Reitoria de Pesquisa e Inovação – EDITAL 01/2020/PRPI/UFCA. J.G.C. is likewise grateful to the support of CNPq (421265/2018-3 and 305369/2018-0), FAPESP Project No. 2015/15897-1, and NAPI “Fenômenos Extremos do Universo” of Fundação de Apoio á Ciência, Tecnologia e Inovação do Paraná. M.M. acknowledges financial support from FAPESP under the thematic project 13/26258-4, Capes, CNPq and INCT-FNA (Proc. No. 464898/2014-5). S.P.N. thanks Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Grant No. 140863/2017 − 6 and CAPES for the financial support. F.W. is supported by the National Science Foundation (USA) under Grant PHY-1714068 and PHY-2012152.
References
- Ashley, R. P., Marsh, T. R., Breedt, E., et al. 2020, MNRAS, 499, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Becerra, L., Rueda, J. A., Lorén-Aguilar, P., & García-Berro, E. 2018, ApJ, 857, 134 [CrossRef] [Google Scholar]
- Belyaev, V. B., Ricci, P., Šimkovic, F., et al. 2015, Nucl. Phys. A, 937, 17 [CrossRef] [Google Scholar]
- Bera, P., & Bhattacharya, D. 2016, MNRAS, 456, 3375 [NASA ADS] [CrossRef] [Google Scholar]
- Borges, S. V., Rodrigues, C. V., Coelho, J. G., Malheiro, M., & Castro, M. 2020, ApJ, 895, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Boshkayev, K., Rueda, J. A., Ruffini, R., & Siutsou, I. 2013a, ApJ, 762, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Boshkayev, K., Rueda, J., & Ruffini, R. 2013b, Int. J. Mod. Phys. Conf. Ser., 23, 193 [CrossRef] [Google Scholar]
- Buckley, D. A. H., Meintjes, P. J., Potter, S. B., Marsh, T. R., & Gänsicke, B. T. 2017, Nat. Astron., 1, 0029 [NASA ADS] [CrossRef] [Google Scholar]
- Cáceres, D. L., de Carvalho, S. M., Coelho, J. G., de Lima, R. C. R., & Rueda, J. A. 2017, MNRAS, 465, 4434 [CrossRef] [Google Scholar]
- Caiazzo, I., Burdge, K. B., Fuller, J., et al. 2021, Nature, 595, 39 [CrossRef] [Google Scholar]
- Chabrier, G., & Potekhin, A. Y. 1998, Phys. Rev. E, 58, 4941 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Fantina, A. F., & Davis, P. J. 2013, Phys. Rev. D, 88, 081301(R) [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Molter, E., Fantina, A., & Arteaga, D. P. 2014, Phys. Rev. D, 90, 043002 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, D., Fantina, A. F., Chamel, N., Novak, J., & Oertel, M. 2017, MNRAS, 469, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Coelho, J. G., & Malheiro, M. 2012, Int. J. Mod. Phys. Conf. Ser., 18, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Coelho, J. G., & Malheiro, M. 2014, PASJ, 66, 14 [NASA ADS] [Google Scholar]
- Coelho, J. G., Marinho, R. M., Malheiro, M., et al. 2014, ApJ, 794, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., & Kepler, S. O. 2019, A&A Rv, 27, 7 [Google Scholar]
- Eisenstein, D. J., Liebert, J., Harris, H. C., et al. 2006, ApJS, 167, 40 [CrossRef] [Google Scholar]
- Eracleous, M., Horne, K., Robinson, E. L., et al. 1994, ApJ, 433, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, J. L., Ipser, J. R., & Parker, L. 1986, ApJ, 304, 115 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Lorén-Aguilar, P., Aznar-Siguán, G., et al. 2012, ApJ, 749, 25 [CrossRef] [Google Scholar]
- Gasques, L. R., Afanasjev, A. V., Aguilera, E. F., et al. 2005, Phys. Rev. C, 72, 025806 [NASA ADS] [CrossRef] [Google Scholar]
- Geng, J.-J., Zhang, B., & Huang, Y.-F. 2016, ApJ, 831, L10 [CrossRef] [Google Scholar]
- Glendenning, N. K., & Weber, F. 1994, Phys. Rev. D, 50, 3836 [NASA ADS] [CrossRef] [Google Scholar]
- Golf, B., Hellmers, J., & Weber, F. 2009, Phys. Rev. C, 80, 015804 [NASA ADS] [CrossRef] [Google Scholar]
- Hartle, J. B. 1967, ApJ, 150, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Hartle, J. B., & Thorne, K. S. 1968, ApJ, 153, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Ikhsanov, N. R., & Biermann, P. L. 2006, A&A, 445, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilkov, M., & Soker, N. 2013, MNRAS, 428, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Stella, L., Angelini, L., et al. 1997, ApJ, 474, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Kalita, S., & Mukhopadhyay, B. 2019, MNRAS, 490, 2692 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, V. M., & Beloborodov, A. M. 2017, ARA&A, 55, 261 [Google Scholar]
- Kepler, S. O., Kleinman, S. J., Pelisoli, I., et al. 2013, MNRAS, 429, 2934 [NASA ADS] [CrossRef] [Google Scholar]
- Kepler, S. O., Pelisoli, I., Koester, D., et al. 2015, MNRAS, 446, 4078 [Google Scholar]
- Kitaguchi, T., An, H., Beloborodov, A. M., et al. 2014, ApJ, 782, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M. 1999, in Annapolis Workshop on Magnetic Cataclysmic Variables, eds. C. Hellier, & K. Mukai, ASP Conf. Ser., 157, 247 [NASA ADS] [Google Scholar]
- Livio, M., & Pringle, J. E. 1998, ApJ, 505, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Lobato, R. V., Malheiro, M., & Coelho, J. G. 2016, Int. J. Mod. Phys. D, 25, 1641025 [CrossRef] [Google Scholar]
- Lopes de Oliveira, R., Bruch, A., Rodrigues, C. V., Oliveira, A. S., & Mukai, K. 2020, ApJ, 898, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Malheiro, M., Rueda, J. A., & Ruffini, R. 2012, PASJ, 64, 56 [NASA ADS] [Google Scholar]
- Malheiro, M., Otoniel, E., & Coelho, J. G. 2021, Braz. J. Phys., 51, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, T. R., Gänsicke, B. T., Hümmerich, S., et al. 2016, Nature, 537, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S., Tiengo, A., Esposito, P., et al. 2009, Science, 325, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S., Pintore, F., Esposito, P., et al. 2016, MNRAS, 458, 3523 [NASA ADS] [CrossRef] [Google Scholar]
- Mukhopadhyay, B., & Rao, A. R. 2016, J. Cosmol. Astropart. Phys., 2016, 007 [Google Scholar]
- Olausen, S. A., & Kaspi, V. M. 2014, ApJS, 212, 6 [Google Scholar]
- Ostriker, J. P., & Bodenheimer, P. 1968, ApJ, 151, 1089 [Google Scholar]
- Ostriker, J. P., & Mark, J. W. K. 1968, ApJ, 151, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Otoniel, E., Franzon, B., Carvalho, G. A., et al. 2019, ApJ, 879, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J. 1979, ApJ, 234, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Branch, D., Chincarini, G., & Robinson, E. L. 1980, ApJ, 240, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Popov, S. B., Mereghetti, S., Blinnikov, S. I., Kuranov, A. G., & Yungelson, L. R. 2018, MNRAS, 474, 2750 [NASA ADS] [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2000, Phys. Rev. E, 62, 8554 [NASA ADS] [CrossRef] [Google Scholar]
- Rueda, J. A., Boshkayev, K., Izzo, L., et al. 2013, ApJ, 772, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1961, ApJ, 134, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, M. F., Coelho, J. G., & de Araujo, J. C. N. 2020a, MNRAS, 492, 5949 [CrossRef] [Google Scholar]
- Sousa, M. F., Coelho, J. G., & de Araujo, J. C. N. 2020b, MNRAS, 498, 4426 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, S., & Mukhopadhyay, B. 2015, MNRAS, 454, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Terada, Y., Hayashi, T., Ishida, M., et al. 2008, PASJ, 60, 387 [NASA ADS] [Google Scholar]
- Weber, F. 1999, Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics, 1st edn. (Bristol, Philadelphia: CRC Press) [Google Scholar]
- Weber, F., & Glendenning, N. K. 1992, ApJ, 390, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., Gasques, L. R., Afanasjev, A. V., Beard, M., & Wiescher, M. 2006, Phys. Rev. C, 74, 035803 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Theoretically established mass (M), radius (R), and central mass density (ρc) of J2056–3014 set by mass shedding (rotation at the Kepler period of 29.6 s) and pycnonuclear fusion reactions among carbon nuclei in the core of a WD.
Minimum mass (M), equatorial radius (R), and central mass density (ρc) predicted for CTCV J2056–3014 for different matter compositions and temperatures if the star’s rotational period of 29.6 s is the Kepler period.
All Figures
 |
Fig. 1. Mass-radius relationships of WDs computed for the EoSs of Chabrier & Potekhin (black and blue curves) and Chandrasekhar (dashed red curve). |
| In the text | |
 |
Fig. 2. Mass limits on CTCV J2056–3014 determined by rotation at the Kepler period (PK) and the onset of pycnonuclear reactions (for carbon WD). A minimum mass (solid square) of 0.56 M⊙ is obtained if CTCV J2056–3014’s rotational period of 29.6 s is close to the mass-shedding limit. The upper mass limit (solid triangle) of around 1.5 M⊙ results from the onset of pycnonuclear reactions if CTCV is a carbon WD. |
| In the text | |
 |
Fig. 3. Carbon WD mass vs. central mass density. All stars along the dashed curve rotate at P = 29.6 s, as observed for J2056–3014. The solid square marks the least massive WD, whose Kepler period is 29.6 s. For all other stars along the dashed line, the rotation period of 29.6 s is greater than the Kepler period. The most massive WD on the sequence, marked with a solid triangle, has a central density of 9.26 × 109 g cm−3. At this density, pycnonuclear reactions set in and microscopic stability ends. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



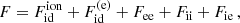
![$$ \begin{aligned} F_{\mathrm{id} }^{\mathrm{ion} }=N_{\rm j} k_{\rm B} T\left[\ln \left(n_{\rm j} \lambda _{\rm j}^{3} / g_{\rm j}\right)-1\right] . \end{aligned} $$](/articles/aa/full_html/2021/12/aa39749-20/aa39749-20-eq3.gif)