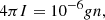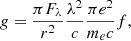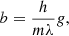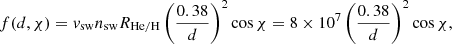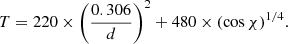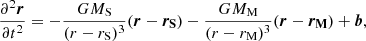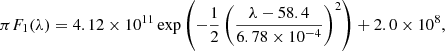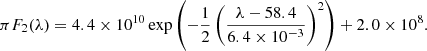EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) L7 Full HTML
Open Access
Issue
A&A
Volume 654, October 2021
Article Number L7
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202142155
Published online 14 October 2021

© M. Yoneda et al. 2021

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

Mercury’s exospheric atmosphere was first detected by the Mariner 10 spacecraft through ultraviolet (UV) observations of emission from neutral atoms of helium, oxygen, and hydrogen (Broadfoot et al. 1976). Furthermore, emission from neutral atoms of sodium, potassium, and calcium have been detected by ground-based observations (Bida et al. 2000; Potter & Morgan 1985, 1988). Magnesium emission was observed by the Messenger spacecraft (McClintock et al. 2009). The emission from neutral helium atoms in Mercury’s exosphere can be observed in the extreme-ultraviolet (EUV) range using the He I 58.4 nm emission line. This emission is due to resonant scattering of solar radiation emitted from the disk. The Mariner 10 spacecraft observed emission from neutral helium during each of its three Mercury flybys (Kumar 1976). The next Mercury surveyor, MESSENGER, carried a UV instrument, but not enough wavelength range to measure He I 58.4 nm emission (McClintock & Lankton 2007). Thus, Mariner 10 remains the only spacecraft that has observed Mercury’s helium emission so far.

There are two possible sources of helium atoms in Mercury’s exosphere. One is from He2+ ions in the solar wind, and the other is from outgassing from Mercury’s crust. Hartle et al. (1975) and Kumar (1976) pointed out that the flux of He2+ in the solar wind is enough to maintain Mercury’s helium exosphere, but they could not establish whether outgassing was an important contributor to the helium exosphere or not.

The He I 58.4 nm brightness in Rayleigh units can be written as

(1)

where g is the g factor that equals the number of photons one atom scatters per unit time (ph s−1) and n is the column density of the atoms along the line of sight (cm−2). The g factor can be derived as

(2)

where πFλ is the solar flux at the radiation wavelength λ at 1 AU from the Sun, e is the electron charge, me is the electron mass, c is the speed of light, f = 0.27 is the oscillation strength factor (Wiese & Fuhr 2009), and r is the distance from the Sun in astronomical units (AU). Also, 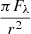is the solar flux per wavelength unit at r (AU), 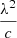is the conversion factor from the wavelength unit to the frequency unit, and 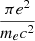is the integrated absorption coefficient per unit f value.

When helium atoms scatter the solar photons, they feel radiation pressure anti-Sunward. The acceleration due to radiation pressure b can be expressed as

(3)

where m is the mass of a single helium atom and h is the Planck constant.

Broadfoot et al. (1976) calculated the g factor for the He I 58.4 nm transition to be 6.8 × 10−5 ph s−1, and subsequent studies have adopted this value. The solar flux at this wavelength is dominated by narrow band emission. Kumar et al. (1973) measured the full width at half maximum (FWHM) of the solar emission line as ≈0.0016 nm based on observations obtained by Hall & Hinteregger (1970). This line width corresponds to a velocity range of ±4.1 km s−1. However, as shown in Fig. 2, Mercury is outside of this range for all true anomaly angles (TAA) other than in ranges of 0 ± 30° (perihelion) and 180 ± 30° (aphelion). All three Mariner 10 Mercury flybys were made when TAA ≈ 185°, and Mercury’s velocity relative to the Sun (heliocentric velocity) was < 1 km s−1. This implies that Mariner 10 would likely not have observed the He I 58.4 nm emission from Mercury if the spacecraft had had flybys at other phases in Mercury’s orbit due to Doppler dimming.

thumbnail Fig. 2.

Range of radial velocities between Mercury and the Sun as a function of the true anomaly angle. The right vertical axis shows the amount of wavelength shift in the solar He I 58.4 nm emission by the Doppler shift due to Mercury’s radial motion. Two lines at ±8.00 × 10−4 nm show the line width of the solar He I 58.4 nm emission estimated by Kumar (1976) and the corresponding velocities.

More recently, Wilhelm et al. (1997) measured line widths ≈0.015 nm for the solar He I 58.4 nm emission using SUMER (Dwivedi 1998), which was a UV spectrograph onboard the NASA Solar and Heliospheric Observatory (SOHO) spacecraft. This value is 10 times larger than that reported by Kumar et al. (1973), and corresponds to a velocity range of ±40 km s−1. This is significantly greater than Mercury’s radial velocity at any phase in the orbit. Still, when Mercury approaches its maximum radial velocity (10 km s−1), the photon flux at 58.4 nm on Mercury is 10% less than when Mercury has no heliocentric radial velocity. In addition to this effect, the solar photon flux varies due to changes in Mercury’s heliocentric distance. The solar radiation at TAA = 0° is 2.15 times greater than that at TAA = 180°.

Emission in the sodium D-line has been measured in Mercury’s exosphere from the ground since the wavelengths are in the visible range (D1: 589.59 nm, D2: 588.99 nm). Similar to the He I 58.4 nm line, the sodium D-line emission is due to resonant scattering of radiation from the solar photosphere. However, the solar spectrum shows absorption at D1 and D2 wavelengths, so sodium D-line emissions from Mercury’s exosphere are strongest at large Mercury heliocentric velocities (Schmidt et al. 2010). Thus, it can be said that helium is not the only constituent of Mercury’s exosphere whose brightness is dependent on the orbital phase, but its behavior can be different from that of sodium. In this study, we present model simulations of the He I 58.4 nm emission from Mercury’s exosphere that takes the effects of Doppler shift into account due to Mercury’s orbital motion.

2. Model simulations

It is not known exactly how helium atoms enter Mercury’s surface or how they are released into the exosphere. However, for the purpose of this work, the specific physical mechanisms are not crucial. We assume an equilibrium is reached so the number of helium atoms released from a unit surface area is the same as the number of helium ions in the solar wind absorbed by the corresponding area. For the sake of simplicity, Mercury’s magnetic field is ignored in our simulations, but it is clear that the spatial distribution of regions where the solar wind reaches the planetary surface is affected by the interactions between the solar wind and Mercury’s magnetosphere.

To focus on the effect of Mercury’s heliocentric velocity and distance, our model is simple. We assume the solar wind is radially streaming only along the Sun-Mercury line, that means we neglected the influence of the interplanetary magnetic field on the solar wind. This means a number of helium ions hitting an area with solar zenith angle χ is proportional to cos χ, and no helium ions strike the night-side hemisphere. The geometric sketch clarifying the positional relations and mathematical symbols that appear in the following equations is shown in Fig. 1. Assuming equilibrium, the number of helium atoms released (and absorbed) from a unit surface, f(d, χ), can be described as

(4)

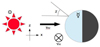thumbnail Fig. 1.

Geometric sketch to show the positional relations and explain the letters in the equations. The directions of axes x and z are the same as the horizontal and vertical axes in Fig. 4, vM and vSW are the velocities of Mercury and the solar wind, and χ is the solar zenith angle at a point on Mercury’s dayside hemisphere.

where d is the distance from Sun in AU, χ is the solar zenith angle at which helium atoms are released, vsw and nsw are the typical velocity and number density in the solar wind at 0.38 AU and given as 400 km s−1 and 40 cm−3 (Sarantos et al. 2007), and RHe/H is the ratio of the helium ions to protons in the solar wind and given as 5% based on Bochsler (2001). We note that these parameters are highly variable, although the same solar wind flux parameters and RHe/H ratio were adopted in the model study of Mercury’s helium atmosphere by Leblanc & Chaufray (2011).

thumbnail Fig. 4.

Two dimensional brightness distributions of the He I 58.4 nm emission of Mercury at three TAAs (0, 180, and 270 degrees) reproduced by model simulation. Horizontal and vertical axes correspond to the x and z directions shown in Fig. 1. The brightness was integrated in each 0.1 RM × 0.1RM box. The line width of the solar He I 58.4 nm emission is assumed to be 0.0016 nm (left column, Kumar et al. 1973) and 0.015 nm (right column, Wilhelm et al. 1997). The horizontal axis is the distance from Mercury’s center along the Sun-Mercury line, and the vertical axis is along Mercury’s rotation axis. The brightest pixels were artificially added to maintain the same color scale for the images within one column.

For the ionization rate of neutral helium atoms due to charge-exchange and photo-ionization at 1 AU, β, we adopted the value 1.08  ×  10−7 (s−1) (Ruciński & Bzowski 1996). Assuming this rate varies inversely with distance from the Sun, we approximated the loss rate scale of neutral helium atoms at radius r (measured in AU) to be 1.08 × 10−7r−2 (s−1).

The initial velocity given to each particle was chosen based on the Maxwell distribution function at the local temperature on the surface. As proposed by Killen et al. (2004) and Leblanc & Johnson (2003), the local temperature in the model, T(K), is expressed as,

(5)

While some studies have suggested that the initial velocity distribution might differ from that obtained from the Maxwell function (Smith et al. 1978; Shemansky & Broadfoot 1977; Leblanc & Chaufray 2011), we did not include these deviations for the sake of simplicity. Helium atoms are under the gravitational forces of the Sun and Mercury as well as solar radiation pressure forces. Therefore, an equation of motion for the helium atoms can be expressed as

(6)

where r, rS, and rM are the position vectors of the helium atoms, the Sun, and Mercury, respectively, G is the gravitational constant, b is the solar radiation pressure vector, and MS and MM are masses of the Sun and Mercury, respectively. The equation of motion was solved using a fourth order Runge–Kutta iteration method in our model.

For the incident solar flux at 58.4 nm, we used two measurements from the literature by Kumar et al. (1973) and Wilhelm et al. (1997). These two values for the solar spectral flux, πF1(λ) and πF2(λ), were normalized so the total integrated He I 58.4 nm photon flux is 0.7 × 109 ph cm−2 s−1 when the solar activity is characterized by a radio flux F10.7 = 100 × 10−20 W m−2 Hz−1, as discussed by Kumar et al. (1973).

Adopting the FWHM = 0.0016 nm value from Kumar et al. (1973), the solar flux (ph nm−1 cm−2 s−1) for our model is given as

(7)

where λ is the Doppler shifted wavelength that corresponds to the radial velocity of each helium atom. In an analogous way, we define the solar flux as πF2(λ) (ph nm−1 cm−2 s−1), which satisfies the wider solar line width (0.015 nm) reported by Wilhelm et al. (1997) as

(8)

The term 2.0 × 108 corresponds to the solar continuum and this value is based on Floyd et al. (2002). The two used emission line widths are shown in Fig. 3. The simulation assumes an optical-thin exosphere that allows the photons to be scattered only once.

thumbnail Fig. 3.

Solar flux at 1 AU as a function of wavelength (lower horizontal axis) and radial velocity between the observer and Sun (upper horizontal axis). The green line with a narrower line width has an FWHM of 0.0016 nm which was reported by Kumar et al. (1973). The broader, purple line has an FWHM of 0.015 nm as reported by Wilhelm et al. (1997). Since the two solar spectral fluxes integrated along the wavelength are assumed to have the same total photon fluxes in our model, the flux with the line width of 0.015 nm shows a lower peak than that with 0.0016 nm. The flux with the line width of 0.015 nm is multiplied by a factor of ten in this panel for scaling.

thumbnail Fig. 5.

Model results for the He I 58.4 nm brightness along the Sun–Mercury line as functions of the distance from the Mercury’s center at a TAA of 0 (filled square), 180 (asterisk), and 270 (filled circles) degrees with the line width of the solar He I 58.4 nm emission of 0.0016 nm (top panel, Kumar et al. 1973) and 0.015 nm (bottom panel, Wilhelm et al. 1997).

3. Results and discussion

The model calculation results are shown as two-dimensional distributions of the He I 58.4 nm emission in Fig. 4 for the narrow line width of 0.0016 nm (left column) and for the broad line width of 0.015 nm (right column). Several interesting findings can be pointed out:

  1. For the same TAA = 0°, the He I 58.4 nm brightness assuming πF1(λ) is larger than using πF2(λ) by an order of magnitude. This is because the solar photon flux per unit wavelength is greater for πF1(λ) than for πF2(λ) (see Fig. 3). They are defined to have the same total solar photon fluxes, but their bandwidths are different by a factor of ten. Therefore, the difference between these two bandwidths at the same TAA is caused by the line widths in our model.

  2. Both line widths show maximum brightness at TAA = 0° when Mercury does not have significant radial velocity with the Sun, and the heliocentric distance is at its minimum, so the fluxes from the solar radiation and wind are at their maximum.

  3. The minimum brightness is seen at TAA = 270° with πF1(λ) and at TAA = 180° with πF2(λ). Mercury’s radial velocity at TAA = 270° is 10 km s−1. At this velocity, the He I 58.4 nm flux on Mercury is 1% compared to when TAA = 0° with πF1(λ).

Figure 5 shows the He I 58.4 nm brightness calculated as a function of the distance from Mercury’s center along the Sun-Mercury line at the Mercury’s equator, assuming πF1(λ) with FWHM = 0.0016 nm (top panel) and πF2(λ) with FWHM = 0.015 nm (bottom panel). The brightness at TAA = 180° is larger than that at TAA = 270° by two orders of magnitude for πF1(λ).

Because of the larger line width, πF2(λ) results in a more modest impact on the brightness due to Mercury’s radial velocity relative to the Sun as compared with the case with πF1(λ). The maximum amplitude of the Doppler shift caused by Mercury’s radial velocity (0.002 nm) is smaller than the line width used with πF2(λ) by one order of magnitude. Most of the observed variation in brightness seen in Fig. 5 with πF2(λ) (bottom panel) is mainly caused by changes in the heliocentric distance rather than by the radial velocity. Mercury’s heliocentric distance is 0.3 AU at perihelion and 0.46 AU at aphelion, respectively. Thus the solar flux varies by approximately a factor of two between these locations. Furthermore, the solar wind flux also varies by around a factor of two. In addition to the solar radiation and wind fluxes, Mercury’s surface temperatures and the solar radiation pressures on the helium atoms are also dependent on the heliocentric distance. Reflecting these factors, the He I 58.4 nm brightness on Mercury varies by an order of the magnitude even if the line width of the solar radiation at this wavelength is remarkably wide as shown in Fig. 5.

As previously mentioned, Mercury’s intrinsic magnetic field is ignored in the model. Schleicher et al. (2004) detected the sodium D-line emission in Mercury’s exosphere concentrated near the polar regions where the solar wind precipitates guided by the magnetosphere. Therefore, the magnetosphere may also localize the He I 58.4 nm emission in the same way as the sodium D-line emission. However, this would not affect the orbital phase dependence of the integrated surface emission.

It is interesting to note that polarimetric observations in both optical sodium and UV helium lines would be sensitive to the distribution of the scattered emission even in the integrated light. Such observations may be a robust way to determine properties of magnetospheres of unresolved planets, such as exoplanets or distant moons and dwarf planets in the Solar System. A similar effect is expected to be observed in other resonance atomic lines, especially in the UV, where the Rayleigh scattering cross section is larger. For example, the Mg II 280 nm line is a good candidate for such a study of exospheres and magnetospheres of rocky planetary bodies. In addition to resonance atomic lines, scattering in near-UV CH, NH, OH, CN, and CO bands can trace the properties of the magnetosphere in the outer atmosphere and exosphere. Scattering in these bands was detected in comets and was also used to study weak magnetic fields in the solar atmosphere (e.g., Berdyugina 2011).

Previously, Yoneda et al. (2017) studied the effect of space weathering on Mercury and the hot super-Earth 61 Vir b using the optical sodium D-line emission. It was shown that the shape and extent of the exosphere strongly depend on the distance between the planet and the star, stellar wind properties, and the mass of the planet. López Ariste et al. (2012) showed that the sodium D2 line and the adjacent continuum emission of Mercury were linearly polarized, correspondingly, up to 17% and 8%, integrated over the planet. The polarization varied with the phase of Mercury, reaching nearly 10% above the continuum in the D2 line near the Mercury elongation (half-moon) phase. This was about a factor of two smaller than expected from a single scattering event by an isolated sodium atom. The authors interpreted the observation to mean that the sodium gas in the Mercury exosphere had the optical thickness of about 1, which decreased the line polarization due to multiple scatterings. However, in the presence of the magnetosphere, the optical thickness is unevenly distributed around the planet. Thus, advancing the model and interpretation would be of interest.

Polarimetric observations of exoplanets also hold promise for detecting their atmospheres (Berdyugina et al. 2008, 2011; Fluri & Berdyugina 2010). A higher Rayleigh cross section in the UV continuum and resonance lines leading to a potentially higher polarization than that in the optical may provide information on exoplanetary exospheres and magnetospheres. We note that for planets and exoplanets with a gravitation-bound atmosphere, the effect of the magnetosphere is expected above the exobase. Variation in the exospheric emission and polarization with the orbital phase is a key observation for a robust detection.

4. Summary and conclusions

We performed model calculations to synthesize the He I 58.4 nm emission from Mercury’s exosphere. The calculations suggest that the brightness of the emission is strongly dependent on Mercury’s orbital phase. Since this emission is due to resonant scattering of solar radiation, it is expected that Mercury’s He I 58.4 nm emission is dependent on the intrinsic line width of the solar emission spectrum. The width of the solar He I 58.4 nm line remains somewhat uncertain because different values have been reported in the literature.

Assuming a narrow line width of 0.0016 nm (Kumar et al. 1973), the model brightness varies by three orders of magnitude depending on Mercury’s orbital phase angle. This effect is primarily dominated by the Doppler shift being significantly larger than the solar line width.

Assuming a larger intrinsic line width of 0.015 nm, (Wilhelm et al. 1997), the model brightness still varies with Mercury’s orbital phase angle, but only by a single order of magnitude. The decreased variability is due to the line width being significantly greater than the Doppler shift due to Mercury’s orbital motion. However, since its orbit is ellipsoidal, the solar wind and photon fluxes vary due to variations in heliocentric distance. These effects are enough to account for the predicted variations in the He I 58.4 nm brightness.

The Hisaki spacecraft is equipped with a UV spectrograph specified for planetary observations (Yoshikawa et al. 2014). Also, one of the observation targets of PHEBUS (Probing of Hermean Exosphere By Ultraviolet Spectroscopy) onboard the BepiColombo spacecraft is He I 58.4 nm emission (Chassefière et al. 2010). Our predictions for the variations in Mercury’s He I 58.4 nm emission along its orbital phase shown in this model study should be testable by these missions.

Finally, we conclude that this research area holds exciting promises for future studies of other Solar System bodies and exoplanets in the UV. In particular, for exoplanets, UV space missions with polarimetric instruments, for example PolStar (Scowen et al. 2021) and LUVOIR (Muslimov et al. 2020) may open new ways of characterizing exoplanets and their exospheres, as well as understanding the role of magnetospheres in planetary composition and habitability.

Acknowledgments

This work was supported by the ERC Advanced Grant HotMol ERC-2011-AdG-291659.

References

  1. Berdyugina, S. V., 2011, in Solar Polarization, eds. J. R. Kuhn, D. M. Harrington, H. Lin, et al., ASP Conf. Ser., 437, 6 [NASA ADS] [Google Scholar]
  2. Berdyugina, S. V., Berdyugin, A. V., Fluri, D. M., & Piirola, V. 2008, ApJ, 673, L83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Berdyugina, S. V., Berdyugin, A. V., Fluri, D. M., & Piirola, V. 2011, ApJ, 728, L6 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bida, T. A., Killen, R. M., & Morgan, T. H. 2000, Nature, 404, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  5. Bochsler, P. 2001, Space Sci. Rev., 97, 113 [NASA ADS] [CrossRef] [Google Scholar]
  6. Broadfoot, A. L., Shemansky, D. E., & Kumar, S. 1976, Geophys. Res. Lett., 3, 577 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chassefière, E., Maria, J. L., Goutail, J. P., et al. 2010, Planet. Space Sci., 58, 201 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dwivedi, B. N. 1998, Bull. Astron. Soc. India, 26, 267 [NASA ADS] [Google Scholar]
  9. Floyd, L., Tobiska, W. K., & Cebula, R. P. 2002, Adv. Space Res., 29, 1427 [CrossRef] [Google Scholar]
  10. Fluri, D. M., & Berdyugina, S. V. 2010, A&A, 512, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Hall, L. A., & Hinteregger, H. E. 1970, J. Geophys. Res., 75, 6959 [NASA ADS] [CrossRef] [Google Scholar]
  12. Hartle, R. E., Curtis, S. A., & Thomas, G. E. 1975, J. Geophys. Res., 80, 3689 [NASA ADS] [CrossRef] [Google Scholar]
  13. Killen, R. M., Sarantos, M., Potter, A. E., & Reiff, P. 2004, Icarus, 171, 1 [NASA ADS] [CrossRef] [Google Scholar]
  14. Kumar, S. 1976, Icarus, 28, 579 [NASA ADS] [CrossRef] [Google Scholar]
  15. Kumar, S., Bowyer, S., & Lampton, M. 1973, J. Geophys. Res., 78, 1107 [NASA ADS] [CrossRef] [Google Scholar]
  16. Leblanc, F., & Chaufray, J. Y. 2011, Icarus, 216, 551 [CrossRef] [Google Scholar]
  17. Leblanc, F., & Johnson, R. E. 2003, Icarus, 164, 261 [NASA ADS] [CrossRef] [Google Scholar]
  18. López Ariste, A., Leblanc, F., Casini, R., et al. 2012, Icarus, 220, 1104 [Google Scholar]
  19. McClintock, W. E., & Lankton, M. R. 2007, Space Sci. Rev., 131, 481 [CrossRef] [Google Scholar]
  20. McClintock, W. E., Vervack, R. J., Bradley, E. T., et al. 2009, Science, 324, 610 [NASA ADS] [PubMed] [Google Scholar]
  21. Muslimov, E., Bouret, J. C., Neiner, C., et al. 2020, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, SPIE Conf. Ser., 11444, 114446G [NASA ADS] [Google Scholar]
  22. Potter, A., & Morgan, T. 1985, Science, 229, 651 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  23. Potter, A. E., & Morgan, T. H. 1988, Science, 241, 675 [NASA ADS] [CrossRef] [Google Scholar]
  24. Ruciński, D., & Bzowski, M. 1996, Space Sci. Rev., 78, 265 [NASA ADS] [CrossRef] [Google Scholar]
  25. Sarantos, M., Killen, R. M., & Kim, D. 2007, Planet. Space Sci., 55, 1584 [NASA ADS] [CrossRef] [Google Scholar]
  26. Schleicher, H., Wiedemann, G., Wöhl, H., Berkefeld, T., & Soltau, D. 2004, A&A, 425, 1119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Schmidt, C. A., Wilson, J. K., Baumgardner, J., & Mendillo, M. 2010, Icarus, 207, 9 [CrossRef] [Google Scholar]
  28. Scowen, P. A., Gayley, K., Neiner, C., et al. 2021, in UV/Optical/IR Space Telescopes and Instruments: Innovative Technologies and Concepts X, eds. A. A. Barto, J. B. Breckinridge, H. P. Stahl, et al., Int. Soc. Opt. Photonics (SPIE), 11819, 58 [Google Scholar]
  29. Shemansky, D. E., & Broadfoot, A. L. 1977, Rev. Geophys. Space Phys., 15, 491 [Google Scholar]
  30. Smith, G. R., Shemansky, D. E., Broadfoot, A. L., & Wallace, L. 1978, J. Geophys. Res., 83, 3783 [CrossRef] [Google Scholar]
  31. Wiese, W. L., & Fuhr, J. R. 2009, J. Phys. Chem. Ref. Data, 38, 565 [Google Scholar]
  32. Wilhelm, K., Lemaire, P., Curdt, W., et al. 1997, Sol. Phys., 170, 75 [NASA ADS] [CrossRef] [Google Scholar]
  33. Yoneda, M., Berdyugina, S., & Kuhn, J. 2017, AJ, 154, 139 [NASA ADS] [CrossRef] [Google Scholar]
  34. Yoshikawa, I., Yoshioka, K., Murakami, G., et al. 2014, Space Sci. Rev., 184, 237 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 2.

Range of radial velocities between Mercury and the Sun as a function of the true anomaly angle. The right vertical axis shows the amount of wavelength shift in the solar He I 58.4 nm emission by the Doppler shift due to Mercury’s radial motion. Two lines at ±8.00 × 10−4 nm show the line width of the solar He I 58.4 nm emission estimated by Kumar (1976) and the corresponding velocities.
In the text
thumbnail Fig. 1.

Geometric sketch to show the positional relations and explain the letters in the equations. The directions of axes x and z are the same as the horizontal and vertical axes in Fig. 4, vM and vSW are the velocities of Mercury and the solar wind, and χ is the solar zenith angle at a point on Mercury’s dayside hemisphere.
In the text
thumbnail Fig. 4.

Two dimensional brightness distributions of the He I 58.4 nm emission of Mercury at three TAAs (0, 180, and 270 degrees) reproduced by model simulation. Horizontal and vertical axes correspond to the x and z directions shown in Fig. 1. The brightness was integrated in each 0.1 RM × 0.1RM box. The line width of the solar He I 58.4 nm emission is assumed to be 0.0016 nm (left column, Kumar et al. 1973) and 0.015 nm (right column, Wilhelm et al. 1997). The horizontal axis is the distance from Mercury’s center along the Sun-Mercury line, and the vertical axis is along Mercury’s rotation axis. The brightest pixels were artificially added to maintain the same color scale for the images within one column.
In the text
thumbnail Fig. 3.

Solar flux at 1 AU as a function of wavelength (lower horizontal axis) and radial velocity between the observer and Sun (upper horizontal axis). The green line with a narrower line width has an FWHM of 0.0016 nm which was reported by Kumar et al. (1973). The broader, purple line has an FWHM of 0.015 nm as reported by Wilhelm et al. (1997). Since the two solar spectral fluxes integrated along the wavelength are assumed to have the same total photon fluxes in our model, the flux with the line width of 0.015 nm shows a lower peak than that with 0.0016 nm. The flux with the line width of 0.015 nm is multiplied by a factor of ten in this panel for scaling.
In the text
thumbnail Fig. 5.

Model results for the He I 58.4 nm brightness along the Sun–Mercury line as functions of the distance from the Mercury’s center at a TAA of 0 (filled square), 180 (asterisk), and 270 (filled circles) degrees with the line width of the solar He I 58.4 nm emission of 0.0016 nm (top panel, Kumar et al. 1973) and 0.015 nm (bottom panel, Wilhelm et al. 1997).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.