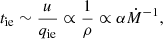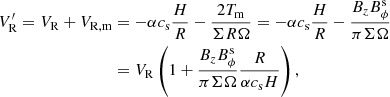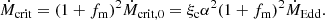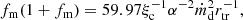EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A81 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A81
Number of page(s) 7
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202141652
Published online 14 October 2021

© ESO 2021

1. Introduction

The variability of X-ray binaries (XRBs) transitions between a thermal state with a substantial thermal component in the continuum spectra and a low or hard state that is dominated by nonthermal emission. It is widely accepted that the states of XRBs correspond to different accretion modes. Hot accretion flows are present in the low or hard state, while black holes (BHs) or neutron stars (NS) are surrounded by geometrically thin accretion disks in the thermal state of XRBs (e.g., Lasota et al. 1996; Esin et al. 1997; Meyer et al. 2000; Zdziarski et al. 2004; Wu & Gu 2008; Belloni 2010; Cao et al. 2014; Dong & Wu 2015).

Outbursts in XRBs are generally believed to be triggered by disk instability, which can explain the basic observed features of the outbursts, such as the observed light curves (e.g., Cannizzo 1993; King & Ritter 1998; Dubus et al. 1999, 2001). In the low or hard state, the mass accretion rate is low, and the inner advection-dominated accretion flow (ADAF) connects to an outer thin disk at a certain radius, namely the transition radius (e.g., Lasota et al. 1996; Esin et al. 1997). During the outburst, the mass accretion rate rises rapidly, and the ADAF is suppressed to a cold disk when its mass accretion rate surpasses a critical value (Narayan & Yi 1994, 1995). As the inner ADAF shrinks, the disk finally approaches the inner stable circular orbits (ISCOs) of BHs or the surface of NS, which corresponds to the thermal state. After the accretion rate reaches a peak value, it declines slowly as the mass of the disk is exhausted because the rate of the gas that is refueled from the companion star is substantially lower than the central accretion rate (e.g., King & Ritter 1998). The state transitions have been extensively studied by many observers. The transitions provide rigourous constraints on theoretical models (e.g., Miyamoto et al. 1995; Zhang et al. 1997; Nowak et al. 2002; Maccarone & Coppi 2003; Zdziarski et al. 2004; Yu & Yan 2009; Wu et al. 2010). The observations of the state transitions give important clues on the accretion mode transitions. It is found that the Eddington-scaled luminosity of the transition from the hard state to the soft state varies in a rather wide range, and furthermore, it is closely correlated with the peak Eddington ratio of the thermal state (Yu et al. 2004, 2007; Yu & Dolence 2007; Yu & Yan 2009). These have challenged the theoretical models because the accretion mode transition is solely triggered by the dimensionless mass accretion rate, as expected by the most of the previous models (see, e.g., Narayan et al. 1998; Yuan & Narayan 2014 for reviews).

In order to explain the hysteretic state transition observed in XRBs (e.g., Miyamoto et al. 1995; Zhang et al. 1997; Nowak et al. 2002; Maccarone & Coppi 2003; Zdziarski et al. 2004; Yu & Yan 2009), Cao (2016) suggested a model of the ADAF with magnetically driven outflows, whose critical mass accretion rate for the ADAF may vary with the strength of the large-scale magnetic field. In this scenario, magnetically driven outflows may carry away a large amount of angular momentum from the ADAF and may thus significantly increase the radial velocity of the ADAF, which leads to a high critical mass accretion rate. Thus, the luminosity for the transition from hard to soft state increases with the field strength. We conjecture that such a large-scale magnetic field may form from the inverse cascade of the small-scale field dynamo generated in the outer disk region (Tout & Pringle 1996), the strength of which increases with the peak mass accretion rate of the disk in the outbursts. We describe the model calculations and the comparison with the observations in Sect. 2. Section 3 contains a brief discussion of the results.

2. Model

In the quiescent state of XRBs, the mass accretion rate is very low, and the outer cold disk connects to an inner ADAF at a certain radius (Esin et al. 1997). If the temperature of the gas approaches the hydrogen ionization temperature somewhere in the cold disks, the instability is triggered at a certain radius of the disk, and this causes the annulus transit to the hot state. Heat diffuses rapidly into the adjacent annuli to stimulate them to make the same transition, which triggers an outburst (e.g., Frank et al. 2002). The mass accretion rate Ṁd of the disk region in the hot state is significantly higher than that in quiescent state. When the heating front moves inward into the ADAF, much gas is fed to the inner ADAF. It is suppressed to a thin disk as its accretion rate is higher than a critical value. The ADAF shrinks with rising accretion rate, and finally, the ADAF is completely suppressed to a thin disk. It is then in the thermal state, and the heating front of the outer disk is still moving inward. The luminosity of the thermal state increases until the heating front approaches the ISCO, which roughly corresponds to the peak luminosity that is observed in the XRB after the outburst. In the outburst state, the disk is quasi-steady, which is well described by the standard disk model (King & Ritter 1998). Thus, we can model the outburst with a series of steady-state disk calculations. We assume that the heating front propagates inward at constant Ṁd. This means that the peak luminosity of the thermal state can be estimated as Lpeak ∼ ηradṀdc2, which is in fact determined by the properties of the disk in quiescent state.

It was suggested that the magnetically driven outflows carry away a substantial fraction of the angular momentum of the ADAF, which significantly increases the radial velocity of the ADAF (see Cao 2016, for the details). This leads to a high critical mass accretion rate, below which an ADAF with magnetic outflows can survive. An external field can be substantially enhanced in an ADAF due to its high radial velocity (Cao 2011). It was therefore suggested that ADAFs with magnetically driven outflows are present in the low or hard states of XRBs (Cao 2016). The external field dragged by the ADAF is taken as a model ingredient because its origin is still unclear.

The magnetic field strength at the surface of the companion stars in low-mass X-ray binaries (LMXRBs) is about several Gauss, and the field advection in a thin turbulent disk is rather inefficient (Lubow et al. 1994). This implies that the field that formed through the advection in the outer thin disk of LMXRBs may probably be too weak to be the external field for the inner ADAF (see the estimate of the field strength that is required for launching outflows from an ADAF in Cao 2016, or the discussion in Sect. 2.1).

Recently, magnetohydrodynamical (MHD) numerical simulations have shown that turbulence in a radially extended accretion disk can generate large-scale poloidal magnetic flux in situ (Liska et al. 2020). We conjecture that the large-scale field in the outer thin disks of LMXRBs is generated locally. One of the possible mechanisms is that the large-scale field is produced from the small-scale field created by dynamo processes in the disk through an inverse cascade process (Tout & Pringle 1992, 1996). The large-scale magnetic field generated in this way in the outer disk can be advected inward by the inner ADAF, which accelerates outflows from the ADAF. The critical mass accretion rate, and correspondingly, the transition luminosity from hard state to soft state, increases with the strength of the magnetic field threading the ADAF, which is roughly proportional to the external field strength, that is, the strength of the large-scale field generated in the outer disk. The field strength increases with the peak accretion rate of the disk in the soft state. Therefore the observed tight correlation between the transition luminosity and the peak luminosity in the soft state of XRBs can be reproduced by this scenario.

2.1. Critical accretion rate for an ADAF with magnetically driven outflows

The hot ADAF switches to an optically thick accretion disk when its accretion rate is increased above a critical value Ṁcrit (Narayan & Yi 1995; Esin et al. 1997). When the ion-electron equilibration timescale is equal to the accretion timescale of an ADAF, the critical mass accretion rate Ṁcrit is estimated (Narayan et al. 1998). For ADAFs, the temperature distributions of ions and electrons are almost independent of the mass accretion rate. The rate of the energy transfer rate qie = ninef(Ti, Te), in which the detailed form of f(Ti, Te) is given in many previous works (e.g., Stepney & Guilbert 1983; Narayan & Yi 1995; Zdziarski 1998). Thus, we estimate the ion-electron equilibration timescale as

(1)

where α is the viscosity parameter, and the relation ρ ∝ α−1 Ṁ for an ADAF is used (Narayan & Yi 1995).

The accretion timescale is

(2)

where H is the thickness of the ADAF, the radial velocity of the ADAF,

(3)

and the viscosity ν = αcsH have been used.

Combing Eqs. (1) and (2), the critical mass accretion rate is estimated as

(4)

Detailed model calculations show

(5)

where ṀEdd = LEdd/0.1c2, ξc = 0.1 and 1 for NS and BHs, respectively (Narayan & Yi 1995).

The structure of the disk is altered if magnetic outflows carry away a fraction of angular momentum of the gas in the disk (e.g., Ferreira et al. 2006; Cao & Spruit 2013; Li & Begelman 2014; Li 2014). In the case of an ADAF with magnetically driven outflows carrying substantial angular momentum away from the accretion flow, its radial velocity will be increased, and therefore the critical mass accretion rate is significantly increased, which has been explored in detail by Cao (2016). We briefly summarize the calculations below (see Cao 2016, for the details).

The magnetic torque exerted by the outflows on unit area of the disk is

(6)

where Bz and are the vertical and azimuthal component of the large-scale magnetic field at the disk surface, respectively. The radial velocity of an ADAF with magnetic outflows is

(7)

which can be rewritten as

(8)

where the dimensionless quantities are defined as

(9)

and

(10)

The ratio ξϕ ≲ 1 (see the detailed discussion in Livio et al. 1999).

The ion-electron equilibration timescale of an ADAF with magnetic outflows is

(11)

and its accretion timescale becomes

(12)

Similar to the conventional ADAF case, the value of Ṁcrit can be estimated with , which leads to

(13)

Here the local structure (ion and electron temperatures) is assumed to be similar to a conventional ADAF without magnetic outflows, which is justified in Cao (2016).

The gravitational energy dissipation rate from the unit area of the disk is

(14)

For a conventional ADAF accreting at the critical rate, its gravitational energy dissipation rate from the unit area of the surface,

(15)

where Eqs. (3) and (5) are used.

Similarly, the gravitational energy dissipation rate of an ADAF with magnetic outflows is calculated with

(16)

where Eqs. (8) and (13) are substituted into Eq. (14).

The radial energy advection is negligible in the ADAF accreting at the critical rate (e.g., Narayan et al. 1998; Yuan & Narayan 2014), and therefore its luminosity is

(17)

The luminosity of an ADAF with magnetic outflows can be approximated as

(18)

which means that the ADAF with magnetic outflows is ∼fm times more luminous than the conventional ADAF that accretes at the critical rate.

2.2. Large-scale magnetic field generated in the outer disk

The origin of a large-scale magnetic field in a thin accretion disk is still uncertain. One possible way is the advection of an external weak field by the disk, but it has been found that the field advection in a thin viscous disk is quite inefficient because its radial velocity is low [vR ∝ (H/R)2] (van Ballegooijen 1989; Lubow et al. 1994). Alternatively, it has been suggested that if most of the angular momentum of the disk is removed by the magnetically driven outflows, the radial velocity of the disk is significantly higher than that of a conventional viscous thin disk, and the external weak field can be substantially enhanced in the inner region (Cao & Spruit 2013; Li & Cao 2019). However, the field strength of the companion stars in LMXRBs is too weak to maintain such a thin disk-outflow system (see Cao & Lai 2019, for a detailed discussion), while an accretion disk with magnetic outflows may be present in the soft state of Cyg X–3 (Cao & Zdziarski 2020), which is a high-mass X-ray binary (HMXRB) containing a Wolf-Rayet star. The observations show that the field strength of Wolf-Rayet stars can be as high as several hundred Gauss (de la Chevrotière et al. 2014; Hubrig et al. 2016). For our present work, we mostly focus on LMXRBs, and therefore efficient field advection in the thin disk seems to be quite unlikely.

Recent MHD numerical simulations showed that the large-scale field can be generated through a dynamo process, that is, turbulence in a radially extended accretion disk generates large-scale poloidal magnetic flux in situ even when it starts from a purely toroidal magnetic field (Liska et al. 2020). The formation of large-scale magnetic fields has been studied with numerical simulations (e.g., Beckwith et al. 2009; Salvesen et al. 2016; Zhu & Stone 2018; Liska et al. 2020) mostly for thick disks or the hot coronal flows above the thin disks. As far as we know, no explicit quantitative relation between the disk properties and the large-scale field strength has been revealed in numerical simulations.

We suggest that a dynamo process takes place in the outer thin disk in LMXRBs, but the length scale of the field generated in this way is about the same as the disk thickness H (Tout & Pringle 1992). In order to launch outflows from the disk, the poloidal magnetic field threading the disk is required to have a length scale of R. Tout & Pringle (1996) suggested that the inverse cascade process of the dynamo that generated the small-scale magnetic field may lead to a large-scale field as B(λ)∝λ−1, where B(λ) is the field strength at a length scale of λ. The strength of this large-scale field is estimated as

(19)

where Hd is the disk thickness, and Bdynamo is the dynamo-generated field strength (Tout & Pringle 1996; Livio et al. 1999; King et al. 2004). The dynamo-generated scale-scale field strength in a thin accretion disk can be estimated as

(20)

(see the last line of Eq. (2.11) in Shakura & Sunyaev 1973), which was adopted by Livio et al. (1999, see Eq. (10) in their paper) together with Eq. (19) to estimate the power of jets produced through the BP and BZ mechanisms. Although this scenario has not been reproduced by MHD simulations so far, it is still a promising mechanism for the large-scale field generation in a thin disk with sufficient solid physical ground. In this work, we employed the same approach as Livio et al. (1999) to estimate the strength of the large-scale magnetic field of the thin disk.

As suggested by King & Ritter (1998), the hot region of the outer disk in the outburst can be described with a quasi-steady disk model. We note that a steady disk model can describe the outburst that occurs close to the peak quite well, while the density profiles during the outburst may deviate from the standard disk model (Dubus et al. 2001). In this work, we focus on the disk conditions near the transition radius during the hard-to-soft state transition when the outer disk extends to a small radius that is connected to the ADAF, and it is close to the peak of the outburst. The large-scale field strength is estimated from the local structure of the thin disk at the transition radius, and the local disk structure can probably be well described by the standard thin disk model.

For a disk in which radiation pressure is dominant, pressure and disk thickness are given by

(21)

and

(22)

where m = M/M⊙, ṁd = Ṁd/ṀEdd, ṀEdd = 4πGM/0.1cκT, and r = Rc2/GM. Although the model of a disk dominated by radiation pressure can describe the outer disk near the transition radius prior to the hard-to-soft state transition quite well for most cases, we also considered the model of a disk dominated by gas pressure for observations with a low Eddington-scaled peak luminosity. When the dimensionless mass accretion rate is low, the disk is dominated by gas pressure, and the disk pressure and thickness are

(23)

and

(24)

The threshold of the mass accretion rate between disks dominated by radiation pressure and gas pressure is calculated by setting the radiation pressure as equal to the gas pressure in the disk, which is

(25)

which depends very weakly on α or m.

Thus, the large-scale field strength of the outer disk is estimated as

(26)

when ṁd ≥ ṁd,rg, and

(27)

when ṁd < ṁd,rg, where Eqs. (19) and (20) are used.

2.3. Transition of the hard to the soft state

In the low or hard state of XRBs, it is generally thought that an inner ADAF is surrounded by a thin disk in the outer region (Lasota et al. 1996; Esin et al. 1997). In the outburst, the heating front passes the transition radius Rtr into the ADAF, and the mass accretion rate in the ADAF rises to Ṁpeak on the order of the thermal timescale (King & Ritter 1998). When the accretion rate becomes higher than the critical value Ṁcrit given by Eq. (13), the ADAF is suppressed to a standard disk. The strength of the magnetic field threading the ADAF at Rtr is roughly the same as that of the outer disk accreting at Ṁpeak close to Rtr because even the field threading the ADAF is predominantly maintained by the same currents in the outer disk that cause the large-scale field threading the disk, which is similar to the BH case considered in Livio et al. (1999).

Considering the heating front of the outer disk just approaching the ADAF at Rtr (see the illustration in Fig. 1), we can estimate the large-scale field strength of the disk very close to the transition radius, as described in Sect. 2.2. Without loss of generality, this large-scale poloidal magnetic field is maintained by the azimuthal currents of the disk, which means that it corresponds to a certain distribution of the currents in the outer disk. The large-scale poloidal field strength of the disk can be calculated with the Biot-Savart law if the current distribution is known (e.g., see Eq. (18) in Lubow et al. 1994). Thus, the strength of the field threading the ADAF at Rtr due to the outer disk can be calculated with the same current distribution with the Biot-Savart law. The field strength only depends on the location for a given current distribution, which means that the strength of the field threading the ADAF at Rtr is almost same as the large-scale field strength of the outer disk close to the transition radius because their radial distance is shorter than the width of the heating front during the state transition, which is on the order of the disk thickness (cf. Frank et al. 2002). This implies that the ADAF feels the field generated in the outer disk even if the gas of the disk has not been entered the ADAF. Thus, the strength of the large-scale field threading the ADAF at rtr can be fairly well estimated with Eq. (26) or Eq. (27).

thumbnail Fig. 1.

Illustration of the model. The large-scale magnetic field is formed through an inverse cascade process of the dynamo-generated small-scale field in the outer thin disk. This large-scale poloidal field is produced by the azimuthal currents in the disk.

The critical mass rate of an ADAF with magnetic outflows is given by Eq. (13) (see Sect. 2.1), so that the gas pressure of the ADAF accreting at the critical rate is

(28)

Combining Eqs. (9), (10), (26), and (28), we derive

(29)

for an outer disk in which radiation pressure is dominant (i.e., ṁd ≥ ṁd,rg), or

(30)

for a disk dominated by gas pressure (i.e., ṁd < ṁd,rg). The peak luminosity of the soft state after the outburst is Lpeak = ηradṀdc2 (see the discussion in the first paragraph of Sect. 2). Adopting a conventional value of the radiation efficiency ηrad = 0.1, we have λpeak = ṁd. Solving the above two equations, we derive how the value of fm varies with mass accretion rate ṁd of the outer disk when the values of the parameters are specified.

For the ADAF accreting at the critical rate, the radial energy advection is negligible (Narayan & Yi 1995), so the Eddington scaled transition luminosity λtr ≃ ṁcrit = ξcα2(1 + fm). Thus, we obtain the relation of λtr with λpeak, when the values of the parameters ξc, α, and rtr are specified. The relations of λpeak with λtr are calculated with λtr = ξcα2(1 + fm), which are shown in Figs. 2 and 3 for rtr = 20 and 30, respectively. In all of the calculations, the approximations ξϕ ∼ 1 and fΩ ∼ 1 are adopted. The neutron star mass m = 1.4 and the BH mass m = 8 are adopted in all calculations.

thumbnail Fig. 2.

Correlation between λtr and λpeak. The circles are NSXRBs, while the dots show the BH counterparts. The data are taken from the literature (Yu & Yan 2009; Yan & Yu 2017; Cúneo et al. 2020). The solid lines are the model calculations for BHXRBs (i.e., ξc = 1), and the dashed lines are for NSXRBs (i.e., ξc = 0.1). The different colors indicate the results calculated with different values of the viscosity parameter: α = 0.05 (yellow), 0.07 (magenta), 0.1 (cyan), 0.15 (red), 0.2 (green), 0.3 (blue), and 0.4 (black). The stars indicate the case of the radiation pressure equaling the gas pressure in the outer disk at Rtr. The transition radius rtr = 20 is adopted in all calculations.

thumbnail Fig. 3.

Same as Fig. 2, but rtr = 30 is adopted.

When the mass accretion rate in the disk is sufficiently high, a strong magnetic field is generated in the outer disk that is dominated by radiation pressure, which leads to strong outflows. In this case, fm ≫ 1, so 1 + fm ∼ fm. Substituting ṁd = λpeak and λtr ≃ ξcα2(1 + fm)∼ξcα2fm into Eq. (29), we obtain

(31)

The linear relation (31) between λtr and λpeak is consistent with the observed correlation derived in Yu & Yan (2009). We note that the transition luminosity can be higher than the peak luminosity, that is, λtr > λpeak, in the case of strong magnetic outflows. For BH X-ray binaries (BHXRBs), ξc = 1, the outbursts would never reach the thermal state if (e.g., α ≳ 0.44 for rtr = 20), while α ≳ 1.4 is required for λtr > λpeak in the case of NS X-ray binaries (NSXRBs) (ξc = 0.1 and ttr = 20 are adopted). This can naturally explain the findings that a substantial fraction of outbursts in BHXRBs do not reach the thermally dominant accretion state (Tetarenko et al. 2016), while no hard-only outburst has been observed in NSXRBs so far.

3. Discussion

We estimated the large-scale magnetic field threading the ADAF at rtr assuming an inverse cascade of the dynamo-generated field in the outer disk without adding any parameter, which is the same as was employed in Livio et al. (1999). The ratios β of the gas to magnetic pressure in the ADAFs are in the range of ∼10−103 at the transition radius. With the derived field strength, we calculated the angular momentum carried away by the magnetic outflows, and then derived the transition luminosity of the ADAF. We find that the observed correlation between λtr and λpeak can be fairly well reproduced by our model calculations without inducing any additional parameter (see Figs. 2 and 3). In our model, strong magnetically driven outflows are present in the outbursts of XRBs, which is indeed consistent with recent observations (Tetarenko et al. 2018).

Although the inner truncation radius rtr in the quiescent state can be as large as ∼104 (e.g., Dubus et al. 2001; Bernardini et al. 2016), our model fittings on the observed correlation require the transition radius to be in the range of ∼20−30 (see Figs. 2 and 3) because all of our calculations are applied for the region at rtr when the state transition takes place. The inner ADAF shrinks with the heating front of the disk moving inward. As most hard X-ray photons are emitted from the inner region of the ADAF, the transition from hard to soft state must take place when the transition radius rtr is very close to the ISCO. Most of the gravitational energy of the gas in the accretion disk is released in the region with R ≲ 2.25 RISCO, that is, r ≲ 15 for a nonrotating BH (Shakura & Sunyaev 1973). Thus, it is reasonable to adopt rtr ∼ 20−30 in the calculations of the state transition. This is supported by the observational constraints on the transition radius: rtr ∼ 10−102 (e.g., García et al. 2015, and the references therein).

In the outburst, the accretion rate of the ADAF at rtr rises in the thermal timescale ∼1/αΩK when the heating front approaches the outer radius of the ADAF (e.g., Frank et al. 2002), which is roughly on the same order as the accretion timescale of an ADAF without magnetic outflows (see Eq. (2)) because the disk thickness of the ADAF H/R ∼ 1. In the case of the ADAF with strong magnetic outflows, fm is substantially higher than unity, the rising timescale of the accretion rate at Rtr is usually longer than the accretion timescale of the ADAF with magnetic outflows (see Eq. (12)). The magnetic coupling between disk and outflows takes place on a much shorter timescale, that is, on the order of the disk dynamical timescale (Cao & Spruit 2002). This implies that the analyses based on the steady model of the ADAF with outflows in this work is a good approximation.

Our model is able to explain the observed correlations naturally for both NSXRBs and BHXRBs, while the values of α are systematically higher for NSXRBs (α ∼ 0.05−0.15 for BHXRBs, and α ∼ 0.15−0.4 for NSXRBs). The traditional ADAF model shows that the dimensionless critical mass accretion rate for NSXRBs is significantly lower than that of the BH counterparts because about half of the gravitational energy is released as soft X-ray photons form the NS surface, part of which are injected into the ADAF as soft seed photons that are inverse-Compton scattered by the hot electrons in the ADAF. This increased the radiation efficiency of the ADAF and therefore reduced the critical mass accretion rate of the ADAF (see Narayan & Yi 1995; Yi et al. 1996, for the detailed calculations). However, there is no obvious difference in the dimensionless transition luminosity λtr between NSXRBs and BHXRBs (see Fig. 2). Thus, higher values of α are required in our model calculations for NSXRBs than for BHXRBs. The averages of typical timescales measured with the observations, that is, rise and decay timescales, and outburst duration, of BHXRBs, are at least twice longer than those of NSXRBs (Yan & Yu 2015). This is roughly consistent with our results because the accretion timescale of the disk is proportional to α−1, although the physics origin of this difference in α is still unclear.

We have only calculated the accretion mode transition condition for an ADAF with magnetic outflows at the transition radius. In principle, the critical mass accretion rate for an ADAF with magnetic outflows given by Eq. (13) is only valid at Rtr. However, the field advection is very efficient in the ADAF, that is, the field threading the ADAF at Rtr will be dragged inward, and the field strength will be substantially amplified in the central part of the flow (Cao 2011). It is found that the value of β increases radially in the ADAF (see Fig. 8 in Cao 2011), which implies that the critical mass accretion rate of an ADAF with magnetic outflows will increase with decreasing radius (see Eqs. (10) and (13)). The ADAF shrinks with the rising mass-feeding rate of the outer disk. We note that the field advection was calculated only for an ADAF without outflows in Cao (2011). If the angular momentum carried away by the outflows from the ADAF is properly considered, the field will be more enhanced than an ADAF without outflows because the radial velocity of the ADAF with outflows is higher than its counterpart without flows. This implies that the whole ADAF can survive if the mass accretion rate is lower than the critical value derived at the transition radius. Our model calculation of the critical mass accretion rate is valid in general for an ADAF with magnetic outflows. The calculation of the global structure of such an ADAF with magnetically driven outflows is desired, and it may help understanding the detailed physics of the hard-to-soft state transition in XRBs, which is beyond the scope of this work.

Acknowledgments

We are grateful to the referee for his/her insightful comments and suggestions. We thank Wenfei Yu for very helpful discussion. This work is supported by the NSFC (11773050, 11833007, 12073023, 11903024, U1838103, U1931203, 11773055, U1838203, and U1938114), the science research grants from the China Manned Space Project with NO. CMS-CSST-2021-A06, the CAS grant QYZDJ-SSWSYS023, and Youth Innovation Promotion Association of CAS (ids. 2020265).

References

  1. Beckwith, K., Hawley, J. F., & Krolik, J. H. 2009, ApJ, 707, 428 [NASA ADS] [CrossRef] [Google Scholar]
  2. Belloni, T. 2010, Lect. Notes Phys., 794, 53 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bernardini, F., Russell, D. M., Shaw, A. W., et al. 2016, ApJ, 818, L5 [NASA ADS] [CrossRef] [Google Scholar]
  4. Cannizzo, J. K. 1993, in Accretion Disks in Compact Stellar Systems, ed. J. C. Wheeler (Singapore: World Scientific Publishing), 6 [NASA ADS] [CrossRef] [Google Scholar]
  5. Cao, X. 2011, ApJ, 737, 94 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cao, X. 2016, ApJ, 817, 71 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cao, X., & Lai, D. 2019, MNRAS, 485, 1916 [NASA ADS] [Google Scholar]
  8. Cao, X., & Spruit, H. C. 2002, A&A, 385, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Cao, X., & Spruit, H. C. 2013, ApJ, 765, 149 [CrossRef] [Google Scholar]
  10. Cao, X., & Zdziarski, A. A. 2020, MNRAS, 492, 223 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cao, X.-F., Wu, Q., & Dong, A.-J. 2014, ApJ, 788, 52 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cúneo, V. A., Alabarta, K., Zhang, L., et al. 2020, MNRAS, 496, 1001 [CrossRef] [Google Scholar]
  13. de la Chevrotière, A., St-Louis, N., Moffat, A. F. J., et al. 2014, ApJ, 781, 73 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dong, A.-J., & Wu, Q. 2015, MNRAS, 453, 3447 [Google Scholar]
  15. Dubus, G., Lasota, J.-P., Hameury, J.-M., & Charles, P. 1999, MNRAS, 303, 139 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dubus, G., Hameury, J.-M., & Lasota, J.-P. 2001, A&A, 373, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Esin, A. A., McClintock, J. E., & Narayan, R. 1997, ApJ, 489, 865 [NASA ADS] [CrossRef] [Google Scholar]
  18. Ferreira, J., Petrucci, P.-O., Henri, G., Saugé, L., & Pelletier, G. 2006, A&A, 447, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics (Cambridge: Cambridge University Press), 398 [Google Scholar]
  20. García, J. A., Steiner, J. F., McClintock, J. E., et al. 2015, ApJ, 813, 84 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hubrig, S., Scholz, K., Hamann, W.-R., et al. 2016, MNRAS, 458, 3381 [NASA ADS] [CrossRef] [Google Scholar]
  22. King, A. R., & Ritter, H. 1998, MNRAS, 293, L42 [NASA ADS] [CrossRef] [Google Scholar]
  23. King, A. R., Pringle, J. E., West, R. G., & Livio, M. 2004, MNRAS, 348, 111 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lasota, J.-P., Narayan, R., & Yi, I. 1996, A&A, 314, 813 [NASA ADS] [Google Scholar]
  25. Li, S.-L. 2014, ApJ, 788, 71 [NASA ADS] [CrossRef] [Google Scholar]
  26. Li, S.-L., & Begelman, M. C. 2014, ApJ, 786, 6 [NASA ADS] [CrossRef] [Google Scholar]
  27. Li, J., & Cao, X. 2019, ApJ, 872, 149 [CrossRef] [Google Scholar]
  28. Liska, M., Tchekhovskoy, A., & Quataert, E. 2020, MNRAS, 494, 3656 [CrossRef] [Google Scholar]
  29. Livio, M., Ogilvie, G. I., & Pringle, J. E. 1999, ApJ, 512, 100 [NASA ADS] [CrossRef] [Google Scholar]
  30. Lubow, S. H., Papaloizou, J. C. B., & Pringle, J. E. 1994, MNRAS, 267, 235 [NASA ADS] [Google Scholar]
  31. Maccarone, T. J., & Coppi, P. S. 2003, MNRAS, 338, 189 [NASA ADS] [CrossRef] [Google Scholar]
  32. Meyer, F., Liu, B. F., & Meyer-Hofmeister, E. 2000, A&A, 354, L67 [NASA ADS] [Google Scholar]
  33. Miyamoto, S., Kitamoto, S., Hayashida, K., & Egoshi, W. 1995, ApJ, 442, L13 [NASA ADS] [CrossRef] [Google Scholar]
  34. Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [NASA ADS] [CrossRef] [Google Scholar]
  35. Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
  36. Narayan, R., Mahadevan, R., & Quataert, E. 1998, in Theory of Black Hole Accretion Disks, eds. M. A. Abramowicz, G. Bjornsson, & J. E. Pringle (Cambridge: Cambridge University Press), 148 [Google Scholar]
  37. Nowak, M. A., Wilms, J., & Dove, J. B. 2002, MNRAS, 332, 856 [NASA ADS] [CrossRef] [Google Scholar]
  38. Salvesen, G., Armitage, P. J., Simon, J. B., & Begelman, M. C. 2016, MNRAS, 460, 3488 [NASA ADS] [CrossRef] [Google Scholar]
  39. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]
  40. Stepney, S., & Guilbert, P. W. 1983, MNRAS, 204, 1269 [NASA ADS] [Google Scholar]
  41. Tetarenko, B. E., Sivakoff, G. R., Heinke, C. O., & Gladstone, J. C. 2016, ApJS, 222, 15 [NASA ADS] [CrossRef] [Google Scholar]
  42. Tetarenko, B. E., Lasota, J.-P., Heinke, C. O., Dubus, G., & Sivakoff, G. R. 2018, Nature, 554, 69 [NASA ADS] [CrossRef] [Google Scholar]
  43. Tout, C. A., & Pringle, J. E. 1992, MNRAS, 259, 604 [NASA ADS] [Google Scholar]
  44. Tout, C. A., & Pringle, J. E. 1996, MNRAS, 281, 219 [NASA ADS] [CrossRef] [Google Scholar]
  45. van Ballegooijen, A. A. 1989, in Accretion Disks and Magnetic Fields in Astrophysics, ed. G. Belvedere (Dordrecht: Kluwer Academic Publishers), Proc. Eur. Phys. Soc. Study Conf., 99 [NASA ADS] [CrossRef] [Google Scholar]
  46. Wu, Q., & Gu, M. 2008, ApJ, 682, 212 [NASA ADS] [CrossRef] [Google Scholar]
  47. Wu, Y. X., Yu, W., Li, T. P., Maccarone, T. J., & Li, X. D. 2010, ApJ, 718, 620 [NASA ADS] [CrossRef] [Google Scholar]
  48. Yan, Z., & Yu, W. 2015, ApJ, 805, 87 [NASA ADS] [CrossRef] [Google Scholar]
  49. Yan, Z., & Yu, W. 2017, MNRAS, 470, 4298 [NASA ADS] [CrossRef] [Google Scholar]
  50. Yi, I., Narayan, R., Barret, D., & McClintock, J. E. 1996, A&AS, 120, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Yu, W., & Dolence, J. 2007, ApJ, 667, 1043 [NASA ADS] [CrossRef] [Google Scholar]
  52. Yu, W., & Yan, Z. 2009, ApJ, 701, 1940 [NASA ADS] [CrossRef] [Google Scholar]
  53. Yu, W., van der Klis, M., & Fender, R. 2004, ApJ, 611, L121 [NASA ADS] [CrossRef] [Google Scholar]
  54. Yu, W., Lamb, F. K., Fender, R., & van der Klis, M. 2007, ApJ, 663, 1309 [NASA ADS] [CrossRef] [Google Scholar]
  55. Yuan, F., & Narayan, R. 2014, ARA&A, 52, 529 [NASA ADS] [CrossRef] [Google Scholar]
  56. Zdziarski, A. A. 1998, MNRAS, 296, L51 [NASA ADS] [CrossRef] [Google Scholar]
  57. Zdziarski, A. A., Gierliński, M., Mikołajewska, J., et al. 2004, MNRAS, 351, 791 [NASA ADS] [CrossRef] [Google Scholar]
  58. Zhang, S. N., Cui, W., Harmon, B. A., et al. 1997, ApJ, 477, L95 [NASA ADS] [CrossRef] [Google Scholar]
  59. Zhu, Z., & Stone, J. M. 2018, ApJ, 857, 34 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Illustration of the model. The large-scale magnetic field is formed through an inverse cascade process of the dynamo-generated small-scale field in the outer thin disk. This large-scale poloidal field is produced by the azimuthal currents in the disk.
In the text
thumbnail Fig. 2.

Correlation between λtr and λpeak. The circles are NSXRBs, while the dots show the BH counterparts. The data are taken from the literature (Yu & Yan 2009; Yan & Yu 2017; Cúneo et al. 2020). The solid lines are the model calculations for BHXRBs (i.e., ξc = 1), and the dashed lines are for NSXRBs (i.e., ξc = 0.1). The different colors indicate the results calculated with different values of the viscosity parameter: α = 0.05 (yellow), 0.07 (magenta), 0.1 (cyan), 0.15 (red), 0.2 (green), 0.3 (blue), and 0.4 (black). The stars indicate the case of the radiation pressure equaling the gas pressure in the outer disk at Rtr. The transition radius rtr = 20 is adopted in all calculations.
In the text
thumbnail Fig. 3.

Same as Fig. 2, but rtr = 30 is adopted.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.