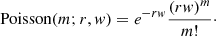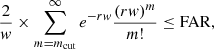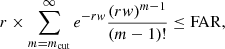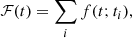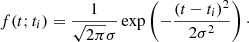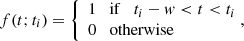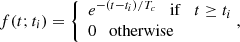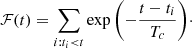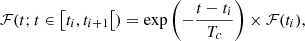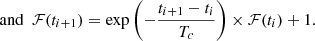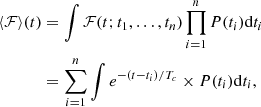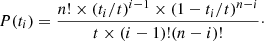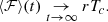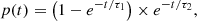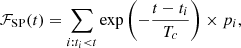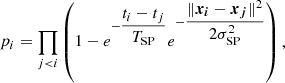| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 5 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202141305 | |
| Published online | 18 October 2021 | |
Identification of neutrino bursts associated to supernovae with real-time test statistic (RTS2) method
INFN Sezione di Padova, 35131 Padova, Italy
e-mail: mathieu.lamoureux@pd.infn.it
Received:
13
May
2021
Accepted:
18
July
2021
Aims. This paper proposes a new approach to detecting 𝒪(MeV) neutrino bursts such as those associated with supernovae.
Methods. A novel ‘real-time test statistic’ (RTS) exploits the temporal structure of the expected signal, discriminating against the diffuse background, to allow detection of very weak signals that would elude standard clustering methods.
Results. For a given background rate, the proposed method increases signal efficiency while keeping the same false alarm rate for a Poisson-distributed background. By adding a spatial penalty term to the definition of RTS, it is also possible to reject spatially correlated backgrounds such as those due to spallation events.
Conclusions. The algorithm can be implemented in a real-time monitoring system for detectors of all sizes, allowing prompt alerts to be sent to the wider community, for example through the SNEWS 2.0 network.
Key words: neutrinos / methods: data analysis / methods: statistical / supernovae: general
© M. Lamoureux 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The detection of low-energy (Eν ∼ 𝒪(MeV)) neutrino bursts is particularly relevant in the search for supernovae. Prompt detection would allow an early warning to be provided, enabling subsequent electromagnetic observations, which are crucial to understanding the underlying mechanisms.
The usual method consists in watching for positive fluctuations from the typical expected background. In most of the neutrino detectors, the main background at energies relevant for supernovae can be modelled with Poisson statistics, which is a constant rate with simple statistical fluctuations. For a given background rate r, the number of background events in a time window w follows the Poisson distribution with λ = r × w:
Let us denote the typical timescale of the physical phenomenon under study, τphys. For instance, τphys ∼ 10 s is expected in the case of supernovae. If rτphys ≫ 1, the search for neutrino bursts can be simplified to a search for an excess with a z-score (Acero et al. 2020). However, if the detector has a relatively low background (rτphys ≲ 1), this method cannot be applied and the usual technique consists in dividing the data into clusters using time windows of size w, covering the physical timescale τphys. For supernovae, w = 20 s is commonly used. There are two different approaches to building these time windows, as illustrated in Fig. 1: sliding windows of width w, with each window starting in the middle of the previous one (Agafonova et al. 2008); and dynamic windows of width w, one starting from each selected event (Ikeda et al. 2007; Abe et al. 2016; Novoseltsev et al. 2020).
 |
Fig. 1. Illustration of the two standard methods used to build the time windows. (a) Sliding windows. (b) Dynamic windows. |
It is then straightforward to define a cut on the cluster multiplicity (number of selected events in the cluster, including the first one in the dynamic case) to achieve a target false alarm rate (FAR; e.g., one per year or one per century) by using the Poisson survival function.
For sliding time windows,
and for dynamic time windows,
where the factor in front of the sum is the ‘rate’ of time windows and the −1 in Eq. (3) accounts for the fact that, as the first event is marking the start of the window, the time window of multiplicity m should only contain m − 1 events; these events are unaffected by the presence of the first event due to the independence property of the Poisson process. For instance, for a background rate of 0.01 s−1 and a FAR of one per century, we get multiplicity cuts of seven and eight events for the sliding and dynamic methods, respectively (16 and 17 for r = 0.1 s−1).
Nevertheless, these methods are limited as neither of them takes into account the fact that signal bursts will have a very different time structure (localised within an interval of a few seconds) than the background (expected to be uniformly distributed within the time window).
Recently, there have been attempts to use additional time-related variables, such as the time difference Δt between the first and the last event in a cluster (Casentini et al. 2018): typically Δt ∼ τphys for signal-only clusters and Δt ∼ w for background-only clusters. This can however suffer from background contamination, in particular at high background rates.
In the present publication, we propose an alternative approach that consists in getting rid of the traditional time window definition while benefiting from the time structure of signal burst. In Sect. 2 we present the new method. In Sect. 3 we present the results when applied to a toy supernova simulation. In Sect. 4, we show that the method can still be useful in the case of remaining non-Poisson background, with slight modifications. In Sect. 5 we present a brief discussion of the different aspects of the new method.
2. Method
A common method to translate discrete event times into a continuous event density consists in using kernel density estimation (KDE) techniques (see e.g., Abbasi et al. 2020 for the application to high-energy neutrinos). It is parametrised by considering that each selected neutrino event i is characterised by a contribution f(t; ti), maximal at t = ti. We then define:
where the sum is performed over all events. This continuous function ℱ can then be used to search for an excess: ℱ(t) > ℱcut. The value of the cut can be optimised to obtain a given FAR. If N centuries of background are simulated and the requested FAR is one per century, we should simply find ℱcut such that ℱ(t) exceeds this threshold less than N times in total.
Usual KDE methods are characterised with a (symmetric) Gaussian kernel,
However, in the following, we are solely interested in identifying whether or not a supernova burst has just occurred, hence the preference for an asymmetric kernel with f(t; ti) = 0 for t < ti.
If we use
the analysis would be fully equivalent to the dynamic time window approach presented in Sect. 1.
In the present publication, we consider the function
where Tc is a characteristic time that plays the role of the bandwidth in standard KDE approaches. The shape of f is not meant to precisely follow the temporal shape of the expected signal (which would introduce model-dependence) but rather to catch its general behaviour with a rapid rising time (< 1 s) where most of the neutrinos will be emitted and still select the events coming from the longer cooling phase (Tc = Tcooling ≳ 𝒪(1 s)).
The choice of Tc = 10 s is conservative enough to catch the main features of the temporal structure of the signal for most of the recent models (e.g., Bollig et al. 2021; Suwa et al. 2021), even though dedicated offline analyses could be performed with f(t) defined to follow a modelled time distribution. Such studies to discriminate between different models are presented in Abe et al. (2021).
The discontinuity at t = ti will introduce some discontinuous jumps in ℱ(t) but this is not problematic for the analysis. Then, ℱ(t) is re-written as:
It can also be expressed in an iterative way:
Average value: In the case of Poisson-distributed background, the average value of ℱ(t) is:
where n is the number of events within the period [0, t] and P(ti) is the distribution of the time of event i. Using order statistic and assuming the events are uniformly distributed between 0 and t, the latter may be written as:
By taking the limit t → ∞ (n → rt), we derived the full computation and obtained:
This ensures that ℱ remains stable in case of background-only events.
For simplicity, in the following, the method is named RTS2 for real-time test statistic for supernovae.
Figure 2 shows the typical distribution of ℱ(t) (using Tc = 10 s) if it is computed regularly for the background-only scenario (with r = 0.05 s), compared with the distribution of the maximum value reached for a supernova signal (see Sect. 3.1 for the description of the latter). As expected from Eq. (13), the background distribution remains at relatively small values and the average value is ⟨ℱ⟩∼0.50 = rTc.
 |
Fig. 2. Distribution of ℱ(t), computed every second on a background simulation with Poisson rate r = 0.05 s−1 and assuming Tc = 10 s, with its corresponding anticumulative (dark blue). The signal histograms show the distributions of the maximal ℱ values obtained for a signal injection of 5, 8, or 10 events (τ1 = 1 s, τ2 = 0.01 s). |
3. Results
In this section, various background rates are considered. The performance of the new method presented in Sect. 2 is compared to that of the simple clusterisation in dynamic time windows (Eq. (3)), referred to as the multiplicity method. In the following, Tc = 10 s is used as it is found to be a good compromise in the search for supernova signals with a similar timescale.
3.1. Signal simulation
The simulation is performed in a generic way, so that it is relatively independent of the supernova models and of the neutrino detector. First, a given number of signal events nS is supposed to be detected. This could be converted to a supernova distance for a given detector (fixed mass, target, and efficiency) using SNOwGLoBES (Beck 2016). Their time distribution is then parametrised by a double-exponential shape as in (Casentini et al. 2018):
with typically τ1 = 10 − 100 ms and τ2 ≳ 1 s, representing respectively the rising time and the decaying time of the signal. In the following, when not explicitly specified, τ1 = 10 ms and τ2 = 1 s are used, which show a close fit to the current supernova models and SN1987a data.
Each signal burst is simulated on a short time interval (typically τ = 30 − 50 s) on top of simulated background events with rate rbkg. The signal selection efficiency for a given cut 𝒞 is obtained by simulating a large number of signal bursts and by computing the fraction of bursts satisfying 𝒞 during the period τ (one cluster passing the multiplicity cut or ℱ(t) exceeding given threshold).
3.2. Raw performance
Independently of the signal simulation, we can first directly compare the cuts applied on ℱ and multiplicity to achieve a given FAR in the RTS2 and multiplicity methods, respectively, as illustrated in Fig. 3. This is relevant as these cuts correspond to the minimal number of events needed to trigger an alert.
 |
Fig. 3. Evolution of the applied cuts on ℱ for the RTS2 method (solid line) and on multiplicity m for the multiplicity method (dashed line) for different values of FAR (FAR = 1 century−1, 1 year−1, 1 day−1), as a function of fixed background rate. |
Figure 3 clearly shows that the new method is reaching lower multiplicities (e.g., down to m = 4 − 5 instead of m = 8 for r = 0.01 s−1 and FAR = 1 century−1) and is more robust with increasing background rate r, as the needed cut increases more softly as a function of r. The penultimate point on the right in Fig. 3 corresponds to the scenario presented in the Fig. 2, with r = 0.05 s−1 and with a typical cut ℱ ≳ 4 − 5 as already visible in the histogram.
3.3. Signal selection efficiency
Figure 4 presents the obtained signal efficiency (computed using the procedure detailed in Sect. 3.1) for different fixed background rates and numbers of injected signal neutrinos, and confirms the results presented in the previous paragraph: the RTS2 method performs much better for bursts with low-multiplicity signal and the effect is visible for all background rates. Referring back to the example of r = 0.05 s−1 from Fig. 2, we can achieve non-negligible efficiencies for nsig > 6, as seen in the clear separation between background and signal in the histogram.
 |
Fig. 4. Comparison of the signal selection efficiency for the RTS2 method (solid line) and for the multiplicity method (dashed line), as a function of the number of true signal neutrinos in the detected burst, for FAR = 1 century−1 and for different background rates (that impact both the simulation toys and the required cut). |
For a fixed FAR and background rate, one may then reduce the detection threshold (and therefore increase the distance horizon) of the supernova search.
3.4. Stability with signal shape
Figure 5 illustrates how the signal efficiency changes with different signal shapes (Eq. (14)) and different sizes of time window for the multiplicity method. Reducing the time window down to 5 s allows the efficiency to be increased compared to the longer duration, but it does not reach the performance of the newly proposed method.
 |
Fig. 5. Comparison of the signal-selection efficiency for the RTS2 method (solid line) and for the multiplicity method (dashed line = time window of 20 s, dotted line = time window of 5 s), as a function of the number of true signal neutrinos in the detected burst, for FAR = 1 century−1, different background rates r = 0.01 − 0.1 s−1, and different values of the signal shape parameter τ2. |
4. Non-Poisson background
Neutrino detectors may suffer from spatially correlated backgrounds whose times will not be distributed with a Poisson distribution. This is the case for spallation events, where a radioactive decay may follow the interaction of high-energy cosmic-ray muons with the matter of the detector. In Super-Kamiokande, this is handled by checking the spatial distribution of the identified vertices after clustering (Abe et al. 2016), computing the dimensionality of the vertex distribution and only selecting clusters identified as volume-distributed (vertices uniformly distributed in the volume of the detector).
As an alternative approach, we adapt the RTS defined in Sect. 2 in order to penalise events if they are detected near to previous events (where the term ‘near to’ refers to both the space and time domains), so that spatially correlated clusters are effectively suppressed:
where pi is the weight applied to event i. A naive approach is to define:
where {xi} are event positions, TSP and σSP are the time and spatial characteristics of the spatial penalty that can be adjusted to the typical scales of the background to be considered, and the sum runs over the events with tj ≤ ti. The formula ensures that pi ∼ 1 if there are no events near to event i (δt ≲ TSP, distance ≲ σSP), while pi → 0 otherwise (event will not contribute to ℱ). The weight of a given event is reduced even further if more than one other event is detected nearby.
For a correlated cluster of N events and characterised by a multi-normal distribution with σ = σB, we derived that 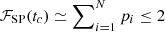 , if σB = σSP and assuming all events arrive at the same time tc, even for N → ∞. The effect of the cluster is effectively suppressed, as long as the term σSP is tuned to the scale of the background of interest in a given detector.
, if σB = σSP and assuming all events arrive at the same time tc, even for N → ∞. The effect of the cluster is effectively suppressed, as long as the term σSP is tuned to the scale of the background of interest in a given detector.
Figure 6 illustrates how the implementation of the spatial penalty terms allows the contamination due to non-Poisson background to be reduced, as peaks related to the latter (assuming point-like sources) are shrunk, while signal bursts remain at the same level as without the spatial penalty. Figure 7 presents the rejection power of the RTS2 method for spatially correlated clusters after applying the cuts on ℱ derived in the previous sections (assuming only Poisson background).
 |
Fig. 6. Illustration of non-Poisson rejection. Top panel: example of event rate as a function of time in a detector with the size of Super-Kamiokande. The injected Poisson background has a rate rbkg = 0.05 s−1. Two additional spatially correlated clusters of background events (with σB = 2 m) and with respectively 10 and 15 events) have been injected. Finally, two signal-like bursts with the parametrisation of Eq. (14) are added, with 7 and 10 neutrinos, respectively. Bottom panel: test statistic time evolution for the RTS2 method without and with the spatial penalty from Eq. (16). |
 |
Fig. 7. Fraction of simulated spatially correlated clusters that are rejected by applying the cut on ℱ(t) optimised in order to ensure FAR of one per century, one per year, one per month, one per week, one per day, or one per hour from Poisson-distributed background (with rbkg = 0.05 s−1), as a function of injected multiplicity of the cluster. The solid lines (resp. dashed lines) show the results without (resp. with) the spatial penalty term in Eq. (15). |
We note that, even though the chosen spatial penalty term is relatively simple, it is quite effective in rejecting point-source background. It is only in the case of very high FAR (e.g., one per hour) that extra care may be needed as the rejection seems to no longer be efficient for such loose cuts on ℱ. Furthermore, the definition of pi = p({xj}j ≤ i, {tj}j ≤ i) may be optimised to reject specific backgrounds related to a given experiment, as the proposed formula only takes care of point-like sources while spallation background may have vertices distributed along a line. To classify each newly detected neutrino as part of a background ‘burst’ (pi → 0) or not (pi ∼ 1), the use of a k-nearest neighbours algorithm or other outlier-detection techniques may be very promising.
5. Discussion
The presented approach would allow supernova bursts to be detected with relatively low multiplicity (∼5 − 10), effectively increasing the horizon compared to more standard approaches. For reference, based on numbers from Table 4 of (Al Kharusi et al. 2021), the Hyper-Kamiokande detector would be able to reach M31-Andromeda (d ∼ 778 kpc) while smaller current detectors would still trigger for most of the Milky Way satellite galaxies (d ≲ 200 kpc; Drlica-Wagner et al. 2020).
The approach can be easily implemented in a real-time monitoring system using Eq. (10) (where +1 may be replaced by pi + 1 to account for the spatial penalty from Sect. 4). The threshold on ℱ may be adjusted to safely reduce contamination by using Monte Carlo simulations of the background or by data-driven methods. The latter ones are particularly relevant if a given experiment wants to achieve FAR of one per day, week, or month, as limited datasets would be sufficient to validate it.
6. Conclusion
In the present paper, we present the RTS2 method and apply it to the detection of neutrino bursts with a generic time spectrum that fits well with current supernova models. We compare the performance to using solely a cut on the multiplicity in the fixed-size time window and show that our new method performs well, even for higher background rates.
The RTS2 method allows for high flexibility as to the choice of the function characterising the contribution of each event and it may be further improved by considering the addition of new variables in the analysis, such as the event energy.
It is possible to simply adapt the RTS2 formula to take care of the non-Poisson distributed background, either with a basic penalty term (e.g., Eq. (16)) or with methods specially adapted to rejecting specific backgrounds in a given detector (outlier-detection techniques or machine learning approaches).
Lastly, even though the present paper focuses on application of the RTS2 method in detecting core-collapse supernovae (CCSNe) in real time, the presented techniques may also be extended beyond the special case of CCSNe, e.g., to bursts of different natures, including binary mergers (Kyutoku & Kashiyama 2018), or beyond real-time applications for single detectors, for instance for offline searches at Super-Kamiokande (Ikeda et al. 2007) or LVD (Vigorito et al. 2021). Similarly, RTS2 may also be promising in the context of the SNEWS network, as it would allow individual high false alarm rate detections to be combined into a significant joint alert.
Acknowledgments
I would like to thank the local group in the Department of Physics of the University of Padova, as well as the astrophysics working group of the Hyper-Kamiokande collaboration, for useful discussions. CloudVeneto is acknowledged for the use of computing and storage facilities. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłosdowska-Curie grant agreement No 754496.
References
- Abbasi, R., Ackermann, M., Adams, J., et al. 2020, ArXiv e-prints [arXiv:2011.05096] [Google Scholar]
- Abe, K., Haga, Y., Hayato, Y., et al. 2016, Astropart. Phys., 81, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Abe, K., Adrich, P., Aihara, H., et al. 2021, ApJ, 916, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, M. A., Adamson, P., Agam, G., et al. 2020, JCAP, 10, 014 [Google Scholar]
- Agafonova, N., Aglietta, M., Antonioli, P., et al. 2008, Astropart. Phys., 28, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Al Kharusi, S., BenZvi, S. Y., Bobowski, J. S., et al. 2021, New J. Phys., 23, 031201 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, A. 2016, SNOwGLoBES: SuperNova Observatories with GLoBES https://github.com/SNOwGLoBES/snowglobes [Google Scholar]
- Bollig, R., Yadav, N., Kresse, D., et al. 2021, ApJ, 915, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Casentini, C., Pagliaroli, G., Vigorito, C., & Fafone, V. 2018, JCAP, 08, 10 [Google Scholar]
- Drlica-Wagner, A., Bechtol, K., Mau, S., et al. 2020, ApJ, 893, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ikeda, M., Takeda, A., Fukuda, Y., et al. 2007, ApJ, 669, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Kyutoku, K., & Kashiyama, K. 2018, Phys. Rev. D, 97, 103001 [NASA ADS] [CrossRef] [Google Scholar]
- Novoseltsev, Y. F., Boliev, M., Dzaparova, I., et al. 2020, Astropart. Phys., 117, 102404 [NASA ADS] [CrossRef] [Google Scholar]
- Suwa, Y., Harada, A., Nakazato, K., & Sumiyoshi, K. 2021, PTEP, 2021, 013E0 [Google Scholar]
- Vigorito, C. F., Bruno, G., Fulgione, W., & Molinario, A. 2021, PoS, ICRC2019, 1028 [Google Scholar]
All Figures
 |
Fig. 1. Illustration of the two standard methods used to build the time windows. (a) Sliding windows. (b) Dynamic windows. |
| In the text | |
 |
Fig. 2. Distribution of ℱ(t), computed every second on a background simulation with Poisson rate r = 0.05 s−1 and assuming Tc = 10 s, with its corresponding anticumulative (dark blue). The signal histograms show the distributions of the maximal ℱ values obtained for a signal injection of 5, 8, or 10 events (τ1 = 1 s, τ2 = 0.01 s). |
| In the text | |
 |
Fig. 3. Evolution of the applied cuts on ℱ for the RTS2 method (solid line) and on multiplicity m for the multiplicity method (dashed line) for different values of FAR (FAR = 1 century−1, 1 year−1, 1 day−1), as a function of fixed background rate. |
| In the text | |
 |
Fig. 4. Comparison of the signal selection efficiency for the RTS2 method (solid line) and for the multiplicity method (dashed line), as a function of the number of true signal neutrinos in the detected burst, for FAR = 1 century−1 and for different background rates (that impact both the simulation toys and the required cut). |
| In the text | |
 |
Fig. 5. Comparison of the signal-selection efficiency for the RTS2 method (solid line) and for the multiplicity method (dashed line = time window of 20 s, dotted line = time window of 5 s), as a function of the number of true signal neutrinos in the detected burst, for FAR = 1 century−1, different background rates r = 0.01 − 0.1 s−1, and different values of the signal shape parameter τ2. |
| In the text | |
 |
Fig. 6. Illustration of non-Poisson rejection. Top panel: example of event rate as a function of time in a detector with the size of Super-Kamiokande. The injected Poisson background has a rate rbkg = 0.05 s−1. Two additional spatially correlated clusters of background events (with σB = 2 m) and with respectively 10 and 15 events) have been injected. Finally, two signal-like bursts with the parametrisation of Eq. (14) are added, with 7 and 10 neutrinos, respectively. Bottom panel: test statistic time evolution for the RTS2 method without and with the spatial penalty from Eq. (16). |
| In the text | |
 |
Fig. 7. Fraction of simulated spatially correlated clusters that are rejected by applying the cut on ℱ(t) optimised in order to ensure FAR of one per century, one per year, one per month, one per week, one per day, or one per hour from Poisson-distributed background (with rbkg = 0.05 s−1), as a function of injected multiplicity of the cluster. The solid lines (resp. dashed lines) show the results without (resp. with) the spatial penalty term in Eq. (15). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.