EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A21 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A21
Number of page(s) 13
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/202141163
Published online 01 October 2021

© ESO 2021

1 Introduction

Coherent radio emission from stellar systems can be produced by two mechanisms: plasma emission that occurs at the ambient plasma frequency and its harmonics, and cyclotron emission that occurs at the ambient cyclotron frequency and its harmonics (Melrose & Dulk 1982). Since plasma and cyclotron frequencies depend only on plasma density and magnetic field strength respectively, radio observations provide a unique opportunity to determine fundamental plasma parameters in the coronae of stars and magnetospheres of planets.

Both plasma and cyclotron emission are expected to be circularly polarised (Dulk 1985), whereas the vast majority of radio sources are weakly (≲1%) or not circularly polarised and of extragalactic origin. We exploited the fact that the majority of radio sources are not circularly polarised to conduct an unbiased survey of stellar radio emissions via cross-matching circularly polarised radio sources in the ongoing LOFAR Two-Meter Sky Survey (LoTSS; Shimwell et al. 2019) with known stars (Vedantham et al. 2020; Callingham et al. 2021a). Here we present the discovery and initial characterisation of 14 radio-emitting RS Canum Venaticorum (RS CVn) binaries detected by this technique. Our detections of individual main-sequence stars and wide-separation binaries will be presented elsewhere. With only a singular instance of coherent radio emission from an RS CVn binary known before (Slee et al. 2008), our sample represents a significant advance towards employing radio observations to study the dynamics of plasma in close stellar binaries.

RS CVn binaries usually consist of two stars with late spectral types (F, G or K) on the main sequence (Hall 1976). They are short-period binaries, with periods ranging from ~1 day to ~30 days. The individual stars are in close proximity to each other (~0.01 AU). The systems also display strong Ca II H and K emission lines, and a prominent Balmer Hα line. The prominent lines are due to an active chromosphere, which is why these stars are often called chromospherically active binaries. They are tidally locked, which leads to high rotational velocities, which in turn leads to strong magnetic fields (Song et al. 2013; Reiners et al. 2014). These high velocities twist the magnetic flux loops in the stars, extending them through the photosphere at various points, leading to a large portion (up to 30%) of the surface to be covered by starspots (Rodonò 1992). Such a large spot covering is used to explain the large optical photometric variability observed for these stars (Oliver 1974).

Chromospheric flares, as well as magnetic interactions within the binary can accelerate electrons that emit radio waves (Dulk 1985; Slee et al. 2008). While their magnetic interaction is interesting in its own right, it also provides a laboratory to study a more general class of sub-Alfvénic plasma interactions that can occur between a star and its planet or a planet and its moon (Goldreich & Lynden-Bell 1969; Zarka 2007; Lanza 2009; Saur et al. 2013).

Polarised and unpolarised radio emission from RS CVns has primarily been studied at gigahertz frequencies (Donati et al. 1992; Kochukhov et al. 2013; White & Franciosini 1995; van den Oord & de Bruyn 1994; Drake et al. 1989; Morris & Mutel 1988; Mutel et al. 1987; Willson & Lang 1987; Mutel & Lestrade 1985). The observed gigahertz emission is typically long-lasting and weakly polarised, and is interpreted as gyrosynchrotron radiation (Dulk 1985; Kuijpers & van der Hulst 1985; Chiuderi Drago & Klein 1990). Only in a few instances has long-lasting (≳hours) polarised (≳40%) emission, reminiscent of planetary aurorae, been seen. For example, White & Franciosini (1995) interpreted the different circular-polarised handedness between 1 and 8 GHz observations as a suggestion that a coherent emission mechanism is likely operating atlow frequencies. Furthermore, Slee et al. (2008) postulated that this emission might be the result of an electrodynamic binary interaction that accelerates electrons which cause the emission – a scenario that shares similarities with the well-known Jupiter-Io ‘unipolar-induction’ model (Goldreich & Lynden-Bell 1969).

Radio observations at metre-wavelengths provide the best opportunity to test the electrodynamic interaction models for two reasons. Firstly, the surface cyclotron frequency νe ≈ 2.8 × 106 B Hz, above which the radio emission cuts off, in the vast majority of stars in RS CVn binaries, may lie below the gigahertz regime. This frequency limit is due to typical surface magnetic fields being around B ≈ 100 Gauss (Donati et al. 1992). In this case, only sub-gigahertz observations would be able to access their cyclotron emission from electrodynamic interaction. Secondly, cyclotron emission is inherently beamed, which means only a small fraction of radio-loud systems are visible to an observer. Low-frequency telescopes have wider fields of view than gigahertz-frequency telescopes, providing a high survey rate to identify the sources that have a fortuitous viewing geometry. The ongoing LoTSS survey (Shimwell et al. 2019), whose data we use here, is particularly well-suited for this purpose. Its long eight-hour exposures allow us to identify long-duration auroral-type emission against minute-timescale bursts that can occur on Sun-like stars due to flaring activity.

The rest of the paper is organised as follows. In Sect. 2, we present the radio detections, fundamental properties of the RS CVns detected, and arguments in favour of a cyclotron maser interpretation. In Sect. 3, we model the emission geometry and brightness temperature of our detections using theoretical considerations and numerical calculations of the emitter’s beaming geometry. We also outline two plausible mechanisms that accelerate charges that radiate the observed radio waves. We end in Sect. 4 with a summary and outlook towards determining the mechanism of acceleration in RS CVn systems.

2 Radio observations and properties

2.1 Discovery

LoTSS routinely produces 144 MHz images with ≲100 μJy root-mean-square noise and with an astrometric accuracy of ~0′′.2 (Shimwell et al. 2019), making it an unparalleled widefield low-frequency survey to blindly search for radio-bright stellar systems. To discover coherently-emitting stellar systems, and to dramatically minimise our false-positive association rate (Callingham et al. 2019), we isolated our crossmatch to only circularly-polarised sources in LoTSS. The number density of sources with a circularly-polarised fraction >2% is ≈ 0.1 per sq. degree (Callingham et al. 2021a). After identifying ≥4σ circularly-polarised LoTSS sources, we associated a Gaia data release 2 (DR2) (Brown et al. 2018) counterpart if the Gaia DR2 source was within 1″ of the radio position and had a parallax over error of ϖ∕ϖerr ≥ 3. Since the LoTSS data available at the time of writing only covers ≈20% of the northern sky at Galactic latitudes |b| > 20°, where the Gaia DR2 source density is relatively low, the chance-coincidence associations between a Gaia Galactic source and the Stokes V LoTSS sample is ≈0.05 (Callinghamet al. 2021a). Therefore, we consider our associations highly reliable.

From this sample of coherently-emitting stellar systems with Gaia DR2 counterparts, we identified three classes of objects: isolated (or wide binary) M dwarfs (presented in Callingham et al. 2021a), millisecond pulsars, and different types of variable stars such as the FK Comae Berenices (FK Com), W Ursae Majoris (W UMa), BY Draconis (BY Dra), and RS Canum Venaticorum (RS CVn) types. Since the main science goal of this manuscript is associated with binary interactions, we only present the stellar systems that are known to be close binaries with periods less than tens of days. This list includes binaries classified as RS CVn and BY Dra systems. We plan to present the other sources in a followup paper. The LoTSS photometry of our sample is given in Table 1, while Figs. 1 and 2 show the Stokes I and Stokes V discovery images. The known stellar parameters and orbital parameters of the individual systems are given in Tables 2 and 3 respectively.

2.2 Images and lightcurves

Once a source of interest was identified in the LoTSS data, we performed some post-processing to extract the highest signal-to-noise images and lightcurves. The post-processing steps are described in van Weeren et al. (2021) and were also employed in Callingham et al. (2021b) and Vedantham et al. (2020). Briefly, each dataset was phase shifted to the position of the source of interest, taking account of the LOFAR station beam attenuation. Residual phase errors were solved for by applying a self-calibration loop on 10–20 s timescales. This was followed by several rounds of diagonal gain calibration on timescales of ≈20 min.

Stokes I and V images of each source were then created from these reduced datasets using a robust parameter of −0.5 via WSCLEAN (v 2.6.3; Offringa et al. 2014). For the time series analysis, each image was synthesised over all of the available bandwidth to maximise the signal. The flux density of each source was measured using the Background And Noise Estimator (BANE) and source finder AEGEAN (v 2.1.1; Hancock et al. 2012, 2018). We used the priorised fitting option of AEGEAN at the location of each source to account for uncertainties associated with non-detections in our time series analysis.

Our time sampling function of the radio data for each stellar system was determined by the Stokes I detection in each 8 hour integrated epoch and the period of the system. The lightcurves of some of our brightest detections and shortest-period binaries are discussed in more detail in Sect. 3.4.

Table 1

144 MHz flux densities (Stokes I and V) of our population.

thumbnail Fig. 1

Stokes I discovery images of our RS CVn population. Each panel is a zoom-in of a LoTSS pipeline-produced image of the field containing the target. The circles are centred on the proper-motion corrected position of the targets and have a radius of 30″. The point spread function is about 5″ wide. The color scale runs from −15 (blue), through 0 (white), to + 15 (red) median absolute deviations, which corresponds to a range of −10σ to + 10σ for Gaussian noise. The date reported in each panel is the date of observation in YYYY-MM-DD format.

2.3 Mechanism of emission

We determined the mechanism of emission using the approximate brightness temperature and degree of circular polarisation. The brightness temperature, normalised to characteristic values for stars in our sample is 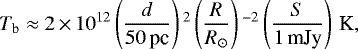(1)

where d is the distance to the star, S is the radio flux-density, and R is the projected radius of the emitter (assumed to be circular). Conservatively, using the values of R for the larger binary component, we find that Tb ranges from ~1011 to ~ 1012.5 K in our sample. The high implied brightness temperature, in combination with the high circular polarisation fraction, implies the radio emission can not be produced by any incoherent emission mechanism (Dulk 1985). Therefore, only coherent plasma and cyclotron maser emission are plausible emission mechanisms.

Plasma emission is thought to be caused by conversion of Langmuir waves to transverse electromagnetic waves (Ginzburg & Zhelezniakov 1958; Melrose 1991). 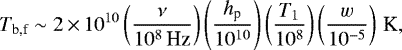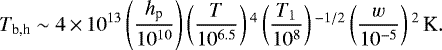At low radio frequencies (ν ~ 102 MHz), induced emission can be neglected for reasonable coronal parameters (Vedantham 2021) and we arrive at the following expressions for the anticipated brightness temperature of fundamental and second harmonic plasma emission, respectively (Vedantham 2021) (2) (3)

Here hp is the plasma density scaleheight, T1 is the hot plasma component temperature that drives the generation of Langmuir turbulence via the bump-on-tail instability, T is the ambient plasma temperature, and w is the fractional energy in the Langmuir-wave turbulence. The normalisation values are chosen to be representative values. The turbulence level, w is thought to be limited to ~ 10−5 at which point the Langmuir wave packets collapse due to non-linear effects (Benz 1993). The ambient coronal temperature of RS CVns determined from X-ray observations is T ≈ 106.5K (Ness et al. 2003) which gives a density scale height of hp ≈ 0.3 R*. T1 has not been observationally determined for our targets and we have taken T1 =30T as a typical value based on hard X-ray observations of flares on dMe stars and RS CVn binaries (Franciosini et al. 2001; Favata & Schmitt 1999).

Although second harmonic plasma emission can attain the observed brightness temperature (see Eqs. (1) and (3)), it cannot attain the high levels of observed circular polarisation (Vedantham 2021) and is therefore disfavoured. Fundamental plasma emission can, in principle, be 100% circularly polarised, but it cannot attain the observed brightness temperature unless R ≳ a few to ten R* for stars in our sample (see Eqs. (1) and (2)). Because we are detecting quasi-quiescent emission in eight-hour-long exposures, the source size must be smaller than the closed-field region in the corona where turbulent gas can be trapped by the magnetic field. In other words, the source must lie within the Alfvén surface. We can approximately determine the Alfvén radius by equating the plasma and magnetic energy densities. For a characteristic base plasma density of n0 = 1010 cm−3 (Ness et al. 2003) and a dipolar magnetic field with a surface field strength of B, the Alfvén point is at a radial distance of 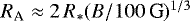. Hence confining turbulent plasma at a radial distance of ≈10 R* is theoretically problematic which disfavours the plasma emission hypothesis for a significant fraction of our sample. Although this leads us to favour the cyclotron maser as the mechanism of emission, the plasma hypothesis cannot be conclusively ruled out because our calculations are based only on nominal values for parameters such as w, T, T1 and hp. We note here that Slee et al. (2008) also identify the electron cyclotron maser as the mechanism of emission for their observations of HR 1099 at gigahertz frequencies. While they arrived at this conclusion based on the detection of millisecond-timescale structure in the radio emission, the low frequency of our observations has allowed us to use the brightness temperature and polarisation fraction of the hours-long-duration emission to arrive at the same conclusion. Although Slee et al. (2008) only had a sample of one, our larger RS CVn sample size suggests that close stellar binaries can generate quasi-quiescent cyclotron maser emission. This conclusion can be reconciled with previous attribution of gigahertz frequency observations mainly to gyrosynchrotron emission, if the large-scale magnetic fields of RS CVn stars have surface values well below a kiloGauss. In this case, their cyclotron emission does not extend to high enough frequencies to have been observed before.

thumbnail Fig. 2

Same as Fig. 1, but for Stokes V. The point spread function width is about 20″ and the radius of the circle is 30″. The images are not de-convolved.
Table 2

Relevant stellar properties found in the literature search for the stars detected by LOFAR.

Table 3

Orbital parameters of our targets.

3 Emission modelling

3.1 Energetics

The isotropic-equivalent radio luminosity of our sample is of the order 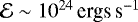, which is many orders of magnitude below the typical X-ray luminosity of RS CVn coronae. Therefore, chromospheric flares, that are thought to power the X-ray corona, certainly have sufficient energy to power the radio emission. Next, we consider models that posit the magnetic interaction between the stars as the source of electron acceleration. RS CVns are likely tidally locked (Song et al. 2013), but deviate from strict magnetospheric co-rotation by about η = 1% (Hall 1981). This differential motion can potentially accelerate electrons and power the emission. Let Ω be the rotation rate, a the orbital separation, B0 the surface magnetic field of the emitter, and R1 its radius. The field at the conducting obstacle (binary companion) is 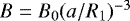. The magnetic energy intercepted by the companion of radius, say R2, per unit time is 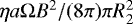which in convenient units for a Keplerian relationship between a and Ω, and assuming solar mass stars is 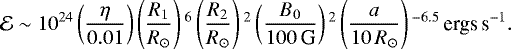(4)

Alternatively, the intercepted energy flux may be dominated by the ram-pressure of the stellar windfluid instead of the energy stored in the magnetic field. In this case we have 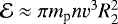. where mp is the proton mass, n is the stellar wind density at the location of the companion, and v is the wind velocity. We make the simplifying assumption that the wind has reached its terminal velocity which gives 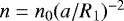where n0 is the base coronalplasma density. In convenient units, we get 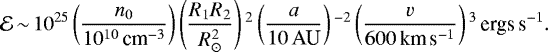(5)

We shall now compare these estimates to the power necessary to support the radio emission. Assuming the radio emission to have a beam solid angle of 10−1 sr, comparable to that of Jovian emission due to Io’s interaction (Queinnec & Zarka 1998) and an emission bandwidth going up to the surface cyclotron cut-off of 2.8(B0∕G) MHz the inferred radio power is 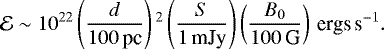(6)

A quick comparison of Eqs. (4)–(6) with the tabulated properties of our RS CVns systems shows that there is sufficient intercepted magnetic pressure and ram pressure in the binary interaction to drive the radio emission if the radio emission efficiency is ≳ 10−2 and ≳ 10−3 respectively. A comparison of the radio power of solar system planets and the interplanetary magnetic pressure as well as the solar wind’s ram pressure yields efficiencies of 2 × 10−3 and 10−5 respectively (Zarka 2007; Zarka et al. 2001). Therefore, although both mechanisms are energetically feasible in principle, the empirical scaling law from solar system planets suggests that magnetic interaction is causing the radio emission. We note here that the X-ray luminosity of RS CVns is typically ≳ 1032 ergs s−1 which is clearly not powered by such interactions; a point also noted by Schrijver & Zwaan (1991). Indeed, the cyclotron emission comes from a small population of supra-thermal (~10 keV to ~1 Mev) electrons that represent a minuscule fraction of the overall coronal thermal-energy budget.

3.2 Brightness temperature

We next check if the cyclotron maser mechanism can plausibly generate the necessary brightness temperature by comparing theoretical limits with observationally inferred values for our sample. Because cyclotron emission is inherently beamed (emitted nearly perpendicular to the magnetic field) and narrowband, the ‘observed’ brightness temperature must itself be inferred via computation of the projected source size, A, at any givenfrequency.

We computed the source size taking beaming into consideration numerically (details in the Appendix), but here provide an approximateanalytic expression to develop intuition. For simplicity, let us consider a large scale dipolar structure for the magnetosphere of the emitter. Cyclotron maser emission from the loss-cone instability is beamed into the surface of a cone with a large opening angle θ ≲ π∕2 and narrow thickness Δθ ≈ β, where βc is the speed of the emittingelectrons (Melrose & Dulk 1982). The cone-axis is parallel to the ambient magnetic field. The emission therefore fills a solid-angle fraction β ≈ Δθ of the visible hemisphere. Seen conversely, a given observer can only view emission from the same fraction of the visible stellar disk. Hence, the apparent emitter area for brightness temperature calculation is 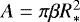, which we confirm to be a good approximation using numerical calculations (see appendix). Taking β =0.2 as a characteristic value (basedon Io-induced Jovian emission models Hess et al. 2010), we see that the observed brightness temperature from Eq. (1) is of the order ~1012−1013.5 K, the upper end of which is comparable to the theoretical limit for maser emission driven by the loss-cone instability (Melrose & Dulk 1982). In other words, a loss-cone maser requires the instability to operate in a large fraction (of order unity) of a dipolar magnetosphere. However, the emitting region in known instances of the loss-cone maser, such as planetary auroral emission, is confined to a thin oval around the magnetic poles. Furthermore, if the loss-cone instability were omnipresent it should have made most of our targets continuously visible because at any given instant, there would be a part of the magnetosphere whose magnetic field orientation allows for the emission to be beamed towards the Earth.

To test if this is the case, we exploited the fact that some of our targets were observed by multiple neighbouring LoTSS pointings. Figure 3 shows a montage of images of our targets where such multi-epoch data with sufficient signal-to-noise ratio for detection was available. We find that most of our targets are detected only in a single epoch which suggests that the maser sites do not occupy a large fraction of the magnetosphere in these objects. We therefore disfavour the loss-cone instability as the cause of emission, particularly for systems at the upper end of the observed brightness temperature range in our sample.

Let us now consider models where only a small fraction of the magnetosphere of the emitting star is ‘live’ with cyclotron emitting electrons. In the specific model of Jupiter-Io type interaction, only the magnetic flux tube connecting the two bodies is live with emitting electrons (see Fig. A.3 for an illustration). Because the loss-cone driven maser in such instances is infeasible due to the above brightness temperature arguments, we suggest that a more efficient instability such as the horseshoe or shell-type maser (Treumann 2006) is responsible. The source size in this case is best computed numerically (as shown in the appendix). The beaming geometry of the horseshoe and shell-type masers is similar to that of the loss-cone maser (all emit nearly perpendicular to the magnetic field)1. We therefore use the loss-cone maser code for our predictions in Sect. 3.4. Here we first provide an approximate expression for analytic intuition. Along a given live field-line, the source size at some frequency is limited by the evolution of the cyclotron frequency beyond the maser bandwidth. The scale length for magnetic field variation in a dipole is ~ R*∕3 and if the maser bandwidth is Δν∕ν, then the source size along the field lines is (Δν∕ν)R*∕3. Across the field lines, the source size is dictated by the thickness of the flux tube that has emitting electrons. Let the radial extent of this ‘live’ flux tube in the equatorial plane be ΔL. The thickness close to the emitting star’s surface is 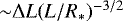. An approximate value for the source area at a given frequency is then 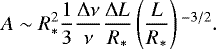(7)

For characteristic values of Δν∕ν ~ 0.01, L∕R*~ 10, ΔL ≈ R* (size of the companion), we have 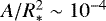. Hence, using Eq. (1), we obtain a maser brightness temperature of Tb ~ 1015−1017 K. A maser driven by the shell or horseshoe instability, thought to power the Earth’s auroral kilometric radiation, can reach brightness temperatures of ~ 1020 K (Louarn et al. 1990; Ergun et al. 2000) which can readily accommodate the inferred values.

In summary, we find that cyclotron maser emission from the loss-cone instability is unlikely to generate the necessary brightness temperature in some of our targets. Instead, the horseshoe of shell-type maser must be invoked to account for the estimated brightness temperature. We note, however, that the horseshoe and shell instabilities require a potential drop directed parallel to the magnetic field lines. It is presently unclear theoretically whether a sufficiently large field-aligned potential can be sustained in the corona of a star whose dense plasma will tend to ‘short’ such voltage drops. In a planetary magnetosphere, the field-aligned potentials are created in density cavities. Although the same has been suggested for stellar coronae in the context of short bursts (Melrose & Wheatland 2016), whether such cavities can be long-lived to generate quasi-quiescent emission must await deeper theoretical work.

thumbnail Fig. 3

Multi-epoch Stokes-I images of our targets. The color scale in each panels runs from − S (blue) through zero (white) to + S (red) where S is the flux density in the discovery epoch (see Table 1). The annotated text also provides the Juliandate at the mid-point of the eight-hour exposure. The circular target-marker has a radius of 5″. The full-width at half-maximum of the point spread function is about 5″. EZ Peg and DG CVn are not included here because both only had one detection of sufficient sensitivity.

3.3 Mechanism of acceleration

Although our blind survey detected a population of M-dwarfs (Callingham et al. 2021a), we have not yet detected a significant population of isolated stars of earlier spectral types. The large number of RS CVn detections whose components span F, G and K stars clearly show that interaction with an orbital companion is essential to the observed radio emission. We foresee two mechanisms by which binarity is causally related to the emission of detectable coherent radio emissions. (i) Chromospheric acceleration: the radio emission may simply be the result of significantly enhanced magnetic activity which in turn is caused by faster rotation (due to tidal locking) and the influence of tidal forces on the underlying dynamo (sometimes called breakdown of co-rotation) (Schrijver & Zwaan 1991). (ii) Magnetospheric acceleration: alternatively, charge acceleration may be a direct result of electrodynamic interaction in the binary similar to the Jupiter-Io engine. In particular, the velocity shear between the wind of one star and the magnetosphere of the other can accelerate charges (Slee et al. 2008). In the first case, the acceleration site is located in the chromosphere and the mechanism is likely similar to that seen in isolated stars, whereas in the second case, it is located away from the star (i.e. it is external to the emitting star) and is likely similar to that seen in magnetospheres of gas-giant planets and brown dwarfs. Discriminating between these two mechanisms will be a significant step in identifying the source of high-energy electrons in RS CVn systems.

We propose that the geometric modulation of the observed emission is an avenue to discriminate between the two mechanisms stated above. Magnetospheric acceleration due to electrodynamic interaction will isolate the ‘live’ azimuthal sectors to those containing the flux tube connecting the two stars, whereas chromospheric acceleration need not have the same preferred azimuthal sector. Due to the beamed nature of cyclotron maser emission, the chromospheric acceleration scenario will likely lead to emission that is always ‘on’, whereas magnetospheric acceleration will lead to emission that has a periodic ‘on-off’ modulation as the ‘live’ flux tube’s orientation changes with respect to the observer during the binary orbit.

There isan important caveat to the discriminant proposed above. Long term photometry of RS CVn starspots, that are the likely sites of particle acceleration, has shown that the spots tend to cluster in so-called Active Longitude Bands (ALBs; Berdyugina & Tuominen 1998). Because the rotation and orbital periods of RS CVns are nearly identical, periodic modulation from this ALB-clustering could masquerade as magnetospheric acceleration. However, the starspot-dip in lightcurves of RS CVns where both stars are on the main sequence appear at quadrature points in the orbit (as opposed to conjunctions); the implication being that the active regions are separated in longitude from the line joining the two stars by ± 90° (Oláh 2006)2. On the other hand, the magnetospheric acceleration scenario posits that the longitude of the ‘live’ flux tube is the same as that of the line joining the two stars. Therefore, even in presence of ALBs, canonical radio and starspot monitoring should be able to discriminate between the two scenarios for systems where both stars are on the main sequence.

3.4 Application to short-period main-sequence binaries

Although we currently do not have long-term radio monitoring data, we applied the discriminant proposed in Sect. 3.3 to existing LoTSS data to elucidate the methodology. We chose a sub-set of our population with the following properties: (a) short orbital periods of a few days or less (semi-major axis of ≲ 10 R⊙) for which the interaction is plausibly sub-Alfvénic, (b) both stars on the main-sequence which avoids the ALB-phenomenon from masquerading as magnetospheric acceleration (see Sect. 3.3), (c) systems for which the orbital inclination is known such that their cyclotron-maser visibility can be computed using known theory, and (d) systems for which the orbital ephemeris is known with sufficient accuracy so that the orbital phase at the radio observation epoch can be calculated with sufficient accuracy. With these criteria, we selected Sig CrB, BF Lyn, EV Dra and YY Gem to apply our discriminant between the two acceleration mechanisms.

The orbital phase of the low-frequency radio emission, including epochs in which the source was not detected, and our model prediction for these four systems is presented in Fig. 4. The predictions for the ten systems for which we had all necessary parameters are shown in Fig. 5.

thumbnail Fig. 4

Orbital phase of the low-frequency total intensity (SI) and circularly-polarised (SV) emission for BF Lyn (top left), EV Dra (top right), Sig CrB (bottom left) and YY Gem (bottom right). The orbital phase for which our model predicts we should observe emission is shown as red-lines at arbitrary flux densities. For Stokes V we use red and blue to distinguish between the two polarisations. Sig CrB was observed in three independent 8 h epochs, while all other stellar systems were only observed in two independent epochs. The prediction for Sig CrB has been shifted 0.5 in phase, which corresponds with emission originating on the secondary, to show the good correspondence with the data. The polarity of the Stokes V prediction is arbitrary because we do not know which magnetic pole is pointed towards us. Therefore the prediction for the stars where we see emission from both poles (YY Gem and EV Dra) can be flipped in sign.

3.4.1 Sig CrB

The first system in our subset is Sigma2 Corona Borealis (TZ CrB, HD 146361), a F9V+G0V type star. It has an orbital period of 1.13979045 ± 0.00000008 days. Rosén et al. (2018) find that conjunction, with the secondary (G0V) closest to us, happens at JD = 2 450 127.9054 ± 0.0004. From this we can determine the orbital phase during the LOFAR epochs. They can be seen in Fig. 4. Our prediction is shown in Fig. 5. We see that our prediction aligns nicely with the observations if we shift the prediction 0.5 in phase. The shifted prediction is shown as the red line in Fig. 4. A 0.5 phase shift is equivalent to saying that the emission originates on the ‘companion’ in our model, i.e. the secondary (G0V). This alignment is consistent with the magnetospheric acceleration model.

3.4.2 BF Lyn

The second star we studied is BF Lynx (HD 80715), a K2V+dK type star. It has an orbital period of 3.804067 ± 0.000008 days. Halbwachs et al. (2018) find that conjunction happens at JD = 2 447 456.2383 ± 0.0025. The only credible detection here overlaps with our prediction, but the phase-binned data lacks a sufficient signal-to-noise ratio to draw a secure conclusion.

3.4.3 EV Dra

The third star in our subset is EV Draconis (HD 144110), a G5V+K0V type star. It has an orbital period of 1.67140121 +- 0.00000065 days. Fekel et al. (2005) find that maximum radial velocity for the primary (G5V) happens at JD = 2 452 182.0226 ± 0.0006. This corresponds to an orbital phase of 0.75. EV Dra’s radio detection is offset by a phase of 0.25 with respectto the predictions, which is inconsistent with the electrodynamic interaction model but consistent with the chromospheric acceleration scenario.

thumbnail Fig. 5

Predicted visible emitter area as a function of orbital phase for our targets that have measured inclinations. We have assumed a theoretical model for the emission geometry given by Melrose & Dulk (1982) with electron speed β = 0.2 as an estimate. The ‘step’-like variations between adjacent points are gridding artefacts. We have assumed that the observer’s line of sight always hits the northern magnetic hemisphere of the emitting star. Solid lines are for electrons travelling from the north magnetic pole to the south magnetic pole, dashed lines are for electrons travelling vice versa. Sincewe do not know if we are observing the northern or southern magnetic hemisphere, these definitions are interchangeable. BQ CVn, DM UMa, DG CVn and BD+334462 have been left out because we lacked the necessary parameters to make an accurate prediction (namely the semi-major axis for the first three star systems, and the inclination for the last one).

3.4.4 YY Gem

The fourth and final star in our subset is YY Geminorum (Castor C, HD 60179C), a M1Ve+M1Ve type star. It has an orbital period of 0.81428290 ± 0.00000005 days. Gary et al. (2012) find that conjunction happens at BJD = 2 456 024.67475 ± 0.00006. The stars have the same spectral type, so there is no point in speaking of primary and secondary. This is the most puzzling case. The predicted epoch of visibility is offset in phase by ≈0.1 of the rotation period, which neither supports the magnetospheric nor the chromospheric acceleration mechanism.

4 Summary and outlook

We have uncovered a population of highly circularly polarised radio-emitting RS CVn stars. We argue based on the low frequency of detection (144 MHz), high circular polarisation fraction (≳70%) and high implied brightness temperatures (≳1013 K) that we are seeing cyclotron maser emission from these systems. All previous radio detections of RS CVn systems were carried out at gigahertz frequencies, and with the notable exception of Slee et al. (2008), interpreted as incoherent gyrosynchrotron emission. We argue that the surface strength of the large scale magnetic fields of RS CVn systems is likely ~ 100 G which allows us to systematically probe their cyclotron emission for the first time due to the low frequency of our observations.

We find that the commonly-invoked loss cone maser can only account for the inferred brightness temperature for unreasonably large source sizes at any given frequency (of the order 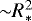) for a significant fraction of our detections. We therefore suggest that the radio emission is being driven by the horseshoe or shell-type instability that also power radio emission in the Earth’s magnetosphere. These types of masers require field-aligned potentials that accelerate charges. It is unclear if such a potential difference could be maintained in the dense corona of a star (plasma flows tend to ‘short’ such voltage drops) and further theoretical work is necessary to gauge the feasibility of such a maser in stellar coronae.

We propose two plausible mechanisms that accelerate the cyclotron emitting electrons: enhanced chromospheric flaring due to tidal forces and an electrodynamical interaction between the two stars (similar to the Jupiter-Io interaction). We propose that quasi-contemporaneous radio monitoring and star-spot photometry could be used to conclusively establish the mechanism of acceleration. To this end, we have developed a code to predict the visibility of the emission and the projected source area for given stellar parameters (details in the Appendix). The limited radio data in hand do not point to a clear conclusion as to the mechanism of acceleration.

We end up noting that the orbital ephemeris of some of our detections were determined using observations that are decades old. The error on the orbital period is often too large to predict the orbital phase during the newer LOFAR exposures sufficiently accurately to be able to constrain the mechanism of acceleration. In addition, some of the systems in our sample haveunknown orbital inclination – a necessary parameter to predict radio visibility. We therefore urge photometricobservations of our targets by advanced amateur astronomers (see e.g. Gary et al. 2012) and spectroscopic observationsby 1-metre class telescopes to accurately constrain the ephemeris, inclination and the longitude of active regions.

Movies

Movie 1 animated image associated with Figure A.3 left (Magnetic_Field_Lines_Through_Binary_Sig_CrB_TZ_Crb_BR_0.96_BD_5.21_28_degrees_0point2c_frame0) Access here

Movie 2 animated image associated with Figure A.3 right (Magnetic_Field_Lines_Through_Binary_Zoomed_In_On_Central_Star_Sig_CrB_TZ_Crb_BR_0.96_BD_5.21_28_degrees_0point2c_frame0) Access here

Movie 3 animated image associated with Figure A.4 left (Source_Site_Binary_Interaction_NtoS_Sig_CrB_TZ_Crb_BR_0.96_BD_5.21_28_degrees_0point2c_frame0) Access here

Movie 4 animated image associated with Figure A.4 right (Emitter_Site_Binary_Interaction_NtoS_Sig_CrB_TZ_Crb_BR_0.96_BD_5.21_28_degrees_0point2c_frame0) Access here

Acknowledgements

J.R.C. thanks the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) for support via the Talent Programme Veni grant. This paper is based on data obtained with the International LOFAR Telescope as part of the LoTSS survey. LOFAR is the Low Frequency Array designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, that are owned by various parties (each with their own funding sources), and that are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefitted from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d’Orléans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK. This research made use of the Dutch national e-infrastructure with support of the SURF Cooperative (e-infra 180169) and the LOFAR e-infra group. The Jülich LOFAR Long Term Archive and the German LOFAR network are both coordinated and operated by the Jülich Supercomputing Centre (JSC), and computing resources on the supercomputer JUWELS at JSC were provided by the Gauss Centre for Supercomputing e.V. (grant CHTB00) through the John von Neumann Institute for Computing (NIC). A.D.acknowledges support by the BMBF Verbundforschung under the grant 05A20STA. This research made use of the University of Hertfordshire high-performance computing facility and the LOFAR-UK computing facility located at the University of Hertfordshire and supported by STFC [ST/P000096/1], and of the Italian LOFAR IT computing infrastructure supported and operated by INAF, and by the Physics Department of Turin university (under an agreement with Consorzio Interuniversitario per la Fisica Spaziale) at the C3S Supercomputing Centre, Italy. Software used: python, numpy, scipy, astropy, matplotlib, vector3d. Telescopes used: LOFAR.

Appendix A Cyclotron maser geometry

Here we describe our modelling of the geometry of the loss cone maser. We begin with the following assumptions:

  • 1.

    The rotational and orbital axis of the binaries are aligned. This assumption is justified for synchronous binaries (Prot = Porb) but not for asynchronous ones (Prot≠Porb) (Glebocki & Stawikowski 1995). As can be seen in Table 3, all our binaries except FG Cam (and potentially BH CVn and DG CVn as the rotational period and orbital period respectively are unknown) are synchronous.

  • 2.

    The stellar magnetic field resembles a dipole and its magnetic axis aligns with the rotational axis (Lehmann et al. 2018). The surface magnetic field at the equator is taken to be 100 G which is a representative value for RS CVn systems (Donati et al. 1992).

  • 3.

    The orbit is circular. As can be seen in Table 3, the eccentricity is 0 or unknown for all binaries except BH CVn.

  • 4.

    The wind from the companion does not significantly distort the magnetic topology of the primary star near the emissionsite. This may not be true in a subset of close contact binaries but we retain this assumption for simplicity.

We model the magnetic field and emission geometry on a grid of points in the magnetosphere of the emitter. We refer to the region where the magnetic field has the right value to generate emission at a given frequency range (and the field lines intercept the binary companion in the case of binary interaction) as the source site. A sub-set of this region from where the beamed emission reaches the Earth is referred to as the emitter site.

We adopted the beaming geometry of Melrose & Dulk (1982) where the emission is directed into a hollow cone with opening angle θ0 and thickness Δθ0 where cos θ0 ≈ Δθ0 ≈ β. In reality, the precise beaming geometry of the emergent radiation depends on the nature of the instability and refraction near the emitter which are not directly accessible, so we take these as representative values. Similarly, we assume that the emitting electrons have an energy of about 10 keV (β ≈ 0.2) as a representative value. With these values, any grid point in the source site where the magnetic field vector makes an angle between θ0 − Δθ0∕2 and θ0 + Δθ0∕2 with the vector pointing towards the observer will fall within the emitter site.

We also adopted the maser bandwidth from Melrose & Dulk (1982): Δν∕ν ≈ 0.5β2 cos2α0, where α0 is the loss-cone angle. We considered α0 = 0.5 as a representative value, which along with β = 0.2 gives Δν ≈ 2 MHz in the LOFAR band. Because we compared the inferred brightness temperature with the theoretical value for a single maser site, we restricted the source site to a region whose cyclotron frequency is within Δν of the central observational frequency of 144 MHz. Finally, we computed the area of the emitter for brightness temperature calculation by projecting the three-dimensional emitter site on to a plane that is normal to the line of sight to Earth.

Figure A.1 shows the emitter site for an example run where we have assumed that the entire magnetosphere of the star is live with cyclotron emitting electrons. Figure A.2 shows the variation of the projected emitter size with β and the observer angle, defined as the inclination of the system. Our numerical calculation for the size of the emitter agrees with the approximate expression 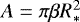used in the main text.

thumbnail Fig. A.1

The emitter site in colour with beaming taken into account. The blue arrow points towards the observer. β is 0.2 and the observing angle is 45 degrees in this example. The transverse emitter site is depicted in black and white. The star is located at the origin.
thumbnail Fig. A.2

The transverse emitter site area as a function of β and observerangle. β has a much larger effect than the observer angle. This is due to the fact that the thickness of the emission cone gets wider with β.

To model the binary interaction scenario we additionally restrict the source site to the flux tube connecting the radio emitting star with its companion. To determine whether a point is on a magnetic field line passing through the companion, we use the equation for magnetic streamlines of a dipole: l = rsin2θ, where θ is the polar angle, l is the distance at which the field line crosses the equator and r is the radial distance. If R2 is the radiusof the companion, then only field lines that have equatorial intercepts in the range (A.1)

can be live. Similarly, in the azimuthal direction, only field lines within 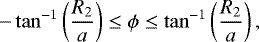(A.2)

where ϕ is the azimuthal angle, can be live. Equations (A.1) and (A.2) completely determine the live flux tube in case of binary interaction. Figure A.3 shows the field lines of the central star passing through the binary companion. Figure A.4 shows the source and emitter sites. The grid was set to a step size of 0.003 in units of R* for r, and 0.003 radians for θ and ϕ.

We have also incorporated the orbital motion of the binary system. This brings along the time variability that we see in our data. As can be seen in the right gif in Fig. A.4 (animation may be viewed using Adobe Reader), the emitter site is only visible at certain orbital phases. At other phases, when it is not visible, we place a single point with magnetic field strength 0 at the origin. This makes it immediately clear from the colour bar there is no emitter site at that particular orbital phase.

thumbnail Fig. A.3

Simulations showing the magnetic field lines from the central star passing through the binary. In the left image we have zoomed out so the binary is constantly visible. The image on the right is zoomed in on the central star because the region we are interested in, with |B| ≈ 50 Gauss, islocated there. Normally as described in the text the magnetic field strength criterion is applied first, but for illustrative purposes we show that in the next figure. The blue arrow depicts the direction towards the observer, its angle corresponds with the inclination of the system. When viewed in Adobe Acrobat Reader these images will appear as gifs, showcasing the fact that the celestial bodies orbit around each other. If the embedded animated images do not display correctly, you can also access them online.
thumbnail Fig. A.4

Simulations showing the source and emitter sites. In the image on the left we have applied the criterion that the magnetic field strength converted to frequency must be inside the bandwidth of a single maser site. In the image on the right we have taken into account on top of the bandwidth criterion that the radiation is beamed in a hollow cone with a solid rim. Therefore the emitter is not always visible. The blue arrow depicts the direction towards the observer, its angle corresponds with the inclination of the system. When viewed in Adobe Acrobat Reader these images will appear as gifs, showcasing the fact that the celestial bodies orbit around each other. Only in certain frames the emitter site will be visible. If it is not visible, a single point with magnetic field strength 0 is placed at the origin so it is clear from the colour bar that the emitter site is not visible at this phase. If the embedded animated images do not display correctly, you can alsoaccess them online.

References

  1. Aurière, M., Konstantinova-Antova, R., Charbonnel, C., et al. 2015, A&A, 574, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Barrado y Navascues, D., de Castro, E., Fernandez-Figueroa, M. J., Cornide, M., & Garcia Lopez, R. J. 1998, A&A, 337, 739 [NASA ADS] [Google Scholar]
  3. Benz, A. O. 1993, Plasma Astrophysics: Kinetic Processes in Solar and Stellar Coronae (Berlin: Springer), 184 [Google Scholar]
  4. Berdyugina, S. V., & Tuominen, I. 1998, A&A, 336, L25 [NASA ADS] [Google Scholar]
  5. Berdyugina, S. V., Jankov, S., Ilyin, I., Tuominen, I., & Fekel, F. C. 1998, A&A, 334, 863 [NASA ADS] [Google Scholar]
  6. Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
  7. Boyajian, T. S., von Braun, K., van Belle, G., et al. 2013, ApJ, 771, 40 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brown, A. G., Vallenari, A., Prusti, T., et al. 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Brown, A., Vallenari, A., Prusti, T., et al. 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Callingham, J. R., Vedantham, H. K., Pope, B. J. S., Shimwell, T. W., & LoTSS Team 2019, Res. Notes Am. Astron. Soc., 3, 37 [Google Scholar]
  11. Callingham, J.R., Vedantham, H. K., Shimwell, T. W., et al. 2021a, Nat. Astron., submitted [Google Scholar]
  12. Callingham, J. R., Pope, B. J. S., Feinstein, A. D., et al. 2021b, A&A, 648, A13 [EDP Sciences] [Google Scholar]
  13. Chiuderi Drago, F., & Klein, K. L. 1990, Ap&SS, 170, 81 [NASA ADS] [CrossRef] [Google Scholar]
  14. Conti, P. S. 1967, ApJ, 149, 629 [NASA ADS] [CrossRef] [Google Scholar]
  15. Crampton, D., Dobias, J., & Margon, B. 1979, ApJ, 234, 993 [NASA ADS] [CrossRef] [Google Scholar]
  16. Donati, J. F., Semel, M., & Rees, D. E. 1992, A&A, 265, 669 [Google Scholar]
  17. Drake, S. A., Simon, T., & Linsky, J. L. 1989, ApJS, 71, 905 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dulk, G. A. 1985, ARA&A, 23, 169 [NASA ADS] [CrossRef] [Google Scholar]
  19. Eker, Z., & Doherty, L. R. 1987, MNRAS, 228, 869 [NASA ADS] [CrossRef] [Google Scholar]
  20. Eker, Z., Ak, N. F., Bilir, S., et al. 2008, MNRAS, 389, 1722 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ergun, R. E., Carlson, C. W., McFadden, J. P., et al. 2000, ApJ, 538, 456 [NASA ADS] [CrossRef] [Google Scholar]
  22. Favata, F., & Schmitt, J. H. M. M. 1999, A&A, 350, 900 [NASA ADS] [Google Scholar]
  23. Fekel, F. C. 1997, PASP, 109, 514 [NASA ADS] [CrossRef] [Google Scholar]
  24. Fekel, F. C., Henry, G. W., Eaton, J. A., Sperauskas, J., & Hall, D. S. 2002, AJ, 124, 1064 [NASA ADS] [CrossRef] [Google Scholar]
  25. Fekel, F. C., Henry, G. W., & Lewis, C. 2005, AJ, 130, 794 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fernandez-Figueroa, M. J., Montes, D., de Castro, E., & Cornide, M. 1994, ApJS, 90, 433 [NASA ADS] [CrossRef] [Google Scholar]
  27. Franciosini, E., Pallavicini, R., & Tagliaferri, G. 2001, A&A, 375, 196 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Frasca, A., & Catalano, S. 1994, A&A, 284, 883 [NASA ADS] [Google Scholar]
  29. Frasca, A., Guillout, P., Marilli, E., et al. 2006, A&A, 454, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Gary, B. L., Hebb, L. H., Foote, J. L., et al. 2012, Soc. Astron. Sci. Ann. Symp., 31, 17 [Google Scholar]
  31. Ginzburg, V. L., & Zhelezniakov, V. V. 1958, Sov. Astron., 2, 653 [Google Scholar]
  32. Glebocki, R., & Stawikowski, A. 1995, Acta Astron., 45, 725 [NASA ADS] [Google Scholar]
  33. Goldreich, P., & Lynden-Bell, D. 1969, ApJ, 156, 59 [NASA ADS] [CrossRef] [Google Scholar]
  34. Griffin, R. F. 1985, The Observatory, 105, 81 [Google Scholar]
  35. Griffin, R. F. 2009, The Observatory, 129, 317 [NASA ADS] [Google Scholar]
  36. Griffin, R. F., Church, R. P., & Tout, C. A. 2006, New Astron., 11, 431 [NASA ADS] [CrossRef] [Google Scholar]
  37. Gunn, A. G., Mitrou, C. K., & Doyle, J. G. 1998, MNRAS, 296, 150 [NASA ADS] [CrossRef] [Google Scholar]
  38. Halbwachs, J. L., Mayor, M., & Udry, S. 2018, A&A, 619, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Hall, D. S. 1976, Astrophys. Space Sci. Lib., 60, 287 [NASA ADS] [CrossRef] [Google Scholar]
  40. Hall, D. S. 1981, Solar Phenomena in Stars and Stellar Systems, eds. R. M. Bonnet, & A. K. Dupree (Berlin: Springer), 68, 431 [NASA ADS] [CrossRef] [Google Scholar]
  41. Hamaker, J. P., & Bregman, J. D. 1996, A&AS, 117, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Hancock, P. J., Murphy, T., Gaensler, B. M., Hopkins, A., & Curran, J. R. 2012, MNRAS, 422, 1812 [NASA ADS] [CrossRef] [Google Scholar]
  43. Hancock, P. J., Trott, C. M., & Hurley-Walker, N. 2018, PASA, 35, e011 [CrossRef] [Google Scholar]
  44. Heckert, P. A., Summers, D., Harkey, R., Sandoval, V., & Pilkey, C. 1988, Information Bull. Variable Stars, 3274, 1 [Google Scholar]
  45. Henry, G. W., Fekel, F. C., & Hall, D. S. 1995, AJ, 110, 2926 [NASA ADS] [CrossRef] [Google Scholar]
  46. Hess, S. L. G., Delamere, P., Dols, V., Bonfond, B., & Swift, D. 2010, J. Geophys. Res. Space Phys., 115, A06205 [NASA ADS] [Google Scholar]
  47. Kochukhov, O., Mantere, M. J., Hackman, T., & Ilyin, I. 2013, A&A, 550, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Kuijpers, J., & van der Hulst, J. M. 1985, A&A, 149, 343 [NASA ADS] [Google Scholar]
  49. Lanza, A. F. 2009, A&A, 505, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Lehmann, L. T., Jardine, M. M., Mackay, D. H., & Vidotto, A. A. 2018, MNRAS, 478, 4390 [NASA ADS] [CrossRef] [Google Scholar]
  51. Little-Marenin, I. R., Simon, T., Ayres, T. R., et al. 1986, ApJ, 303, 780 [NASA ADS] [CrossRef] [Google Scholar]
  52. Louarn, P., Roux, A., de Féraudy, H., et al. 1990, J. Geophys. Res., 95, 5983 [NASA ADS] [CrossRef] [Google Scholar]
  53. Marino, G., Catalano, S., Frasca, A., Marilli, E., & Teriaca, L. 2002, Information Bull. Variable Stars, 5227, 1 [Google Scholar]
  54. Melrose, D. B. 1991, ARA&A, 29, 31 [NASA ADS] [CrossRef] [Google Scholar]
  55. Melrose, D., & Dulk, G. A. 1982, ApJ, 259, 844 [NASA ADS] [CrossRef] [Google Scholar]
  56. Melrose, D. B., & Wheatland, M. S. 2016, Sol. Phys., 291, 3637 [CrossRef] [Google Scholar]
  57. Montes, D., de Castro, E., Fernandez-Figueroa, M. J., & Cornide, M. 1995, A&AS, 114, 287 [NASA ADS] [Google Scholar]
  58. Montes, D., Sanz-Forcada, J., Fernandez-Figueroa, M. J., de Castro, E., & Poncet, A. 1998, A&A, 330, 155 [NASA ADS] [Google Scholar]
  59. Montes, D., Fernández-Figueroa, M. J., De Castro, E., et al. 2000, A&AS, 146, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Morris, D. H., & Mutel, R. L. 1988, AJ, 95, 204 [NASA ADS] [CrossRef] [Google Scholar]
  61. Mutel, R. L., & Lestrade, J. F. 1985, AJ, 90, 493 [NASA ADS] [CrossRef] [Google Scholar]
  62. Mutel, R. L., Morris, D. H., Doiron, D. J., & Lestrade, J. F. 1987, AJ, 93, 1220 [NASA ADS] [CrossRef] [Google Scholar]
  63. Ness, J. U., Audard, M., Schmitt, J. H. M. M., & Güdel, M. 2003, Adv. Space Res., 32, 937 [NASA ADS] [CrossRef] [Google Scholar]
  64. Offringa, A. R., McKinley, B., Hurley-Walker, N., et al. 2014, MNRAS, 444, 606 [NASA ADS] [CrossRef] [Google Scholar]
  65. Oláh, K. 2006, Ap&SS, 304, 145 [NASA ADS] [CrossRef] [Google Scholar]
  66. Oliver, J. P. 1974, PhD thesis, California University, Los Angeles, USA [Google Scholar]
  67. O’Neal, D., Neff, J. E., Saar, S. H., & Cuntz, M. 2004, AJ, 128, 1802 [NASA ADS] [CrossRef] [Google Scholar]
  68. Osten, R. A., Kowalski, A., Drake, S. A., et al. 2016, ApJ, 832, 174 [Google Scholar]
  69. Padmakar, Singh, K. P., Drake, S. A., & Pandey, S. K. 2000, MNRAS, 314, 733 [NASA ADS] [CrossRef] [Google Scholar]
  70. Popper, D. M. 1988, AJ, 96, 1040 [NASA ADS] [CrossRef] [Google Scholar]
  71. Qian, S., Liu, D., Tan, W., & Soonthornthum, B. 2002, AJ, 124, 1060 [NASA ADS] [CrossRef] [Google Scholar]
  72. Queinnec, J., & Zarka, P. 1998, J. Geophys. Res., 103, 26649 [NASA ADS] [CrossRef] [Google Scholar]
  73. Reiners, A., Schüssler, M., & Passegger, V. M. 2014, ApJ, 794, 144 [NASA ADS] [CrossRef] [Google Scholar]
  74. Rodonò, M. 1992, in Symposium-International Astronomical Union (Cambridge: Cambridge University Press), 151, 71 [Google Scholar]
  75. Rosén, L., Kochukhov, O., Alecian, E., et al. 2018, A&A, 613, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Saur, J., Grambusch, T., Duling, S., Neubauer, F. M., & Simon, S. 2013, A&A, 552, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Schrijver, C. J., & Zwaan, C. 1991, A&A, 251, 183 [NASA ADS] [Google Scholar]
  78. Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Slee, O. B., Wilson, W., & Ramsay, G. 2008, PASA, 25, 94 [NASA ADS] [CrossRef] [Google Scholar]
  80. Song, H. F., Maeder, A., Meynet, G., et al. 2013, A&A, 556, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
  82. Strassmeier, K. G., & Rice, J. B. 2003, A&A, 399, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Strassmeier, K. G., Hooten, J. T., Hall, D. S., & Fekel, F. C. 1989, PASP, 101, 107 [NASA ADS] [CrossRef] [Google Scholar]
  84. Strassmeier, K. G., Serkowitsch, E., & Granzer, T. 1999, A&AS, 140, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Tokovinin, A., Thomas, S., Sterzik, M., & Udry, S. 2006, A&A, 450, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Torres, G., & Ribas, I. 2002, ApJ, 567, 1140 [NASA ADS] [CrossRef] [Google Scholar]
  87. Treumann, R. A. 2006, A&ARv, 13, 229 [NASA ADS] [CrossRef] [Google Scholar]
  88. van den Oord,G. H. J., & de Bruyn, A. G. 1994, A&A, 286, 181 [NASA ADS] [Google Scholar]
  89. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. van Straten, W., Manchester, R. N., Johnston, S., & Reynolds, J. E. 2010, PASA, 27, 104 [NASA ADS] [Google Scholar]
  91. van Weeren, R. J., Shimwell, T. W., Botteon, A., et al. 2021, A&A, 651, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Vedantham, H. K. 2021, MNRAS, 500, 3898 [Google Scholar]
  93. Vedantham, H. K., Callingham, J. R., Shimwell, T. W., et al. 2020, Nat. Astron., 4, 577 [CrossRef] [Google Scholar]
  94. White, S. M., & Franciosini, E. 1995, ApJ, 444, 342 [NASA ADS] [CrossRef] [Google Scholar]
  95. Willson, R. F., & Lang, K. R. 1987, ApJ, 312, 278 [CrossRef] [Google Scholar]
  96. Zarka, P. 2007, Planet. Space Sci., 55, 598 [NASA ADS] [CrossRef] [Google Scholar]
  97. Zarka, P., Treumann, R. A., Ryabov, B. P., & Ryabov, V. B. 2001, Ap&SS, 277, 293 [Google Scholar]
1

The level of refraction experienced by the radiation will vary between the masers, however this is beyond the scope of this paper.

2

In any case, starspot longitude can be measured with quasi-contemporaneous optical photometry.

All Tables

Table 1

144 MHz flux densities (Stokes I and V) of our population.

In the text
Table 2

Relevant stellar properties found in the literature search for the stars detected by LOFAR.

In the text
Table 3

Orbital parameters of our targets.

In the text

All Figures

thumbnail Fig. 1

Stokes I discovery images of our RS CVn population. Each panel is a zoom-in of a LoTSS pipeline-produced image of the field containing the target. The circles are centred on the proper-motion corrected position of the targets and have a radius of 30″. The point spread function is about 5″ wide. The color scale runs from −15 (blue), through 0 (white), to + 15 (red) median absolute deviations, which corresponds to a range of −10σ to + 10σ for Gaussian noise. The date reported in each panel is the date of observation in YYYY-MM-DD format.
In the text
thumbnail Fig. 2

Same as Fig. 1, but for Stokes V. The point spread function width is about 20″ and the radius of the circle is 30″. The images are not de-convolved.
In the text
thumbnail Fig. 3

Multi-epoch Stokes-I images of our targets. The color scale in each panels runs from − S (blue) through zero (white) to + S (red) where S is the flux density in the discovery epoch (see Table 1). The annotated text also provides the Juliandate at the mid-point of the eight-hour exposure. The circular target-marker has a radius of 5″. The full-width at half-maximum of the point spread function is about 5″. EZ Peg and DG CVn are not included here because both only had one detection of sufficient sensitivity.
In the text
thumbnail Fig. 4

Orbital phase of the low-frequency total intensity (SI) and circularly-polarised (SV) emission for BF Lyn (top left), EV Dra (top right), Sig CrB (bottom left) and YY Gem (bottom right). The orbital phase for which our model predicts we should observe emission is shown as red-lines at arbitrary flux densities. For Stokes V we use red and blue to distinguish between the two polarisations. Sig CrB was observed in three independent 8 h epochs, while all other stellar systems were only observed in two independent epochs. The prediction for Sig CrB has been shifted 0.5 in phase, which corresponds with emission originating on the secondary, to show the good correspondence with the data. The polarity of the Stokes V prediction is arbitrary because we do not know which magnetic pole is pointed towards us. Therefore the prediction for the stars where we see emission from both poles (YY Gem and EV Dra) can be flipped in sign.
In the text
thumbnail Fig. 5

Predicted visible emitter area as a function of orbital phase for our targets that have measured inclinations. We have assumed a theoretical model for the emission geometry given by Melrose & Dulk (1982) with electron speed β = 0.2 as an estimate. The ‘step’-like variations between adjacent points are gridding artefacts. We have assumed that the observer’s line of sight always hits the northern magnetic hemisphere of the emitting star. Solid lines are for electrons travelling from the north magnetic pole to the south magnetic pole, dashed lines are for electrons travelling vice versa. Sincewe do not know if we are observing the northern or southern magnetic hemisphere, these definitions are interchangeable. BQ CVn, DM UMa, DG CVn and BD+334462 have been left out because we lacked the necessary parameters to make an accurate prediction (namely the semi-major axis for the first three star systems, and the inclination for the last one).
In the text
thumbnail Fig. A.1

The emitter site in colour with beaming taken into account. The blue arrow points towards the observer. β is 0.2 and the observing angle is 45 degrees in this example. The transverse emitter site is depicted in black and white. The star is located at the origin.
In the text
thumbnail Fig. A.2

The transverse emitter site area as a function of β and observerangle. β has a much larger effect than the observer angle. This is due to the fact that the thickness of the emission cone gets wider with β.
In the text
thumbnail Fig. A.3

Simulations showing the magnetic field lines from the central star passing through the binary. In the left image we have zoomed out so the binary is constantly visible. The image on the right is zoomed in on the central star because the region we are interested in, with |B| ≈ 50 Gauss, islocated there. Normally as described in the text the magnetic field strength criterion is applied first, but for illustrative purposes we show that in the next figure. The blue arrow depicts the direction towards the observer, its angle corresponds with the inclination of the system. When viewed in Adobe Acrobat Reader these images will appear as gifs, showcasing the fact that the celestial bodies orbit around each other. If the embedded animated images do not display correctly, you can also access them online.
In the text
thumbnail Fig. A.4

Simulations showing the source and emitter sites. In the image on the left we have applied the criterion that the magnetic field strength converted to frequency must be inside the bandwidth of a single maser site. In the image on the right we have taken into account on top of the bandwidth criterion that the radiation is beamed in a hollow cone with a solid rim. Therefore the emitter is not always visible. The blue arrow depicts the direction towards the observer, its angle corresponds with the inclination of the system. When viewed in Adobe Acrobat Reader these images will appear as gifs, showcasing the fact that the celestial bodies orbit around each other. Only in certain frames the emitter site will be visible. If it is not visible, a single point with magnetic field strength 0 is placed at the origin so it is clear from the colour bar that the emitter site is not visible at this phase. If the embedded animated images do not display correctly, you can alsoaccess them online.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.