| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202140746 | |
| Published online | 01 October 2021 | |
Follow-up of non-transiting planets detected by Kepler
Confirmation of three hot-Jupiters and validation of three other planets★
1
Centro de Astrobiología (CAB, CSIC-INTA), Depto. de Astrofísica,
ESAC campus 28692 Villanueva de la Cañada
(Madrid),
Spain
e-mail: jorge.lillo@cab.inta-csic.es
2
Department of Astrophysical Sciences, Princeton University,
Princeton,
NJ
08544,
USA
3
Department of Astronomy, Yale University,
New Haven,
CT
06511,
USA
Received:
8
March
2021
Accepted:
30
July
2021
Context. The direct detection of new extrasolar planets from high-precision photometry data is commonly based on the observation of the transit signal of the planet as it passes in front of its star. Close-in planets, however, leave additional imprints in the light curve even if they do not transit. These are the so-called phase curve variations that include ellipsoidal, reflection and beaming effects.
Aims. In a previous paper, we scrutinized the Kepler database looking for these phase variations from non-transiting planets. They found 60 candidates whose signals were compatible with planetary companions. In this paper, we perform a ground-based follow-up of a subsample of these systems with the aim of confirming and characterizing these planets and thus validating the detection technique.
Methods. We used the CAFE and HERMES instruments to monitor the radial velocity (RV) of ten non-transiting planet candidates along their orbits. We additionally used AstraLux to obtain high-resolution images of some of these candidates to discard blended binaries that contaminate the Kepler light curves by mimicking planetary signals.
Results. Among the ten systems, we confirm three new hot-Jupiters (KIC 8121913 b, KIC 10068024 b, and KIC 5479689 b) with masses in the range 0.5–2 MJup and set mass constraints within the planetary regime for the other three candidates (KIC 8026887 b, KIC 5878307 b, and KIC 11362225 b), thus strongly suggestive of their planetary nature.
Conclusions. For the first time, we validate the technique of detecting non-transiting planets via their phase curve variations. We present the new planetary systems and their properties. We find good agreement between the RV-derived masses and the photometric masses in all cases except KIC 8121913 b, which shows a significantly lower mass derived from the ellipsoidal modulations than from beaming and RV data.
Key words: planets and satellites: detection / planets and satellites: gaseous planets / planet-star interactions / planets and satellites: fundamental parameters
Based on observations collected at Centro Astronómico Hispano en Andalucía (CAHA) at Calar Alto, jointly operated by Instituto de Astrofísica de Andalucía (CSIC) and Junta de Andalucía and observations made with the Mercator Telescope, operated on the island of La Palma by the Flemish Community, at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias.
© ESO 2021
1 Introduction
In the era of high-precision photometric space-based missions, the detection of extrasolar planets through the transit technique has been very fruitful. So far, more than 4300 planets have been found around other stars, with around three-fourths of them detected by this technique. Since the launch of the CoRoT mission (Auvergne et al. 2009), the subsequent NASA planet hunter Kepler (Borucki et al. 2010) and its extended K2 mission (Howell et al. 2014) as well as its successor TESS (Ricker et al. 2014) have scrutinized the sky looking for these planetary fingerprints in the light curves of stellar sources. According to the NASA Exoplanet archive, more than 2400 planets were discovered with Kepler and more than 400 with K2, and presently 137 have been detected and confirmed by TESS using the transit method (Akeson et al. 2013).
Several years after the end of the prime Kepler mission, the high-quality data provided by this telescope are still being profitably mined. Although Kepler was tasked to find Earth-sized planets around Solar-like stars, it explored an unexpectedly large range of planetary and orbital properties, including the first circumbinary planets, super-Earths, planets in highly eccentric orbits, and planets around giant stars, etc. (e.g., Doyle et al. 2011; Borucki et al. 2012; Ciceri et al. 2015; Lillo-Box et al. 2014, respectively).
The transit technique, however, does not provide a full confirmation of the planet candidate signal by itself, as other non-planetary configurations can mimic the imprint of a symmetric dip in the light curve (e.g., background eclipsing binaries, grazing binary eclipses, etc.). Also, any blended source residing inside the photometer aperture can contaminate the light curve and provide inaccurate estimates of the planet candidate’s parameters. Hence, additional follow-up is necessary from the ground. In practice, the confirmation of transiting planet candidates primarily stems from radial velocity (RV) follow-up, which can provide the mass of the transiting body and thus confirm its planetary nature.
The extraordinary quality of the Kepler photometry motivated the proposal of an alternate technique to detect and fully characterize new planets, that is measure the mass and orbital configuration. Previously used in binary systems, the detection of periodic modulations coupled with the orbital phase of the planet arose as a new potential detection technique (e.g., Faigler & Mazeh 2011). These photometric variations are mainly due to three effects: reflected stellar light, ellipsoidal modulations, and Doppler beaming (hereafter the REB modulations, see Fig. 1). The reflection effect depends directly on the planet-to-star separation, size, and the geometric albedo of the planet. The ellipsoidal variations are known to be caused by tidal effects produced by a close-in object (e.g., a planet) on the external layers of the star (Morris 1985). Since the amplitude of this modulation depends on the mass of the planet, it can potentially be used to both detect,confirm, and characterize planets. Finally, the Doppler beaming effect represents the photometric signature of the RV variations of the star induced by the planet motion when photometry is obtained on a fixed wavelength range (Hills & Dale 1974; Rybicki & Lightman 1979). The induced RV implies that the stellar spectrum is periodically blue-shifted and red-shifted. As a consequence, more or less light enters in the wavelength domain of the photometric filter, yielding sinusoidal flux variations with an amplitude that depends on the mass of the planet.
The REB modulations have already been used to detect and characterize close-in transiting planets from the Kepler sample (e.g., Mazeh et al. 2012; Lillo-Box et al. 2014). These systematic searches have established several interesting findings, including generally low (but occasionally quite large) hot Jupiter albedos (Demory & Seager 2011) and repeated detections of shifts in the maximum of the phase curve away from the substellar point. Though it is substantial, the sample size (~15) of Kepler transiting planets with detectable photometric variations (less than 5 with RV confirmations) is short of the count necessary toadequately understand the atmospheric properties in a population sense. It is therefore worthwhile to increase the number of planets with well-characterized optical phase curves by expanding the search to non-transiting planets. Moreover, the masses derived from these modulations seem to not fully match the measurements from RVs in the few (less than 5) cases where both techniques could be applied. This is theoretically attributed to the presence of hot stream clouds in the atmosphere of the hot-Jupiters causing a phase shift in the light curve modulations.
Millholland & Laughlin (2017) used a supervised machine learning approach to perform a systematic search of these modulations in the whole sample of 142 630 FGK Kepler stars without confirmed planets or KOIs (Kepler Objects of Interest). They identified 60 high-probability (>98%) non-transiting hot Jupiter candidates that could readily be confirmed with RVs (see Fig. 1). In this paper, we present the ground-based follow-up of the brightest subsample of these candidates. In Sect. 2, we present the targets and the observations. In Sect. 3, we perform a joint analysis of the light curve and RV data to confirm the planetary nature of some of the candidates and constrain the masses of the remaining subsample. In Sect. 4, we discuss the results of the analysis, and we conclude in Sect. 5.
2 Follow-up observations
2.1 Target selection
This work is based on the follow-up of the Kepler non-transiting planet candidates detected by Millholland & Laughlin (2017) through the phase variations technique. Among the 60 candidates, we focused on those feasible with the Calar Alto Fiber-fed Echelle spectrograph (CAFE, Aceituno et al. 2013; Lillo-Box et al. 2020). We selected ten of the brightest candidates (Kp < 14 mag) displaying photometric periods of a few days (P < 5 days) and with estimated RV amplitudes (K sin i)1 from the photometric phase curve analysis feasible with CAFE (K sini > 10 m s−1). Table 1 lists our initial selection of targets.
 |
Fig. 1 Schematic representation of the reflection, ellipsoidal and beaming (REB) modulations. Top panel: orbital path of the planet at different phases and two orbital inclinations. Middle panel: corresponding shape of the REB effects (dotted labelled lines) and the composite phase curve (green solid line). Bottom panel: corresponding RV signal with its appropriate phase relationship. |
2.2 Kepler light curves
In Sect. 3.2, we perform a joint fit of the RV and light curve data. For the Kepler light curves, we use the same pre-processing techniques as Millholland & Laughlin (2017); further details can be found therein. We began with the pre-search data conditioning (PDC) photometry (Smith et al. 2012; Stumpe et al. 2012, 2014) provided by the Kepler Science Center. We performed two types of detrending: (1) an initial sliding polynomial fit, which was first used to identify candidate periodic signals using a Lomb-Scargle periodogram, and (2) a two-component detrending on the candidate signals, which simultaneously fit a sinusoidal phase curve component and a sliding polynomial stellar variability component. Using this latter fit, we created the detrended light curve by dividing the PDC light curve by the polynomial component of the fit. These detrended light curves are used in Sect. 3.2, where we phase fold and bin the light curve data for our joint fit.
List of targets selected for initial follow-up.
2.3 Astralux high-spatial resolution imaging
We used the AstraLux instrument (Hormuth et al. 2008) at the 2.2 m telescope in Calar Alto observatory to obtain high-spatial resolution images of seven of the selected candidates. AstraLux is a simple fast-readout camera that performs the so-called lucky imaging technique on a 24 × 24 arcsec maximum field-of-view (FOV), with the possibility of windowing to smaller FOVs in order to gain in readout time and thus reduce the exposure time. The instrument has demonstrated an excellent performance and has already shown a key contribution to the Kepler Follow-up Observing program (KFOP) in Lillo-Box et al. (2012, 2014); Furlan et al. (2017) and in key results from the K2 (e.g., Santerne et al. 2018; Barros et al. 2017) and TESS (e.g., Armstrong et al. 2020; Bluhm et al. 2020; Soto et al. 2021) missions.
Seven of the targets were observed with AstraLux on 13 August 2019 under 1.2 arcsec mean seeing conditions and good transparency conditions. One of the images (corresponding to KIC 8026887) is too noisy to be useful given a sudden worsening of the weather conditions. Hence, we here analyze the remaining images for six of our targets. The datacubes were reduced with the automatic pipeline running at the observatory (Hormuth et al. 2008). This pipeline performs the basic reduction of the data and then selects the 10% best frames (according to their Strehl ratio, Strehl 1902) and aligns and stack the frames to get the final high-spatial resolution image. These images are subsequently analyzed by our pipeline to detect possible blended sources and to obtain the contrast curves and estimate the maximum contamination in the Kepler light curves (see Lillo-Box et al. 2012, 2014 for details on how these contrast curves are estimated). The resulting contrast curves and AstraLux images are presented in Fig. 2.
The high-resolution images2 do not show any signs of close companions within 3 arcsec for any of the observed targets. Additionally, the contrast curves discard photometric contamination from undetected companions below 1%. This is sufficient to ensure that the source of the photometric phase variations detected in Millholland & Laughlin (2017) is the bright (and only) target in the field of view. Given this result, we assume throughout our analysis that the only source in the Kepler aperture and hence the only contributor to the photometric signal is the target star.
2.4 CAFE high-resolution spectra
We used the CAFE instrument (Aceituno et al. 2013) with its recently upgraded capabilities (Lillo-Box et al. 2020) to perform a systematic RV follow-up of the selected planet candidates. CAFE is a fiber-fed high-resolution (R = 63 000) echelle spectrograph located in the coudé room of the 2.2 m telescope at the Calar Alto observatory (Almería, Spain). Although the instrument has been operating since 2012, in 2016 its grating suffered a strong degradation that affected its efficiency and necessitated its retirement. This was taken as an opportunity to perform additional upgrades alongside the exchange of the grating. These improvements included a new double scrambler, introduction of temperature control of the isolated room where the instrument is located, and development of a new Python-based public pipeline (CAFExtractor, see Lillo-Box et al. 2020) that automatically reduces the data and provides high-level data-products like precise RV measurements using the cross-correlation technique (Baranne et al. 1996). These new capabilities were commissioned during 2018 and 2019, and the instrument was brought to full operation in April 2019. We refer the interested reader to Lillo-Box et al. (2020) for additional details on the new capabilities of CAFE.
The observations were carried out in May–August 2019 under the approved program ID H19-2.2-007 (PI: Lillo-Box). In total, we obtained 53 spectra from the ten targets. We used the new CAFExtractor pipeline to reduce the spectra and obtain the RVs. The pipeline includes an option to fit the CCF by using either a Gaussian profile (by default) or a rotational profile for the rapidly rotating stars (recommended for stars with v sin i > 10 km s−1). The rotational profile is defined as in Gray (2005) and it has already been used in several programs that obtained precise RV measurements of rapidly rotating stars (e.g., Santerne et al. 2012; Aller et al. 2018). For cases with v sin i > 10 km s−1, we used this approach, while for v sin i < 10 km s−1, we used the usual Gaussian profile. In four out of the ten observed targets, either the CCF was too broad to extract meaningful RVs (KIC 6783562 and KIC 10931452) or the phase coverage was insufficient to perform a relevant analysis (KIC 5001685 and KIC 8042004). Hence, these targets are not further addressed in this paper. The extracted RVs and the properties of the CCF for the remaining six targets are shown in Tables A.1–A.6.
2.5 HERMES/Mercator high-resolution spectra
We observed five of the targets from the selected sample with the high-resolution fiber-fed HERMES spectrograph (Raskin et al. 2011) at the Mercator telescope in La Palma in August 2020. HERMES is a sibling of the CORALIE instrument at La Silla. It provides a resolution of R = 85 000 and a wavelength coverage of 377–900 nm. We used the simultaneous wavelength calibration mode, which uses a second fiber to inject a thorium-argon spectrum in between the science orders to monitor the nightly drift of the wavelength calibration for precise RV measurements. The instrument’s automatic pipeline provides the basic reduction of the spectra. We measured the RVs by following a similar procedure as described for the CAFE spectra, with a new mask adapted for this wavelength coverage and resolution. The extracted RVs and the properties of the CCF are shown in Tables A.1–A.6.
 |
Fig. 2 Results of the analysis of the high-spatial resolution images obtained with the AstraLux lucky-imaging instrument. Each panel shows the contrast curve calculated as in Lillo-Box et al. (2014) as a white line. The color-code of the contrast curve represents the contamination produced by a blended star of the given magnitude contrast as shown in the color bar. The inset panel displays the AstraLux image, with redder colors indicating more intensity. |
3 Analysis
3.1 Radial velocity standalone modeling
We first performed a RV analysis of the CAFE data, since the number of RV measurements from the HERMES instrument was low for this preliminary analysis. Given the limited number of observations for most of the systems, we used a simplistic RV model that assumes circular orbits (likely a good approximation given the short periods of these candidates) and adopts Gaussian priors on the period and time of conjunction obtained from the light curve analysis in Millholland & Laughlin (2017). Consequently, the only two free parameters of the model are the systemic velocity (Vsys) and the semi-amplitude of the RV signal (K). For each of these parameters, we assumed a uniform prior with broad ranges corresponding to 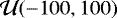 km s−1 for Vsys and
km s−1 for Vsys and 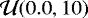 km s−1 for K.
km s−1 for K.
We used the Markov chain Monte Carlo affine invariant ensemble sampler emcee (Goodman & Weare 2010; Foreman-Mackey et al. 2013)to explore the posterior probability of the two parameters. We ran a first set of 20 walkers with 10 000 steps per walker to identify the maximum likelihood location of the parameter space. Then we ran another 10 walkers with 10 000 steps per walker in a nearby region around this maximum likelihood location of the parameter space to properly sample the posterior distributions. The results are shown in Figs. 3 and 4, and the priors, median and confidence levels of the posterior distributions for each parameter are shown in Tables A.7–A.12.
Among the six systems with appropriate phase coverage, we find clear detection in three of the targets (KIC 8121913, KIC 10068024, and KIC 5479689), see Fig. 3. In these cases, the RV semi-amplitude is detected with a confidence larger than 99.7% (corresponding to 3σ) and thus are considered as confirmed planets. In two other cases (KIC 5878307 and KIC 11362225, see Fig. 4), the data is insufficient to measure the planet mass but the low amplitude of the RV variations and the absence of contaminants in the AstraLux images validate their planetary nature. In the case of KIC 8026887, we find either a large amplitude of several hundred of meters per second or a strong linear trend with a smaller RV amplitude. Additionally, by using a period equal to twice the photometric period (2 × P = 3.8464 days), we find a clear signal compatible with a Keplerian model with K ~ 610 ± 180 m s−1 (see Fig. 4, right panel). This is further investigated in the joint light curve and radial velocity analysis in the next section.
 |
Fig. 3 Phase-folded radial velocity curves for the three planets confirmed in this paper. The solid open symbols represent nightly binned values when more than one observation are available on a given night (although we note that the analysis in the paperhas been done using the individual measurements). The median radial velocity model is represented by the black dashed line and the 67.8 and 95% confidence intervals are displayed as dark gray and light gray shaded regions around the median model. |
 |
Fig. 4 Phase-folded radial velocity curves for the two planets where only upper limits to the planet mass are possible (left and middle panels) and the case of KIC 8026887 with the period equal to twice the photometric period found in Millholland & Laughlin (2017). The solid open symbols represent nightly binned values when more than one observation are available on a given night (although we note that the analysis in the paper has been done using the individual measurements). The median radial velocity model is represented by the black dashed line and the 67.8 and 95% confidence intervals aredisplayed as dark gray and light gray shaded regions around the median model. |
3.2 Joint radial velocity and light curve modeling
To examine the consistency of the RV observations and Kepler light curves, we performed a simultaneous fit of the two datasets for the four targets with sufficiently precise RVs: KIC 8121913, KIC 10068024, KIC 5479689, and KIC 8026887. The key goal of this simultaneous fit is to verify that the periods and phases suggested by the photometricdetections are consistent with the RVs. Moreover, we also wish to investigate whether the companion mass estimates agree between the two datasets. Here we adopt a fitting approach that is as simplified as possible, on account of our relatively small number of RV data points and our goal to simply demonstrate RV and light curve consistency.
We model the phase curve variations using a four-component sum of sinusoids at the orbital phase
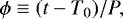 (1)
(1)
where T0 is the epoch ofinferior conjunction (or the transit time if the companion is transiting):
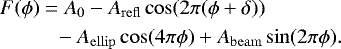 (2)
(2)
Here, δ is a phase offset in peak brigtness of the reflection component, and Arefl, Aellip, and Abeam are positive quantities representing the photometric amplitudes of the atmospheric/reflection, ellipsoidal, and beaming components of the phase curve (Esteves et al. 2015; Shporer 2017). These amplitudes will be treated as free parameters in our model. In Sect. 4.1, we describe the origin of these phase curve components and their approximate relationships to fundamental physical and orbital parameters. We also verify that they have been fit with reasonable values.
This four-component phase curve model is fit to the detrended Kepler light curves introduced in Sect. 2.2. These light curves are phase-folded using the period P and epoch T0 from Eq. (1) (both of which are free parameters in the fit) and binned into 400 bins, with the jth bin having mean flux, Fj, and standard deviation, σF,j.
We now proceed to the RV component of the joint fit. We model the Doppler velocities simply as
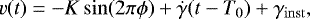 (3)
(3)
where we have assumed a negligible orbital eccentricity. The RV semi-amplitude, K, is strictly positive, and ϕ and T0 are the same phase and epoch as defined in Eq. (1). In addition to the sinusoidal signal, we include a long-term linear trend with acceleration 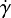 and instrument-specific offset, γinst.
and instrument-specific offset, γinst.
We perform a joint RV and phase curve fit to the observations using the standard practices of Bayesian inference. The log-likelihood is here composed of the sum of the individual log-likelihoods of the RV and light curve datasets:
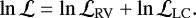 (4)
(4)
Assuming Gaussian-distributed noise, the RV log-likelihood is
![\begin{equation*}\ln\mathcal{L}_{\mathrm{RV}} = -\frac{1}{2}\sum_j\left[{\frac{(v_j - v_{\mathrm{mod}}(t_j)){}^2}{(\sigma_{v,j}^2 + \sigma_{\mathrm{jit, inst}}^2)}} + \ln(2\pi[\sigma_{v,j}^2 + \sigma_{\mathrm{jit, inst}}^2])\right].\end{equation*}](/articles/aa/full_html/2021/10/aa40746-21/aa40746-21-eq8.png) (5)
(5)
Here, vj and σv,j are the jth velocity measurement and measurement error, and vmod(tj) is the model RV (Eq. (3)) at time tj.
Similarly, the light curve log-likelihood is given by
![\begin{equation*}\ln\mathcal{L}_{\mathrm{LC}}= -\frac{1}{2}\sum_j{\left[\frac{(F_j - F_{\mathrm{mod}}(\phi_j)){}^2}{\sigma_{F,j}^2} + \ln(2\pi\sigma_{F,j}^2)\right]},\end{equation*}](/articles/aa/full_html/2021/10/aa40746-21/aa40746-21-eq9.png) (6)
(6)
where Fj and σF,j are the jth measurement and error resulting from the folded and binned light curve data. Fmod (ϕj) is the model phase curve (Eq. (2)) at phase ϕj.
The posterior distributions of the parameters were sampled through the Markov chain Monte Carlo affine invariant ensemble sampler emcee (Goodman & Weare 2010; Foreman-Mackey et al. 2013) using uniform priors and the likelihood function given by Eqs. (4)–(6). We collect 20 000 samples across 200 chains, discarding the first 5000 samples as burn-in. Convergence was assessed by inspecting trace plots to see that the chains were well-mixed. We provide corner plots of the joint posterior parameter distributions in Appendix B.
The results of the joint fit are presented in Table 2, and the best-fitting models for KIC 8121913, KIC 10068024, and KIC 5479689 are displayed in Fig. 5. We observe that consistent solutions for the joint RV/phase curve fit can be found for these systems. Specifically, there are sets of P and T0 for which the two datasets agree within uncertainties. The amplitudes of the phase curve and RV signals are also generally consistent in terms of the physical system parameters they correspond to, as we discuss in Sect. 4.1.
In the case of KIC 8026887, the phase curve clearly shows ellipsoidal variations when folded at P = 1.9232 days. Hence the double period hypothesis is unlikely. In any case, we tested it to ensure that the P = 1.9 days is able to jointly model the RV and LC data. We then tested four models including priors on the period and turning on and off the linear trend. We then estimated the Bayesian evidence for the four models and concluded that the model with P = 1.9 and the linear trend shows the largest evidence for the current dataset. This model is able to reconcile both RVs and light curve modulations and provides a planet mass of 3.44 ± 0.42 Mjup. The difference in log-evidence is + 7 compared to the modelwithout a linear trend and + 135 compared tothe model with 2 × P. The candidate absolute mass is hence significantly detected and we can hence validate the planetary nature of this candidate. Given the poor radial velocity phase coverage, however, we remain conservative and do not claim confirmation yet.
 |
Fig. 5 Results of the joint phase curve (upper panels) and radial velocity (lower panels) fits for KIC 8121913, KIC 10068024, and KIC 5479689 (see Sect. 3.2). |
Results of the joint fits to the radial velocity and light curve data.
4 Discussion
4.1 Consistency of RVs and phase curve component amplitudes
In the previous section, we treated the phase curve component amplitudes as free parameters within the joint RV/phase curve fit. These amplitudes are not truly free parameters, however, since they stem from physical effects in the star-planet system. Thus, the comparison of the phase curve component amplitudes to one another and to the RV semi-amplitudes can inform whether the joint fits are physically consistent. Here we describe the relation of the amplitudes to physical parameters and assess their consistency. Within this, we adopt stellar parameters from the Gaia-Kepler Stellar Properties Catalog (Berger et al. 2020); these are provided in Table 3.
The atmospheric component of optical phase curves, Arefl, includes both light from the primary star reflected off the companion, as well as thermal emission from the companion itself. It is generally difficult to separate reflected light from thermal emission, and it depends on the system as to which dominates. The amplitude of the atmospheric component is given by (Shporer 2017),
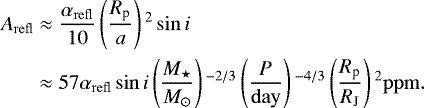 (7)
(7)
Here αrefl is an order-unity coefficient that depends on the planet’s albedo and the efficiency of heat redistribution.
In addition to phase modulations from the planet’s atmospheric brightness, there are also gravitationally-induced photometric signals from the host star. The phase component due to Doppler beaming (also known as Doppler boosting) stems from periodic blueshifts and redshifts of the stellar spectrum in response to the orbiting planet. The amplitude of the beaming component is given by
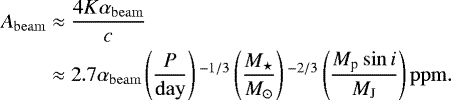 (8)
(8)
Here, K is the radial velocity semi-amplitude, c is the speed of light and αbeam is an order-unity coefficient equal to the photon-weighted bandpass-integrated beaming factor.
The second gravitational signal results from the ellipsoidal distortion of the host star due to tidal potential of the companion. This signal is dominated by a cos(4πϕ) term, although a more complete expansion includes smaller amplitude harmonics such as cos (2πϕ) and cos (6πϕ), which we have ignored in Eq. (2) for simplicity. The photometric amplitude of the ellipsoidal distortion is approximately
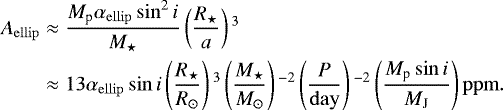 (9)
(9)
The αellip coefficient isorder-unity, and it relates to the stellar limb darkening and gravity darkening,
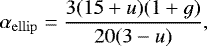 (10)
(10)
where u is the linear limb darkening coefficient and g is the gravity darkening coefficient (Claret & Bloemen 2011).
To investigate the consistency of the phase curve components and the RV semi-amplitudes for each system, we compare their respective constraints on Mp sini. The minimum mass Mp sini is most robustly constrained from the RV semi-amplitude K, but Abeam and Aellip also provide weak estimates. We first solve Eqs. (8) and (9) for Mp sini. Next, we use the posterior samples from the joint fits in Sect. 3.2 and the stellar parameter estimates (Table 3) to calculate the posterior distributions of Mp sini. Specifically, for the stellar parameters, we sample from distributions of M⋆ and R⋆ consistent with the observed means and error estimates in Table 3. The Aellip amplitude includes an extra factor of sini (Aellip ∝ Mp sin2i; Eq. (9)), so we average over it by assuming an isotropic distribution of the inclination. As for the order-unity coefficients αbeam and αellip, we set them to fixed values based on simple linear relationships with Teff, which were shown to be good fits to these coefficients in the Kepler bandpass (Millholland & Laughlin 2017):
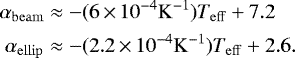 (11)
(11)
This is an appropriate simplification because the uncertainties in the derived Mp sini are primarily driven by the spread in posterior samples of Abeam and Aellip. Finally, putting all of this together, we calculate the posterior distributions of Mp sini. The resulting means and 1σ ranges are given in Table 2.
We find that the Mp sini estimates from RV, Abeam, and Aellip are consistent in almost all cases for our three targets. The one exception arises within the Mp sini estimates derived from Aellip, which are systematically lower than those derived from K and Abeam in all three cases, up to ~4σ lower in the case of KIC 8121913. This discrepancy could arise from the extra factor of sin i, which we marginalized over. Additionally, it could be related to uncertainties in αellip, which we ignored. More broadly, however, this mass discrepancy is common in photometric phase curve analyses and has been pointed out in previous studies (see Shporer 2017 and references therein). An inconsistency between the ellipsoidal and RV-derived masses was found for KOI-74 by Bloemen et al. (2011), an eclipsing binary composed by an A-type and a white dwarf star, with the mass ratio derived by RVs being larger than from ellipsoidal modulations, as in the case of KIC 8121913. Although the reason for this discrepancy is not yet understood, several studies have pointed out different possible causes (e.g., van Kerkwijk et al. 2010; Pfahl et al. 2008).
The above analysis provided a consistency check on both the RVs and the beaming and ellipsoidal components of the phase curve. It is also worthwhile to check the reflection phase curve component amplitude, Arefl, although this is complicated by the unknown αrefl, Rp, and sin i. One approach is to use the posterior samples of Arefl from Sect. 3.2 to calculate the combination of parameters 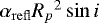 via Eq. (7). We can then examine whether the constraints are reasonably consistent with the RVs. The derived values of
via Eq. (7). We can then examine whether the constraints are reasonably consistent with the RVs. The derived values of 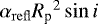 are given in Table 2. The values for KIC 8121913 and KIC 10068024 are unity or greater, thus consistent with Rp ≳ RJup planets, whereas KIC 5479689 suggests a somewhat smaller Rp and/or smaller sin i. This constraint is independently consistent with the inferred Mp sini for KIC 5479689, which was found to be smaller than the other two systems.
are given in Table 2. The values for KIC 8121913 and KIC 10068024 are unity or greater, thus consistent with Rp ≳ RJup planets, whereas KIC 5479689 suggests a somewhat smaller Rp and/or smaller sin i. This constraint is independently consistent with the inferred Mp sini for KIC 5479689, which was found to be smaller than the other two systems.
Stellar parameters adopted for KIC 8121913, KIC 10068024, and KIC 5479689, taken from the Gaia-Kepler Stellar Properties Catalog (Berger et al. 2020).
5 Summary and conclusions
We performed ground-based follow-up observations of ten non-transiting planet candidates detected through their phase curve modulationsvia a supervised machine learning approach by Millholland & Laughlin (2017). Adequate phase coverage was obtained forsix of them. High-spatial resolution images and radial velocity monitoring with the CAFE and HERMES instruments was obtained, yielding planet confirmation for three of the candidates (KIC 8121913 b, KIC 10068024 b, and KIC 5479689 b) and adding credence to the planetary nature of the other three (KIC 5878307 b, KIC 11362225 b, and KIC 8026887 b). These follow-up observations highlight the potential of phase curve modulations as a detection technique for non-transiting planets.
We find KIC 10068024 b is a massive hot-Jupiter (Mp = 2.0 ± 0.4 MJup) around a F8-G0 type star potentially in the early stages of the subgiant phase. KIC 5479689 b is found to be a sub-Jupiter-mass planet (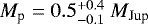 ) orbiting with a 1.7 days orbital period around a main-sequence solar-like star. Finally, we find KIC 8121913 b is a Jupiter-mass planet with a RV-derived mass in the Jupiter regime (Mp = 2.1 ± 0.4 MJup), in agreement with the beaming amplitude of the phase curve. However, in this case, we find a significant discrepancy with the ellipsoidal amplitude, which points toward a lower mass for this planet of
) orbiting with a 1.7 days orbital period around a main-sequence solar-like star. Finally, we find KIC 8121913 b is a Jupiter-mass planet with a RV-derived mass in the Jupiter regime (Mp = 2.1 ± 0.4 MJup), in agreement with the beaming amplitude of the phase curve. However, in this case, we find a significant discrepancy with the ellipsoidal amplitude, which points toward a lower mass for this planet of 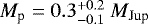 . This discrepancy has already been reported in other systems with phase curve modulations, but its origin remains unknown. Hence, KIC 8121913 b, and additional systems like it can help in the interpretation of this discrepancy and the physics behind it.
. This discrepancy has already been reported in other systems with phase curve modulations, but its origin remains unknown. Hence, KIC 8121913 b, and additional systems like it can help in the interpretation of this discrepancy and the physics behind it.
Additionally, our RV data suggests that the orbital period of the candidate planet in KIC 8026887 is actually twice the photometric period derived in Millholland & Laughlin (2017). Under such an assumption, our RV analysis provides a significant detection with a planet mass corresponding to a massive gaseous giant (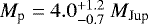 ). However, because we cannot obtain a strong joint fit of both the light curve and RV data with the same orbital period, we do not consider this as a confirmed planet. Finally, we obtained an upper limit to the masses of the other two candidates of 8.5 MJup (KIC 5878307 b) and 4.4 MJup (KIC 11362225 b).
). However, because we cannot obtain a strong joint fit of both the light curve and RV data with the same orbital period, we do not consider this as a confirmed planet. Finally, we obtained an upper limit to the masses of the other two candidates of 8.5 MJup (KIC 5878307 b) and 4.4 MJup (KIC 11362225 b).
These hot Jupiters are not known to posses nearby planetary companions and are thus of less interest from the perspective of planetary orbital architectures. However, this phase curve detection technique offers the most promising approach for detecting hot Jupiters in multi-planet systems with mutually-inclined orbits (Millholland et al. 2016). Specifically, if we consider a hypothetical system with a known, transiting super-Earth/sub-Neptune on a ≳ 10 day orbit, we can inspect the stellar light curve for photometric variations from a non-transiting hot Jupiter on an interior ≲ 5 day orbit. As shown by Millholland et al. (2016), the detection of astrometrically induced transit-timing variations for the exterior transiting planet may serve as an additional predictor for the existence of the potential non-transiting hot Jupiter. Systems containing a mutually-inclined hot Jupiter and exterior, small-mass planet are predicted to exist if some fraction of hot Jupiters form in situ (Batygin et al. 2016). The search for phase curve detections of non-transiting hot Jupiters (and the subsequent radial velocity monitoring) offers a means toward a direct test of this hypothesis.
The targets presented in this paper are the first non-transiting planets to be confirmed after initial detection of their full-phase photometric variations3. The photometric detection of non-transiting planets will continue to be relevant to exoplanet exploration as new space-based missions are launched. The Kepler mission provided several candidates in this regime and many more will come from TESS (Ricker et al. 2014) and the future PLATO mission (Rauer et al. 2014). Currently, the Cheops mission through one of its working packages is also focused on the study of phase curves through high-precision and high-cadence observations. The targets presented here, and especially KIC 8121913 b, offer excellent opportunities to probe hot Jupiter atmospheres and understand the possible discrepancies between RV-derived and photometric masses. Moreover, the method as a whole can be used as a test of theories of hot Jupiter formation, which is still one of the biggest open questions in the field of exoplanets today.
Acknowledgements
J.L.-B. acknowledges financial support received from “la Caixa” Foundation (ID 100010434) and from the European Union’s Horizon 2020 research and innovation programme under the Marie Sk?odowska-Curie grant agreement No 847648, with fellowship code LCF/BQ/PI20/11760023. This research has also been partly funded by the Spanish State Research Agency (AEI) Projects No.ESP2017-87676-C5-1-R and No. MDM-2017-0737 Unidad de Excelencia “María de Maeztu” – Centro de Astrobiología (INTA-CSIC). S.M. was supported by NASA through the NASA Hubble Fellowship grant #HST-HF2-51465 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. S.M. was also supported by the NSF Graduate Research Fellowship Program under Grant DGE-1122492. Partly based on observations obtained with the HERMES spectrograph, which is supported by the Research Foundation – Flanders (FWO), Belgium, the Research Council of KU Leuven, Belgium, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland and the Thüringer Landessternwarte Tautenburg, Germany.
Appendix A Tables
Cross-correlation funtion properties for KIC5479689.
Cross-correlation funtion properties for KIC5878307.
Cross-correlation funtion properties for KIC8026887.
Cross-correlation funtion properties for KIC8121913.
Cross-correlation funtion properties for KIC10068024.
Cross-correlation funtion properties for KIC11362225.
Prior and posterior distributions for the analysis of CAFE radial velocities of KIC8026887 from Sect. 3.1.
Prior and posterior distributions for the analysis of CAFE radial velocities of KIC11362225 from Sect. 3.1.
Prior and posterior distributions for the analysis of CAFE radial velocities of KIC5878307 from Sect. 3.1.
Appendix B Posterior distributions from the joint radial velocity and light curve fit
 |
Fig. B.1 Corner plot of the joint posterior parameter distributions for KIC 8121913. |
 |
Fig. B.2 Corner plot of the joint posterior parameter distributions for KIC 10068024. |
 |
Fig. B.3 Corner plot of the joint posterior parameter distributions for KIC 5479689. |
References
- Aceituno, J., Sánchez, S. F., Grupp, F., et al. 2013, A&A, 552, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akeson, R. L., Chen, X., Ciardi, D., et al. 2013, PASP, 125, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Aller, A., Lillo-Box, J., Vučković, M., et al. 2018, MNRAS, 476, 1140 [NASA ADS] [CrossRef] [Google Scholar]
- Armstrong, D. J., Lopez, T. A., Adibekyan, V., et al. 2020, Nature, 583, 39 [CrossRef] [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barros, S. C. C., Gosselin, H., Lillo-Box, J., et al. 2017, A&A, 608, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batygin, K., Bodenheimer, P. H., & Laughlin, G. P. 2016, ApJ, 829, 114 [Google Scholar]
- Berger, T. A., Huber, D., van Saders, J. L., et al. 2020, AJ, 159, 280 [Google Scholar]
- Bloemen, S., Marsh, T. R., Østensen, R. H., et al. 2011, MNRAS, 410, 1787 [NASA ADS] [Google Scholar]
- Bluhm, P., Luque, R., Espinoza, N., et al. 2020, A&A, 639, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Borucki, W. J., Koch, D. G., Batalha, N., et al. 2012, ApJ, 745, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Ciceri, S., Lillo-Box, J., Southworth, J., et al. 2015, A&A, 573, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demory, B.-O., & Seager, S. 2011, ApJS, 197, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, L. R., Carter, J. A., Fabrycky, D. C., et al. 2011, Science, 333, 1602 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Esteves, L. J., De Mooij, E. J. W., & Jayawardhana, R. 2015, ApJ, 804, 150 [Google Scholar]
- Faigler, S., & Mazeh, T. 2011, MNRAS, 415, 3921 [Google Scholar]
- Faigler, S., Tal-Or, L., Mazeh, T., Latham, D. W., & Buchhave, L. A. 2013, ApJ, 771, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Furlan, E., Ciardi, D. R., Everett, M. E., et al. 2017, AJ, 153, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres (Hoboken, NJ: Wiley) [CrossRef] [Google Scholar]
- Hills, J. G., & Dale, T. M. 1974, A&A, 30, 135 [NASA ADS] [Google Scholar]
- Hormuth, F., Brandner, W., Hippler, S., & Henning, T. 2008, J. Phys. Conf. Ser., 131, 012051 [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Lillo-Box, J., Barrado, D., & Bouy, H. 2012, A&A, 546, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Barrado, D., Moya, A., et al. 2014, A&A, 562, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Aceituno, J., Pedraz, S., et al. 2020, MNRAS, 491, 4496 [CrossRef] [Google Scholar]
- Mathur, S., Huber, D., Batalha, N. M., et al. 2017, ApJS, 229, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Mazeh, T., Nachmani, G., Sokol, G., Faigler, S., & Zucker, S. 2012, A&A, 541, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millholland, S., & Laughlin, G. 2017, AJ, 154, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Millholland, S., Wang, S., & Laughlin, G. 2016, ApJ, 823, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, S. L. 1985, ApJ, 295, 143 [Google Scholar]
- Pfahl, E., Arras, P., & Paxton, B. 2008, ApJ, 679, 783 [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, SPIE Conf. Ser., 9143, 20 [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (Hoboken, NJ: Wiley) [Google Scholar]
- Santerne, A., Moutou, C., Barros, S. C. C., et al. 2012, A&A, 544, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Brugger, B., Armstrong, D. J., et al. 2018, Nat. Astron., 2, 393 [Google Scholar]
- Shporer, A. 2017, PASP, 129, 072001 [Google Scholar]
- Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [Google Scholar]
- Soto, M. G., Anglada-Escudé, G., Dreizler, S., et al. 2021, A&A, 649, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strehl, K. 1902, Astron. Nachr., 158, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Stumpe, M. C., Smith, J. C., Van Cleve, J. E., et al. 2012, PASP, 124, 985 [Google Scholar]
- Stumpe, M. C., Smith, J. C., Catanzarite, J. H., et al. 2014, PASP, 126, 100 [Google Scholar]
- van Kerkwijk, M. H., Rappaport, S. A., Breton, R. P., et al. 2010, ApJ, 715, 51 [NASA ADS] [CrossRef] [Google Scholar]
Estimation of K sin i is non-traditional, but it arises directly from a measurement of the photometric amplitude of the ellipsoidal variation, Aellip. That is, K sin i ∝ Aellip ∝ Mp sin2 i. (See Eq. (9) ahead or equation 27 of Millholland & Laughlin 2017.) This explains the extra factor of sin i.
All processed AstraLux images are publicly available through the Calar Alto Archive maintained by the Spanish Virtual Observatory at http://caha.sdc.cab.inta-csic.es/calto/
We note that Faigler et al. (2013) first found Kepler-76 through phase curve modulations, but it was subsequently found to transit its host star.
All Tables
Stellar parameters adopted for KIC 8121913, KIC 10068024, and KIC 5479689, taken from the Gaia-Kepler Stellar Properties Catalog (Berger et al. 2020).
Prior and posterior distributions for the analysis of CAFE radial velocities of KIC8026887 from Sect. 3.1.
Prior and posterior distributions for the analysis of CAFE radial velocities of KIC11362225 from Sect. 3.1.
Prior and posterior distributions for the analysis of CAFE radial velocities of KIC5878307 from Sect. 3.1.
All Figures
 |
Fig. 1 Schematic representation of the reflection, ellipsoidal and beaming (REB) modulations. Top panel: orbital path of the planet at different phases and two orbital inclinations. Middle panel: corresponding shape of the REB effects (dotted labelled lines) and the composite phase curve (green solid line). Bottom panel: corresponding RV signal with its appropriate phase relationship. |
| In the text | |
 |
Fig. 2 Results of the analysis of the high-spatial resolution images obtained with the AstraLux lucky-imaging instrument. Each panel shows the contrast curve calculated as in Lillo-Box et al. (2014) as a white line. The color-code of the contrast curve represents the contamination produced by a blended star of the given magnitude contrast as shown in the color bar. The inset panel displays the AstraLux image, with redder colors indicating more intensity. |
| In the text | |
 |
Fig. 3 Phase-folded radial velocity curves for the three planets confirmed in this paper. The solid open symbols represent nightly binned values when more than one observation are available on a given night (although we note that the analysis in the paperhas been done using the individual measurements). The median radial velocity model is represented by the black dashed line and the 67.8 and 95% confidence intervals are displayed as dark gray and light gray shaded regions around the median model. |
| In the text | |
 |
Fig. 4 Phase-folded radial velocity curves for the two planets where only upper limits to the planet mass are possible (left and middle panels) and the case of KIC 8026887 with the period equal to twice the photometric period found in Millholland & Laughlin (2017). The solid open symbols represent nightly binned values when more than one observation are available on a given night (although we note that the analysis in the paper has been done using the individual measurements). The median radial velocity model is represented by the black dashed line and the 67.8 and 95% confidence intervals aredisplayed as dark gray and light gray shaded regions around the median model. |
| In the text | |
 |
Fig. 5 Results of the joint phase curve (upper panels) and radial velocity (lower panels) fits for KIC 8121913, KIC 10068024, and KIC 5479689 (see Sect. 3.2). |
| In the text | |
 |
Fig. B.1 Corner plot of the joint posterior parameter distributions for KIC 8121913. |
| In the text | |
 |
Fig. B.2 Corner plot of the joint posterior parameter distributions for KIC 10068024. |
| In the text | |
 |
Fig. B.3 Corner plot of the joint posterior parameter distributions for KIC 5479689. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


