EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A102 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A102
Number of page(s) 12
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202039983
Published online 19 October 2021

© ESO 2021

1. Introduction

In low-mass X-ray binaries harbouring neutron stars (hereafter NS-LMXBs), a weakly magnetised neutron star (NS) accretes matter from a low-mass (< 1 M⊙) companion star through Roche-lobe overflow. One of the main sub-classifications of NS-LMXBs is based on the spectral and timing variability of the sources (Hasinger & van der Klis 1989). The pattern is traced by a single source in its X-ray colour-colour diagram (CD) or hardness-intensity diagram (HID). Thus we distinguish the so-called Atoll-class (with a luminosity of ∼0.01−0.1 of the Eddington luminosity LEdd) and Z-class (with a luminosity close to LEdd) systems. The CD of the Z sources shows the typical three-branch pattern, in which we identify the horizontal branch (HB) at the top of the track, the normal branch (NB) in the middle, and flaring branch (FB) at the bottom (see Hasinger & van der Klis 1989). The evolution of an individual source along the Z track occurs on a timescale of a few days and it is (probably) driven by the variability in the mass accretion rate Ṁ (Hasinger et al. 1990).

The power spectrum of a Z source shows quasi-periodic oscillations (QPOs), which are low-amplitude X-ray modulation with frequencies between 5 and 1250 Hz. According to the standard scenario, QPOs arise from the interaction between the weak (< 1010 G) magnetic field of the NS and transient blobs of accreting matter in the innermost region of the accretion disc (see van der Klis 1989, 2006a, for a review). The QPO frequencies could be compatible with the beat between the NS spin frequency and the Keplerian frequency of the blobs (Alpar & Shaham 1985) and might result in a modulation in the mass accretion rate Ṁ caused by the X-ray intensity variation (Lamb et al. 1985). Because the highest frequency oscillations, the so-called kHz QPOs (see e.g. Strohmayer et al. 1996; van der Klis 2000, 2006b; Jonker et al. 2000), occur near the orbital frequencies of matter in the inner accretion disc, a model-dependent constraint on the mass and the radius of the NS can be inferred assuming a stable orbital motion around the NS with a radius between the NS surface and the innermost stable circular orbit (ISCO = 6GM/c2). Under these hypotheses, it is possible to find an upper limit on the observable frequency at the ISCO in the range 1000−1250 Hz, assuming an NS with mass MNS = 2 M⊙ (Zhang et al. 1997; Miller et al. 1998; Miller & Lamb 2016).

In the continuum of the X-ray spectra of NS-LMXBs, we identify in general a soft thermal component due to the blackbody emission from the NS and/or the accretion disc, and a hard component due to the Comptonisation of soft photons from a hot electron corona located (probably) in the inner region of the system, around the NS or above the inner disc (see e.g. D’Aì et al. 2010; Pintore et al. 2015). Furthermore, the spectra of these sources show often a reflection component that originates in direct Compton scattering of the Comptonised photons that leave the hot corona with the cold electrons in the top layers of the inner accretion disc. In most of the cases, the reflection spectrum can show the so-called Compton hump above 10 keV (see e.g. Egron et al. 2013; Miller et al. 2013; Ludlam et al. 2017; Coughenour et al. 2018; Ludlam et al. 2020, 2021). The reflection component also shows some discrete features due to the fluorescence emission and photoelectric absorption by heavy ions in the accretion disc. The strength of the reflection is mainly indicated by the strong broad (full width at half maximum, FWHM, up to 1 keV) emission line from Fe atoms between 6.4 and 6.97 keV (Fe-K region), identified with the Kα radiative transition of iron at different ionisation states (e.g. Iaria et al. 2007, 2009, 2016, 2019; Papitto et al. 2013; Sanna et al. 2013; Miller et al. 2013; Di Salvo et al. 2009). These features most likely originate in the region of the accretion disc that lies closer to the compact object, where matter rotates rapidly and reaches velocities of up to a few tenths of the speed of light (see e.g. Mazzola et al. 2019; Di Salvo et al. 2015, and references therein). The whole reflection spectrum is therefore thought to be modified by transverse Doppler shifts, Doppler broadening, relativistic Doppler boosting, and gravitational redshift, which produce the characteristic broad and skewed line profile (Fabian et al. 1989). On the other hand, in some Z-sources, reflection spectral components are absent (e.g. the source GX 5–1, see Bhulla et al. 2019; Homan et al. 2018; Jackson et al. 2009), suggesting different geometries, accretion flow properties, or metallicities.

Z sources also present a hard power-law component predominant above 20 keV (e.g. Reig & Kylafis 2016; Paizis et al. 2006; Iaria et al. 2001; Di Salvo et al. 2001), whose strength is usually related with the position of the source in the CD, being highly significant in the HB up to disappear in the FB (see e.g. Di Salvo et al. 2000; D’Aì et al. 2007). The origin of the hard tail is still a matter of debate. It may originate in the Comptonisation in a hybrid thermal/non-thermal electron corona (see e.g. Farinelli et al. 2005; Poutanen & Coppi 1998), or in the mildly relativistic bulk motion of matter close to the compact object (e.g. Farinelli et al. 2008; Psaltis 2001).

We study the spectral emission of Scorpius X–1 (hereafter Sco X–1), the brightest X-ray persistent source in the sky. Identified as the first X-ray extra-solar source by Giacconi et al. (1962), Sco X–1 is an NS-LMXB system classified as a Z source (Hasinger & van der Klis 1989) in which the companion star is an M-type star with a mass of ∼0.4 M⊙ (Steeghs & Casares 2002). Sco X–1 was also the first X-ray binary found to exhibit radio emission (Andrew & Purton 1968), and based on a monitoring campaign performed with the Very Long Baseline Array, Bradshaw et al. (1999) inferred a distance to the source of 2.8 ± 0.3 kpc1, while Fomalont et al. (2001) determined an inclination angle θ = 46° ±6° of the system with respect to the line of sight.

Similar to all Z sources, Sco X–1 exhibits QPOs along all the branches of the Z track: observed for the first time by Middleditch & Priedhorsky (1986), we can distinguish in general between low- (< 10 Hz) and high- (≫10 Hz) frequency QPOs. These QPOs were extensively studied. The horizontal branch oscillations (HBOs) in Sco X–1 were observed for the first time by van der Klis et al. (1996), with a peak of 45 Hz (and a harmonic near 90 Hz). Twin kHz HBOs were also detected in the range 800−1100 Hz. They shift simultaneously in frequency with a constant peak-to-peak separation (Zhang et al. 2006; Yin et al. 2007; Yin & Zhao 2007). Normal branch oscillations (NBOs) and flaring branch oscillations (FBOs) were observed with peak frequencies in the range 4.5−7 Hz and 6−25 Hz, respectively, and seemed to be related to each other because the two peak frequencies converge when the source moves from NB to FB (see e.g. Casella et al. 2006; Yu 2007).

Because of the strong brightness of Sco X–1, which makes it hard to collect high statistical data in the soft X-ray band without damaging the instruments, the study of the spectral emission of this source was mainly directed to the highest energies. Using several HEXTE (on board the Rossi X-ray Timing Explorer satellite, Rothschild et al. 1998) observations, D’Amico et al. (2001) searched for the hard tail in the spectra of Sco X–1, modelling the data with a thermal bremsstrahlung model. The authors found that the addition of a power law was necessary to model the data in 5 out of the 16 analysed observations. Barnard et al. (2003) used the HEXTE and PCA instruments to study the broadband spectrum of this source, fitting the data with a model composed of a blackbody from the NS and a cut-off power law interpreted as Comptonised emission from an extended accretion disc corona (ADC, White & Holt 1982) plus a broad Gaussian line. Bradshaw et al. (2003) applied a model composed of a blackbody emission plus a bulk motion Comptonisation and a broad Gaussian line to analyse PCA data in the range 2.5−18 keV. Di Salvo et al. (2006) exploited the monitoring carried out by INTEGRAL to follow the spectral evolution of the source along the Z track. The authors analysed the data in the 20−200 keV energy range that were collected by IBIS/ISGRI (Ubertini et al. 2003; Goldwurm et al. 2003) during two entire revolutions of the satellite (∼300 ks each), using a thermal Comptonisation model. They observed that the spectra were dominated above 30 keV by a power law with a photon index of Γ ∼ 3, whose intensity slightly decreased from the HB along the other branches to become insignificant in the FB. The absence of a cut-off detection at the highest energy suggested the non-thermal origin of this hard component. D’Aì et al. (2007) analysed 43 spectra collected by RXTE between 1997 and 2003 using a thermal and a hybrid Comptonisation model plus a Gaussian and power-law component. The authors followed the spectral variation along the Z pattern and obtained that in this case as well, the flux of the hard X-ray tail (with a photon index between 1.9 and 3) was correlated with the position of the source in the CD. They reported that the contribution of this component to the total flux was anti-correlated to the mass accretion rate. Church et al. (2012) exploited PCA+HEXTE observations to test the ADC model for Sco X–1 and Sco-like sources, finding that the behaviour in their NB is broadly similar to Cyg-like sources. The authors also proposed a general model for the Z sources in which the mass accretion rate does not increase monotonically along the Z track, but rises from the soft apex to the hard apex, determining a constant high luminosity and high NS temperature, and consequently a high radiation pressure that causes the emission of relativistic radio jets also in the FB. Titarchuk et al. (2014) followed the evolution of Sco X–1 between the HB and FB by studying several RXTE observations collected between 1996 and 2002. The authors fitted the 3−250 keV spectra with a model consisting of two Comptonised components with different seed-photon temperatures and a broad iron line, observing a stability in the value of the photon index during the HB and NB until a slight decrease in the FB. Finally, Revnivtsev et al. (2014) studied 4 Ms of data collected by the SPI (Vedrenne et al. 2003) and IBIS instruments on board INTEGRAL and related simultaneous RXTE observations in order to obtain a coverage from 2 keV up to 10 MeV. The authors showed that the hard tail was well described by a power-law shape without cut-off up to 200−300 keV, proposing that it originates in a Compton up-scattering of soft seed photons on electrons with a non-thermal distribution.

Homan et al. (2018) partially analysed the NuSTAR observation of Sco X–1 reported here in order to compare the results with those obtained in their study of the Z source GX 5–1. Here, we extend the analysis of NuSTAR data by studying the 3−60 keV spectra extracted for NB and FB with two different classes of models. This leads to the same physical description of the source.

2. Observations and data reduction

The Nuclear Spectroscopic Telescope Array satellite (NuSTAR, Harrison et al. 2013) observed Sco X–1 between 2014 October 8, 06:46:07 UTC, and 2014 October 8, 16:16:07 UTC (ObsId 30001040002), for a total of ∼30 ks. The data were processed using the NuSTAR Data Analysis Software (NuSTAR-DAS) v1.9.3 for both data sets collected by the two focal plane modules, FPMA and FPMB.

The source events were extracted from a circular region with radius 250″ and 200″ for FPMA and FPMB, respectively, centred on the source coordinates. For the background events, we used a circular region with a radius of 120″ far away from the source for both instruments. Because of the extremely high count rate of the source, the statusexpr parameter in nupipeline was modified to avoid artificially excluding events from the noise filter.

The filtered events, the background-subtracted light curves, the spectra, and the arf and rmf files were created using the nuproducts tool. Live-time, point-spread function, exposure, and vignetting corrections were applied.

We observed the flaring activity of the source in the FPMA and FPMB light curves with a count rate between 5000 c/s and 12 500 c/s. We show the 1.6−80 keV FPMA background-subtracted light curve in Fig. 1.

thumbnail Fig. 1.

FPMA background-subtracted light curve of Sco X–1 in the 1.6−80 keV energy range, showing the flaring activity of the source (in red). The bin time is 64 s.

Furthermore, we built the CD of the source for the two instruments using the hardness ratio between the count rate in the 6−10 keV and 3−6 keV energy bands and in the 10−20 keV and 6−10 keV energy bands to obtain the “soft colour” (SC) and “hard colour” (HC) light curves, respectively.

Comparing the NuSTAR CD with previous analyses reported in literature, we observe the same Z-track shape as highlighted by CDs and HIDs obtained from RXTE data (although the energy ranges and the intensity are slightly different), in which only the lower normal branch and the flaring branch are visible and there are no evidence of the HB (see e.g. Church et al. 2012; Ding et al. 2021; Wang et al. 2020). We combined the CD of the two instruments and divided the two branches by performing a selection in HC and SC intervals in order to group the data. In particular, we selected data between 0.58−0.62 SC and 0.22−0.25 HC, between 0.55−0.645 SC and 0.25−0.285 HC, and between 0.58−0.7 SC and 0.285−0.35 HC for NB (black points in Fig. 2). For FB (red points in Fig. 2), we selected data in the following intervals: 0.62−0.66 SC and 0.22−0.25 HC, 0.66−0.74 SC and 0.225−0.228 HC and 0.74−0.82 SC and 0.25−0.33 HC. The grouped data are shown in Fig. 2 using different colours.

thumbnail Fig. 2.

Colour-colour diagram of Sco X–1 from combined FPMA and FPMB data. The SC is the ratio of the count rate in the energy bands 6−10 keV and 3−6 keV, while the HC is the ratio of the count rate in the energy bands 10−20 keV and 6−10 keV. The bin time is 128 s.

Because of the high count rate of the source, we explored the possibility of pile-up effects in our data. As reported by Grefenstette et al. (2016), a possible pile-up effect can occur in two different situations: when two photons arrive at the same pixel and are counted as one, or when two photons arrive at adjacent pixels and are then combined during the reprocessing stage of the data.

For the first type of pile-up, Grefenstette et al. (2016) estimated for this NuSTAR observation a pile-up fraction of 5.3 × 10−4 per pixel. This is a negligible contribution. For the second type, the same authors estimated a pile-up fraction of 8 × 10−4 per pixel, taking into account only the events with values of the grades parameter (which is a qualifier assigned to each event to identify the pattern of the detected photon on a 3 × 3 grid) between 21 and 24. As suggested by Grefenstette et al. (2016), we extracted the spectrum of the source using grades = 0−32 (total events), grades = 0 (single-photon events only), and grades = 1−32 (multiple-photon events only), but we did not observe a variation in the counts per energy channel related to a possible pile-up.

Using the standard nuproducts pipeline, we obtained a total spectrum with an exposure time of about 800 s for FPMA and FPMB because of the dead-time correction factor due to the high count rate of the source. Finally, we extracted an NB spectrum of ∼500 s exposure time and an FB spectrum of ∼276 s exposure time for the FPMA and FPMB.

3. Data analysis

Because the spectral shapes for the two instruments were compatible above 3 keV, they were fitted simultaneously in the 3−60 keV energy range in order to avoid the predominant contribution of the background at the highest energies. The spectra are indeed background dominated above 60 keV. All the spectra were grouped to have a minimum of 25 counts per energy bin.

We used XSPEC v12.10.1q to perform the spectral fit. We set the abundances and the photoelectric absorption cross-sections to the values found by Wilms et al. (2000) and by Verner et al. (1996), respectively, for all the spectral models discussed in the following. We applied the same models to the NB and the FB spectra.

3.1. Model 1A

Initially, we fitted the direct emission of the continuum with a model composed of a blackbody component (bbodyrad in XSPEC), which mimics a saturated Comptonisation associated with a boundary layer, plus a thermal Comptonisation (nthComp, Zdziarski et al. 1996; Życki et al. 1999), with the inp_type parameter set to 1, indicating that the seed photons have a disc-blackbody distribution. To take the photoelectric absorption by neutral matter in the interstellar medium (ISM) into account, we used the Tübingen-Boulder model (TBabs component), keeping the value of the equivalent hydrogen column associated with the interstellar matter fixed to 0.3 × 1022 cm−2 (Ding et al. 2021; Church et al. 2012; D’Aì et al. 2007; Christian & Swank 1997) due to the lack of coverage below 3 keV. From this model, called Model 1A, we obtained a χ2/d.o.f. of 2149/1186 and 1772/1104 for NB and FB, respectively, but we observed large residuals around 6 keV, in the Fe-K region (top left and top right panels in Fig. 3).

thumbnail Fig. 3.

Comparison between residuals obtained adopting Model 1A (left, top panel), Model 1A plus a Gaussian component (middle panel), and Model 2A (bottom panel) for NB. On the right, we show the same comparison for FB. The FPMA and FPMB data are shown in black and red, respectively. The residuals are graphically re-binned in order to have at least 100σ per bin.

We then added a Gaussian component to the model, leaving all the line parameters free to vary. We obtained a significant improvement of the fit, with a χ2/d.o.f. of 1428/1183 and 1190/1101 for NB and FB, respectively, and a significance of the line component (estimated as the ratio between the intensity of the line and the associated error calculated at 68% c.l.) of 13σ for NB spectrum and 15σ for FB spectrum. The emission line showed a centroid energy of about 6.6 keV and a line width σ ∼ 0.3 keV.

3.2. Model 2A

The residuals (central panels in Fig. 3) still show some features in the Fe-K region, especially in the NB spectrum. We therefore added a second Gaussian component, keeping the width linked to the σ parameter of the first component, under the hypothesis that the two lines are associated with the emission from the same ion in the same region of the accretion flow, and so that their dispersion velocity did not depend on the atomic weight of the element and they were affected by the same broadening effects. From this Model 2A, we obtained χ2/d.o.f. = 1395/1181 with a significance of the new line component of 7.3σ for NB and χ2/d.o.f. = 1181/1099 with a 3σ of significance for FB, implying that the detection of this feature is barely significant in the flaring branch spectrum. The centroid energy of this line is about 7.8 keV, suggesting an emission related to the Kβ transition of the Fe XXV ion. The best-fit results and residuals are shown in Table 1 (second and sixth columns for NB and FB, respectively) and Fig. 3 (bottom panels).

Table 1.

Best-fit results.

3.3. Model 3A

Because we still observed large residuals above 30 keV, we added a powerlaw component to Model 2A to fit this hard excess, leaving the photon index and the normalisation free to vary. We obtained a χ2/d.o.f. of 1285/1179 and 1145/1097 for NB and FB, respectively, corresponding to a Δχ2 with respect to Model 2A of 110 and 36 (with 2 d.o.f. gap), which represent an improvement of the fits. Furthermore, we obtained an F-test probability of chance improvement of 8.8 × 10−22 for NB and of 4.6 × 10−8 for FB, corresponding to a significance higher than 6σ and about 5.7σ, respectively, suggesting that the power-law component is required in both cases. We also added a low-energy exponential roll-off to the model using the expabs component in order to mimic a cut-off at the seed photon temperature, keeping the low-energy cut-off fixed to a value equal to three times the blackbody peak temperature kT. We called this model Model 3A. We obtained a χ2/d.o.f. of 1336/1179 with an F-test probability of chance improvement of 9 × 10−12 (significance > 6σ) for NB and χ2/d.o.f. = 1167/1097 with an F-test of 0.0018 (significance ∼3σ) for FB. In this case, the statistical weight of the power law also decreases in the flaring branch spectrum. The significance of this component was also confirmed using Monte Carlo simulations (see Appendix A).

For the NB spectrum, we observe a total unabsorbed flux Fbol = 6.20 × 10−7 erg cm−2 s−1 in the 0.1−100 keV energy range, corresponding to a luminosity of 5.79 × 1038 erg s−1 for a distance to the source of 2.8 ± 0.3 kpc (Bradshaw et al. 2003). The 0.1−100 keV bolometric flux associated with the power-law component is Fpow = 2.85 × 10−9 erg cm−2 s−1. For the FB spectrum, the total unabsorbed flux in the 0.1−100 keV energy range is Fbol = 8.0 × 10−7 erg cm−2 s−1, corresponding to a luminosity of 7.5 × 1038 erg s−1. The bolometric flux associated with the power-law component is Fpow = 0.78 × 10−9 erg cm−2 s−1. The best-fit values of the parameters are shown in the fourth and eighth column of Table 1. The unfolded spectrum and the corresponding residuals are shown in Fig. 4.

thumbnail Fig. 4.

Unfolded spectrum and corresponding residuals obtained using Model 3A for NB (left) and FB (right). The FPMA and FPMB data are shown in black and red, respectively. The spectra and the residuals are graphically re-binned in order to have at least 100σ per bin.

3.4. B models

As an alternative description, we substituted the blackbody component with a multi-colour disc-blackbody (diskbb in XSPEC, Mitsuda et al. 1984; Makishima et al. 1986), varying the inp_type value of nthComp accordingly to 0. This indicates that the seed photons have a blackbody incoming spectrum. We called this model Model 1B. Following the same steps as described above, we added two Gaussian lines and obtained our Model 2B:TBabs*(Gaussian+Gaussian+diskbb+nthComp). The Kα line has a significance of 12σ in the two branch spectra, while the Kβ line has a significance of 8.7σ in NB and only 2σ in FB. The values of the line parameters are compatible with those obtained from Model 2A. The best-fit results are shown in Table 1 (third and seventh columns for NB and FB, respectively). The residuals for each model step are presented in Fig. 5.

thumbnail Fig. 5.

Comparison between residuals obtained adopting Model 1B (left, top panel), Model 1B plus a Gaussian component (middle panel), and Model 2B (bottom panel) for NB. On the right, we show the same comparison for FB. The FPMA and FPMB data are shown in black and red, respectively. The residuals are graphically re-binned in order to have at least 100σ per bin.

Then we added a power law to the model, obtaining χ2/d.o.f. = 1307/1179 for NB with an F-test probability of chance improvement of 6.7 × 10−7, corresponding to a significance of ∼5σ, which suggests that the addition of this component is statistically significant. For FB, however, we obtained χ2/d.o.f. = 1146/1097 with an F-test of 0.0156 (significance < 2.8σ), suggesting that the power law is not significant.

The addition of expabs is not required by the data in this case. However, in order to perform a self-consistent analysis, we decided to take this component also into account in this model, called Model 3B, and kept the low-energy cut-off fixed to the seed-photon temperature kTbb.

We tested the significance of the power-law component using Monte Carlo simulations also in this case (see Appendix A). The total unabsorbed flux observed in the 0.1−100 keV energy range is Fbol = 7.55 × 10−7 erg cm−2 s−1, corresponding to a luminosity of 7.1 × 1038 erg s−1 in NB and Fbol = 6.46 × 10−7 erg cm−2 s−1 in FB, corresponding to a luminosity of 6.1 × 1038 erg s−1. The 0.1−100 keV bolometric flux associated with the power-law component is Fpow = 1.06 × 10−9 erg cm−2 s−1 and Fpow = 1.77 × 10−9 erg cm−2 s−1 in NB and FB, respectively. The best-fit values of the parameters are shown in the fifth and ninth column of Table 1. The unfolded spectrum and the corresponding residuals are shown in Fig. 6.

thumbnail Fig. 6.

Unfolded spectrum and corresponding residuals obtained using Model 3B for NB (left) and FB (right). The FPMA and FPMB data are shown in black and red, respectively. The spectra and the residuals are graphically re-binned in order to have at least 100σ per bin.

3.5. Model 4

We then explored the hypothesis that the iron emission lines originate from a smeared reflection. We therefore replaced the Gaussian components in Model 3B with a diskline (Fabian et al. 1989). We kept the outer radius of the reflection region Rout and the inclination angle θ of the binary system fixed to the value of 3000 gravitational radii (Rg = GM/c2) and 46° (Fomalont et al. 2001), while the inner radius Rin, the power-law dependence of the emissivity Betor, and the energy of the emission line were left free to vary. In order to lead the fit to convergence, we kept the photon index of the power-law component fixed to the value obtained from Model 3B for the NB and FB spectra. We called this Model 4. We obtained a χ2/d.o.f. of 1374/1181 and 1155/1099 for NB and FB, respectively. The line energy and best-fit values of the continuum parameters are compatible at 90% c.l. with the results obtained from Model 3B for both NB and FB. On the other hand, the inner radius Rin is not well constrained: we obtained only an upper limit of 14 Rg in NB and 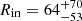Rg in FB. The emissivity parameter is 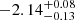for the NB spectrum and Betor = 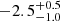in FB, according to the value expected for an LMXB ranging between −2 (in the case of a dominating central illuminating flux) and −3, which approximately describes the intrinsic emissivity of a disc (see e.g. Dauser et al. 2013; Ponti et al. 2018; Di Salvo et al. 2019; Mazzola et al. 2019; Marino et al. 2019; Iaria et al. 2019, 2020).

Slightly large residuals are observed around 7.8 keV, especially for the NB spectrum (see the central panels in Fig. 7). Furthermore, we obtained a Δχ2 of 67 and 9 (2 d.o.f. apart) with respect to Model 3B for the NB and FB spectra, respectively. This shows that we did not obtain an improvement of the fit.

thumbnail Fig. 7.

Comparison between residuals obtained adopting Model 3B (left, top panel), Model 4 (middle panel), and Model 5 (bottom panel) for NB. On the right, we show the same comparison for FB. The FPMA and FPMB data are shown in black and red, respectively. The residuals are graphically re-binned in order to have at least 120σ per bin.

3.6. Model 5

We then replaced the diskline component with a self-consistent reflection model (rfxconv, Kolehmainen et al. 2011) in order to fit the emission line in the Fe-K region and to also take the reflection continuum into account. We kept the iron abundance fixed to the solar abundance, the redshift parameter z fixed to 0, and the cosine of the inclination angle fixed to 0.6947, again considering θ = 46° (Fomalont et al. 2001). We left the ionisation parameter log ξ of the reflecting matter in the accretion disc and the relative reflection normalisation rel_refl free to vary. The incident emission onto the accretion disc is provided by the Comptonisation component. We call this model Model 5. The best-fit results are shown in Table 2. We obtained a χ2/d.o.f. of 1316/1183 with a Δχ2 of 9 with respect to Model 4B for the NB spectrum and a χ2/d.o.f. = 1145/1101 and Δχ2 = 3 for the FB spectrum, suggesting that the reflection model does not provide an improvement of the fit.

Table 2.

Best-fit results from Model 5: TBabs*(expabs*powerlaw+diskbb+rfxconv*nthComp).

To take the possible relativistic smearing effects in the inner region of the accretion disc into account, we added a multiplicative rdblur component to Model 6 using the same values of the parameters as described for the diskline in Model 4. We did not obtain any constraints on the inner radius Rin at which the reflection component originates. Under the hypothesis that the reflection occurs in a region of the disc in which the relativistic effects are not predominant, we therefore arbitrary decided to tie the inner reflection radius to the inner radius of the accretion disc. This is related to the normalisation of the disc-blackbody component by the relation 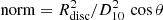, where D10 is the distance to the source in units of 10 kpc and θ is the inclination angle of the source. Under this assumption, we found a constraint on the emissivity factor Betor of 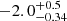in NB and >  − 1.7 in FB. This model provides a χ2/d.o.f. of 1305/1182 with an F-test probability of chance improvement of 0.0005, corresponding to a significance ∼3σ for the NB spectrum and χ2/d.o.f. = 1146/1100 with an F-test value of 0.0698 (significance < 2σ) for the FB spectrum. These results suggest that the addition of rdblur component is not significant. We therefore assume that the iron emission line is not affected by relativistical smearing, but only by Compton broadening.

Although the best-fit values of the parameters are compatible at 90% c.l. with those obtained from Model 3B for both the branches, Model 5 still shows slightly larger residuals around 7.8 keV, especially in the NB spectrum (see the comparison in Fig. 7). For this reason, together with the evidence that the reflection does not produce an improvement for the fit, we consider the two Gaussian models (i.e. models 3A and 3B) as our best-fit models. Finally, we can infer that the Fe-K region of the spectrum is well described by the presence of two Compton-broadened iron emission lines, related to the Kα and Kβ transition of the Fe XXV ions in the accretion disc.

We finally also tested the model used by Homan et al. (2018), composed of two thermal components, a power law, and a Gaussian component, to fit the iron emission line at 6.6 keV, plus a TBabs component to take the absorption due to the ISM into account. For the NB spectrum, we inferred a χ2/d.o.f. of 1380/1184 and reproduced the same results as were obtained by Homan et al. (2018), but we did not attain an improvement of the fit with respect to models 3A and 3B. For the FB spectrum, which was not analysed by Homan et al. (2018), we did not obtain a good fit using this model. We inferred a photon index of the power law of about 7, and large residuals remain in the Fe-K region of the spectrum and above 20 keV. The two blackbody components try to fit the residuals related to the Kβ emission line as a soft excess, which is not expected from the source, and the power-law component alone is not sufficient to model both the Comptonised emission and the hard excess observed above 20 keV.

4. Discussion

We analysed the first NuSTAR observation of the source Sco X–1, collected in October 2014. From the obtained CD, we pointed out that the observation covers the lower normal branch and the flaring branch of its Z track. We therefore extracted an almost complete spectrum for NB and a partial spectrum for FB. For both branches, we find that the 3−60 keV spectrum is well fitted by a model composed of a thermal emission, a thermal Comptonisation, and two Gaussian components corresponding to the Fe Kα and Fe Kβ emission line of the Fe XXV ion. A hard tail was detected above 20 keV and modelled by a power law limited at low energies with a photon index value of 2. We adopted two different descriptions for the thermal emission: a blackbody component (Model 3A), and a multi-colour disc-blackbody (Model 3B).

From Model 3A, assuming a distance to the source of 2.8 kpc, we inferred a blackbody radius Rbb = 13 ± 2 km and 13 ± 1 km for NB and FB, respectively, according to the hypothesis that this emission is generated in the innermost region of the system, which is generally identified with the NS surface and the so-called boundary layer. Furthermore, we estimated the radius of the seed-photon-emitting region Rseed using the relation Rseed = 3 × 104 d[FCompt/(1 + y)]1/2(kTseed)−2 (in ’t Zand et al. 1999), where d is the distance to the source in units of kpc, y = 4kTemax[τ, τ2]/(mec2) is the Compton parameter, kTseed is the seed-photon temperature in units of keV, and FCompt is the bolometric flux of the Comptonisation component. Using the best-fit values (fourth and seventh column in Table 1), we find Rseed = 303 ± 2 km and 286 ± 30 km for the NB and FB spectra, respectively. In this case, we assumed that the seed photons come from an equivalent spherical surface with a radius Rseed.

We then estimated the optical depth τ of the Comptonising cloud using the relation provided by Zdziarski et al. (1996),

finding that τ = 9.8 ± 0.2 and τ = 9.6 ± 0.02 for NB and FB, respectively. The electron corona is then optically thick and is likely responsible for the shielding of the emission coming from the innermost region of the system, as hypothesised for other NS-LMXBs (see e.g. Mazzola et al. 2019; Iaria et al. 2019, and references therein).

In the NB and FB spectra, a broad emission line with energy ElineKα ∼ 6.6 keV and width σKα around 0.35 keV was detected. It corresponds to the fluorescence of the Fe XXV and is compatible with the results obtained by D’Aì et al. (2007) for NB/FB spectra. We also observed an emission line around 7.8 keV, corresponding to the Kβ transition of the Fe XXV ion. We infer an equivalent width of 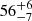eV and 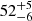eV for the Fe-Kα line in NB and FB, respectively. The Fe-Kβ emission line shows an equivalent width of 17 ± 4 eV in NB and 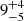eV in FB. These features are compatible with the two intercombination lines belonging to the He-like triplets of Fe XXV (see e.g. Iaria et al. 2005). Because of the NuSTAR energy resolution, the forbidden and resonance lines of the triplets are probably blended to the intercombination line, which is predominant.

We estimated the branching ratio Kβ/Kα of the intensity of the detected lines as the ratio of the normalisation values of the corresponding Gaussian components obtained from the best-fit parameters. It is 0.20 ± 0.04 and 0.11 ± 0.04 in NB and FB, respectively. The uncertainties are calculated at the 68% confidence level. These values are compatible with each other within 3σ and with the theoretical value of 0.27 (expected for the resonance lines)2, precisely within 2σ for the NB spectrum and within about 3σ for the FB spectrum, respectively. The difference between the Kβ/Kα values in NB and FB is due to the reduced intensity of the Kβ line in the flaring branch. This might be related to the different statistics of the data for the two spectra. We indeed infer a total number of photons of ∼3.6 × 106 and ∼2.51 × 106 for NB and FB, respectively. Unfortunately, no other information about the plasma diagnostic can be obtained due to the limited spectral resolution of the data for the emission lines. Further observations with higher spectral resolution in the Fe-K region of the spectrum are necessary for this purpose.

From Model 3B, under the same assumption discussed above, we inferred an inner radius of the accretion disc 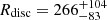km and 107 ± 21 km for NB and FB, respectively. In order to convert this value into the realistic inner disc radius Rreal, we used the relation Rreal ∼ f2Rdisc, where f ∼ 1.7 is the colour correction factor, and it depends on the mass accretion rate Ṁ (see Shimura & Takahara 1995, for details). We find that 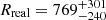km and 310 ± 61 km in NB and FB, respectively, which indicates that we are not able to observe the innermost region of the disc. This is compatible with the results obtained from Model 3A. A possible explanation could be provided by taking the high value of the mass accretion rate Ṁ into account, which is ∼ 2.5 ṀEdd (for an NS with a mass of 1.4 M⊙ and a radius of 10 km). For these values of Ṁ, the inner regions of the accretion disc are thermally unstable and are dominated by radiation pressure. This inflates the inner disc and generates an optically thick bulge of matter, which may act as a shielding corona for the inner soft emission (Shakura & Sunyaev 1976; Sincell & Krolik 1997).

Furthermore, we estimated the optical depth τ of the Comptonising cloud using the relation described above, finding that τ = 7.58 ± 0.09 in NB and τ = 6.2 ± 0.3 in FB. In this case, the electron corona is also optically thick and the value of τ is compatible with those obtained by Di Salvo et al. (2006) in FB and by D’Aì et al. (2007) in NB/FB. For this scenario, we also estimated the average electron density Ne of the cloud using the relation τ = NeσTR, in which τ is the optical depth, σT is the Thomson cross-section, and R = Rreal − RNS is the geometrical dimension of the Comptonising corona, assuming that it covers the innermost region of the system from the NS surface up to the inner radius of the accretion disc. Thus, we obtained Ne = 1.48 × 1017 cm−3 and Ne = 3.01 × 1017 cm−3 for RNS = 10 km, under the assumption that Rreal is the real inner radius of the accretion disc. Furthermore, we also estimated the radius Rseed from which the seed photons are emitted using the relation provided by in ’t Zand et al. (1999). We find Rseed = 45 ± 5 km in NB and 23 ± 3 km in FB, suggesting that the seed photons were mainly emitted from a region near the NS surface.

Lastly, in this case, we also observed two broadened Gaussian lines in the Fe-K region of both NB and FB spectrum around 6.6 keV and 7.8 keV, corresponding to the Fe-Kα and Fe-Kβ transition of the Fe XV, respectively. We infer an equivalent width of 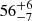eV and 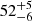eV for the Fe-Kα line in NB and FB, respectively, while the Fe-Kβ emission line shows an equivalent width of 21 ± 5 eV in NB and 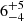eV in FB. The branching ratio Kα/Kβ is 0.24 ± 0.04 in NB and 0.10 ± 0.05 in FB, with uncertainties calculated at 68% c.l. These values are compatible with each other within 3σ in these cases also, and with the theoretical value within 1σ for the NB spectrum and within 3σ for the FB spectrum.

As mentioned in the previous section, the reflection component does not represent an improvement for the fit, and the smearing component is also unnecessary to describe these features. This suggests that reflection occurs at such a distance from the NS surface that the relativistic and Doppler effect do not rule. This hypothesis is supported by the higher value inferred from the diskbb model for the inner radius of the accretion disc, which would locate the radius at which the reflection originates at more than 250 km. In addition, because the source is ultra bright, it is possible that the irradiation due to incident emission from the NS/boundary layer ionises the inner regions of the accretion disc to such a degree that are mainly composed of neutral matter and thus prevents the formation of discrete features in the reflection component, as suggested by Homan et al. (2018) for the Z source GX 5–1. However, it is even possible that the lack of coverage of the data at lower energy leads to an inefficiency of the self-consistent model in the description of the reflection continuum. Further investigations in a broader energy band are required to shed light on these hypothesis.

A weak hard tail above 30 keV was finally detected. It contributes to less than 5% to the total unabsorbed luminosity in the 0.1−100 keV energy range in NB and FB, in disagreement with the contribution of the power law around 10%−12% of the total luminosity observed by Di Salvo et al. (2006), D’Aì et al. (2007) and Ding et al. (2021) in the 2−200 keV energy range, who found a correlation between the intensity of the power law and the position of the source in CD. This correlation was demonstrated also by Revnivtsev et al. (2014), who studied the variation in amplitude of this component along the Z track and the relation of the hard tail with the other spectral components. A similar analysis is not possible in our case due to the weakness of the power law, which is probably related to the lack of coverage above 60 keV. On the other hand, although the photon index Γ lies within the range 1.9−3 determined by D’Aì et al. (2007) and Ding et al. (2021) in NB, it seems to be beyond the range of 0.2−0.8 identified by the same authors for the FB. However, the uncertainties on Γ are large here, thus it is unconstrained and hampers the possibility of evaluating the variation in power law along the Z track. The lack of a high-energy cut-off suggests a non-thermal origin for the hard tail (see e.g. Di Salvo et al. 2006, and reference therein), which could be the result of synchrotron emission from energetic electrons (Riegler 1970), a Comptonisation of the soft seed-photons on non-thermal electrons (Revnivtsev et al. 2014), a non-thermal Comptonisation due to the bulk motion in the nearest of the NS (Farinelli et al. 2008; Ding et al. 2021), or again the result of Compton up-scattering of the soft photons in the relativistic radio jets (Reig & Kylafis 2016, 2015). In order to distinguish between these models and determine the correlation between the X-ray hard tail and the other spectral components, broad-band observations with good statistics along the complete Z track of the source are needed, especially with simultaneous radio coverage, to eventually correlate it with strong outflows or jets.

5. Conclusions

We analysed the 3−60 keV spectrum of Sco X–1 collected by NuSTAR in 2014. From the CD of this observation, we separated the spectrum of the normal branch and the flaring branch.

We fitted the two spectra using a model composed of a blackbody component, a thermal Comptonisation, and a power-law component that is absorbed by the ISM at the lower energies. Alternatively, a good fit was represented by a model in which the thermal component is provided by a multi-colour blackbody.

In both cases, two Compton-broadened emission lines were detected at 6.6 keV and 7.8 keV, corresponding to the Kα and Kβ transition of the He-like Fe XXV ion. The detection of the Fe kα line is significant in the two CD branches, while the Fe Kβ line seems to be weaker in the flaring branch. A reflection component is not required to model these features.

A power law with a photon index between 2 and 3 is required for both models, although the associated parameters are poorly constrained. The power law is very weak and contributes to the total flux with ≲1% in both branches.

The two models depict equivalent physical scenarios for the source: the spectrum softens between the normal and the flaring branch.

1

A more recent estimate of the distance can be inferred from the parallax measured by Gaia, and it is 2.1 ± 0.1 kpc. See the Gaia EDR3 catalogue at https://gaia.ari.uni-heidelberg.de/tap.html.

2

See the NIST Atomic Spectra Database Lines Data, https://www.nist.gov/pml/atomic-spectra-database

Acknowledgments

This research has made use of data and/or software provided by the High Energy Astrophysics Science Archive Research Center (HEASARC), which is a service of the Astrophysics Science Division at NASA/GSFC and the High Energy Astrophysics Division of the Smithsonian Astrophysical Observatory. The authors thank B.W. Grefenstette of NuSTAR SOC for the kind and helpful discussion about NuSTAR data reduction procedures. The authors acknowledge financial contribution from the agreement ASI-INAF n.2017-14-H.0, from INAF mainstream (PI: T. Belloni; PI: A. De Rosa) and from the HERMES project financed by the Italian Space Agency (ASI) Agreement n. 2016/13 U.O. RI and TDS acknowledge the research grant iPeska (PI: Andrea Possenti) funded under the INAF national call Prin-SKA/CTA approved with the Presidential Decree 70/2016. S.M. Mazzola extends her utmost gratitude to the anonymous Referee for their useful contribution and their patience during a prolonged refereeing process, due to an unforeseen personal issue of the author herself.

References

  1. Alpar, M. A., & Shaham, J. 1985, Nature, 316, 239 [NASA ADS] [CrossRef] [Google Scholar]
  2. Andrew, B. H., & Purton, C. R. 1968, Nature, 218, 855 [Google Scholar]
  3. Barnard, R., Osborne, J. P., Kolb, U., & Borozdin, K. N. 2003, A&A, 405, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bhulla, Y., Misra, R., Yadav, J. S., & Jaaffrey, S. N. A. 2019, Res. Astron. Astrophys., 19, 114 [CrossRef] [Google Scholar]
  5. Bradshaw, C. F., Fomalont, E. B., & Geldzahler, B. J. 1999, ApJ, 512, L121 [Google Scholar]
  6. Bradshaw, C. F., Geldzahler, B. J., & Fomalont, E. B. 2003, ApJ, 592, 486 [CrossRef] [Google Scholar]
  7. Casella, P., Belloni, T., & Stella, L. 2006, A&A, 446, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Christian, D. J., & Swank, J. H. 1997, ApJS, 109, 177 [NASA ADS] [CrossRef] [Google Scholar]
  9. Church, M. J., Gibiec, A., Bałucińska-Church, M., & Jackson, N. K. 2012, A&A, 546, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Coughenour, B. M., Cackett, E. M., Miller, J. M., & Ludlam, R. M. 2018, ApJ, 867, 64 [CrossRef] [Google Scholar]
  11. D’Aì, A., Życki, P., Di Salvo, T., et al. 2007, ApJ, 667, 411 [CrossRef] [Google Scholar]
  12. D’Aì, A., Di Salvo, T., Ballantyne, D., et al. 2010, A&A, 516, A36 [CrossRef] [EDP Sciences] [Google Scholar]
  13. D’Amico, F., Heindl, W. A., Rothschild, R. E., & Gruber, D. E. 2001, ApJ, 547, L147 [CrossRef] [Google Scholar]
  14. Dauser, T., Garcia, J., Wilms, J., et al. 2013, MNRAS, 430, 1694 [Google Scholar]
  15. Di Salvo, T., Stella, L., Robba, N. R., et al. 2000, ApJ, 544, L119 [CrossRef] [Google Scholar]
  16. Di Salvo, T., Robba, N. R., Iaria, R., et al. 2001, ApJ, 554, 49 [NASA ADS] [CrossRef] [Google Scholar]
  17. Di Salvo, T., Goldoni, P., Stella, L., et al. 2006, ApJ, 649, L91 [NASA ADS] [CrossRef] [Google Scholar]
  18. Di Salvo, T., D’Aì, A., Iaria, R., et al. 2009, MNRAS, 398, 2022 [NASA ADS] [CrossRef] [Google Scholar]
  19. Di Salvo, T., Iaria, R., Matranga, M., et al. 2015, MNRAS, 449, 2794 [NASA ADS] [CrossRef] [Google Scholar]
  20. Di Salvo, T., Sanna, A., Burderi, L., et al. 2019, MNRAS, 483, 767 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ding, G. Q., Chen, T. T., & Qu, J. L. 2021, MNRAS, 500, 772 [Google Scholar]
  22. Egron, E., Di Salvo, T., Motta, S., et al. 2013, A&A, 550, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [Google Scholar]
  24. Farinelli, R., Frontera, F., Zdziarski, A. A., et al. 2005, A&A, 434, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Farinelli, R., Titarchuk, L., Paizis, A., & Frontera, F. 2008, ApJ, 680, 602 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fomalont, E. B., Geldzahler, B. J., & Bradshaw, C. F. 2001, ApJ, 558, 283 [Google Scholar]
  27. Giacconi, R., Gursky, H., Paolini, F. R., & Rossi, B. B. 1962, Phys. Rev. Lett., 9, 439 [NASA ADS] [CrossRef] [Google Scholar]
  28. Goldwurm, A., David, P., Foschini, L., et al. 2003, A&A, 411, L223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Grefenstette, B. W., Glesener, L., Krucker, S., et al. 2016, ApJ, 826, 20 [Google Scholar]
  30. Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
  31. Hasinger, G., & van der Klis, M. 1989, A&A, 225, 79 [NASA ADS] [Google Scholar]
  32. Hasinger, G., van der Klis, M., Ebisawa, K., Dotani, T., & Mitsuda, K. 1990, A&A, 235, 131 [NASA ADS] [Google Scholar]
  33. Homan, J., Steiner, J. F., Lin, D., et al. 2018, ApJ, 853, 157 [NASA ADS] [CrossRef] [Google Scholar]
  34. Iaria, R., Burderi, L., Di Salvo, T., La Barbera, A., & Robba, N. R. 2001, ApJ, 547, 412 [NASA ADS] [CrossRef] [Google Scholar]
  35. Iaria, R., Di Salvo, T., Robba, N. R., et al. 2005, ApJ, 634, L161 [NASA ADS] [CrossRef] [Google Scholar]
  36. Iaria, R., Lavagetto, G., D’Aì, A., Di Salvo, T., & Robba, N. R. 2007, A&A, 463, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Iaria, R., D’Aì, A., Di Salvo, T., et al. 2009, A&A, 505, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Iaria, R., Di Salvo, T., Del Santo, M., et al. 2016, A&A, 596, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Iaria, R., Mazzola, S. M., Bassi, T., et al. 2019, A&A, 630, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Iaria, R., Mazzola, S. M., Di Salvo, T., et al. 2020, A&A, 635, A209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. in ’t Zand, J. J. M., Verbunt, F., Strohmayer, T. E., et al. 1999, A&A, 345, 100 [NASA ADS] [Google Scholar]
  42. Jackson, N. K., Church, M. J., & Bałucińska-Church, M. 2009, A&A, 494, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Jonker, P. G., Méndez, M., & van der Klis, M. 2000, ApJ, 540, L29 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kolehmainen, M., Done, C., & Díaz Trigo, M. 2011, MNRAS, 416, 311 [NASA ADS] [Google Scholar]
  45. Lamb, F. K., Shibazaki, N., Alpar, M. A., & Shaham, J. 1985, Nature, 317, 681 [NASA ADS] [CrossRef] [Google Scholar]
  46. Ludlam, R. M., Miller, J. M., Bachetti, M., et al. 2017, ApJ, 836, 140 [CrossRef] [Google Scholar]
  47. Ludlam, R. M., Cackett, E. M., García, J. A., et al. 2020, ApJ, 895, 45 [NASA ADS] [CrossRef] [Google Scholar]
  48. Ludlam, R. M., Jaodand, A. D., García, J. A., et al. 2021, ApJ, 911, 123 [Google Scholar]
  49. Makishima, K., Maejima, Y., Mitsuda, K., et al. 1986, ApJ, 308, 635 [NASA ADS] [CrossRef] [Google Scholar]
  50. Marino, A., Del Santo, M., Cocchi, M., et al. 2019, MNRAS, 490, 2300 [NASA ADS] [CrossRef] [Google Scholar]
  51. Mazzola, S. M., Iaria, R., Di Salvo, T., et al. 2019, A&A, 621, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Middleditch, J., & Priedhorsky, W. C. 1986, ApJ, 306, 230 [NASA ADS] [CrossRef] [Google Scholar]
  53. Miller, M. C., & Lamb, F. K. 2016, Eur. Phys. J. A, 52, 63 [NASA ADS] [CrossRef] [Google Scholar]
  54. Miller, M. C., Lamb, F. K., & Cook, G. B. 1998, ApJ, 509, 793 [NASA ADS] [CrossRef] [Google Scholar]
  55. Miller, J. M., Parker, M. L., Fuerst, F., et al. 2013, ApJ, 779, L2 [NASA ADS] [CrossRef] [Google Scholar]
  56. Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
  57. Paizis, A., Farinelli, R., Titarchuk, L., et al. 2006, A&A, 459, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Papitto, A., D’Aì, A., Di Salvo, T., et al. 2013, MNRAS, 429, 3411 [NASA ADS] [CrossRef] [Google Scholar]
  59. Pintore, F., Di Salvo, T., Bozzo, E., et al. 2015, MNRAS, 450, 2016 [NASA ADS] [CrossRef] [Google Scholar]
  60. Ponti, G., Bianchi, S., Muñoz-Darias, T., et al. 2018, MNRAS, 473, 2304 [NASA ADS] [CrossRef] [Google Scholar]
  61. Poutanen, J., & Coppi, P. S. 1998, Phys. Scr. Vol. T, 77, 57 [NASA ADS] [CrossRef] [Google Scholar]
  62. Psaltis, D. 2001, ApJ, 555, 786 [NASA ADS] [CrossRef] [Google Scholar]
  63. Reig, P., & Kylafis, N. 2016, A&A, 591, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Reig, P., & Kylafis, N. D. 2015, A&A, 584, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Revnivtsev, M. G., Tsygankov, S. S., Churazov, E. M., & Krivonos, R. A. 2014, MNRAS, 445, 1205 [NASA ADS] [CrossRef] [Google Scholar]
  66. Riegler, G. R. 1970, Nature, 226, 1041 [NASA ADS] [CrossRef] [Google Scholar]
  67. Rothschild, R. E., Blanco, P. R., Gruber, D. E., et al. 1998, ApJ, 496, 538 [NASA ADS] [CrossRef] [Google Scholar]
  68. Sanna, A., Hiemstra, B., Méndez, M., et al. 2013, MNRAS, 432, 1144 [NASA ADS] [CrossRef] [Google Scholar]
  69. Shakura, N. I., & Sunyaev, R. A. 1976, MNRAS, 175, 613 [NASA ADS] [CrossRef] [Google Scholar]
  70. Shimura, T., & Takahara, F. 1995, ApJ, 445, 780 [Google Scholar]
  71. Sincell, M. W., & Krolik, J. H. 1997, ApJ, 476, 605 [CrossRef] [Google Scholar]
  72. Steeghs, D., & Casares, J. 2002, ApJ, 568, 273 [Google Scholar]
  73. Strohmayer, T. E., Zhang, W., Swank, J. H., et al. 1996, ApJ, 469, L9 [Google Scholar]
  74. Titarchuk, L., Seifina, E., & Shrader, C. 2014, ApJ, 789, 98 [NASA ADS] [CrossRef] [Google Scholar]
  75. Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. van der Klis, M. 1989, ARA&A, 27, 517 [NASA ADS] [CrossRef] [Google Scholar]
  77. van der Klis, M. 2000, ARA&A, 38, 717 [NASA ADS] [CrossRef] [Google Scholar]
  78. van der Klis, M. 2006a, Adv. Space Res., 38, 2675 [NASA ADS] [CrossRef] [Google Scholar]
  79. van der Klis, M. 2006b, in Compact Stellar X-ray Sources, eds. W. H. G. Lewin, & M. Van der Klis, Camb. Astrophys. Ser., 39, 39 [NASA ADS] [CrossRef] [Google Scholar]
  80. van der Klis, M., Swank, J. H., Zhang, W., et al. 1996, ApJ, 469, L1 [NASA ADS] [CrossRef] [Google Scholar]
  81. Vedrenne, G., Roques, J. P., Schönfelder, V., et al. 2003, A&A, 411, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [Google Scholar]
  83. Wang, D.-H., Zhang, C.-M., Qu, J.-L., & Jia, S.-M. 2020, A&A, 642, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. White, N. E., & Holt, S. S. 1982, ApJ, 257, 318 [NASA ADS] [CrossRef] [Google Scholar]
  85. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
  86. Yin, H. X., & Zhao, Y. H. 2007, Adv. Space Res., 40, 1522 [NASA ADS] [CrossRef] [Google Scholar]
  87. Yin, H. X., Zhang, C. M., Zhao, Y. H., et al. 2007, A&A, 471, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Yu, W. 2007, ApJ, 659, L145 [NASA ADS] [CrossRef] [Google Scholar]
  89. Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
  90. Zhang, W., Strohmayer, T. E., & Swank, J. H. 1997, ApJ, 482, L167 [CrossRef] [Google Scholar]
  91. Zhang, C. M., Yin, H. X., Zhao, Y. H., Zhang, F., & Song, L. M. 2006, MNRAS, 366, 1373 [CrossRef] [Google Scholar]
  92. Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [Google Scholar]

Appendix A: Testing the hard-tail significance with Monte Carlo simulations

We used an alternative method to the F-test probability to evaluate the significance of the presence of the hard tail, employing the Monte Carlo technique to simulate a set of 1000 spectra for each NuSTAR instrument.

Assuming as null hypothesis that the spectrum does not require a power-law component, we used the corresponding best-fit model (Model 2A) and the fakeit task of XSPEC for the simulations, obtaining 1000 spectra for the FPMA and FPMB. We used the NuSTAR FPMA and FPMB ancillary response file (ARF), response matrix (RMF), and background spectrum for each instrument. We simulated each spectrum for the same exposure time for the source and background. Each pair of simulated FPMA+FPMB spectra was fitted using the best-fit models 3A and 2A (including and excluding the power-law component, respectively). For each fit, we evaluated the discrepancy Δχ2 between the two obtained χ2. Each value of the obtained Δχ2 was compared with the same Δχ2 value obtained from the real data.

We evaluated the distribution of the Δχ2 reporting the number of times in which the simulated value of Δχ2 is higher than that obtained with the real data (i.e. good trials). The probability of chance improvement was finally evaluated by considering the good-trial values divided by the total number of simulations.

We followed the described approach for the two branches. For the NB, we obtained a Δχ2 that exceeded the real one by 0/1000 times. This means that the probability of chance improvement is < 0.1%. For the FB, the obtained Δχ2 is larger than the real one by 9/1000 times, which means a probability of 0.9%. In both cases, the simulations confirm what was predicted by the F-test.

We applied the same procedure to the B models and simulated the spectra with Model 2B and fitted them with models 2B and 3B. We obtained a probability of chance improvement < 0.1% in NB and of 0.7% in FB. This confirms the F-test prediction in these cases as well. By relying on the Monte Carlo tests, we can conclude that the power-law component is required in both branches with the confidence level reported in the text.

All Tables

Table 1.

Best-fit results.

In the text
Table 2.

Best-fit results from Model 5: TBabs*(expabs*powerlaw+diskbb+rfxconv*nthComp).

In the text

All Figures

thumbnail Fig. 1.

FPMA background-subtracted light curve of Sco X–1 in the 1.6−80 keV energy range, showing the flaring activity of the source (in red). The bin time is 64 s.
In the text
thumbnail Fig. 2.

Colour-colour diagram of Sco X–1 from combined FPMA and FPMB data. The SC is the ratio of the count rate in the energy bands 6−10 keV and 3−6 keV, while the HC is the ratio of the count rate in the energy bands 10−20 keV and 6−10 keV. The bin time is 128 s.
In the text
thumbnail Fig. 3.

Comparison between residuals obtained adopting Model 1A (left, top panel), Model 1A plus a Gaussian component (middle panel), and Model 2A (bottom panel) for NB. On the right, we show the same comparison for FB. The FPMA and FPMB data are shown in black and red, respectively. The residuals are graphically re-binned in order to have at least 100σ per bin.
In the text
thumbnail Fig. 4.

Unfolded spectrum and corresponding residuals obtained using Model 3A for NB (left) and FB (right). The FPMA and FPMB data are shown in black and red, respectively. The spectra and the residuals are graphically re-binned in order to have at least 100σ per bin.
In the text
thumbnail Fig. 5.

Comparison between residuals obtained adopting Model 1B (left, top panel), Model 1B plus a Gaussian component (middle panel), and Model 2B (bottom panel) for NB. On the right, we show the same comparison for FB. The FPMA and FPMB data are shown in black and red, respectively. The residuals are graphically re-binned in order to have at least 100σ per bin.
In the text
thumbnail Fig. 6.

Unfolded spectrum and corresponding residuals obtained using Model 3B for NB (left) and FB (right). The FPMA and FPMB data are shown in black and red, respectively. The spectra and the residuals are graphically re-binned in order to have at least 100σ per bin.
In the text
thumbnail Fig. 7.

Comparison between residuals obtained adopting Model 3B (left, top panel), Model 4 (middle panel), and Model 5 (bottom panel) for NB. On the right, we show the same comparison for FB. The FPMA and FPMB data are shown in black and red, respectively. The residuals are graphically re-binned in order to have at least 120σ per bin.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.