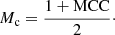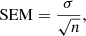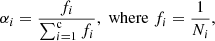| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 16 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202140369 | |
| Published online | 03 September 2021 | |
Deep transfer learning for the classification of variable sources
1
Electronics and Telecommunications Research Institute (ETRI), 218 Gajeong-ro, Daejeon, Yuseong-gu, South Korea
e-mail: dwk@etri.re.kr
2
Max Planck Institute for Astronomy (MPIA), Königstuhl 17, 69117 Heidelberg, Germany
Received:
18
January
2021
Accepted:
31
May
2021
Ongoing or upcoming surveys such as Gaia, ZTF, or LSST will observe the light curves of billions or more astronomical sources. This presents new challenges for identifying interesting and important types of variability. Collecting a sufficient amount of labeled data for training is difficult, especially in the early stages of a new survey. Here we develop a single-band light-curve classifier based on deep neural networks and use transfer learning to address the training data paucity problem by conveying knowledge from one data set to another. First we train a neural network on 16 variability features extracted from the light curves of OGLE and EROS-2 variables. We then optimize this model using a small set (e.g., 5%) of periodic variable light curves from the ASAS data set in order to transfer knowledge inferred from OGLE and EROS-2 to a new ASAS classifier. With this we achieve good classification results on ASAS, thereby showing that knowledge can be successfully transferred between data sets. We demonstrate similar transfer learning using HIPPARCOS and ASAS-SN data. We therefore find that it is not necessary to train a neural network from scratch for every new survey; rather, transfer learning can be used, even when only a small set of labeled data is available in the new survey.
Key words: methods: data analysis / stars: variables: general / surveys / techniques: miscellaneous
© ESO 2021
1. Introduction
In recent years deep learning has achieved outstanding success in various research areas and application domains. For instance, convolutional neural networks (CNNs; Lecun et al. 2015) use convolutional layers to regularize and build space-invariant neural networks to classify visual data (Krizhevsky et al. 2012; Goodfellow et al. 2014; Szegedy et al. 2015). AlphaGo, which is one of the most astonishing achievements of deep learning and is based on reinforcement learning, defeated several world-class Go players (Silver et al. 2016). In astronomy, deep learning has become popular and has been used in many types of studies, such as star-galaxy classification (Kim & Brunner 2017), asteroseismology classification of red giants (Hon et al. 2017), photometric redshift estimation (D’Isanto & Polsterer 2018), galaxy-galaxy strong lens detection (Lanusse et al. 2018), exoplanet finding (Pearson et al. 2018), point source detection (Vafaei Sadr et al. 2019), and fast-moving object identification (Duev et al. 2019), to name just a few examples.
Training a deep learning classification model requires a huge amount of labeled data, which are not always readily available. This can be addressed using “transfer learning”, a method that preserves prior knowledge inferred from one problem that has sufficient samples (the “source”) and applies it to a related problem (the “target”) (Hinton et al. 2015; Yim et al. 2017; Yeo et al. 2018). Transfer learning starts with a machine learning model that has been trained on a large number of labeled samples from the source. It then optimizes parameters in the model using a small number of labeled samples from the target. The source and target samples can be different but need to be related such that extracted features to train the model are general and relevant in both samples. Period, amplitude, and variability indices could be such features when the problem is one of classifying the light curves of variable stars.
Transfer learning has been used in a number of ways, such as for medical image classification (Shin et al. 2016; Maqsood et al. 2019; Byra et al. 2020), recommender-system applications (Pan et al. 2012; Hu et al. 2019), bioinformatics applications (Xu et al. 2010; Petegrosso et al. 2016), transportation applications (Di et al. 2018; Wang et al. 2018; Lu et al. 2019), and energy saving applications (Li et al. 2014; Zhao & Grace 2014). Some studies in astronomy have also used transfer learning, such as Ackermann et al. (2018), Domínguez Sánchez et al. (2019), Lieu et al. (2019), and Tang et al. (2019). These studies used transfer learning to analyze image data sets of either galaxies or Solar System objects and confirmed that transfer learning is successful even when using a small set of data.
The advantages of transfer learning are as follows. First, transfer learning uses accumulated knowledge from the source. Therefore, it works with a small set of samples from the target. Second, transfer learning uses a pretrained model, obviating the need to design a deep neural network from scratch for every survey, which is a challenging and time-consuming task. A pretrained model furthermore contains better initialization parameters than randomly initialized parameters. Thus, it is likely that transferring a pretrained model shows faster convergence than training from scratch. Finally, it is possible to either add or remove certain output classes from the pretrained model during transfer-learning processes. This is particularly useful because the classes in the target data set are mostly different from the classes of the source data set.
In our previous work, UPSILoN: AUtomated Classification for Periodic Variable Stars using MachIne LearNing (Kim & Bailer-Jones 2016), we provided a software package that automatically classifies light curves into one of seven periodic variable classes. Other groups have used UPSILoN to classify light curves of periodic variable stars (e.g., Jayasinghe et al. 2018; Kains et al. 2019; Hosenie et al. 2019).
In this paper we introduce UPSILoN-T: UPSILoN using Transfer Learning. UPSILoN-T is substantially different from UPSILoN in several respects. First, UPSILoN-T can be transferred to other surveys, whereas the UPSILoN’s random forest model cannot. Second, UPSILoN-T is not only able to classify periodic or semi-periodic variables but also nonperiodic variables, such as quasi-stellar objects (QSOs) or blue variables. Third, UPSILoN-T uses the Matthews correlation coefficient (MCC; Matthews 1975) rather than F1 as a performance metric. The MCC is known to give a relatively robust performance measure for imbalanced samples (Boughorbel et al. 2017). We use the generalized MCC (Chicco 2017) for multi-class classification. Finally, UPSILoN-T uses deep learning, whereas UPSILoN used a random forest. The UPSILoN-T model has three hidden layers, with 64, 128, and 256 neurons, respectively. This is a much smaller model (∼200 KB) than UPSILoN’s random forest model (∼3 GB).
As far as we know, no previous work has applied transfer learning based on deep learning to time-variability features extracted from light curves. In addition to developing the method, we provide a python library so that readers can easily adapt our method to their data sets (see the appendix). The library classifies a single-band light curve as one of nine variable classes. If multiple optical bands exist, the library can be applied to each of them independently. It should be noted that one of the goals of our method, as with its predecessor UPSILoN, is to not be dependent on colors and, as such, to be independent of the availability or number of bands in a survey.
We give an introduction of a neural network in Sect. 2. In Sect. 3.1 we introduce the training set, and in Sect. 3.2 we explain the 16 time-variability features that we use to train a classification model. From Sects. 3.3–3.5, we explain training processes and the feature importance of the trained model. Section 4 demonstrates the application of transfer learning to other light-curve data sets: the All Sky Automated Survey (ASAS; Pojmanski 1997), HIPPARCOS (Dubath et al. 2011), and the All-Sky Automated Survey for Supernovae (ASAS-SN; Jayasinghe et al. 2018) data sets. Section 5 gives the classification performance of the transferred model as a function of light-curve lengths and sampling. Section 6 gives a summary.
2. Artificial neural network
An artificial neural network (ANN) consists of multiple layers comprising an input layer, hidden layer(s), and an output layer. An ANN with at least two hidden layers is usually called a deep neural network (DNN). Each layer contains one or more nodes (neurons) that are connected to the nodes in the next layer. Each connection has a particular weight that can be interpreted as how much impact that node has on the connected node in the next layer. Data are propagated through the network, and the value on each node is computed using an activation function (Agatonovic-Kustrin & Beresford 2000). The Heaviside function, hyperbolic tangent function, and rectified linear unit (ReLU; Nair & Hinton 2010) are typical examples of nonlinear activation functions that are often used between intermediate layers. The softmax function is widely used in the output layer when solving a classification problem (Nair & Hinton 2010). Due to the nonlinearity, the function space that can be expressed using ANNs is diverse.
An example of ANN architecture is shown in Fig. 1. We define input nodes, hidden nodes, and output nodes as x, h, and y, respectively, and these are vectors. Let the weights and biases between x and h and weights between h and y be W1, b1 and W2, b2, respectively. Then, W1 and W2 are matrices and b1 and b2 are vectors. We can then express x, h, and y as follows:
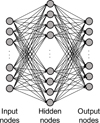 |
Fig. 1. DNN architecture with one hidden layer. |
where σ1(⋅) and σ2(⋅) denote the activation function between x and h and between h and y, respectively. In classification problems, σ1 and σ2 are typically the ReLU function and the softmax function, respectively. The values of the output nodes give the probabilities of the input (i.e., x) belonging to each of the output classes. The goal of a classification problem is learning the weights so that the true classes receive the highest probabilities. Given an input X = {x1,x2,⋯,xm}, this learning process is done by minimizing a loss function such as cross entropy, which defined as follows:
where li is the true label for each xi and is a one-hot encoded vector, which is a vector representation of categorical data, such as class labels. That is, lk = [lk, 1, lk, 2, …, lk, c] and lk, j ∈ {0, 1} for k = {1, 2, …, m} and j = {1, 2, …, c}. The c is the number of classes, W = {W1,b1,W2,b2}, and “⋅” denotes an inner product. In the cases of imbalanced data set classification, a weighted cross entropy is often used, which is defined as follows:
where α = [α1, α2, …, αc] and ° denotes an element-wise product. The αi is a weight for a given class and is a nonnegative real number, where 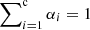 .
.
Inferring the weights (i.e., learning) is done by minimizing a loss function, such as that in Eqs. (2) or (3), using a gradient descent method:
where λ is a learning rate for the gradient descent optimization and is a positive constant. The minimization is often done by using a stochastic gradient descent (SGD) optimization (Hinton et al. 2012; Graves et al. 2013) or a modified SGD optimization (Kingma & Ba 2014). In the case of SGD optimization, the input data are split into several batches (i.e., mini-batches), and then SGD is applied to each mini-batch as the pseudo-code shown in Algorithm 1.
Input:
Initialized weights of ANN to be learned: W = {W1, b1, W2, b2}
Output:
Learned weights of ANN: W
1: While W does not converge do
2: Choose a mini-batch Xℬ of size n
Xℬ = {xℬ,1,…,xℬ,n}⊂ X
Wnew ← Wold − λ ∇WLCE(Xℬ; Wold)
UpdateW using SGD
4: end while
3. UPSILoN-T classifier
3.1. Training set
The training set consists of single-band light curves of variable sources from two independent surveys, Optical Gravitational Lensing Experiment (OGLE; Udalski et al. 1997) and Expérience pour la Recherche d’Objets Sombres (EROS-2; Tisserand et al. 2007). We mixed variable sources from the two surveys in order to build a rich training set. The training set comprises non-variables and seven classes of periodic variables: δ Scuti stars, RR Lyraes, Cepheids (CEPHs), Type II Cepheids (T2CEPHs), eclipsing binaries (EBs), and long period variables (LPVs). We also used the subclasses (e.g., CEPH F, 1O, and Other) of each class if these exist. These seven classes of variable sources are from Kim & Bailer-Jones (2016), who originally compiled and cleaned the list of periodic variable stars from several sources, including Soszynski et al. (2008), Soszyński et al. (2008, 2009, 2009), Poleski et al. (2010), Graczyk et al. (2011), and Kim et al. (2014). As described in these papers, light curves are visually examined and cleaned in order to remove light curves that do not show variability. In the present work we also added the QSOs and blue variables from Kim et al. (2014) to the training set. These two types of variables generally show nonperiodic and irregular variability. It should be noted that the training set is not exhaustive, since it does not contain all types of variable sources in the real sky. Thus, a model trained on the training set will classify a light curve that does not belong to the training classes into a “most similar” training class based on variability.
The observation duration is about eight years for the OGLE light curves and about seven years for the EROS-2 light curves. We used OGLE I-band light curves and EROS-2 blue-band, BE, light curves because these generally have more data points and better photometric accuracy than OGLE V-band and EROS-2 red-band, RE, respectively. The average number of data points in the light curves is about 500. Table 1 shows the number of objects per class in the training set. There is a total of 21 variable classes.
Number of sources per true class in the OGLE and EROS-2 training set.
3.2. Variability features
We extracted 16 variability features from each light curve in the training set. These features, listed in Table 2, are taken from von Neumann (1941), Shapiro & Wilk (1965), Lomb (1976), Ellaway (1978), Grison (1994), Stetson (1996), Long et al. (2012), Kim et al. (2014), and Kim & Bailer-Jones (2016). These features have proven to be useful for classifying both periodic and nonperiodic variables (e.g., QSOs) in our previous works (Kim et al. 2011, 2012, 2014; Kim & Bailer-Jones 2016). They are generic and can be extracted from any single-band light curves. Four of the features (ψη, ψCS, mp90, and mp10) are based on a phase-folded light curve. We excluded survey-dependent features, such as colors, because we want to transfer accumulated knowledge from one survey to another.
16 variability features.
We took the logarithm base 10 of nine of the features (period, γ1, γ2, ψη, ψCS, Q3 − 1, A, H1, and mp90) because we found empirically that a model trained using these log10 applied features improved the performance over using the features directly. We scaled each of the nine feature sets as follows: First, we derived the minimum value of a feature set; second, we subtracted the minimum value minus one from each feature in the feature set; and third, we took the logarithm base 10 of the features.
Performance did not improve when taking the logarithm of the other features, so those features were used directly. Finally, we normalized each of the 16 feature sets by calculating the standard score.
3.3. Model training
3.3.1. Classification performance metric
In order to measure the classification performance of a trained model and then select the one that gives the best performance, we used the MCC metric (Matthews 1975) rather than the mode traditional F1 or accuracy metrics. For two-class problems, the MCC, accuracy, and F1 are defined as follows:
where TP, TN, FP, and TN are the numbers of true positives, true negatives, false positives, and false negatives, respectively. Precision and recall in Eq. (7) are defined as follows:
The MCC is a more informative measure for imbalanced data sets than the other two measures because the MCC utilizes all four categories of a confusion matrix (Powers 2011; Boughorbel et al. 2017). The F1 does not take account of true negative and thus is less informative for imbalanced data sets. Accuracy is inappropriate for imbalanced data sets because high accuracy does not necessarily indicate high classification quality, due to the “accuracy paradox” (Fernandes et al. 2010; Valverde-Albacete & Peláez-Moreno 2014). The MCC ranges from −1.0 to 1.0, where 1.0 indicates that the predictions match exactly with the true labels, 0.0 indicates that the predictions are random, and −1.0 means that the predictions are completely opposite to the true labels. It is claimed that the MCC is the most informative value for measuring the classification quality using a confusion matrix (Chicco 2017). In the case of multi-class problems, the MCC is generalized as follows (Gorodkin 2004):
For convenience, we mapped MCC to the range [0,1], as suggested in Chicco & Jurman (2020):
Hereinafter, we use Mc to report the classification quality of neural networks.
3.3.2. Training DNN models
In order to find the best architecture for classifying the OGLE and EROS-2 training set, we trained many DNN models with different combinations of the number of hidden layers, the number of neurons in each hidden layer, loss functions, and activation functions between layers. The model training processes are as follows.
First, we randomly split the data set shown in Table 1 into an 80% training set and a 20% validation set while preserving the class ratio (i.e., stratified sampling).
Second, we trained a DNN model from scratch using the training set with the batch size of 1024 and learning rate = 0.1. This counts as one training epoch. The Mc was then calculated using the validation set.
Third, we ran the training process in the second step for 500 iterations (i.e., 500 training epochs). If Mc is not improved for three consecutive epochs, we decreased the learning rate by 10. If the learning rate becomes lower than 10−10, we increased it back to 0.1, according to a technique called the cyclical learning rate (CLR; Smith 2015).
Fourth, we took the highest Mc value (i.e., the best Mc value) from the 500 epochs. Finally, we repeated steps 1 to 4 a total of 30 times and calculated the mean of the best Mc values and the standard error of this mean (SEM), which is defined as:
where σ is the standard deviation of the nMc values from the n = 30 cycles.
The loss function that we chose is cross entropy, which is explained in Sect. 2. While training DNN models, we used the SGD (Hinton et al. 2012; Graves et al. 2013) optimizer because we empirically found that SGD gives a better classification performance than other optimizers (e.g., ADAM: Kingma & Ba 2014; ADADELTA: Zeiler 2012; and ADAGRAD: Duchi et al. 2011). We also used a batch normalization method that converts the inputs to layers into a normal distribution in order to mitigate “internal covariate shift” (Ioffe & Szegedy 2015). Ioffe & Szegedy (2015) showed that this method makes training faster and more stable.
After training many DNN models, we finally chose the architecture that had the highest validation-set Mc, which was 0.9043. This is shown in Fig. 2. It should be noted that we used Mc to choose the best model, but we did not use it as a loss function to optimize neural networks. We refer to this best model as the “U model”, an abbreviation of “UPSILoN-T model”. The number of trainable parameters in the U model is 48 799. Given that the number of training samples is 144 823 and that there are 16 features per sample, we presumed that there exist enough features to train the parameters. Furthermore, the parameters in a network are not, and need not be, independent. Therefore, it is not theoretically necessary to have more training features than the number of trainable parameters.
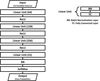 |
Fig. 2. Neural network architecture that we adopted in this work. The input is a vector of 16 variability features. Each linear unit contains one batch normalization layer and one fully connected layer. We use ReLU as an activation function between layers. The last linear unit has 21 outputs, which is the number of variable classes in our training set. We use the softmax function before the output layer to scale the outputs to lie between 0 and 1 in order to represent probabilities for the 21 output classes. |
Some examples of the DNN architectures that we trained are shown in Table 3, where the U model is shown in bold text. As the table shows, increasing the number of layers and the number of neurons in each hidden layer increases the classification performance. On the other hand, using too many neurons degrades the classification performance, as can be seen in the bottom three rows, due to an overfitting of the training data. The Mc differences between the models are statistically significant at the several sigma level. Whether the differences are practically significant or not is, however, another issue. In order to confirm that the differences are practically significant, we would need to apply every trained DNN model to many different time-series databases that have labels for light curves and then check their classification performances. We have not done this, as we just chose the best model, but this does not preclude a simpler model being almost as good in practice.
Classification performance of the neural network models.
We classified each light curve according to the highest probability of all the classes. The top panel in Fig. 3 shows the highest and the second highest probabilities for each source in the training sample. As the panel shows, the majority of the highest probabilities are larger than 0.8, while the majority of the second highest probabilities are lower than 0.2. In the bottom panel, we show the histogram of the differences between the two. As expected, the differences are generally larger than 0.5. This means that the classifier is reasonably confident about its class assignments. The U model returns both the predicted class and the probabilities of all classes, so users can set a threshold on a probability if they desire.
 |
Fig. 3. Class probability distribution of the light curves in the training set. Upper panel: highest and the second highest probabilities. Bottom panel: differences between the two. |
3.3.3. Classification quality of the U model
In Fig. 4 we show the U model’s confusion matrix normalized by the number of true objects per class. The numbers on the leading diagonal represent recall values for each variable class. The recall values are higher than ∼0.8 for all but a few classes, such as T2CEPH and QSO. The figure also shows confusion within subclasses of a certain variable class, such as LPVs or EBs. This confusion is expected because variability patterns residing in their light curves are likely to be similar.
 |
Fig. 4. Confusion matrix of the U model. Labels on the vertical axis are the true classes, and labels on the horizontal axis are the predicted classes. Each row is divided by the number of true objects per variable class. Thus, the values on each diagonal are recall. We show the value if it is larger than or equal to 0.01. |
In the top panel of Fig. 5, we show Mc and the learning rate as a function of the training epoch. The figure shows 500 epochs of the n = 18 cycle (see the training processes in Sect. 3.3.2), where the highest validation-set Mc (annotated with the red arrow) is achieved. As the figure shows, the training-set Mc keeps increasing as a function of epoch. This indicates that the model eventually starts to overfit the training samples. We note that the U model was chosen based on the validation-set Mc, not based on the training-set Mc. The lower panel of Fig. 5 shows the change in the learning rate during the training processes. We see the learning rate cycling decreasing and increasing, a consequence of our using CLR. The Mc value (the top panel) derived using the training sets and validation sets varies according to the changes in learning rate. The highest validation-set Mc is obtained after several iterations of CLR.
 |
Fig. 5. Mc and the learning rate as a function of the training epoch. Top panel: training-set Mc (blue line) and validation-set Mc (orange line) as a function of training epochs. Bottom panel: changes in the learning rate as a result of the CLR application. The red arrow indicates the training epoch where the best validation-set Mc is achieved. |
For comparison purposes, we trained random forest (Breiman 2001) models with the same data set and variability features. We trained the models using 80% of the data as a training set and then derived Mc using the remaining 20%, just as we did for the DNN model training. We optimized the model hyper-parameters using the 80% training set and using ten-fold cross-validation and a brute-force grid search over a two-dimensional grid of t and m, where t is the number of trees and m is the number of randomly selected features for each node in a tree. The grid values of t and m are [100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 1100, 1200] and [4, 6, 8, 10, 12, 14], respectively1. We repeated the training processes ten times. The highest Mc after the training is 0.8996, which is lower than the Mc of the DNN. The average of Mc and SEM2 are 0.8963 and 7.7 × 10−4, respectively. Thus, we concluded that the random forest model gives a slightly worse performance than the U model. Nevertheless, this result does not mean that DNN is always superior than random forest for variable source classification using variability features.
In the case of “random” light curves that do not belong to any of the training classes, we found empirically that most of them are classified as non-variables as follows.
First, we generated 1000 light curves consisting of purely random values, extracted 16 variability features from them, and predicted their classes using the U model. The U model predicted ∼800 of them as non-variables and ∼100 as LPVs. The predicted classes of the remaining ∼100 light curves were dispersed through other variable classes.
Second, we randomly shuffled data points in each light curve of the ASAS variable stars (Table 4 in Sect. 3.4), extracted 16 variability features, and used the U-model to predict their classes. As a result, ∼7000 light curves were classified as non-variables, and ∼3000 light curves were classified as detached eclipsing binaries (EB ED in Table 1). The predicted classes of the remaining ∼1000 light curves were dispersed through other classes.
Number of objects per true class in the ASAS data set.
3.4. Application to ASAS light curves of periodic variable stars
To validate the classification quality of the U model in general, we applied it to the ASAS light curves of periodic variable stars that contain δ Scuti stars, RR Lyraes, CEPHs, EBs, and LPVs (Pojmanski 1997). The duration of the light curves is about nine years. The average number of data points is about 500. We collected the light curves from Kim & Bailer-Jones (2016). The number of samples per true variable class and the classification quality is shown in Table 4. We derived the F1 measure of the same data set as well, and it was 0.87. This is slightly higher than the F1 = 0.85 from Kim & Bailer-Jones (2016), who used the same training set and the 16 variability features to train a random forest. Nevertheless, this does not necessarily mean that the U model is always superior to the random forest. For instance, we applied the U model to light curves from the MACHO data set that Kim & Bailer-Jones (2016) also used. In this case, the F1 measures for both the U model and the random forest model are identical at 0.92.
3.5. Feature importance
We used the SHapley Additive exPlanations (SHAP; Lundberg & Lee 2017) method to measure the feature importance in the U model. SHAP values represents how strongly each feature impacts a model’s predictions. They are derived from the Shapley value (Shapley 1953) used in cooperative game theory. Conceptually, the Shapley value measures the degree of contribution of each player to a game where all the players cooperate. Although there are few SHAP applications in physics, Pham et al. (2019), Amacker et al. (2020), and Scillitoe et al. (2021) used SHAP to measure feature importances for their machine learning applications, such as predicting solar flare activities, Higgs self-coupling measurements, and data-driven turbulence modeling.
Figure 6 shows the SHAP feature importance for the U model. This shows the mean absolute value of SHAP over all samples for each feature. We see that the period is the most important feature, which has also been found in other studies (e.g., Kim et al. 2014; Kim & Bailer-Jones 2016; Elorrieta et al. 2016). All other features also contribute to the classification of variable classes, although their contributions are lower than the period’s contribution.
 |
Fig. 6. SHAP feature importance Lundberg & Lee (2017). The larger the SHAP value, the more important a feature is. The mean absolute SHAP value shows the accumulated feature importance for all variable classes, which are depicted in different colors. |
We trained two independent DNN models with the same architecture as shown in Fig. 2. Both were trained with periods removed, and the second with the period-related features (ψη, ψCS, mp90, and mp10) also removed. As a result, the Mc drops from 0.90 to 0.87 in the first case and to 0.82 in the second case. Given that the SEM values (Table 3) are quite small, these decreases are significant, again confirming that periods are critical for variable classification. We note, however, that periods of some training classes do not have a strict physical “period” meaning, such as in the case of quasars. In such cases, they are just used as a variability feature.
4. Transferring the U model’s knowledge to other light-curve data sets of variable sources
4.1. Transfer learning
Transfer learning is a research field in machine learning that aims to preserve knowledge accumulated while solving one problem (source) and then utilize this knowledge to solve other related problems (target; Cowan et al. 1994; Pan & Yang 2010). Depending on the problem at hand, conditions of the source and target could vary in several ways. In this work, which aims to transfer the U model to data from other surveys, we deal with the following three issues.
The first issue is a different class label space. The number of variable classes (21, as shown in Table 1) of the OGLE and EROS-2 training set is different from the number of variable classes of the ASAS data set (9, as shown in Table 4). Moreover, not only does the number of variable classes differ, but so do the variable types. For instance, there are no QSOs or blue variables in the ASAS data set.
The second issue is the different frequencies of class members. The number of contacted eclipsing binaries (EB EC in Table 1) in the OGLE and EROS-2 training set is 1398 (see Table 1), which is less than 1% of the data set, but their number in the ASAS data set is 2550 (see Table 4), which is ∼24% of the data set.
The third issue is the different distribution of variability features. Magnitude ranges, filter wavelengths, and noise characteristics differ between surveys. This implies that the distribution of the 16 variability features extracted from light curves is not identical between source and target.
The widely used transfer-learning approach for dealing with these issues is to transfer the weights from the pretrained model. We started with the same neural network model with the same weights (i.e., the U model). We then continued with the training in one or two different ways. The first was to optimize the weights of every layer, and the second was to optimize the weights of only the last fully connected layer while freezing the other layers. In Fig. 2 the last fully connected layer is in the fourth linear unit (i.e., the last linear unit). In both approaches we adjusted the number of output nodes at the last linear unit so that the number of output nodes is equal to the number of variable classes from the target data set3. By doing this, we were able to obtain appropriate prediction results with regard to the target data set’s classes.
In order to show the benefit of transfer learning, we defined a base model as the non-transferred and directly trained model, and compared it to the transferred models. We also compared a model directly trained on a small data set (scratch models) with the transferred models. The six-step process for the transfer learning that we applied to each target data set (i.e., ASAS, HIPPARCOS, and ASAS-SN) is as follows.
First, we randomly split the target data set into the 80% and 20% groups while preserving the class ratio (stratified sampling). We call the 80% data set D0.8 and the 20% data set the test set.
Second, we trained a DNN model from scratch with the same architecture shown in Fig. 2. We used the entire D0.8 to train the model. We call this the “base model”. The training process is the same as that from Sect. 3.3.2. We then calculated the Mc of the base model using the test set. We note that this base model does not use any accumulated knowledge from the U model (i.e., weights in the U model).
Third, we randomly chose a 3% subset of D0.8 and then used this subset to train a DNN model from scratch, which has the same architecture as the one shown in Fig. 2. We used the same training process in Sect. 3.3.2. We call this the “scratch model”. It should also be noted that we did not transfer any of the U model’s accumulated knowledge. After the training, we computed the Mc for the scratch model on the test set.
Fourth, we used the same 3% subset of D0.8 used for training the scratch model to transfer the U model. As mentioned above, we transferred the U model according to two different approaches (1) optimizing weights of every layer and (2) optimizing weights of only the last fully connected layer while freezing the weights of all other layers. We call the former an “every-layer model” and the latter a “last-layer model”. We note that both approaches start from the initial weights of the U model rather than from random initialization. We again used the same training process as in Sect. 3.3.2 to optimize the weights. We computed the Mc of these models using the test set.
Fifth, we repeated the third and fourth steps using 5%, 10%, 15%, 20%, 50%, and 100% of D0.8. Theoretically, the classification quality of the base model should be identical to that of the scratch model trained using 100% of D0.8 because the base model is also trained using the same 100% of D0.8.
Sixth, we repeated the steps one to five a total of 30 times and used these values to compute the mean and SEM value of Mc.
In the following three subsections, we show and analyze the results of using this transfer-learning procedure on three different data sets.
4.2. Application to the ASAS data set
The results of applying the transfer-learning process to the ASAS data set described in Sect. 3.4 are given in Fig. 7. The base model’s average Mc is 0.9501, and its SEM is 1.8 × 10−3. The figure also shows the results for the other models (described in the previous section), which we now briefly discuss.
 |
Fig. 7. Average Mc with SEM as error bars for the last-layer, every-layer, and scratch models. The Mc of the every-layer models are slightly higher than those of the scratch models. The last-layer models show higher Mc for small training sets, and vice versa for large training sets. We add a small offset on the x-axis to the scratch models in order to prevent its error bars from lying on top of the other error bars. |
The Mc of the scratch models increase as the size of a subset of D0.8 increases. The scratch model trained using 100% of D0.8 shows Mc = 0.9513, which is very similar to the Mc of the base model.
The Mc of the every-layer models are generally higher than those of the scratch models, even when their training set is small. This result shows the benefit of transfer learning, even with a small target data set. For larger samples (50%−100% subset), the results of the transferred models and scratch models are similar.
The last-layer models preserve more knowledge from the U model than the every-layer models do. For the same reason, the last-layer model could give a worse performance because new knowledge from the target data set cannot be transmitted to every layer. The results show that which effect dominates depends on the training sample size. For small training sets, the last-layer models produce a higher Mc, and vice versa for large training sets. We also see that the SEM values of the last-layer models are smaller than those of other models because optimizing the weights in only the last layer gives less freedom to update the weights than optimizing the weights in every layer does.
Overall, we see that transfer learning produces good results when the size of the target data set is small, which is one of the advantages of using transfer learning. Transferring only the last layer is not a good choice when there is a relatively large number of target samples. In such cases, training from scratch (base model) or transferring every layer works better, although it requires more computation time. In addition, we show a confusion matrix of the every-layer model trained on the 100% subset in Fig. 8. This shows a good classification performance.
4.3. Application to the HIPPARCOS data set
We then applied transfer learning to the HIPPARCOS data set (Dubath et al. 2011), which has more classes but fewer samples than the ASAS data set (see Table 5). The 1570 HIPPARCOS light curves that we extracted from Kim & Bailer-Jones (2016) is substantially smaller than the 10 779 light curves in the ASAS data set. The duration of the light curves varies from one to three years, and the average number of data points is about 100.
Number of objects per true class in the HIPPARCOS data set.
Overall, the training process is the same as the one described in Sect. 4.1. To ensure sufficient samples for training, however, we split the HIPPARCOS data into 50% training and 50% testing sets (D0.5), rather than the 80% and 20% that we used for ASAS. We used the entire set of D0.5 to train scratch models and also to transfer the U model. We did not train separate base models since these are now the same as the scratch models.
The result of transfer learning is shown in Table 6. The scratch model’s average Mc is 0.7398, whereas the every-layer model’s average Mc is 0.7770. The last-layer model achieves the highest average Mc of all models tested, 0.8230. Due to the small number of target samples, learning from scratch is significantly inferior to transfer learning in this case. Figure 9 is a confusion matrix of the last-layer model, which also shows a relatively high confusion between the classes because of the insufficient target samples.
Transfer learning application using the HIPPARCOS data set.
4.4. Application to the ASAS-SN data set
In this section we apply transfer learning to the ASAS-SN database of variable stars (Shappee et al. 2014; Jayasinghe et al. 2019). We obtained a catalog of the variable stars and their corresponding light curves from the ASAS-SN website4. We selected only the light curves with class probabilities higher than 95% and whose classification results are certain. The average number of data points in the light curves is about 200, and the duration is about four years. We extracted 16 time-variability features from each light curve, excluding light curves that had fewer than 100 data points. In Table 7 we show the number of selected light curves for each variable class and their corresponding classes5 in the training set (if any). The larger number of samples, 288 698, is sufficient to train DNNs from scratch. Yet even in such cases transfer learning could be useful because it could achieve the highest Mc faster than training from scratch would.
Number of objects per true class in the ASAS-SN data set.
We trained scratch, every-layer, and last-layer models using the entire set of D0.8 according to the training process described in Sect. 4.1. Because base models are now the same as the scratch models, we did not train them. The average of Mc and the SEM are shown in Table 8. The average Mc of the scratch model and the every-layer model are similar, as expected, whereas that of the last-layer model is smaller. It should be noted that we did not train models using a subset of the ASAS-SN data set because its result would be similar to what we explained in Sects. 4.2 and 4.3. Figure 10 is a confusion matrix of the every-layer model. The classification quality is relatively good, but a lot of the yellow semi-regular variables (SRDs), red irregular variables (Ls), young stellar objects (YSOs), long secondary period variables (LSPs), and variable stars of unspecified type (VARs) are misclassified as long period semi-regular variables (SRs). Most of these variables are either semi-regular or irregular variables, and thus their variability characteristics are expected to be similar to one another (i.e., no clear periodicities in their light curves). Furthermore, the number of SRDs, YSOs, LSPs and VARs is relatively small, a few hundred per class, whereas the number of SRs is 108 943, which could cause the bias toward the majority (SR).
Transfer learning application using the ASAS-SN data set.
Figure 11 shows four examples of validation-set Mc at the first 40 training epochs from the n = 30 cycles (see Sect. 3.3.2). From the figure, we see that the every-layer models reach the highest Mc faster than the scratch models do. We confirmed that the remaining 26 cases out of the n = 30 cycles show similar behavior. However, the difference is not significant, which implies that, given enough training samples and computing resources, transfer learning is not really necessary because training from scratch gives as good a classification performance as transfer learning does.
 |
Fig. 11. Examples of the ASAS-SN validation-set Mc of the scratch models (blue line) and the every-layer models (orange line). As the figure shows, transferring the UT model reaches the highest Mc faster than training from scratch does. |
5. Performance of a transferred model as a function of light-curve length and sampling
In this section we examine the classification performance of the transferred model as a function of the observation durations, d, and the number of data points in a light curve, n. For this experiment, we used the every-layer model transferred using the 20% subset of ASAS D0.8 (see Sect. 4.2). The Mc of the model is 0.94.
We constructed a set of light curves by resampling the ASAS light curves shown in Table 4 using d = 30, 60, 90, 180, 365, 730, and 1470 days and n = 20, 40, 80, 100, 150, 200, and 300. In order to resample a given light curve, we first extracted measurements observed between the starting epoch and d days after the starting epoch. We then randomly selected n unique data points from the extracted measurements to make a resampled light curve. The left panel of Fig. 12 shows the classification quality of the transferred model applied to these resampled light curves. As the panel shows, Mc quickly reaches its maximum value once the number of data points reaches 300. Even with a lower n, 100 or 150, or a lower d, 365 or 730, Mc is fairly high. When n = 20, we see that Mc decreases as d increases. This is because n = 20 is too small a number of data points to construct a well-sampled light curve.
 |
Fig. 12. Classification quality, Mc, of the resampled ASAS light curves as a function of duration, d (horizontal axis), and the number of data points, n (different lines), in the light curve. Left: Mc of the transferred model. Right: Mc of the U model. |
From this experiment, we see that if the number of data points, n, is larger than or equal to 100, Mc is not significantly lower than what we can achieve using more data points. For comparison, we show the Mc of the U model for the same data set in the right panel of Fig. 12. The Mc of the U model is lower than that of the transferred model, as expected, but the overall patterns of Mc are similar to those of the transferred model. For the HIPPARCOS and ASAS-SN data sets, we did not resample their light curves to carry out the same experiment due to a lack of either n or d. Nevertheless, if enough n and d are given, we would expect to see similar variations in Mc for the other data sets considered because those models were also derived from the U model using transfer learning.
6. Summary
We have introduced deep transfer learning for classifying light curves of variable sources in order to diminish difficulties in collecting sufficient training samples with labels, in designing an individual neural network for every survey, and in applying inferred knowledge from one data set to another. Our approach starts with training a DNN using 16 variability features that are relatively survey independent. These features were extracted from a training set composed of the light curves of OGLE and EROS-2 variable sources. We then applied transfer learning to optimize the weights in the trained network to be able to extend the original model to new data sets, here ASAS, HIPPARCOS, and ASAS-SN. From these applications we see that transfer learning successfully utilizes knowledge inferred from the source data set (i.e., OGLE and EROS-2) to the target data set even with a small number of the target samples. In particular, we see that:
-
Transferring only the last layer of the network shows better classification quality than transferring every layer when there are few samples. For instance, the last-layer models’ classification performance is 3%−7% higher than that of the scratch models when a small number of ASAS samples (i.e., 3%−15% of the entire ASAS data set) is used (see Fig. 7).
-
As shown in Fig. 7, when there exists a sufficient number of samples (i.e., 20%−100% of the entire ASAS data set), the every-layer models give a better classification performance, 1%−2% higher than the last-layer models.
-
Transfer learning works successfully even when label spaces are different between the source and the target. For instance, the HIPPARCOS data set contains many types of variable sources that differ from those of the training samples (i.e., OGLE and EROS-2), as shown in Table 5. Transfer learning works: The every-layer and the last-layer models show ∼4% and ∼9% better classification performances, respectively, relative to the scratch models (see Table 6).
From these results of using transfer learning, we see that transfer learning is useful for the classification of variable sources from time-domain surveys that have a few training samples. This is a significant benefit since it is not always possible to build a robust training set with a sufficient number of samples. For instance, many ongoing and upcoming time-domain surveys, such as Gaia (Gaia Collaboration 2016), the Zwicky transient facility (ZTF; Bellm et al. 2019), SkyMapper (Keller et al. 2007), and Pan-STARRS (Chambers et al. 2016), will produce a large number of light curves of astronomical sources. Assembling a sufficiently large set of labeled light curves for training for each survey, however, is a difficult and time-consuming task, especially in the early stage of the survey. Given that transfer learning works even when using a small set of data, transfer learning would prove useful for classifying light curves and thus building an initial training set for such surveys. Nevertheless, if enough training samples are readily available, transfer learning does not provide much benefit; however, it does not do any worse, as can be seen from the results of the every-layer models (e.g., Fig. 7 and Table 8).
We have not used any survey-specific features, such as colors. It would nonetheless be interesting to test whether including such features improves the classification performance. For instance, one could replace the lowest important feature, ϕ21 (see Fig. 6), with a color. One could then train a DNN model from scratch with this and transfer the trained model to another survey that uses different colors.
We provide a python software package containing a pretrained network (the U model) and functionality to transfer the U model to any time-domain survey. The package can also train a DNN model from scratch and deal with imbalanced data sets. Details about the package are given in the appendix.
The grid values are from our previous work, Kim & Bailer-Jones (2016).
In this case, the n in Eq. (11) is 10.
Due to Electronics and Telecommunications Research Institute (ETRI) policy, permission is required to access the UPSILoN-T repository after registration for the ETRI GitLab website. The access permission can be obtained simply by emailing the author (D.-W. Kim).
Acknowledgments
This work was supported by a National Research Council of Science and Technology (NST) grant by the Korean government (MSIP) [No. CRC-15-05-ETRI].
References
- Ackermann, S., Schawinski, K., Zhang, C., Weigel, A. K., & Turp, M. D. 2018, MNRAS, 479, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Agatonovic-Kustrin, S., & Beresford, R. 2000, J. Pharm. Biomed. Anal., 22, 717 [Google Scholar]
- Amacker, J., Balunas, W., Beresford, L., et al. 2020, J. High Energy Phys., 2020, 115 [Google Scholar]
- Bailer-Jones, C. A. L., Fouesneau, M., & Andrae, R. 2019, MNRAS, 490, 5615 [CrossRef] [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002 [NASA ADS] [CrossRef] [Google Scholar]
- Boughorbel, S., Jarray, F., & El-Anbari, M. 2017, PLoS ONE, 12, e0177678 [NASA ADS] [CrossRef] [Google Scholar]
- Breiman, L. 2001, Mach. Learn., 45, 5 [CrossRef] [Google Scholar]
- Byra, M., Wu, M., Zhang, X., et al. 2020, Magn. Reson. Med., 83, 1109 [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Chawla, N., Bowyer, K., Hall, L., & Kegelmeyer, W. 2002, J. Artif. Intell. Res. (JAIR), 16, 321 [Google Scholar]
- Chicco, D. 2017, BioData Mining, 10, 35 [Google Scholar]
- Chicco, D., & Jurman, G. 2020, BMC Genom., 21, 6 [Google Scholar]
- Cowan, J., Tesauro, G., & Alspector, J. 1994, Advances in Neural Information Processing Systems 6 (Morgan Kaufmann) [Google Scholar]
- Di, S., Zhang, H., Li, C., et al. 2018, IEEE Trans. Intell. Transp. Syst., 19, 745 [Google Scholar]
- D’Isanto, A., & Polsterer, K. L. 2018, A&A, 609, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domínguez Sánchez, H., Huertas-Company, M., Bernardi, M., et al. 2019, MNRAS, 484, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Dubath, P., Rimoldini, L., Süveges, M., et al. 2011, MNRAS, 414, 2602 [NASA ADS] [CrossRef] [Google Scholar]
- Duchi, J., Hazan, E., & Singer, Y. 2011, J. Mach. Learn. Res., 12, 2121 [Google Scholar]
- Duev, D. A., Mahabal, A., Ye, Q., et al. 2019, MNRAS, 486, 4158 [CrossRef] [Google Scholar]
- Ellaway, P. 1978, Electroencephalogr. Clin. Neurophysiol., 45, 302 [Google Scholar]
- Elorrieta, F., Eyheramendy, S., Jordán, A., et al. 2016, A&A, 595, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fernandes, J. A., Irigoien, X., Goikoetxea, N., et al. 2010, Ecol. Model., 221, 338 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodfellow, I., Pouget-Abadie, J., Mirza, M., et al. 2014, in Advances in Neural Information Processing Systems 27, eds. Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, & K. Q. Weinberger (Curran Associates, Inc.), 2672 [Google Scholar]
- Gorodkin, J. 2004, Comput. Biol. Chem., 28, 367 [Google Scholar]
- Graczyk, D., Soszyński, I., Poleski, R., et al. 2011, Acta Astron., 61, 103 [Google Scholar]
- Graves, A., Mohamed, A. R., & Hinton, G. 2013, ArXiv e-prints [arXiv:1303.5778] [Google Scholar]
- Grison, P. 1994, A&A, 289, 404 [NASA ADS] [Google Scholar]
- He, H., Bai, Y., Garcia, E. A., & Li, S. 2008, IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), 1322 [Google Scholar]
- Hinton, G., Deng, l., Yu, D., et al. 2012, Sign. Process. Mag. IEEE, 29, 82 [Google Scholar]
- Hinton, G., Vinyals, O., & Dean, J. 2015, ArXiv e-prints [arXiv:1503.02531] [Google Scholar]
- Hon, M., Stello, D., & Yu, J. 2017, MNRAS, 469, 4578 [NASA ADS] [CrossRef] [Google Scholar]
- Hosenie, Z., Lyon, R. J., Stappers, B. W., & Mootoovaloo, A. 2019, MNRAS, 488, 4858 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, G., Zhang, Y., & Yang, Q. 2019, ArXiv e-prints [arXiv:1901.07199] [Google Scholar]
- Ioffe, S., & Szegedy, C. 2015, ArXiv e-prints [arXiv:1502.03167] [Google Scholar]
- Jayasinghe, T., Kochanek, C. S., Stanek, K. Z., et al. 2018, MNRAS, 477, 3145 [Google Scholar]
- Jayasinghe, T., Stanek, K. Z., Kochanek, C. S., et al. 2019, MNRAS, 485, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Kains, N., Calamida, A., Rejkuba, M., et al. 2019, MNRAS, 482, 3058 [NASA ADS] [Google Scholar]
- Keller, S. C., Schmidt, B. P., Bessell, M. S., et al. 2007, PASA, 24, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D.-W., & Bailer-Jones, C. A. L. 2016, A&A, 587, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, E. J., & Brunner, R. J. 2017, MNRAS, 464, 4463 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D.-W., Protopapas, P., Byun, Y.-I., et al. 2011, ApJ, 735, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D.-W., Protopapas, P., Trichas, M., et al. 2012, ApJ, 747, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D.-W., Protopapas, P., Bailer-Jones, C. A. L., et al. 2014, A&A, 566, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kingma, D. P., & Ba, J. 2014, ArXiv e-prints [arXiv:1412.6980] [Google Scholar]
- Krizhevsky, A., Sutskever, I., & Hinton, G. E. 2012, Commun. ACM, 60, 84 [Google Scholar]
- Lanusse, F., Ma, Q., Li, N., et al. 2018, MNRAS, 473, 3895 [NASA ADS] [CrossRef] [Google Scholar]
- Lecun, Y., Bengio, Y., & Hinton, G. 2015, Nature, 521, 436 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Li, R., Zhao, Z., Chen, X., Palicot, J., & Zhang, H. 2014, IEEE Trans. Wirel. Commun., 13, 2000 [Google Scholar]
- Lieu, M., Conversi, L., Altieri, B., & Carry, B. 2019, MNRAS, 485, 5831 [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Long, J. P., El Karoui, N., Rice, J. A., Richards, J. W., & Bloom, J. S. 2012, PASP, 124, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, C., Hu, F., Cao, D., et al. 2019, IEEE Trans. Intell. Transp. Syst., 1 [Google Scholar]
- Lundberg, S. M., & Lee, S. I. 2017, in Advances in Neural Information Processing Systems 30, eds. I. Guyon, U. V. Luxburg, S. Bengio, et al. (Curran Associates, Inc.), 4765 [Google Scholar]
- Maqsood, M., Nazir, F., Khan, U., et al. 2019, Sensors (Basel), 19, 2645 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, B. 1975, Biochim. Biophys. Acta (BBA) – Protein Struct., 405, 442 [Google Scholar]
- Nair, V., & Hinton, G. E. 2010, Proceedings of the 27th International Conference on Machine Learning (ICML-10), 807 [Google Scholar]
- Pan, S. J., & Yang, Q. 2010, IEEE Trans. Knowl. Data Eng., 22, 1345 [Google Scholar]
- Pan, W., Xiang, E. W., & Yang, Q. 2012, Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence, AAAI’12 (AAAI Press), 662 [Google Scholar]
- Pearson, K. A., Palafox, L., & Griffith, C. A. 2018, MNRAS, 474, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Petegrosso, R., Park, S., Hwang, T. H., & Kuang, R. 2016, Bioinformatics, 33, 529 [Google Scholar]
- Pham, C., Pham, V., & Dang, T. 2019, 2019 IEEE International Conference on Big Data (Big Data), 5844 [CrossRef] [Google Scholar]
- Pojmanski, G. 1997, Acta Astron., 47, 467 [Google Scholar]
- Poleski, R., Soszyñski, I., Udalski, A., et al. 2010, Acta Astron., 60, 1 [NASA ADS] [Google Scholar]
- Powers, D. M. W. 2011, J. Mach. Learn. Technol., 2, 37 [NASA ADS] [Google Scholar]
- Scillitoe, A., Seshadri, P., & Girolami, M. 2021, J. Comput. Phys., 430, 110116 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, S. S., & Wilk, M. B. 1965, Biometrika, 52, 591 [Google Scholar]
- Shapley, L. S. 1953, Contributions to the Theory of Games (AM-28) (Princeton: Princeton University Press), 2 [Google Scholar]
- Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, ApJ, 788, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Shin, H. C., Roth, H. R., Gao, M., et al. 2016, ArXiv e-prints [arXiv:1602.03409] [Google Scholar]
- Silver, D., Huang, A., Maddison, C. J., et al. 2016, Nature, 529, 484 [CrossRef] [PubMed] [Google Scholar]
- Smith, L. N. 2015, ArXiv e-prints [arXiv:1506.01186] [Google Scholar]
- Soszynski, I., Poleski, R., Udalski, A., et al. 2008, Acta Astron., 58, 163 [NASA ADS] [Google Scholar]
- Soszyñski, I., Udalski, A., Szymañski, M. K., et al. 2009, Acta Astron., 59, 239 [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2008, Acta Astron., 58, 293 [NASA ADS] [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2009, Acta Astron., 59, 1 [NASA ADS] [Google Scholar]
- Stetson, P. B. 1996, PASP, 108, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Szegedy, C., Liu, W., Jia, Y., et al. 2015, Computer Vision and Pattern Recognition (CVPR) (IEEE) [Google Scholar]
- Tang, H., Scaife, A. M. M., & Leahy, J. P. 2019, MNRAS, 488, 3358 [Google Scholar]
- Tisserand, P., Le Guillou, L., Afonso, C., et al. 2007, A&A, 469, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udalski, A., Kubiak, M., & Szymanski, M. 1997, Acta Astron., 47, 319 [NASA ADS] [Google Scholar]
- Vafaei Sadr, A., Vos, E. E., Bassett, B. A., et al. 2019, MNRAS, 484, 2793 [NASA ADS] [CrossRef] [Google Scholar]
- Valverde-Albacete, F. J., & Peláez-Moreno, C. 2014, PLoS ONE, 9, e84217 [NASA ADS] [CrossRef] [Google Scholar]
- von Neumann, J. 1941, Ann. Math. Stat., 12, 367 [Google Scholar]
- Wang, J., Zheng, H., Huang, Y., & Ding, X. 2018, IEEE Trans. Intell. Transp. Syst., 19, 2913 [CrossRef] [Google Scholar]
- Xu, Q., Xiang, E. W., & Yang, Q. 2010, IEEE International Conference on Bioinformatics and Biomedicine (BIBM), 62 [CrossRef] [Google Scholar]
- Yeo, D., Bae, J., Kim, N., et al. 2018, 2018 25th IEEE International Conference on Image Processing (ICIP), 674 [CrossRef] [Google Scholar]
- Yim, J., Joo, D., Bae, J., & Kim, J. 2017, 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 7130 [CrossRef] [Google Scholar]
- Zeiler, M. D. 2012, ArXiv e-prints [arXiv:1212.5701] [Google Scholar]
- Zhao, Q., & Grace, D. 2014, 1st International Conference on 5G for Ubiquitous Connectivity, 152 [Google Scholar]
Appendix A: Python library
A.1. How to predict variable classes using UPSILoN-T
The following pseudo-code shows how to use the UPSILoN-T python software library67 to extract variability features from a set of light curves and then predict their classes.
from upsilont import UPSILoNT
from upsilont.features import VariabilityFeatures
# Extract features from a set of light-curves.
feature_list = []
for light_curve in set_of_light_curves:
# Read a light-curve.
date = np.array([:])
mag = np.array([:])
err = np.array([:])
# Extract features.
var_features = VariabilityFeatures(date, mag, err).get_features()
feature_list.append(var_features)
features = pd.DataFrame(feature_list)
ut = UPSILoNT()
label, prob = ut.predict(features, return_prob=True)
label and prob are lists of predicted classes and class probabilities, respectively.
A.2. How to transfer UPSILoN-T knowledge to another data set
The library can transfer the U model as follows:
ut.transfer(features, labels, "/path/to/transferred/
model/")features is a list of features extracted from a set of light curves, and labels is a list of corresponding labels. The library writes the transferred model and other model-related parameters to a specified location (i.e., “/path/to/transferred/model/” in the above pseudo-code). The transferred model can predict variable classes as follows:
ut.load("/path/to/transferred/model/")
label, prob = ut.predict(features, return_prob=True)
A.3. How to deal with an imbalanced data set
As shown in Table 1, the training set is often imbalanced. For instance, there are approximately 179 more OGLE small amplitude red giant branch pulsating stars (OSARG RGBs) than QSOs (i.e., 29 516/165 ≈ 179). Due to such class imbalance, the training of a network could be biased toward the more dominant classes, even though this dominance is just a consequence of the relative frequency of available training samples that we do not want to learn.
There are several approaches to deal with imbalanced data sets, such as weighting a loss function according to the sample frequencies, synthesizing artificial samples (e.g., SMOTE, introduced in Chawla et al. 2002, or ADASYN, introduced in He et al. 2008), over- or under-sampling methods that repeat or remove samples in order to balance the sample frequency per class, and Bayesian methods (Bailer-Jones et al. 2019). Bailer-Jones et al. (2019) introduced a method to accommodate class imbalance in probabilistic multi-class classifiers. The UPSILoN-T library provides two of these approaches when training or transferring a model.
A.3.1. Weighting a loss function
In Eq. (3) we weight a loss function using α, which is proportional to the number of samples per class. In brief, we give a higher weight to the minority class, and vice versa. The α for each class is defined as follows:
where Ni is the number of samples per class and c is the number of variable classes.
A.3.2. Over-sampling technique
Conceptually, an over- or under-sampling method builds an artificial training set by balancing the number of each class in the original training set. The over-sampling method resamples the original training set by randomly duplicating samples from the minority class. For instance, if there are 20 samples of class A and 40 samples of class B, over-sampling randomly selects twice as many samples from class A as class B. The disadvantage of this approach to addressing imbalance is that the training time is increased. Another disadvantage is that a trained model could overfit the minority class since it just duplicates samples.
The following pseudo-code shows how to use these two methods.
# Over-sampling.
ut.train(features, labels, balanced_sampling=True)
# Weighting a loss function.
ut.train(features, labels, weight_class=True)
# Do both.
ut.train(features, labels, balanced_sampling=True,
weight_class=True)All Tables
All Figures
 |
Fig. 1. DNN architecture with one hidden layer. |
| In the text | |
 |
Fig. 2. Neural network architecture that we adopted in this work. The input is a vector of 16 variability features. Each linear unit contains one batch normalization layer and one fully connected layer. We use ReLU as an activation function between layers. The last linear unit has 21 outputs, which is the number of variable classes in our training set. We use the softmax function before the output layer to scale the outputs to lie between 0 and 1 in order to represent probabilities for the 21 output classes. |
| In the text | |
 |
Fig. 3. Class probability distribution of the light curves in the training set. Upper panel: highest and the second highest probabilities. Bottom panel: differences between the two. |
| In the text | |
 |
Fig. 4. Confusion matrix of the U model. Labels on the vertical axis are the true classes, and labels on the horizontal axis are the predicted classes. Each row is divided by the number of true objects per variable class. Thus, the values on each diagonal are recall. We show the value if it is larger than or equal to 0.01. |
| In the text | |
 |
Fig. 5. Mc and the learning rate as a function of the training epoch. Top panel: training-set Mc (blue line) and validation-set Mc (orange line) as a function of training epochs. Bottom panel: changes in the learning rate as a result of the CLR application. The red arrow indicates the training epoch where the best validation-set Mc is achieved. |
| In the text | |
 |
Fig. 6. SHAP feature importance Lundberg & Lee (2017). The larger the SHAP value, the more important a feature is. The mean absolute SHAP value shows the accumulated feature importance for all variable classes, which are depicted in different colors. |
| In the text | |
 |
Fig. 7. Average Mc with SEM as error bars for the last-layer, every-layer, and scratch models. The Mc of the every-layer models are slightly higher than those of the scratch models. The last-layer models show higher Mc for small training sets, and vice versa for large training sets. We add a small offset on the x-axis to the scratch models in order to prevent its error bars from lying on top of the other error bars. |
| In the text | |
 |
Fig. 8. Confusion matrix of the transferred ASAS model. Labels are the same as in Table 4. |
| In the text | |
 |
Fig. 9. Confusion matrix of the transferred HIPPARCOS model. Labels are the same as in Table 5. |
| In the text | |
 |
Fig. 10. Confusion matrix of the transferred ASAS-SN model. Labels are the same as in Table 7. |
| In the text | |
 |
Fig. 11. Examples of the ASAS-SN validation-set Mc of the scratch models (blue line) and the every-layer models (orange line). As the figure shows, transferring the UT model reaches the highest Mc faster than training from scratch does. |
| In the text | |
 |
Fig. 12. Classification quality, Mc, of the resampled ASAS light curves as a function of duration, d (horizontal axis), and the number of data points, n (different lines), in the light curve. Left: Mc of the transferred model. Right: Mc of the U model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



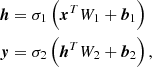
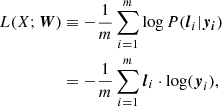
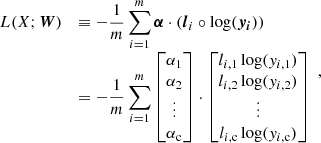
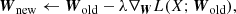
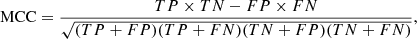
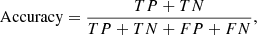
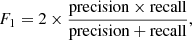
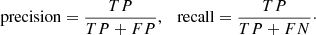
![$$ \begin{aligned} \mathrm{MCC} =&\left[ \sum _k \sum _l \sum _m C_{kk} C_{lm} - C_{kl} C_{mk} \right]\nonumber \\& \times \left[ \sum _k \left( \sum _l C_{kl} \right) \left( \sum _{k^\prime | k^\prime \ne k} \sum _{l^\prime } C_{k^\prime l^\prime } \right) \right]^{- \frac{1}{2}}\nonumber \\& \times \left[ \sum _k \left( \sum _l C_{lk} \right) \left( \sum _{k^\prime | k^\prime \ne k} \sum _{l^\prime } C_{l^\prime k^\prime } \right) \right]^{-\frac{1}{2}}. \end{aligned} $$](/articles/aa/full_html/2021/09/aa40369-21/aa40369-21-eq10.gif)