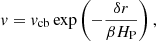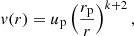EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 652 (August 2021) A&A, 652 (2021) A100 Full HTML
Free Access
Issue
A&A
Volume 652, August 2021
Article Number A100
Number of page(s) 7
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202141173
Published online 17 August 2021

© ESO 2021

1. Introduction

Understanding the cosmic origin of fluorine is one of the most interesting topics in the field of nuclear astrophysics. The production of its sole stable isotope, 19F, largely depends on the physical conditions characterizing stellar interiors. The primary source of fluorine in the Universe is currently widely debated, and several sites have been proposed as potential candidates: asymptotic gaint branch (AGB) stars (Forestini et al. 1992), rapidly rotating massive stars (Limongi & Chieffi 2018), Wolf–Rayet stars (Meynet & Arnould 2000), core-collapse supernovae (Woosley & Haxton 1988), and novae (José & Hernanz 1998). While the contributions from many of these sources are required to explain the galactic chemical evolution of fluorine abundance (see, e.g., Meynet & Arnould 2000; Renda et al. 2004; Kobayashi et al. 2011; Spitoni et al. 2018; Prantzos et al. 2018; Olive & Vangioni 2019; Grisoni et al. 2020), the only direct observation of fluorine production is provided by spectroscopic findings of photospheric [F/Fe] enhancements in intrinsic AGB carbon stars (Jorissen et al. 1992; Abia et al. 2009, 2010, 2011, 2019) and metal-poor extrinsic stars (Lucatello et al. 2011; Abia et al. 2019).

Asymptotic giant branch stars consist of a degenerate C-O core surrounded by a He-shell and a H-shell that are separated by a He-rich intermediate zone (He-intershell), and an extended convective envelope. Recurrently, on a timescale of tens of thousands of years of quiescent H-shell burning, the He-burning shell becomes thermally unstable. The large amount of energy released during this thermal pulse (TP), mainly due to the triple-α reaction, induces convective motions throughout the He-intershell and causes an expansion and thus a cooling of the H-burning shell. As a consequence, the latter is switched off until the star contracts, and the rising temperature is high enough to reignite it. This process repeats until the complete erosion of the envelope by stellar winds. It characterizes the thermally pulsing AGB (TP-AGB) phase of these stars (e.g., Iben & Renzini 1983). During the expansion of the envelope, convection may penetrate deep into the H-He discontinuity beyond the H-burning shell and carry fresh products of the nucleosynthesis to the surface. This phenomenon is known as third dredge-up (TDU). At each TDU episode, protons are partially mixed from the envelope into the He-intershell, and as the H-burning shell reignites, they are captured by the abundant 12C nuclei to produce a 13C-enriched layer, the so-called 13C pocket. 13C nuclei are then efficiently burned through the 13C(α, n)16O reaction at T ≈ 9 × 107 K (see Cristallo et al. 2018 and references therein) and so produce the free neutrons necessary for the synthesis of heavy elements in low-mass AGB stars (M ≲ 3 M⊙) through the so-called s(low)-process (see Busso et al. 1999; Herwig 2005; Straniero et al. 2006; Karakas & Lattanzio 2014 for reviews). A second neutron burst is driven by the 22Ne(α, n)25Mg reaction, which is efficiently activated at the base of the convective zone produced by a TP when the temperature reaches about 3 × 108 K (mostly in more massive AGBs; see, e.g., Karakas & Lattanzio 2014).

During the interpulse phase, part of the neutrons released within the He-intershell are captured by 14N through the 14N(n, p)14C reaction to synthesize 15N by means of the chain 14C(α, γ)18O(p, α)15N. 15N is then burnt to primary 19F through the 15N(α, γ)19F reaction in the subsequent convective TP (Goriely & Mowlavi 2000; Lugaro et al. 2004; Cristallo et al. 2014). An additional contribution to fluorine production comes from secondary 13C and 14N synthesized in the H-burning ashes and from the eventual unburnt 13C in the pocket (Cristallo et al. 2009a). In both cases, 13C is engulfed in the convective shell generated by the TP and produces further secondary 19F through the same reaction chains. Fluorine is then carried to the surface by convective motions during the TDU. Therefore its envelope abundance is expected to be correlated with the abundances of carbon and s-process elements (see Abia et al. 2019 and references therein).

One of the most debated topics in AGB modeling is the formation of the 13C pocket. The solution to this problem is strictly connected to a deep understanding of the physical processes governing mass-exchange at the interface of the convective envelope and the radiative core. Latest research has focused on studying nonconvective transport mechanisms that are usually ignored by the canonical theory of stellar structure and evolution. Different types of additional transport processes were invoked for the penetration of proton-rich material from the convective envelope into the He-intershell: convective overshoot (Herwig et al. 1997), opacity-induced overshoot (Cristallo et al. 2009a, 2011, 2015b), mixing induced by rotation (Herwig et al. 2003; Siess et al. 2004; Piersanti et al. 2013) or internal gravity waves (Denissenkov & Tout 2003; Battino et al. 2016), and mixing induced by magnetic buoyancy (Trippella et al. 2014, 2016). Focusing on the production of fluorine, it was suggested that a mechanism leading to the formation of an extended 13C pocket and at the same time, to a small amount of 14N, could solve the problem of 19F overproduction with respect to s-elements in low-mass metal-poor objects (Abia et al. 2019).

Post-process neutron-capture models for AGB stars in which the formation of the required 13C reservoir is ascribed to mixing induced by magnetic buoyancy were shown to be able to account for the solar distributions of s-only isotopes (Trippella et al. 2016), isotopic ratios of s-elements measured in presolar SiC grains (Palmerini et al. 2018), and for a large part of the abundance observations in evolved low-mass stars (Busso et al. 2021). The theory of mixing triggered by magnetic buoyancy developed by Nucci & Busso (2014) was used for this. The latter has recently been adopted by Vescovi et al. (2020), who contextualized magnetic mixing in the more complex framework of FRUITY stellar evolutionary models, obtaining a satisfactory fit to presolar grain isotopic ratios. The same stellar models also provide a consistent explanation for the observed yttrium abundance trends in the inner region of the Galactic disk (Magrini et al. 2021). FRUITY magnetic models predict that deep profiles of low proton abundances are generated below the convective envelope border. The low proton concentration severely limits local 14N formation because protons are almost entirely consumed for the synthesis of 13C, thereby affecting 19F production as well.

We investigate fluorine nucleosynthesis in low-mass AGB stars by computing a new series of stellar models accounting for the formation of a 13C pocket induced by magnetic buoyancy. The structure of the paper is as follows. In Sect. 2 we present the stellar evolutionary code, the nuclear network, and the mixing algorithm adopted to calculate the AGB models. In Sect. 3 we compare our models with available F spectroscopic abundances in a sample of Galactic and extragalactic AGB carbon stars, as well as with other metal-poor Ba-type and CH-type evolved stars. Finally, we summarize our conclusions in the last section.

2. Stellar models

The stellar models presented in this work were computed using the FUNS code (see Straniero et al. 2006 and references therein) by following the chemical evolution of approximately 500 isotopes (from hydrogen to bismuth) linked by more than 800 reactions (charged-particle reactions, neutron captures, and β-decays). The baseline nuclear network is essentially the same as was described in Cristallo et al. (2009a), with the addition of some recently updated reaction rates. In particular, the list of adopted reaction rates relevant to the nucleosynthesis of fluorine is reported in Table 1.

Table 1.

Reaction rates of relevance to fluorine nucleosynthesis.

For radiative opacities, we computed opacity tables by means of the OPAL Web tool1. At the low temperatures (log T ≤ 4.05) that are typical of the external layers of stars, we used the ÆSOPUS tool (Marigo & Aringer 2009), which includes molecular and atomic species relevant for AGB atmospheres to compute the opacity tables. In particular, ÆSOPUS allows taking changes in opacity into account that are due to eventual oxygen and α-enhancement (see Table 2) and to chemical composition variations in the envelope when the star becomes carbon rich (Marigo 2002; Cristallo et al. 2007; Ventura & Marigo 2010).

Table 2.

Initial mass, [Fe/H], total metallicity (including αO − Ca enhancements), and helium.

The opacity tables used in this work were calculated with the scaled-solar element distribution by Lodders (2020). Accordingly, a solar-calibrated value of the mixing length parameter αml = 1.86 was adopted (see Vescovi et al. 2019 for more details). Regarding the mass-loss rate, we adopted a Reimers formula with η = 0.4 for the pre-AGB evolution and the rate used by Abia et al. (2020) for the AGB phase (this rate is slightly different from that of Straniero et al. 2006 because they adopted recalculated bolometric corrections).

The surface enrichment of C and s-process elements in AGB stars is related to the complex coupling between convective mixing and nuclear processes. The problem of the neutron source in AGB stars, and in particular, the physical process driving the formation of a 13C pocket in the He-rich intershell, is still a matter of debate (see Sect. 1). In previous FRUITY models, the partial mixing of hydrogen from the envelope that is required to produce fresh 13C was accounted for by the so-called opacity-induced overshoot (Straniero et al. 2006; Cristallo et al. 2009a). This powers an additional mixing and the formation of a chemically smooth transition zone between the fully convective envelope and the radiative region. At the inner border of the convective envelope, the velocity of the descending material accelerated by convection is estimated as

v = v cb exp ( − δ r β H P ) , $$ \begin{aligned} { v} = { v}_{\rm cb} \, {\exp } \left(-\frac{\delta r}{\beta H_{\rm P}} \right), \end{aligned} $$(1)

where vcb is the velocity at the convective border, δr is the distance from the border, HP is the pressure scale height at the convective border, and β is a free parameter whose value was set to 0.1 in order to maximize the s-process production in low-mass AGB stars (see Cristallo et al. 2009a; Guandalini & Cristallo 2013). The free parameter β regulates the number of protons that is mixed beyond the bare convective border, and it also affects the TDU efficiency. In standard FRUITY models, the partially mixed zone is extended below the formal Schwarzschild convective boundary down to 2 HP (Straniero et al. 2006). Instead, in FRUITY Tail models (Cristallo et al. 2015a), the penetration limit is fixed to the layer where the convective velocity is 10−11 times lower than the value attained at the Schwarzschild border. The ensuing 13C pockets were shown to be remarkably larger than those obtained in standard FRUITY models, which results in a substantial increase in surface s-process enrichment.

Vescovi et al. (2020) found that when updated physical inputs are included, the slope of the exponential decline of convective velocities has to be reduced to β = 0.025 to avoid altering the efficiency of the TDU and obtain a sizable amount of dredged-up material. However, models computed with this parameter choice show additional mixing that is so inefficient to almost inhibit the production of s-process nuclei. Thus, mixing triggered by magnetic fields has been introduced as an additional mixing mechanism. Vescovi et al. (2020) assumed that a toroidal field is present in the radiative He-intershell at the beginning of the TDU and triggers the buoyant rise of magnetic flux tubes. As a consequence, a matter flow is pushed to the envelope. For mass conservation, this induces a matter downflow of H-rich material to the He-intershell that is required for the formation of the 13C pocket. The downflow velocity can be expressed as

v ( r ) = u p ( r p r ) k + 2 , $$ \begin{aligned} { v}(r) = u_{\rm p} \left(\frac{r_{\rm p}}{r} \right)^{k+2}, \end{aligned} $$(2)

where rp is the distance from the stellar center from which magnetic flux tubes, generated in the He-intershell, start to rise. rp can be identified from the critical toroidal Bφ necessary for the onset of magnetic buoyancy instabilities (Vescovi et al. 2020). k is the exponent quantifying the density decline, being ρ(r) ∝ rk, in the He-rich radiative layers below the convective envelope during a TDU, and it is typically lower than −3 (see also Busso et al. 2021). The identification of the critical field necessary for the occurrence of instabilities by magnetic buoyancy allows identifying the corresponding radial position rp from which magnetic structures arise. up is the effective starting buoyant velocity. The magnetized domains are rather fast and occupy only a small fraction of the total mass of the stellar layer (≃1/105; see, e.g., Busso et al. 2007; Trippella et al. 2016), thus transporting mass at a rate equal to assuming an effective buoyant velocity for all the material in the layer. Vescovi et al. (2020) found that most of the heavy-element isotope ratios measured in presolar SiC grains from AGB stars are consistently explained by stellar AGB models computed with a unique choice for the toroidal field strength and the initial buoyant velocity, namely Bφ = 5 × 104 G and up = 5 × 10−5 cm s−1. Nonetheless, we expect a nontrivial mass-metallicity dependence of the mixing triggered by magnetic buoyancy (as for other type of mixing; see, e.g., Joyce & Chaboyer 2018; Battino et al. 2021). In particular, the toroidal field strength is determined by the differential rotation profile established in the He-intershell that amplifies the magnetic field through dynamo action (see Sect. 4). In this framework, the compactness of a star at the pre-AGB and AGB stages is a fundamental property that affects the dynamo process and the following mixing induced by magnetic buoyancy. The stellar models presented here have H-exhausted core masses at the beginning of the TP-AGB phase very similar to the 2 M⊙ close-to-solar metallicity models presented in Vescovi et al. (2020). We therefore adopted for all the computed models their parameter choice for Bφ and up without further adjustments. We defer the analysis of the dependence of the magnetic mixing on the stellar core mass to a future work.

3. Results and discussion

In the following, we compare literature data and new FRUITY magnetic models. To do this, we adopted data from previous studies of intrinsic AGB carbon stars (Abia et al. 2010, 2011, 2015, 2019) and extrinsic CH/Ba stars (Lucatello et al. 2011). In Fig. 1 we report the [F/Fe] ratios of our selected sample as a function of the iron content [Fe/H]. We plot four group data: galactic (N-type) carbon stars, SC-type stars, extragalactic carbon stars, and extrinsic CH/Ba stars. Observational data are compared with stellar models of 1.5 M⊙ and 2 M⊙ at different TPs. Within the observational errors there is a good agreement, confirming the expected F-enhancement trend with the metallicity (see e.g. Lugaro et al. 2004; Cristallo et al. 2014). One word of caution has to be used regarding fluorine abundances in extrinsic CH/Ba stars, for which [F/Fe] ratios only represent lower limits due to dilution effects of binary mass-transfer phenomena (Abia et al. 2019).

thumbnail Fig. 1.

Comparison of observed [F/Fe] ratios as a function of the metallicity and FRUITY magnetic models. Symbols refer to the four data groups: circles represent galactic carbon stars, triangles show SC-type stars, squares stand for extragalactic carbon stars, and pentagons show extrinsic CH/Ba stars. The lines represent theoretical predictions for 2 (for [Fe/H] ≥ −0.7) and 1.5 M⊙ (for [Fe/H] < −0.7) AGB stars at different TPs. A typical error bar is indicated.

The top panel of Fig. 2 shows the comparison between theoretical predictions of FRUITY magnetic models with initial mass M = 2 M⊙ and [Fe/H] ≥ −0.4 and spectroscopic observations for [F/Fe] ratios versus the average s-element enhancement. Four observational indices are commonly used to represent s-process distributions and overabundances: [ls/Fe] (representative of the first s-process peak), [hs/Fe] (representative of the second s-process peak), [s/Fe], and [hs/ls]. Given the inhomogeneity of the available elemental abundance of heavy s-elements for the selected sample, we used the mean of the relative abundances of only Y and Zr to express the ls-index, and Ba and La to express the hs-index. The difference between the hs- and the ls-index quantifies the s-element index [hs/ls], while the total average s-element enhancement is given by the mean of the relative abundances of Y, Zr, Ba, and La. For close-to-solar metallicity galactic N-type carbon stars (dots) and SC-type stars (triangles), the observed increase in fluorine with s-element enhancement is well reproduced by theoretical models. The predicted [F/Fe] are always positive because 19F is overall produced in low-mass AGB stars (see also Lugaro et al. 2004). On the other hand, a few observational data show negative values that are still consistent within the errors with no fluorine production, however. The comparison with N-type and extrinsic CH/Ba type stars (pentagon) with [Fe/H] < −0.2 is more challenging because less information is available at these metallicities. In particular, two out of the three stars appear to exhibit the same trend as is observed at higher metallicity and agree well with theoretical predictions, while the fluorine and s-elements abundances derived for TX Psc are slightly out of the trend and are not fully reproduced by stellar models. This interpretation is confirmed even when [F/s] ratios are considered (see the bottom panel of Fig. 2). This index shows that the fluorine enhancement for the extrinsic stars is not affected by the uncertainties related to the dilution factor and provides a more robust tool for comparison. Confirming the previous analysis, models are able to replicate the quasi-linear decreasing trend of [F/s] with the surface s-process enrichment, except for the marginally outside TX Psc. Given the typical uncertainties affecting observational data, however, it is difficult to firmly conclude that model predictions and observations disagree for this single star.

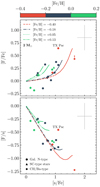thumbnail Fig. 2.

Observed [F/Fe] (top panel) and [F/s] (bottom panel) vs. average s-element enhancements compared with theoretical predictions for 2 M⊙ and close-to-solar metallicity models. Symbols are the same as in Fig. 1. Data points and theoretical lines are color-coded by [Fe/H]. The continuous portion of the lines represents the theoretical C-rich phase, and the discontinuous portion represents the O-rich phase. Typical uncertainties are shown. See text for details.

In our computations we used the 13C(α, n)16O reaction rate provided by Trippella & La Cognata (2017), which combined the latest asymptotic normalization coefficient values and the Trojan horse method, to determine the astrophysical S-factor with a indirect approach. At the typical temperature of ∼90 MK corresponding to the radiative 13C burning phase, the most recent direct measurement, given by Heil et al. (2008), is almost 20% higher. Adopting this rate has no effect on the production of s-nuclei if the 13C pocket is fully consumed during the interpulse period (see also Trippella & La Cognata 2017), however. Instead, if some amount of 13C survives due to the lower reaction rate, it will be swallowed by the convective shell generated by the following TP and burnt at a rather high temperature (∼200 MK). This provides an additional neutron burst and possibly affects the production of s-nuclei and 19F. This burst was shown to occur only during the very first TPs in low-mass AGB stars with high metallicity (Z ≥ 0.01; see Cristallo et al. 2009a; Karakas 2010). In our 2 M⊙Z = 0.02 model, switching from the Trippella & La Cognata (2017) to the Heil et al. (2008) reaction rate produces variations of less than 3% in the [F/Fe], [ls/Fe], and [hs/Fe] indexes, which is much lower than the typical uncertainties affecting spectroscopic observations of s-process-rich stars. Stellar models of lower metallicity are expected to produce even minor variations (Cristallo et al. 2009a; Karakas 2010) unless their mass and metallicity are so low (M ≲ 1.3 M⊙ and [Fe/H] ≲ −2.5) that they experience a proton ingestion episode at the first fully developed TP (see Cristallo et al. 2009b; Campbell et al. 2010; Choplin et al. 2021).

In Figs. 3 and 4 we perform a similar comparison at low metallicities. Because there is no homogeneous sample of stars with both Ba and La, we compared the model predictions separately. For both figures, we present in different panels theoretical expectations from new “FRUITY Magnetic” models (top panels), from standard “FRUITY” models (middle panels) and from “FRUITY Tail” models (bottom panels). Magnetic models are capable of reproducing the observed spread well at different metallicities for the [F/Ba] and [F/La] ratios as a function of the corresponding overall s-process enhancement. Conversely, standard FRUITY models fail in reproducing both the Ba and La enrichment, as well as the [F/Ba] and [F/La] ratios. Finally, FRUITY Tail models are sufficiently enriched in s-elements because the 13C pockets are larger than those obtained in standard FRUITY models, but they still show a systematic overproduction of fluorine with respect to Ba and La. As a whole, FRUITY magnetic models show a reduction of fluorine production that agrees well with spectroscopic observations for low-metallicity stars.

thumbnail Fig. 3.

[F/Ba] vs. [Ba/Fe] in the sample stars with [Fe/H] ≤ −1.0. The squares show extragalactic carbon stars, and the pentagons represent extrinsic CH/Ba stars. The lines are theoretical predictions for 1.5 M⊙ TP-AGB stars with low metallicity, assuming different mechanisms for the formation of the 13C pocket (see text for details). At these low metallicities, theoretical AGB models predict that the star becomes C-rich from first TDU episodes. Data points and theoretical lines are color-coded by [Fe/H]. Typical error bars are indicated.

thumbnail Fig. 4.

Same as Fig. 3, but for [F/La] vs. [La/Fe].

As previously mentioned, 19F is primarily synthesized in AGB stars through the 15N(α, γ)19F reaction reaction in the convective zone generated by a TP. The production of 15N in the He-intershell involves a complex nuclear chain of successive n- (or p-) and α–captures starting from 13C nuclei. A first source of 13C is represented by the 13C pocket itself, whose radiative burning leads to the accumulation of 15N. A second source is the 13C left in the H-burning shell ashes, which is engulfed in the convective zone generated by the TP and is rapidly burned through the 13C(α, n)16O reaction. In standard FRUITY models, the two channels contribute almost equally to the fluorine nucleosynthesis, especially at close-to-solar metallicity. On the other hand, at low metallicities, the contribution of 13C left in the H-burning ashes is lower (Cristallo et al. 2009a). Instead, in FRUITY Tail models, the larger 13C pockets guarantee a net increase of s-process abundances and a large fluorine decrease at fixed s-process surface enhancement (Abia et al. 2015). However, these models barely reach negative values for [F/Ba] and [F/La] (see the lower panels of Figs. 3 and 4), which indicates that fluorine production needs to be further suppressed without altering the s-process enrichment (see also Abia et al. 2019). The extended profile and the low proton abundance characterizing FRUITY magnetic models (Vescovi et al. 2020) have the twofold effect of forming large 13C pockets and reducing the formation of primary 14N. In this framework, the few available protons first produce 13C through the 12C(p, γ)13C reaction, preventing more proton captures from forming 14N and thereby inhibiting the nuclear chain 14N(n, p)14C(α, γ)18O(p, α)15N(α, γ)19F. Hence, any fluorine appearing in AGB envelopes in these models is of secondary nature, generated by 14N concentrations left behind by H-shell burning. This results in low fluorine enhancements and high s-enhancements, which places FRUITY magnetic models in close agreement with observations in very metal-poor AGB stars.

4. Conclusions

The fluorine production in low-mass AGB stars has been revisited in the light of upgraded FRUITY stellar models in which the 13C neutron source is related to phenomena induced by magnetic buoyancy. The predicted fluorine enhancements agree with those observed in carbon stars at different metallicities. The observed correlation between F and the s-element enhancements is also reproduced. On one hand, new FRUITY magnetic models show a reduced net 19F production with respect to models in which the partial mixing of hydrogen during a TDU is attributed to overshooting below the convective envelope of an AGB star. This is a consequence of the low abundance of 14N in the 13C pocket, which leads to a negligible production of fluorine during the 13C radiative burning. The 19F envelope abundance is therefore only ascribed to the amount of the secondary 13C in the H-shell ashes, which depends on the CNO abundances in the star. On the other hand, mixing induced by magnetic buoyancy leads to extended 13C pockets, which results in high surface s-process enrichments. As a whole, the new FRUITY magnetic models simultaneously account for the observed fluorine and the average s-element enhancements in intrinsic AGB carbon stars and extrinsic CH/Ba stars.

Different types of data (presolar grain measurements and spectroscopic observations) related to stars belonging to different components of our Galaxy (disk and halo) indicate a single configuration of mixing induced by magnetic buoyancy. This scenario suggests that magnetism probably also is a quite common phenomenon in evolved low-mass stars. In this respect, several observations of magnetic fields of a few G in the envelopes of AGB stars have been made (see, e.g., Vlemmings 2019 and references therein). Another piece of evidence for magnetic fields in low-mass stars is provided by the increasing number of observed magnetic white dwarfs (WDs). During the least decades, many WDs lying within 20 pc from the Sun were shown to have a field strength above ∼1 MG, while the available data were not sufficient to asses the presence or absence of a magnetic field for most of them. These studies suggested that about 10% of all WDs are magnetic (e.g., Kawka et al. 2007). However, the advent of increasingly precise spectroscopic and spectropolarimetric observations, which improve the capability of detecting magnetic fields of low strength, revealed that at least ∼20% of the WDs possess magnetic fields ranging from a few kG to about 1000 MG (Landstreet & Bagnulo 2019; Bagnulo & Landstreet 2020), indicating that magnetism is a widespread and not a rare property of WDs. These magnetic fields are most likely the remain of previous phases, and they may be the result of a complicated interaction between fossil and dynamo generated fields during stellar evolution and/or stellar merger events (Ferrario et al. 2020). In our scenario, we propose that below the extended convective envelope of low-mass AGB stars, strong toroidal magnetic fields exist and trigger a mixing induced by magnetic buoyancy that is adequate for the formation of the 13C pocket. The required mixing rate places constraints on the field strength. In this picture, the toroidal field is assumed to originate from a dynamo operating in the AGB interiors that amplifies a small seed poloidal field by draining the available differential rotation energy.

This study provides another independent confirmation (see Magrini et al. 2021) that the calibration performed by Vescovi et al. (2020) on the free parameters characterizing mixing induced by magnetic buoyancy is extremely robust. However, additional analyses are needed to validate this statement before we can claim a definitive theory.

Acknowledgments

DV and SC acknowledge S. Bagnulo for fruitful discussions. DV acknowledges financial support from the German-Israeli Foundation (GIF No. I-1500-303.7/2019). CA acknowledges financial support from the Agencia Estatal de Investigación of the Spanish Ministerio de Ciencia e Innovación through the FEDER founds projects PGC2018-095317-B-C2.

References

  1. Abia, C., Recio-Blanco, A., de Laverny, P., et al. 2009, ApJ, 694, 971 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abia, C., Cunha, K., Cristallo, S., et al. 2010, ApJ, 715, L94 [NASA ADS] [CrossRef] [Google Scholar]
  3. Abia, C., Cunha, K., Cristallo, S., et al. 2011, ApJ, 737, L8 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abia, C., Cunha, K., Cristallo, S., & de Laverny, P. 2015, A&A, 581, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Abia, C., Cristallo, S., Cunha, K., de Laverny, P., & Smith, V. V. 2019, A&A, 625, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Abia, C., de Laverny, P., Cristallo, S., Kordopatis, G., & Straniero, O. 2020, A&A, 633, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [Google Scholar]
  8. Bagnulo, S., & Landstreet, J. D. 2020, A&A, 643, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Battino, U., Pignatari, M., Ritter, C., et al. 2016, ApJ, 827, 30 [Google Scholar]
  10. Battino, U., Lederer-Woods, C., Cseh, B., Denissenkov, P., & Herwig, F. 2021, Universe, 7, 25 [NASA ADS] [CrossRef] [Google Scholar]
  11. Best, A., Pantaleo, F. R., Boeltzig, A., et al. 2019, Phys. Lett. B, 797, 134900 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bruno, C. G., Scott, D. A., Aliotta, M., et al. 2016, Phys. Rev. Lett., 117, 142502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  13. Bruno, C. G., Aliotta, M., Descouvemont, P., et al. 2019, Phys. Lett. B, 790, 237 [NASA ADS] [CrossRef] [Google Scholar]
  14. Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [Google Scholar]
  15. Busso, M., Wasserburg, G. J., Nollett, K. M., & Calandra, A. 2007, ApJ, 671, 802 [NASA ADS] [CrossRef] [Google Scholar]
  16. Busso, M., Vescovi, D., Palmerini, S., Cristallo, S., & Antonuccio-Delogu, V. 2021, ApJ, 908, 55 [Google Scholar]
  17. Campbell, S. W., Lugaro, M., & Karakas, A. I. 2010, A&A, 522, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Choplin, A., Siess, L., & Goriely, S. 2021, A&A, 648, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Cristallo, S., Straniero, O., Lederer, M. T., & Aringer, B. 2007, ApJ, 667, 489 [NASA ADS] [CrossRef] [Google Scholar]
  20. Cristallo, S., Straniero, O., Gallino, R., et al. 2009a, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cristallo, S., Piersanti, L., Straniero, O., et al. 2009b, PASA, 26, 139 [Google Scholar]
  22. Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
  23. Cristallo, S., Di Leva, A., Imbriani, G., et al. 2014, A&A, 570, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Cristallo, S., Abia, C., Straniero, O., & Piersanti, L. 2015a, ApJ, 801, 53 [NASA ADS] [CrossRef] [Google Scholar]
  25. Cristallo, S., Straniero, O., Piersanti, L., & Gobrecht, D. 2015b, ApJS, 219, 40 [Google Scholar]
  26. Cristallo, S., La Cognata, M., Massimi, C., et al. 2018, ApJ, 859, 105 [Google Scholar]
  27. D’Agata, G., Pizzone, R. G., La Cognata, M., et al. 2018, ApJ, 860, 61 [CrossRef] [Google Scholar]
  28. Denissenkov, P. A., & Tout, C. A. 2003, MNRAS, 340, 722 [NASA ADS] [CrossRef] [Google Scholar]
  29. Di Leva, A., Scott, D. A., Caciolli, A., et al. 2014, Phys. Rev. C, 89, 015803 [NASA ADS] [CrossRef] [Google Scholar]
  30. Ferrario, L., Wickramasinghe, D., & Kawka, A. 2020, Adv. Space Res., 66, 1025 [NASA ADS] [CrossRef] [Google Scholar]
  31. Forestini, M., Goriely, S., Jorissen, A., & Arnould, M. 1992, A&A, 261, 157 [NASA ADS] [Google Scholar]
  32. Goriely, S., & Mowlavi, N. 2000, A&A, 362, 599 [NASA ADS] [Google Scholar]
  33. Grisoni, V., Romano, D., Spitoni, E., et al. 2020, MNRAS, 498, 1252 [CrossRef] [Google Scholar]
  34. Guandalini, R., & Cristallo, S. 2013, A&A, 555, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Heil, M., Detwiler, R., Azuma, R. E., et al. 2008, Phys. Rev. C, 78, 025803 [NASA ADS] [CrossRef] [Google Scholar]
  36. Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
  37. Herwig, F., Langer, N., & Lugaro, M. 2003, ApJ, 593, 1056 [NASA ADS] [CrossRef] [Google Scholar]
  38. Herwig, F., Bloecker, T., Schoenberner, D., & El Eid, M. 1997, A&A, 324, L81 [NASA ADS] [Google Scholar]
  39. Iben, I., Jr., & Renzini, A. 1983, ARA&A, 21, 271 [NASA ADS] [CrossRef] [Google Scholar]
  40. Iliadis, C., Longland, R., Champagne, A. E., Coc, A., & Fitzgerald, R. 2010, Nucl. Phys. A, 841, 31 [NASA ADS] [CrossRef] [Google Scholar]
  41. Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Indelicato, I., La Cognata, M., Spitaleri, C., et al. 2017, ApJ, 845, 19 [NASA ADS] [CrossRef] [Google Scholar]
  43. Johnson, E. D., Rogachev, G. V., Mitchell, J., Miller, L., & Kemper, K. W. 2009, Phys. Rev. C, 80, 045805 [CrossRef] [Google Scholar]
  44. Jorissen, A., Smith, V. V., & Lambert, D. L. 1992, A&A, 261, 164 [NASA ADS] [Google Scholar]
  45. José, J., & Hernanz, M. 1998, ApJ, 494, 680 [NASA ADS] [CrossRef] [Google Scholar]
  46. Joyce, M., & Chaboyer, B. 2018, ApJ, 856, 10 [Google Scholar]
  47. Karakas, A. I. 2010, MNRAS, 403, 1413 [Google Scholar]
  48. Karakas, A. I., & Lattanzio, J. C. 2014, PASA, 31, e030 [NASA ADS] [CrossRef] [Google Scholar]
  49. Kawka, A., Vennes, S., Schmidt, G. D., Wickramasinghe, D. T., & Koch, R. 2007, ApJ, 654, 499 [NASA ADS] [CrossRef] [Google Scholar]
  50. Kobayashi, C., Izutani, N., Karakas, A. I., et al. 2011, ApJ, 739, L57 [NASA ADS] [CrossRef] [Google Scholar]
  51. Landstreet, J. D., & Bagnulo, S. 2019, A&A, 628, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Leblanc, P. J., Imbriani, G., Görres, J., et al. 2010, Phys. Rev. C, 82, 055804 [NASA ADS] [CrossRef] [Google Scholar]
  53. Limongi, M., & Chieffi, A. 2018, ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
  54. Lodders, K. 2020, Solar Elemental Abundances (Oxford: Oxford University Press) [Google Scholar]
  55. Lucatello, S., Masseron, T., Johnson, J. A., Pignatari, M., & Herwig, F. 2011, ApJ, 729, 40 [NASA ADS] [CrossRef] [Google Scholar]
  56. Lugaro, M., Ugalde, C., Karakas, A. I., et al. 2004, ApJ, 615, 934 [NASA ADS] [CrossRef] [Google Scholar]
  57. Magrini, L., Vescovi, D., Casali, G., et al. 2021, A&A, 646, L2 [EDP Sciences] [Google Scholar]
  58. Marigo, P. 2002, A&A, 387, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Marigo, P., & Aringer, B. 2009, A&A, 508, 1539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Meynet, G., & Arnould, M. 2000, A&A, 355, 176 [NASA ADS] [Google Scholar]
  61. Nucci, M. C., & Busso, M. 2014, ApJ, 787, 141 [NASA ADS] [CrossRef] [Google Scholar]
  62. Olive, K. A., & Vangioni, E. 2019, MNRAS, 490, 4307 [CrossRef] [Google Scholar]
  63. Palmerini, S., Trippella, O., Busso, M., et al. 2018, Geochim. Cosmochim. Acta, 221, 21 [NASA ADS] [CrossRef] [Google Scholar]
  64. Piersanti, L., Cristallo, S., & Straniero, O. 2013, ApJ, 774, 98 [NASA ADS] [CrossRef] [Google Scholar]
  65. Prantzos, N., Abia, C., Limongi, M., Chieffi, A., & Cristallo, S. 2018, MNRAS, 476, 3432 [Google Scholar]
  66. Renda, A., Fenner, Y., Gibson, B. K., et al. 2004, MNRAS, 354, 575 [NASA ADS] [CrossRef] [Google Scholar]
  67. Siess, L., Goriely, S., & Langer, N. 2004, A&A, 415, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Spitoni, E., Matteucci, F., Jönsson, H., Ryde, N., & Romano, D. 2018, A&A, 612, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Straniero, O., Gallino, R., & Cristallo, S. 2006, Nucl. Phys. A, 777, 311 [NASA ADS] [CrossRef] [Google Scholar]
  70. Trippella, O., & La Cognata, M. 2017, ApJ, 837, 41 [NASA ADS] [CrossRef] [Google Scholar]
  71. Trippella, O., Busso, M., Maiorca, E., Käppeler, F., & Palmerini, S. 2014, ApJ, 787, 41 [NASA ADS] [CrossRef] [Google Scholar]
  72. Trippella, O., Busso, M., Palmerini, S., Maiorca, E., & Nucci, M. C. 2016, ApJ, 818, 125 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  73. Ventura, P., & Marigo, P. 2010, MNRAS, 408, 2476 [NASA ADS] [CrossRef] [Google Scholar]
  74. Vescovi, D., Piersanti, L., Cristallo, S., et al. 2019, A&A, 623, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Vescovi, D., Cristallo, S., Busso, M., & Liu, N. 2020, ApJ, 897, L25 [Google Scholar]
  76. Vlemmings, W. 2019, IAU Symp., 343, 19 [NASA ADS] [Google Scholar]
  77. Wallner, A., Bichler, M., Buczak, K., et al. 2016, Phys. Rev. C, 93, 045803 [NASA ADS] [CrossRef] [Google Scholar]
  78. Woosley, S. E., & Haxton, W. C. 1988, Nature, 334, 45 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Reaction rates of relevance to fluorine nucleosynthesis.

In the text
Table 2.

Initial mass, [Fe/H], total metallicity (including αO − Ca enhancements), and helium.

In the text

All Figures

thumbnail Fig. 1.

Comparison of observed [F/Fe] ratios as a function of the metallicity and FRUITY magnetic models. Symbols refer to the four data groups: circles represent galactic carbon stars, triangles show SC-type stars, squares stand for extragalactic carbon stars, and pentagons show extrinsic CH/Ba stars. The lines represent theoretical predictions for 2 (for [Fe/H] ≥ −0.7) and 1.5 M⊙ (for [Fe/H] < −0.7) AGB stars at different TPs. A typical error bar is indicated.
In the text
thumbnail Fig. 2.

Observed [F/Fe] (top panel) and [F/s] (bottom panel) vs. average s-element enhancements compared with theoretical predictions for 2 M⊙ and close-to-solar metallicity models. Symbols are the same as in Fig. 1. Data points and theoretical lines are color-coded by [Fe/H]. The continuous portion of the lines represents the theoretical C-rich phase, and the discontinuous portion represents the O-rich phase. Typical uncertainties are shown. See text for details.
In the text
thumbnail Fig. 3.

[F/Ba] vs. [Ba/Fe] in the sample stars with [Fe/H] ≤ −1.0. The squares show extragalactic carbon stars, and the pentagons represent extrinsic CH/Ba stars. The lines are theoretical predictions for 1.5 M⊙ TP-AGB stars with low metallicity, assuming different mechanisms for the formation of the 13C pocket (see text for details). At these low metallicities, theoretical AGB models predict that the star becomes C-rich from first TDU episodes. Data points and theoretical lines are color-coded by [Fe/H]. Typical error bars are indicated.
In the text
thumbnail Fig. 4.

Same as Fig. 3, but for [F/La] vs. [La/Fe].
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.