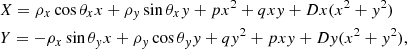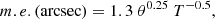| Issue |
A&A
Volume 652, August 2021
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 16 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202140472 | |
| Published online | 30 July 2021 | |
The NAROO digitization center
Overview and scientific program
1
Institut Polytechnique des Sciences Avancées IPSA, 63 bis Boulevard de Brandebourg, 94200 Ivry-sur-Seine, France
e-mail: vincent.robert@obspm.fr, vincent.robert@ipsa.fr
2
IMCCE, Observatoire de Paris, PSL Research University, CNRS UMR 8028, Sorbonne Universités, UPMC, Univ. Lille 1, 77 avenue Denfert- Rochereau, 75014 Paris, France
3
GEPI, Observatoire de Paris, PSL Research University, CNRS UMR 8111, Sorbonne Universités, Université de Paris, 5 place Jules Janssen, 92195 Meudon, France
4
LESIA, Observatoire de Paris, PSL Research University, CNRS UMR 8109, Sorbonne Universités, Université de Paris, 5 place Jules Janssen, 92195 Meudon, France
5
Université Nice Côte d’Azur, Observatoire de la Côte d’Azur, Service Culture et Patrimoine, CNRS UMS2202, Nice, France
6
SAF, Société Astronomique de France, 3 rue Beethoven, 75016 Paris, France
7
OSU Institut Pythéas, Observatoire de Haute-Provence, 04870 Saint-Michel-l’Observatoire, France
8
Central Astronomical Observatory, Russian Academy of Sciences, 65/1 Pulkovskoye Chaussee, St. Petersburg 196140, Russia
9
SYRTE, Observatoire de Paris, PSL Research University, CNRS UMR 8630, Sorbonne Universités, LNE, 61 avenue de l’Observatoire, 75014 Paris, France
10
United States Naval Observatory USNO (retired), 3458 Massachusetts Ave NW, Washington, DC 20392, USA
11
LUTH, Observatoire de Paris, PSL Research University, CNRS UMR 8102, Sorbonne Universités, Université de Paris, 5 place Jules Janssen, 92195 Meudon, France
12
Université Nice Côte d’Azur, Observatoire de la Côte d’Azur, Laboratoire Lagrange, CNRS UMR7293, Nice, France
13
LERMA, Observatoire de Paris, PSL Research University, CNRS UMR 8112, Sorbonne Universités, Université de Paris, 61 avenue de l’Observatoire, 75014 Paris, France
Received:
1
February
2021
Accepted:
21
April
2021
The New Astrometric Reduction of Old Observations (NAROO) center can be found at the Paris Observatory in Meudon, and it is dedicated to the measurement of astrophotographic plates and the analysis of old observations. The NAROO digitizer consists of a granite-based Newport-Microcontrol open-frame air-bearing XY positioning table, a scientific sCMOS camera, and a telecentric optical system. The plate holder assembly is suited for mounting glass plates up to 350 mm squared. The machine positioning stability is better than 15 nm, and its repeatability is better than 40 nm. With real photographic plate data, we were able to produce measurements with an accuracy better than 65 nm. The renewed interest about photographic plates concerns the expansion of the database of transient objects evolving in time, since digitization now makes it possible to measure images with a high level of accuracy and to identify all the available objects. The information extracted from such materials can be of an astrometric, photometric, and spectroscopic nature, when not purely imaging, with consequences in planetology, near-Earth asteroid risk assessment, astrophysical phenomena, and general relativity, to mention but a few. Through our scientific program in the Gaia era, we detail examples of current and upcoming uses for the community. We invite researchers to use our facilities and digitize their collection by answering our call for proposals.
Key words: instrumentation: high angular resolution / techniques: image processing
© V. Robert et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
This paper introduces the current New Astrometric Reduction of Old Observations (NAROO) digitization center and its hardware, operation, and scientific program. The center represents a project resulting from the work of researchers of the Institut de Mécanique Céleste et de Calcul des Éphémérides (IMCCE) and Institut Polytechnique des Sciences Avancées (IPSA). It is not part of any preservation or archiving effort since it is mainly dedicated to science with the measurement of astrophotographic plates and the analysis of old observations. The first measurements for astrometry and spectroscopy are in progress, and results will be presented in respective upcoming papers. The first digitization call for proposals is scheduled for publication in May 2021 via our project website1.
Studying the dynamics of Solar System bodies, in particular, requires astrometric observations sampled over a long time span to quantify the long period terms which may help to analyze the evolution of the motion. Searching for old data is obviously useful for this purpose, and since we have demonstrated that a precise digitization and a new astrometric reduction of old photographic plates could provide very accurate positions (Robert et al. 2011, 2015, 2016), researchers involved in various scientific topics began to (re-)consider such materials. As a consequence, the Paris Observatory decided to acquire such an instrument and to build a scientific community for its exploitation. The NAROO machine has been installed and housed in a temperature- and humidity-stabilized ISO-5 clean room with adjacent archive room. It can digitize photographic plates up to 350 mm squared on glass plates, and is able to process all known transparent photographic plate material automatically. Almost all kinds of celestial bodies have been observed with photographic plates since 1890: natural satellites, planets, Solar System small bodies, stars, galaxies, and nebula. Renewed interest about such materials concerns the broadening of transient object databases, which evolve with time, since digitization now makes it possible to measure images with a high level of accuracy and to identify all the available objects. The information extracted from such materials can be of astrometric, photometric and spectroscopic nature, when not purely imaging, with consequences in planetology, near-Earth asteroids risk assessment, astrophysical phenomena, and general relativity, to mention but a few.
In Sect. 2 of this paper, we present details on the current NAROO machine hardware and digitization process, while Sect. 3 describes the calibration steps with real data. Section 4 deals with improvements in astrometric accuracy, and Sect. 5 presents details about the very first, current and upcoming scientific uses of the center, which are examples for the community and may lead to interactions between researchers. Section 6 summarizes technical performances of the digitizer and provides information about our call for proposals, which is accessible to the whole community.
2. NAROO features
2.1. Hardware
Figure 1 shows the NAROO digitizer as of April 2020. The machine consists of a granite-based Newport-Microcontrol open-frame and air-bearing XY positioning table, with a plate holder assembly suited for mounting glass plates up to 350 mm squared. The NAROO machine is able to process almost all known transparent photographic plate materials automatically.
 |
Fig. 1. NAROO machine at the Paris Observatory, Meudon. |
The granite base measures 1.3 m × 1.3 m × 0.2 m. It is mounted on dynamic feet to compensate for the building and environment vibrations. The position of the XY-table is read by Heidenhain encoders with an accuracy better than 2 nm. The linearity and orthogonality of XY-axes were calibrated by Newport-Microcontrol using a laser interferometer. The local XY-table positioning was measured by the manufacturer with a capacitance up to 7 nm. The repeatability, how closely the XY-table can return to an initial position following movement over the entire XY-axes, was also measured by the manufacturer with a capacitance up to 40 nm. These results are even better than those previously obtained from the StarScan machine at USNO (Zacharias et al. 2008), and the DAMIAN machine at ROB (Robert et al. 2011). In order to reach and maintain a high geometric and radiometric accuracy, the digitizer is placed in an overpressure, air-conditioned, ISO-5 clean room, at a temperature of 20 °C ± 0.1 °C and a relative humidity of 50% RH ± 5% RH.
The optical unit consists of an Andor Neo sCMOS Camera, mounted on a VST VS-TCM-130/S telecentric 1:1 objective. This system is attached to the Z-axis above the XY-table. The photographic plates are illuminated from below with light emitting diodes (LEDs), controlled by a high-precision DC power supply. We paid particular attention to the complete optical system which was specifically designed by the instrumentation pole of the Paris Observatory to evenly illuminate the plate and avoid vignetting. The 2D sCMOS Camera generates images with 2560 by 2160 pixels of 6.5 μm by 6.5 μm. The maximum dynamic range is 30 000:1. Each frame results in a 16-bit FITS file with 11 MB disk space. For instance, the digitization of a classical 5 by 7 inch Kodak plate requires about 1.2 GB of disk space, while that of a 350 mm squared Schmidt plate is up to 5.9 GB.
2.2. Lighting device
There are several ways to light photographic plates to digitize them. The first approach is to use a LED array located under the material, but the field would not have been homogeneous. A diffuser would have been necessary, and these light sources would have heated up the plates, affecting the position accuracy of the mobile carriage. Thus, we preferred to move the light source away from the XY-table. In order to be independent with regard to the homogeneity of the source, we chose an optical combination with two microlens arrays to ensure the homogeneity of the illuminated field. Actually, this system provides the same illumination homogeneity whether the light source is punctual or extended and homogeneous or not. Figure 2 shows the optical system designed by the instrumentation pole of the Paris Observatory for the NAROO machine. The incoming beam is sampled behind a first lens then a microlens array in sub-apertures, which are superimposed with a second microlens array before a second lens on the photographic material. First microlens array sees a small part of the beam small enough, so its illumination is considered homogeneous. Each point of the light source is spread over the entire illuminated field on the photographic plate so, whatever the emission of these points, the whole illuminated field is the sum of these source points. The size of the illuminated field depends on the focal length of the microlenses and that of the second lens in the system.
 |
Fig. 2. NAROO lighting optical scheme. |
The light source is a monochromatic LED emitting at the maximum of sensibility of the camera (590 nm). A condenser collects the light and collimates the beam. The microlenses and the collimator project the beam on the photographic plate. The lighting beam’s F number is adapted to that of the shooting lens. Figure 2 shows that even if the profile of the intensity beam is not homogeneous, the profile of the illumination field is.
2.3. Shooting lens
The Andor Neo sCMOS camera was mainly chosen for the size of its chip, with a field of view of about 16.6 by 14.0 mm squared. The magnification of the shooting lens depends on the number of photon tokens per plate (i.e. the integration time) and the desired spatial resolution. The chosen compromise is a magnification of −1. In addition, we chose a double telecentric lens to avoid the variation of magnification as a result of a focusing defect (non-flatness of the photographic plate). In fact, with a conventional objective, the field is an angular dimension, so the size of the image depends on the distance to the object. On the other hand, with a telecentric objective, the field is a linear dimension, so the size of the object and the distance to the object are independent. When the photographic material is not at the nominal distance from the lens, the image is blurred, but the gravity center does not move.
We studied a number of lenses and objectives with very little optical distortion below 10 nm, but we must state that such systems are very difficult to manufacture or expensive to buy. Thus, we chose the VS-TCM-130/S commercial objective made by VS Technology: the diameter of the field of view is 22 mm, so it covers that of the camera, and its F number is 6.25. The distance between the photographic material and the lens is 131 mm, and the announced distortion is 0.00% (see Sect. 3.2 for the estimation of the optical distortion with real data). The complete optical system integration is shown in Fig. 3.
 |
Fig. 3. NAROO opto-mechanical drawing. |
2.4. Digitization process
Most of the NAROO functions are computer controlled. Depending on their size, one or several photographic plates are put inside a plate holder that is mounted on the XY-table. At the beginning of each digitization process, the supports are automatically put into focus, with the emulsion facing up, by clamping the plate holder upward against the counterpressure rack. The illumination is set to 3/4 of the saturation on the plate’s sky background by adjusting the DC power supply unit to the LED. The plate is automatically digitized in step-and-stare mode with steps corresponding to user-defined moves in the X and Y directions. The local XY-table position is read by the Heidenhain encoders and inserted into the image header. After the plate digitization is complete, the XY-table automatically returns to its home position, and the plate holder is unclamped in anticipation of a new cycle. As a final product of digitization, an overall mosaic FITS image of the whole photographic plate is generated from the individual images with or without overlapping. Both mosaic and individual images are archived on a dedicated disk space.
The time needed to digitize a single classical 5 by 7 inches Kodak plate with about of 120 individual images is 5 min, taking into account the overall movement from the XY-table home position and return. That of a complete Schmidt plate with about 550 individual images is 22 min. Figures 4 and 5 show mean dark and mean flat frames, respectively, obtained by averaging 100 individual images taken at the same integration time of 0.2 s, which are used to correct the individual raw plate images. Images are taken with a camera temperature set to −35 ° C to minimize the dark current and ensure low noise. The camera is used with the global shutter readout mode. In particular, the mean flat image shows different defects. One can see a parasitic reflection in the mean flat frame (bottom left in the blue circle) of the microlenses used to homogenize the light beam. Optical simulations did not show such an effect inside the lighting device, so it probably comes from the shooting lens, but we do not have the optical scheme to verify this hypothesis. One can also see dust on the lenses of the shooting lens and dust on the glass before the detector. The lighting device using direct light is very sensitive to the problem of dust, but it gives a sharper image than diffused light. By the end, the mean flat image is maintained with 10% homogeneity. Figure 6 shows the first scientific image (positive) of the NAROO machine as of April 2019, with a 1975 USNO photographic plate of the Saturnian system.
 |
Fig. 4. NAROO mean dark image. Color values on the x-axis denote pixel ADU counts. |
 |
Fig. 5. NAROO mean flat image. Color values on the x-axis denote pixel ADU counts. A parasitic reflection of the microlenses is shown in the blue circle. |
 |
Fig. 6. First NAROO scientific image (positive): center of a 1975 USNO photographic plate of Saturn. The image of Saturn is seen through a neutral metallic Inconel film filter. |
3. Calibration
3.1. XY-table stability
Newport-Microcontrol provides tools for the user to check and control the XY-table operation, and Fig. 7 is a typical result of the machine’s stability control. In step-stare mode, the movement between images is up to about 16 mm. Following such a movement with a 300 mm s−1 velocity, it shows that the displacement is realized in about of 250 ms and that the machine needs 550 ms more to stabilize the new position with an accuracy better than 15 nm on the X-axis and 7 nm on the Y-axis. Here, one should note that the 7 nm local XY-table positionings that were measured by the manufacturer are independent unidirectional data. Thus, the difference in results between our measurements and the manufacturer’s on the X-axis, and the difference in results between our measurements on both axes are due to the XY-table design itself, because the X-axis is physically mounted on the Y-axis. As a consequence, the X-axis is more impacted by pitch and roll, which can also be seen in Fig. 7 since oscillations before complete stability on the X-axis are slightly higher. As a security measure, during the digitization process we used an extra delay of 300 ms before an image was acquired, to make sure that the XY-table was completely stabilized.
 |
Fig. 7. NAROO XY-table stability. Red line denotes a 16 mm movement on both X and Y axes. Green line denotes the machine compensation before X-axis stability, enlarged 1000 times. Blue line denotes the machine compensation before Y-axis stability, enlarged 1000 times. |
3.2. Camera mapping
The NAROO mapping parameters for the sCMOS pixel coordinates to global XY-table coordinates transformation are determined from real data by stepping a well-exposed star dot in the field of view of the digital camera. This makes it possible to correct for scales and orientations, for the second order tilt terms, and most importantly, for the third-order optical distortion term. We use the following functional model with seven-parameter third-order polynomials to calculate corrected X and Y plate coordinates as a function of x and y measured coordinates, with respect to the center of individual images:
where X and Y are the coordinates of a star dot in the XY-table plate axes with respect to the current position of the frame center, ρx and ρy are the scale factors on the XY-table plate axes, θx and θy are the orientations of the XY-table plate axes, p and q are the second-order tilt terms denoting tilts between the camera chip and the XY-table plate axes, and D is the third-order distortion term. Here, we chose a mapping functional model, by opposition with a general conventional model (de Vegt & Ebner 1974; Zacharias et al. 1992), so that the linear terms explicitly express the free unknowns that characterize the isotropy of the field of view through the scale factors, and its orthogonality through the orientation parameters, for comparison. There are no offset constant terms since the zero point of the transformation is arbitrary.
We developed a new program based on the MovingDot software (Winter 2008) for the alignment of the sCMOS camera with the axes of the XY-table, and for the calculation of a correct mapping model. After centering a star dot in the camera’s field of view, we moved the XY-table by steps of 0.65 mm (theoretically ≃100 pixels) on both X and Y axes, to compose a virtual dot calibration plate of the same object, resulting in the analysis of 525 images for the complete working area given by the sCMOS chip. We fitted the aimed star dot positions from each individual image and generated a table with the (xi, yi) star positions as functions of the (Xi, Yi) table positions. We then determined the seven parameters of Eq. (1) using a least-squares method.
We repeated the complete set of measures each week for six months, with many other plate measurements in between. We found the field of view to be isotropic with an error less than 5 nm, and orthogonal with an error less than 2.10−4 rad. We found the tilt terms to be insignificant, and we found a small contribution of the distortion term. Figure 8 shows the corrections of the optical distortion of the objective/camera unit below 0.01%, which is very low for a commercial objective, in the 2560 by 2160 pixels field of view of the camera as vectors scaled by a factor of 100; thus, the largest vector is about 1.0 μm long. The magnitude of the optical correction at the edges of the field of view is 0.8 μm on the X-axis and 0.6 μm on the Y-axis. The difference between the two is mainly due to the shape of the chip itself, which is not square.
 |
Fig. 8. Correction of the optical distortion in micrometers of the objective/camera unit, in the 2560 by 2160 pixels field of view of the camera, shown as vectors enlarged 100 times (the largest vector is about 1.0-μm long). |
More generally, the complete design of the NAROO optomechanical system is ideal for our needs, providing calibration results better than those previously obtained from comparable scientific machines. For instance, one should note that the maximum correction of the optical distortion is about of 65% that of the DAMIAN machine (Robert et al. 2011) but in our case, the usable field of view is four times larger. Lastly, at the same temperature and in the same humidity conditions, we found the mapping parameters to be stable to within 1σ of their individual formal errors.
3.3. Repeatability
According to the definition given by Zacharias et al. (2008), the comparison between various measurements of the same dot and in the same measurement orientation reflects the absolute repeatability of the NAROO machine. One can use even a dot calibration plate DCP or real photographic plate data, without any assumptions on the errors of the photographic material since the measurement conditions and methods used remain the same for the comparison set. For this purpose, we measured the USNO Praesepe cluster plate n°21004 of 1994 in four orientations (0°, 90°, 180°, and 270°) with exactly 145 star dots. We repeated the complete set of measurements each week for one month, with many other plate measurements in between. We used a linear transformation model between these four sets of measurements, and for each orientation, to give the rms-corrected table position differences in Table 1. The mean absolute repeatability is 66 nm on the x-axis and 60 nm on the y-axis. As explained in Sect. 3.1, the difference in results on both axes could be due to the XY-table design itself. Nevertheless, these results denote the overall accuracy of the NAROO machine with real photographic data.
Comparisons between four sets of measurements; 145 star dots on a USNO Praesepe cluster plate.
Finally, we divided the rms differences by 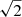 to estimate the absolute repeatability error of a single NAROO measure per coordinate, and we obtain 47 nm on the x-axis, and 42 nm on the y-axis. These results denote the limit of accuracy of the XY-table coordinate measurements with real photographic data.
to estimate the absolute repeatability error of a single NAROO measure per coordinate, and we obtain 47 nm on the x-axis, and 42 nm on the y-axis. These results denote the limit of accuracy of the XY-table coordinate measurements with real photographic data.
3.4. Direct-reverse effect
We evaluated the direct-reverse effect to check for systematic errors introduced by the measuring process as a function of the magnitude, and to check if the mapping process and 2D calibration correction were suitable. We measured the same USNO Praesepe cluster plate in the “direct” (0°) and “reverse” (180°) orientations. After correcting the measured positions of the 145 dot stars using Eq. (1), we used a simple orthogonal four-parameter first-order polynomial for the reverse set to match the direct set. Figure 9 shows the corresponding position differences as a function of the V-magnitude.
 |
Fig. 9. Direct-reverse residuals as a function of the V magnitude, in microns. Red dots denote the X-axis residuals, and blue dots denote the Y-axis residuals. Each dot denotes a single star coordinate. |
One can see that there is no obvious magnitude equation in the measuring process, indicating that the NAROO machine is not affected by any systematic error due to a direct-reverse effect. There are also no obvious unexplained glitches.
4. Improving astrometric accuracy of photographic plates with NAROO and Gaia
4.1. Introduction
The astrometry, in particular, aims to map and measure objects on the celestial sphere. Visually mapping the celestial sphere using meridian transit instruments took many years to produce the first reference star catalogs. With the introduction of refractor instruments mounted with micrometers, including heliometers with a 0.15 arcsec accuracy (Arlot 1986), it became possible to link Solar System objects to the stars of the first reference catalogs. Following the development of the (photographic) astrograph in France by the Henry brothers, the “Carte du Ciel” international program was initiated. The basis for this first photographic star catalog included the fundamental meridian transit catalogs that had already been developed. Thus, the Carte du Ciel consisted of a “densification” of these catalogs, providing the positions of about 10 million stars to the twelfth magnitude, and insuring that accurate positional reference stars were available in the small fields of view of the long-focus telescopes.
The projection of part of the celestial sphere on the plane of a photographic plate is gnomonic, which is biunique. Since a minimum of two reference stars is needed to produce the spherical equatorial coordinates in right ascension and declination of a Solar System object, this would provide the least accurate result as no account was made of the myriad sources of error. These sources include aberrations due to the telescope optics, its alignment, its drive errors, the plate and emulsion errors, the atmospheric refraction and prismatic effects, biases and misalignments of the plate measuring instrument, and plate modeling errors. An account of these sources is generally made in the plate reduction model, if a sufficient number of reference stars are available on the plate.
The NAROO digitizing machine will make it possible to reduce the errors made during the measurement. Moreover, new algorithms allow us to detect more stars on plates compared with the former manual method. As an example, with USNO long-focus plates, 4–5 stars were manually detected and often not cataloged, since 15–20 stars are now detected by the NAROO machine. All these stars were cataloged by Gaia with a proper motion that was accurate to one mas one century ago (Lindegren et al. 2016, 2018; Arénou 2020). We then detail which errors could be eliminated thanks to NAROO and Gaia.
4.2. Contribution of the focal length to the astrometric error
Short focal length astrographs and Schmidt telescopes were developed to provide large field plates with a high number of stars. However, some of these instruments have complex fields and are very difficult to model. For example, the classical Schmidt has a curved focal plane, so the thin plates were bent to approximate its shape and then released to flatten again before measurement. Modeling such large fields after the bending of the plate is a huge challenge leading to a poor accuracy of all objects on these plates. A better method is to obtain the position of an object by selecting a small region around it with enough reference stars to calibrate the zone more specifically and accurately. With a dense and accurate catalog such as Gaia releases, this might be the best method with plates of short-focus astrographs, especially since the atmospheric component in the error budget would be minimized while modeling a small field.
An analysis of the Carte du Ciel plates was realized by Lehtinen et al. (2018) with the conclusion that their intrinsic accuracy is about of 0.15 arcsec using the Gaia catalog, which is supposed to provide an accuracy of 1 mas for stars on these materials. Since they used a commercial digitizer, the intrinsic accuracy of the plates also includes that of the machine. On the other hand, we aim to provide a better intrinsic accuracy using a sub-micrometric digitizer. With regard to its specifications, the NAROO machine provides an astrometric accuracy as shown in Table 2. All values are below the limits due to the grain of the emulsion and, of course, due to the abnormalities of the refraction, which arbitrarily move the images outside the isoplanatic zone. Table 2 (theoretical) data that are derived from NAROO’s stability (relative) and repeatability (absolute) show the same trend as the one in Fig. 10 (observational).
 |
Fig. 10. Accuracy of observations of the Galilean satellites obtained with telescopes of various focal lengths (Ferraz-Mello 1983). |
Angular astrometric accuracy of the NAROO digitizer depending on the focal length of the telescope used for the realization of the plates.
Long-focus refractors were developed to study the orbits of the planetary satellites and double stars, and to measure stellar parallaxes. The long focal lengths provided scales of the satellite and stellar orbits, which were large relative to the calibration and measuring errors, resulting in an improved system mass. These instruments have fields with fewer stars, and the plate-reduction models are less complex. Combining a more accurate measurement with highly accurate Gaia reference stars will result in a substantial improvement in the positional accuracy of such objects. Digitizing measuring devices, such as the NAROO digitizer, which provides and centroids 3D images, are superior in accuracy to the older automatic measuring machines that measure the transparency of images, especially for fainter images (Robert et al. 2016).
Several studies have been realized on the astrometric accuracy of the photographic observations, which took into consideration many error sources. Some of the observational errors are due to the telescope, others are due to the atmosphere, the measuring device, and to the photographic material itself. Ferraz-Mello (1983) found that the highest accurate observations were correlated with the focal length of the telescope as shown in Fig. 10: the longer the focal length, the more accurate the observation. A correlation was also confirmed by Pascu (1994). If the error had been a simple measuring error, the correlation would have to be linear, but this is not in any of the studies. Moreover, the measuring errors in question appear too large. As a consequence, the total error must be due to several sources, and remeasurement of the long- and short-focus plates with new-generation digitizers will effectively remove the measuring error (see Table 2).
4.3. Contribution of the atmosphere to the astrometric error
It has been known for over a century that the atmosphere significantly contributes to astrometric error. There are three main sources: the atmospheric seeing, the refraction, and the color dispersion. While one can correct for the two latter effects if colors and magnitudes are available for the reference stars, there is no possible correction for the atmospheric seeing. However, this effect can be minimized by increasing the integration time (exposure time), but for historical photographs this is academic. Lindegren (1980) quantified the expected error at the zenith as
where m.e. is the mean error in arcsec depending on θ the separation between two objects, such as natural satellites, in radians, and T is the exposure time in seconds. This formulation was found to be consistent with an analysis of a large set of photographic observations of the main satellites of Saturn (Robert et al. 2016). However, the intersatellite residuals in the photographic observations of the Galilean satellites of Jupiter, made with the USNO 26-inch refractor in the years 1986–1990, were consistent with this equation only for the years 1986 and 1987. For the 1988 and 1989–90 observations, the residuals were considerably larger, suggesting a more complicated involvement of the atmospheric seeing in the astrometric error (Pascu 1994). Revisiting this issue with the expected high measuring accuracy of the NAROO machine and the reduction of these measurements with the high-precision Gaia catalog will help to resolve this problem.
For satellite astrometry, Eq. (2) tells us that the smallest error due to seeing is for small separations of the satellites and for longer exposures. Since exposure times are prescribed by a balance between motions in the satellite system and the faintness of reference stars on the plate, the smallest errors are for close separations of the satellites, and an accuracy premium occurs for satellite separations below 50 arcsec due to the increasing correlation of the seeing excursions of the pair as the separation approaches isoplanatic patch size, where the seeing excursions are completely correlated. Thus, for the long-focus telescopes, the atmospheric seeing will dominate the error budget (for separations larger than 50 arcsec), but not for the short-focus astrographs. The improved measuring accuracy of the NAROO machine will benefit the observations made with telescopes of small focal length the most.
4.4. Color- and magnitude-related errors
Errors arising from color differences are important, especially in planetary systems astrometry, due to the large color differences between objects. For example, Mars is much redder than its moons, Io is redder than the other Galilean satellites, Titan is considerably redder than the other Saturnians, and so on. Sources of color errors are the telescope optics and the atmosphere. Color-dependent errors due to the optics can be corrected if the colors of the reference stars and the target objects are known. Two exposures, taken with the objective rotated by 180 with respect to the target field are averaged together. This was done with short-focus astrographs, but not with long-focus telescopes. In those cases, standard calibration fields such as Pleiades or Praesepe clusters were used, since most of the long-focus target fields do not have a sufficient distribution of reference stars with a good range of colors. Color-dependent errors due to the atmosphere are (chromatic) refraction and dispersion. These are in the zenith direction, and in the absence of a good distribution of reference star colors in the target field, corrections are made using calibration constants determined through specific calibration plates made with images of star clusters (Pleiades or Praesepe) and valid for any plates made during the same observational season. The use of the Gaia catalog should make it possible to avoid such calibration.
Sources of magnitude errors are the telescope drive, the optics, and the plate-measuring machine. Sidereal drive errors are magnitude and declination dependent. These are more important for unguided longer exposures. For instance, exposures taken with the USNO 26-inch are unguided short in duration, so this is not an issue. However, the USNO 26-inch does have a 90-second periodic drive error (a glitch) caused by the worm gear. It results in some elongated images that are rejected in the reductions. Magnitude-related displacements due to the optics are dealt with in the same way as color-dependent sources.
The principal magnitude-related error for long-focus telescopes is caused by coma, which produces a comet-like image noticeable at some distance from the center of the plate, when the distorted image is larger than the seeing image and difficult to measure. This aberration is magnitude dependent and produces the coma-magnitude error: zero at the center of the plate but increasing radially outward. While the error can be reduced by diaphragming the objective, Ianna (1965) showed that one should correct the reference star positions for the variability of such an aberration.
4.5. Photographic emulsions
Early photographic emulsions were sensitive to the blue part of the spectrum, though most long-focus telescopes were visual refractors. When emulsions sensitive to the visual (green) part of the spectrum were invented, atmospheric color effects were reduced. While the greatest precision can be obtained with fine-grain, high-contrast emulsions, the choice to move an object’s astrometry focuses on the reduction of the exposure time by choosing an emulsion that will provide the faintest image desired in the shortest exposure time. With the need for adequate reference star configuration, the coma-free field of the telescope becomes an important consideration.
For example, with the USNO 26-inch, f/15 visual refractor, using 5 by 7 inches photographic glass plates required the aperture to be diaphragmed to 16 inches to provide round stellar images to the corners of the plates. The telescope, now at f/24, will require longer exposure times. Using Kodak 103aG + Schott GG14, the yellow filter provided good stellar images of a tenth-magnitude visual in a 20-second exposure. A composite, neutral density filter was used to prevent overexposure of planets and satellites. The larger grain size of the 103aG emulsion means that the signal to noise will be decreased, and thus both the representational error and the measuring error will increase.
5. Science program
In this section, we provide details of current and upcoming scientific programs, in which the NAROO center is involved, as examples for the community and to possible interactions. The information extracted from photographic plates are of an astrometric, photometric, and spectroscopic nature, when not purely imaging. Digitizations are in progress and corresponding results will be published in various forthcoming papers.
5.1. Planets and satellites
The astrometric monitoring of planets and moons is extremely useful for both ephemerides accuracy and theoretical research. In the first case, accurate astrometry is at the core of planets’ and natural satellites’ ephemerides. While modern ephemerides strongly rely on spacecraft data (Fienga et al. 2009; Lainey et al. 2021, 2020), ground-based data are still extremely useful for most distant objects. Because of observational error and mismodelling, ephemerides will drift after a certain period of time. Moreover, each generation of space missions is regularly pushing the limit of space navigation, continually requiring more accurate ephemerides. To mitigate the drift of such ephemerides, it is extremely valuable to obtain highly accurate data over a long time span of observations, and especially close to the bounds of the time interval, to better constrain the frequencies involved in the dynamical system (mean motions, pericenter, and node frequencies). Thanks to the NAROO facility, very old photographic plates of the planets of the Solar System, including their main and outer moons will be digitized and astrometrically reduced. With regard to planets, this is particularly relevant for Uranus and Neptune, which did not benefit much from spacecraft radio-science data. In the case of natural satellites, the much faster motions make the reprocessing of old photographic plates useful, despite the sometimes large amount of space data available. Moreover, the reprocessing of old photographic plates can sometimes even provide astrometric accuracy comparable to the one derived from space missions themselves (Robert et al. 2015).
Of as much importance will be the implication of NAROO machine to more theoretical studies. Thanks to its high accuracy and the availability of very old photographic plates, the NAROO project will tackle several important questions. In the case of planets, successful fundamental physics experiments have been carried out using the INPOP planetary ephemerides (Fienga et al. 2011; Bernus et al. 2019). Similarly, these ephemerides have been used to constrain the possible position of the planet candidate P9 (Fienga et al. 2020). In both former cases, a reprocessing of old photographic plates will allow for a tighter physical constraint by strongly reducing the uncertainty on the celestial position of the outer planets at the beginning of the twentieth century.
Using observations of natural satellites, NAROO will also be extremely useful for planetology studies. Indeed, moons can be used to test tidal mechanisms at play in giant planets (Lainey et al. 2012), tidal dissipation inside very active satellites such as Io (Lainey et al. 2009), characterizing the mass distribution inside moons (Lainey et al. 2019), or simply determining the mass of an outer moon (Emelyanov 2005). To give just a few examples of what NAROO will be able to do, the availability of old plates of the Jovian system will allow us to test the Fuller hypothesis of a possible tidal lock mechanism currently at play within Jupiter (Fuller et al. 2016). In the same vein, the Alden and O’Connell plates (Alden & O’Connell 1928) will allow for a much better characterization of tidal dissipation within Saturn at the innermost mid-sized moon’s tidal frequency (Lainey et al. 2020).
5.2. Asteroids
As for planets and satellites, dynamics of small Solar System bodies (SSSBs) can benefit from long-term astrometry provided by the NAROO machine. Among the SSSBs, around 1 million asteroids and 4400 comets have been discovered so far. SSSBs can appear in many plates, even if they were not the purpose of the original observation. Knowing the metadata of the plates, that is, the exact time of the exposure, the coordinates of the center of the plate, and the size of the field of view, the objects that could “appear” on the plate can be identified with SkyBoT (Berthier et al. 2006). Although, SkyBoT is built to seek and identify of Solar System objects in astronomical images. It allows us to identify objects in a cone with a given radius pointing, in a given direction, and on a given date.
In the general case, for every type of asteroid, including near-Earth asteroids (NEAs), main belt asteroids, or trans-Neptunian objects, the NAROO data will help us to refine orbits of asteroids and to study small effects on their dynamics. Here, we present expected results for NEAs, in particular the refinement of the orbits of such objects and the study of nongravitational accelerations.
5.2.1. Refinement of orbits
Orbits of SSSB are determined thanks to dynamical models fit to observations. The extrapolation of a model provides an ephemeris of the body in the past and future. The precision of the ephemeris can be derived and extrapolated through time with various techniques (Desmars et al. 2009). The precision is usually good during the observational period, whereas it gets worse outside this period. Furthermore, orbits have a better precision as the observational period is large (Desmars et al. 2013). In that context, regular observations are necessary to maintain the quality of the ephemerides. Moreover, the new reduction of old photographic plates (as we propose with the NAROO program) providing new accurate astrometric positions from the past, will allow us to improve the precision of ephemerides.
Some plates also refer to observations that are archived at the Minor Planet Center (MPC). Even if this astrometry is available to the community, a remeasurement of the original plate remains entirely interesting for two reasons. First, the archived data have no uncertainty on the positions (except for recent years, when submissions with a revised format was permitted). The uncertainty, putting a weight on each observation, is still a fundamental quantity to orbital fitting. Second, the astrometry calibrated in the past has considerable patterns of systematic errors due to the catalogs used. Today, a re-reduction using Gaia reference stars can completely eliminate this issue, which is usually one of the most severe limitations of the orbit improvement process.
As an example, we analyzed the database of 3600 Schmidt plates made at the Observatoire de la Côte d’Azur (OCA) between 1978 and 1996. These are large plates enabling us to observe a large field of view of the sky, and they were realized with long exposure times. Hence, objects with a maximum magnitude up to 20–21 could be measured on these plates, and a large number of SSSBs may have been recorded on these plates. Because of the large number of objects up to an apparent magnitude of 20, we focused on potentially hazardous asteroids2 (PHAs), and with SkyBoT 166 we identified PHAs with an apparent magnitude below 20 on 284 OCA plates among the 3600 of the database. Approximately 90% of identified PHAs have prediscovery observations among these old observations that have never been measured and used for orbit determination.
To estimate the improvement in the precision of the ephemeris by reducing old photographic plates with the NAROO digitizer, we made simulations with the PHA 2015 OL35 identified in the OCA database. It was discovered on 2015-07-23, and its observational period goes from 2015-07-23 to 2020-04-28, according to the MPC (as of 2021-01-28). In the OCA database, we identified three potential prediscoveries for 2015 OL35 in 1995, which is 20 years before the observational period. Simulations were made using the numerical integration of the motion of an asteroid (NIMA) method developed by Desmars (2015), and allowing orbit determination and estimation of the ephemeris precision. We have tested various cases representing various levels of precision we expected after a reduction by the NAROO machine and Gaia references. Figure 11 shows the estimated precision in equatorial coordinates of the 2015 OL35 orbit, using the current set of available astrometric positions on MPC and assuming that the three additional prediscovery observations are reduced with an astrometric precision of 200 mas and 50 mas, respectively. The addition of the three observations shows, as expected, a significant improvement in the orbit precision, not only on the past but over all the considered period (1900–2100). Other simulations with other PHAs detected on the database show similar results. These simulations reveal that only few observations of old photographic plates that could be measured with the NAROO machine are enough to significantly improve the orbit precision. Moreover, having a better astrometric measurement over a long period of time will ensure better estimations of impact probabilities.
 |
Fig. 11. Simulation of the evolution of the uncertainty of the ephemeris of 2015 OL35 from 1900 to 2100. The blue curve denotes the uncertainty of the ephemeris using the original astrometric observations from MPC. The orange and green curves denote the uncertainties of the ephemeris taking three additional potential prediscoveries and assuming astrometric precisions of 50 mas and 200 mas, respectively. |
5.2.2. Nongravitational acceleration
The NAROO machine will not only be helpful to improve the orbit determination and precision of SSSBs, it will also be helpful to detect small accelerations in the dynamics of such objects. Thanks to new astrometric measurements over a long period of time, in particular in the past with old photographic plates, nongravitational acceleration such as the Yarkovsky effect may be measured. Yarkovsky acceleration produces a drift in the semi-major axis of the asteroids, which can be measured in some cases (Vokrouhlický et al. 2000).
Indeed, the first measure of Yarkovsky acceleration using astrometric observations was done for (152 563) 1992 BF (Vokrouhlický et al. 2008) with new reduction of astrometric plates made in 1953. This new astrometry of four observations in 1953 made it possible to detect a drift in the semi-major axis between 1953 and recent observations in 2008. This acceleration is explained by the Yarkovsky effect. A small drift in semi major-axis can also be measurable thanks to accurate astrometry deriving, for example from radar measurements, but they remain rare. Since this study, various papers have identified NEAs with a measurable drift in semi-major axis using astrometry (Nugent et al. 2012; Farnocchia et al. 2013; Desmars 2015; Del Vigna et al. 2018; Greenberg et al. 2020). Thanks to better recent astrometry, such a drift is now measurable with reliability for more than 200 objects. New perspectives of measurements have also been identified using Gaia star catalogs and via direct observations from Gaia (Spoto et al. 2019).
With new digitization and measurements of old photographic plates, the NAROO machine will provide accurate astrometry of old observations allowing the measure of small accelerations in the motion of some asteroids. Desmars (2015) already investigated the impact of a program like NAROO by exploiting old photographic plates in the measure of nongravitational acceleration. He highlighted that by reducing only a few old photographic plates (2–10) with a precision of 30 mas, the determination of the reliable drift in semi-major axis (at more than 3 sigma) would be possible for about 100 asteroids.
The detection of a Yarkovsky acceleration can provide new constraints on NEAs. As the drift in semi-major axis depends on physical characteristics such as the diameter, the bulk density, the spin, and so on, those parameters can be constrained by the value of the drift itself. Moreover, the drift in semi-major axis can provide constraints on the orbital evolution of asteroids such as the transportation from the main belt to the near-Earth orbit (Bottke 2006), and the ratio of prograde and retrograde objects in the NEA population (La Spina et al. 2004).
5.3. Solar physics
The Paris Observatory owns about 100 000 photographic plates of the Sun, mostly observed in Hα, Ca II K center line wavelength, and continuum (near Ca II K line). These observations were made from 1870 to 1999 with photographic plates, while new observations are still being realized today using digital recording, with a recent update in 2018 (Malherbe & Dalmasse 2019).
For most of the time, the plates were homemade, and we lack information on their coating. Making photometric estimation with such materials would be expensive and challenging. However, the French solar database BASS20003 contains a heliophysics feature catalog4, which is a database of solar and heliophysic features obtained from automatic detections with various kinds of observations realized in the frame of the HELIO European project (Bentley et al. 2011). For now, most of the detections extend from 1996 until today. Those features are a signature of the solar activity and magnetic field underneath the solar surface (photosphere), and we know that the behavior of some of them is an indicator of the beginnings of solar flares. It is especially the case for a filament’s “disparition brusque” (sudden disappearance), which can lead to eruptive filament behavior. Filaments can disappear during a certain period of time, typically a few days, then appear again due to variations in opacity. The way they disappear gives clues as to the composition of the surrounding atmosphere. This should not be mistaken with disparition brusque, where the filament is really breaking. Throughout its lifetime, a filament changes in shape, twisting, bending. An example of a filament changing in shape, contrast, and visibility is shown in Fig. 12.
 |
Fig. 12. Solar filament as seen on 2001-07-03 (lower image) and 2001-07-04 (upper image). Its visibility strongly varies from one day to the next. Images from the Meudon spectroheliograph (available in the BASS2000 database). |
The size of the grains of silver on a typical photographic plate of the Sun is about 10 μm. Making extrapolation and combining observations, we estimate that we could obtain between 1/10 and 1/20 in precision of location on the solar surface, for instance 500 nm. Thus, the overall accuracy of the NAROO machine is ideal to measure the best possible location of the contours of filaments. Obviously, this will not be done for all filaments in all observations, but it will be possible to digitize the boundaries of filaments involved in strong flares to deduce the behavior of the magnetic field leading to them. This work can be achieved quite easily as we can benefit from filament detections (Fuller et al. 2005) and time tracking (Bonnin et al. 2013) to identify the photographic plates and digitize them in the collection.
Another application of the NAROO program deals with the exact determination of the boundaries of active regions (AR). First, we could analyze digitizations to determine the place between two opposite polarities, called the neutral line, where filaments can appear. Then, it will allow us to accurately study the extension of an AR and its evolution in time, which gives clues to the strength of the underlying magnetic field. Lastly, and probably the most prospective scientific application, is the fact that it will help us to precisely determine, at various altitudes, the shape of the ARs, giving 3D information on the magnetic field extension and evolution. Figure 13 shows the change of an AR from one day to the next, in the upper solar atmosphere, upper chromosphere, and lower chromosphere.
 |
Fig. 13. Left panel: upper thumbnail shows an AR in high chromosphere (center of Ca II K3 line), while the lower one shows the same region at the same time, in low chromosphere (Hα line). Right panel: same active region, in low corona, on 2001-07-03 (upper image) and on 2001-07-04 (lower image). Left observations were realized with the Meudon spectroheliograph and are available in BASS2000. Right observations come from the SOHO/EIT instrument and are available at NASA. Automatic detections come from Barra et al. (2009). |
Using the NAROO machine with older photographic plates of the Sun will allow us to tackle the problem of morphology and topology of various Solar features. It will help us to understand the way the magnetic field evolves in time, how it behaves before strong flares, and maybe discover initiator of flares, or at least determine pre-flare behaviors, which would be a major advance for space weather science.
5.4. Be stars
Classical Be stars are hot stars that sporadically eject material from their surface into a Keplerian disk (Rivinius et al. 2013). This disk can be witnessed in the spectra of Be stars through emission in spectral lines, in particular hydrogen lines such as Hα, helium lines such as He I 6678, and Fe II lines. As new outbursts occur and as the disk dissipates in the interstellar medium, the properties (size, density, homogeneity, etc.) of the disk change, and so do the emission lines. Therefore, by studying the variation of spectral emission from Be stars, one can learn about the history of the disk and matter ejections. This is particularly important because the mechanism at the origin of the outbursts is still debated. According to current observational and theoretical knowledge, the most probable explanation is that the outbursts are due to a combination of very rapid rotation and pulsations (Neiner et al. 2020). Indeed, Be stars are known to rotate at ∼90% of the critical velocity (Frémat et al. 2005) and have been shown to undergo pulsations due to the κ mechanism (e.g., Floquet et al. 2002; Neiner et al. 2009; Semaan et al. 2018). Recently, it was shown that they also host stochastically excited gravito-inertial pulsations (Neiner et al. 2012), and that these pulsation modes can efficiently transport angular momentum to the surface of the star and accelerate it to reach critical velocity and thus eject material (Neiner et al. 2020).
To observationally characterize Be outbursts, in particular how the nature and occurrence of outbursts correlate with the properties of the star (such as its temperature or rotational velocity), it is necessary to collect spectra over a very long time frame. Indeed, outbursts occur over a time frame of a few months to several decades. To this aim, the BeSS database5 was set up (Neiner et al. 2011). It includes a catalog of the brightest ∼2300 Be stars known, together with available spectra obtained by both professional and amateur astronomers (Neiner 2018). At the time of writing, this includes ∼245 000 spectra, all of which were collected on charge coupled device cameras (CCDs) from the end of the 1980s onwards.
To increase the time frame of the observations, it is necessary to include older spectra obtained on glass plates. The Paris Observatory hosts a collection of such observations of Be stars on plates, obtained at the Haute-Provence Observatory (OHP 193, 152, and 120 cm), the European Southern Observatory (ESO 152 cm), and San Pedro Mártir Observatory in Mexico, from the 1960s to the 1980s. This collection is estimated to have ∼30 000 plates, including calibration plates. The NAROO machine will allow us to digitize the plates and retrieve the spectra. Calibration plates or calibration spectra recorded on the science plates will allow us to convert the density recorded on the science plate into the stellar spectral intensity. In addition, a part of the plates exposed with a calibration lamp will be used to perform the wavelength calibration. Metadata, such as the date and time of observations, are available on paper logs and have already been digitized. Final spectra will be saved in FITS format and added to the BeSS database to contribute to the study of long-term variations (in particular outbursts) of Be stars. Since the BeSS database is open to anyone, the spectra will be available to any researcher wishing to use them.
5.5. Solar System and Earth visitors
Some celestial objects may just be temporarily passing through the Solar System or even the Earth’s atmosphere. We will use the NAROO digitizations to search for those that could have visited in the past.
5.5.1. Interstellar objects
In 2017 and 2019, two Solar System objects were discovered on hyperbolic orbits: 1I/Oumuamua with an eccentricity of 1.2 (MPEC 2017-U181 2017), and 2I/Borisov with an eccentricity of 3.5 (MPEC 2019-R106 2019). These high eccentricities indicate an extrasolar origin, and these interstellar objects (ISOs) presumably originated from other planetary systems, from which they would have been ejected. Actually, such objects have been anticipated for several years (Sekanina 1976), and the Vera Rubin Observatory’s Legacy Survey of Space and Time (LSST) detects from one to a few of them each year, with a 24.5-limit magnitude (Trilling et al. 2017). A new estimation states as many as seven objects per year (Eubanks et al. 2021).
It is therefore natural to envision that such visitors did hit the Solar System in the past, and some of them may be dormant in old observations. Even if ISOs are as faint as 24 mag, instruments such as the Palomar 5 m telescope, the Mount Wilson 2.5 m telescope, or the 48 inch Palomar Survey telescope were able to observe them. In fact, 2I/Borisov itself, first discovered in August 2019, was retrospectively discovered with December 2018 observations, using images taken by the Catalina Sky Survey (CSS), Pan-STARRS, and the Zwicky Transient Facility (ZTF; Ye et al. 2020).
The scientific interest of these anterior discoveries are mainly to contribute to the statistics of ISOs and to assess their frequency in time. Indeed, galactic tides may change their apparition frequency in the Solar System (Eubanks 2019). For instance, Siraj & Loeb (2020) showed that they may present a directional asymmetry leading a better understanding of planetary system origin and nature. We also suggest that some of these visitors may not be asteroids or comets, but bona fide planets ejected from a planetary system of origin. Such ejections have indeed been predicted by several authors such as Matsumoto et al. (2020), and several free-floating planets have already been detected (Mróz et al. 2018).
Our methodology consists of combining plates from different origins in the same sky area. If we suppose that there are N such plates, we process them using the following steps. We first sort the plates according to their epoch of exposure, and we digitize them. Then we search for a difference in the position of objects and if a difference is found, two things may have happened: the difference is due to the displacement of the same object, or the difference comes from two different objects, one having disappeared, the other having appeared. At this step, one could provisionally conclude that there is a displacement if the two objects have the same magnitude and color. If a displacement is found, we digitize the third plate and we search for a new displacement. We repeat this last step for all remaining plates. It will lead to positions (xi, yi)i = 1, N on the sky at times ti = 1, N. Finally, we fit the positions and epochs with a Kepler law of motion. The fit will lead the eccentricity e. If e > 1, the object is a candidate for an ISO.
5.5.2. The 1908 Tunguska meteorite
The Tunguska event was a massive explosion that occurred near the Podkamennaya Tunguska River in Yeniseysk Governorate (now Krasnoyarsk Krai), Russia, on the morning of 1908-06-30 (NS). The explosion over the sparsely populated Eastern Siberian Taiga flattened an estimated 80 million trees over an area of 2150 km2 of forest, and eyewitness reports suggest that at least three people may have died in the event. The explosion is generally attributed to the air burst of a stony meteoroid about 100 m in size. It is classified as an impact event, even though no impact crater has been found. The object is thought to have disintegrated at an altitude of 5–10 km rather than hitting the surface of the Earth. No consensus has yet been reached with regard to an explanation. Recently, Khrenikov et al. suggested that it resulted from the passage of an iron asteroid across the Earth’s atmosphere. The latter would have hit the upper atmosphere at about 10–15 km and then escaped to the interplanetary space (Khrennikov et al. 2020).
We propose searching for it outside the Earth’s atmosphere on photographic plates realized a few hours or days before and after the morning of June 8 (Siberian time). A few observatories in the region could have such materials: the 38-cm telescope of the Pulkovo Observatory near Saint-Petersburg, the 12 inch telescope of Engelgardt Observatory near Kazan, or the 40 cm refractor of Sheshan Observatory near Shanghai.
The procedure to find this object would be different from that of ISOs. Due to its high speed and low altitude on 1908-06-30, it would not appear as a single point but as a segment with an angular length VθTexp, where Vθ is its angular speed and Texp the duration of the exposure. In addition, the aspect of the image should not be the same during its passage through the atmosphere and before or after the passage in the atmosphere.
5.6. General relativity: Physics tests
The Solar System is a laboratory for testing the laws of gravitation and many of the most important tests of general relativity have been made using Solar System bodies: advance of Mercury perihelion, deflection of light near the Sun, the motion of the Earth-Moon System, etc. Studying the dynamics of Solar System bodies requires astrometric observations of very good accuracy and over a long time span, in order to be able to quantify long period and secular terms, the latter being the signature of relativistic precessions. From this point of view, the contribution of Gaia data is fundamental to build orbits very precisely; however, these data are valid for a nominal period of five years, or even longer in the case of a mission extension. That said, building orbits over several decades is essential to perform quality relativity tests. This is exactly the contribution of the NAROO instrument: a precise digitization and a new astrometric reduction of old photographic plates provide very accurate positions, and by combining them with the Gaia data, we obtain a long time span, which is exactly what we need to precisely quantify relativistic effects.
NAROO even shows its interest in fundamental physics tests if we consider as study objects the population of known asteroids, which is enormously increasing with Gaia and LSST. Indeed, this large population is characterized by a wide variety of orbital elements, both in semi-major axis, eccentricity, and especially inclination. Three phenomenologies are of interest for carrying out relativity tests with NAROO data: the parameterized post-Newtonian (PPN) and fifth force formalisms, as well as the standard model extension (SME).
Parameterized post-Newtonian formalism is a phenomenological framework in which the spacetime metric is parameterized by ten dimensionless coefficients (Will 2014 and references therein). The two most important PPN parameters are γ, which describes the spatial space-time curvature, and β, which parameterizes the nonlinearity in the time component of the space-time metric. Perihelion precession of asteroids is directly connected with β. NAROO, combined with Gaia data (Mouret 2011) and Radar data (Verma et al. 2017) will lead to a substantial improvement of the constraints of β. Another approach is to consider a violation of the strong equivalence principle (SEP) which can appear in many alternative theories to GR. SEP violation produces indeed an effect on orbits that depend on the gravitational self-energy of the bodies; it is characterized by a difference between gravitational and inertial mass, usually described by the Nordtvedt parameter η, which can be related to the other PPN parameters through the relation η = 4β − γ − 3. As demonstrated in Hees et al. (2018), this approach combined with Gaia and NAROO data will lead to a significant improvement in the determination of the β parameter.
The fifth force formalism first emerged as a reinterpretation of Eotvos’ experiment in late 1980s (Fischbach et al. 1986) and since is considered as a potential candidate to explain dark energy as a quintessence field (Cicoli et al. 2012). This formalism considers deviations from Newtonian gravity in which the gravitational potential is modified by a Yukawa term, characterized by two parameters: the length and the strength of the interaction. The use of NAROO data on asteroids can help to improve the current constraints above one astronomical unit.
Standard model extension framework has been developed to systematically search for a breaking of Lorentz symmetry in all sectors of physics (Colladay & Kostelecký 1998). At lowest order, in its gravitational sector, SME parameterizes a breaking of Lorentz invariance by a symmetric traceless tensor (Bailey & Kostelecký 2006). These coefficients have been constrained by various observations, including very long baseline interferometry (Le Poncin-Lafitte et al. 2016), lunar laser ranging (Bourgoin et al. 2016, 2017), and binary pulsars (Shao 2014) (for a complete review, see Hees et al. 2016). Nevertheless, it is still impossible to decorrelate all the SME coefficients satisfactorily. The big advantage of asteroid observations comes from the huge number of observed objects and from the variety of their orbital parameters, which allow us to decorrelate these coefficients by using NAROO data to enlarge the dynamical time span.
5.7. General relativity: Gravitational deflection of light
The gravitational deflection of light was a key prediction of general relativity, first confirmed by the expedition that observed the eclipse of May 29, 1919 (Gilmore & Tausch-Pebody 2020). A set of 38 surviving plates were reanalyzed with microdensitometers in 1979 at the Royal Greenwich Observatory, confirming the original result. Although in contrast with the differential astrometry carried out by the members of the eclipse expedition (Dyson et al. 1920), relative astrometry was attempted using reference plates (Harvey 1979). There is a huge interest in analyzing these plates with state-of-the-art astrometry machines such as NAROO, given the controverted history of the subject and the claims made of deviations from the general relativity prediction (e.g., Merat et al. 1974), even though modern CCD observations during eclipses have fully confirmed the results (Bruns 2018). The analysis of eclipse plates up to the early 1930s was thoroughly discussed by Danjon (1932), and whilst there were attempts in the 1920s to measure the effect in other plates, they were usually not suitable due to several factors such as a small field of view, lack of comparison plates, tracking set to the solar rate rather than to the sidereal one, and above all, lack of reference stars in the field. For example, a copy of a fraction of one of the original 1919 eclipse plates is available in the archives of the Paris Observatory and was digitized with the NAROO machine, confirming the relative positions of four stars (Fig. 14). A full astrometric reduction is currently underway. Yet, there is a large body of plates in many archives that could be exploited, in particular those related to the search for the planet Vulcan.
 |
Fig. 14. NAROO digitization of a partial copy of one of the 1919 eclipse plates found in the archives of the Paris Observatory. The result mosaic is composed by 60 subimages. Four stars are detected. |
5.8. Archival collections and NAROO
A number of plate archives could be digitized with the NAROO facility, and here we provide a few examples to highlight their potential use for various scientific topics. It also shows differences and varieties between collections.
5.8.1. Juvisy archive
The famous French astronomer C. Flammarion lived in Juvisy-sur-Orge, in the suburbs of Paris, a century ago. There, he built his own observatory with a 240 mm Zeiss refractor, and various secondary optics and astrographic cameras. His assistant, F. Quénisset, took most of the thousands of photographic plates over 50 years, starting in 1893. The results from many of these plates were published in the Astronomie journal, the main publication of the Société Astronomique de France (SAF), which Flammarion founded in 1887. All this astronomical material needs to be preserved, because it is officially considered as national scientific heritage. Beyond reconditioning the plates in new envelopes, the digital scan of the collection is the main operation for the people in charge of this project, and for this purpose the NAROO machine was regarded as the most efficient. Figure 15 shows the center of the NAROO digitization of plate 00192, realized on July 16th 1906, with M6 and M20 objects.
 |
Fig. 15. Center of the NAROO digitization of Juvisy plate 00192, realized on July 16th 1906, with M6 and M20 objects. |
Metadata were recorded in hand-written logbooks, which have been meticulously transcribed into a database to allow easy queries, looking for dates, objects, instruments, or astronomical events. In the collection, there are many plates targeting the Sun, the Moon, and planets. Among them are 18 plates looking for Pluto, starting on March 20th 1930, only six days after the official release of the discovery by Tombaugh (1946). The planet was not yet designated by its current name, but as the “transneptunian object”, or the “Lowell object”.
Another significant group of plates consists of star fields and a comet search. Quénisset is a co-discoverer of two comets. For such a quest, the field is close to the ecliptic and, as described in Sect. 5.2, may enclose small Solar System bodies. Quénisset captured the Eros asteroid on several plates from September 1930, as it passed close to Earth. Dedicated astrometry has been performed using a very accurate microscope image (one single local digitzation) to evaluate the astrometric potential of the plate (Guérard & Robert 2018). Comparing the astrometric reduction from PanSTARRS background reference and Eros prediction by MPC, the position of the asteroid was recovered within one arcsec rms, while the plate has never been used in the Eros ephemeris construction.
The Flammarion collection project is driven by a collaboration between professionals and amateurs6.
5.8.2. OCA archive
The Observatoire de la Cote d’Azur (OCA), formerly the Observatoire de Nice, owns a collection of 8200 astronomical photographic plates taken with a double Zeiss astrograph (1935–1978) and 3600 plates from the Calern observatory’s Schmidt telescope (1978–1996). Table 3 shows details about the OCA archive.
Details of the OCA archive.
The double Zeiss astrograph has been provided as war damages by the German optical manufacturer C. Zeiss. Since its first light in 1935, two main observing teams were involved: A. Patry and M. Laugier, who produced some 2700 plates from 1935 to 1961, and B. Milet, who produced 5500 plates from 1965 to 1978. Most of these plates focus on Solar System minor objects. The Calern Schmidt telescope, also known as TElescope de SChmidt de CAlern (TESCA), is a pure Schmidt instrument with a 1.52 m spherical primary mirror. It was constructed at the Calern observatory (some 60 km away from the Observatoire de Nice), formerly administrated from 1974 by the Centre d’Études et de Recherches en Géodynamique et en Astrométrie (CERGA). In 1988, the CERGA and the Observatoire de Nice merged into the OCA.
Between 1978 and 1996, the observing team produced around 3600 astronomical images on glass plates and soft films. For those 18 years, several scientific topics were addressed: Solar System objects, stellar dynamics in clusters, optical counterparts for gamma, UV, IR and radio objects detected by space-borne instruments, supernovae and variable stars, quasars, nebulas, and space debris location.
The OCA historical plate collection has also been enriched by several astronomical images from other institutes. It gathers 3293 images on soft films taken by the Schmidt telescope at the Meudon observatory from 1961 to 1975, a few plates from the Carte du Ciel program taken at various observatories (Algiers and non-identified observatories), some 50 glass plates taken by O. Calame in the 1960s at the Pic du Midi observatory, and approximately 200 plates with various formats mostly from C. Veillet taken at La Silla, CFHT, Observatoire de Haute Provence, Observatoire du Pic du Midi, and Chiran observing station.
5.8.3. OHP archive
The Observatoire de Haute Provence (OHP) holds a large collection of photographic plates taken with different OHP telescopes and instruments over nearly half a century. Spectroscopic, direct, and objective-prism plates have been conserved at OHP with the observing logs containing complete metadata.
The 193 cm “coudé spectrograph” telescope was active from 1959 to 1985, and produced about 17 000 plates with different dispersion and sizes. Five Schmidt cameras and two gratings offered 19 different combinations of wavelength (resolution), ranging from 3.1 Å mm−1 (V-camera in the yellow band) to 78 Å mm−1 (I-camera in the infrared band). The 152 cm coudé spectrograph telescope was active from 1970 to 1989 and produced about 20 000 plates. Three Schmidt cameras and three gratings offered nine different combinations of wavelength, ranging from 7.2 Å mm−1 (C-camera in the blue or yellow bands) to 31.3 Å mm−1 (A-camera in the red-infrared band). Two other spectrographs were built and operated at the 120-cm telescope: the C spectrograph between 1944 and 1974 with a single prism that gave a dispersion of 77 Å mm−1 at Hγ, and the Marly spectrograph between 1980 and 1995 with two gratings for dispersions of 40 or 80 Å mm−1. About 8500 plates were realized with these two spectrographs.
Direct plates were mainly realized with the 60/87-cm Schmidt telescope, active from 1970 to 1997. More than 7300 plates were produced. 17.5 cm round films were used until July 1974 and 16 × 16 cm glass plates were used thereafter. The research programs focused on minor planets and comets; studies of HII regions and galaxies; and variability of novae, supernovae, radio, and X-ray sources. Various direct plates were also realized with other OHP telescopes: 193-cm, 120-cm, and 80-cm telescopes. Finally, more than 18 000 plates were realized with 40 cm “Grand Prisme-Objectif” GPO astrographs (1957–1984), with the 16-cm “Petit Prisme Objectif” PPO (1946–1993), and the 60/87-cm Schmidt telescope with a 62-cm prism (1974–1993).
5.8.4. Pulkovo archive
Photographic observations performed with the Normal Astrograph in the 1890s resulted in the creation of the Pulkovo collection of astronegatives7. Observations were accumulated throughout the twentieth century using the Pulkovo Normal Astrograph and 26-inch refractor, and small parts of the archive were also produced with various telescopes from distant stations of the Pulkovo Observatory (e.g., Bolivian expedition, Bolivian National Observatory at Tarija). The plate archive now contains more than 50 000 photographic plates. Table 4 shows details about the Pulkovo archive.
Details of the Pulkovo archive.
Observations were realized for proper motion surveys of selected sky areas and open clusters (Bobylev et al. 2004), astrometric observations of the Solar System bodies (Kiseleva et al. 2015), and photographic surveys used to construct astrometric catalogs (Khrutskaya et al. 2004). One of the primary goals was to determine the orbital parameters and masses of binary stars, therefore the archive is half composed of the 26-inch refractor plates (Izmailov et al. 2016). The Normal Astrograph plates are limited by 17 mag. The 26-inch refractor plates are usually limited by 10–12 mag (up to 17 mag in some astronegatives). The Bolivian plates include stellar images up to 14 mag. Most of the observations were realized in the second part of the twentieth century, but a significant part of the materials were lost from 1893 to 1941 because of WWII.
Properties of the Pulkovo collection are shown in Fig. 16. The dots distributed along the ecliptic denote the Solar System body observations (planetary satellites and asteroids), and the black dots denote the binary star plates. The homogeneous filling of the Southern hemisphere shows the FOCAT-S astronegatives catalog (Bystrov et al. 1994).
 |
Fig. 16. Properties of the Pulkovo archive of photographic plates: distribution of observations over the celestial sphere in equatorial coordinates. PNA denotes observations realized with the Normal Astrograph, P26 denotes those realized with the 26-inch refractor, and EA denotes those realized with the Expeditionary Astrograph. |
6. Summary and conclusions
The value of a new analysis of old photographic plates has been demonstrated, and the community is beginning to worry about the use and preservation of such materials for science. As recommended by the resolution B3 of the XXX IAU General Assembly in 20188, the preservation, digitization, and scientific exploration of the plates must be realized. The recent Science White Paper by Pevtsov et al. (2019) covers the range of problems to be addressed by the community. While a few digitization programs exist mainly through preservation or archiving efforts, the NAROO center is especially dedicated to science with the measurement of photographic plates and the analysis of old observations. We have paid special attention to the design of our sub-micrometric digitizer: the Newport-Microcontrol XY-table, Andor Neo sCMOS camera, shooting lens and lighting device, in order to automatically process all known transparent astrophotographic plate material with the best technical elements, processes and accuracy. The NAROO machine positioning stability is better than 15 nm. With real data, that is, for fine-grain and well-exposed stellar images and after applying the 2D calibration correction, the overall accuracy of the NAROO machine is better than 65 nm. The absolute repeatability error of a single measure per coordinate is 45 nm, denoting the limit of accuracy of the XY-table coordinate measures. Comparisons of direct and reverse measures show that the digitizer is not affected by any systematic error due to the measuring process, and that the mapping process and 2D calibration are also adequate.
We have composed a team of researchers of the Paris Observatory involved in various scientific topics: astrometry, photometry, and spectroscopy, with consequences in Planetology, NEA risk assessment, Solar physics, astrophysical phenomena, and general relativity. Plate collections of the Paris Observatory and other French and international institutions are being digitized to provide data spanning more than one century for our works. Corresponding results will be presented in upcoming papers. Digitized raw data will also be available for the community.
Furthermore, the NAROO machine is available for researchers to digitize their own collections for scientific purposes, since digitization time is reserved for external users. A call for proposals will be issued every six months via our project website9. The projects received will be evaluated and ranked by a dedicated panel. The very first digitization call will be published in May 2021. From this date to the end of 2022, there will be no call for large programs since we intend to allow as many researchers as possible to estimate the value of their collection with “small” sets limited to 200 plates.
NAROO webpage https://omekas.obspm.fr/s/naroo-project/
BASS2000 webpage http://bass2000.obspm.fr
HFC webpage http://voparis-helio.obspm.fr/hfc-gui/
BeSS webpage http://basebe.obspm.fr
Gemini portal https://proam-gemini.fr/
Pulkovo database http://www.puldb.ru/db/plates/
NAROO webpage https://omekas.obspm.fr/s/naroo-project/
Acknowledgments
The NAROO program was supported by the DIM-ACAV of Ile-de-France region, PSL Research University, the Programme National GRAM and the Programme National de Planétologie (PNP) of CNRS/INSU with INP and IN2P3, co-funded by CNES. The authors are grateful to the Archive and Heritage Commission of LESIA. The Pulkovo astronegatives program was funded by RFBR according to the research projects No 19-02-00843 A, and partially supported by the Ministry of Science and Higher Education of Russian Federation under the contract 075-15-2020-780.
References
- Alden, R. L., & O’Connell, W. 1928, AJ, 38, 53 [Google Scholar]
- Arlot, J. E. 1986, A&A, 167, 371 [Google Scholar]
- Arénou, F. 2020, Newsletter, AF Gaia [Google Scholar]
- Bailey, Q. G., & Kostelecký, V. A. 2006, Phys. Rev. D, 74, 045001 [Google Scholar]
- Barra, V., Delouille, V., Kretzschmar, M., & Hochedez, J. F. 2009, A&A, 505, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bentley, R. D., Csillaghy, A., Aboudarham, J., et al. 2011, Adv. Space Res., 47, 2235 [Google Scholar]
- Bernus, L., Minazzoli, O., Fienga, A., et al. 2019, Phys. Rev. Lett., 123, 161103 [Google Scholar]
- Berthier, J., Vachier, F., Thuillot, W., et al. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, S. Enrique, et al., ASP Conf. Ser., 351, 367 [Google Scholar]
- Bobylev, V. V., Bronnikova, N. M., & Shakht, N. A. 2004, Astron. Lett., 30, 469 [Google Scholar]
- Bonnin, X., Aboudarham, J., Fuller, N., Csillaghy, A., & Bentley, R. 2013, Sol. Phys., 283, 49 [Google Scholar]
- Bottke, W. F., Vokrouhlický, D., Rubincam, D. P., & Nesvorný, D. 2006, Ann. Rev. Earth Planet. Sci., 34, 157 [Google Scholar]
- Bourgoin, A., Hees, A., Bouquillon, S., et al. 2016, Phys. Rev. Lett., 117, 241301 [Google Scholar]
- Bourgoin, A., Le Poncin-Lafitte, C., Hees, A., et al. 2017, Phys. Rev. Lett., 119, 201102 [Google Scholar]
- Bruns, D. G. 2018, CQG, 35, 075009 [Google Scholar]
- Bystrov, N. F., Polojentsev, D. D., Potter, H. I., et al. 1994, Bulletin d’Information du Centre de Donnees Stellaires, 44, 3 [Google Scholar]
- Cicoli, M., Pedro, F. G., & Tasinato, G. 2012, JCAP, 2012, 044 [Google Scholar]
- Colladay, D., & Kostelecký, V. A. 1998, Phys. Rev. D, 58, 116002 [Google Scholar]
- Danjon, A. 1932, J. Phys. Radium, 7, 21 [Google Scholar]
- de Vegt, C., & Ebner, H. 1974, MNRAS, 167, 169 [Google Scholar]
- Del Vigna, A., Faggioli, L., Milani, A., et al. 2018, A&A, 617, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmars, J. 2015, A&A, 575, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmars, J., Arlot, S., Arlot, J. E., Lainey, V., & Vienne, A. 2009, A&A, 499, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmars, J., Bancelin, D., Hestroffer, D., & Thuillot, W. 2013, A&A, 554, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dyson, F. W., Eddington, A. S., & Davidson, C. 1920, Phil. Trans. R. Soc. London Ser. A, 220, 291 [Google Scholar]
- Emelyanov, N. V. 2005, A&A, 438, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eubanks, T. M. 2019, ApJ, 874, L11 [Google Scholar]
- Eubanks, T. M., Hein, A. M., Lingam, M., et al. 2021, AJ, submitted, [arXiv:2103.03289] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Vokrouhlický, D., et al. 2013, Icarus, 224, 1 [Google Scholar]
- Ferraz-Mello, S. 1983, An. Acad. Brasil. Cienc, 55, 219 [Google Scholar]
- Fienga, A., Laskar, J., Morley, T., et al. 2009, A&A, 507, 1675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fienga, A., Laskar, J., Kuchynka, P., et al. 2011, Celest. Mech. Dyn. Astron., 111, 363 [Google Scholar]
- Fienga, A., Di Ruscio, A., Bernus, L., et al. 2020, A&A, 640, A6 [CrossRef] [EDP Sciences] [Google Scholar]
- Fischbach, E., Sudarsky, D., Szafer, A., Talmadge, C., & Aronson, S. H. 1986, Phys. Rev. Lett., 56, 3 [CrossRef] [PubMed] [Google Scholar]
- Floquet, M., Neiner, C., Janot-Pacheco, E., et al. 2002, A&A, 394, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frémat, Y., Zorec, J., Hubert, A. M., & Floquet, M. 2005, A&A, 440, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuller, N., Aboudarham, J., & Bentley, R. D. 2005, Sol. Phys., 227, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fuller, J., Luan, J., & Quataert, E. 2016, MNRAS, 458, 3867 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., & Tausch-Pebody, G. 2020, Notes Rec. Roy. Soc., 2020, 0040 [Google Scholar]
- Greenberg, A. H., Margot, J.-L., Verma, A. K., Taylor, P. A., & Hodge, S. E. 2020, AJ, 159, 92 [Google Scholar]
- Guérard, J., & Robert, V. 2018, in SF2A 2018 workshop [Google Scholar]
- Harvey, G. M. 1979, Observatory, 99, 195 [Google Scholar]
- Hees, A., Bailey, Q., Bourgoin, A., et al. 2016, Universe, 2, 30 [CrossRef] [Google Scholar]
- Hees, A., Le Poncin-Lafitte, C., Hestroffer, D., & David, P. 2018, Astrometry and Astrophysics in the Gaia Sky, 330, 63 [Google Scholar]
- Ianna, P. A. 1965, Vistas Astron., 6, 93 [CrossRef] [Google Scholar]
- Izmailov, I. S., Roshchina, E. A., Kiselev, A. A., et al. 2016, Astron. Lett., 42, 41 [CrossRef] [Google Scholar]
- Khrennikov, D. E., Titov, A. K., Ershov, A. E. E., Pariev, V. I., & Karpov, S. V. 2020, MNRAS, 493, 1344 [CrossRef] [Google Scholar]
- Khrutskaya, E. V., Khovritchev, M. Y., & Bronnikova, N. M. 2004, A&A, 418, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiseleva, T. P., Vasil’eva, T. A., Izmailov, I. S., & Roshchina, E. A. 2015, Sol. Syst. Res., 49, 72 [NASA ADS] [CrossRef] [Google Scholar]
- La Spina, A., Paolicchi, P., Kryszczyńska, A., & Pravec, P. 2004, Nature, 428, 400 [Google Scholar]
- Lainey, V., Arlot, J.-E., Karatekin, Ö., & van Hoolst, T. 2009, Nature, 459, 957 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lainey, V., Karatekin, Ö., Desmars, J., et al. 2012, ApJ, 752, 14 [Google Scholar]
- Lainey, V., Noyelles, B., Cooper, N., et al. 2019, Icarus, 326, 48 [Google Scholar]
- Lainey, V., Casajus, L. G., Fuller, J., et al. 2020, Nat. Astron., 4, 1053 [CrossRef] [Google Scholar]
- Lainey, V., Pasewaldt, A., Robert, V., et al. 2021, A&A, 650, A64 [CrossRef] [EDP Sciences] [Google Scholar]
- Le Poncin-Lafitte, C., Hees, A., & Lambert, S. 2016, Phys. Rev. D, 94, 125030 [NASA ADS] [CrossRef] [Google Scholar]
- Lehtinen, K., Prusti, T., de Bruijne, J., et al. 2018, A&A, 616, A185 [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L. 1980, A&A, 89, 41 [Google Scholar]
- Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malherbe, J. M., & Dalmasse, K. 2019, Sol. Phys., 294, 52 [CrossRef] [Google Scholar]
- Matsumoto, Y., Gu, P.-G., Kokubo, E., Oshino, S., & Omiya, M. 2020, A&A, 642, A23 [CrossRef] [EDP Sciences] [Google Scholar]
- Merat, P., Pecker, J. C., Vigier, J. P., & Yourgrau, W. 1974, A&A, 32, 471 [Google Scholar]
- Mouret, S. 2011, Phys. Rev. D, 84 [CrossRef] [Google Scholar]
- MPEC 2017-U181, 2017, Minor Planet Electronic Circular [Google Scholar]
- MPEC 2019-R106, 2019, Minor Planet Electronic Circular [Google Scholar]
- Mróz, P., Ryu, Y. H., Skowron, J., et al. 2018, AJ, 155, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Neiner, C., et al. 2018, in SF2A-2018: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. P. Di Matteo, F. Billebaud, F. Herpin, et al. [Google Scholar]
- Neiner, C., Gutiérrez-Soto, J., Baudin, F., et al. 2009, A&A, 506, 143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neiner, C., de Batz, B., Cochard, F., et al. 2011, AJ, 142, 149 [Google Scholar]
- Neiner, C., Floquet, M., Samadi, R., et al. 2012, A&A, 546, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neiner, C., Lee, U., Mathis, S., et al. 2020, A&A, 644, A9 [EDP Sciences] [Google Scholar]
- Nugent, C. R., Margot, J. L., Chesley, S. R., & Vokrouhlický, D. 2012, AJ, 144, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Pascu, D. 1994, in Galactic and Solar System Optical Astrometry, eds. L. V. Morrison, & G. F. Gilmore, 304 [Google Scholar]
- Pevtsov, A., Griffin, E., Grindlay, J., et al. 2019, BAAS, 51, 190 [Google Scholar]
- Rivinius, T., Carciofi, A. C., & Martayan, C. 2013, A&ARv, 21, 69 [Google Scholar]
- Robert, V., de Cuyper, J. P., Arlot, J. E., et al. 2011, MNRAS, 415, 701 [Google Scholar]
- Robert, V., Lainey, V., Pascu, D., et al. 2015, A&A, 582, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robert, V., Pascu, D., Lainey, V., et al. 2016, A&A, 596, A37 [CrossRef] [EDP Sciences] [Google Scholar]
- Sekanina, Z. 1976, Icarus, 27, 123 [Google Scholar]
- Semaan, T., Hubert, A. M., Zorec, J., et al. 2018, A&A, 613, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shao, L. 2014, Phys. Rev. Lett., 112, 111103 [Google Scholar]
- Siraj, A., & Loeb, A. 2020, ApJ, 903, L20 [Google Scholar]
- Spoto, F., Tanga, P., & Carry, B. 2019, in EPSC-DPS Joint Meeting 2019, 2019, EPSC-DPS2019-1361 [Google Scholar]
- Tombaugh, C. W. 1946, Leafl. Astron. Soc. Pac., 5, 73 [Google Scholar]
- Trilling, D. E., Robinson, T., Roegge, A., et al. 2017, ApJ, 850, L38 [Google Scholar]
- Verma, A. K., Margot, J.-L., & Greenberg, A. H. 2017, ApJ, 845, 166 [Google Scholar]
- Vokrouhlický, D., Milani, A., & Chesley, S. R. 2000, Icarus, 148, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Chesley, S. R., & Matson, R. D. 2008, AJ, 135, 2336 [Google Scholar]
- Will, C. M. 2014, Liv. Rev. Rel., 17, 4 [Google Scholar]
- Winter, L. 2008, Annual Report, Tech. rep., Royal Observatory of Belgium [Google Scholar]
- Ye, Q., Kelley, M. S. P., Bolin, B. T., et al. 2020, AJ, 159, 77 [Google Scholar]
- Zacharias, N., de Vegt, C., Nicholson, W., & Penston, M. J. 1992, A&A, 254, 397 [Google Scholar]
- Zacharias, N., Winter, L., Holdenried, E. R., et al. 2008, PASP, 120, 644 [Google Scholar]
All Tables
Comparisons between four sets of measurements; 145 star dots on a USNO Praesepe cluster plate.
Angular astrometric accuracy of the NAROO digitizer depending on the focal length of the telescope used for the realization of the plates.
All Figures
 |
Fig. 1. NAROO machine at the Paris Observatory, Meudon. |
| In the text | |
 |
Fig. 2. NAROO lighting optical scheme. |
| In the text | |
 |
Fig. 3. NAROO opto-mechanical drawing. |
| In the text | |
 |
Fig. 4. NAROO mean dark image. Color values on the x-axis denote pixel ADU counts. |
| In the text | |
 |
Fig. 5. NAROO mean flat image. Color values on the x-axis denote pixel ADU counts. A parasitic reflection of the microlenses is shown in the blue circle. |
| In the text | |
 |
Fig. 6. First NAROO scientific image (positive): center of a 1975 USNO photographic plate of Saturn. The image of Saturn is seen through a neutral metallic Inconel film filter. |
| In the text | |
 |
Fig. 7. NAROO XY-table stability. Red line denotes a 16 mm movement on both X and Y axes. Green line denotes the machine compensation before X-axis stability, enlarged 1000 times. Blue line denotes the machine compensation before Y-axis stability, enlarged 1000 times. |
| In the text | |
 |
Fig. 8. Correction of the optical distortion in micrometers of the objective/camera unit, in the 2560 by 2160 pixels field of view of the camera, shown as vectors enlarged 100 times (the largest vector is about 1.0-μm long). |
| In the text | |
 |
Fig. 9. Direct-reverse residuals as a function of the V magnitude, in microns. Red dots denote the X-axis residuals, and blue dots denote the Y-axis residuals. Each dot denotes a single star coordinate. |
| In the text | |
 |
Fig. 10. Accuracy of observations of the Galilean satellites obtained with telescopes of various focal lengths (Ferraz-Mello 1983). |
| In the text | |
 |
Fig. 11. Simulation of the evolution of the uncertainty of the ephemeris of 2015 OL35 from 1900 to 2100. The blue curve denotes the uncertainty of the ephemeris using the original astrometric observations from MPC. The orange and green curves denote the uncertainties of the ephemeris taking three additional potential prediscoveries and assuming astrometric precisions of 50 mas and 200 mas, respectively. |
| In the text | |
 |
Fig. 12. Solar filament as seen on 2001-07-03 (lower image) and 2001-07-04 (upper image). Its visibility strongly varies from one day to the next. Images from the Meudon spectroheliograph (available in the BASS2000 database). |
| In the text | |
 |
Fig. 13. Left panel: upper thumbnail shows an AR in high chromosphere (center of Ca II K3 line), while the lower one shows the same region at the same time, in low chromosphere (Hα line). Right panel: same active region, in low corona, on 2001-07-03 (upper image) and on 2001-07-04 (lower image). Left observations were realized with the Meudon spectroheliograph and are available in BASS2000. Right observations come from the SOHO/EIT instrument and are available at NASA. Automatic detections come from Barra et al. (2009). |
| In the text | |
 |
Fig. 14. NAROO digitization of a partial copy of one of the 1919 eclipse plates found in the archives of the Paris Observatory. The result mosaic is composed by 60 subimages. Four stars are detected. |
| In the text | |
 |
Fig. 15. Center of the NAROO digitization of Juvisy plate 00192, realized on July 16th 1906, with M6 and M20 objects. |
| In the text | |
 |
Fig. 16. Properties of the Pulkovo archive of photographic plates: distribution of observations over the celestial sphere in equatorial coordinates. PNA denotes observations realized with the Normal Astrograph, P26 denotes those realized with the 26-inch refractor, and EA denotes those realized with the Expeditionary Astrograph. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.