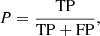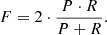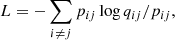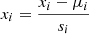| Issue |
A&A
Volume 652, August 2021
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202038911 | |
| Published online | 03 August 2021 | |
Interpreting automatic AGN classifiers with saliency maps⋆
1
Dipartimento di Fisica e Astronomia “G. Galilei”, Università degli Studi di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
e-mail: tobia.peruzzi@studenti.unipd.it
2
Center for Astro, Particle and Planetary Physics (CAP 3), New York University Abu Dhabi, Abu Dhabi, United Arab Emirates
e-mail: mp5757@nyu.edu
3
INAF, Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
4
INFN-Sezione di Padova, Via Marzolo 8, 35131 Padova, Italy
5
Finnish Centre for Astronomy with ESO (FINCA), University of Turku, Vesilinnantie 5, 20014 Turku, Finland
6
Aalto University Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
7
Dipartimento di Fisica e Astronomia, Università di Firenze, via G.Sansone 1, 50019 Sesto Fiorentino, Firenze, Italy
8
INAF, Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
Received:
13
July
2020
Accepted:
21
April
2021
Classification of the optical spectra of active galactic nuclei (AGN) into different types is currently based on features such as line widths and intensity ratios. Although well founded on AGN physics, this approach involves some degree of human oversight and cannot scale to large datasets. Machine learning (ML) tackles this classification problem in a fast and reproducible way, but is often (and not without reason) perceived as a black box. However, ML interpretability and are active research areas in computer science that are providing us with tools to mitigate this issue. We apply ML interpretability tools to a classifier trained to predict AGN types from spectra. Our goal is to demonstrate the use of such tools in this context, obtaining for the first time insight into an otherwise black box AGN classifier. In particular, we want to understand which parts of each spectrum most affect the predictions of our classifier, checking that the results make sense in the light of our theoretical expectations. We trained a support-vector machine on 3346 high-quality, low-redshift AGN spectra from SDSS DR15. We considered either two-class classification (type 1 versus 2) or multiclass (type 1 versus 2 versus intermediate-type). The spectra were previously and independently hand-labeled and divided into types 1 and 2, and intermediate-type (i.e., sources in which the Balmer line profile consists of a sharp narrow component superimposed on a broad component). We performed a train-validation-test split, tuning hyperparameters and independently measuring performance via a variety of metrics. On a selection of test-set spectra, we computed the gradient of the predicted class probability at a given spectrum. Regions of the spectrum were then color-coded based on the direction and the amount by which they influence the predicted class, effectively building a saliency map. We also visualized the high-dimensional space of AGN spectra using t-distributed stochastic neighbor embedding (t-SNE), showing where the spectra for which we computed a saliency map are located. Our best classifier reaches an F-score of 0.942 on our test set (with 0.948 precision and 0.936 recall). We computed saliency maps on all misclassified spectra in the test set and on a sample of randomly selected spectra. Regions that affect the predicted AGN type often coincide with physically relevant features, such as spectral lines. t-SNE visualization shows good separability of type 1 and type 2 spectra. Intermediate-type spectra either lie in-between, as expected, or appear mixed with type 2 spectra. Misclassified spectra are typically found among the latter. Some clustering structure is apparent among type 2 and intermediate-type spectra, though this may be an artifact. Saliency maps show why a given AGN type was predicted by our classifier resulting in a physical interpretation in terms of regions of the spectrum that affected its decision, making it no longer a black box. These regions coincide with those used by human experts, for example relevant spectral lines, and are even used in a similar way; the classifier effectively measures the width of a line by weighing its center and its tails oppositely.
Key words: methods: statistical / galaxies: active / quasars: general / galaxies: Seyfert
The code on which this work is based can be found at the following link https://gitlab.com/tobia.peruzzi/agn_spectra
© ESO 2021
1. Introduction
Active galactic nuclei (AGN) are the most energetic non-transient phenomena in the Universe. AGN can be found in the nuclei of galaxies characterized by highly ionized gas not correlated with stellar activity. The gas surrounding the AGN can be photoionized by photons produced by accretion mechanisms onto a supermassive black hole (SMBH), with MBH ≈ 106 − 109 M⊙, which accretes material from the surrounding interstellar medium (Salpeter 1964; Zel’Dovich & Novikov 1965; Lynden-Bell 1969; Rees 1984).
Classically AGN, and in particular Seyfert galaxies, are divided into two groups (Khachikyan & Weedman 1971; Khachikian & Weedman 1974): type 1 and type 2. The corresponding physical interpretation, called the Unified Model, is that for type 1 the observer looks directly into the unobscured accretion disk surrounded by fast-moving gas clouds, and for type 2 the line of sight into the accretion disk is blocked by an obscuring medium (Antonucci 1993; Urry & Padovani 1995).
AGN emit radiation in virtually all bands, and consequently have historically been described in terms of several classes of objects depending on the band they were discovered in. AGN classification is reviewed in detail by Padovani et al. (2017), which also includes a systematic discussion of the definitions of different but sometimes overlapping classes of AGN defined over time by observational astronomers in bands ranging from the radio to the gamma rays, known as the AGN zoo. In the following we focus on the problem of classification into type 1 and type 2 because of its implications for statistical analyses (see Elitzur 2012, which also discusses a refinement of the original unified model) on large catalogs and to illustrate an application of machine learning (ML) interpretability tools.
Classification of sources into type 1 and type 2 is typically based on features observed in the optical spectrum, such as the full width at half maximum (FWHM) of the broad Hβ line: type 1 AGN are classically defined as having FWHM of permitted broad lines in excess of those of the forbidden lines that rarely exceed 1000 km s−1, generally accompanied by an intense blue continuum; type 2 show permitted and forbidden emission lines of comparable width (Khachikian & Weedman 1974). Among type 1 AGN, the ratio of equivalent widths between FeII optical emission and the HI Balmer emission line Hβ helps to classify large samples of quasars along a main sequence (Boroson & Green 1992). This approach may be supplemented by observables in different bands, leading to the four-dimensional Eigenvector 1 (4DE1) parameter space (Sulentic et al. 2000a,b, 2007). These methods of AGN classification are firmly grounded in our understanding of AGN physics, but are hard to automate and require at least some human oversight. Direct quantification of the classification performance attained by humans is obviously hard, as it would involve setting up a controlled classification experiment, but there are documented instances of spurious source identifications which were overturned on closer inspection (e.g., Järvelä et al. 2020). The performance of automatic approaches on the other hand can be easily evaluated on an unseen test set. For these reasons, AGN classification for extremely large datasets, such as the Sloan Digital Sky Survey (SDSS), is likely to require an automated approach. The challenge we are facing is to make classification fast and accurate, without turning the classification process into a black box and losing physical interpretability.
Surprisingly, automatic ML classification of AGN optical spectra was attempted only a few times based on artificial neural networks (Rawson et al. 1996; González-Martín et al. 2014) and nearest neighbor schemes (Zhao et al. 2007). In all cases the focus was on correct automatic classification rather than on the interpretability of the resulting model. This is also the case for the most recent and to our knowledge most accurate AGN classification result based on a supervised ML framework presented by Tao et al. (2020). They trained various black box ML models on 10000 SDSS DR-14 spectra, achieving remarkably high classification performance (≈93% in terms of the F-score metric, which we discuss below). The authors also use random forest feature importance to gain some insight into which principal components of the feature space of spectra are more informative, but do not discuss their physical meaning. Despite the great classification performance, the current state of the art in automated AGN classification lacks interpretability: how are these models achieving such high performance? In the following we focus on this question, while pointing the reader interested in a general discussion of ML in astronomy to the excellent review by Fluke & Jacobs (2020).
Interpretability and explainability are open research areas in ML, and a variety of techniques have been proposed depending on the context in which the need for model explanation arises (see Molnar 2019, for a review). In astronomy and science in general, the ability to provide an explanation in addition to a bare prediction is likely crucial for adoption of ML methods.
While interpretability techniques are increasingly being applied to a variety of astronomical problems (see, e.g., Peek & Burkhart 2019; Villanueva-Domingo & Villaescusa-Navarro 2021; Zhang et al. 2020), along with natively interpretable models such as simple decision trees (e.g., Askar et al. 2019), they are still far from the norm in the field. Generally speaking, interpretability tools are either model specific or model agnostic. The former apply only to a specific set of ML models, while the latter potentially apply to any model, including a black box model; model agnostic tools are clearly more interesting for application to astronomy. In the following we visualize the gradient of our classifier’s prediction (more precisely the relative change in the predicted probability or confidence for the predicted class), which is applicable to any underlying ML model as long as it is differentiable. The gradient is inexpensive to compute, clearly indicates how to modify a given instance (an AGN spectrum in our case) to change the associated prediction, and can be readily visualized.
In this paper we obtain comparable accuracy to that found by Tao et al. (2020), also using a support-vector machine (SVM; Cortes & Vapnik 1995). We then explain our trained classifier’s decision on an individual basis by visualizing its gradient by a so-called saliency map (Simonyan et al. 2013) given any AGN spectrum. SVMs are differentiable, allowing us to compute the gradient of the predicted class probability at any given point in feature space. Since the coordinates of this space are the fluxes measured for each wavelength in our spectra, we can use the gradient computed at any given spectrum to visualize which parts of the spectrum are responsible for a type 1 classification (slightly increasing the flux at those wavelengths increases the predicted probability of being type 1), which parts are irrelevant (increasing the flux has no effect), and which parts pull in the opposite direction toward a type 2 classification (increasing the flux decreases the predicted probability of being type 1). This can be conveniently shown as a color-coding of the spectrum under consideration, and is an easy way to check what the model is basing its predictions on.
In addition to interpretability tools applied to classifiers, visualization and visual clustering based on dimensionality reduction approaches where high-dimensional data is mapped to a low-dimensional space, such as a plane for visualization purposes, are also becoming more commonplace in astronomy (see, e.g., Kos et al. 2018; Anders et al. 2018; Lamb et al. 2019; Furfaro et al. 2019; Steinhardt et al. 2020a,b; Kline & Prša 2020), with applications also to AGN ranging from time-tested linear methods such as principal component analysis (Yip et al. 2004a,b) to advanced deep learning approaches (Ma et al. 2019; Portillo et al. 2020). Since we use saliency maps as an instance-by-instance explanation of our ML model it is natural to leverage dimensionality reduction to represent AGN spectra on a plane, where we then show which instances (data points) we are examining. This also allows us to visualize the position of misclassified instances with respect to the other data in our set.
In Sect. 2 we describe the dataset used, and in Sect. 3 the supervised classification setup. In Sect. 4 we present the SVM performance (4.1), the AGN spectra space visualized with the dimensionality reduction algorithm t-distributed stochastic neighbor embedding t-SNE (4.2), and the application of saliency map interpretability tool to AGN spectra (4.3). In Sect. 5 we provide a summary of the results reached in this work.
2. Data
Our dataset is composed of 680 type 1, 2145 type 2, and 521 intermediate-type AGN spectra from the SDSS survey. All of them have been accurately classified by previous works in the literature, and are expected to have a lower rate of misclassification than what is typically achieved with unsupervised sample selection (see Sect. 2 of Berton et al. 2020). For this reason they are well-suited to testing our automatic classification procedure.
The selection of type 1 spectra is described in detail by Marziani et al. (2013). First, they selected sources cataloged as quasars in the SDSS DR7 in the redshift range 0.4–0.75 and with magnitudes brighter than 18.5 in g, r, or i band, to ensure a good spectral quality. They also included sources with FWHM(Hβ) < 1000 km s−1 selected by Zhou et al. (2006), which are usually not classified as quasars by SDSS. After a visual inspection to remove low-quality spectra, they included 680 sources in the final sample.
The selection of the type 2 and intermediate-type spectra was carried out by Vaona et al. (2012). In SDSS DR7 they selected all the sources showing the [O II]λ3727, [O III]λ5007, and [O I]λ6300 lines, with an additional criterion on the signal-to-noise ratio (S/N)([O I]λ6300) > 3. This sample of 119226 sources was subsequently reduced by applying a redshift threshold 0.02 ≤ z ≤ 0.1. The lower limit was needed to ensure the presence of the [O II] line, while the upper limit to avoid contamination from extranuclear sources within the fiber aperture. An empirical criterion based on line ratios suggested by Kewley et al. (2006) was applied to remove sources without AGN activity (see Eq. (1) in Vaona et al. 2012). The remaining objects were further analyzed on the basis of the diagnostic diagrams by Veilleux & Osterbrock (1987) and their Hα widths, and were finally divided into two samples of 2153 Seyfert 2 and 521 intermediate-type AGN. Thanks to these strict selection criteria, their spectra had a typical S/N, defined here as the ratio of the mean flux of the 5100 Å continuum to the standard deviation in the same spectral region, between 10 and 40, directly comparable to that of the type 1 sample.
Intermediate-type AGN show Balmer line profiles that consist of a sharp narrow component superimposed on a broad component (Osterbrock & Koski 1976; Osterbrock 1981, 1991). Following the classification proposed by Osterbrock, they are classified as 1.2, 1.5, and 1.8 in order of decreasing prominence of the broad component. For the context of the classification task presented in this work, they are considered as a single type since an additional subdivision would require a level of sophistication that is not necessary at this stage.
Every spectrum was shifted to rest frame using the values of z given by the SDSS and normalized to the flux value at 5100 Å in the rest frame. This value was chosen in order to normalize on a flux that belongs to the continuum and not to an emission line or some other component.
In order to perform classification on a fixed number of spectral features, we needed to turn each spectrum into an array of normalized fluxes of the same length. Every spectrum in the dataset was thus interpolated over 1000 points at equally spaced wavelengths obtaining flux values at the same wavelengths for every spectrum. Over the range of wavelength overlap, this results in an effective resolution in wavelength strictly higher than the nominal SDSS resolution in the same range, and therefore no information is lost in the interpolation. These flux values constitute our features, so our feature space has 1000 dimensions. We restricted the range of our interpolation to the shared overlap of our spectra (i.e., between the maximum among the minimum wavelengths of all the spectra and the minimum among the maximum wavelengths of all the spectra) so that we could include all spectra in the final sample without having to add padding. We note that this approach somewhat reduces the amount of information available to our classifier with respect to that used during human classification because some lines used in the latter may end up outside our adopted range. The values of the resulting wavelength range are reported in Table 1.
Extremes of the wavelength interpolation ranges for type 1, type 2, and intermediate-type AGN spectra.
3. Supervised classification setup
To classify AGN spectra we selected a support-vector machine (SVM) classifier (Cortes & Vapnik 1995) for two-class classification between type 1 versus type 2, and multiclass with type 1 versus type 2 versus intermediate-type. SVMs look for a maximum margin hyperplane separator between the classes, possibly after an implicit transformation into a higher dimensional space where data that is not linearly separable may become so. Maximizing the margin means that the separation surface is as far as possible from any data point, which is an additional constraint with respect to other methods that just find a separation surface. Intuitively this reduces the uncertainty in the classification (since points are far away from the separation surface, they are firmly classified) and results in a boundary between classes that depends only on a handful of training data points near the surface, the eponymous support vectors. It was shown empirically that SVMs perform well on a variety of structured data, text, and other classification tasks (see, e.g., Manning et al. 2008). In the following we use SVMs in the scikit-learn (Pedregosa et al. 2011) implementation for python. We make use of soft-margin classification, so the separating hyperplane is allowed to make some classification mistakes if this increases the margin, but these mistakes are weighted negatively within the cost function that is optimized to train the SVM. The cost of mistakes is a hyperparameter that we fine-tune in validation together with other hyperparameters, such as the kernel used for a nonlinear SVM, as described in the following.
The whole dataset was randomly divided into a training and a test set with an 80%−20% split. The training set was further randomly split into training and validation sets, again with an 80%−20% split, so the final proportions are training 64%, validation 16%, and testing 20%. The hyperparameter optimization (see below) took place within a five-fold cross-validation loop, while the test set was kept as a holdout set from the beginning (i.e., it was not involved in any cross-validation loop). The train-validation-test split was adopted in order to have a subset used to select the best set of parameters for the classifier (the validation set) and a subset of unseen data in order to test the performance of the best model on unseen data. The latter is one of the techniques used in ML to avoid overfitting, which happens when a ML model is unable to generalize well to new data. The random partitioning was unstratified, meaning that it is performed without imposing any kind of fixed ratio between the number of samples belonging to different classes, given the relatively balanced nature of our dataset with respect to the different class frequencies. However during all training steps of our SVM, we applied weights inversely proportional to class frequency in an attempt to counter class inbalance, using the class_weight=balanced option in scikit-learn. In Table 2 we show the frequency of the classes in training, validation, and test sets.
Class frequency in training, validation, and test sets.
We then performed a hyperparameter optimization for our SVM classifier using a grid search approach. The parameters optimized were cost C, which is the regularization parameter (the strength of the regularization is inversely proportional to C, which represents the cost of misclassification for a soft-margin SVM), and γ, which is a kernel coefficient used only for polynomial kernels or radial basis function (RBF) kernels that can be seen as the inverse of the radius of influence of samples selected by the model as support vectors. The choice of the kernel used was also itself subject to optimization. The grid search optimization was first applied to a wide range for parameter C, from 5 × 10−4 to 5 × 104 on an equally spaced logarithmic grid, and then interactively restricted around the best value until the F-score stopped improving (i.e., the fourth decimal digit remained constant). The range investigated for γ was narrower, going from 0.005 to 5.0. Both ranges were selected while keeping in mind the trade-off between computational requirements and the ability to satisfactorily cover hyperparameter space.
The hyperparameter optimization was performed for four different kernels: linear, polynomial of degree 2 and 3, and RBF. The performance was evaluated with the F-score, which is defined as the harmonic mean of precision and recall (Van Rijsbergen 1979; Chinchor 1992), where precision is the number of true positives (TP) divided by the total number of samples classified as positive (i.e., TP plus false positive, FP) and recall is the number of true positives divided by the number of all the actual positive samples (i.e., true positive plus false negatives, FN).
Based on these definitions, we can express precision, recall, and F-score as follows:
In the astronomical literature precision is often referred to as purity and recall as completeness.
A high value (close to 1) of the F-score means that the classifier is able to correctly classify most of the data, achieving both good precision and good recall. These definitions of course apply to a given class, where positive means a member of that class and negative a non-member. Their extension to a multiclass setting is straightforward by taking the mean over the different classes.
It was found that the kernel with the highest performance, that is the highest F-score, for multiclass classification was the linear one and the best regularization parameter was C = 0.07, while for two-class classification all the kernels achieved nominally perfect results except for the polynomial of degree 3. These metrics were calculated on the validation set. The performances of the four different models corresponding to the four kernels can be seen in Table 3 for multiclass classification, and in Table 4 for two-class classification.
F-score on validation set for the multiclass classification problem for four different models corresponding to different SVM kernels (from top to bottom): linear, radial basis, polynomial of degree two, polynomial of degree three.
F-score on validation set for four different models (two-class classification).
We then trained the SVM using both the training and validation subsets and evaluated the model performance on the test set.
3.1. Dependence on signal-to-noise ratio
We explored how the performance of our SVM (trained on both the training and validation subsets) changes when we add Gaussian noise onto the test-set spectra. The noise’s standard deviation was taken proportional to the flux value corresponding to 5100 Å, with the following values as proportionality factors: 0.1, 0.2, 0.3, 0.4, 1.0, 2.0, 3.0, and 4.0. The metrics can be seen in Table 5 and in Fig. 1a and b. As can be seen, for small values of the noise, the mean F-score remains above 0.8, but decreases almost linearly with increasing noise factor, while the type 1 F-score initially remains equal to 1.0. The type 2 F-score decreases similarly to the mean F-score, but remains above 0.85. On the contrary, the intermediate-type F-score decreases rapidly with the noise factor, reaching 0.63 for noise factor 0.4. With higher values for the noise factor, all the F-scores are below 0.8, the only exception being for the first two values of the type 1 F-score that remain above 0.8 for noise factor 1.0 and noise factor 2.0. It is worth noting that for higher values of the noise factor, the type 1 F-score decreases rapidly, in contrast to the F-scores of type 2 and intermediate-type. This can indicate that in general spectra characterized by a low S/N are harder to classify, and that the SVM classifier we used also begins to misclassify type 1 AGN for high values of the noise, but the confidence for type 2 and intermediate-type does not change considerably after some values of the noise factor.
 |
Fig. 1. F-scores for linear SVM on data with incremental noise. Blue: mean F-scores; orange: F-scores for type 1; green: F-scores for type 2; and red: F-scores for intermediate-type. (a) Noise factor values: 0.1, 0.2, 0.3, 0.4. (b) Noise factor values: 1.0, 2.0, 3.0, 4.0. |
Performance metrics calculated on test set with incremental additive Gaussian noise.
4. Interpretability framework
4.1. Classifier gradient visualized as saliency map
In order to gain insights on what our SVM classifiers have learned, we followed the saliency map approach that found wide application in the context of deep neural networks (Simonyan et al. 2013) and has proven very useful in the interpretation of image classifiers, showing which parts of a given image contribute the most to the image’s predicted classification. In this paper we refer exclusively to the second meaning of the term “saliency map” defined in the Simonyan et al. (2013) paper, which is an image (in our case a one-dimensional array representing a given AGN spectrum) where each pixel represents the derivative of the class score with respect to the value of the corresponding pixel of a given image as per their Eq. (4).
In the context of our work we built saliency maps as follows. We considered the class score or, loosely speaking, the probability associated by our classifier with a given sample’s predicted class, pc(fi), where fi is the flux at wavelength λi for a given spectrum and c is the predicted class, for example, type I. We then computed a numerical approximation to the gradient gi = ∇f log pc(fi), which yields a vector the same length as the original spectrum. Finally, we visualized the computed gradient vector as a color-coding in addition to the original spectrum, with blue (orange) corresponding to wavelengths for which the associated component of the gradient is positive (negative).
To compute the gradient gi, each feature fi of a chosen sample is individually perturbed by a certain value ei, forming n spectra with the ith feature perturbed, where n is the number of features (in this work equal to 1000). Then our SVM model is used to reclassify these perturbed spectra, obtaining a value of pc(fj + δijei) for each one. Since the perturbation was chosen as ei = 0.01fi (i.e., a 1% perturbation), pc(fj + δijei)−pc(fi)/ei approximates the ith component of the gradient of log pc.
A gi value close to zero (shown in white in the map) means that a perturbation of the ith feature does not change the confidence of the classifier in classifying the spectrum as belonging to a specific class; a positive value means that a perturbation of the ith feature strengthens the confidence of the classifier’s prediction for the given class (increases the class score) and a negative value reduces it.
4.2. Dimensionality reduction for visualization
t-SNE (van der Maaten & Hinton 2008) is an unsupervised dimensionality reduction algorithm used for visualization and data exploration in many ML settings. The goal of dimensionality reduction is to map high-dimensional data to a lower-dimensional space (in our case the plane) while preserving the pairwise distances of points. This is impossible to do rigorously, because the high-dimensional space cannot be embedded in the plane, but t-SNE achieves this approximately by prioritizing the distances of points that are near to each other, so short distances are distorted the least, while the large-scale structure of the dataset is mostly lost. This is obtained by minimizing a loss
where pij is a similarity measure between points i and j in the original high-dimensional space and qij is a (different) similarity measure in the low-dimensional space. While pij decays as a Gaussian with the distance between point i and j, qij decays like a Student’s t-distribution with one degree of freedom, hence the name of the algorithm. We can see from Eq. (4) that points that are far from each other in the high-dimensional space do not contribute much to the loss as their pij goes to zero exponentially with squared distance. The outcome of t-SNE depends on the perplexity hyperparameter, which drives the standard deviation of the Gaussian used to define pij and can be loosely interpreted as the typical size of the subgroups expected in a given dataset. A practical illustration of the effect of varying perplexity can be found in Wattenberg et al. (2016). Since perplexity can be set at the discretion of the user of t-SNE, results that depend strongly on this parameter, such as clustering structure that shows up only for a narrow range of values of perplexity, should not be blindly trusted. In the following we make sure to test a wide range of perplexity values. We use t-SNE in the scikit-learn implementation (Pedregosa et al. 2011) for Python. While our main use for t-SNE visualization is to show where the AGN spectra that we selected for inspection through saliency maps are located, which is particularly useful for misclassified spectra, we also gain some useful insight on the structure of our dataset through this approach, as shown below.
5. Results
5.1. Classifier performance
The metrics values reached by our models on our test set are reported in Table 6 for multiclass classification and in Table 7 for two-class classification. We find that they are comparable to those obtained on the validation set, suggesting that no overfitting is occurring. Table 8 lists the values of precision, recall, and F-score obtained by our best model for the three classes: type 1, type 2, and intermediate-type AGN. It is clear that separating type 1 and type 2 can be easily done by every kernel with the right choice of hyperparameters. On the other hand, the multiclass classification including intermediate-type spectra is a more difficult task to solve, requiring a careful choice of hyperparameters in order to achieve high performance.
Metrics values on test set for linear, RBF, and polynomial kernels for multiclass classification.
Metrics values on test set for linear, RBF, and polynomial kernels for two-class classification.
Precision, recall, and F-score obtained by SVM with linear kernel for every class in the test set.
The confusion matrix for the two best models for multiclass classification can be seen in Fig. 2 and the normalized confusion matrix in Fig. 3. Even if the linear kernel performs slightly better than the RBF, both models are able to classify the majority of the spectra, failing only in the classification of a small number of type 2 and intermediate-type spectra. Specifically, 22 intermediate-type spectra (out of 115) were classified as type 2 by the RBF model, and 12 type 2 (out of 423) as intermediate; the linear model failed to classify 19 intermediate spectra (out of the same 115) and classified them as type 2, and 12 type 2 (out of the same 423) were classified as intermediate. This was an expected result because the distinction between type 2 and intermediate AGN is difficult in the presence of spectra with low S/N. Therefore, this uncertainty in the distinction between intermediate-type and type 2 AGN spectra in presence of a low S/N can affect the automated classification result.
 |
Fig. 2. Confusion matrix heatmaps for SVM classification over test set. Horizontal axis: labels predicted by the classifier. Vertical axis: true labels for the samples. (a) Confusion matrix for RBF kernel. (b) Confusion matrix for linear kernel. |
 |
Fig. 3. Normalized confusion matrix heatmaps for SVM classification over test set. Horizontal axis: labels predicted by the classifier. Vertical axis: true labels for the samples. (a) Normalized confusion matrix for RBF kernel. (b) Normalized confusion matrix for linear kernel. |
5.2. Training time complexity
Every kernel was also evaluated in terms of the computational time of the training. The computational time is evaluated by taking the time average of ten different trainings for every kernel (using both train and validation sets for this purpose). The results presented in Table 9 show that the two polynomial kernels are the fastest, in particular the polynomial of degree 2. Surprisingly, the linear kernel appears to be the slowest. A possible explanation could be that the scikit-learn implementation used in this work (libsvm-based; Chang & Lin 2011) is less efficient for the linear case, as stated in the scikit-learn documentation (Pedregosa et al. 2011). The documentation also provides an estimation of the time complexity, in big O notation, of the SVM implementation, that scales between 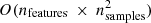 and
and 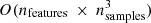 (Pedregosa et al. 2011). Every computation in this step was performed on an Intel(R) Core(TM) i7 − 6700HQ CPU (2.60 GHz).
(Pedregosa et al. 2011). Every computation in this step was performed on an Intel(R) Core(TM) i7 − 6700HQ CPU (2.60 GHz).
Training computational time for various kernels.
5.3. Visualizing spectra with t-SNE
Thanks to the interpolation used in this work, the AGN spectra space turns out to be 1000-dimensional, while the original spectra comprised a variable number of points typically on the order of a few thousands. The dimensionality of feature space is still quite high, however. We then used t-SNE to map our spectra dataset to a plane. The algorithm was first applied to data not scaled and not mean normalized to compare the results of this case to the case with pre-processed features, as described below.
The result of t-SNE applied only to type 1 and type 2 AGN can be seen in Fig. A.1. In the embedded plane, type 1 AGN and type 2 AGN are clearly separated, with just a few outliers. The perplexity parameter was set to 50 in Fig. A.1. With lower perplexities the separation between the two types was somewhat less clear, but still persisted as can be seen in Fig. A.2. Additionally, some smaller-scale structures can be seen. We also applied t-SNE to the whole dataset, including intermediate-type AGN. The result can be seen in Fig. 4 (in this case as well the perplexity was set to 50). Predictably, intermediate-type AGN cannot be well separated from the other two classes, in particular from type 2 spectra with which they appear somewhat mixed. However, there is a clear cluster of intermediate-type spectra connecting the regions occupied by type 1 and type 2 spectra, true to the definition of intermediate-type. While spurious groups may sometimes appear in t-SNE plots, this is likely a physically motivated feature since it persists even when the perplexity is varied (see below). At the moment we can only speculate on the physical meaning of the other two subclusters of intermediate-type spectra that appear to gather in distinct “islands” at the extremes of the region occupied by type 2 spectra. Perhaps this should be addressed by direct visual inspection of the spectra as part of a future work. In Fig. A.3 we plot the embedded spaces for various values of perplexity, showing that the main results we outlined here are robust to changes in the perplexity parameter; this is discussed further in Appendix.
 |
Fig. 4. t-SNE embedded plane for type 1, type 2, and intermediate-type AGN. Perplexity: 50. Blue points: type 1; yellow points: type 2; red points: intermediate-type; red circles: possible intermediate-type subgroups identified by the t-SNE algorithm. |
5.4. Saliency maps
In the following we consider directly the multiclass problem (type 1, type 2, intermediate-type) because of its higher scientific interest and because we find no misclassified instances in the two-class problem (i.e., we have a nominally perfect accuracy), as discussed above. We thus used saliency maps to investigate misclassified and correctly classified spectra in the multiclass problem. The saliency maps for a correctly classified spectrum (Fig. 5) and a misclassified spectrum (Fig. 6) show that the main optical lines used by humans to classify AGN spectra are also recognized by the SVM as important features. In every saliency map we plot the main lines that can be used to classify AGN spectra: [O II] 3727, He I 3889, Hδ4101, Hγ4340, Hβ4861, [O III] 4959, and [O III] 5007). The region around the Hβ line plays an especially important role, as can be seen in both Fig. 5 and Fig. 6, where the center of the line and its tails appear in opposite colors, signifying the opposite effect on the class score of an increase in flux. In particular, Fig. 6 is an intermediate-type confidently (76%) misclassified as type 2, with the model’s decision depending mostly on the Hβ line. This is apparent by looking at the region next to the Hβ line where the continuum is the reddest spot in the saliency map. This shows that the misclassification is largely due to the absence of a broad component in Hβ (we recall here that red means that increasing the flux value at that location would reduce the confidence in the predicted class). Other regions of the saliency map that appear to contribute to the misclassification are the other hydrogen lines, but their contribution is minor as evidenced by the color-coding. Even so, the pattern of color-coding is similar, suggesting that lack of a broad component is the main driving feature for misclassification here. To properly classify this spectrum we likely would need to observe the Hα line, which is not included in the current spectral range, otherwise an intermediate-type 1.9, which would show a broadening only on the Hα line, may appear as a type 2 because it has a virtually unbroadened Hβ line. These findings should be contrasted with Fig. 5, where the color-coding shows the same behavior, but in reverse: the tails of the Hβ appear colored in blue, showing that increasing the flux there would lead to an even more confident classification as intermediate-type. This applies similarly to the other hydrogen lines.
 |
Fig. 5. Intermediate-type spectrum correctly classified by our SVM. The regions of the spectrum shown in blue are those that most contributed toward its classification as an intermediate-type, whereas those shown in red would reduce the SVM classification confidence if their flux increased. Several regions surrounding lines conventionally used for classification appear in blue, suggesting that our SVM model relied, in this case, on clues similar to those used by human experts; in particular, the center of the Hβ line appears in red and the tails in blue, which corresponds to the classifier using the width of the Hβ line for its decision. |
 |
Fig. 6. Intermediate-type spectrum misclassified as type 2 with 76% confidence. The regions of the spectrum shown in blue are those that most contributed toward its classification as a type 2, whereas those shown in red would reduce the SVM classification confidence if their flux increased. |
For example, increasing the flux in the tails of the Hβ line (i.e., increasing its width for a given height of the central peak) reduces the classification probability of classifying the spectrum in Fig. 5 as intermediate-type, while it increases the probability of classifying it as type 1, as one would expect; increasing the flux in the center has exactly the opposite effect. This result is expected because a broader Hβ profile, indicative of a type 1 AGN, would significantly change the shape of the spectrum next to the line. Interestingly, the saliency maps show that the continuum between the Hγ and Hβ also affects the classification results. This is also reasonable, considering how the continuum differs between type 1 spectra and type 2–intermediate.
In Fig. 7 we show the spectra for which we calculated a saliency map projected onto the t-SNE embedded plane. In the figure the red panels correspond to misclassified spectra and the green ones to correctly classified spectra. The corresponding saliency maps can be seen in Fig. 8 for misclassified spectra, and in Fig. 9 for correctly classified spectra. The numbering corresponds to that reported in Fig. 7.
 |
Fig. 7. Randomly selected spectra for which there are computed and visualized saliency maps, shown in the t-SNE embedded plane. Spectra that were correctly classified by our SVM are shown in green, while misclassified spectra are shown in red. Color-coding for the points as in Fig. 4. Green rectangles: correctly classified spectra for which saliency maps were calculated; red rectangles: misclassified spectra for which saliency maps were calculated. |
 |
Fig. 8. Saliency maps for misclassified spectra. The regions of the spectrum shown in blue are those that most contributed toward the classification chosen by our model, whereas those shown in red would reduce the SVM classification confidence if their flux were to increase. (1) Type 2 misclassified as Int. (2) Type 2 misclassified as Int. (3) Type 2 misclassified as Int. (4) Int. misclassified as type 2 (5) Int. misclassified as type 2 (6) Int. misclassified as type 2. |
 |
Fig. 9. Saliency maps for correctly classified spectra. Color-coding and axes as in Fig. 8. (7) Type 1, correctly classified (8) Type 2, correctly classified (9) Int. type, correctly classified (10) Type 2, correctly classified (11) Type 2, correctly classified (12) Int. type, correctly classified (13) Type 1, correctly classified (14) Type 1, correctly classified. |
For the spectra in Fig. 8 where an intermediate had been misclassified as type 2, the cause of misclassification as inferred from the saliency map is the same as discussed above for Fig. 6. When the opposite misclassification occurs, we note that the Hβ line often appears embedded in the underlying stellar absorption, a situation that is likely not common enough in our training set for the model to learn to deal properly with it.
Classification probabilities calculated by the SVM classifier can be seen for misclassified spectra in Table 10 and for correctly classified spectra in Table 11.
Classification probabilities for misclassified spectra for which saliency maps were calculated.
Classification probabilities for misclassified spectra for which saliency maps were calculated.
The classification of spectra to a high level of confidence, like the 14th spectrum in Fig. 9, does not change considerably under small perturbations, as are the ones used in this work to calculate the confidence derivative. This can be interpreted as the fact that single features, even if perturbed, do not change a high confidence prediction, showing that the results obtained with the SVM are robust.
6. Conclusions
We trained a support-vector machine model to classify AGN spectra, obtaining fairly accurate results on a test set not seen in training (F-score of ≈94%). While it is tempting to just apply the trained model to a large sample of spectra, we argue that it is crucial to first understand why the classifier returns the prediction it does. We showed that simple interpretability tools, such as a saliency map, allow us to easily accomplish this, at least on a spectrum-by-spectrum basis. Even though a general explanation of the criteria used by a classifier (as would be achieved by some natively interpretable ML method) is in general impossible to achieve for a black box classifier, saliency maps make it possible to understand the workings of an otherwise black box classifier in the neighborhood of any given data point.
We computed saliency maps of a random sample of correctly classified and misclassified spectra. In general we find that the regions of the spectrum that most affect the classifier prediction are similar to those used by a human expert, namely those around the spectral lines [O II] 3727, He I 3889, Hδ4101, Hγ4340, Hβ4861, [O III] 4959, and [O III] 5007. In addition, the way in which the model uses the information in these regions conforms to our expectations; for example, it implicitly relies on the width of the Hβ line which increases the probability of classifying a spectra as type 1. We thus conclude, at least for the spectra we considered, that our classifier operates much in the same way as a human would, just automatically and much faster. This is extremely reassuring regarding the possibility of applying ML classifiers to the large datasets of spectra that will result from upcoming surveys, which will not be amenable to direct human classification.
We also visualized the high-dimensional feature space of the spectra using the t-SNE algorithm, which maps spectra to points in a plane while attempting to preserve the local pairwise distances. We find that type 1 and type 2 spectra are mapped to distinct regions of the plane, forming two islands separated by a clear-cut isthmus. If intermediate-type spectra are also included, some of them happen to populate the isthmus, forming a bridge between type 1 and type 2, as expected from the very definition of intermediate-type spectra. However, several intermediate-types end up in the same region occupied by type 2 spectra, apparently mixed with them. It may be that labeling these spectra as intermediate-type is questionable in the first place. Interestingly, both intermediate-type and type 2 spectra show subclustering structure in the t-SNE plane. While this may be an artifact of t-SNE, it persists when different values of the perplexity hyperparameter are used (perplexity roughly corresponding to the expected size of groups in the dataset), which suggests that the result is genuine. Further work is needed to characterize these subgroups, perhaps comparing them with proposed AGN subtypes; we plan to carry this out in a subsequent paper.
Acknowledgments
This project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No. 664931. This material is based upon work supported by Tamkeen under the NYU Abu Dhabi Research Institute grant CAP3. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
References
- Anders, F., Chiappini, C., Santiago, B. X., et al. 2018, A&A, 619, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Askar, A., Askar, A., Pasquato, M., & Giersz, M. 2019, MNRAS, 485, 5345 [Google Scholar]
- Berton, M., Björklund, I., Lähteenmäki, A., et al. 2020, Contrib. Astron. Obs. Skalnate Pleso, 50, 270 [NASA ADS] [Google Scholar]
- Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [Google Scholar]
- Chang, C. C., & Lin, C. J. 2011, ACM Transactions on Intelligent Systems and Technology, 2, 1, software available at http://www.csie.ntu.edu.tw/cjlin/libsvm [Google Scholar]
- Chinchor, N. 1992, in Proceedings of the 4th conference on Message understanding, Association for Computational Linguistics, 30 [Google Scholar]
- Cortes, C., & Vapnik, V. 1995, Mach. Learn., 20, 273 [Google Scholar]
- Elitzur, M. 2012, ApJ, 747, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Fluke, C. J., & Jacobs, C. 2020, WIREs Data Mining and Knowledge Discovery, 10 [Google Scholar]
- Furfaro, R., Linares, R., & Reddy, V. 2019, in Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, 17 [Google Scholar]
- González-Martín, O., Díaz-González, D., Acosta-Pulido, J. A., et al. 2014, A&A, 567, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Järvelä, E., Berton, M., Ciroi, S., et al. 2020, A&A, 636, L12 [CrossRef] [EDP Sciences] [Google Scholar]
- Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Khachikian, E. Y., & Weedman, D. W. 1974, ApJ, 192, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Khachikyan, É. Y., & Weedman, D. W. 1971, Astrophysics, 7, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kline, T. R., & Prša, A. 2020, Am. Astron. Soc. Meeting Abstr., 52, 170.30 [Google Scholar]
- Kos, J., Bland-Hawthorn, J., Freeman, K., et al. 2018, MNRAS, 473, 4612 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, K., Malhotra, G., Vlontzos, A., et al. 2019, ArXiv e-prints [arXiv:1910.03085] [Google Scholar]
- Lynden-Bell, D. 1969, Nature, 223, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, Z., Xu, H., Zhu, J., et al. 2019, ApJS, 240, 34 [CrossRef] [Google Scholar]
- Manning, C. D., Schütze, H., & Raghavan, P. 2008, Introduction to Information Retrieval (Cambridge University Press) [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Plauchu-Frayn, I., & del Olmo, A. 2013, A&A, 555, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molnar, C. 2019, Interpretable machine learning (Lulu.com) [Google Scholar]
- Osterbrock, D. E. 1981, ApJ, 249, 462 [Google Scholar]
- Osterbrock, D. E. 1991, Rep. Prog. Phys., 54, 579 [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Koski, A. T. 1976, MNRAS, 176, 61P [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Alexander, D. M., Assef, R. J., et al. 2017, A&ARv, 25, 2 [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Peek, J. E. G., & Burkhart, B. 2019, ApJ, 882, L12 [Google Scholar]
- Portillo, S. K. N., Parejko, J. K., Vergara, J. R., & Connolly, A. J. 2020, AJ, 160, 45 [Google Scholar]
- Rawson, D. M., Bailey, J., & Francis, P. J. 1996, PASA, 13, 207 [NASA ADS] [Google Scholar]
- Rees, M. J. 1984, ARA&A, 22, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1964, ApJ, 140, 796 [CrossRef] [Google Scholar]
- Simonyan, K., Vedaldi, A., & Zisserman, A. 2013, ArXiv preprint [arXiv:1312.6034] [Google Scholar]
- Steinhardt, C. L., Weaver, J. R., Maxfield, J., et al. 2020a, ApJ, 891, 136 [CrossRef] [Google Scholar]
- Steinhardt, C. L., Kragh Jespersen, C., Severin, J. B., et al. 2020b, Am. Astron. Soc. Meeting Abstr., 52, 440.04 [Google Scholar]
- Sulentic, J. W., Marziani, P., & Dultzin-Hacyan, D. 2000a, ARA&A, 38, 521 [Google Scholar]
- Sulentic, J. W., Zwitter, T., Marziani, P., & Dultzin-Hacyan, D. 2000b, ApJ, 536, L5 [Google Scholar]
- Sulentic, J. W., Bachev, R., Marziani, P., Negrete, C. A., & Dultzin, D. 2007, ApJ, 666, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Tao, Y., Zhang, Y., Cui, C., & Zhang, G. 2020, ASP Conf. Ser., 522, 421 [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [Google Scholar]
- van der Maaten, L., & Hinton, G. 2008, J. Mach. Learn. Res., 9, 2579 [Google Scholar]
- Van Rijsbergen, C. J. 1979 in Proceedings of the Joint IBM/University of Newcastle uponTyne Seminar on Data Base Systems, 1 [Google Scholar]
- Vaona, L., Ciroi, S., Di Mille, F., et al. 2012, MNRAS, 427, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Villanueva-Domingo, P., & Villaescusa-Navarro, F. 2021, ApJ, 907, 44 [CrossRef] [Google Scholar]
- Wattenberg, M., Viégas, F., & Johnson, I. 2016, Distill, http://distill.pub/2016/misread-tsne [Google Scholar]
- Yip, C. W., Connolly, A. J., Vanden Berk, D. E., et al. 2004a, AJ, 128, 2603 [Google Scholar]
- Yip, C. W., Connolly, A. J., Szalay, A. S., et al. 2004b, AJ, 128, 585 [Google Scholar]
- Zel’Dovich, Y. B., & Novikov, I. D. 1965, Sov. Phys. Dokl., 9, 834 [Google Scholar]
- Zhang, C., Wang, C., Hobbs, G., et al. 2020, A&A, 642, A26 [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, M.-F., Wu, C., Luo, A.-L., Wu, F.-C., & Zhao, Y.-H. 2007, Chin. Astron. Astrophys., 31, 352 [CrossRef] [Google Scholar]
- Zhou, H., Wang, T., Yuan, W., et al. 2006, ApJS, 166, 128 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Effects of feature scaling and perplexity on t-SNE results
The t-SNE algorithm depends on perplexity, a tunable parameter that loosely corresponds to the expected number of neighbors of the typical point in the dataset under consideration. The visualization produced by t-SNE can vary strongly as perplexity is changed, and there is no general rule on how to pick the right value for this parameter. This may result in misleading visualizations, so it is best to try different values of perplexity and be wary of features (e.g., data subclusters) that only show up in a narrow range of perplexities (Wattenberg et al. 2016). In Fig. A.2 we explore the effects of varying perplexity between 5 and 40 for type 1 and type 2 AGN, while in Fig. A.3 we also include intermediate-type AGN.
 |
Fig. A.1. t-SNE embedded plane for type 1 and type 2 AGN. Blue points: type 1; yellow points: type 2. |
 |
Fig. A.2. t-SNE for type 1 and type 2 with various perplexity values. Color-coding of points as in Fig. A.2. (a) Perplexity: 5 (b) Perplexity: 15 (c) Perplexity: 30 (d) Perplexity: 40. |
 |
Fig. A.3. t-SNE for whole dataset with various perplexity values. Color-coding of points as in Fig. 4. (a) Perplexity: 5 (b) Perplexity: 15 (c) Perplexity: 30 (d) Perplexity: 40. |
After that, the t-SNE algorithm was fed with scaled and mean normalized data, which means that every feature xi is expressed by
where μi is the average of the ith feature and si is the standard deviation of the ith feature. The results can be seen in Fig. A.4, with a perplexity of 50. The result for other perplexity values can be seen in Fig. A.5.
 |
Fig. A.4. t-SNE embedded plane for type 1, type 2, and intermediate-type AGN spectra scaled and mean normalized. Color-coding of points as in Fig. 4. |
 |
Fig. A.5. t-SNE for whole dataset scaled and mean normalized with various perplexity values. Color-coding of points as in Fig. 4. (a) Perplexity: 5 (b) Perplexity: 15 (c) Perplexity: 30 (d) Perplexity: 40. |
Overall, the outcome is similar to the un-normalized case, and t-SNE (with the right choice of perplexity) seems to perform just as well after feature scaling and mean normalization. The result presented in Fig. A.4 can be interpreted even more clearly as a transition from type 1 spectra (characterized by broad lines and strong continuum) to intermediate-type spectra (characterized by narrower lines and lower continuum), and from intermediate-type to type 2 spectra (characterized by narrow lines and almost constant continuum). Some intermediate-type spectra will still be clustered together with type 1, or more often with type 2 spectra, but this is an expected result. The distinction between intermediate-type and type 2 spectra is not strict, and spectra of the two types may appear similar. Nonetheless the figure shows a clear transition region between type 1 and type 2 populated by intermediate-type spectra.
All Tables
Extremes of the wavelength interpolation ranges for type 1, type 2, and intermediate-type AGN spectra.
F-score on validation set for the multiclass classification problem for four different models corresponding to different SVM kernels (from top to bottom): linear, radial basis, polynomial of degree two, polynomial of degree three.
Performance metrics calculated on test set with incremental additive Gaussian noise.
Metrics values on test set for linear, RBF, and polynomial kernels for multiclass classification.
Metrics values on test set for linear, RBF, and polynomial kernels for two-class classification.
Precision, recall, and F-score obtained by SVM with linear kernel for every class in the test set.
Classification probabilities for misclassified spectra for which saliency maps were calculated.
Classification probabilities for misclassified spectra for which saliency maps were calculated.
All Figures
 |
Fig. 1. F-scores for linear SVM on data with incremental noise. Blue: mean F-scores; orange: F-scores for type 1; green: F-scores for type 2; and red: F-scores for intermediate-type. (a) Noise factor values: 0.1, 0.2, 0.3, 0.4. (b) Noise factor values: 1.0, 2.0, 3.0, 4.0. |
| In the text | |
 |
Fig. 2. Confusion matrix heatmaps for SVM classification over test set. Horizontal axis: labels predicted by the classifier. Vertical axis: true labels for the samples. (a) Confusion matrix for RBF kernel. (b) Confusion matrix for linear kernel. |
| In the text | |
 |
Fig. 3. Normalized confusion matrix heatmaps for SVM classification over test set. Horizontal axis: labels predicted by the classifier. Vertical axis: true labels for the samples. (a) Normalized confusion matrix for RBF kernel. (b) Normalized confusion matrix for linear kernel. |
| In the text | |
 |
Fig. 4. t-SNE embedded plane for type 1, type 2, and intermediate-type AGN. Perplexity: 50. Blue points: type 1; yellow points: type 2; red points: intermediate-type; red circles: possible intermediate-type subgroups identified by the t-SNE algorithm. |
| In the text | |
 |
Fig. 5. Intermediate-type spectrum correctly classified by our SVM. The regions of the spectrum shown in blue are those that most contributed toward its classification as an intermediate-type, whereas those shown in red would reduce the SVM classification confidence if their flux increased. Several regions surrounding lines conventionally used for classification appear in blue, suggesting that our SVM model relied, in this case, on clues similar to those used by human experts; in particular, the center of the Hβ line appears in red and the tails in blue, which corresponds to the classifier using the width of the Hβ line for its decision. |
| In the text | |
 |
Fig. 6. Intermediate-type spectrum misclassified as type 2 with 76% confidence. The regions of the spectrum shown in blue are those that most contributed toward its classification as a type 2, whereas those shown in red would reduce the SVM classification confidence if their flux increased. |
| In the text | |
 |
Fig. 7. Randomly selected spectra for which there are computed and visualized saliency maps, shown in the t-SNE embedded plane. Spectra that were correctly classified by our SVM are shown in green, while misclassified spectra are shown in red. Color-coding for the points as in Fig. 4. Green rectangles: correctly classified spectra for which saliency maps were calculated; red rectangles: misclassified spectra for which saliency maps were calculated. |
| In the text | |
 |
Fig. 8. Saliency maps for misclassified spectra. The regions of the spectrum shown in blue are those that most contributed toward the classification chosen by our model, whereas those shown in red would reduce the SVM classification confidence if their flux were to increase. (1) Type 2 misclassified as Int. (2) Type 2 misclassified as Int. (3) Type 2 misclassified as Int. (4) Int. misclassified as type 2 (5) Int. misclassified as type 2 (6) Int. misclassified as type 2. |
| In the text | |
 |
Fig. 9. Saliency maps for correctly classified spectra. Color-coding and axes as in Fig. 8. (7) Type 1, correctly classified (8) Type 2, correctly classified (9) Int. type, correctly classified (10) Type 2, correctly classified (11) Type 2, correctly classified (12) Int. type, correctly classified (13) Type 1, correctly classified (14) Type 1, correctly classified. |
| In the text | |
 |
Fig. A.1. t-SNE embedded plane for type 1 and type 2 AGN. Blue points: type 1; yellow points: type 2. |
| In the text | |
 |
Fig. A.2. t-SNE for type 1 and type 2 with various perplexity values. Color-coding of points as in Fig. A.2. (a) Perplexity: 5 (b) Perplexity: 15 (c) Perplexity: 30 (d) Perplexity: 40. |
| In the text | |
 |
Fig. A.3. t-SNE for whole dataset with various perplexity values. Color-coding of points as in Fig. 4. (a) Perplexity: 5 (b) Perplexity: 15 (c) Perplexity: 30 (d) Perplexity: 40. |
| In the text | |
 |
Fig. A.4. t-SNE embedded plane for type 1, type 2, and intermediate-type AGN spectra scaled and mean normalized. Color-coding of points as in Fig. 4. |
| In the text | |
 |
Fig. A.5. t-SNE for whole dataset scaled and mean normalized with various perplexity values. Color-coding of points as in Fig. 4. (a) Perplexity: 5 (b) Perplexity: 15 (c) Perplexity: 30 (d) Perplexity: 40. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.