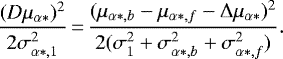| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 7 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202140807 | |
| Published online | 26 May 2021 | |
Characterizing and correcting the proper motion bias of the bright Gaia EDR3 sources
1
Institut de Ciències del Cosmos, Universitat de Barcelona (IEEC-UB),
Martí i Franquès 1,
08028
Barcelona,
Spain
e-mail: tcantat@fqa.ub.edu
2
Department of Physics, University of California,
Santa Barbara,
Santa Barbara, CA
93106,
USA
e-mail: tbrandt@ucsb.edu
Received:
14
March
2021
Accepted:
15
April
2021
In this paper, we characterize magnitude-dependent systematics in the proper motions of the Gaia EDR3 catalog and provide a prescription for their removal. The reference frame of bright stars (G ≲ 13) in EDR3 is known to rotate with respect to extragalactic objects, but this rotation has proven difficult to characterize and correct. We employ a sample of binary stars and a sample of open cluster members to characterize this proper motion bias as a magnitude-dependent spin of the reference frame. We show that the bias varies with G magnitude, reaching up to 80 μas yr−1 for sources in the range G = 11–13, several times the formal EDR3 proper motion uncertainties. We also show evidence for an additional dependence on the color of the source, with a magnitude up to ~10 μas yr−1. However, a color correction proportional to the effective wavenumber is unsatisfactory for very red or very blue stars, and we do not recommend its use. We provide a recipe for a magnitude-dependent correction to align the proper motion of the Gaia EDR3 sources brighter than G = 13 with the International Celestial Reference Frame.
Key words: astrometry / proper motions / methods: data analysis / methods: statistical
© ESO 2021
1 Introduction
The early third data release (EDR3) of the Gaia mission (Gaia Collaboration 2021) provides the positions, proper motions, and parallaxes of more than 1 billion sources. This astrometry is relative to the International Celestial Reference Frame (ICRF; Charlot et al. 2020), which is defined by distant radio quasars. Gaia EDR3 spans more than 15 magnitudes in source brightness (more than a factor of 106 in flux). The Gaia satellite uses different readout modes, called window classes, and even different exposure times, which are implemented through gatings, to handle this huge dynamic range. Different classes of observations must be calibrated to one another in order to align them with the ICRF. This is particularly true for bright stars (G ≲ 13), which have a different observation mode than faint stars and for which there are no quasars of similar brightness.
In the second Gaia data release (DR2), the bright star reference frame is rotated at ~0.15 mas yr−1 relative to the faint stars and quasars (Brandt 2018; Lindegren et al. 2018)1. In EDR3, this rotation was tentatively removed by anchoring the window class 0 (WC0) reference frame (corresponding to G ≲ 13) to the positional difference of stars between the HIPPARCOS and Gaia missions (see Sect. 4.5 of Lindegren et al. 2021). The Gaia bright star reference frame thus carries with it the 0.6 mas uncertainty in the HIPPARCOS realization of the ICRF (Kovalevsky et al. 1997) divided by the ≈25-year interval between HIPPARCOS and Gaia. Throughout the magnitude range G < 13, Gaia uses a wide range of gatings; each transition carries with it the potential for systematic offsets in the reference frame. HIPPARCOS provides almost no sources at magnitudes 11–13 to serve as references.
A proper motion bias affecting stars differently depending on their apparent magnitude can bias the eccentricity distributions inferred from a sample of binaries or can incorrectly suggest that massive stars in young associations exhibit a different kinematic behavior from that of low-mass stars. Despite representing only ~4% of the EDR3 catalog, the sources brighter than G = 13 include most O- and B-type stars within 4 kpc and represent over 70% of the subset with currently available radial velocities. A good understanding of the systematics is therefore necessary in order to fully exploit the exquisite proper motion precision provided by the Gaia astrometry.
Here, we use two independent sets of sources (resolved binaries and open clusters) to show that significant systematics are still present. We propose an additional correction to align the reference frame of the proper motions of the bright Gaia EDR3 sources with that of the fainter sources and, by extension, the ICRF. Section 2 presents the data used in this study. Section 3 investigates the dependence of the spin parameters on the magnitude and color of the sources. We conclude with Sect. 4.
2 Data used
We calibrated the proper motions of the bright stars in Gaia EDR3 to those of the faint stars without referring to external data. Our calibration sample consisted of binaries with a bright (G <14) and faint (G > 14) component and of bound star clusters whose mean proper motions we estimated using their faint members. Gaia EDR3 calibrates the faint stars to quasars of similar magnitude. This section describes our samples of binaries and open clusters, whose magnitude and sky distributions are shown in Fig. 1.
 |
Fig. 1 Sky and magnitude distribution of the sources in our two samples. Top: equatorial coordinate distribution of the binaries and cluster members with G < 14 in healpix with Nside = 8. The center is (α,δ) = (0,0), with α increasing toward the left. Bottom: G-magnitude distribution in equal bins and with the binning used in Sect. 3.3. |
2.1 Binary stars
The two components of a widely separated binary have similar motions through the Galaxy and nearly identical parallaxes. El-Badry et al. (2021) used these two facts to select pairs of stars in EDR3 whose parallaxes and proper motions are consistent with binarity. Their catalog forms the basis of our binary star sample. We sought to measure a frame rotation at the level of tens of μas yr−1. For a pair of Solar mass stars at 500 pc, the orbital motion is ~ 100 μas yr−1, even at a separation of 104 AU. Our measurement of the frame rotation required hundreds of widely separated binaries to average over this motion.
We selected stars from the El-Badry et al. (2021) catalog using thresholds in angular separation and parallax and requiring 1 μm−1 < νeff < 2 μm−1. The latter criterion excludes six-parameter astrometric solutions (Gaia Collaboration 2021). We required stars to be separated by at least 5′′ to minimizethe primary star’s effect on the secondary’s Gaia astrometry (Lindegren et al. 2021). We then required that a star’s rotational Keplerian velocity at its projected separation not exceed 0.2 mas yr−1, assuming a system mass of 1 M⊙. This last criterion is equivalent to
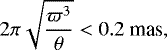 (1)
(1)
with parallax ϖ and angular separation θ both measured in mas. Most binaries will have a nonzero eccentricity and will preferentially be observed at apastron. Their physical separations will also be larger than their projected separations. Both of these effects make the typical orbital motion a factor of a few smaller than our formal limit of 0.2 mas yr−1. Finally, we wished to select only true binaries, but spurious matches become increasingly common at wide angular separations. We applied an additional cut: that the chance alignment probability supplied by El-Badry et al. (2021) be no higher than 5%.
The above cuts produced a sample of about 160 000 binaries. We studied the dependence of the reference frame on magnitude, anchoring the reference frame to that of the faint stars (G ≳ 14). Within this sample of binaries, about 55 000 have a primary brighter than G = 14 and a secondary fainter than G = 14. These 55 000 stars, further divided by the magnitude of the primary, form the basis of the analysis in Sect. 3.
2.2 Open clusters
Our open cluster sample uses the 1903 clusters listed in Cantat-Gaudin et al. (2020) that have members brighter than G = 14. These clusters are distant and weakly bound, making them suitable calibrators for the EDR3 reference frame. We selected stars from Gaia EDR3 within the central radius of each cluster, applying thresholds of 0.3 mas in parallax and 0.5 mas yr−1 in proper motion around each cluster’s listed centroids.
Since Cantat-Gaudin et al. (2020) determined the clusters’ mean astrometric parameters using Gaia DR2, we recomputed the median proper motion and parallax using our initial sample selected from EDR3. We then repeated the query on EDR3 based on those updated values. After this second iteration we obtained about 358 000 stars, of which 37 000 are brighter than G = 14. We considered the reference proper motion of each cluster to be the median proper motion of its members fainter than G = 14.
 |
Fig. 2 Median proper motion bias computed in healpix with Nside = 8 for the sources in our sample in the magnitude range 11 < G < 13, mapped in equatorial coordinates. The center is (α, δ) = (0, 0), with α increasing toward the left. The lower panels show the results after applying the correction derived in Sect. 3 using the prescription supplied in Appendix A. |
3 Aligning to the ICRF
We began by visualizing the proper motion bias across the sky using our combined sample of binaries and open cluster members. We divided the sky into healpix tiles with Nside = 8 and computed the median proper motion of stars in the magnitude range 11 < G < 13 relative to the faint (G > 14) stars. The top panels of Fig. 2 show clear evidence for frame rotation, closely resembling that seen in DR2(cf. Fig. 6 of Brandt 2018). This likely reflects the magnitude dependence of the anchoring of the WC0 reference frame to the HIPPARCOS positions at epoch 1991.25 (ESA 1997; van Leeuwen 2007). In this section, we derive the magnitude dependence of this frame rotation and supply a prescription for its removal. The lower panel of Fig. 2 shows the results of applying this correction to our full sample of 11 < G < 13 stars.
3.1 The spin
We represent the ICRF as a vector triad C = [X Y Z], where X, Y, and Z are orthogonal unit vectors pointing toward (α,δ) = (0,0), (90°,0), and (0,90°), respectively. An arbitrary reference frame ![$\tens{\tilde{C}}\,{=}\,[\vec{\tilde{X}}~\vec{\tilde{Y}}~\vec{\tilde{Z}}]$](/articles/aa/full_html/2021/05/aa40807-21/aa40807-21-eq2.png) can be obtained by rotating C around the three axes X, Y, and Z, as shown in Fig. 3.
can be obtained by rotating C around the three axes X, Y, and Z, as shown in Fig. 3.
Following the formalism presented in Sect. 2 of Lindegren (2020), if the overall rotation ω = [ωX ωY ωZ] is small, the proper motion of a given source in the reference frame  is related to its proper motion in C through the approximation:
is related to its proper motion in C through the approximation:
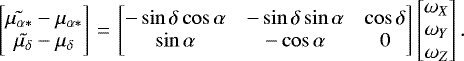 (2)
(2)
The proper motion bias (Δμα*, Δμδ) introduced by the spin of the reference frame therefore depends on the (α, δ) coordinates of the source. Over the whole sky, Δμδ averages to zero, while Δμα* is on average proportional to ωZ. This effect is illustrated in Fig. 2 for the stars with 11 < G < 13 and is consistent with the findings of Fabricius et al. (2021), who point out a low-significance offset of the μα* of bright stars, and no detectable offset in μδ.
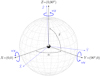 |
Fig. 3 ICRF modeled as an orthogonal vector triad C = [X Y Z]. The transformation from C to |
3.2 Fitting the spin components
The proper motion difference between a bright source and its faint companion, or the bulk motion of the fainter cluster stars, is due to multiple factors. Part of the difference is due to measurement errors (assumed to be Gaussian) on the proper motions, which we denote as (σα*,b, σδ,b) and (σα*,f, σδ,f) for the bright and faint source, respectively. For a cluster member, σα*,f and σδ,f are negligible because they represent medians over many stars. An intrinsic velocity difference is also expected owing to the orbital motion of binaries and to internal velocity dispersion in clusters. We denote this intrinsic dispersion by σ1.
We also accounted for the fact that both the binary and cluster star samples contain a fraction 1 − g of outliers that are background contaminants. Since our sources are distributed across the entire sky, the overall contributionof these contaminants does not skew the proper motion distribution, but it adds tails that cannot be reproduced with a single Gaussian component. Rather than performing, for example, a sigma clipping, we modeled the proper motion distribution as a two-component Gaussian mixture by adding a broader component of dispersion σ2.
The three spin components ωX, ωY, and ωZ give a proper motion shift (Δμα*, Δμδ) at each star’s position according to Eq. (2). We optimized these three components by maximizing the likelihood given by the Gaussian mixture model
![\begin{align*} & {\cal L}\,{=}\,\prod_{\textrm{stars}\,i} \Bigg(\frac{g}{2\pi\sigma_{\alpha*,1}\sigma_{\delta,1}} \exp\left[-\frac{(D\mu_{\alpha*})^2}{2\sigma_{\alpha*,1}^2} -\frac{(D\mu_{\delta})^2}{2\sigma_{\delta,1}^2} \right] \nonumber \\ &\qquad + \frac{1 - g}{2\pi\sigma_{\alpha*,2}\sigma_{\delta,2}} \exp\left[-\frac{(D\mu_{\alpha*})^2}{2\sigma_{\alpha*,2}^2} -\frac{(D\mu_{\delta})^2}{2\sigma_{\delta,2}^2} \right] \Bigg)\end{align*}](/articles/aa/full_html/2021/05/aa40807-21/aa40807-21-eq5.png) (3)
(3)
For the binary sample, we took σ1 = 100 μas yr−1, which is comparable to the typical orbital motion that we expect for these stars. For the clusters, σ1 is the quadrature sum of 10 μas yr−1 (which represents the effect of small-scale correlations on the proper motion precision) and the intrinsic proper motion dispersion (which corresponds to 0.5 km s−1 at the cluster distance). For both samples we used 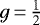 and σ2 = 0.3 mas yr−1. Varying g, σ1, and σ2 within reasonable value ranges does not change our results, but it affects the uncertainties by ~ 10%.
and σ2 = 0.3 mas yr−1. Varying g, σ1, and σ2 within reasonable value ranges does not change our results, but it affects the uncertainties by ~ 10%.
Maximizing Eq. (3) gives the best-fit frame rotation ω via the proper motion shifts (Δμα*, Δμδ). To assign uncertainties to these values, we used bootstrap resampling within each magnitude bin. We report the mean and standard deviations of 400 bootstrap re-samples for each magnitude bin.
3.3 Spin parameters as a function of magnitude
The best-fit spin components that we obtained in different magnitude bins are shown in Fig. 4 and listed in Table 1. The values obtained from binaries and from clusters are consistent, although the cluster sample provides slightly larger uncertainties due to a lower number of sources and larger intrinsic velocity dispersions. Both categories of sources show that the bias becomes much more significant for G < 13, clearly indicating an instrumental origin for this effect. The bottom panel of Fig. 4 shows the results obtained with the combined sample of binaries and cluster stars.
The ωX and ωY componentsof the spin are very significant for the sources brighter than G = 13, while ωZ only appears significant at G < 10.5. The ωY component varies strongly with magnitude, reaching up to 80 μas yr−1 for stars in the magnitude range G = 12–13. This bias is five times larger than the typical proper motion error quoted in the Gaia EDR3 catalog in this magnitude range.
Figure 5 shows running medians of the difference between a star’s proper motion and that of its cluster. This bias depends on position; we divided the sky in half to avoid having it average to zero. The median bias reaches ~ 40 μas yr−1 for G ≲ 13, roughly double the formal EDR3 uncertainties, but would reach higher values if computed on smaller portions of the sky. The bottom row of Fig. 5 shows a correction of the proper motions of the cluster stars based on the spin computed from binary stars. We aligned the proper motions of stars brighter than G = 13 to the ICRF through the relation
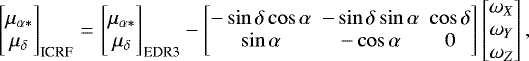 (5)
(5)
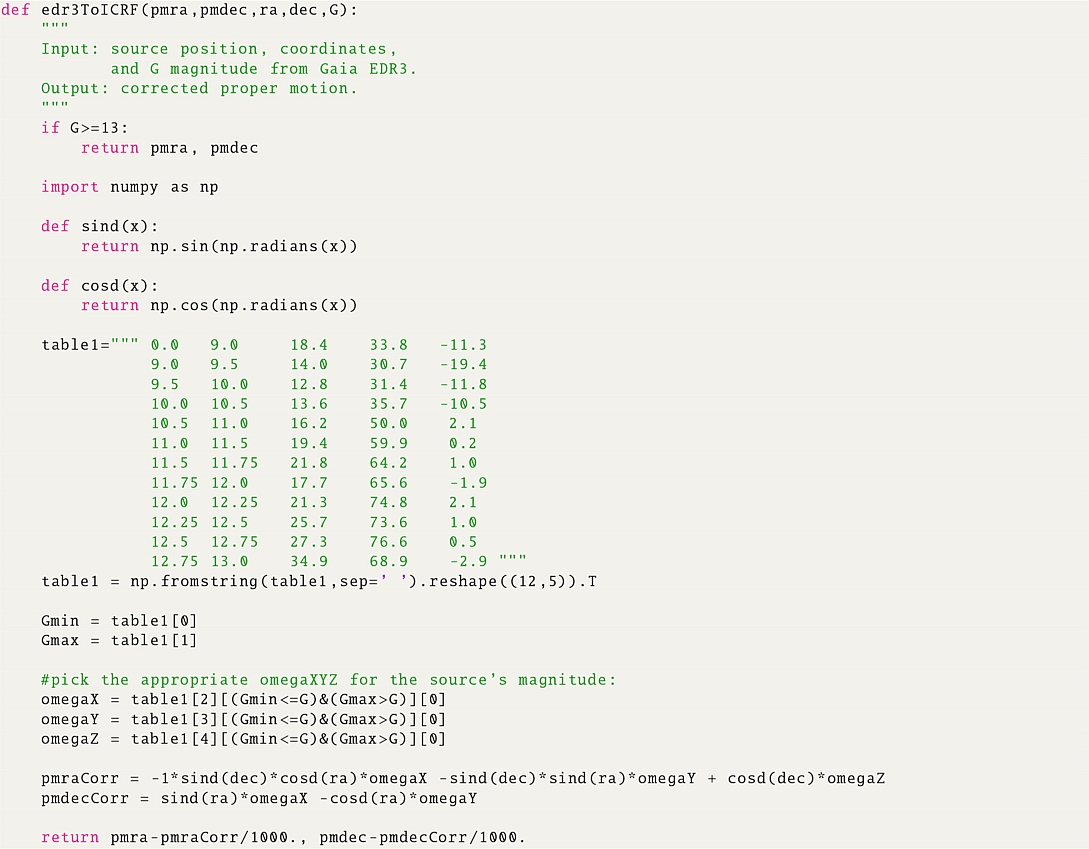
where the values of ωX, ωY, and ωZ are the best-fit spin parameters obtained in the corresponding magnitude bin. We include in Appendix A a Python function that performs the correction calibrated on the combined sample of cluster members and binaries.
For bright magnitudes (G ≲ 10), the bias that we find likely reflects errors in the alignment of HIPPARCOS with the ICRF. These were estimated to be 0.6 mas (ESA 1997), or about 25 μas yr−1 if dividing by the difference between the HIPPARCOS and Gaia catalog epochs. At G = 13, the bias is similar to the rotation of (ωX, ωY, ωZ) = (–16.6, –95.0, +28.3) μas yr−1 applied to bright sources (Lindegren et al. 2021), with the signs reversed. This suggests that the systematics in the bright source reference frame build gradually with magnitude away from the boundary between WC0 and WC1.
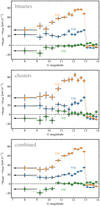 |
Fig. 4 Components of the best-fit frame rotation derived from a sample of wide-separation binaries (top), open cluster members (middle), and both samples combined (bottom). The uncertainties are derived from bootstrap resampling within each magnitude bin. |
 |
Fig. 5 Proper motion bias before and after correction. Top panels: running medians of the differences between proper motions of bright open cluster members and the proper motions of their host clusters as traced by the faint stars. Bottom panels: same running medians after correcting the proper motions of the bright stars using the spin of the reference frame derived from binary stars. The shaded areas correspond to 1σ and 2σ intervals computed using bootstrap resampling. |
3.4 Evidence for a color dependence
In order to calibrate color-dependent spread functions, the Gaia astrometric processing relies on prior color information given by the effective wavenumberνeff. This is available in the EDR3 catalog for each source as nu_eff_used_in_astrometry. To investigate a color dependence of ω, we allowed the three spin parameters to vary linearly with νeff by expressing them as
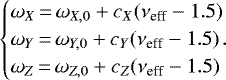 (6)
(6)
This adds three free parameters to the fitting procedure described in Sect. 3.2.
The best-fit values we obtain for these coefficients in each magnitude bin are shown in Fig. 6, along with the uncertainty estimated by bootstrapping. We obtain negative values for cX and cY, indicating that the bias is stronger for smaller values of νeff (corresponding to redder sources). We find mostly positive values for cZ.
To assess whether these values could be the result of statistical fluctuations, and whether cX, cY, and cZ are constant with magnitude, we applied χ2 statistics. In Fig. 6, we report the p values corresponding to the hypothesis that the true value of cX, cY, or cZ is zero (pno), and to the hypothesis that they are nonzero and constant with G magnitude (pdep). We obtain small values for pno, providing conclusive evidence that ωX varies with νeff, as well as marginal evidence that ωY and ωZ do so as well. The pdep values indicate that, within the statistical precision allowed by our sample, cX, cY, and cZ do not appear to vary with G magnitude.
We next tested whether this color correction, computed mainly from the binary stars, improves the proper motion residuals for the clusters members. The binary stars and cluster members have systematically different νeff, with the bright cluster stars being more distant and bluer than the bright components of nearby wide binaries. The cluster stars also show a larger dispersion of νeff values.
We find that adding a color correction to the magnitude correction given by Eq. (5) slightly increases the dispersion of the cluster stars’ proper motion residuals (i.e., it degrades the quality of the correction). We hypothesize that a linear dependence of the spin parameters on νeff is a poor approximation for the wider range of colors represented by bright open cluster members: Eq. (5) tends to overcorrect these stars. Unfortunately, our sample is insufficient to fully characterize the dependence of the reference frame on color. We therefore recommend only the magnitude correction given by Eq. (5) but advise that color-dependent frame rotations are present at ~ 10 μas yr−1 for a star somewhat bluer or redder than the Gaia median of νeff ≈ 1.5.
Spin best-fit parameters computed from the combined sample of binary stars and cluster members.
 |
Fig. 6 Coefficients obtained in different magnitude bins when fitting color-dependent spin parameters as defined in Eq. (6). The shaded areas correspond to 1σ and 2σ uncertainties obtained by bootstrapping, and pno and pdep are defined in the text. While cX in particular is significantly nonzero, we do not recommend the application of a color correction proportional to νeff. Our sample lacks the statistical power to fully characterize the chromaticity of the spin. |
4 Summary and conclusion
The large magnitude range covered by the Gaia observations requires the use of different gatings and readout modes. The reference frame of the faint sources can be calibrated directly to the ICRF using distant radio quasars that have an optical counterpart.Due to the unprecedented astrometric capabilities of the Gaia spacecraft, no reference external sample of sufficient quality is available for brighter sources; the bright observations are calibrated to the fainter ones to align them with the ICRF.
In this paper we have shown that the reference frame of the proper motions of the bright EDR3 sources (G < 13) rotates with respect to that of the faint EDR3 sources. The resulting proper motion bias reaches 80 μas yr−1 in the magnitude range G = 11–13, five times larger than the nominal uncertainty listed in the Gaia EDR3 catalog for these sources. We have also shown evidence for a second-order dependence of the spin parameters on the color of the source when modeled as a linear function of the effective wavenumber νeff. A color correction proportional to νeff, however, proves unsatisfactory over the wide range of colors present in our open cluster sample. We recommend the use of only a magnitude-dependent correction and caution that color-dependent systematics of up to ~ 10 μas yr−1 will still be present.
Our main result is a magnitude-based correction to be applied to the Gaia EDR3 proper motions of bright stars in order to align them with the ICRF. The correction can be computed using Eq. (5) with the spin parameters listed in Table 1. Appendix A provides sample Python code to realize this correction for a list of stars in Gaia EDR3.
Acknowledgments
We thank L. Lindegren, C. Fabricius, and F. Arenou for their feedback and helpful comments, as well as the referee and editor who helped improve this manuscript. TCG acknowledges support by the Spanish Ministry of Science, Innovation and University (MICIU/FEDER, UE) through grants RTI2018-095076-B-C21 and the Institute of Cosmos Sciences University of Barcelona (ICCUB, Unidad de Excelencia ‘María de Maeztu’) through grant CEX2019-000918-M. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC; https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
Appendix A Python implementation of the frame spin correction
This function applies Eq. (5) using the values listed in Table 1.
References
- Brandt, T. D. 2018, ApJS, 239, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Cantat-Gaudin, T., Anders, F., Castro-Ginard, A., et al. 2020, A&A, 640, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charlot, P., Jacobs, C. S., Gordon, D., et al. 2020, A&A, 644, A159 [EDP Sciences] [Google Scholar]
- El-Badry, K., Rix, H.-W., & Heintz, T. M. 2021, MNRAS, in press [arXiv:2101.05282] [Google Scholar]
- ESA 1997, ESA Special Publication, 1200, The HIPPARCOS and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission [Google Scholar]
- Fabricius, C., Luri, X., Arenou, F., et al. 2021, A&A 649, A5 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovalevsky, J., Lindegren, L., Perryman, M. A. C., et al. 1997, A&A, 323, 620 [NASA ADS] [Google Scholar]
- Lindegren, L. 2020, A&A, 633, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A 649, A2 [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
We refer the reader to Appendix B of Lindegren et al. (2018) for further discussion of the origin of this calibration issue.
All Tables
Spin best-fit parameters computed from the combined sample of binary stars and cluster members.
All Figures
 |
Fig. 1 Sky and magnitude distribution of the sources in our two samples. Top: equatorial coordinate distribution of the binaries and cluster members with G < 14 in healpix with Nside = 8. The center is (α,δ) = (0,0), with α increasing toward the left. Bottom: G-magnitude distribution in equal bins and with the binning used in Sect. 3.3. |
| In the text | |
 |
Fig. 2 Median proper motion bias computed in healpix with Nside = 8 for the sources in our sample in the magnitude range 11 < G < 13, mapped in equatorial coordinates. The center is (α, δ) = (0, 0), with α increasing toward the left. The lower panels show the results after applying the correction derived in Sect. 3 using the prescription supplied in Appendix A. |
| In the text | |
 |
Fig. 3 ICRF modeled as an orthogonal vector triad C = [X Y Z]. The transformation from C to |
| In the text | |
 |
Fig. 4 Components of the best-fit frame rotation derived from a sample of wide-separation binaries (top), open cluster members (middle), and both samples combined (bottom). The uncertainties are derived from bootstrap resampling within each magnitude bin. |
| In the text | |
 |
Fig. 5 Proper motion bias before and after correction. Top panels: running medians of the differences between proper motions of bright open cluster members and the proper motions of their host clusters as traced by the faint stars. Bottom panels: same running medians after correcting the proper motions of the bright stars using the spin of the reference frame derived from binary stars. The shaded areas correspond to 1σ and 2σ intervals computed using bootstrap resampling. |
| In the text | |
 |
Fig. 6 Coefficients obtained in different magnitude bins when fitting color-dependent spin parameters as defined in Eq. (6). The shaded areas correspond to 1σ and 2σ uncertainties obtained by bootstrapping, and pno and pdep are defined in the text. While cX in particular is significantly nonzero, we do not recommend the application of a color correction proportional to νeff. Our sample lacks the statistical power to fully characterize the chromaticity of the spin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\tens{\tilde{C}}\,{=}\,[\vec{\tilde{X}}~\vec{\tilde{Y}}~\vec{\tilde{Z}}]$](/articles/aa/full_html/2021/05/aa40807-21/aa40807-21-eq10.png)