| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 10 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202140418 | |
| Published online | 28 April 2021 | |
Validation of the accuracy and precision of Gaia EDR3 parallaxes with globular clusters
1
Centro de Astrobiología, CSIC-INTA. Campus ESAC. C. bajo del castillo s/n 28692 Villanueva de la Cañada,
Madrid,
Spain
e-mail: jmaiz@cab.inta-csic.es
2
Departamento de Astrofísica y Física de la Atmósfera, Universidad Complutense de Madrid. 28040 Madrid, Spain
3
Departamento de Astronomía, Universidad de La Serena. Av. Cisternas 1200 Norte.
La Serena, Chile
Received:
25
January
2021
Accepted:
3
March
2021
Context. The recent early third data release (EDR3) from the Gaia mission has produced parallaxes for 1.468 × 109 sources with better quality than those reported in the previous data release. Nevertheless, there are calibration issues with the data that require corrections to the published values and uncertainties.
Aims. We want to properly characterize the behavior of the random and systematic uncertainties of the Gaia EDR3 parallaxes in order to maximize the precision of the derived distances without compromising their accuracy. We also aim to provide a step-by-step procedure for the calculation of distances to stars and stellar clusters when using these parallaxes.
Methods. We reanalyzed some of the data presented in the calibration papers for quasar and Large Magellanic Cloud (LMC) parallaxes and combine these results with measurements for six bright globular clusters. We calculated the angular covariance of EDR3 parallaxes at small separations (up to a few degrees) based on the LMC results and combined it with the results for larger angles using quasars to obtain an approximate analytical formula for the angular covariance over the whole sky. The results for the six globular clusters were used to validate the parallax bias correction as a function of magnitude, color, and ecliptic latitude and to determine the multiplicative constant k used to convert internal uncertainties to external ones.
Results. The angular covariance at zero separation is estimated to be 106 μas2, yielding a minimum (systematic) uncertainty for EDR3 parallaxes of 10.3 μas for individual stars or compact stellar clusters. This value can be slightly reduced for globular clusters that span ≳30′ after considering the behavior of the angular covariance of the parallaxes for small separations. A recent parallax bias correction is found to work quite well, except perhaps for the brighter magnitudes, where improvements may be possible. The value of k is found to be 1.1–1.7 and to depend on G. We find that stars with moderately large values of the renormalized unit weight error can still provide useful parallaxes, albeit with larger values of k. We give accurate and precise Gaia EDR3 distances to the six globular clusters, and for the specific case of 47 Tuc we are able to beat the angular covariance limit through the use of the background Small Magellanic Cloud as a reference and derive a high-precision distance of 4.53 ± 0.06 kpc. Finally, a recipe for the derivation of distances to stars and stellar clusters using Gaia EDR3 parallaxes is given.
Key words: astrometry / globular clusters: general / methods: data analysis / parallaxes / stars: distances / surveys
© ESO 2021
1 Introduction
The early third Gaia data release (EDR3; Gaia Collaboration 2021a) was presented on 3 December 2020 and included photometry for 1.8 × 109 sources and astrometry for ~80% of them. The “early” in EDR3 refers to the fact that the associated spectrophotometry will be presented at a later date. The astrometric solution is presented in Lindegren et al. (2021a) (hereafter L21a), and includes an analysis of the angular covariance of the parallaxes at different angular scales using data for quasars (large separations θ) and stars in the Large Magellanic Cloud (LMC; small separations). Lindegren et al. (2021b) (hereafter L21b) analyzes the parallax bias (or zero point, ZEDR3) in the data as a function of magnitude (G, the primary very broadband optical photometry provided by Gaia), color (νeff, the effective wavenumber, which for most well-behaved sources is a function of the GBP−GRP color provided by Gaia; see Fig. 2 in L21a), and ecliptic latitude (β). The median parallax for quasars measured by L21b is −17 μas, which can be understood as the typical parallax bias given that quasars are too far away to have parallaxes measurable by Gaia, but systematic variations as a function of position in the sky at the level of 10 μas are detected (Fig. 2 in L21b). Furthermore, L21b use data from LMC stars and physical binaries to show that ZEDR3 has a complex behavior when going from the (mostly faint) quasar regime to brighter objects with even larger deviations from the median parallax value (see Fig. 20 in that paper), hence the need to characterize ZEDR3 at least as a function of G, νeff, and β.
In this paper we have three objectives: (1) to validate the results from L21b and L21a with an independent dataset built from globular clusters, (2) to provide a general recipe for the use of Gaia EDR3 parallaxes to derive precise and accurate1 distances to stars and stellar clusters, and (3) to analyze cases where it may be possible to beat the parallax bias to reduce the uncertainty on those distances. First, we present the formalism we use throughout the paper; second, we reevaluate the angular covariance of the Gaia EDR3 parallaxes; third, we briefly discuss the anchoring of the parallaxes to distant objects; and fourth, we use a sample of six globular clusters to validate the ZEDR3 from L21b and toestimate the external uncertainties of the parallaxes. We then discuss the possibility of obtaining even more precise distances for globular clusters using Gaia EDR3 data, and we conclude by presenting a summary of the paper and our proposed recipe for the calculation of distances from Gaia EDR3 parallaxes.
2 Formalism for the analysis of Gaia EDR3 parallaxes
In this section we present the formalism that is used in this paper and that follows for the most part that of Lindegren et al. (2018) (hereafter L18), and L21b and L21a.
2.1 Correcting the parallax bias
The relationship between the measured EDR3 parallax, ϖ, and the corrected EDR3 parallax, ϖc, is given by
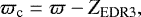 (1)
(1)
where, following L21b, ZEDR3 is a function of G, νeff, and β and takes different forms for five-parameter solutions as Z5(G, νeff, β) and for six-parameter solutions as Z6(G, νeff, β). The separation is needed because Gaia EDR3 astrometry comes in two flavors. For those with measured νeff, five parameters are fitted (two coordinates, one parallax, and two proper motions), while for those where νeff is not known a priori it has to be added as a sixth parameter (the pseudocolor). Five-parameter solutions are of better quality and are the majority for stars brighter than G = 19 (Fig. 5 in L21a) but a minority (40%) of the total Gaia EDR3 sample, which is dominated by sources in the G = 19–21.5 range. In this paper we are interested mostly in bright stars, we thus pay attention primarily to those with five-parameter solutions; however, forthe globular cluster sample we also include a small fraction of stars with six-parameter solutions. The solutions Z5 (G, νeff, β) and Z6 (G, νeff, β) are defined from three orthogonal polynomial basis functions b0, b1, b2 of the ecliptic latitude (of zeroth, first, and second order in sinβ, respectively); five piecewise basis functions c0, c1, c2, c3, c4 that depend on νeff (Appendix A in L21b); and tabulated qjk coefficients for 13 values of G between 6 and 21,
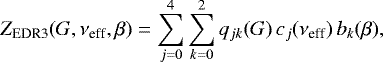 (2)
(2)
where two different tables are given for Z5(G, νeff, β) and Z6 (G, νeff, β) (Tables 9 and 10 in L21b, respectively). From the tabulated values of qjk we can interpolate to any G magnitude. For Z5 (G, νeff, β), only 8 of the possible 15 combinations of cj and bk have non-zero values of qjk, and of these only 4 have non-zero values for the whole G = 6–21 range, q00, q01, q02, and q11, which are the three color-independent β terms and the term that depends linearly on both νeff (in the 1.24–1.48 μm−1 range) and β. The remaining four combinations with non zero-terms, q10, q20, q30, and q40, are all β-independent and apply to stars brighter than G =13.1 (q10, linear term in the 1.24–1.48 μm−1 range), brighter than G = 17.5 (q20, applicable for stars redder than νeff = 1.48 μm−1), between G = 13.1 and 17.5 (q30, applicable for stars redder than νeff = 1.24 μm−1), and between G = 13.1 and 19.0 (q40, applicable for stars bluer than νeff = 1.72 μm−1).
2.2 Accounting for the uncorrected parallax bias
The L21b ZEDR3 (G, νeff, β) parallax bias corrections improve the consistency of the parallaxes of stars in stellar clusters, as shown in Figs. 17 and 18 of Fabricius et al. (2021) and as we also show later on in this paper. An empirical correction like that of L21b can always be improved with better data, but for the time being we can assume that it removes most of the bias associated with magnitude and color and with the spherical harmonics of degree ≤ 2 of the angular power spectrum of the parallax bias. However, L21a used the parallaxes of one million quasars to show that the angular power spectrum of the parallax bias is dominated by the contributions of the spherical harmonics of higher order. Putting it in another way, L21a determined that the angular covariance Vϖ of the quasar parallaxes can be approximately described by
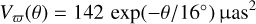 (3)
(3)
for separations 0.5° < θ < 80°. Taking Eq. (3) at face value, the square root of its value at zero separation (11.9 μas) represents the dispersion of the uncorrected parallax bias; it can be thought of as an additional uncertainty source for any Gaia EDR3 parallax, which we refer to in this paper as σs. Furthermore, as any star located a short distance away from the source of interest will have a similar uncorrected parallax bias, σs acts as a systematic effect, meaning that it affects all stars in a compact cluster in the same (unknown for a specific object) manner and sets a limit on the overall uncertainty of the cluster parallax when combining data from many stars. However, there are at least two reasons why Eq. (3) does not tell the whole story. The first is that the quasar sample used by L21a is very faint, with a median G of 19.9 mag. This raises the question of whether the angular spectrum of the parallax bias for brighter sources has the same characteristics, which we answer below. The second reason is that Eq. (3) does not reflect the behavior of Vϖ at small separations (from a fraction of a degree to a few degrees) as the value of the first bin (θ < 0.125°) for the quasar covariance reported by L21a has a significantly larger value of 700 μas2 (albeit with a large uncertainty) that leads to σs = 26.5 μas. That small-angle behavior is better captured by the checkered pattern seen in the smoothed parallaxes for LMC sources with G = 16–18 mag shown in Fig. 14 of L21a. The pattern has a similar triangular disposition of maxima and minima with peak-to-peak or valley-to-valley separation of ~ 1° in Gaia DR2 and EDR3, but the RMS amplitude decreased from 13.1 μas to 6.9 μas between the two data releases. In the next section we combine these pieces of information to generate an approximate analytical form for Vϖ for any separation.
A different issue that appears when comparing Gaia parallaxes with external data is that the (random) internal uncertainties σint do not reflect the true dispersion of the values listed in the catalog. Here we follow L18 to define the total or external uncertainty σext for a parallax as
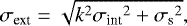 (4)
(4)
where k is a multiplicative constant that needs to be determined and that may depend on magnitude or other quantities. For a well-characterized catalog it is expected to be close to one. Fabricius et al. (2021), who call it unit-weight uncertainty (uwu), find that for most of the Gaia EDR3 samples they analyzed it is between 1.0 and 1.8 (see their Table 1 and their Fig. 21). Later in this paper we provide an independent evaluation of k.
2.3 Combining parallaxes
Using Eq. (4) to obtain the total parallax uncertainty of a source leads to a problem: it is neither a random nor a systematic uncertainty, but a combination of both. More specifically, it can be treated as a random uncertainty only if we are dealing with a single source and calculating its distance, but not if we are dealing with several sources assumed to be at the same distance. If we want to obtain an improved parallax by combining the individual corrected parallaxes ϖc,i from the members of a multiple stellar system or cluster, we should treat each type of uncertainty properly. Furthermore, when combining information from stars at non-negligible separations we should use Vϖ to determine how to treat the correlated uncertainties. The answer is to use a slightly modified version of the Campillay et al. (2019) procedure to obtain the group parallax ϖg,
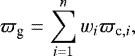 (5)
(5)
where the weights are given by
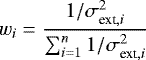 (6)
(6)
and the group parallax uncertainty is given by
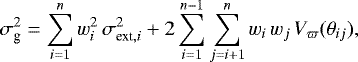 (7)
(7)
where the first term reflects the contributions from the individual stars and the second term is a sum over all pairs of stars to properly account for the correlations introduced by the angular covariance. For the simple case where all external uncertainties are the same and the same applies to the angular covariance, the first term becomes 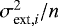 and the second term becomes Vϖ(θij)(n − 1)∕n; that is, the first term makes σg improve with the square root of the number of stars, while the second term is relatively insensitive to how many objects are in the group. Therefore, in the limit of a cluster with a large number of stars its parallax uncertainty becomes the square root of the angular covariance averaged over all stellar pairs2. This effect is seen in Table 3 of Maíz Apellániz et al. (2020), who used this strategy to obtain the group parallaxes of OB stellar groups from Gaia DR2 parallaxes. Most group uncertainties have values close to 43 μas as that paper used a value of Vϖ(0) of 1850 μas2 (L21a and references therein) and most of the stellar groups have small angular sizes. The two most notable exceptions are Villafranca O-015 (Collinder 419) and Villafranca O-016 (NGC 2264) (see also Maíz Apellániz 2019) as these two stellar groups are nearby and have larger angular sizes, allowing Vϖ to be averaged over longer separations and hence become lower. This effect reduces the group parallax uncertainties to 34 μas and 29 μas, respectively.
and the second term becomes Vϖ(θij)(n − 1)∕n; that is, the first term makes σg improve with the square root of the number of stars, while the second term is relatively insensitive to how many objects are in the group. Therefore, in the limit of a cluster with a large number of stars its parallax uncertainty becomes the square root of the angular covariance averaged over all stellar pairs2. This effect is seen in Table 3 of Maíz Apellániz et al. (2020), who used this strategy to obtain the group parallaxes of OB stellar groups from Gaia DR2 parallaxes. Most group uncertainties have values close to 43 μas as that paper used a value of Vϖ(0) of 1850 μas2 (L21a and references therein) and most of the stellar groups have small angular sizes. The two most notable exceptions are Villafranca O-015 (Collinder 419) and Villafranca O-016 (NGC 2264) (see also Maíz Apellániz 2019) as these two stellar groups are nearby and have larger angular sizes, allowing Vϖ to be averaged over longer separations and hence become lower. This effect reduces the group parallax uncertainties to 34 μas and 29 μas, respectively.
Below we apply this procedure to determine the group parallaxes and their uncertainties for six globular clusters using Gaia EDR3 data. The results are then used to validate the parallax bias and to determine k.
2.4 Calculating distances
The last step that is usually required to use a parallax is to convert it into a distance d or, more precisely, a posterior distribution of distances p(d|ϖc). To obtain such a distribution for given values of ϖc and σext it is necessary to use a likelihood distribution p(ϖc|d) (a Gaussian is typically assumed) and a prior distribution for the distances to the population to which the object belongs. It has been known for a long time (Lutz & Kelker 1973) that a flat prior that extends to infinity makes the posterior distribution diverge at large distances. Therefore, a prior that goes to zero faster than 1∕d3 is required (see Eq. (1) in Maíz Apellániz 2005). Given the finite extent of the Milky Way, this should not be a problem when dealing with Galactic sources; nevertheless, a prior should not be applied blindly as the underlying spatial distribution is not the same depending on whether the star is a red giant or an early-type star, for example, or whether it belongs to the disk or the halo populations. This issue is even more relevant when a sightline contains objects concentrated at very different distances, such as the solar neighborhood, a globular cluster, and a Local Group galaxy. On the other hand, Pantaleoni González et al. (2021) have compared Gaia DR2 distances to OB stars using three different priors, one specific for OB stars (Maíz Apellániz 2001; Maíz Apellániz et al. 2008) and two for the general Galactic (mostly disk) population (Bailer-Jones et al. 2018; Anders et al. 2019), and have found out that the results are quite similar. There are some systematic differences, but they are well within the posterior uncertainties. This result means that as long as the prior is a reasonable description of the underlying population, distances derived from Gaia parallaxes are robust and mostly independent of the details of the prior itself.
3 Angular covariance of the Gaia EDR3 parallaxes
In this section we re-evaluate the angular covariance of the Gaia EDR3 parallaxes. We analyze first the small separations case (θ < 4°) and we then extend the analysis to larger values of θ.
3.1 Small-separation angular covariance
To determine the angular covariance for small values of θ we use the Gaia EDR3 LMC parallaxes to extend the work of L21a. We start by obtaining the sample in a circular region with a radius of 10° centered at α = 81.28° and δ = −69.78° using the selection algorithm and coordinate transformation of Gaia Collaboration (2021b). We obtain a bright subsample defined by G< 19.019, the median magnitude, to study magnitude-dependent effects. We apply ZEDR3 from L21b to calculate ϖc for each star and calculate the weighted (from σext) average in the central 10° × 10° region smoothed using a Gaussian kernel with a standard deviation of 0.1°. This is the same technique as L21a, but with the differences of (a) using either the whole magnitude range or that with G < 19.019 as opposed to that with G = 16−18 and (b) applying the L21b parallax correction beforehand.
For the full sample the smoothed parallax is 24.2 ± 7.0 μas, which is 4.0 μas larger than the 20.2 μas value derived from the Pietrzyński et al. (2019) distance but within one sigma3. The equivalent result for the bright subsample is 24.7 ± 6.8 μas. The similarity between the full and bright samples indicates that the L21b correction does a good job of removing magnitude- and color-dependent effects in the G = 18−20 range, though we note that the dispersion for the faint subsample is 14.8 μas as it is dominated by the significantly larger individual uncertainties. Furthermore, the dispersion is nearly identical to the 6.9 μas value found by L21a using the G = 16−18 range, indicating that it has little magnitude dependence and that the application of the L21b correction does not introduce changes in the dispersion, as expected. Therefore, we conclude that the covariance at zero separation from the LMC data is well established to be Vϖ,LMC(0) = 46.2 μas2 within a few μas2, where we used the value for our bright subsample.
The left panel of Fig. 1 shows the smoothed parallax for the bright subsample (the full subsample is not shown, but the equivalent plot is nearly identical), a plot equivalent to Fig. 14 in L21b. This pattern is commonly referred to as the checkered pattern. We use these data to measure the angular covariance at 0.05° intervals in the 0° –4° range. The results are shown in the right panel of Fig. 1. We also tried different analytical functions to use as an approximation to the fitted data and we settled on
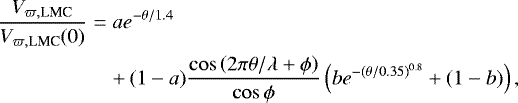 (8)
(8)
where θ is in degrees, λ = 1.05°, a = 0.6, b = 0.94, and ϕ = −5π∕18. There are two advantages to fitting an approximate analytical function. First, it is easier to implement than a tabulated form, and second, it allows a better analysis of its behavior. However, one should be careful that no large discrepancies or anomalous asymptotic behaviors are introduced. With respect to the first issue, we verified that in the 0°–4° range the difference between the analytical function and the data has a mean of 0.3 μas2 and a standard deviation of 1.0 μas2, which is sufficient for our needs. Regarding the asymptotic behavior at large separations, we generated a numerical model with a periodic checkered pattern similar to the one seen in the left panel of Fig. 1 (and even more clearly in the right panel of Fig. 14 in L21b) and an infinite extent, and repeated the calculation up to separations of 40°. The object of such a numerical model is to evaluate the periodic component of the checkered pattern to separate it from other contributions to the angular covariance.
The analytical function is the sum of an exponential and a damped sinusoid with the highest values at very small angles. The exponential component (first term in Eq. (8)) indicates the existence of an uncorrected parallax bias that is correlated on scales of a few degrees. As we show in the next subsection, this effect has to be taken in conjunction with the angular covariance at larger separations. The damped sinusoid (second term in Eq. (8)) is the effect of the checkered pattern itself and its behavior is very nicely reproduced by the numerical model with infinite extent. The wavelength λ as measured in the angular covariance is 1.05°, but we note that there is a − 5π∕18 phase in the cosine (the fitted function does not have a positive slope at zero due to the effect of the other terms). The oscillation is quickly damped, but a small residual with a 2.4% amplitude of the initial value (~ 1 μas2) is maintained at large separations in the numerical model, where the phase is also conserved for at least several tens of cycles. This behavior is ultimately unphysical (the celestial sphere is finite and curved, among other reasons, so the pattern cannot be maintained), but given the small amplitude compared to other effects (see Fig. 2 in the next subsection), its effect in our model is insignificant.
 |
Fig. 1 Left: smoothed corrected Gaia EDR3 parallaxes for the bright LMC subsample. The axes arerectangular coordinates in degrees and the color table shows the parallax scale in μas. Right: angular covariance in the LMC data with respect to the mean measured parallax. The points are the measured values and the red line is the analytical function described in the text. |
3.2 Adding quasars for larger angles
To analyze the contribution from larger angles to the spatial covariance, we follow the same strategy of L21a, but with two differences. First, we restrict the quasar sample of L21a (1 214 779 objects) to G < 19 mag and Galactic latitude |b| > 25° to better simulate brighter objects and to minimize contamination effects close to the Galactic plane. This leaves us with a sample of 139 036 objects with a median G = 18.58 mag. Second, we consider both uncorrected and corrected parallaxes.
We group the quasar pairs in 1° bins and calculate the mean angular covariance in each bin. The results are shown in Fig. 2.
The qualitative behavior of the quasar covariance Vϖ,QSO in Fig. 2 is similar to that in Fig. 15 of L21a: a maximum at small separations, a nearly flat regime for most values of θ, and a minimum at large separations that is antisymmetric with respect to that at small values. However, the amplitude at the extremes is significantly lower. The overall behavior using ϖc is well fitted by the function
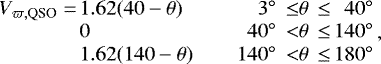 (9)
(9)
with θ in degrees and Vϖ,QSO in μas2, where for the linear fit we use the 3° –40° range. The value at 3° (60 μas2) is substantially lower than the 142 μas2 value of L21a for zero separation. This is a combination of three effects. Two are the use of a linear function instead of an exponential, which contributes to a reduction of ~ 10 μas2, and the use of ϖc instead of ϖ, which is a smaller effect of ~ 5 μas2 (see Fig. 2). The third effect is the use of brighter quasars, which seems to be the dominant one.
We obtain our final full covariance model by combining the results from the LMC and quasars from Eqs. (8) and (9)
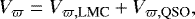 (10)
(10)
where for the 0–3° range one should take Vϖ,QSO = 60 μas2 (Fig. 2). We note that the checkered pattern is also detected in the cumulative angular power spectrum for quasars (Fig. 16 in L21a), and its effect is seen as deviations from the linear behavior at small separations in the left panel of Fig. 2, but we excluded these angles from the linear fit (where the error bars from the quasars are large in any case). Nevertheless, the sum of the two components in Eq. (10) is not far from what is seen for quasars at small separations.
 |
Fig. 2 Large-angle angular covariance of the Gaia EDR3 parallaxes.Left panel: 0°–20° separation range with the quasar data in 1° bins using either ϖ (blue asterisks) or ϖc (black error bars), the linear fit to the quasar corrected data in the 5°–40° separation range (green line), and the analytical fit to the LMC data (red line). The error bars associated with the quasar ϖ data are not shown, but they are similar to those for ϖc. Right panel: full 0°–180° separation range and includes the total quasar+LMC model. |
 |
Fig. 3 Smoothed corrected Gaia EDR3 parallaxes for the RC bulge sample. The axes are in Galactic coordinates in degrees and the color table shows the parallax scale in units of μas. |
3.3 Limitations and validity
There are two issues to analyze regarding the limitations and validity of these results: the angular covariance for small scales and the overall angular covariance.
In order to test the validity of the angular covariance for small angles in other parts of the sky we chose the region of the Galactic bulge shown in Fig. 3, which has already been used by Arenou et al. (2018) for the validation of the Gaia DR2 parallaxes. We refined the exact location of the area in Galactic latitude by selecting a region that is not too close to the Galactic plane (where extinction effects dominate), but also not too far (where there are not enough stars). We selected the Gaia EDR3 sources with reduced unit weight error (RUWE) < 1.4 and σint < 0.1 mas and filtered the sample by choosing sources that are within a proper motion radius of the expected center and are in the region of the GBP −GRP versus G CMD, which corresponds to red clump (RC) stars at the distance of the bulge (accounting for possible extinction). The results were then smoothed inthe same manner as for the LMC sample. The outcome, shown in Fig. 3, has a standard deviation of 6.7 μas, which is remarkably similar to the LMC result, and is much smaller than the equivalent value estimated from Fig. 13 in Arenou et al. (2018) for Gaia DR2. Furthermore, the sample has G magnitudes in the 14.5–17.6 range (i.e., significantly brighter than the LMC sample).
Two other analyses of the small-separation angular covariance for Gaia EDR3 parallaxes became available shortly after this paper was submitted. Vasiliev & Baumgardt (2021) uses globular clusters to obtain a value of Vϖ (0) around 50 μas2, which is very similar to ours. In the second paper Zinn (2021) uses data from the Kepler field for this purpose. In Fig. 5 of that work the first data point for the angular covariance has a value of ~ 45 μas2, but the trend is for separation points towards a lower value of around 16 μas2. In terms of the standard deviation, the corresponding values are in the range of 4–7 μas, similar to our results. Therefore, the value of Vϖ(0) derived from regions of small angular size seems to be relatively independent of sky position and magnitude, but we cannot discard thatsmall changes are present.
Regarding larger separations, given that the covariance from (mostly fainter) quasars in L21a is larger than the one here, it is possible that the effect may be smaller for even brighter targets. However, the coherence between the LMC results for different magnitude ranges indicates that there is a limit to those possible improvements and, as we show above, it is also possible that the small-separation angular covariance may be slightly different in other parts of the sky from the LMC. In summary, Eq. (10) is a conservative estimate for the covariance in Gaia EDR3 parallaxes, but it may not be the final word in the matter. Using that equation leads to a total Vϖ (0) = 106 μas, with similar contributions from the LMC (small separations) and quasars (large separations) components, and to σs = 10.3 μas as the proposed value to be used in Eq. (4) for Gaia EDR3 parallaxes.
4 Anchoring of the Gaia EDR3 parallaxes
Next, we briefly discuss the anchoring of the EDR3 parallaxes as a distance measurement. Most distance measurements in astronomy are derived from photometric magnitudes. In that case, a constant uncertainty (random or systematic) in magnitude translates into a constant σd∕d, meaning that relative distance uncertainties derived from magnitudes are (to first order) independent of distance. Parallaxes are different, as to first order the uncertainty in distance derived from a parallax measurement grows as d2 (ignoring issues with priors; see Maíz Apellániz 2005). This means that for nearby objects parallactic distances will generally be more precise than photometric distances, but for distant objects the situation will be reversed. Therefore, from the calibration point of view we should use distant objects to calibrate parallaxes under the assumption that two objects in the same region of the sky and with the same magnitude and color will have the same parallax bias in Gaia (see below). In this way, if we have an object at infinity with an accurate (i.e., bias-free) parallax of zero, the relative parallax between the distant and the nearby object will effectively be an absolute parallax.
The approach described in the previous paragraph is the logic behind the L21b and L21a analysis: Gaia EDR3 parallaxes are ultimately anchored in the values for quasars, which are forced to be zero through the use of parallax bias corrections. However, as discussed in the previous paragraph, parallaxes can also be anchored with galaxies for which accurate and precise distances exist because in those cases the uncertainties associated with their photometric distances can be significantly lower than the uncertainties associated with their parallactic distances. Here and in Table 1 we present further lines of evidence that indicate that the Gaia EDR3 parallaxes are correctly anchored:
-
Could there be a magnitude dependency of the quasar EDR3 parallaxes? We checked this by using the bright quasar subsample described in the previous subsection (as opposed to the full sample used by L21b). Their corrected mean parallax is within one sigma of zero (see Table 1), where for the uncertainty we simply used the standarddeviation of the mean given that quasars are spread over the whole sky, so the answer to the question is no.
-
What is the average EDR3 corrected parallax of the LMC? The values given above were calculated using a spatial smoothing in the region shown in Fig. 1. Doing a straight application of Eqs. (5) and (7) in the region located within 10° of the LMC center for the Gaia Collaboration (2021b) sample instead yields the value in Table 1, with the second term in Eq. (7) being the dominant contribution. This is just 0.4 σ above the expected value.
-
We canask the same question about the Small Magellanic Cloud (SMC).. If we do the same application of Eqs. (5) and (7) to the region located within 10° of the SMC center for the Gaia Collaboration (2021b) sample, we obtain a (corrected) group parallax that is within 0.6 σ of the expected value.
-
We also calculated the (corrected) group parallaxes for M 31 and M 33 using a similar procedure to that described below for globular clusters. For M 31 we selected 1229 Gaia EDR3 stars and for M 33 we selected 2309 Gaia EDR3 stars. The results in Table 1 are within one sigma of the expected values, one above zero and one below, providing another indication of the absence of a significant bias in the EDR3 parallaxes.
Therefore, we conclude that Gaia EDR3 parallaxes are well anchored with respect to distant objects and can be considered bias-free in the sense that the values of a large sample located at an infinite distance and with a wide variety of sky positions, magnitudes, and colors will have an average corrected parallax close to zero. Problems may arise when we restrict the sample in position, magnitude, and color, which is the subject of the next section.
Objects used to anchor the Gaia EDR3 parallaxes.
Filters applied to the globular clusters and the reference SMC field in this paper used for the 47 Tuc analysis.
5 Validating Gaia EDR3 parallaxes with globular clusters
Once we have a model covariance for Gaia EDR3 parallaxes, we can apply it to determine the distance uncertainties for stellar clusters. Gaia provides an unparalleled combination of parallaxes, proper motions, and photometry that can be used to first select a clean sample of cluster members and then derive the distance to the system. For our analysis we followed a modification of the technique developed by Maíz Apellániz (2019) and used for 16 stellar groups in Maíz Apellániz et al. (2020), and applied it to six globular clusters. The results are used in this section to validate the Gaia EDR3 parallaxes and in the next to derive the distances to the globular clusters. The selected globular clusters are the six richest known examples located far from the Galactic plane. We use rich clusters to have a sample of stars that is as large and clean as possible. The distance from the Galactic plane also minimizes contamination and differential extinction. The globular clusters and the filters used to select the sample are given in Table 2. We use the results to test the parallax bias correction, derive the value of k, and characterize RUWE.
We downloaded from the Gaia EDR3 archive the sources in a 1° × 1° or 2° × 2° square (depending on the angular size of the object) centered on each cluster, and we selected first the stars with G < 18, RUWE < 1.4, and σext < 0.1 mas (for the last we assume k = 1.0; see below). We then applied a cut in angular distance to the center of the cluster r and an equivalent cut in proper motion distance rμ. We did not apply a CMD cut as we did in the previous papers; our objects are the dominant population in the region and there is no significant differential extinction along their sightlines. We made the final selection by dropping the outliers in normalized parallax
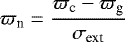 (11)
(11)
using a 4σ cut. As explained in Maíz Apellániz et al. (2020), the goal of this strategy is to have a final sample that is as clean as possible by sacrificing completeness. In other words, there must be many more stars in these clusters with Gaia EDR3 entries.
5.1 Testing the parallax bias correction as a function of G
To test the parallax bias correction we first assume k = 1.0 in Eq. (4) and use either a constant ZEDR3 value of −17 μas or the variable correction from Eq. (2). We perform the two selection procedures independently, and obtain the cluster parallaxes and their uncertainties from Eqs. (5)–(7). We then select the stars with five-parameter solutions (i.e., we only analyze Z5(G, νeff, β)), subtract thecorresponding cluster parallax from each star, and combine the resulting relative parallaxes Δϖ (star minus cluster) for all clusters, noting that the individual uncertainty for each star is larger than the spread expected from line-of-sight distance differences, which means that the relative parallaxes are almost exclusively caused by the random and systematic uncertainties and not by cluster-depth effects (see Soltis et al. 2021). The CMD resulting from combining the six globular clusters is shown in Fig. 4, where the conversion from νeff to GBP −GRP is taken from Eq. (2) in L21b. The CMD has the typical appearance of globular clusters, starting at the bottom from main-sequence stars, continuing to the top with red giants, and extending towards the left with horizontal branch (HB) stars, but as it is a composite of six globular clusters, it shows multiple sequences.
As shown in Fig. 20 of L21b, for a given color and ecliptic latitude Z5 (G, νeff, β) is nearly-constant in a series of magnitude ranges and has abrupt changes at their boundaries. Therefore, to validate Z5 (G, νeff, β) we divide our CMD using those magnitude ranges in Fig. 4 and Table 3. The next logical step would be to also divide the CMD into color ranges as the changes in Z5 (G, νeff, β) as a function of νeff are comparable to those as a function of G. Unfortunately, the CMD shows little spread in color for a given magnitude; the only exception is the G = 13−16 range wheremost of the HB stars are found, so that is the only range where we make such a division. This leaves us with seven ranges, and in each of these ranges we compute the mean and the standard deviation of Δϖ assuming either the constant ZEDR3 or the variable Z5 (G, νeff, β) (Table 3).
The comparison between Δϖconst and Δϖvar shows two clear magnitude ranges. For G < 13 the variable Z5(G, νeff, β) is a significant improvement over the constant ZEDR3, especially for 11 < G < 13. On the other hand, for G > 13 the differences are small: in all ranges |Δϖ| is at most 4.2 μas, with the variable Z5(G, νeff, β) being better for 13 < G < 16 and the constant ZEDR3 better for 16 < G < 18. The advantage of Δϖvar for G > 13 is that it is sometimes positive and sometimes negative, leading to a small effect when combining magnitude ranges, while Δϖconst is always negative. In either case, |Δϖ| is significantly smaller than σext, which is the most relevant comparison.
As it is clear that the variable Z5(G, νeff, β) yields significantly lower residuals overall when combining large magnitude ranges (especially for brighter stars), our main conclusion is that using it is recommended. However, we note that Δϖvar is relatively large for G < 11, that we have left blue stars mostly unstudied, and that our sampling of ecliptic latitudes is poor. A similar effect but with larger error bars is seen in Fig. 4 of Zinn (2021). Therefore, further testing is needed, which may lead to tweaking Z5 (G, νeff, β).
 |
Fig. 4 Combined CMD for the six globular clusters using a logarithmic intensity scale. The dotted lines separate the CMD regions described in the text. |
Globular cluster results for the parallax bias Z5(G, νeff, β) and k5 for five-parameter solutions (see text for a description of the columns).
5.2 Deriving the values for k
We now turn to the analysis of k5, the multiplicative constant in Eq. (4) for Gaia EDR3 five-parameter solutions. We evaluate it in each of the ranges defined above by forcing the distribution in ϖn in each one of them to have a standard deviation of 1.0. We do it by assuming [a] the constant ZEDR3 (k5,const), [b] the variable Z5 (G, νeff, β) (k5,var), or [c] the variable Z5(G, νeff, β) plus an additional correction introduced for all the stars in the range to force Δϖ to be zero (k5,new). The results are listed in the three last columns of Table 3. A comparison between them shows that from k5,const to k5,var there is (a) a small reduction for bright stars, (b) a small increase for the HB range, and (c) little change for red faint stars. Between k5,var and k5,new differences are negligible. This indicates that the origin of k being largerthan one lies mostly in the underestimation of the random uncertainties, as it should, and not in the uncorrected parallax bias. If we want to use a simple approximate formula to implement k, one possibility is
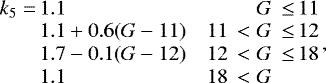 (12)
(12)
which is quite similar to the results found in Fig. 19 of Fabricius et al. (2021) for G > 12, but significantly lower for bright stars. The same structure as a function of G and similar values for k are seen in Fig. 16 of El-Badry et al. (2021).
Globular cluster results as a function of RUWE for five-parameter solutions (see text for a description of the columns).
5.3 How bad is a bad RUWE?
The RUWEis the goodness-of-fit statistic recommended by L21a as the main filtering criterion to exclude stars with poor astrometric solutions. It is an adimensional quantity with an average of ~ 1.0, and the most common value used for filtering is 1.4 (as we use above for the globular clusters in this paper). However, if a star with a RUWE of 1.3, for example, is considered to have a good astrometric solution, a valid question would be, how bad is the solution for another one with 1.5? And what if the RUWE were 2.5? Here we do a simple analysis to quantify that.
As described in our procedure above, the last step in the selection of the sample for each globular cluster is a cut in ϖn where we drop the 4σ outliers. Following Maíz Apellániz et al. (2020), we define the numbers in the sample before and after the cut as N*,0 and N*, respectively.Their values are given in Table 4 for the whole sample considering only stars with five-parameter solutions and in Table 5 cluster by cluster for stars with five- and six-parameter solutions. After the application of k, the final sample should have a ϖn distribution with an average close to zero and a standard deviation σn close to one, and this is indeed the case for RUWE < 1.4 in Table 4.
To evaluate the degradation of the quality of the parallaxes with increasing RUWE we include in our analysis the five-parameter stars selected by our algorithm but excluded solely on the basis of their RUWE. We divide them into two RUWE ranges (see Table 4), introduce a multiplicative factor k5,ext in addition to the one from Eq. (12), and increase it from 1 until we force the standard deviation of ϖn to be ~ 1 (hence σn ~ 1). When we do this we find that for RUWE between 1.4 and 2.0 (a) less than 1% of the points are farther away than 4σ, (b) the required value for k5,ext is moderately small, and (c) the resulting distribution has an average close to zero. This indicates that those parallaxes are likely safe to use after introducing the extra uncertainty. For RUWE between 2.0 and 3.0, on the other hand, k5,ext is already close to two, the average ϖn has started to deviate from zero (very slightly), and our sample is small. Therefore, these values can still be used, but the possibility of them being biased may be larger.
Membership and astrometric results for the globular clusters and the reference SMC field in this paper used for the 47 Tuc analysis.
6 Gaia EDR3 distances to globular clusters and going beyond the angular covariance limit
The results for the globular clusters are given in Table 5. To calculate the distance we used a flat prior truncated at 20 kpc, so no a priori knowledge of the spatial distribution of globular clusters is used. Nevertheless, given the small relative uncertainties for ϖg (all better than 10%), the results are robust. For example, changing the distance at which the prior is truncated to 15 kpc or 30 kpc leaves the results unchanged (see Fig. 1 in Maíz Apellániz 2005).
We also list in Table 5 the literature results for the globular clusters in the sample. There is good agreement overall, which is especially significant in some cases. For the two closest clusters, NGC 6397 and NGC 6752, the discrepancies are very small, at the level of 0.1 kpc or less. For 47 Tuc there is very good agreement with the high-precision results from Thompson et al. (2020) using eclipsing binaries.
A special situation is that of the Soltis et al. (2021) result for ω Cen using the same Gaia EDR3 parallaxes that we use. Their distance value is essentially the same as ours (difference of 0.01 kpc, within the rounding error), but their uncertainty is significantly smaller as their result for ϖg is 191 ± 1 (stat.) ±4 (syst.) μas, where the statistical uncertainty should be understood as being from the first term in our Eq. (7) and the systematic uncertainty from the second term. The authors claim that the 4 μas is derived from the L21a analysis of the LMC, but, as we show in this paper, this value is actually 6.8 μas, and when the effect of terms from larger separations is included it grows to 10.3 μas. The reduction to 9.6 μas in Table 5 is achieved by the averaging effect introduced by the considerable size of the cluster (Fig. 2).
We wanted to understand if there is a way to beat the Gaia EDR3 angular covariance limit of ~ 10 μas. In principle,it can be done if one has a collection of additional sources with an external high-precision distance measurement and the same spatial distribution as the cluster in question. These additional sources can be used as a reference to trace the uncorrected Gaia EDR3 parallax bias. This is the principle behind using quasars to study the spatial covariance, as their true parallaxes are on the order of nanoarcseconds. Could quasars be used as a reference for a particular cluster? Unfortunately, no. There are few known quasars per square degree, and their individual Gaia EDR3 uncertainties are too large to be useful.
A background galaxy such as that of the MCs is a different story. As one of our clusters, 47 Tuc, is notoriously located in front of the SMC, it can be used to see whether it is possible to beat the angular covariance limit. 47 Tuc and the SMC are highly differentiated in proper motions, so it is easy to distinguish between thecomponents from the two systems in exactly the same region. We did this here using the filters in Table 2 and processing the Gaia EDR3 parallaxes for the SMC population behind in 47 Tuc to derive the SMC results listed in Table 5. The distance to the SMC given by Cioni et al. (2000) is 62.8 ± 0.8 (stat.) ±2.3 (syst.) kpc, which corresponds to a parallax of 15.9 ± 0.6 μas. The value we derive from Gaia EDR3 parallaxes is 22.8 ± 9.0 μas, but it includes both the random and systematic components4. The latter is not needed if we want to calculate relative parallaxes in the same region and with a similar spatial distribution. The random component for the SMC is just 1.5 μas. Therefore, the uncorrected parallax bias is 6.9 ± 1.6 μas, including in the error budget that of the SMC distance. The value for the ϖc uncertainty for 47 Tuc in Table 5 also includes the systematic component; eliminating it leaves an uncertainty of just 0.4 μas. This leads to a final ϖc for 47 Tuc corrected from the SMC parallax bias of 220.9 ± 1.7 μas, where the uncertainty is purely statistical. However, we should remember the results of Table 3 and that the SMC sample is significantly fainter than the 47 Tuc, leading to a possible magnitude-dependent bias. A more realistic uncertainty including these effects is 3 μas, which yields a final distance of 4.53 ± 0.06 kpc. Therefore, for 47 Tuc we are able to beat the angular covariance limit and derive a precise distance that is in excellent agreement with the eclipsing-binary result of Thompson et al. (2020). The result is also within one sigma of the Gaia DR2 value by Chen et al. (2018), who used a similar (but not identical) method to the one we used here and whose uncertainty is twice as large as ours (a good example of the improvement from DR2 to EDR3).
7 Summary and recipe for using Gaia EDR3 parallaxes
In this paper we presented a procedure for obtaining accurate and precise Gaia EDR3 parallaxes. The procedure includes the correction of the known parallax biases and the addition of the unknown biases into the error budget. To do this correctly, we performed an analysis of the angular covariance of the Gaia EDR3 parallaxes combining LMC and quasar data, and verified it with Galactic bulge data. A sample of six globular clusters was used to validate the procedure, and while doing so we derived accurate distances to them. For 47 Tuc we showed that it is possible to go beyond the angular covariance limit with the help of the background stars in the SMC.
The biases related to angular covariance are likely to be hard to eliminate. The hope is that DR4 will significantly reduce them, as EDR3 did for the biases present in DR2. However, it may be possible to reduce the magnitude, color, and position biases that remain in the data without having to wait for DR4, especially for the brightest stars. We plan to do so in the near future by combining the results presented in this paper with an analysis of open clusters that may lead to an improvement of Z5 (G, νeff, β).
We propose the following recipe for the derivation of Gaia EDR3 distances based on the analysis in this paper:
- 1.
Do a preliminary filtering by RUWE, five- or six-parameter solutions, and other criteria (e.g., parallax uncertainty) to eliminate objects with undesirable properties (which depend on the specific task at hand);
- 2.
Apply the known parallax bias correction using Eqs. (1) and (2) from this paper and the information in the L21b tables;
- 3.
Convert from internal to external parallax uncertainties using Eq. (4) with σs = 10.3 μas and k from Eq. (12), with the corrections from Table 4 if using objects with RUWE in the 1.4–3.0 range;
- 4.
When combining two or more parallaxes, apply Eqs. (5)–(7) with the angular covariance taken from Eqs. (8)–(10);
- 5.
Select an appropriate prior and calculate the posterior distribution for the distance;
- 6.
If background or foreground targets of a known distance are present in the field, consider using them to beat the angular covariance limit.
With that recipe we conclude this paper.
Acknowledgements
The authors thank Lennart Lindegren and the rest of the DPAC astrometry team for their extraordinary work in producing Gaia EDR3 and Stefano Casertano and Adam Riess for useful discussions on the topics of this paper. We also thank Xavier Luri for letting us have access to the LMC Gaia EDR3 selection script. J.M.A. and M.P.G. acknowledge support from the Spanish Government Ministerio de Ciencia through grant PGC2018-095049-B-C22. R.H.B. acknowledges support from the ESAC visitors program. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of the SIMBAD and VizieR databases, operated at CDS, Strasbourg, France. The Gaia data is processed with the computer resources at Mare Nostrum and the technical support provided by BSC-CNS.
References
- Anders, F., Khalatyan, A., Chiappini, C., et al. 2019, A&A, 628, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arenou, F., Luri, X., Babusiaux, C., et al. 2018, A&A, 616, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Campillay, A. R., Arias, J. I., Barbá, R. H., et al. 2019, MNRAS, 484, 2137 [NASA ADS] [CrossRef] [Google Scholar]
- Cerny, W., Freedman, W. L., Madore, B. F., et al. 2020, AAS J., submitted [arXiv:2012.09701] [Google Scholar]
- Chen, S., Richer, H., Caiazzo, I., & Heyl, J. 2018, ApJ, 867, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Cioni, M. R. L., van der Marel, R. P., Loup, C., & Habing, H. J. 2000, A&A, 359, 601 [Google Scholar]
- Conn, A. R., Ibata, R. A., Lewis, G. F., et al. 2012, ApJ, 758, 11 [Google Scholar]
- El-Badry, K., Rix, H.-W., & Heintz, T. M. 2021, MNRAS, in press [arXiv:2101.05282] [Google Scholar]
- Fabricius, C., Luri, X., Arenou, F., et al. 2021, A&A, 649, A5 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021a, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Luri, X., et al.) 2021b, A&A, 649, A7 [EDP Sciences] [Google Scholar]
- Harris, W. E. 2010, ArXiv e-prints [arXiv:1012.3224] [Google Scholar]
- Lindegren, L. et al. 2018, https://www.cosmos.esa.int/documents/29201/1770596/Lindegren_GaiaDR2_Astrometry_extended.pdf [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021a, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021b, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Lutz, T. E., & Kelker, D. H. 1973, PASP, 85, 573 [Google Scholar]
- Maíz Apellániz, J. 2001, AJ, 121, 2737 [Google Scholar]
- Maíz Apellániz, J. 2005, ESA SP, 576, 179 [Google Scholar]
- Maíz Apellániz, J. 2019, A&A, 630, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., Alfaro, E. J., & Sota, A. 2008, ArXiv eprints [arXiv:0804.2553] [Google Scholar]
- Maíz Apellániz, J., Crespo Bellido, P., Barbá, R. H., Fernández Aranda, R., & Sota, A. 2020, A&A, 643, A138 [CrossRef] [EDP Sciences] [Google Scholar]
- Pantaleoni González, M., Maíz Apellániz, J., Barbá, R. H., & Reed, B. C. 2021, MNRAS, in press [arXiv:2103.02748] [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200 [Google Scholar]
- Recio-Blanco, A., Piotto, G., de Angeli, F., et al. 2005, A&A, 432, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soltis, J., Casertano, S., & Riess, A. G. 2021, ApJ, 908, L5 [Google Scholar]
- Thompson, I. B., Udalski, A., Dotter, A., et al. 2020, MNRAS, 492, 4254 [Google Scholar]
- Vasiliev, E., & Baumgardt, H. 2021, ArXiv e-prints [arXiv:2102.09568] [Google Scholar]
- Watkins, L. L., van der Marel, R. P., Bellini, A., & Anderson, J. 2015, ApJ, 812, 149 [Google Scholar]
- Zinn, J. C. 2021, AJ, 161, 214 [Google Scholar]
We define a result as “precise” when it has a small total uncertainty and as “accurate” when its systematic uncertainty is either small or is properly corrected for. See Sect. 2 for a further description of how we define the different uncertainty types.
It is possible in principle to play with a selection of which stars to use and which ones to discard to minimize even further the result from Eq. (7). However, when attempting this process with real stellar clusters the improvement in σg is usually very small, of the order of 10% at most.
7.0 μas is the dispersion of the smoothed values, not the standard deviation of the mean, which is much lower but irrelevant for the Gaia EDR3 overall measurement for the LMC due to the second term in Eq. (7). The average of the individual parallax values is also different, as we discuss below, due to the non-uniform spatial coverage of the sample.
The parallax is similar but not identical to the value in Table 1, which is calculated from the whole SMC, as expected given the effect of the angular covariance at separations of a few degrees.
All Tables
Filters applied to the globular clusters and the reference SMC field in this paper used for the 47 Tuc analysis.
Globular cluster results for the parallax bias Z5(G, νeff, β) and k5 for five-parameter solutions (see text for a description of the columns).
Globular cluster results as a function of RUWE for five-parameter solutions (see text for a description of the columns).
Membership and astrometric results for the globular clusters and the reference SMC field in this paper used for the 47 Tuc analysis.
All Figures
 |
Fig. 1 Left: smoothed corrected Gaia EDR3 parallaxes for the bright LMC subsample. The axes arerectangular coordinates in degrees and the color table shows the parallax scale in μas. Right: angular covariance in the LMC data with respect to the mean measured parallax. The points are the measured values and the red line is the analytical function described in the text. |
| In the text | |
 |
Fig. 2 Large-angle angular covariance of the Gaia EDR3 parallaxes.Left panel: 0°–20° separation range with the quasar data in 1° bins using either ϖ (blue asterisks) or ϖc (black error bars), the linear fit to the quasar corrected data in the 5°–40° separation range (green line), and the analytical fit to the LMC data (red line). The error bars associated with the quasar ϖ data are not shown, but they are similar to those for ϖc. Right panel: full 0°–180° separation range and includes the total quasar+LMC model. |
| In the text | |
 |
Fig. 3 Smoothed corrected Gaia EDR3 parallaxes for the RC bulge sample. The axes are in Galactic coordinates in degrees and the color table shows the parallax scale in units of μas. |
| In the text | |
 |
Fig. 4 Combined CMD for the six globular clusters using a logarithmic intensity scale. The dotted lines separate the CMD regions described in the text. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


