EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 649 (May 2021) A&A, 649 (2021) A156 Full HTML
Free Access
Issue
A&A
Volume 649, May 2021
Article Number A156
Number of page(s) 8
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202038964
Published online 31 May 2021

© ESO 2021

1 Introduction

With the discovery on an increasing number of extrasolar planets in the past decade, we are in the fortunate position to have an ever increasing statistical sample, probing the outcome of the planet formation process. However, some of the properties of this sample are not yet fully characterized. One important aspect is the presence of additional stellar bodies in the system. Raghavan et al. (2010) found that close to half of all solar-type stars in the Galaxy reside in binary or higher order stellar multiple systems (see also earlier results by Abt & Levy 1976; Duquennoy & Mayor 1991). Thus the influence of additional stellar companions on the planet formation process is a highly relevant question. In fact, the closest known extrasolar planet to the sun, orbiting α Cen B, is located in a stellar multiple system (Dumusque et al. 2012).

In an early hydrodynamical study, Nelson (2000) found that planet formation should be inhibited in close (~50 au), equal mass binary systems due to the additional source of potential energy that heats up the circumstellar disk, thus preventing fragmentation of the disk. This was supported by some observational results, for example, Eggenberger et al. (2011) found that planets are less frequent in systems with additional stellar components between 35 au and 100 au.

Several observational studies have investigated the influence of additional companions on the lifetimes of circumstellar disks. In particular Cieza et al. (2009) and Kraus et al. (2012) independently found that the lifetime of disks in known binary systems seems to be significantly shorter (0.1–1 Myr as opposed to the canonical ~10 Myr, e.g., Haisch et al. 2001).

On the other hand, Pascucci et al. (2008) found with Spitzer observations, while tracing the silicate emission feature at 10 μm, that the dust evolution in young systems in Taurus is not significantly influenced by the presence of stellar companions between 10 au and 450 au. Finally, several recent studies find that close binaries may in fact lead to an enhanced presence of giant planets (Ngo et al. 2016; Fontanive et al. 2019).

Adaptive optics (AO) imaging with large aperture telescopes is the best method to find stellar companions to exoplanet host stars at separations between a few tens of au and a few hundred au, that is to say at separations where they are not picked up by wide field surveys, but where they may also not be apparent in spectroscopic observations. Several such surveys have been conducted in the past with VLT/NACO (e.g., Eggenberger et al. 2007; Mugrauer & Ginski 2015) and with Keck/NIRC2 (e.g., Ngo et al. 2015, 2017; Wang et al. 2015). Bohn et al. (2020) recently used, for the first time, an extreme1 AO system on an 8 m-class telescope to image a large sample of transiting host stars.

In this study, we present the first results of our stellar multiplicity survey of radial-velocity (RV) exoplanet host stars using the Spectro-Polarimetric High-contrast Exoplanet REsearch (SPHERE) instrument (Beuzit et al. 2019) at the ESO/VLT. Over the course of this survey, we have observed 122 systems between 2016 and 2019 with detected RV planets, making this the largest survey of its kind with an extreme AO instrument to date. The detailed results of the survey will be presented in a forthcoming publication by Vogt et al. (in prep.). Here we highlight four systems in which we have detected new stellar companions, one of which we cross-matched with the catalog of the second data release of the ESA-Gaia mission (Gaia DR2 from here on, Gaia Collaboration 2018) and thus identified as white dwarf.

In Sect. 2, we give a brief overview of the systems where we detected these new companions, and we describe theobservations and the data reduction strategy as well as the astrometric and photometric extraction in Sects. 3 and 4. Using the photometry of the companions and the systems age estimates, we compute mass estimates in Sect. 5 and detection limits in Sect. 6. Finally we discuss the properties of these planetary systems in the context of these new detections in Sect. 7.

2 Properties of observed systems

In the following, we summarize the basic stellar parameters and previously discovered planets in our target sample. As the orbital inclinations of the planets are not known, the mass estimates are always minimum masses, that is to say m sin (i).

HD 1666

Is a F7 main sequence star (Houk & Smith-Moore 1988), which is located at a distance2 of 118.3 ± 0.7 pc (Gaia DR2, Gaia Collaboration 2018). Harakawa et al. (2015) report a Jovian mass planet (Mp sin i = 6.4MJup) around HD 1666 with a period of P = 270 days and an eccentricity of e = 0.63. They computed the stellar parameters from isochrone fitting and found a mass of 1.50 ± 0.07 M⊙ and an age of 1.76 ± 0.20 Gyr.

HD 109271

Is an old, solar type main sequence star of spectral type G5 with a mass of 1.05 ± 0.02 M⊙ and an age of 7.3 ± 1.2 Gyr (Girardi et al. 2000). It is located at a distance of 56.0 ± 0.2 pc (Gaia DR2, Gaia Collaboration 2018). Lo Curto et al. (2013) detected two approximately Neptune-mass planets (17 ± 1 M⊕ and 24 ± 2 M⊕) in the system with orbital periods of 7.9 and 30.9 days, respectively. Both of the recovered planetary signals indicate moderately eccentric orbits with an eccentricity of 0.25 ± 0.08 for the less massive, closer-in planet and 0.15 ± 0.09 for the outer planet. The authors also speculate on the presence of a further out planet with a roughly 400 day period, but they cannot confirm the detection with their data set.

HIP 68468

Is a solar twin, main sequence star with a spectral type of G3 (Houk 1982). It is located at a distance of 99.9 ± 0.7 pc (Gaia DR2,Gaia Collaboration 2018). Meléndez et al. (2017) estimated the stellar parameters from high resolution spectra and, in particular, element abundances and found an age of 6.4 ± 0.8 Gyr. They also detected RV variations, which were best fit by a two-planet solution: one super Earth (2.9 ± 0.8 M⊕) on a 1.8 day orbit and a super Neptune (26 ± 4 M⊕) in a much wider 194 day orbit. Remarkably, the best fit orbit for the inner super Earth is highly eccentric with an eccentricity of 0.41, while this is not the case for the outer, more massive planet.

HIP 107773

Is a horizontal branch giant of spectral type K1 (van Leeuwen 2007). It is located at a distance of 105.5 ± 0.8 pc (Gaia DR2, Gaia Collaboration 2018). An age estimate for the star has not been given in the literature; however, Jones et al. (2015) find a mass of 2.42 ± 0.27 M⊙ from a study of the available photometry of the system. Given this mass and that the star is already on the horizontal branch, the age is certainly more than 1 Gyr. Jones et al. (2015) find RV variations, which they fit with a roughly Jupiter mass planet (1.98 ± 0.21 MJup) on a 144 day orbit. The planet shows a small eccentricity of 0.09 ± 0.06. Additionally, they detect a significant linear trend of 14.6 ± 1.8 m s−1 yr−1 in the RV that is longer than the observation period. They speculate that there is a second Jupiter class planet in a significantly larger orbit, but they could not fit a specific solution with the available data. We summarize all of the basic parameters of the target systems and their planetary companions in Table 1.

3 Observations and data reduction

All observations were conducted with SPHERE/IRDIS (Infra-Red Dual Imager and Spectrograph, Dohlen et al. 2008) at the ESO/VLT in field stabilized classical imaging mode with the broad-band Ks filter. The bright primary star was always placed behind an apodized Lyot coronagraph with an inner working angle3 of 120 mas. Individual frame exposure times (3 s–16 s) were adjusted such that the residual light from the primary star does not reach saturation levels. The total integration time for all targets was between 3.2 and 6 min. The observation conditions were highly variable between individual observation epochs and targets since our program was executed as filler for nonideal or unstable weather conditions. We give an overview of integration times and key weather parameters in Table 2. For all systems but HD 1666, we have at least one observation epoch with excellent seeing conditions (< 0.8′′) and an atmosphere coherence time ( >5 ms). For HD 1666, we have a high coherence time of 5.3 ms and seeing within the tolerances of the AO system (< 1.2′′) in the first observation epoch in 2016, leading to a stable AO performance.

In all observation, epochs we took flux and center reference frames as well as dedicated sky images for background subtraction. Flux calibration frames were taken with the primary star removed from the coronagraphic mask and the individual integration time adjusted to prevent saturation. Additionally, neutral density filters were employed when necessary. The center reference frames were taken after the primary star was aligned behind the coronagraphic mask and the AO system was used to introduce a waffle pattern on the wavefront to create equidistant calibration spots outside of the coronagraphic mask. Sky frames were taken with the AO loop open and the telescope pointing away from the primary star with no other (bright) sources in the field of view.

For data reduction, we used a modified version of the IRDIS Data reduction for Accurate Polarimetry (IRDAP, van Holstein et al. 2020)pipeline. All of the basic data processing steps (flat-fielding with lamp flats, sky subtraction, and bad pixel masking) were executed as described in van Holstein et al. 2020. Since our data were nonpolarimetric, we then modified the pipeline to simply center and stack all frames. The final results are shown in Fig. 1.

Table 1

Summary of the properties of our target systems.

Table 2

Observation parameters for all four systems.

4 Astrometry and photometry of new companions

For astrometric and photoemtric extraction, we used a multistage fitting process which will be described in detail in van Holstein et al. (in prep.). As a first step, we fit a Moffat function to the position of the detected companions. To account for the stellar halo of the primary star, we added an inclined plane to the fit. We then performed point spread function (PSF) fitting, using the unsaturated PSF of the primary star from the flux calibration frames as a model. The initial guess for the peak location and scaling between primary and companion PSF was taken from the Moffat fitting results. The fitting procedure uses the simplex method as implemented in the minimize function in the SciPy package (Virtanen et al. 2020). To derive accurate statistical uncertainties of the fitting results, we performed a Markov-chain Monte-Carlo (MCMC) analysis using the emcee Python package (Foreman-Mackey et al. 2013). We used Gaussian priors for the flux ratio between the companion and primary as well as the companion position with the simplex fitting results as mean values of the Gaussians. We explored the parameter space in all cases with 32 walkers which perform a total of 20 000 steps.

The resulting values of the companion position in detector coordinates is converted to a relative astrometric position with respect to the primary star. For this, we used the astrometric calibration given in Maire et al. (2016) for SPHERE/IRDIS, that is, a pixel scale of 12.265 ± 0.009 mas/pixel and a true north detector position angle of −1.75° ± 0.10°. The detector position of the primary star is, in all cases, determined by fitting Gaussians to the satellite spots after the subtraction of the residual stellar light as outlined in van Holstein et al. (2020).

The flux ratio between the companion and primary star is converted to a magnitude contrast, taking into account the different exposure times for flux and science frames as well as the profiles of neutral density filters that were inserted for the flux calibration images in some cases. The resulting astrometry and photometry are listed in Table 3. We note that the relative photometry for all companions changed significantly between epochs (changes are up to 0.9 mag with a significance between 3σ and 7σ). In all likelihood, this is due to the unstable weather conditions of one of the observations epochs for each of the candidates. Since flux reference frames and science frames are not taken simultaneously with SPHERE, the AO corrected PSF will change between these observations. In particular, during highly unstable conditions, this introduces a systematic error in photometry (see e.g., Esslinger & Edmunds 1998 for a discussion on this effect for AO systems). As we report in Table 2, for HD 1666, the second epoch coherence time was well below the limit of 3 ms after which the SPHERE AO system can no longer sufficiently keep up with atmosphere changes. For HD 109271, the seeing in the second observation epoch was close to the specification limit of SPHERE at 1.2′′. Additionally thin clouds were reported in both observation epochs of HD 109271, which may have introduced a variable sky transparency. For HIP 68468, the photometry of the first and third observation epoch are in perfect agreement. Both of these epochs had above average atmosphere coherence times of 7 ms4 and good seeing conditions. The second observation epoch varies significantly from the other two, but it was taken under an average seeing of 1.4′′, that is to say well outside of the SPHERE specification limit and with coherence times shorter than 3 ms. Finally, HIP 107773 shows a 3.1σ variation between both observation epochs, despite good average seeing conditions and atmosphere coherence times above 3 ms, as reported in Table 2. However, in the second observation epoch, the seeing and coherence time degraded significantly during the between science and flux calibration exposures. While the average seeing during the science sequence was 0.49′′, it degraded to 0.79′′ during the flux calibration. The atmosphere coherence time dropped at the same time to 2.3 ms, that is, below the threshold at which the SPHERE AO has problems keeping up with the changes in atmospheric distortions.

To test if the different magnitudes may indeed be explained by a degradation in AO performance, we performed aperture photometry in the second epoch of the HD 1666 system, using a large aperture radius of 30 pixels to include all flux of the companion. Using this technique, we arrive at a brighter companion contrast of 5.1 ± 0.1 mag compared to the 5.70 ± 0.31 mag extracted with PSF fitting photometry for the same data set. This result is in better agreement with the magnitude difference of 4.83 ± 0.07 mag, which was measured in the first epoch under significantly better weather conditions. The remaining discrepancy in the first epoch can be explained if some signal of the companion dropped below the noise floor in the image due to the lower quality AO correction. Since for all systems the first observation epoch was taken in excellent atmospheric conditions, we adopt these magnitudes for the subsequent analysis, but report all results in Table 3 for completeness.

To confirm that the newly detected companions are bound to the observed host stars, we performed a common proper motion analysis. Proper motions for all systems were taken from the Gaia DR2 catalog. In Fig. 2, we show, for each system, the separation and position angle of the companion relative to the primary star versus time. The solid, oscillating lines indicate the expected position for a distant and thus nonmoving background object given the primary stars’ proper and parallactic motion and the position of the companion in the first observing epoch. We find that, in all four systems, the astrometry is inconsistent with such a background object with a high significance. In all systems, the extracted astrometry is consistent with a primary star and companion exhibiting the same proper motion on the sky. Given our small field of view and that all stars in our study are evolved and not part of young co-moving groups, we thus conclude that we identified new and gravitationally bound companions to these exoplanet host stars in all cases.

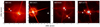thumbnail Fig. 1

SPHERE/IRDIS observations of the new co-moving low-mass stellar companions to exoplanet host stars. The gray hatched disk marks the utilized coronagraphic mask.
Table 3

Astrometric and photometric measurements (in Ks-band) of companions.

5 Characterization of companions

We used the extracted photometry together with the system ages and distances from Sect. 2 as well as the 2MASS (Skrutskie et al. 2006) K-band magnitudes of the primary stars to compute mass estimates for the companions. We first converted the magnitude differences from Table 3 into apparent K-band magnitudes using the primary star K-band magnitude. In all cases, we use the epoch with the smaller uncertainties (and better weather conditions) for the mass estimates. Given the apparent magnitudes, we converted these into absolute magnitudes using the known distances and then compared these with (sub)stellar BT-SETTL model isochrones (Baraffe et al. 2015). To derive masses, we interpolated the model grid and took uncertainties in all parameters into account, that is to say the age, distance, and magnitude. We find companion masses of 0.39 ± 0.01 M⊙ for HD 1666B, 0.36 ± 0.01 M⊙ for HIP 68468 B, and 0.63 ± 0.04 M⊙ for HIP 107773 B. We summarize the masses and projected separations of all companions in Table 4.

The new companion in the HD 109271 system is, in principle, faint enough in the Ks -band to be in the brown dwarf mass range. Since it is located at a very wide separation of 5.4′′, we cross-checked the Gaia DR2 catalog to see if it was picked up by Gaia as well. We indeed find that the object with Gaia identifier Gaia DR2 3578137911427752704 is located at the correct separation and position angle relative to HD 109271 (separation of 5.4250′′ ± 0.0007′′ and position angle of 267.354° ± 0.004°). This objectshows a Gaia magnitude of 16.125 ± 0.009 mag. Given the very faint Ks-band magnitude of 16.06 ± 0.04 mag, this magnitude in the optical Gaia band is surprising. If we only take our Ks -band measurement, we find that the object should be a brown dwarf with a mass of 72.9 ± 0.3 MJup. In this case, we would expect a G-band magnitude of roughly 21.8 mag. The significantly brighter G-band magnitude indicates, however, the different nature of the object.

We used the G-band photometry of both components of the HD 109271 system as well as the parallax (π = 17.8697 ± 0.066 mas) and the G-band extinction estimate (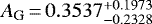 mag) of the primary, listed in the Gaia DR2, to determine the absolute G-band magnitudes of both stars. We obtain 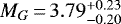mag for HD 109271 A and 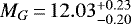mag for its co-moving companion, respectively.

Furthermore, with the G-band extinction of the primary, its 2MASS Ks-band magnitude (Ks = 6.495 ± 0.026 mag), as well as the photometry of the companion, as measured in our SPHERE images, we derived the intrinsic (G − Ks) color of both stars by adopting 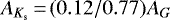. This yields 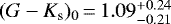mag for the primary and 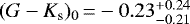mag for the fainter secondary, respectively.

The derived photometry of both components of the HD 109271 system is illustrated in a color-magnitude diagram in Fig. 3. The stars are plotted in this diagram together with the main-sequence (gray line) from Pecaut & Mamajek (2013)5, as well as the evolutionary track (dashed black line) of 0.6 M⊙ DA white dwarfs, as predicted by the models of Holberg & Bergeron (2006), Kowalski & Saumon (2006), Tremblay et al. (2011), and Bergeron et al. (2011). While the photometry of HD 109271 A is fully consistent with what is expected for a main-sequence star, the companion is clearly located below the main-sequence. However, its photometry agrees well with that of DA white dwarfs. Hence, we conclude that HD 109271 B is a white dwarf companion of the exoplanet host star. Spectroscopic follow-up observations are needed to further constrain the properties of this degenerated star.

Mugrauer (2019) computed detection limits for low-mass companions around a solar-mass, main-sequence star within a distance of 240 pc. They find that around these targets, Gaia is generally not sensitive to companions inside an angular separation of 1′′ and has detection limits corresponding to masses of 0.5 M⊙ inside of 2′′. Accordingly, the other three detected companions are at too small a separation and are too low in mass (and thus too faint) to be detected by Gaia.

thumbnail Fig. 2

Proper motion diagrams of all detected stellar companions. The separations and position angles of the companion relative to the primary stars are plotted versus time. The “oscillating,” solid lines show the area in which a nonmoving background object would be expected. The dashed lines show the area where a co-moving, bound object would be expected; this also takes possible orbital motion into account.
Table 4

Mass estimates and projected separations.

thumbnail Fig. 3

Both components of the HD 109271 system plotted in a (G − Ks) − MG diagram. The main-sequence is shown with the gray line and the evolutionary track of DA white dwarfs with a mass of 0.6 M⊙ is shown with the black dashed line. The photometry of the exoplanet host star HD 109271 A is consistent with a main-sequence star, as expected. In contrast, the detected co-moving companion HD 109271 B is clearly located below the main-sequence, but its photometry agrees well with that of DA white dwarfs.

6 Detection limits

While a detailed analysis of the detection limits for our entire survey sample will be presented in Vogt et al. (in prep.), we did compute individual detection limits for the four systems presented here. We determined the attained contrast as a function of separation using star-centered rings for comparison purposes, similar to the method described in Mawet et al. (2014) and implemented in IRDAP. Using the 2MASS magnitudes of the systems, the contrast was then converted to the apparent magnitude detection limit. The result is shown in Fig. 4. Using the system ages and distances, we can convert these magnitude limits to mass limits. For the conversion, we used (sub)stellar model isochrones by Baraffe et al. (2015). For HD 109271 and HIP 68468, we can rule out additional stellar companions down to 0.15′′. For HD 1666, this separation increases to 0.4′′. For HIP 107773, the oldest system in this sample, we can rule out a stellar companion down to 1.3′′. At larger separations, outside of 3′′, we are on average sensitive to wide brown dwarf companions with masses down to ~ 60 MJup. Due to the high system ages, we are not sensitive to objects in the planetary mass range, that is, below the deuterium burning mass limit.

7 Discussion and conclusion

In this study, we present the discovery of four new stellar companions to exoplanet host stars; one of which was identified asa white dwarf. Of the discovered stellar companions, HIP 107773 B is certainly the most interesting object located at a projected separation of only 40 au. HIP 107773 B is one of only approximately ten systems with known extrasolar planets and stellar companions at orbital separations smaller than 100 au (see Thebault & Haghighipour 2015 for a summary of these systems and Ngo et al. (2017) for updated statistics). At such small separations, the stellar companion likely has a significant influence on the evolution of the planet-forming disk around the primary star. In particular, Rosotti & Clarke (2018) report that for companion separations of 20–30 au, the disk dispersal mechanism around the primary component changes from the photo-evaporation dominated (inside-out) regime to the tidal torque driven (outside-in) regime. Roell et al. (2012) found that systems with close stellar companions tend to harbor more massive planets, that is to say they find that for stellar separations of ~ 40 au, all planetary masses were above 0.3 MJup. Indeed the minimum mass of the detected RV planet in the HIP 107773 system is ~ 2 MJup, which fits into this picture. In addition to the Jupiter-mass planet in the system, Jones et al. (2015) find a linear trend in the RV data. We investigated if this signal may be caused by the detected stellar companion. At its current projected separation of 40 au, the orbital period would be on the order of 145 yr. Assuming a circular orbit and an inclination of 90° of the orbital plane, we find a semi-amplitude of the induce RV signal in HIP 107773 A of 2.1 km s−1. The linear trend observed by Jones et al. (2015) changes the RV of the A component by several 10 m s−1. Thus, in principle, the stellar companion can explain this signal well, especially if it is currently close to the projected apastron and thus the induced signal is small, or if the inclination of the orbit is much smaller than 90°. For the other three systems in this study, the projected separations are much larger and thus the expected RV signal is much smaller and consistent with not being detected in the existing RV data.

The white dwarf companion around HD 109271 is one of a growing number of such objects detected around exoplanet hosts (see e.g., Mugrauer 2019, who reports nine new white dwarf companions). It appears increasingly common that planets around the less massive component in a binary system survive the post main sequence phase of the more massive component.

For the HD 1666 system, there is some indication that the stellar companion may have an influence on the orbital dynamics of the detected long period, super Jupiter in the system, which shows a very high eccentricity of 0.63. In principle, it may be possible that HD 1666 b and B are locked in a Kozai–Lidov-type resonance (Kozai 1962). Using the formula by Ford et al. (2000), we estimate that the period for such a resonance would be on the order of 43 Myr if the stellar companion is currently on a circular orbit or it may be as low as 3.5 Myr if the companion orbit is highly eccentric (e = 0.9). Given that the system age is above 1 Gyr, such resonances are thus in principle possible and indeed the HD 1666 system occupies a parameter space for which Takeda & Rasio (2005) found that Kozai–Lidov-type oscillations should be effective. However, we note that Ngo et al. (2017) did not find a systematic difference between orbital parameters of planets located between 0.1 au and 5 au from the primary star in stellar multiple and single star systems. This may make HD 1666 an exceptional case.

The parameter space probed by our new study using VLT/SPHERE in classical imaging mode is significantly different than other studies and complements those. Mugrauer (2019) has recently demonstrated that, using Gaia DR2, wide stellar companions to exoplanet host stars, which are of a similar brightness as the primary star, can be discovered in principle down to 1′′ (few tens of au). However, the majority of the systems that were picked up with Gaia are at separations larger than 1000 au. With SPHERE, we probe significantly closer to the primary star and for fainter and thus lower mass objects and cover a complementary parameter space compared to Gaia. The three main-sequence stellar companions that we recovered are located on projected separations between 40 au and 250 au and they are not listed in the Gaia DR2 catalog. In principle, our imaging data are sensitive to all stellar companions down to the hydrogen-burning mass limit for minimum projected separations ranging between 8 au and 140 au, depending on the system’s ages and distances. SPHERE with its extreme AO system thus enables one to probe closer to the exoplanet host stars than was done previously with AO surveys, for example, the contrast limit reached at 1.5′′ is roughly 2–4 mag deeper than the observations reported in Ngo et al. (2017) with Keck/NIRC2 in the K-band. This highlights the necessity for large surveys of exoplanet host stars with extreme AO instruments to extend our picture of stellar multiplicity in exoplanet host stars to the smallest separations and companion masses.

thumbnail Fig. 4

5 σ detection limits for possible companions around the four discussed systems of our survey. We show the average magnitude limit, assuming a distance of 95 pc and age of 4.5 Gyr; this translates into a companion mass at the stellar-brown dwarf boarder.

Acknowledgements

SPHERE is an instrument designed and built by a consortium consisting of IPAG (Grenoble, France), MPIA (Heidelberg, Germany), LAM (Marseille, France), LESIA (Paris, France), Laboratoire Lagrange (Nice, France), INAF – Osservatorio di Padova (Italy), Observatoire de Genève (Switzerland), ETH Zurich (Switzerland), NOVA (Netherlands), ONERA (France), and ASTRON (The Netherlands) in collaboration with ESO. SPHERE was funded by ESO, with additional contributions from CNRS (France), MPIA (Germany), INAF (Italy), FINES (Switzerland), and NOVA (The Netherlands). SPHERE also received funding from the European Commission Sixth and Seventh Framework Programmes as part of the Optical Infrared Coordination Network for Astronomy (OPTICON) under grant number RII3-Ct2004-001566 for FP6 (2004–2008), grant number 226604 for FP7 (2009–2012), and grant number 312430 for FP7 (2013–2016). C.G. acknowledges funding from the Netherlands Organisation for Scientific Research (NWO) TOP-1 grant as part of the research program Herbig Ae/Be stars, Rosetta stones for understanding the formation of planetary systems, project number 614.001.552. This research has used the SIMBAD database, operated at CDS, Strasbourg, France (Wenger et al. 2000). We used the Python programming language6, especially the SciPy (Virtanen et al. 2020), NumPy (Oliphant 2006), Matplotlib (Hunter 2007), photutils (Bradley et al. 2016), and astropy (Astropy Collaboration 2013, 2018) packages. We thank the writers of these software packages for making their work available to the astronomical community.

References

  1. Abt, H. A., & Levy, S. G. 1976, ApJS, 30, 273 [NASA ADS] [CrossRef] [Google Scholar]
  2. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  4. Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bergeron, P., Wesemael, F., Dufour, P., et al. 2011, ApJ, 737, 28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bohn, A. J., Southworth, J., Ginski, C., et al. 2020, A&A, 635, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bradley, L., Sipocz, B., Robitaille, T., et al. 2016, Photutils: Photometry Tools, Astrophys. Source Code Libr. [record ascl:1609.011] [Google Scholar]
  9. Cieza, L. A., Padgett, D. L., Allen, L. E., et al. 2009, ApJ, 696, L84 [Google Scholar]
  10. Dohlen, K., Langlois, M., Saisse, M., et al. 2008, in SPIE Conf. Ser., 7014, Proc. SPIE, 70143L [Google Scholar]
  11. Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [Google Scholar]
  12. Duquennoy, A., & Mayor, M. 1991, A&A, 500, 337 [NASA ADS] [Google Scholar]
  13. Eggenberger, A., Udry, S., Chauvin, G., et al. 2007, A&A, 474, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Eggenberger, A., Udry, S., Chauvin, G., et al. 2011, in IAU Symposium, 276, The Astrophysics of Planetary Systems: Formation, Structure, and Dynamical Evolution, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss, 409 [Google Scholar]
  15. Esslinger, O., & Edmunds, M. G. 1998, A&AS, 129, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Fontanive, C., Rice, K., Bonavita, M., et al. 2019, MNRAS, 485, 4967 [Google Scholar]
  17. Ford, E. B., Kozinsky, B., & Rasio, F. A. 2000, ApJ, 535, 385 [Google Scholar]
  18. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  19. Gaia Collaboration 2018, VizieR Online Data Catalog: I/345 [Google Scholar]
  20. Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Guyon, O. 2018, ARA&A, 56, 315 [Google Scholar]
  22. Haisch, Karl E., J., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [Google Scholar]
  23. Harakawa, H., Sato, B., Omiya, M., et al. 2015, ApJ, 806, 5 [NASA ADS] [CrossRef] [Google Scholar]
  24. Holberg, J. B., & Bergeron, P. 2006, AJ, 132, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Houk, N. 1982, Michigan Catalogue of Two-dimensional Spectral Types for the HD stars, Volume_3, Declinations −40.0 to −26.0. (University of Michigan) [Google Scholar]
  26. Houk, N., & Smith-Moore, M. 1988, Michigan Catalogue of Two-dimensional Spectral Types for the HD Stars, 4, Declinations −26.′′0 to −12.′′0.4 (University of Michigan) [Google Scholar]
  27. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  28. Jones, M. I., Jenkins, J. S., Rojo, P., Olivares, F., & Melo, C. H. F. 2015, A&A, 580, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Kowalski, P. M., & Saumon, D. 2006, ApJ, 651, L137 [Google Scholar]
  30. Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
  31. Kraus, A. L., Ireland, M. J., Hillenbrand, L. A., & Martinache, F. 2012, ApJ, 745, 19 [NASA ADS] [CrossRef] [Google Scholar]
  32. Lo Curto, G., Mayor, M., Benz, W., et al. 2013, A&A, 551, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Maire, A.-L., Langlois, M., Dohlen, K., et al. 2016, in SPIE Conf. Ser., 9908, Proc. SPIE, 990 834 [Google Scholar]
  34. Mawet, D., Milli, J., Wahhaj, Z., et al. 2014, ApJ, 792, 97 [NASA ADS] [CrossRef] [Google Scholar]
  35. Meléndez, J., Bedell, M., Bean, J. L., et al. 2017, A&A, 597, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Mugrauer, M. 2019, MNRAS, 490, 5088 [Google Scholar]
  37. Mugrauer, M.,& Ginski, C. 2015, MNRAS, 450, 3127 [NASA ADS] [CrossRef] [Google Scholar]
  38. Nelson, A. F. 2000, ApJ, 537, L65 [NASA ADS] [CrossRef] [Google Scholar]
  39. Ngo, H., Knutson, H. A., Hinkley, S., et al. 2015, ApJ, 800, 138 [NASA ADS] [CrossRef] [Google Scholar]
  40. Ngo, H., Knutson, H. A., Hinkley, S., et al. 2016, ApJ, 827, 8 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ngo, H., Knutson, H. A., Bryan, M. L., et al. 2017, AJ, 153, 242 [NASA ADS] [CrossRef] [Google Scholar]
  42. Oliphant, T. E. 2006, A Guide to NumPy, 1 (USA: Trelgol Publishing) [Google Scholar]
  43. Pascucci, I., Apai, D., Hardegree-Ullman, E. E., et al. 2008, ApJ, 673, 477 [NASA ADS] [CrossRef] [Google Scholar]
  44. Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
  45. Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Roell, T., Neuhäuser, R., Seifahrt, A., & Mugrauer, M. 2012, A&A, 542, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Rosotti, G. P., & Clarke, C. J. 2018, MNRAS, 473, 5630 [NASA ADS] [CrossRef] [Google Scholar]
  48. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  49. Takeda, G., & Rasio, F. A. 2005, ApJ, 627, 1001 [NASA ADS] [CrossRef] [Google Scholar]
  50. Thebault, P., & Haghighipour, N. 2015, Planet Formation in Binaries, 309 [Google Scholar]
  51. Tremblay, P.-E., Bergeron, P., & Gianninas, A. 2011, ApJ, 730, 128 [NASA ADS] [CrossRef] [Google Scholar]
  52. van Holstein, R. G., Girard, J. H., de Boer, J., et al. 2020, A&A, 633, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
  55. Wang, J., Fischer, D. A., Xie, J.-W., & Ciardi, D. R. 2015, ApJ, 813, 130 [NASA ADS] [CrossRef] [Google Scholar]
  56. Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
1

For a detailed discussion of extreme AO systems, we refer readers to Guyon (2018).

2

Calculated from the inverse parallax.

3

Defined as separation with 50% transmission.

4

Coherence times longer than 5.2 ms are achieved in less than 10% of the available observation time, see: https://www.eso.org/sci/observing/phase2/ObsConditions.SPHERE.html.

6

Python Software Foundation, https://www.python.org/

All Tables

Table 1

Summary of the properties of our target systems.

In the text
Table 2

Observation parameters for all four systems.

In the text
Table 3

Astrometric and photometric measurements (in Ks-band) of companions.

In the text
Table 4

Mass estimates and projected separations.

In the text

All Figures

thumbnail Fig. 1

SPHERE/IRDIS observations of the new co-moving low-mass stellar companions to exoplanet host stars. The gray hatched disk marks the utilized coronagraphic mask.
In the text
thumbnail Fig. 2

Proper motion diagrams of all detected stellar companions. The separations and position angles of the companion relative to the primary stars are plotted versus time. The “oscillating,” solid lines show the area in which a nonmoving background object would be expected. The dashed lines show the area where a co-moving, bound object would be expected; this also takes possible orbital motion into account.
In the text
thumbnail Fig. 3

Both components of the HD 109271 system plotted in a (G − Ks) − MG diagram. The main-sequence is shown with the gray line and the evolutionary track of DA white dwarfs with a mass of 0.6 M⊙ is shown with the black dashed line. The photometry of the exoplanet host star HD 109271 A is consistent with a main-sequence star, as expected. In contrast, the detected co-moving companion HD 109271 B is clearly located below the main-sequence, but its photometry agrees well with that of DA white dwarfs.
In the text
thumbnail Fig. 4

5 σ detection limits for possible companions around the four discussed systems of our survey. We show the average magnitude limit, assuming a distance of 95 pc and age of 4.5 Gyr; this translates into a companion mass at the stellar-brown dwarf boarder.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.