| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202038545 | |
| Published online | 07 May 2021 | |
Asteroid spectral taxonomy using neural networks
1
Department of Physics, PO Box 64,
00014
University of Helsinki,
Finland
e-mail: antti.i.penttila@helsinki.fi
2
Finnish Geospatial Research Institute FGI, National Land Survey,
Geodeetinrinne 2,
02430
Kirkkonummi, Finland
Received:
1
June
2020
Accepted:
11
March
2021
Aims. We explore the performance of neural networks in automatically classifying asteroids into their taxonomic spectral classes. We particularly focus on what the methodology could offer the ESA Gaia mission.
Methods. We constructed an asteroid dataset that can be limited to simulating Gaia samples. The samples were fed into a custom-designed neural network that learns how to predict the samples’ spectral classes and produces the success rate of the predictions. The performance of the neural network is also evaluated using three real preliminary Gaia asteroid spectra.
Results. The overall results show that the neural network can identify taxonomic classes of asteroids in a robust manner. The success in classification is evaluated for spectra from the nominal 0.45–2.45 μm wavelength range used in the Bus-DeMeo taxonomy, and from a limited range of 0.45–1.05 μm following the joint wavelength range of Gaia observations and the Bus-DeMeo taxonomic system.
Conclusions. The obtained results indicate that using neural networks to execute automated classification is an appealing solution for maintaining asteroid taxonomies, especially as the size of the available datasets grows larger with missions like Gaia.
Key words: methods: data analysis / techniques: spectroscopic / surveys / minor planets, asteroids: general
© A. Penttilä et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
There seems to be a trend. Whenever a new spectral asteroid dataset is introduced, a new way to classify asteroids is born. For example, one of the historically most well-known taxonomic systems was developed by Tholen (1984, 1989) based on the data collected by the Eight-Color Asteroid Survey (ECAS; Zellner et al. 1985). Another leap toward a system with greater detail was made when Bus & Binzel (2002) introduced their taxonomic system consisting of 26 classes, defined by the data of the second phase of the Small Main-Belt Asteroid Spectroscopic Survey (SMASS II). However, neither of the systems considered the near-infrared (NIR) range because to the surveys did not record any data there. This was amended by DeMeo et al. (2009) when they refined the previous Bus taxonomy by utilizing a new dataset that extended into the infrared.
The asteroid datasets we have had access to in the past have not been particularly large, typically consisting of less than a few thousand samples. However, this soon began to change with missions like the European Space Agency’s Gaia. Launched in 2013, Gaia’s main objective is to form the most accurate three-dimensional map of the objects within the Milky Way. The mission goals emphasize astrometry in combination with photometric and spectrometric surveys, focusing mainly on the stars within our galaxy. However, because of Gaia’s sensitivity to faint and small objects, it has also detected a considerable number of asteroids (Gaia Collaboration 2016). Consequently, the near future is exciting for asteroid spectroscopy: the Gaia Data Release 3 will be made available in 2022. It will include a significant amount of data on the asteroids in our Solar System, which will help constrain their spectra considerably (Delbo et al. 2019).
Therefore, if past trends are to be believed, it is extremely likely that with the data provided by Gaia, a new taxonomic system for asteroids must be developed. A plan for the purpose has already been developed by, for example, Delbo et al. (2012a). The formation of a new taxonomy is especially relevant for the mission because the spectra are in a different wavelength range from the previous systems; Gaia’s operation range falls between 0.33 and 1.05 μm (Gaia Collaboration 2016). The wavelengths are unique due to the lack of modern asteroid taxonomies extending to the ultraviolet.
If and when a new Gaia taxonomy is formed, there will still be a demand to evaluate the class of a Gaia-observed asteroid within the other taxonomies. This is true in general for all the asteroid spectral observations that do not fall in the wavelength range of a particular taxonomic system. In this study we particularly concentrate on the Bus-DeMeo taxonomy (B-DM) since it is the most recent one, and seems to be very frequently used in modern asteroid studies (Delbo et al. 2012a; Sanchez et al. 2012; Reddy et al. 2014).
The official B-DM classification system1 cannot really deal with wavelength ranges other than (0.45, 2.45) μm, except that it can try the classification using only NIR data from 0.85 μm onward. For the small missing parts at the end of the wavelength range they recommend extrapolation, but this is a reasonable option only in the case of very small missing ranges. There is an approach where the B-DM classification is done for Gaia wavelengths using linear discriminant analysis for the B-DM original asteroids at Gaia wavelengths, and then applying naïve Bayesian classification (Torppa et al. 2018). While this approach seems to work quite well, it is not easily automatically applied to any given wavelength range. Therefore, in this article, we study the possibility of using artificial neural networks (ANNs) and deep learning for the task of classifying spectra taken at arbitrary but somewhat overlapping ranges with the B-DM wavelengths.
The following sections explore the topic and the application of ANNs in practice. First, the preparation of the datasets utilized within the study is presented. Next, the theory of neural networks is discussed in the context of the specific example used in this application. Classification of base B-DM system samples, along with those that would be obtained by the Gaia mission, is then executed and the obtained results are presented. Additionally, three real preliminary Gaia samples are tested against a network trained with simulated Gaia data. The significance and implications of the results are then discussed, after which our conclusions are presented.
2 Materials and methods
Before the classification process can be executed, the dataset supplied to the neural network must be defined and constructed. Additionally, the properties of the network itself have to be specified.
2.1 Data
The data provided to the neural network must be labeled according to a classification system. Since we want to utilize the B-DM taxonomy, we ideally need spectral data that covers the entire current wavelength range the system is based on (0.45 to 2.45 μm). However, acquiring infrared data for asteroids is still complicated due to the hindering effects of the atmosphere. As a consequence, sets that present infrared data for asteroids are either small in size, or they are incorporated into larger sets that have samples that do not necessarily all extend into the infrared. Because of this, no universally used large dataset exists that has both visible and infrared data for all asteroid samples. Consequently, for this study the primary dataset used is a novel combination of two medium-sized datasets: that used by DeMeo et al. (2009) in the construction of the B-DM taxonomy, and the MIT-Hawaii Near-Earth Object Spectroscopic Survey (MITHNEOS; Binzel et al. 2019).
In order to develop the new dataset (hereafter VisNIR), several steps need to be taken (see Appendix A). The full VisNIR dataset includes 591 individual asteroid spectra; each spectra covers wavelengths from 0.45 to 2.45 μm with 0.01 μm steps. There is a problem with using this dataset as the training set for the ANN; there are 33 B-DM taxonomic classes in the set, but for some of the classes there are only a few objects or even a single object. The automated classification, especially if applied to limited wavelengths, will not be very successful with this level of detail in the taxonomy. We note that some ambiguous classifications in the B-DM implementation are left to the user’s visual inspection. Therefore, we must simplify the classes in our tasks.
We compiled the reduced B-DM taxonomy and reduced VisNIR dataset by combining the subclasses into their main equivalents. In practice, this means reducing classes like Sa, Sq, Sr, and Sv to simply the S-class. Out of the remaining main classes, we removed the single-target classes O and R, as well as the “unknown” class (U), a total of five samples. Hence, the reduced set has 11 classes and 586 samples. The 11 classes in the reduced set are A, B, C, D, K, L, Q, S, T, V, and X. The number of asteroids in each class is presented in Table 1.
Finally, we created a simulated set for the ANN training. In general, ANN training data is often augmented with synthesized samples in order to reproduce enough variability and to obtain enough example cases per class. Our synthesized samples are formed using the principle component transform of the spectra, adding random noise to the uncorrelated principle components, and transforming back to wavelength space. This method is described in more detail in Appendix B. One additional benefit of having synthesized samples is that we can balance the number of training samples per class. In this work we always train our ANNs with 200 samples in each (reduced) taxonomic class.
In this study we are not only interested in the B-DM wavelength range, but also in other wavelength ranges, especially that of the Gaia mission. Gaia’s asteroid data will be between 0.33 and 1.05 μm. We can build a B-DM classification for the Gaia data by using our synthesized training set, but limiting the wavelengths of the objects to the overlapping range between B-DM and Gaia, so between 0.45 and 1.05 μm. The reduced VisNIR spectra (before synthesizing new samples) is illustrated in Fig. 1. The wavelength ranges for the B-DM and Gaia systems and the resulting number of data points each spectrum has in this application are described in Table 2.
Number of samples (#) per each reduced B-DM taxonomic class in our VisNIR dataset.
Wavelength ranges of the B-DM and Gaia data.
2.2 Artificial neural networks
Artificial neural networks are an example of supervised learning, and as such, they must be provided a dataset along with labels that describe the classes the samples fall into. The network learns to classify the samples by training itself with a set of data that has access to the labels, and then testing its performance by predicting the labels itself. The extent of success in the predictions can be evaluated by comparing the suggested labels to the real ones in the constructed label set.
The basic components of a neural network are the processing elements, neurons, and the connections between them (Zhang et al. 2003). The learning process revolves mostly around adjusting the connections until they describe the features in the defined training set. Each connection is represented by a weight. The neurons themselves reside in layers within the network. The simplest way to describe the layers is to define three types: the input layer, the hidden layers, and the output layer. Further descriptions involve defining the functions the layers utilize. There also are some governing functions that adjust the performance of the entire network. There is no automatic way to find the best structure for the neural network; for example, it is left to the user to decide the parameters that define how many layers the network has, what functions the layers utilize, and how many neurons are in each of the hidden layers.
 |
Fig. 1 Illustration of the 586 asteroid spectra in the reduced VisNIR set. The vertical lines indicate the cutoff point between theB-DM and Gaia wavelengths. The red part of spectra is what remains in the Gaia wavelength range. The x-axes hold the wavelengths from 0.45 to 2.45 μm, while the y-axes are the reflectances normalized to unity at 0.55 μm. |
2.2.1 Classification neural network algorithm
The neural network structure utilized in the study is a specific type of feed-forward network, constructed to excel in classification tasks (see, e.g., Hietala 2020). A feed-forward network is a structure in which the connections between the neurons cannot and will not form a cycle, meaning that information flows in only one direction (Ganesh & Anderson 2009). The overall structure of the network that we utilize has one input layer, one hidden layer, and one output layer.
The input layer is essentially a vector of length s, where s is the number of data points (i.e., wavelengths) each sample has. Each of the input elements can be described as an input neuron, which connects to the neurons on the next layer. Typically some kind of data pre-processing also takes place within the neural network, and these processes can be attributed to take place in the input layer. A common example of pre-processing is deciding how to handle any possible unknown inputs. The size of the input layer can vary greatly between applications because it is based on the utilized dataset’s number of variables, which consequently affects the design of the hidden layers.
The hidden layer contains the number of neurons chosen by the user. These neurons produce an output by utilizing the weighted inputs, biases, and activation functions through the equation
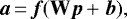 (1)
(1)
where the vector a is the output of a layer, f is the vector-valued mapping of the layer’s activation function f to its argument vector, W is the weight matrix, p is the input vector, and b is the bias vector. The operational power of neural networks lies in the capability to adjust the weights and “learn” the features of the data in this way. The adjustment process takes place in the training phase, where the network can fine-tune the weights based on the provided samples with their corresponding labels. The user can also choose to increase the number of hidden layers if the classification task seems to require it. In the multi-layer case, the preceding layer’s outputs become the next layer’s inputs, and they are once again adjusted by the weights and biases. We conducted studies of the network accuracy and the variation of this accuracy between consequent training runs, and found that with the full B-DM wavelength range (input dimension 200), a hidden layer with about 30 neurons is enough to reach good accuracy, but still small enough so that the deviation between runs due to possible overfitting or underfitting will be small. With the B-DM and Gaia overlapping wavelengths only, the number of the neurons in the hidden layer can be decreased to about 20.
The activation function (or alternatively the transfer function) that all the neurons utilize on the hidden layer in this implementation is the hyperbolic tangent sigmoid function, tansig. It is a specific case of the sigmoid function and mathematically equivalent to the hyperbolic tangent function
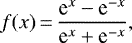 (2)
(2)
which ranges from −1 to 1, making it a scaled and shifted version of the logistic function. Sigmoid functions are some of the most widely used activation functions in neural networks, mostly due to their simplicity and because they are differentiable with a positive derivative everywhere (Han et al. 2012). The differentiability is a key aspect in neural network design since it facilitates the ability to optimize the performance in a robust but efficient manner using gradient-based methods.
The output layer has as many neurons as there are classes to place objects into. Although typically of a different size and utilizing a different activation function, the output layer’s operation principle is very similar to that of the hidden layers, and can be also described by Eq. (1). The activation function of the output layer here is known as softmax. The result produced by utilizing softmax is that all the inputs are scaled to true probabilities that add up to 1. Based on these values it is possible to choose the value with the highest probability as the assigned class. Because the network structure and the task in this case are relatively simple, in a well-performing case it is typical to see one of the values close to 1 and the others very close to 0, implying that the network is very sure about the label it assigns to that particular sample.
The basic structure for this network is described in Fig. 2. It includes the three outlined layers, as well as the connections between them. The illustration here is simplified in the sense that connections are described as vectors or matrices. This allows the focus to be on the overall processes taking place in the structure instead of on the individual components. As mentioned previously, the size of the input layer depends on the number of data points each spectrum has in the dataset. Here the number of data points is equal to 200 for the B-DM range, and 60 for the shorter Gaia range. The input data points are supplied to the rest of the network by the column vector p. Each individual data point connects to each of the neurons in the hidden layer with a unique weight. Therefore, an overall weight matrix W1 of size r × s exists between the first two layers. The superscript is included in order to discriminate between the arrays in different layers. The symbol r represents the number of neurons in the hidden layer. In this study, r is equal to 30 or 20, as explained before.
Each of the hidden layer neurons, which are connected to all the input data points, forms a connection to the layer’s activation function after it has added up the weighted input and the bias factor. These connections together form the r × 1 vector n1 in Fig. 2. Since each neuron has its own bias, they can be generalized into an r × 1 vector b1. Each layer produces a final output, which is represented by ai. The components p, W, b, and a listed here are the constituents of Eq. (1).
The output layer has as many neurons as there are classes to place objects into, represented by c. The value of c is 11 with our reduced VisNIR dataset. Overall, the connections on the output layer function similarly to those of the hidden layer. The individual final outputs are included in vector a2, which consists of the class probabilities between 0 and 1.
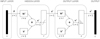 |
Fig. 2 Simplified structure of the neural network. The input layer provides the hidden layer s data points per sample. It is equal to 200 and 60 for the full B-DM and Gaia wavelength ranges, respectively. The hidden layer has r neurons, which is equal to 30 or 20 in our implementation. Finally, the output layer has as many neurons as there are output classes, represented by c. Therefore, c is equal to 11 for the reduced VisNIR set. |
2.2.2 Training the neural network
Before the neural network can be applied, it must be trained. In the training process the unknown values for the weight and bias parameters are estimated. The estimation is, in practice, a high-dimensional nonlinear minimization task. The function to be minimized is the loss function J (average of the cross entropy H), computed from the training data and the difference between the labels predicted by the ANN and the correct labels as
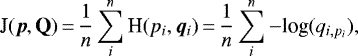 (3)
(3)
where vector p holds the correct labelindex 1, …, k for each sample i, and matrix Q consists of rows qi, which are the predicted probabilities for the categories 1, …, k. In this paper the dimension of the optimization task is (200 × 30 + 30) + (30 × 11 + 11) = 6371 for the full B-DM wavelengths, and 1451 for the Gaia wavelengths only.
Taking into account the very high dimension of the typical ANN training task, the optimization algorithm must be highly efficient. A stochastic gradient descent algorithm Adam is used here (Kingma & Ba 2014). In the stochastic version of the steepest gradient descent, only one stochastic sample of the whole training data, a batch, is used in each evaluation round. This decreases the computation time when the complete training set is large. A parameter called the learning rate controls how much the current batch can affect the global gradient estimate in each round.
The ANN training process is affected by the training data, the random starting values of the weight and bias parameters, the batch size and the value of the learning parameter, the random batch selection when training, and the number of complete optimization rounds employing all the batches in the training data (i.e., number of epochs). Taking this into account, it is natural that successive training of the ANN using the same training data, but with a new random initialization of the system, can lead to a slightly different result with finite number of epochs.
Insufficient training or a too simple ANN structure can lead to underfitting the data, while excessive training with a complicated ANN structure can lead to overfitting. We tackled the underfitting problem by increasing the size of the first layer only as long as the prediction accuracy kept increasing significantly, and the deviation in the prediction accuracy between successive training runs did not increase significantly. For the overfitting, we introduced a dropout layer between the hidden layer and the output layer for the training. The dropout layer removes a given percentage (in this case 10%) of the connections between the layers at random during the training rounds. Effectively, this makes the network more robust, and less bound to overfitting. In addition, the dropout layer is good in our application with spectral data, which has very high local correlations between nearby wavelengths. The ANN can easily lock down to one value or a few single wavelength values for a specific spectral feature. However, if the real data to be used has more noise than the training data, and the one wavelength has an outlier value, the whole prediction can go wrong. With the dropout layer, the ANN is forced not to trust a single input from a neuron, but rather the combination of many neuron inputs to tackle the possible missing connection.
2.2.3 Applying the neural network in classification
As explained in Sect. 2.2.2, there is a certain level of randomness in the estimated weight and bias values of a trained network, due to the random starting values and the stochastic optimization algorithm. This can be somewhat frustrating when building the final “production use” version of the ANN. Two identically built models can give slightly different results in the classification. To reduce this effect, we propose using a method of multiple ANNs as “voters” (see, e.g., Auda et al. 1995; Cao et al. 2012). In this method, a number of ANNs (e.g., 5) are trained with random initializations. In the classification task, each of the networks classifies, but the final answer is based on the majority of the votes given by the ANNs. This decreases the effect of randomness during the training process with individual networks, not only in the classification, but especially when asking the probabilitiesof each taxonomic class for a given object. The output neurons produce, after the softmax operation, a “probability distribution” for the different classes, where each neuron correspond to a certain class. It can be very fruitful to not only examine the “winning class” of an object, but also the probability estimate of the winning class and the competing classes. In cases where the ANN is very sure about the classification, the majority of the probability mass is with the corresponding neuron. In unclear cases, however, the second-best class could have a probability that is almost as high as that of the winner, and these cases might be interesting to study further.
The idea of voting is extended here also to the class probabilities. When evaluating them for a spectrum, the class probability estimates are collected from the individual voters (i.e., the ANNs). Then, a trimmed mean over the voters is used to compute a preliminary probability estimate for a given class. Finally, the estimates are scaled so that their sum is 1. The final step is needed because the trimmed mean operation can eliminate different voters for different classes, so the resulting mean does not necessarily sum up to 1anymore.
While the training process of the ANN, or multiple ANNs, is a resource-demanding task, the classification using the final trained network or multiple voter networks is a much lighter task. In the training phase, each round of the numerical optimizer requires the evaluation of the ANN for each case in the training data. In the final production use, the classification requires only one evaluation of the ANN for one single object. While this still requires a matrix-vector multiplication of size (30 × 200) matrix and size 200 vector in our case (full B-DM wavelengths), and some smaller operations for each voter, it is still relatively cheap.
2.2.4 Cross-validating the network performance
Finally, the performance of the ANN voter network needs to be evaluated. We accomplish this by cross-validation, where one part of the data is left out from the data synthesizing and ANN training, but is used to assess the accuracy of the system in predicting the correct classes. In our VisNIR dataset some taxonomic classes have only a few spectra, such as the T type with four samples and the A type with seven samples (see Table 1). Therefore, we decided to perform the cross-validation by the leave-one-out method, where at every validation round, only one observation is left out from the training set and then classified. This method is optimal regarding the sample size left for training, but also requires the most validation rounds. We completed a full validation sequence by running the leave-one-out round for each of the 586 asteroids. The left-out spectrum was completely isolated from both the data synthesizing and the ANN training. This means that we trained the ANN network 586 × 5 = 2930 times (five voter ANNs for every round). Our validation round benefited greatly from GPU acceleration using the Nvidia Tesla P100 card.
Summary of the ANN properties in this study.
2.2.5 Overfitting
Taking into account the fact that a feed-forward ANN is basically a very pliable nonlinear model with a vast number of free parameters, there is always the risk of overfitting. In an ideal case, the labeled data can be divided into training, validation, and testing sets. In this approach the validation set is used to check if the model accuracy remains close enough to the accuracy evaluated using the training set. If the validation set accuracy differs significantly from the training set value, the ANN is probably overfitting the data, and model hyperparameters should be adjusted toward a simpler model. The model hyperparameters can include the number of nodes in a layer, the number of layers, the number of epochs in training, and the type of activation function.
In our case the amount of labeled data, especially with some taxonomic types, does not really support the separation into validation data. Therefore, we needed to take other measures to avoid model overfitting. First, when we designed the model, we did not try to optimize the model performance. Rather, we tried to optimize the simplicity of the model. Our ANN has only one hidden layer, and a modest number of 30 or 20 nodes. This ANN structure was found by starting with larger node numbers and two hidden layers, and simplifying as long as the performance kept on a good level.
Second, we introduced a dropout layer between the hidden layer and the output layer. The purpose was to force the network not to lock down on a single spectral wavelength or a feature, but also to make the network more robust against overfitting.
Third, instead of training one ANN with a large number of epochs, we trained five ANNs with somewhat modest number of epochs, 5000. Increasing the number of epochs in training would allow the ANN to adapt to the learning set with increasing accuracy, but due to an evident overfitting risk, this is not the desired behavior. However, to tackle the possible underfitting with a smaller number of epochs, we joined these five ANNs and made the final classification based on their votes. The summary of all our ANN structure and training parameters are given in Table 3.
However, we would like to note that our procedure is a compromise. We optimized the model and its hyperparameters with all the data, although we wanted to find the simplest model possible. If it were possible to use labeled datasets with thousands or tens of thousands of spectra, we would have preferred to divide the data into separate training, validation, and testing sets. When this data is available, we will be able to use it to re-evaluate our ANN accuracy. Also, we should critically evaluate the results of classification with our suggested method when the Gaia spectral data becomes available, most probably with Gaia Data Release 3.
 |
Fig. 3 Confusion matrix from the ANN classification of the VisNIR dataset. The known classes are organized in rows of the matrix, and the distribution of the predicted class labels for each correct class are organized as columns. The blue shade of thecell background color highlights the diagonal with the correct classifications, while the orange shade shows the misclassifications. |
 |
Fig. 4 Confusion matrix from the ANN classification of the VisNIR dataset using only the intersection of the Gaia and Bus-DeMeo wavelengths. For the structure of the matrix, see Fig. 3. |
3 Results and discussion
Once the structure of the neural network has been decided, and the networks have been trained, the classification can begin. We are interested in how well the neural network succeeds in classifying the asteroids correctly, that is, how many of the predicted classes match the true, known classes of those samples. The degree of success is described by the classification success rate, which is expressed in percentage points.
3.1 Classification of samples with the full Bus-DeMeo wavelength range
We begin by establishing a baseline for our ANN performance by classifying samples from our VisNIR dataset using the full B-DM wavelength range. The so-called confusion matrix of the results is presented in Fig. 3, where the distribution of the predicted classes is cross-tabulated with the distribution of the correct classes. The cases that are correctly predicted are located in the diagonal of the matrix, and their sum, 531, is the number of correct classifications out of the total 586 cases, making the overall classification accuracy 90.6%.
With many taxonomic classes, the resulting accuracy is 100%. The S types are sometimes misclassified, mainly as Q types. If C types are misclassified, it is mostly as X types. Of all the types, the L type is the most difficult to classify (75.8% accuracy). If L-types are misclassified, they can fall into K, S, or X types.
3.2 Classification of samples with the joint Gaia and Bus-DeMeo wavelength range
If we now turn to the task of classifying objects with the wavelength range of the Gaia observations into the B-DM taxonomic system, the accuracy decreases. This occurs because the wavelength range of the spectra is reduced from 0.45–2.45 μm to 0.45–1.05 μm. The result of this classification for our VisNIR dataset as a confusion matrix is presented in Fig. 4. The overall accuracy comes now from the cases in the diagonal, 507, divided by the total number of 586, so 86.5%. The drop in accuracy does not seem very dramatic, especially taking into account that we are now completely missing the NIR part above the 1.05 μm wavelength. It seems that the ANN classification of Gaia-observed asteroids can be quite promising.
If we look at individual taxonomic types in the classification, we find that the L types are still relatively difficult to classify (66.7% accuracy). In addition, now with the limited wavelength range, the C types are more difficult (75.4% accuracy). In particular, the difference between B and C types is somewhat difficult without the longer NIR wavelengths. The third lowest accuracy is for X types (82.4% accuracy). Its misclassified objects are spread quite widely into B, C, D, K, L, or T types.
3.3 Classification of real Gaia samples
Thus far we have motivated the need to simulate Gaia classifications by the fact that no true Gaia asteroid data is available yet. However, some preliminary samples do exist (Galluccio et al. 2017). Here we test the performance of the neural network with three asteroids, (19) Fortuna, (21) Lutetia, and (279) Thule, with real Gaia spectra.
To prepare the new data, a spline fit is done to the three spectra to obtain the same number of data points as the training set samples. Additionally, the Lutetia data stops at 1.01 μm, so its splinefit is followed by a linear extrapolation to estimate values until the 1.05 μm endpoint. The samples are presented to the network without any class labels.
The classes the neural network predicts for the asteroids are presented in Table 4. We report all taxonomic classes with greater than 1% probability. The asteroid (19) Fortuna is generally taken as a C-type asteroid, Ch to be exact (Fornasier et al. 2014). Our ANN also suggests C type with a probability of 77%, but also predicts X or D types with low probabilities. Asteroid (21) Lutetia is Xc in the B-DM taxonomy, and is also classified by our ANN as X with 71% probability. Additionally, for Lutetia the classes L, K, and S are predicted with >1% probabilities. Finally, (279) Thule should be D type in B-DM, and is also classified as such with some probability also on T or X types.
The classification of the three real Gaia samples, Fortuna, Lutetia, and Thule, when the neural network has been trained with simulated Gaia data shows overall encouraging results. All three samples are predicted as their expected correct class with high probability. However, sometimes the prediction is not absolutely certain, as seen with Fortuna and Lutetia. Context for what might cause the uncertainty in prediction is provided by Fig. 5, which plots the spectra of the three asteroids on top of the simulated spectra of the predicted classes. With Lutetia it is easy to understand how the network might sometimes mistake the spectrum as being from the L class. With Fortuna, it seems that the overall slope of the spectra may be on the high end for C types, but on the low end for X or D types, therefore justifying the lower probabilities also for the X or D taxonomies.
Torppa et al. (2018) studied the same three asteroids and their Gaia spectra, but using a linear discriminant analysis (LDA) and a naïve Bayesian classifier that were adjusted for the Gaia wavelengths. Their probabilistic classification results were somewhat similar. The D class was not proposed at any significant level for Fortuna, and for Lutetia, the most probable classification in their assessment was the K-class. The interpretation for their results was that the LDA probably noticed the downturn in the Gaia spectra of Lutetia after 1 μm, and gave that a large weight and an association with the K type.
 |
Fig. 5 Comparison of the spectra of (19) Fortuna, (21) Lutetia, and (279) Thule to the spectra of the simulated samples in their predicted classes. Top row: Fortuna with the samples from the C, X, and D classes. Middle row: Lutetia with the samples from the X, L, K, and S classes. Bottom row: Thule with the samples from the D, T, and X classes. The red lines are thespectra of the real asteroids, while the gray lines show the synthesized samples in the training data. |
Reduced classes predicted for Fortuna, Lutetia, and Thule using the Gaia spectral observations.
3.4 Training, training data, and the accuracy measure of our neural network
The training of the ANN is a process where the network parameters are optimized against a chosen merit function. Usually in classification tasks, and in our case, the merit function is the cross-entropy (i.e., the sum of the logarithms of the predicted class probabilities times the true binary class indicator). The choice might seem quite objective, but it is not completely objective. The merit function will weight each class according to their fraction in the training data. In our case, we chose to have 200 cases for each class in our synthesized training data. In practice, this means that we are weighting the importance of each class uniformly. We could also choose to, for example, follow the estimated frequencies of the asteroid classes in the asteroid population in the training data, thus giving more importance to the classification of the most common classes. The caveat in this kind of approach is that it can lead to situations where the classification accuracy of the rare taxonomic classes does not really weigh at all in the merit function, and therefore the ANN does not need to learn to classify them.
The similar weighting issue is also valid when we estimate the final accuracy of the trained ANN using the test dataset. Unlike in our training dataset, our test dataset is a real collection (i.e., not augmented or simulated) of the asteroid spectra in the combined Bus-DeMeo and MITHNEOS datasets. Therefore it will also weight the accuracy measure using the taxonomic frequencies of our combined VisNIR dataset. We hope that the frequency distribution is somewhat similar to the real taxonomic distribution of the asteroids, although with a probable observational bias. By estimating the accuracy separately for each class, we can apply all kinds of weights. For example, giving each taxonomic class the same weight, the total accuracy of our ANN would be 92.1% with all the B-DM wavelengths (it was 90.6% with weights from the VisNIR dataset frequencies) and 88.3% for the joint B-DM and Gaia wavelengths only (previously 86.5%). We could also apply other weighting schemes for evaluating the expected accuracy in different situations, for example by taking the best estimate for the main belt asteroid population.
4 Conclusions
The aim of our study was to verify how well artificial neural networks can classify asteroids into their taxonomic classes, particularly when the wavelength range of the spectra differs from the range used to define the taxonomy. We were especially interested in investigating the neural network Bus-DeMeo classification with the Gaia wavelengths. For this purpose a novel asteroid VisNIR dataset was constructed. A feed-forward neural network was designed with parameters that yield the best possible success rate of classification with the VisNIR samples.
The results seem to imply that a neural network can classify Gaia samples robustly, even with a taxonomic system that was not designed specifically for their wavelength range. Compared to earlier work on the same subject by Torppa et al. (2018), the neural network is much more flexible and can be automatically trained for various wavelengths. For further improvements, it would be beneficial to have access to a considerably larger set of real spectral data with solid taxonomic information. Further studies of how the neural network prioritizes features in the data within the Gaia wavelength range could also be done. Finally, specifically regarding the Gaia data, it would be beneficial if the blue end of the Gaia spectra could also be employed. This is possible with suitable training data with taxonomic labels.
We aim to study the possibilities of neural network-based classifiers further with the upcoming survey data from Gaia and the Large Synoptic Survey Telescope observations over photometric colors (Jones et al. 2015), and with the disk-resolved spectral data from the spacecraft observations such as the JAXA Hayabusa observations of the asteroid (25143) Itokawa (Abe et al. 2006) or NASA OSIRIS-REx observations of the asteroid (101955) Bennu (Simon et al. 2020).
Acknowledgements
We would like to kindly acknowledge Francesca E. DeMeo for providing us with the base asteroid datasets of the Bus-DeMeo taxonomic system, utilized in this study, and for graciously answering our questions regarding that data. The funding from Academy of Finland project no. 325805 is acknowledged. Computing resources were provided by CSC – IT Center for Science Ltd., Finland.
Appendix A Creating the combined dataset
To create the VisNIR spectral dataset with taxonomically labeled asteroids we combined two sets of asteroid data, the original dataset used by DeMeo et al. (2009) when creating the B-DM taxonomy, and the quite recent MITHNEOS dataset2 (Binzel et al. 2019). To our understanding, the B-DM dataset is not publicly available per se, and we thank F. DeMeo for providing uswith the original data.
The B-DM data consists of 371 asteroids, and the MITHNEOS data with both visual and NIR wavelengths of 316 asteroids. When combined, there are spectral data of 602 unique asteroids, since there are overlaps in the datasets. We chose to deal with the asteroids present in both datasets in a simple manner; the more recent MITHNEOS data is selected in these 85 cases.
Our VisNIR dataset was created by resampling the original observed spectra between wavelengths 0.45 and 2.45 μm in 0.01 μm steps. The resampling was done on the cubic regression spline fitted to the original spectra. The knots of the regression spline were placed on the percentiles of the data, and the number of these percentiles (and thus, the number of knots and the number of individual splines) in the spline system was found by optimizing the Bayesian Information Criteria (BIC), which is a function of the squared residual errors between the fit and the data, and the number of free parameters. The resulting number of splines varied between 10 and 30.
We visually inspected all 602 regression spline fits to the data. In most cases the results were visually very good. In some cases the fit was found to be poor, either on the small or large end of the wavelength range. This was always due to different wavelength sampling densities in the original data. For example, in some cases the visual rangewas covered only with about five data points, while the NIR part was densely sampled. In these cases we first did a separate, low-order fit to the less-sampled wavelengths, resampled that part more densely, and then fitted a global regression spline. In some rare cases, we needed to extrapolate the data a bit to reach the 2.45 μm wavelength. In seven cases it was not possible, in our subjective opinion, to credibly know how to extrapolate the data, and these cases were left out from the final data.
With the scrutinized combined dataset now having 595 asteroids, we organized the asteroids according to their taxonomic classes, and plotted all the spectra together for each taxonomic class. By doing this, we could visually spot one strange case in each class C, Q, Srw, and Xe, and removed them. This left us with the final VisNIR dataset of 591 asteroid spectra from 0.45–2.45 μm range, 0.01 μm sampling, and with the B-DM taxonomic label attached.
Appendix B Method for simulating asteroid spectra
The synthesized spectral data for each taxonomic class is simulated using the spectral data from that class as the base dataset. The methodis described in detail in this section.
Let thebase dataset from one taxonomic class be in the data matrix X. The individual spectra from our VisNIR dataset for that class (n) are the rows of the matrix, and the columns (k) are the 200 (full range) or 60 (only Gaia range) wavelengths. For the principle component analysis (PCA) transform we need the column mean vectorof X as 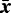 with k components, and the covariance matrix Σ, dimension k × k, of X. Furthermore, X needs to be centered, i.e.,
with k components, and the covariance matrix Σ, dimension k × k, of X. Furthermore, X needs to be centered, i.e., 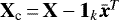 , where 1k is a vector of ones, with length k.
, where 1k is a vector of ones, with length k.
Now, the PCA transform of Xc is given with the help of eigenvalue decomposition of Σ as
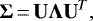 (B.1)
(B.1)
where U is a k × k orthogonal matrix of eigenvectors, and Λ is a diagonal matrix with eigenvalues. Now the original (centered) spectra Xc can be transformed into observations Z in the PCA space with
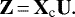 (B.2)
(B.2)
When simulating one synthesized spectra, we take at random one real spectra in PCA space z from Z. Since the PCA transform projects the original variables into uncorrelated variable space, the components in z are uncorrelated. Therefore, we can add simple uncorrelated Gaussian noise to z. The eigenvalues give variances for the noise components. We scale these variances slightly down by a factor of 0.36 (factor 0.6 for standard deviations) to keep the variation of the simulated spectra on a reasonable level, based on visual inspection. Now with a vector of Gaussian random numbers e with expected values of 0 and standard deviations of 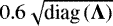 , our synthesized spectra in PCA space is zs = z + e.
, our synthesized spectra in PCA space is zs = z + e.
Finally, the vector zs can be transformed back in the original wavelength space by
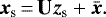 (B.3)
(B.3)
An example of the seven original spectra in the A class and 200 synthesized spectra using the above method is shown in Fig. B.1.
 |
Fig. B.1 Seven original A-type spectra in our VisNIR dataset (left), and 200 synthesized A-type spectra (right). |
References
- Abe, M., Takagi, Y., Kitazato, K., et al. 2006, Science, 312, 1334 [Google Scholar]
- Auda, G., Kamel, M., & Raafat, H. 1995, Proceedings of ICNN’95 – International Conference on Neural Networks, Perth, WA, Australia, 1240 [Google Scholar]
- Binzel, R. P., DeMeo, F. E., Turtelbloom, E. V., et al. 2019, Icarus, 324, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Bus, S. J., & Binzel, R. P. 2002, Icarus, 158, 1 [Google Scholar]
- Cao, J., Lin, Z., Huang, G.B., & Liu, N. 2012, Information Sci., 185, 66 [Google Scholar]
- Delbo, M., Gayon-Markt, J., Busso, G., et al. 2012a, Planet. Space Sci., 73, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., Avdellidou, C., & Morbidelli, A. 2012b, A&A, 624, A69 [Google Scholar]
- DeMeo, F. E., Binzel, R. P., Slivan, S. M., & Bus, S. J. 2009, Icarus, 202, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fornasier, S., Lantz, C., Barucci, M. A., & Lazzarin, M. 2014, Icarus, 233, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galluccio, L., DeAngeli, F., Delbo, M., et al. 2017, Image of the Week – Gaia Reveals the Composition of Asteroids, https://www.cosmos.esa.int/web/gaia/iow_20170424 [Google Scholar]
- Ganesh, N., & Anderson, N. G. 2017, in Dissipation in Neuromorphic Computing: Fundamental Bounds for Feedforward Networks, Proceedings of the 17th IEEE International Conference on Nanotechnology (IEEE, Pittsburgh) [Google Scholar]
- Goodfellow, I., Bengio, Y., & Courville, A. 2016, Deep Learning (Cambridge: MIT Press) [Google Scholar]
- Guenther, F., & Fritsch, S. 2010, The R Journal, 2, 1 [Google Scholar]
- Han, J., Kamber, M., & Pei, J. 2012, Getting to Know Your Data, in Morgan Kaufmann Series in Data Management Systems, Data Mining, 3rd edn., eds. W. Bottke, A. Cellino, P. Paolicchi, & R. Binzel (Waltham: Elsevier) [Google Scholar]
- Hietala, H. 2020, Master’s thesis, University of Helsinki, Helsinki [Google Scholar]
- Jones, R., Jurić, M., & Ivezić, ž. 2015, Proc. Int. Astron. Union, 10, 282 [Google Scholar]
- Kingma, D., & Ba, J, 2014, International Conference on Learning Representations [Google Scholar]
- Møller, M. F. 1993, Neural Networks, 6, 525 [CrossRef] [Google Scholar]
- Prechelt, L. 2012, Early Stopping – But When?, in Neural Networks: Tricks of the Trade, eds. G. Mantavon, G. B. Orr, & K. R. Müller (Berlin: Springer) [Google Scholar]
- Reddy, V., Sanchez, J. A., Cloutis, E. A., et al. 2014, Lunar Planet. Sci. Conf., 45, 1646 [Google Scholar]
- Sanchez, J. A., Reddy, V., Nathues, A., & et al. 2012, Icarus, 220, 1 [CrossRef] [Google Scholar]
- Silva, T. C., & Zhao, L. 2016, Machine Learning, in Machine Learning in Complex Networks (Cham: Springer) [Google Scholar]
- Simon, A. A., Kaplan, H. H., Cloutis, E., et al. 2020, A&A, 644, A148 [EDP Sciences] [Google Scholar]
- Tholen, D. J. 1984, Doctoral Dissertation (Tucson: University of Arizona), USA [Google Scholar]
- Tholen, D. J. 1989, Asteroid Taxonomic Classification, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson: University of Arizona) [Google Scholar]
- Torppa, J. Granvik, M., Penttilä, A., et al. 2018, Adv. Space Res. 62, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Zellner, B., Tholen, D. J., & Tedesco, E. F. 1985, Icarus, 61, 3 [Google Scholar]
- Zhang, Q. J., Gupta, K. C., & Devabhaktuni, V. K., 2003, IEEE Trans. Microw. Theory Techn., 51, 4 [Google Scholar]
B-DM spectral classification implementation at http://smass.mit.edu/busdemeoclass.html, thanks to Stephen M. Slivan at MIT.
The dataset Binzel2019.zip, from http://smass.mit.edu/minuspubs.html
All Tables
Number of samples (#) per each reduced B-DM taxonomic class in our VisNIR dataset.
Reduced classes predicted for Fortuna, Lutetia, and Thule using the Gaia spectral observations.
All Figures
 |
Fig. 1 Illustration of the 586 asteroid spectra in the reduced VisNIR set. The vertical lines indicate the cutoff point between theB-DM and Gaia wavelengths. The red part of spectra is what remains in the Gaia wavelength range. The x-axes hold the wavelengths from 0.45 to 2.45 μm, while the y-axes are the reflectances normalized to unity at 0.55 μm. |
| In the text | |
 |
Fig. 2 Simplified structure of the neural network. The input layer provides the hidden layer s data points per sample. It is equal to 200 and 60 for the full B-DM and Gaia wavelength ranges, respectively. The hidden layer has r neurons, which is equal to 30 or 20 in our implementation. Finally, the output layer has as many neurons as there are output classes, represented by c. Therefore, c is equal to 11 for the reduced VisNIR set. |
| In the text | |
 |
Fig. 3 Confusion matrix from the ANN classification of the VisNIR dataset. The known classes are organized in rows of the matrix, and the distribution of the predicted class labels for each correct class are organized as columns. The blue shade of thecell background color highlights the diagonal with the correct classifications, while the orange shade shows the misclassifications. |
| In the text | |
 |
Fig. 4 Confusion matrix from the ANN classification of the VisNIR dataset using only the intersection of the Gaia and Bus-DeMeo wavelengths. For the structure of the matrix, see Fig. 3. |
| In the text | |
 |
Fig. 5 Comparison of the spectra of (19) Fortuna, (21) Lutetia, and (279) Thule to the spectra of the simulated samples in their predicted classes. Top row: Fortuna with the samples from the C, X, and D classes. Middle row: Lutetia with the samples from the X, L, K, and S classes. Bottom row: Thule with the samples from the D, T, and X classes. The red lines are thespectra of the real asteroids, while the gray lines show the synthesized samples in the training data. |
| In the text | |
 |
Fig. B.1 Seven original A-type spectra in our VisNIR dataset (left), and 200 synthesized A-type spectra (right). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


