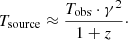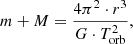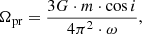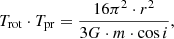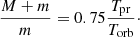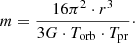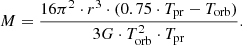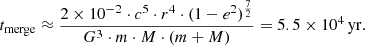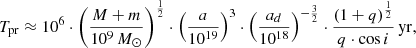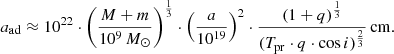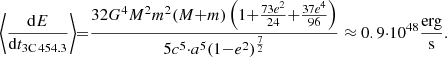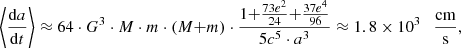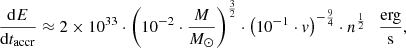| Issue |
A&A
Volume 648, April 2021
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202039124 | |
| Published online | 07 April 2021 | |
Most massive double black hole 3C 454.3 and powerful gravitational wave radiation
1
Radio Astronomy Laboratory of Crimean Astrophysical Observatory, Katsively RT-22, Crimea
e-mail: volvach@meta.ua
2
Astro Space Center, Lebedev Physical Institute, Russian Academy of Sciences, Profsoyuznaya ul. 84/32, Moscow 117997, Russia
Received:
7
August
2020
Accepted:
29
January
2021
Aims. A new method for determining the parameters of close double systems of supermassive black holes is proposed.
Methods. We used the ground-based radio telescope in Simeiz (RT-22). Observational data were collected and processed automatically. Harmonic and wavelet data analyses were used to find the components of changes in the flux densities of 3C 454.3.
Results. 3C 454.3 may be the most massive double system in the Universe. We show that when the bulk Lorentz (γ-factor) is taken into account, it is possible to obtain the agreed parameters of the 3C 454.3. We present first estimates of the size and thickness of the accretion disk of the 3C 454.3 obtained directly from the observation data. Based on the obtained data, we consider the characteristics of the gravitational radiation of this system, as well as the lifetime before merging, and possible variations in companion orbits.
Key words: galaxies: active / black hole physics / gravitational waves
© ESO 2021
1. Introduction
Supermassive black holes (SMBHs) in the centers of galaxies can be important sources of gravitational waves (GWs) and very powerful objects in a wide spectrum of electromagnetic radiation. However, there are no practically active galactic nuclei (AGNs) with double SMBHs for which the kinematic and dynamical characteristics of the components have been precisely defined, and these latter are necessary to determine the parameters of GW radiation. Models of BH orbits can be obtained by studying the physical conditions in the central regions of AGNs. In this sense, a multi-frequency monitoring campaign of flux densities on single dishes can be of paramount importance in finding the required SMBH parameters. Blazar 3C 454.3 is considered to be representative of AGNs in the Universe and a candidate double SMBH that is capable of emitting powerful nanohertz GWs (Dey et al. 2019).
The SMBH parameters required to determine the power of GW radiation include the masses of their components, the semi-major axis of the orbit, its eccentricity, orbital and precession periods, the rotation period of the central SMBH, and the value of the percenter motion. We cannot obtain a set of these parameters unambiguously from observational data. Important parameters that are not directly determined from monitoring observations are a Lorentz-factor (γ) and values of the orbital sizes of SMBHs. Therefore, it is necessary to use the model solution within reasonable assumptions and limitations. In this paper, we analyze multi-frequency data of 3C 454.3 based on the proposed model of SMBHs to obtain system parameters. A 2014–2020 prolonged flare in 3C 454.3 is considered and the interpretation of this unusual phenomenon is proposed. In addition, the power of GWs radiated by 3C 454.3 is estimated.
2. Observations
Monitoring at frequencies of 8 and 14.5 GHz was performed on the 26 m radio telescope of the University of Michigan Observatory in the period 1966 to 2012, the databases have been published elsewhere and used in several works (Volvach et al. 2010, 2011, 2013a). Since 2012, observations at 8 GHz have also been made on RT-22 in Simeiz. Monitoring at a frequency of 15 GHz was carried out using the 40 m Owens Valley Radio Observatory radio telescope in the period 2013 to 2019 (Richards et al. 2011) at a frequency of 22 GHz in Simeiz (RT-22).
Here we use the following sources of data: optical data obtained by the Steward Observatory spectropolarimetric monitoring project (Smith et al. 2009) from 2008 to 2018; optical data from 2008 to 2020 obtained as part of the Frankfurt Quasar Monitoring Project by Stefan Karge (Frankfurt, the Taunus Observatory of Physikalischer Verein, Germany); and optical data borrowed from the Open Science Observatories of the Open University (United Kingdom), the Bradford Robotic Telescope of the University of Bradford (United Kingdom), and the Tzec Maun Observatory of the Tzec Maun Foundation (USA).
Furthermore, data in the gamma range were obtained as part of the Fermi mission on the LAT instrument1. Each point corresponds to the photon flux averaged per day, integrated in the energy range 100 MeV–300 GeV. The gamma-ray source 1FGL 2253.9+1608 is positionally associated with the quasar 3C 454.3 (Abdollahi et al. 2020).
3. Results
Data from long-term monitoring of 3C 454.3 in the radio, optical, and gamma wavelength ranges are shown in Figs. 1 and 2. Periodograms were obtained from a harmonic analysis using the Schuster method (Volvach et al. 2013b). The first three rows of Table 1 show the results averaged over radio frequencies 8, 14.5+15, and 22.2 GHz, and optical and gamma wavelengths. The first row shows the averaged harmonic analysis data for all the specified frequencies for the entire observation period since 1966. The second row contains the averaged harmonic analysis data also for all frequencies, but for the time-interval of observations from 1966 to 2008. The third row shows the same data, but for the time interval from 2009 to 2020, given the start time of the Fermi satellite.
 |
Fig. 1. Data of 3C 454.3 multi-frequency monitoring for the period 1966 to 2020. |
 |
Fig. 2. Prolonged flare events in blazar 3C 454.3. |
Results of harmonic analysis of multi-frequency monitoring of 3C 454.3.
Here we propose a possible interpretation of the phenomena occurring in the SMBHs. The period of 14 years is confidently allocated as in Volvach et al. (2007). This period could be connected with the presence of precession movements of the central SMBH and associated with the accretion disk (AD) areas. Shorter periods allocated on all frequencies are 2.3 and 1.1 years. These can be related to the period and semi-period of the orbital motion of the companion. The semi-period of 1.1 years is explained by the double companions crossing the AD during a single orbital period. The semi-period of the precession also clearly stands out from analysis of the observational data.
For the reliability of the analysis, the observation data at all radio frequencies were divided into two samples. The first one included the results of monitoring conducted before 2008 (line 2), and the second, after 2008 until 2020 (line 3). The first row of Table 1 shows the harmonic components obtained for a complete sample of monitoring data. In the fourth row of Table 1, periods are taken in the coordinate system associated with the source for the values z = 0.86 and the bulk Lorentz factor γ = 5 using Eq. (1) of Rieger (2007):
In the following, we take the value γ = 5 for the blazar 3C 454.3. This value was obtained from comparing flare durations in other blazars, where estimates of γ-values were made. It is believed that the shorter the flare have the greater value of γ. The basis for applying this formula is the fact that we accept radiation from an object in a narrow angle between the directions of the ejection (“jet”) and the observer’s line of sight, assuming that γ2 = 1/θ, where θ is the angle between the ejection from the source and the direction to the observer (Volvach et al. 2009). The value of the precession period in the third row of Table 1 is omitted due to the comparability of the data sample length with the analyzed period. Data from the second and third rows of Table 1 are in good agreement with each other, despite being based on independent samples of experimental data.
For the “general” sample (first row of Table 1), we obtain more accurate periods, which are consistent with two independent samples from data analysis in different years. In the paper we use results obtained from the analysis of multi-frequency monitoring data from 1966 to 2020.
In support of our choice of orbital and precession periods in 3C 454.3, we note that many authors have concluded that bright AGNs are double systems of SMBHs. By harmonic analysis of long-term monitoring data of flux densities at different frequencies, authors have also established the presence of precession and orbital periods in these systems. The ranges of changes in precession and orbital periods in different AGNs are small. This may indicate the relative proximity between the masses of the companions in double systems (the ratio of companion masses is less than ten), which leads to the ratio of Tpr/Torb which is also less than ten (in accordance with the laws of celestial mechanics; see equations herein).
Here we provide some examples. For 3C 120, the values of Tpr = 12.3 years and Torb = 1.4 years are given (Caproni & Abraham 2004). Two periods (one 11.65 years, the second – 1.1 or 1.6 years) have been identified in the source OJ 287 based on optical and radio data (Sillanpaa et al. 1988, 1996; Pietila et al. 1999; Aller et al. 1992; Shukla & Stoner 1996). Precession and orbital periods of 12.4 and 3.0 years were allocated in 3C 273 (Volvach et al. 2013a).
Our further calculations using celestial mechanics and an eccentricity of zero are only a first-order estimation. In order to describe the orbits, the post-Newtonian second-order approximation is needed or the weak-field approximation.
Within the framework of the proposed close double systems model, it can be assumed that the axes of rotation of a more massive SMBH and central regions of AD are not perpendicular to the plane of the orbit of the companions. Moreover, the rotation periods of the central BH of the Trot and the outer regions of the AD may not coincide. This is due to the lack of “a frozen magnetic field” (Volvach et al. 2007) in the disk plasma in the peripheral regions of the AD. In this case, in accordance with the generalized Kepler’s third law we can write:
where m is the mass of the companion, M is the mass of the central BH, r is the radius of the companion’s orbit, and G is the gravitational constant.
On the other hand, the precession of the central BH in conjunction with the central regions of AD can occur due to gravitational perturbation of the companion moving in orbit. The angular velocity of precession of the central body Ωpr is determined from the standard ratio:
where i is half the angle of the precession cone, and ω is the angular velocity of the central body rotation. Given that Ωpr = 2π/Tpr and ω = 2π/Trot, the ratio (3) can converted to the form:
from where, taking into account (Eq. (2)), we can write:
Thus, the mass function depends only on the ratio of the precession period to the orbital period. In blazars, the value of i does not exceed 10°, and therefore we take cos i ≈ 1. From expression (4) it follows that:
Here we keep in mind the position that in the close double systems, due to the strong tidal interaction between the central SMBH and the supermassive companion, Trot = Torb. Then, for the mass of the central SMBH (Eqs. (5), (6)) we get the expression:
If the radiation that we receive from blazars comes to us from the “jet” component, emission from the source is observed at small angles between the observer beam of vision and the direction of the “jet” θ. In such cases, corrections are required for durations of processes in the source coordinate system (Eq. (1)).
With γ = 5, z = 0.86, for 3C 454.3 we obtain Tpr ≈ 188 years and Torb ≈ 31 years (line 4 Table 1). Using expressions (6) and (7), we define the orbit and masses of the 3C 454.3 companions (Table 2). Formulas (2)–(7) can, in principle, be used for calculations and in stellar kinematics.
Values of the 3C 454.3 companion masses for the three values of the orbit of the companion.
4. Discussion
Before proceeding to our interpretation of the phenomena occurring in the SMBHs, we consider the jet activity of the sources. A positive correlation has been found between the jet power and the luminosity of the accretion disk in broad-line blazars. In these objects, the total power of the jet is of the same order as the luminosity of the disc (Ghisellini et al. 2010). The nature of the connection between jet activity and disk activity has not yet been established. Although some draw an analogy with microquasars (Marscher et al. 2002).
This strongly suggests that, for flares, the mechanisms and locations of the high-energy events are the same for all outbursts. The γ-ray variations are strongly correlated with those at optical, far-infrared (FIR) and millimeter (mm) wavelengths with a delay of < 1 day. It has been determined that the synchrotron component is responsible for the variability from UV to IR wavelengths during an outburst (Jorstad et al. 2013).
The role of BLR clouds is not yet fully clear. A likely interaction of BLR clouds with the origin of the jet might contribute to the observed levels of high-energy emission (Araudo et al. 2010; Bosch-Ramon et al. 2012). This finding crucially links the broad-emission-line fluctuations to the nonthermal continuum emission produced by relativistically moving material in the jet and hence to the presence of broad-line region clouds surrounding the radio core. If the radio core were located at several parsecs from the central BH, then results would suggest the presence of broad-line region material outside the inner parsec where the canonical broad-line region is thought to be located.
However, these latter authors propose a more complex situation. The results suggest the presence of an outflowing BLR, which might be filled with BLR material dragged up by the relativistic jet as it propagates downstream from the BH. Perhaps it could be a subrelativistic outflow arising from an accretion disk wind. The dynamic and extended BLR notion has already been proposed (e.g., Popovic et al. 2001; Elitzur & Shlosman 2006). For source like 3C 273 (Paltani & Turler 2003) and 3C 454.3 (Finke & Dermer 2010), it could serve as an alternative source of seed photons for the inverse Compton scattering as proposed by Leon-Tavares et al. (2011).
Exiting the core was accompanied with a rotation of the optical polarization plane and strong optical polarization degree variations of up to 20%. The optical polarization behavior points to two interacting components in the jet, presumably shock–shock interaction, as one of the underlying mechanisms for the electric vector position angle. Alternatively, the merger of reconnection plasmoids in a moving stripe could reproduce > 180° rotations with similar polarization behavior (Zhang et al. 2018). The interaction of relativistic jets with the surrounding clouds of matter is the most important element of the jet activity of the AGN, as well as the dynamics of the jet itself. The continuum variability in AGNs is related to both the jet and the instabilities of accretion-disk flows (Mushotzky et al. 1993; Ulrich et al. 1997). In these objects the beaming of continuum emission is less, but optical synchrotron radiation from the core of the jet can be significant (3C 273; Soldi et al. 2008). The emission from the accretion disk or hot corona can be hidden by an obscuring torus. Hence, the bulk of the optical continuum and broad-line emission can be attributed to the relativistic jet rather than the central engine (the jet is intrinsically luminous and highly relativistic).
The bulk of optical continuum emission on timescales from a few months to years is likely to be generated by knots of high-energy electrons propagating in the innermost 0.4 pc region of the jet. In that sense, the timescale, amplitude, and frequency of optical synchrotron flares depend on energetics, kinematics, and the rate of ejected radio knots. The beamed continuum emission from the jet ionizes a gas in a subrelativistic outflow along the jet, which results in the formation of two outflowing BLRs along the jet and counter-jet (Arshakian et al. 2010).
As in the previous case, all optical flares are associated with the jet-ejection events when a flare rises after the time of ejection of a new jet component. A flare reaches its maximum in the epoch at which the ejected radio knot passes the stationary radio component downstream from the jet. The time passage of a component is in the average by 0.1 year (Leon-Tavares et al. 2010). The flaring component of the X-ray, optical, and radio emission is different in its nature from the underlying, quiescent emission associated with the accretion disk; it may be produced by a relativistically moving material in the jet (Leon-Tavares et al. 2010).
However, there are examples where the activity of the AGN cannot be linked to the jet, for example, in OJ 287 (Valtonen et al. 2011).
We propose an alternative scenario that should be considered as one of the possible interpretations of the phenomena occurring in the SMBHs.
By expressions (6) and (7) we see that the masses of the companions depends significantly on the sizes of they orbits. This means that to great sizes for the companion orbits can lead to unrealistic values of they masses. The lower limit for the mass of the SMBH is determined by the Eddington’s restriction on mass. The Eddington mass is related to the Eddington luminosity by the ratio Ledd ≈ 1.4 × 1038(M/M⊙). It is known that when the mass of the SMBH reaches the value M = 5 × 1010 M⊙, its size begins to interfere with the formation of AD. This leads to the destruction of the AD and the loss of accreting matter. For this reason, the resulting masses of the companions in the first row of Table 2 appear clearly improbable.
On the other hand, the total apparent luminosity of 3C 454.3 from radio to UV has been estimated as 6 × 1047 erg s−1 (Volvach et al. 2008). When inverse Compton contributions are added, the total luminosity may be as high as 1048 erg s−1. If we equate this value to the Eddington luminosity, we get a minimum estimate (low limit) for the mass of the central SMBH, M ≈ 7 × 109 M⊙ (line 3, Table 2).
We select parameters in row 2 of Table 2. With these, acceptable values for the companion masses are obtained at the orbit of 4.5 × 1017 (0.14 pc). The companion of the central SMBH is only a few times smaller in mass. The mass ratio of the components is μ3C 454.3 ≈ M/m ≈ 3.5. This is one of the lowest values known for SMBHs. As a consequence, μ3C 454.3 depends on the ratio of the precession and orbital periods (Eq. (6)). In this case, supermassive companions revolve around a common center of gravity in almost circular orbits with radii of rcomp ≈ 4.5 × 1017 cm and rcentr ≈ rcomp/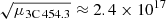 cm. The distance between the companions during their movement around the common center of gravity is a ≈ rcomp + rcentr = 6.9 × 1017 cm. In this situation, the rotation period and orbital period of the central SMBH coincide with the orbital period of the companion.
cm. The distance between the companions during their movement around the common center of gravity is a ≈ rcomp + rcentr = 6.9 × 1017 cm. In this situation, the rotation period and orbital period of the central SMBH coincide with the orbital period of the companion.
The estimated lifetime of the system prior to the merger for data from line 2 of Table 2 is (Fernandez & Kobayashi 2019):
Thus, 3C 454.3 is a short-lived close double systems of SMBHs.
Using the harmonic analysis of radio data during the flare in 3C 454.3, which has been ongoing since the beginning of 2014, the presence of harmonic components of the orbital period and half-period of 2.3 and 1.1 years was establish (Fig. 2). Periods of 2.3 and 1.0 years were also confidently detected in the analysis of optical data. These are also present in the γ-range data. These values indicate that there were no major changes in the γ-factor in the system.
The flare has been ongoing for 7 yr and three orbital periods have passed. This means that the companion does not go beyond the AD for the time of the precession half-period (about 7 years). At the same time, the angle of view to the observer and the jet direction was inside the precession cone i all this time. This allows us to evaluate the AD parameters.
As for the radius of AD, it can be noted that it is larger than rd > 4.5 × 1017 cm, because the companion’s orbit is located inside it. A more precise estimate of its radius can be made based on the central body precession formula (Dunn et al. 2006):
where q = m/M, a = rcomp + rcentr is the distance between the companions, ad is radius AD, and i is the angle between the orbital and AD planes (half angle of the precession cone). This formula can be converted for calculating the radius AD by known values M, m, Tpr, q, a and i:
Substituting the precession period of Tpr ≈ 188 yr (row 4 Table 1) into Eq. (6), together with the masses of the companions (row 2 Table 2), and the distances between them, a = rcomp + rcentr = 6.9 × 1017 cm, i = 0 and q ≈ 0.286, we obtain a value of aad 3C 454.3 ≈ 3.9 × 1018 cm ≈ 1.27 pc.
If we take the semi-cone angle of the precession i ≈ 1/γ2 ≈ 5°, we get the maximum value semi-thickness of AD: had 3C 454.3 ≈ 0.08 ⋅ aad 3C 454.3 ≈ 3.1 × 1017 cm. The gravitational radius of the central SMBH: Rg = 2GM/c2 ≈ 7.1 × 1015 cm. Therefore, in this case, the AD is not a physically thin disk. The minimum estimate of the semi-thickness of the AD follows from the size of the companion’s orbit: 0.08 × 4.5 × 1017 cm ≈3.6 × 1016 cm. Therefore, we obtain restrictions on the semi-thicknessof the AD of 3C 454.3 of 3.6 × 1016 cm < had 3C 454.3 < 3.1 × 1017 cm, or had 3C 454.3 < 0.08 ⋅ aad 3C 454.3. It is known that standard accretion α-disks have a semi-thickness of h ≈ 0.07 ⋅ aad (Suleimanov et al. 2007). X-ray binary systems indicate a significant semi-thickness of accretion disks up to h ≈ 0.25 ⋅ aad (McClintock et al. 1982). Thus, our data in the radio band do not contradict theoretical estimates for standard accretion α-disks.
As far as we know, this is the first estimate of AD parameters obtained from monitoring data in the radio band. Since 2014, companions are inside the AD. At the same time, AD has not yet collapsed, despite the supermassive companion and the central SMBH being passed through the AD.
We now discuss what we mean by flares in general. We consider a flare to be a phenomenon that has a duration of the order of some months or more, because according to our interpretation, a flare occurs when SMBH companions move inside the AD or cross it. Taking into account the estimated parameters of the AD (had ≈ 3.1 × 1017 cm) and the giant velocity of the companion movement (v3C 454.3comp ≈ 3 × 109 cm s−1, discussion section), even if the companion passes the AD on a perpendicular trajectory, the time will be ΔTsource ≈ 108 s in the coordinate system associated with the source. In our coordinate system, this will be ΔTobs ≈ ΔTsource(1 + z)/γ2 ≈ 7.4 × 106 s ≈ 0.4 years ≈ 5 months (z = 1.86, γ = 5). Even if the plasma formation in the jet moves at the speed of light, it will travel a distance of 3 × 1010 cm s−1 0.4 yr 3 × 107 s [γ2/(1 + z)] = 4.8 × 1018 cm ≈ 1.5 pc. Most of the processes we observe in the 3C 454.3 jet in the range from R to radio (1 cm) are deployed within 1.5 pc from its origin. These areas are inaccessible to modern ground-based interferometry.
All phenomena similar to those that are analyzed in the article presented by Liodakis et al. (2020) are subflares according to our criteria; they have durations of approximately 10 days or less. In some representations, these phenomena can be results of blows of companions to heterogeneities of matter in AD. We discuss this subject in Volvach et al. (2008). It is by analyzing short subflares that the distribution of the matter in the AD can be investigated. Some such flare phenomena can also be associated with the passage and interaction of shock waves in the jet (Liodakis et al. 2020). Naturally, we did not take such durations into account in the harmonic analysis.
Let us now look at Fig. 3. Here we see the development of the flare phenomenon in 3C 454.3 in 2004–2006 (optical and radio bands). The time-delay between optical and radio flares (36.8 GHz) is about 8 months. It is necessary to note the main conclusions that follow from the above observations.
 |
Fig. 3. Light curve and spectral flux density of the 3C 454.3 in the optical and radio band at the time of the flare. This is a fragment from our work Volvach et al. (2008). |
1. The duration of the flare is about 1 year at all wavelengths.
2. No dependence of the flare duration on the frequency (distance from the jet origin) is observed.
3. The flare shape is the same at all frequencies. Moreover, the form is identical on all timescales from weeks to years for the interval between data collection (5–7 days).
4. The dependence of the delay variation on frequency excludes the influence of medium between the observer and the source as the cause of the frequency shift of the flare. This means that the observed physical processes occur in the environment of the jet, at its point of origin.
5. It can also be argued that the dispersion properties of the jet environment are insignificant if we do not observe a serious “blurring” of the small details of the flare.
On the basis of the above statements, we can note something about the physical characteristics of the jet environment in principle. Small details at different frequencies allow us to determine the multi-month shift of the flare with an accuracy of days.
Using the orbital radius (middle row of Table 2) and period (row 4 of Table 1), it is possible to determine the velocity of the companion in the orbit: v3C 454.3comp ≈ 2πr/Torb ≈ 3.0 × 104 km s−1. The obtained value even exceeds the velocity of matter during the explosion of type I supernovae vtypeI ≈ 104 km s−1. The velocity of the central SMBH 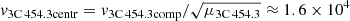 km s−1, which is also comparable with the velocity movement of matter in the explosion of type I supernovae.
km s−1, which is also comparable with the velocity movement of matter in the explosion of type I supernovae.
At a companion speed of 0.1 c (3 × 109 cm s−1), for example, the temperature may rise to 1010 K. The effect of isotropic motion of gas plasma particles occurs behind the shock wave front. In this case, the directed motion of the shock wave is converted into chaotic particle motion, determined by the plasma temperature mv2/2 = 3kT/2. For hydrogen plasma, we get T ≈ 1.5 × 1010 K. For heavier cores, the temperature will be higher. In any case, the plasma temperature is several times higher than the threshold of electron–positron (e–p) pair birth (T ≈ 5 × 109 K). Supersonic shock waves with a factor dilution and cooling of the medium due to a drop in the power of shock waves reach the beginning of the jet and form plasma blobs with a magnetic field. Blobs consist of differently sized knots (inhomogeneities). Near the origin of a jet, electric and magnetic fields may accelerate plasma formations to almost the speed of light, forming “jets” consisting of e–p pairs in addition to clouds of the electron–proton plasma. In this time, the highest level of activity of 3C 454.3 is seen in all wavelength ranges, especially in the gamma range. This is a possible but not directly proven event scenario.
In the observer’s coordinate system, we see flares (blobs in interferometry) lasting many months. The VLBA resolution of 0.1 mas means a value of several parsecs at a distance of 3C 454.3. At such distances, we can reliably determine parts larger than 10 pc. Our phenomena in optics and radio develop at smaller distances from the origin of the jet. The strength of the multi-frequency long-term monitoring method lies precisely in the fact that it can be used to observe processes occurring in such small areas that are inaccessible even for global interferometric systems. With using a wavelet analyze we established that there was no change of the orbital period in 3C 454.3 at the value of about 20% in the time-interval between 1970 and 2020.
This does not exclude minor changes in the angle between the direction to the observer and the jet. The required change in the γ-factor is only ±5%.
Now we discuss the relationship of the processes in the AD with the orbital and precession periods. In our scheme (discussion section), supermassive companions in 3C 454.3 revolve around a common center of gravity at nearly circular orbits with radii rcomp and rcentr. They are in the stage of close binary systems near to the confluence (by cosmic standards). The distance between the companions during their movement around the common center of gravity is a ≈ rcomp + rcentr ≈ 6.9 × 1017 cm. The AD size is 3.9 × 1018 cm. In such a situation, the AD may be common by the companions.
The plane of the companion’s orbit has an angle of inclination to the AD plane in the general case. At any angle of inclination, the companion crosses the AD plane twice during one orbital period (2.3 years), each time at a different distance from the center. Shock waves with a delay in propagation reach the origin of the jet, creating flares. Due to the small difference in the time of two parts of the flare (ΔTflares ≈ 0.3 yr see panel 14.5 GHz), they merge into one creating different slopes as the radiation flux density increases and decreases (14.5 GHz panel). Flares from companions (two parts of the flare) have different amplitudes (see left and right parts of the flare).
Thus, the asymmetric shape of the flare in 3C 454.3 can be explained within the framework of our hypothesis, which considers two SMBHs located in close orbits and rotating in approximately circular orbits around the common center of gravity at different distances from it. Both companions ram the AD and the shock waves reach the jet’s origin with a delay of a fixed value, which is determined by the difference in the distances of the companions from the common center of gravity and difference in their velocity. If the speed of the shock waves depends only on the parameters of the propagation medium (from temperature and density in the first place), then simple estimations can confirm the observed difference in the time of their arrival at the origin of the jet.
The difference in the distance of the companions to the common center of gravity is Δr ≈ 2 × 1017 cm. The time between flares from companions in the rest frame of the source is equal to ΔTsource ≈ ΔTobs ⋅ γ2/(1 + z)≈Δr/vshock. Subsequently, the average speed of the shock waves is vshock ≈ Δr ⋅ (1 + z)/(ΔTobs ⋅ γ2)≈(2 × 1017 cm ⋅ 1.86)/(0.9 × 107 s ⋅ 25)≈1.6 × 109 cm s−1 ≈ 1.6 × 104 km s−1. The speed of the SMBH companion is about twice as fast of SMBH at the moment of the companion’s impact on the environment. Given the gigantic temperatures in the medium and the dependence 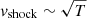 , the described situation appears quite possible.
, the described situation appears quite possible.
Analysis of monitoring data from 2010 to mid-2014 indicates that the rapprochement of AD and companion orbits planes may have begun in 2010 (Fig. 2). Analysis of monitoring data from mid-2011 to mid-2014 indicates that at this time, the precession cone began retiring from the direction to the observer and the Doppler factor δ decreased. Taking into account the dependence of the Doppler brightening on δ as (δ + α)3 (α – spectral index of the dependence of flux density on frequency), the changes in the δ could be insignificant (no more than 1.7 times) in order to achieve a five-fold drop in the observed flux density. Then, in mid-2014, the direction to the observer moved to the center of the precession cone, but the flow density level was restored to only 50% of the previous value. It can be assumed that the 3C 454.3 companions were already in the AD more than 10 years ago. If the companion leaves the central parts of the AD successfully, then it should assumed that the AD is restored after each orbital period. Two factors may contribute to this:
(a) The companion moves with each new revolution along a new trajectory in the AD (because of the displacement of the percenter).
(b) The “swept out” matter by companions is regenerated despite the supersonic speed of the companions, which is provided by high thermal velocity and additional external pressure from the matter in the AD.
Given the high speeds of the 3C 454.3 companions, it is advisable to calculate the kinetic energy using the relativistic formula Ekin = m ⋅ c2 [⋅1/(1 − v2/c2) − 1]. Taking the values of the masses (middle row of Table 2) and speeds of the companions 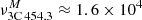 km s−1,
km s−1, 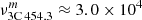 km s−1, we obtain
km s−1, we obtain 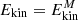 +
+ 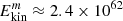 erg. This energy is emitted as gravitational radiation and overcoming dynamic friction against the dense environment of the AD. Based on the data proposed in the model for 3C 454.3 (second row of Table 2, a = rcomp + rcentr ≈ 6.9 × 1017 cm), it is possible to calculate the rate of energy loss due to the radiation of GWs, taking e = 0 (Peters 1964).
erg. This energy is emitted as gravitational radiation and overcoming dynamic friction against the dense environment of the AD. Based on the data proposed in the model for 3C 454.3 (second row of Table 2, a = rcomp + rcentr ≈ 6.9 × 1017 cm), it is possible to calculate the rate of energy loss due to the radiation of GWs, taking e = 0 (Peters 1964).
Bringing the eccentricity into consideration leads to an increase in the rate of energy loss (formula (11)). In the case of e = 0.7 (as for the OJ 287 model used), dE/dT increases by a factor of 30 and becomes equal to dE/dT ≈ 3 × 1049 erg s−1. The rate of change of the orbit increases by a factor of 2.5. This does not fundamentally change anything in our consideration.
The following physical reasons led us to consider the orbit with e = 0.
(a) We have a close double supermassive system with comparable masses at the stage of evolution close to merging.
(b) Within the framework of the proposed model, there can be no significant eccentricity, because there are values of the orbital period and half-period that are half the orbital period within the errors.
Using the formula from Peters (1964), we get:
It is interesting to compare the data obtained for 3C 454.3 with the famous blazar OJ 287. The OJ287, at present, is a unique BH binary with known parameters determined by observations. This double system can be used for the detection of GWs (Valtonen 2007). The orbital angular momentum of close double systems OJ 287 is lost in the process of strong GWs and electromagnetic radiations, which leads to a short lifetime of about 104 yr. This is comparable to our data for 3C 454.3 (row 2 Table 2). The power of the GW radiation for OJ 287 is 1046 − 1047 erg s−1 and reaches a maximum of flaring at 1049 erg s−1 (Sun et al. 2011). However, the average value for OJ 287 is less than that obtained for 3C 454.3 (Eq. (11)). Even taking into account the difference in distance, the 3C 454.3 may provide a greater flux density of GWs on Earth than OJ 287.
Another important difference between 3C 454.3 and OJ 287 is that for the last 10 yr, companions of 3C 454.3 have been located in the AD structure, which exerts increased dynamic friction on the system. Due to the precession of AD, the companions are located in different places in the AD where there are different densities and inhomogeneities. From this, the level of GW radiation increases and varies. The share of GW radiation due to dynamic friction can be significant if not the main fraction of the total. In addition, the system lifetime before merging is reduced.
To determine changes in the orbit of the companion of 3C 454.3 and the possibility of experimental determination of these changes, we calculate the rate of the orbit changes using the formula from Peters (1964):
where G is the gravitational constant, M, m are the masses of the companions (row 2 of Table 2), a = 6.9 × 1017 cm, and e = 0.
Knowing the orbital period (row 4 of Table 1), we get the value of the companion’s orbit change Δa ≈ 1.7 × 1013 cm. The change in the orbital period is ΔTper≈ 0.4 days. Over the entire time of multi-frequency observations of the object (54 years ≈ 23 periods), the change in the period is ΔTobs ≈ 9.2 days ≈ 0.025 years. This value is ten times lower than the errors in determining the period (Table 1) and the accuracy of determining the time of a flare, the duration of which can be a year or more. To reliably determine the change in the period with an accuracy of 4σ, we need to have an error in determining the period of ΔTσ ≈ 0.1 days. It is impossible to determine the time of a complex flare event lasting about a year with such accuracy.
A legitimate question arises as to how the accretion of matter onto a BH behaves at such high velocity of SMBH movement relative to the falling matter on it. The answer may come from the following formula, which shows how this affects the accretion rate (Shvartsman 1971):
where n is the density of the accreting matter, and v is the velocity of movement relative to the speed of the matter falling onto the SMBH. When we enter the values of M ≈ 2.4 × 1010 M⊙, n ≈ 3 × 109 cm−3 and v ≈ 3 × 104 km s−1, the luminosity due to accretion onto a BH is equal to L ≈ 3.4 × 1040 erg s−1, which is seven orders of magnitude less than the luminosity of 3C 454.3 in the entire electromagnetic spectrum (Volvach et al. 2008). This once again supports the hypothesis that in the close double systems of SMBHs, the primary energy release does not occur due to the accretion of matter onto the BH. In our concept, this energy release occurs when the companion and the central SMBH itself pass through the AD. Only close double systemss of SMBHs form bright AGNs.
5. Conclusions
1. We propose a new method for calculating the parameters of the orbits of double SMBHs using only multi-frequency monitoring data in the radio band. Our results suggest that 3C 454.3 may be the most massive close double systems of SMBHs.
2. The shape of the flux density change during the unusual flare in 2014–2020 may indicate the coincidence of planes of the AD and the orbits of the companions.
3. We use a novel combination of data monitoring studies in the radio range and a new method for determining system parameters to obtain estimates of the diameter and thickness of AD 3C 454.
4. According to our study, due to precession, companions will leave the central parts of the AD in a few years if the AD retains its stability and does not collapse before that time.
5. Estimates of the level of GWs coming from 3C 454.3 show that 3C 454.3 is currently the most powerful GW emitter. 3C 454.3 is the most powerful source of radiation in the range of the entire electromagnetic spectrum. Its power is E3C 454.3 ≈ 1048 erg s−1 (Volvach et al. 2008).
6. Estimates of the values of changes in the orbits of 3C 454.3 companions are made. The obtained values of changes in the orbits do not allow them to be detected by modern methods.
7. The calculated lifetimes of the 3C 454.3 system show that this is a short-lived object in the Universe with a lifetime of ∼5 × 104 yr.
8. Due to the constant presence of companions in a dense inhomogeneous AD environment, the role of dynamic friction increases for dynamics of all system. In the first of all that connection with the process of calculate of the GWs level radiation, which increase in that case. This situation allows us to suggests for an increase in the probability of detecting GWs radiating from 3C 454.3.
Acknowledgments
The RT-22 observations, collecting and data processing were done under support of the Ministry of Science and Higher Education of the Russian Federation under the grant 075-15-2020-780. The study uses data from the OVRO 40-meter radio telescope monitoring program, which is partially supporting by NASA grants NNX08AW31G, NNX11A043G, NNX14AQ89G and NSF, as well as grants AST-0808050 and AST-1109911. Optical data was using from the Steward Observatory spectropolarimetric monitoring project supported by Fermi Guest Investigator grants NNX08AW56G, NNX09AU10G, NNX12AO93G, and NNX15AU81G and the Frankfurt-based Steffan Karger quasar-monitoring project. The research was caring out with the financial support of the RFBR in the framework of the scientific project 19-29-11027 (LV) in the part of the gravitational radiation.
References
- Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Aller, M. F., Aller, H. D., Hughes, P. A., & Latimer, G. E. 1992, in Variability of Blazars, eds. E. Valtaoja, & M. Valtonen (Cambridge Univ. Press), 126 [Google Scholar]
- Araudo, A. T., Bosch-Ramon, V., & Romero, G. E. 2010, A&A, 522, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arshakian, T. G., Leon-Tavares, J., Lobanov, A. P., et al. 2010, MNRAS, 401, 1231 [Google Scholar]
- Bosch-Ramon, V., Perucho, M., & Barkov, M. V. 2012, A&A, 539, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caproni, A., & Abraham, Z. 2004, MNRAS, 349, 1218 [Google Scholar]
- Dey, L., Gopakumar, A., Valtonen, M., et al. 2019, Universe, 5, 108 [Google Scholar]
- Dunn, R. J. H., Fabian, A. C., & Sanders, J. S. 2006, MNRAS, 366, 758 [Google Scholar]
- Elitzur, M., & Shlosman, I. 2006, ApJ, 648, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandez, J. J., & Kobayashi, S. 2019, MNRAS, 487, 1200 [Google Scholar]
- Finke, J. D., & Dermer, C. D. 2010, ApJ, 714, L303 [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., et al. 2010, MNRAS, 402, 497 [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Larionov, V. M., et al. 2010, ApJ, 715, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Smith, P. S., et al. 2013, ApJ, 773, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Leon-Tavares, J., Lobanov, A. P., Chavushyan, V. H., et al. 2010, ApJ, 715, 355 [Google Scholar]
- Leon-Tavares, J., Valtaoja, E., Tornikoski, M. L., & Nieppola, E. 2011, A&A, 532, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liodakis, I., Blinov, D., Jorstad, S. G., et al. 2020, ApJ, 902, 61 [Google Scholar]
- Marscher, A. P., Jorstad, S. G., Gomez, J.-L., et al. 2002, Nature, 417, 625 [Google Scholar]
- McClintock, J. E., London, R. A., Bond, H. E., & Grauer, A. D. 1982, ApJ, 258, 245 [Google Scholar]
- Mushotzky, R. F., Done, C., & Pounds, K. 1993, ARA&A, 31, 717 [Google Scholar]
- Paltani, S., & Turler, M. 2003, ApJ, 583, 659 [Google Scholar]
- Peters, P. C. 1964, Phys. Rev. B, 136, 1224 [Google Scholar]
- Pietila, H., Takalo, L. O., Tosti, G., et al. 1999, A&A, 345, 760 [Google Scholar]
- Popovic, L. C., Stanic, N., Kubicela, A., & Bon, E. 2001, A&A, 367, 780 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richards, J. L., Max-Moerbeck, W., Pavlidou, V., et al. 2011, ApJS, 194, 29 [Google Scholar]
- Rieger, F. M. 2007, Astrophys. Space Sci., 309, 271 [Google Scholar]
- Shukla, H., & Stoner, R. E. 1996, ApJS, 106, 41 [Google Scholar]
- Shvartsman, V. F. 1971, Sov. Astron., 15, 342 [Google Scholar]
- Sillanpaa, A., Haarala, S., Valtonen, M. J., et al. 1988, ApJ, 325, 628 [Google Scholar]
- Sillanpaa, A., Takalo, L. O., Pursimo, T., et al. 1996, A&A, 305, 17 [Google Scholar]
- Smith, P. S., Montiel, E., Rightley, S., et al. 2009, 2009 Fermi Symposium, eConf Proceedings C091122 [Google Scholar]
- Soldi, S., Türler, M., Paltani, S., et al. 2008, A&A, 486, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suleimanov, V. F., Lipunova, G. V., & Shakura, N. I. 2007, Astron. Rep., 51, 549 [Google Scholar]
- Sun, Y.-T., Liu, J.-Y., Lin, J.-Z., et al. 2011, Chin. Astron. Astrophys., 35, 123 [Google Scholar]
- Ulrich, M.-H., Maraschi, L., & Urry, C. M. 1997, ARA&A, 35, 445 [Google Scholar]
- Valtonen, M. J. 2007, ApJ, 659, 1074 [Google Scholar]
- Valtonen, M. J., Lehto, H. J., Takalo, L. O., & Sillanpaa, A. 2011, ApJ, 729, 33 [Google Scholar]
- Volvach, A. E., Volvach, L. N., Larionov, M. G., et al. 2007, Astron. Rep., 51, 450 [Google Scholar]
- Volvach, A. E., Volvach, L. N., Larionov, M. G., et al. 2008, Astron. Rep., 52, 867 [Google Scholar]
- Volvach, A. E., Volvach, L. N., Larionov, M. G., et al. 2009, Astron. Rep., 53, 777 [Google Scholar]
- Volvach, A. E., Volvach, L. N., Larionov, M. G., et al. 2010, Astron. Rep., 54, 28 [Google Scholar]
- Volvach, A. E., Volvach, L. N., Larionov, M. G., et al. 2011, Astron. Rep., 55, 608 [Google Scholar]
- Volvach, A. E., Volvach, L. N., Larionov, M. G., et al. 2013a, Astron. Rep., 57, 46 [Google Scholar]
- Volvach, A. E., Volvach, L. N., Larionov, M. G., et al. 2013b, Astron. Rep., 57, 34 [Google Scholar]
- Zhang, H., Li, X., Guo, F., & Giannios, D. 2018, ApJ, 862, L25 [Google Scholar]
All Tables
Values of the 3C 454.3 companion masses for the three values of the orbit of the companion.
All Figures
 |
Fig. 1. Data of 3C 454.3 multi-frequency monitoring for the period 1966 to 2020. |
| In the text | |
 |
Fig. 2. Prolonged flare events in blazar 3C 454.3. |
| In the text | |
 |
Fig. 3. Light curve and spectral flux density of the 3C 454.3 in the optical and radio band at the time of the flare. This is a fragment from our work Volvach et al. (2008). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.