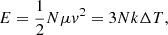| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | L13 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202140295 | |
| Published online | 02 April 2021 | |
Letter to the Editor
Bouncing and sticking collisions of organic nanoparticles: Atomistic study
Physics Department and Research Center OPTIMAS, University Kaiserslautern, Erwin-Schrödinger-Straße, 67663 Kaiserslautern, Germany
e-mail: urbassek@uni-kl.de
Received:
7
January
2021
Accepted:
23
March
2021
Context. Whether nanoparticles bounce or stick during collisions determines whether particles grow or fragment, hence shaping collision-induced agglomeration processes. The collision behavior of organic matter may strongly differ from that of silica or ice grains.
Aims. We explore the microscopic processes underlying the bouncing behavior of organic nanoparticles.
Methods. Molecular dynamics simulations based on a reactive potential, which follow molecular motion on an atomistic scale, are used.
Results. For the exemplary case of glycolic acid molecules, warm nanoparticles (250 K) always show sticking, while at low velocities (2.5 m s−1) cold nanoparticles (100 K) exhibit a considerable probability for bouncing. This behavior can be traced back to the distant electrostatic repulsion of the nanoparticles at certain orientations; this prevents a closer approach, during which van der Waals and H-bonded interactions would lead to sticking. At higher temperatures, molecular vibrations and conformational flexibility average over the nanoparticle interaction, such that attraction dominates and bouncing is prevented. Our results are in qualitative agreement with laboratory experiments.
Conclusions. Organic matter distinctly influences the collision behavior of nanoparticles.
Key words: protoplanetary disks / planets and satellites: formation / methods: numerical
© ESO 2021
1. Introduction
Dust is found everywhere in the universe, both in interplanetary and interstellar space (Li & Greenberg 2003). While grains consist mostly of silicates and ices, carbonaceous material is also frequently found (Greenberg 2002; Draine 2003; Tielens 2005). Collisions between dust grains are relevant for the grain-size distribution in dust clouds and disks: Sticking collisions lead to dust agglomeration, while bouncing – or even fragmenting – collisions may prevent the formation of larger entities in the clouds. While collisions between silica and ice particles have often been studied, both by experiment and simulation (Dominik & Tielens 1997; Blum 2010, 2018), our knowledge of collisions between carbonaceous grains is still poor (Nietiadi et al. 2020).
The organic molecules that form the basis of dust grains have been subdivided into “molecular-cloud” and “diffuse-cloud” organic matter (Briggs et al. 1992; Mendoza-Gómez & Greenberg 1993; Greenberg & Li 1999; Kouchi et al. 2002; Kudo et al. 2002), where the latter category consists of molecules modified by exposure to radiation and includes the class of polycyclic aromatic hydrocarbons. Here, we focus on molecules belonging to the former category, which we found to be fascinating since their collision properties strongly change with temperature. Kouchi et al. (2002) and Kudo et al. (2002) provide extensive tables of molecules belonging to the class of molecular-cloud organic matter and used a mixture for their collision experiments. Taking glycolic acid as a representative material, it behaves elastically at temperatures below 240 K, and it melts above 348 K (Kouchi et al. 2002; Kudo et al. 2002). At intermediate temperatures, it acts as a viscoelastic material (Homma et al. 2019). Similar behavior has been found for other analogous molecular-cloud organic material (Piani et al. 2017). Thus, it has been speculated that organic mantles may strongly mediate collisions between grains and administer their collision-induced agglomeration. In contrast, diffuse-cloud organic matter is more rigid and thus has a different collision behavior (Piani et al. 2017).
In the present study, we use molecular dynamics (MD) simulations to study collisions between nanometer-size nanoparticles (NPs) that consist of glycolic acid. By varying the NP temperature and the collision velocity, we can study the atomistic origin of the sticking or bouncing collision behavior.
2. Methods
The glycolic acid molecule, HOCH2-COOH, is depicted in Fig. 1. It can be taken as a representative organic molecule of grains in molecular clouds (Homma et al. 2019); more complete lists of organic matter in these clouds are available (Kouchi et al. 2002; Kudo et al. 2002). The molecule has a mass of m = 76 amu. Condensed glycolic acid has a melting temperature of 348 K and a density of 1.49 g cm−3 (Ullmann et al. 1985). We modeled this molecule using the reactive force (ReaxFF) potential (Monti et al. 2013), which incorporates not only the covalent bonds between the atoms, but also the van der Waals (vdW) and electrostatic forces between molecules. We note that this potential assigns partial charges to the atoms in glycolic acid, which are recalculated on the fly within the simulations.
 |
Fig. 1. Glycolic acid molecule. |
We considered NPs consisting of N = 62 molecules. We used PACKMOL (Martínez et al. 2009) to fill these molecules into a sphere of radius R = 10.8 Å, such that the density corresponded to the experimental value. The amorphous structure was relaxed for 5.5 ps to get rid of excess potential energy and then thermalized for around 35 ps to the desired temperature. In this study we considered collisions with NPs at 100 K and at 250 K. These temperatures were chosen since the elastic and viscous properties of glycolic acid change strongly with temperature (Kouchi et al. 2002; Kudo et al. 2002; Homma et al. 2019). In the following, the 100 K NP is denoted as “cold” and the 250 K NP as “warm”.
The thermalized NP was duplicated; then, both NPs were shot against each other with relative velocity v; we considered v = 2.5, 5, 10, and 20 m s−1. For the lowest velocity, we simulated six collisions; in each simulation, one of the NPs was rotated with respect to the other in order to assemble statistics. Only central collisions were considered. The collisions were followed for a time between 0.3 and 1.5 ns, until the fate of the collision (bouncing or sticking) was clarified.
The simulations were performed in an NVE ensemble using the LAMMPS software (Plimpton 1995). We studied the time step by performing reference simulations with varied time steps; a value of 0.1 fs guarantees energy conservation and was used for all simulations.
For the analysis of our results, we used a molecule detector that allowed us to detect whether nearby molecules form H bonds. This detector is based on Stoddard’s cluster detector (Stoddard 1978). It uses a distance criterion such that O-H pairs are considered to be bound by an H bond if their distance is smaller than 1.3 Å (Anders & Urbassek 2013; Mücksch et al. 2014).
3. Results
Figure 2a demonstrates that, for the cold NPs, we observed both sticking and bouncing NP collisions. We detected these collision outcomes by following the center-of-mass distance, Δz, of the two colliding NPs for a sufficiently long time to observe whether they separate again after the collision. However, we observed bouncing for the cold NPs only, and only for the lowest velocity, 2.5 m s−1; in this case, two out of the six simulated trajectories resulted in bouncing (i.e., a 33% probability). In all other cases, only sticking was observed.
 |
Fig. 2. Temporal evolution of the center-of-mass distance, Δz. Panel a: data for a bouncing collision and a sticking collision at 100 K with a velocity of 2.5 m s−1. The trajectories correspond to the snapshots shown in Figs. 3b and c. Panel b: data for sticking collisions at 250 K for various velocities. |
The sticking trajectory results in a final center-of-mass distance between the two NPs of around 2 nm, in good agreement with the NP size of 2.15 nm. For higher velocities, the final center-of-mass distance is even smaller (see Fig. 2b), corresponding to an NP compression in the collision zone. The bouncing trajectory (Fig. 2a) shows its distance of closest approach at 3.0 nm. At such large distances, the outermost atoms of the NPs are still around 10 Å apart, such that strong attractive bonding – via H bonds – is impossible. Rather, the atoms are in the range of the vdW and electrostatic forces. Repulsion must therefore be caused by the action of repulsive forces between the partially charged atoms of the glycol acid molecules. Due to the amorphous arrangement of the molecules within the NPs, this arrangement can lead – depending on the mutual orientation of the two NPs – to either attractive or repulsive interaction, and hence sticking or bouncing.
Figure 3 shows several snapshots of collision events illustrating this point, all taken for cold NPs. Figure 3b shows the bounced NPs for the initial orientation shown in Fig. 3a at a low velocity, 2.5 m s−1. We note the strong changes in the local atomic conformations. As the NPs are very “floppy”, they do not only occur in the collision zone, but also in distant regions. An inspection of the NP motion shows that the collision induced NP rotation; this is possible even for the central collisions studied here since the NPs are not spherically symmetric.
 |
Fig. 3. Collision of two NPs at 100 K with a velocity of 2.5 m s−1. Panel a: initial and panel b: final configurations for a bouncing collision. Panel c: final configuration of a sticking collision. Panel d: sticking configuration for a velocity of 20 m s−1. |
Figure 3c shows the structure of a collided NP in the sticking regime for the same initial velocity (but a different initial conformation). We note that the collision zone appears quite dilute; atom density there is small.
Finally, Fig. 3d shows the resulting NP for a faster collision velocity, 20 m s−1. We note that here the collision zone is indeed denser; it was compacted in the collision. Such collisional compression is expected for increased velocities.
A further clue on the nature of the bouncing process for low-velocity cold NPs is provided by counting the number of H-bonded glycolic acid molecules in the NPs. Figure 4 shows that the number of H-bonded dimers only negligibly depends on the collision velocity, but it depends strongly on the NP temperature. The smaller number of H bonds in the warm NP corresponds to a more flexible NP conformation; this allows that during the period of time while the colliding NPs approach NP interaction is averaged over various conformations such that the attractive interaction wins.
 |
Fig. 4. Number of hydrogen-bonded glycolic acid molecules formed in NP collisions at 100 and 250 K. Data for the un-collided NPs are included at v = 0. Error bars included for v = 2.5 m s−1 show the standard deviation. |
The collision does not affect the NP temperature and thus does not affect the number of H bonds. This can readily be rationalized by calculating the maximum change in temperature, ΔT, in the NPs by assuming that all collision energy is transformed into heat:
where k is the Boltzmann constant and μ = m/2 denotes the reduced mass of a glycolic acid molecule. Even for v = 20 m s−1, this amounts to a change of only ΔT = 0.26 K.
4. Conclusions
The sticking of the NPs that we observe for the warm NPs as a rule, and for the cold NPs for all but the smallest velocities, is mediated by the vdW attraction and even more so by the electrostatic interactions of the two NPs. Higher collision velocities (20 m s−1) induce a local compression in the collision zone, in contrast to the open structure retained at 2.5 m s−1.
Bouncing collisions were only observed for the lowest velocity, 2.5 m s−1, and only at 100 K. Even here, bouncing does not occur in all collisions: It only has a 33% probability of occurring. In our simulations, we find that rebound only occurs when electrostatic interactions repel the two NPs when they are already at a distance where vdW and H-bond interactions are insignificant. At higher temperatures, molecular vibrations and conformational flexibility lead to an averaging over the NP interaction in which attraction dominates and bouncing is prevented.
In thermal equilibrium, our NPs will have quite high thermal center-of-mass velocities, amounting to 23 (36) m s−1 at a temperature of 100 (250) K. Hence, the collision velocities of 2.5−20 m s−1 studied in the present work will all contribute in an equilibrium cloud. The situation is different in a cold cloud, where, at a temperature of 2.7 K, the average center-of-mass velocity is only 4 m s−1. Due to the small heat capacity of organic NPs (Draine & Li 2001), single photons may heat NPs up by several hundred K; however, the NPs will cool down via photon emission on a timescale of hours. In such a scenario, the combination of high internal temperature and small center-of-mass velocities is justified.
Our finding is in qualitative agreement with data from experiments (Kouchi et al. 2002; Kudo et al. 2002) in which the collisions of macroscopic spheres were studied. These spheres were coated by an organic mantle consisting of an analog of molecular-cloud organic matter, of which glycolic acid is thought to be a representative constituent. The increased bouncing was rationalized by the order-of-magnitude decrease in the elastic and viscous properties of the organic mantle that begins when temperatures surpass around 200 K (Homma et al. 2019). This macroscopic thermal softening is in agreement with the higher propensity of attractive bonding in the warm NPs.
In future investigations, the effect of an organic mantle on the collision behavior of silica NPs will be studied. Such composite grains have been proposed (Li & Greenberg 1997) as an explanation for observed interstellar spectral features and may have mantle thicknesses of 0.1 μm. It has been found experimentally (Kouchi et al. 2002; Kudo et al. 2002) that, in a certain temperature window (250−400 K), organic mantles may act as a “glue”, increasing the sticking probability of colliding silica NPs, whereas at low temperatures they are too stiff and may evaporate or undergo pyrolysis at higher temperatures. Recent extensions of the ReaxFF potential (Kulkarni et al. 2013) allow us to realistically model the interaction of silica with organic molecules; they will hence facilitate such simulation studies and may supplement recent considerations based on (macroscopic) granular mechanics (Homma et al. 2019).
Acknowledgments
We acknowledge financial support by the Deutsche Forschungsgemeinschaft within project Ur 32/27-2. Simulations were performed at the High Performance Cluster Elwetritsch (RHRK, TU Kaiserslautern, Germany).
References
- Anders, C., & Urbassek, H. M. 2013, Nucl. Instrum. Meth. B, 303, 200 [Google Scholar]
- Blum, J. 2010, Res. Astron. Astrophys., 10, 1199 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J. 2018, Space Sci. Rev., 214, 52 [Google Scholar]
- Briggs, R., Ertem, G., Ferris, J. P., et al. 1992, Orig. Life Evol. Biosph., 22, 287 [Google Scholar]
- Dominik, C., & Tielens, A. G. G. M. 1997, ApJ, 480, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg, J. M. 2002, Surf. Sci., 500, 793 [Google Scholar]
- Greenberg, J. M., & Li, A. 1999, Adv. Space Res., 24, 497 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Homma, K. A., Okuzumi, S., Nakamoto, T., & Ueda, Y. 2019, ApJ, 877, 128 [Google Scholar]
- Kouchi, A., Kudo, T., Nakano, H., et al. 2002, ApJ, 566, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Kudo, T., Kouchi, A., Arakawa, M., & Nakano, H. 2002, Meteorit. Planet. Sci., 37, 1975 [Google Scholar]
- Kulkarni, A. D., Truhlar, D. G., Goverapet Srinivasan, S., et al. 2013, J. Phys. Chem. C, 117, 258 [Google Scholar]
- Li, A., & Greenberg, J. M. 1997, A&A, 323, 566 [NASA ADS] [Google Scholar]
- Li, A., & Greenberg, J. M. 2003, in Solid State Astrochemistry, NATO Science Series II: Mathematics, Physics and Chemistry, eds. V. Pirronello, J. Krelowski, & G. Manicò (Dordrecht: Kluwer Academic Publishers), 120, 37 [Google Scholar]
- Martínez, L., Andrade, R., Birgin, E. G., & Martínez, J. M. 2009, J. Comput. Chem., 30, 2157 [Google Scholar]
- Mendoza-Gómez, C. X., & Greenberg, J. M. 1993, Orig. Life Evol. Biosph., 23, 23 [Google Scholar]
- Monti, S., Corozzi, A., Fristrup, P., et al. 2013, Phys. Chem. Chem. Phys., 15, 15062 [Google Scholar]
- Mücksch, C., Anders, C., Gnaser, H., & Urbassek, H. M. 2014, J. Phys. Chem. C, 118, 7962 [CrossRef] [Google Scholar]
- Nietiadi, M. L., Valencia, F., Gonzalez, R. I., Bringa, E. M., & Urbassek, H. M. 2020, A&A, 641, A159 [EDP Sciences] [Google Scholar]
- Piani, L., Tachibana, S., Hama, T., et al. 2017, ApJ, 837, 35 [Google Scholar]
- Plimpton, S. 1995, J. Comput. Phys., 117, 1 [Google Scholar]
- Stoddard, S. D. 1978, J. Comput. Phys., 27, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Ullmann, F., Gerhartz, W., Yamamoto, Y. S., et al. 1985, Ullmann’s Encyclopedia of Industrial Chemistry (Weinheim: VCH Publishers) [Google Scholar]
All Figures
 |
Fig. 1. Glycolic acid molecule. |
| In the text | |
 |
Fig. 2. Temporal evolution of the center-of-mass distance, Δz. Panel a: data for a bouncing collision and a sticking collision at 100 K with a velocity of 2.5 m s−1. The trajectories correspond to the snapshots shown in Figs. 3b and c. Panel b: data for sticking collisions at 250 K for various velocities. |
| In the text | |
 |
Fig. 3. Collision of two NPs at 100 K with a velocity of 2.5 m s−1. Panel a: initial and panel b: final configurations for a bouncing collision. Panel c: final configuration of a sticking collision. Panel d: sticking configuration for a velocity of 20 m s−1. |
| In the text | |
 |
Fig. 4. Number of hydrogen-bonded glycolic acid molecules formed in NP collisions at 100 and 250 K. Data for the un-collided NPs are included at v = 0. Error bars included for v = 2.5 m s−1 show the standard deviation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.