| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A179 | |
| Number of page(s) | 10 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202040088 | |
| Published online | 31 March 2021 | |
Rotational spectroscopy of isotopic cyclopropenone, c-H2C3O, and determination of its equilibrium structure★,★★
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln, Germany
e-mail: hspm@ph1.uni-koeln.de
2
Univ Rennes, Ecole Nationale Supérieure de Chimie de Rennes, CNRS, ISCR−UMR 6226,
35000
Rennes, France
Received:
8
December
2020
Accepted:
21
January
2021
Context. Cyclopropenone was first detected in the cold and less dense envelope of the giant molecular cloud Sagittarius B2(N). It was found later in several cold dark clouds and it may be possible to detect its minor isotopic species in these environments. In addition, the main species may well be identified in warmer environments.
Aims. We aim to extend existing line lists of isotopologs of c-H2C3O from the microwave to the millimeter region and create one for the singly deuterated isotopolog to facilitate their detections in space. Furthermore, we aim to extend the line list of the main isotopic species to the submillimeter region and to evaluate an equilibrium structure of the molecule.
Methods. We employed a cyclopropenone sample in natural isotopic composition to investigate the rotational spectra of the main and 18O-containing isotopologs as well as the two isotopomers containing one 13C atom. Spectral recordings of the singly and doubly deuterated isotopic species were obtained using a cyclopropenone sample highly enriched in deuterium. We recorded rotational transitions in the 70−126 and 160−245 GHz regions for all isotopologs and also in the 342−505 GHz range for the main species. Quantum-chemical calculations were carried out to evaluate initial spectroscopic parameters and the differences between ground-state and equilibrium rotational parameters in order to derive semi-empirical equilibrium structural parameters.
Results. We determined new or improved spectroscopic parameters for six isotopologs and structural parameters according to different structure models.
Conclusions. The spectroscopic parameters are accurate enough to identify minor isotopic species at centimeter and millimeter wavelengths while those of the main species are deemed to be reliable up to 1 THz. Our structural parameters differ from earlier ones. The deviations are attributed to misassignments in the earlier spectrum of one isotopic species.
Key words: molecular data / methods: laboratory: molecular / techniques: spectroscopic / radio lines: ISM / ISM: molecules / astrochemistry
The data are only available at CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/647/A179
Transition frequencies from this work as well as related data from earlier work are given for each isotopic species as supplementary material. We also provide quantum numbers, uncertainties, and residuals between measured frequencies and those calculated from the final sets of spectroscopic parameters.
© ESO 2021
1 Introduction
Cyclopropenone is one of the smallest aromatic molecules (Wang et al. 2011), after cyclopropenylidene (c-C3H2), and the first cyclic molecule with a ketone functional group that has been detected in space. It was first found in the cold and less dense envelope of the giant star-forming region Sagittarius B2(N) (Hollis et al. 2006). More recently, c-H2C3O was detected in four dark clouds or prestellar cores, TMC-1, B1-b, L483, and Lupus-1A (Loison et al. 2016), and in the low-mass star-forming region L1527 (Araki et al. 2017).
Benson et al. (1973) presented the first account on the rotational spectrum of cyclopropenone. These latter authors reported between 6 and 14 rotational transitions for five isotopic species recorded between 9 and 40 GHz. The main isotopolog and the two isotopomers containing one 13C atom were studied in a sample in natural isotopic composition. Benson et al. (1973), employed isotopic enriched samples to investigate isotopologs containing 18O or two D. Additionally, they derived structural parameters of c-H2C3O and determined its dipole moment and rotational g values through Stark and Zeeman measurements, respectively. Later, Guillemin et al. (1990) extended the data set of the main isotopic species to 247 GHz. These data are sufficient to identify c-H2C3O in cold astronomical sources up to the lower submillimeter region, possibly up to ~500 GHz, but are not enough for searches in warmer astronomical environments. Although cyclopropenone has so far only been identified in colder sources, it may well be detected in the warmer and denser parts of star-forming regions in the future. Propanal (Lykke et al. 2017), propene, and propenal (Manigand et al. 2021) are recent examples of molecules initially found only in cold astronomical sources later found in the hot corino, the warmer and denser parts of a low-mass star-forming region – of IRAS 16293−2422 B in these latter cases. The isotopic data may be suitable for astronomical searches in cold environments in the microwave and possibly lower millimeter regions if good estimates of the lowest order centrifugal distortion parameters are available, but are certainly too limited for searches throughout the entire millimeter region. Moreover, no data are available for c-HDC3O, which is the most promising isotopolog to be found in cold dark molecular clouds. Therefore, we investigated the rotational spectra of five isotopologs of cyclopropenone in the millimeter region to facilitate their detection in space and extended measurements of the main isotopic species to the lower submillimeter region to enable more secure searches in warmer astronomical sources.
2 Experimental details
2.1 Sample preparation
The synthesis of normal cyclopropenone was the same as in Guillemin et al. (1990) and followed the procedure described by Breslow et al. (1977). The synthesis of the cyclopropenone sample highly enriched in deuterium followed largely Breslow & Oda (1972) with n-Bu3SnH replaced by n-Bu3SnD. Please note that cyclopropenone decomposes at room temperature. It is very stable in a sealed container at temperatures below ~240 K. We kept the sample in dry ice or liquid nitrogen for our experiments.
2.2 Spectroscopic measurements
The investigation of the rotational spectra of cyclopropenone isotopologs was carried out with two different spectrometers. We employed two 7 m coupled glass cells, each with an inner diameter of 10 cm, in a double path arrangement for measurements in the 70−126 GHz region, yielding an optical path length of 28 m. We used a 5 m double path cell with a 10 cm inner diameter for the 160−245 GHz and the 342−505 GHz ranges. Both spectrometers use Virginia Diode, Inc. (VDI), frequency multipliers driven by Rohde & Schwarz SMF 100A synthesizers as sources, and Schottky diode detectors. Frequency modulation was employed to reduce baseline effects with demodulation at twice the modulation frequency. This causes absorption lines to appear approximately as second derivatives of a Gaussian. Additional information on the spectrometers is available in Ordu et al. (2012) and Martin-Drumel et al. (2015), respectively.
We recorded individual transition frequencies in all three frequency windows covering 10 MHz for well-predicted lines up to 100 MHz in the search for first lines of the singly deuterated isotopolog. The pressure was around 1.0 Pa in the 3 mm region as test measurements showed that the peak intensity was best between ~0.75 and ~1.5 Pa. The pressure was between 1.0 and 2.0 Pa at shorter wavelengths. We refilled the cells after roughly one hour because the molecule is only moderately stable at room temperature; its half-life was close to one hour in our cells. Uncertainties were evaluated mostly based on the symmetry of the line shape and were as small as 5 kHz for isolated and very symmetric lines. Such small uncertainties were achieved earlier, for example, in the case of 2-cyanobutane with a much richer rotational spectrum (Müller et al. 2017). Uncertainties for good lines were 10−20 kHz, and larger uncertainties up to ~100 kHz were used for example for weaker lines and lines close to other lines.
Initial measurements using the highly deuterated cyclopropenone sample yielded no clear signs of rotational transitions of c-D2 C3O, but instead strong signals of c-H2 C3O. We suspected rapid D-to-H exchange on the cell walls, even though this may appear unusual for a molecule with substantial aromatic character. On the other hand, at least some unsaturated molecules are known to exchange D and H quite readily; for example, the reaction between HC3 N and D2 O was used to generate DC3 N (Spahn et al. 2008). We conditioned the cell walls with ~200 Pa D2 O for two hours and observed strong signals of c-D2 C3O and very weak ones of c-H2 C3O afterwards. The signals of c-HDC3O, identified later, were in between, roughly a factor of four weaker than those of c-D2 C3O.
3 Quantum-chemical calculations
We carried out quantum-chemical calculations at the Regionales Rechenzentrum der Universität zu Köln (RRZK) using the commercially available program Gaussian 09 (Frisch et al. 2013). We performed B3LYP hybrid density functional (Becke 1993; Lee et al. 1988), Møller-Plesset second- (MP2) and third-order perturbation theory (MP3) calculations (Møller & Plesset 1934), along with coupled cluster calculations with single and double excitations augmented by a perturbative correction for triple excitations, CCSD(T) (Raghavachari et al. 1989). We employed correlation consistent basis sets which were augmented with diffuse basis functions aug-cc-pVXZ (X = T, Q, 5; Dunning 1989), which we abbreviate here to 3a, 4a, and 5a, respectively. These basis sets were further augmented with core-correlating basis functions in some cases, yielding the aug-cc-pwCVXZ basis sets (Peterson & Dunning 2002), which we denote 3aC, 4aC, and 5aC, respectively.
Equilibrium geometries were determined by analytic gradient techniques, harmonic force fields by analytic second derivatives, and anharmonic force fields by numerical differentiation of the analytically evaluated second derivatives of the energy. The main goals of these anharmonic force field calculations were to evaluate initial spectroscopic parameters for the minor isotopic species of cyclopropenone and first-order vibration-rotation parameters (Mills 1972); see also Sect. 6. Core electrons were kept frozen in MP2, MP3, and CCSD(T) calculations unless “ae” indicates that all electrons were correlated.
4 Spectroscopic properties of cyclopropenone
Cyclopropenone is a planar asymmetric rotor with κ = (2B − A − C)∕(A − C) = −0.8801, which is somewhat close to the prolate symmetric limit of −1. Its dipole moment of 4.39 D (Benson et al. 1973) is along the a-inertial axis which is aligned with the CO bond; see Fig. 1. The strongest transitions are R-branch transitions (ΔJ = +1) with ΔKa = 0 and ΔKc = +1. The Boltzmann peak at 300 K is near 480 GHz. Q-branch transitions with ΔKa = 0 and ΔKc = −1 and transitions with ΔKa = ±2 are much weaker, but can be observed quite readily under favorable circumstances.
Carbon has two stable isotopes with mass numbers 12 and 13 and with terrestrial abundances of 98.89 and 1.11%, respectively (Berglund & Wieser 2011). The respective abundances are 99.76, 0.04, and 0.20% for 16 O, 17 O, and 18O, and 99.98 and ~0.015% for H and D.
The main isotopolog and those with 18O or 13C in the keto group (C1) have C2v symmetry. Spin-statistics caused by the two equivalent H lead to ortho and para states with a 3:1 intensity ratio; see Fig. 2. The ortho states are described by Ka being odd. The doubly deuterated isotopolog also has C2v symmetry, but the ortho to para ratio is 2:1, and the ortho states are described by Ka being even. The effect of substituting 13C at C2 or C3 is the same because the two carbon atoms are structurally equivalent. The corresponding species is therefore referred to as the 13C2 isotopolog. We note that we do not consider isotopologs with more than one 13C. The abundance of the 13C2 isotopolog is ~2.2% in a sample of natural isotopic composition. Its symmetry is CS, as is that of the HD isotopolog. No nontrivial spin statistics exist in these two isotopologs. The HD isotopolog has a very small b-dipole moment component of ~0.21 D as derived from the structure and from quantum-chemical calculations; the corresponding value for the 13C2 isotopolog is ~0.06 D.
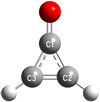 |
Fig. 1 Model of the cyclopropenone molecule. Carbon atoms are symbolized by gray spheres which are numbered. Hydrogen atoms are indicated by small, light gray spheres and the oxygen atom by a red sphere. |
 |
Fig. 2 Section of the submillimeter spectrum of c-H2C3O. The Kc = J−1 transitions are approaching oblate pairing, that is, the two lines coalesce at somewhat higher J. Also demonstrated is the 1:3 para to ortho ratio for transitions with Ka being even and odd, respectively; see Sect. 4 for further details. |
5 Spectroscopic results
Pickett’s programs SPCAT and SPFIT (Pickett 1991) were used to calculate and fit the rotational spectra of the cyclopropenone isotopologs. The results of Guillemin et al. (1990) were used for the main species. Too few transition frequencies have been published for the minor isotopic species to reliably determine quartic centrifugal distortion parameters. We evaluated ground-state rotational and equilibrium quartic centrifugal distortion parameters for six isotopic species of cyclopropenone at the B3LYP/3a quantum-chemical level; vibrational corrections to centrifugal distortion parameters are, to our knowledge, not available in publicly available quantum-chemical programs. We approximated the experimental value 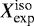 of isotopic spectroscopic parameters by scaling the calculated value
of isotopic spectroscopic parameters by scaling the calculated value 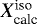 with the ratio of the experimental and calculated value
with the ratio of the experimental and calculated value 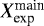 /
/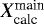 of the main isotopolog. These values were used as starting parameters to reproduce the limited sets of transition frequencies of the minor isotopic species. One important aspect in this procedure, and in all of our fitting, was to determine or to float as few parameters as possible to improve the weighted rms (wrms) of the fit as a useful measure of the quality of the fit. This implies that we searched in each fitting round for the spectroscopic parameter that led to the greatest reduction of the wrms, and that was useful in the context of parameters already determined or floated in the fit. It was sufficient to float B and C in the cases of the 13C1, 13C2, and 18O isotopologs of cyclopropenone. One transition of the 18O species, 41,3−41,4, and two transitions of the 13C2 species, 102,8−102,9 and 153,12−153,13, had large residuals between the reported experimental frequency and the calculated one that we decreased the weights of these transitions initially; eventually, these were omitted from the final fits. The reported frequencies were larger than in our final calculations by 0.46 MHz for the line attributed to the 18O species and by 43.51 and 92.56 MHz, respectively, for the two lines assigned to the 13C2 isotopolog. We also had to float A in order to satisfactorily reproduce the transition frequencies of the doubly deuterated isotopolog. The adjusted rotational parameters of c-D2C3O differed somewhat more from the initial parameters than the adjusted B and C values of the other minor isotopic species. We assumed the deviations in the case of c-HDC3O would be roughly half as large as those of c-D2C3O. We corrected the c-HDC3O accordingly to improve the calculations of this isotopolog for the first searches of rotational transitions.
of the main isotopolog. These values were used as starting parameters to reproduce the limited sets of transition frequencies of the minor isotopic species. One important aspect in this procedure, and in all of our fitting, was to determine or to float as few parameters as possible to improve the weighted rms (wrms) of the fit as a useful measure of the quality of the fit. This implies that we searched in each fitting round for the spectroscopic parameter that led to the greatest reduction of the wrms, and that was useful in the context of parameters already determined or floated in the fit. It was sufficient to float B and C in the cases of the 13C1, 13C2, and 18O isotopologs of cyclopropenone. One transition of the 18O species, 41,3−41,4, and two transitions of the 13C2 species, 102,8−102,9 and 153,12−153,13, had large residuals between the reported experimental frequency and the calculated one that we decreased the weights of these transitions initially; eventually, these were omitted from the final fits. The reported frequencies were larger than in our final calculations by 0.46 MHz for the line attributed to the 18O species and by 43.51 and 92.56 MHz, respectively, for the two lines assigned to the 13C2 isotopolog. We also had to float A in order to satisfactorily reproduce the transition frequencies of the doubly deuterated isotopolog. The adjusted rotational parameters of c-D2C3O differed somewhat more from the initial parameters than the adjusted B and C values of the other minor isotopic species. We assumed the deviations in the case of c-HDC3O would be roughly half as large as those of c-D2C3O. We corrected the c-HDC3O accordingly to improve the calculations of this isotopolog for the first searches of rotational transitions.
5.1 The main isotopic species
Our investigations started with measurements of the main isotopic species in the 342−505 GHz region. We targeted the strongest R-branch transitions with Ka ≤ 5 in a first step, extending to Ka = 29 in subsequent steps. Transitions with Ka ≤ 14 were found within 0.3 MHz of the initial calculations. The deviations increased rapidly with Ka and exceeded 10 MHz for the highest Ka transitions. We then searched for Q-branch transitions with ΔKa = 0 and for various types of ΔKa = 2 transitions, most of them had also ΔJ = 0. Later, very limited measurements were carried out in the 160−245 GHz region and then again more extensive ones in the 70−126 GHz region. The ΔKa = ΔJ = 0 transitions reached Ka = 8, and the ΔKa = 2 transitions extended to Ka = 5 ↔ 7. Whereas the rotational spectrum of cyclopropenone is quite sparse on the level of the strongest lines, it is much richer on the level of the weakest transitions recorded, which means that the desired line has an increased chance of being blended with or being close to a usually unassigned line.
In the end, we recorded 398 different, novel transitions, which corresponds to 311 different frequencies because of 87 unresolved asymmetry doublets. The majority of these doublets are prolate paired transitions, which have the same J and Ka for each pair, as maybe expected for an asymmetric rotor somewhat close to the prolate symmetric limit; seven are oblate paired transitions with Kc = J in each case.In addition, we remeasured three transitions already reported by Guillemin et al. (1990). These data were combined with 14 transition frequencies from Benson et al. (1973) and 45 from Guillemin et al. (1990), which corresponded to 51 transitions. Uncertainties of 30 kHz were used for these lines as stated by Guillemin et al. (1990) for their data and commensurate for the data of Benson et al. (1973).
We subjected the transition frequencies initially to fits employing Watson’s A reduction, as done previously (Guillemin et al. 1990). We also tried Watson’s S reduction because cyclopropenone is quite close to the prolate symmetric limit, in which case the S reduction is usually preferable. As can be seen in Table 1, we required an almost complete parameter set up to sixth order in the A reduction; only ΦK was not used in the fit. Two fewer parameters were used in the S reduction, albeit with a slightly larger wrms of 0.972 compared to 0.921. Nevertheless, we decided to view the S reduced fit as the preferred one. Trial fits with ΦK or HK, HJ, and h1 from B3LYP/3a calculations added to the fit as fixed parameters did not improve the quality of the fits and resulted in changes of the remaining spectroscopic parameters roughly corresponding to their uncertainties. Moreover, we were uncertain as to the reliability of the quantum-chemically calculated sextic distortion parameters; see also Sect. 7.1. Therefore, these parameters were omitted from the final fits. The quantum-chemically calculated spectroscopic parameters are given in Table 1 for comparison, along with the parameters from Guillemin et al. (1990). We also provide rms values for the whole data set and for the individual sources for completeness. The rms is meaningful if only one uncertainty was used in all instances or if the uncertainties differ only by a factor of a few. In the present case, the uncertainties differ by around a factor of ten. In this and similar cases, the rms is dominated by the lines with large residuals.
Present and previous experimental spectroscopic parameters (MHz) of the main isotopolog of cyclopropenone and details of the fits in comparison to values calculated at the B3LYP/3a level.
5.2 The 13C1, 13C2, and 18O isotopologs
We began our investigations of the minor isotopologs of cyclopropenone containing one 13C or 18O in the 160−245 GHz region searching for the stronger R-branch transitions first with Ka ≤ 2 and then up to Ka = 5. Additional measurements were carried out in the 70−126 GHz region, in which we recorded R-branch transitions up to Ka = 7 and several ΔKa = ΔJ = 0 transitions for the two isotopomers with one 13C. The extent of measured lines was more limited for the 18O because of its lower abundance.
The final line lists of the 13C1, 13C2, and 18O isotopologs consist of 104, 95, and 48 different and new transition frequencies, respectively, in addition to the small number of previously reported lines (Benson et al. 1973) for which uncertainties of 70 kHz were assigned. The resulting sets of spectroscopic parameters, determined as described at the beginning of this section, had not only B and C floated for 13C1 and 13C2, but also A and two respectively three quartic distortion parameters. It was sufficient to float only B and C in the case of the 18O isotopolog. The parameter values, their uncertainties, and additional details of the fits are presented in Table 2 as minimum parameter sets which are the preferred parameter sets. We also tested the number of parameters that can be determined with sufficient significance. These were all quartic centrifugal distortion parameters for the isotopomers with one 13C and all but ΔDK for the 18O isotopolog. The resulting values are given as maximum parameter sets in the same table along with the initial parameters whose derivation was also described at the beginning of this section.
Spectroscopic parameters (MHz) from a minimum parameter set, a maximum parameter set, and initial parameters along with details of the fits of the 13C1, 13C2, and 18O isotopologs of cyclopropenone.
 |
Fig. 3 Section of the millimeter spectrum of cyclopropenone highly enriched in deuterium. Transitions with small but rapidly increasing asymmetry splitting are shown for Ka = 6 of c-HDC3O. We assignedthese transitions first because of their easily recognizable patterns. |
5.3 The singly and doubly deuterated isotopic species
Our procedure for studying the rotational spectrum of the D2 isotopolog was very similar to that for the minor isotopic species described in the previous section. The use of a sample highly enriched in deuterium made it possible to record considerably more transitions extending to higher quantum numbers. The spectral recordings were richer in lines than those of the sample in natural isotopic composition because of the presence of lines caused by the HD species and even some of the main species. In addition, we identified lines of traces of CH2Cl2 which was used as a solvent in the course of the preparation of the deuterated sample and was difficult to remove completely.
The R-branch transitions with ΔKa = 0 were recorded up to Ka = 9, transitions with ΔKa = ΔJ = 0 up to 2, and those with ΔKa = 2 up to Ka = 5 ← 3.
We employed a different strategy to search for transitions of the HD isotopolog because no previous data exist. A pattern of two or more transitions is obviously more decisive than a single line. The best candidates are nearly prolate or nearly oblate paired R-branch transitions because the small asymmetry splitting changes rapidly with J. The asymmetry splitting of the Kc = J nearly oblate paired transitions was deemed to be too large in the 160−245 GHz region. As can be seen in Fig. 3, the Ka = 6 nearly prolate paired transitions were suited very well, even though they were considerably weaker. The measured asymmetry splittings of about 1.8, 4.4, and 9.5 MHz for J″ = 12 to 14 compared very well with the calculated splittings. We searched for R-branch transitions with equal or lower Ka with an improved calculation of the rotational spectrum. Subsequently, we sought Q-branch transitions with ΔKa = 0 and 2, respectively. Our line list reached Ka = 3 in the first case and Ka = 3 ← 1 in the second case of these weaker transitions.
We did not target any b-type transitions of c-HDC3O as these were calculated to be even weaker than many of the ΔKa = 2 transitions. Some b-type transitions were covered by accident; even much longer integration times may not have helped because the number of lines with similar or larger intensities was so large that it would be difficult to identify unblended lines unambiguously. In addition, it is important to note that ΔKa = 1 transitions carry less information on the purely K-dependent parameters than transitions with ΔKa = 2 at similar values of Ka.
The minimum parameter sets for both deuterated isotopologs were determined as described above. Interestingly, we obtained a satisfactory fit for 172 different frequencies of c-D2C3O after floating only two of the five quartic centrifugal distortion parameters, whereas we required four for 126 different frequencies of c-HDC3O; this is probably a consequence of the choice of the covered transitions. In the fit of c-D2C3O with the full parameter set, ΔDJ and ΔDJK improved the wrms by similar amounts. The parameter values, their uncertainties, and additional details on the fits are presented in Table 3.
6 Structural parameters of cyclopropenone
Several methods exist to derive structural parameters of a molecule from its moments of inertia, which are inversely proportional to the rotational parameters. The results depend on the model to a varying degree, and some methods do not even yield the same result for different data sets in theory. Data for different isotopologs are required for molecules with three or more symmetry-inequivalent atoms; it is usually desirable to substitute each symmetry-inequivalent atom once to be able to obtain reliable structural parameters.
The ground-state effective (or r0) structure is the most straightforward model in which the structural parameters are fit to the ground-state moments of inertia. The ground-state values are usually the ones determined first, and are often the only ones. The ground-state moments of inertia contain vibrational contributions from the zero-point vibrations, causing the r0 structure to be one of the less meaningful structure models, with sometimes relatively large changes between isotopic data sets.
The differences in the moments of inertia caused by the substitution of one or more symmetry-inequivalent atoms can be used to determine the Cartesian coordinates of these atoms (Kraitchman 1953; Costain 1958). The resulting substitution (or rs) structure reduces the effects of vibrational contributions to the ground-state moments of inertia, albeit to a varying degree. The rs structure is equivalent to rΔI, the structure that is obtained by fitting structural parameters to the differences of the moments of inertia (Rudolph 1991). This structure is, in turn, equivalent to the rI,ϵ structure, in which vibrational contributions ϵi to the ground-state moments of inertia, that is Iii,0 = Iii,e + ϵi, with i = a, b, c, are assumed to be equal for different isotopologs of a given molecule. The advantage of taking ϵi into account explicitly is that rotational parameters of isotopic species to be studied can be estimated much more accurately, in particular for atoms with more than two isotopes or for multiply substituted isotopologs (Epple & Rudolph 1992; Müller & Gerry 1994; Müller et al. 2019), if residuals of known isotopologs can be transferred to the values of the desired isotopolog. In the case of H2 CS, Müller et al. (2019) extrapolated the residuals of H2 C32S, H2 C33S, and H2 C34S to H2 C36S, and those of H2 C32S, H2 C34S, and H CS to H
CS to H C34S.
C34S.
The equilibrium (or re) structure of a molecule in the potential minimum is the most meaningful structure. However, it is also the most elusive structure because data of more than one isotopolog are needed for molecules with three or more symmetry-inequivalent atoms, and for each isotopolog we require the knowledge of several vibration-rotation parameters according to
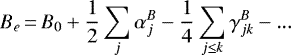 (1)
(1)
in order to evaluate the equilibrium parameter Be from the ground-state value B0. Here, the 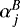 are first-order vibrational corrections, the
are first-order vibrational corrections, the 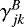 are second-order vibrational corrections, and so on. Equivalent formulations hold for Ae and Ce. An attractive and lately very common approach is to calculate
are second-order vibrational corrections, and so on. Equivalent formulations hold for Ae and Ce. An attractive and lately very common approach is to calculate 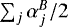 by quantum-chemical means to derive semi-empirical equilibrium rotational parameters Bi,e from the experimental ground-state values (Stanton et al. 1998). Second and higher order vibrational contributions are neglected. Numerous quantum-chemical programs are available to carry out such calculations; examples are mentioned in Sect. 3.
by quantum-chemical means to derive semi-empirical equilibrium rotational parameters Bi,e from the experimental ground-state values (Stanton et al. 1998). Second and higher order vibrational contributions are neglected. Numerous quantum-chemical programs are available to carry out such calculations; examples are mentioned in Sect. 3.
We used B3LYP, MP2, and ae-MP2 calculations with a triple zeta basis set to evaluate the first-order vibrational corrections for isotopologs of cyclopropenone which are summarized in Table 4 together with ground-state values and the resulting semi-empirical equilibrium values. The inertia defect Δ = Icc − Ibb − Iaa is also given for each set of rotational parameters.
We employed the RU111J program (Rudolph 1995) to derive semi-empirical equilibrium structural parameters 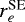 for each of the three quantum-chemical calculations. The results are given in Table 5 together with structural parameters purely from quantum-chemical calculations and with the rs parameters from Benson et al. (1973). The differences between the rs parameters and our
for each of the three quantum-chemical calculations. The results are given in Table 5 together with structural parameters purely from quantum-chemical calculations and with the rs parameters from Benson et al. (1973). The differences between the rs parameters and our 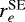 parameters turned out to be larger than expected and are discussed in detail in Sect. 7.2. We calculated subsequently rI,ϵ structures, which are equivalent to rs structures as mentioned above, in order to evaluate the dependence of the resulting parameters on diverse input data. The first set of input data were our present rotational data from six isotopic species as summarized in Table 4. The second set employed our starting values as described in Sect. 5. The third set were the rotational parameters from Benson et al. (1973), but without A(13C2), as it deviated by 61 MHz from the value of our preferred fit. The results of these structure fits are also given (in reverse order) in Table 5.
parameters turned out to be larger than expected and are discussed in detail in Sect. 7.2. We calculated subsequently rI,ϵ structures, which are equivalent to rs structures as mentioned above, in order to evaluate the dependence of the resulting parameters on diverse input data. The first set of input data were our present rotational data from six isotopic species as summarized in Table 4. The second set employed our starting values as described in Sect. 5. The third set were the rotational parameters from Benson et al. (1973), but without A(13C2), as it deviated by 61 MHz from the value of our preferred fit. The results of these structure fits are also given (in reverse order) in Table 5.
Spectroscopic parameters (MHz) from a minimum parameter set, a full parameter set, and initial parameters along with details on the fits of the mono and doubly deuterated isotopologs of cyclopropenone.
Ground-state rotational parameters Bi,0 of cyclopropenone isotopic species, vibrational corrections ΔBi,v (a), resulting semi-empirical equilibrium rotational parameters 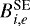 , and inertia defects Δ.(b)
, and inertia defects Δ.(b)
7 Discussion
7.1 Spectroscopic parameters
As can be seen in Table 1, the J and Ka quantum number ranges and also the number of different transition frequencies of the main isotopolog of cyclopropenone have been greatly increased in the course of the present investigation with respect to the previous study (Guillemin et al. 1990). The previous spectroscopic parameters agree well with ours in the A reduction taking into account the uncertainties in that work. The B3LYP/3a quantum-chemically calculated ground-state rotational and equilibrium quartic centrifugal distortion parameters agree quite well with our experimental values in both reductions. The comparison of the sextic centrifugal distortion parameters is more mixed as far as experimental values are available; trial fits showed that the experimental values are only slightly affected by the absence of three and one sextic parameter in the S and A reduction, respectively. This shows that the deviations seen in particular in HKJ and the corresponding ΦKJ are not mainly caused by the omission of the three or one parameter. Moreover, a trial fit with h1 in the fit yielded a value of 19 ± 10 μHz, not compatible with the calculated 96 μHz.
Our final fit in the S reduction has two parameters less than the one in the A reduction at the expense of a slightly larger wrms. We consider this improvement to be sufficient to favor the S reduction. Additional reasons for preferring the S reduction are that it is more versatile than the A reduction as the latter can exhibit convergence problems for molecules close to the prolate or oblate symmetric limit. Moreover, Watson (1977) recommended to use the S reduction because such fits yield smaller correlation coefficients. This conclusion was recently reemphasized in an extensive study of the rotational spectra of SO18O and S18O2 in their lowest two and three vibrational states, respectively, with detailed analyses of the fits (Margulès et al. 2020).
Our spectroscopic parameters for the 13C1, 13C2, and 18O isotopologs in Table 2 agree very well with our initial values both for the minimum and maximum parameter sets. The agreement is good in the cases of the deuterated isotopologs, as can be seen in Table 3. The parameter DK from the full parameter sets of both deuterated isotopologs agrees very well with the initial values, which may indicate that the small changes in DK seen for the isotopomers containing one 13C may nevertheless be too large.
The initial spectroscopic parameters of all minor isotopic species were derived from quantum-chemically calculated ones scaled with the respective ratios between experimental and calculated values of the main species as described in slightly more detail at the beginning of Sect. 5. Such scaling was used, for example, to evaluate some sextic centrifugal distortion parameters of two minor isotopologs of TiO2 (Kania et al. 2011). Cazzoli et al. (2014) demonstrated in a study of the rotational spectrum of H S that such scaling works very well even for heavy-atom substitutions of relatively light molecules such as H2 S. Higher level quantum-chemical calculations, as employed by Cazzoli et al. (2014), may lead to better starting values than the lower level calculations used here. However, higher level calculations are computationally more demanding, in particular for somewhat larger molecules. Moreover, Morgan et al. (2018) showed that considerable computational effort is necessary to obtain good-quality, systematically converged results even for the fairly small molecule formaldehyde, H2 CO. The quality of the scaling of centrifugal distortion parameters may be limited in addition by the lack of vibrational corrections. Quartic and sextic equilibrium centrifugal distortion parameters can be calculated with several quantum-chemical programs, but the derivation of vibrational corrections is, to the best of our knowledge, not possible with any publicly available program.
S that such scaling works very well even for heavy-atom substitutions of relatively light molecules such as H2 S. Higher level quantum-chemical calculations, as employed by Cazzoli et al. (2014), may lead to better starting values than the lower level calculations used here. However, higher level calculations are computationally more demanding, in particular for somewhat larger molecules. Moreover, Morgan et al. (2018) showed that considerable computational effort is necessary to obtain good-quality, systematically converged results even for the fairly small molecule formaldehyde, H2 CO. The quality of the scaling of centrifugal distortion parameters may be limited in addition by the lack of vibrational corrections. Quartic and sextic equilibrium centrifugal distortion parameters can be calculated with several quantum-chemical programs, but the derivation of vibrational corrections is, to the best of our knowledge, not possible with any publicly available program.
Scaling of quantum-chemically derived distortion parameters should be better than scaling by appropriate powers of the ratios of 2A − B − C, B + C, and B − C, as done, for example, in the recent case of isotopic H2CS (Müller et al. 2019). This type of scaling usually works quite well for heavy-atom substitutions, but less so for H to D substitutions, in particular for molecules with few atoms. Fixing parameters of minor isotopologs, which cannot be determined sufficiently well, to values from the main isotopic species usually works less well, but is in most cases better than fixing such parameters to zero.
We mayask ourselves what the advantages and disadvantages of our minimum parameter fits are compared to our maximum parameter fits. Increasing the parameter set beyond the optimum increases the uncertainties, usually the correlation among the parameters, and frequently affects the parameter values outside the initial uncertainties. Therefore, transition frequencies calculated with fewer parameters are often better in cases of interpolation or modest extrapolation compared to values from a larger parameter set. On the other hand, calculated uncertainties quickly become too optimistic upon extrapolation for a smaller parameter set. Extrapolation in J from our present data should be reasonable to two times the upper frequency limit for the strong R-branch transition which is ~1.0 THz for the main isotopolog and 450 to 500 GHz for the minor isotopologs. Extrapolation in Ka is much more limited.
The ground-state inertia defects in Table 4 are relatively small and positive, as is common for planar molecules with small out-of-plane vibrational amplitudes. The semi-empirical equilibrium inertia defects obtained from the ground-state rotational constants after subtracting the first-order vibrational corrections are much smaller in magnitude and negative, which is also very common.
Quantum-chemical and experimental bond lengths (pm) and bond angles (deg) of cyclopropenone.
Equilibrium bond lengths (pm) and selected bond angles (deg) of cyclopropenone in comparison to related molecules.
7.2 Structural parameters
Our semi-empirical equilibrium structural parameters in Table 5 are largely very similar among the three different sets. The CO bond length has fairly large uncertainties, but displays almost no scatter; the C = C bond shows, in contrast, more pronounced,though still modest variations, which are only a few times the combined uncertainties for the parameters employing B3LYP and ae-MP2 corrections. The CH bond varies to an approximately equal degree, albeit with larger uncertainties than the C = C bond.
The previously published rs structure (Benson et al. 1973) agrees, at best, reasonably well with our 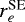 structures; the C = C bond length difference is, with more than 4 pm, particularly large. We calculated rI,ϵ structures that are equivalent to the rs structure (Rudolph 1991). Using our ground-state rotational data of six isotopologs, as summarized in Table 4, we obtained structural parameters close to our
structures; the C = C bond length difference is, with more than 4 pm, particularly large. We calculated rI,ϵ structures that are equivalent to the rs structure (Rudolph 1991). Using our ground-state rotational data of six isotopologs, as summarized in Table 4, we obtained structural parameters close to our 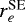 values; the largest difference of 0.4 pm occurs in the CO bond length and is even within the combined uncertainties. The initial parameters of five isotopic species, as derived in Sect. 5, yielded essentially the same parameters, the main differences are larger uncertainties in some parameters, most likely caused by the absence of data of the HD isotopolog; even the fit with values from Benson et al. (1973) yields results quite similar to the other two rI,ϵ fits. The deviation of the rs structure parameters therefore appears to be caused by the difference of 61 MHz in A(13C2) which is mainly caused by two lines falsely attributed to the 13C2 isotopolog; see also Sect. 5.
values; the largest difference of 0.4 pm occurs in the CO bond length and is even within the combined uncertainties. The initial parameters of five isotopic species, as derived in Sect. 5, yielded essentially the same parameters, the main differences are larger uncertainties in some parameters, most likely caused by the absence of data of the HD isotopolog; even the fit with values from Benson et al. (1973) yields results quite similar to the other two rI,ϵ fits. The deviation of the rs structure parameters therefore appears to be caused by the difference of 61 MHz in A(13C2) which is mainly caused by two lines falsely attributed to the 13C2 isotopolog; see also Sect. 5.
The quantum-chemical calculations in Table 5 show very small changes between basis sets and also rather small changes between the different methods. The bond lengths display the usual shortening upon increasing basis set size and upon correlation of all electrons as far as applicable. The bond lengths differ substantially among the different methods. The B3LYP parameters show little change with basis set size and agree quite well with our 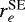 values. The largest deviation is seen for the C = C bond length, which is too short by about 0.5 pm. The C−C bond length is also too short, but by smaller amounts, whereas the CO and CH bonds were calculated slightly too long. The MP2/5a and ae-MP2/5aC structures agree between well and very well with our
values. The largest deviation is seen for the C = C bond length, which is too short by about 0.5 pm. The C−C bond length is also too short, but by smaller amounts, whereas the CO and CH bonds were calculated slightly too long. The MP2/5a and ae-MP2/5aC structures agree between well and very well with our 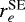 structure, the MP2/5a values are slightly closer for the C−C and CH bonds, whereas the ae-MP2/5aC are slightly closer for the other two bond lengths. Calculations using MP3 are sometimes better than those with MP2, but are usually worse than those with CCSD(T). In the case of cyclopropenone, some bond lengths are already too short at the MP3/3a level, and even more so at ae-MP3/3aC level. Bond lengths at the CCSD(T)/3a level are rather long. The effects of correlating all electrons compared to those with a frozen core are similar to those of MP2 calculations employing basis sets of triple zeta quality. If we assume the relative differences are the same for basis sets of quadruple zeta quality, we can estimate the following ae-CCSD(T)/4aC bond lengths: r(CO) ≈ 120.10 pm, r(C−C) ≈ 142.95 pm, r(C = C) ≈ 134.53 pm, and r(CH) ≈ 108.00 pm, all very close toour
structure, the MP2/5a values are slightly closer for the C−C and CH bonds, whereas the ae-MP2/5aC are slightly closer for the other two bond lengths. Calculations using MP3 are sometimes better than those with MP2, but are usually worse than those with CCSD(T). In the case of cyclopropenone, some bond lengths are already too short at the MP3/3a level, and even more so at ae-MP3/3aC level. Bond lengths at the CCSD(T)/3a level are rather long. The effects of correlating all electrons compared to those with a frozen core are similar to those of MP2 calculations employing basis sets of triple zeta quality. If we assume the relative differences are the same for basis sets of quadruple zeta quality, we can estimate the following ae-CCSD(T)/4aC bond lengths: r(CO) ≈ 120.10 pm, r(C−C) ≈ 142.95 pm, r(C = C) ≈ 134.53 pm, and r(CH) ≈ 108.00 pm, all very close toour 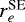 values; this behavior is common for ae-CCSD(T)/4aC calculations.
values; this behavior is common for ae-CCSD(T)/4aC calculations.
Structural parameters of cyclopropenone are compared with those of other molecules in Table 6. Cyclopropenylidene is best suited for comparison as it most closely resembles cyclopropenone, but without the O atom. The O atom withdraws electron density from the rest of the cyclopropenylidene molecule, causing an elongation of all bond lengths; the effect is smallest for the distant CH bond. Formaldehyde is probably the prototypical molecule with a CO double bond. Its CO bond is only slightly longer than that of c-H2C3O. The C = C bond lengths of c-H2C3O and c-C3H2 are essentially equal to the one in C2 H4, and are thus typical CC double bonds. The C−C bonds of both cyclic molecules are nevertheless much shorter than that of ethane, whose C−C bond can probably be viewed as a prototypical CC single bond. We note that these bonds are only slightly longer than the aromatic CC bonds in benzene. Finally, the CH bond lengths in c-H2C3O and c-C3H2 are substantially shorter than in C2 H4, but much longer than ~106.2 pm in acetylene (Liévin et al. 2011; Tamassia et al. 2016). These characteristics highlight the aromatic character of cyclopropenone (Wang et al. 2011) and cyclopropenylidene from a structural point of view.
8 Conclusion and outlook
Our data for five minor isotopic species of cyclopropenone are sufficient for astronomical searches in cold molecular clouds even without any extrapolation, as the Boltzmann peak at 10 K is at ~95 GHz. Extrapolation of the data in J should be reasonable up to 450 or 500 GHz. Such extrapolations should be possible up to 1 THz for the main isotopic species, which is sufficient even for rotational temperatures around 300 K. However, we assume that rotational temperatures of c-H2C3O in warmer sources will be closer to 100 K based on findings for propanal, propenal, and propene in IRAS 16293−2422 B (Lykke et al. 2017; Manigand et al. 2021).
Dedicated searches will probably be necessary to detect minor isotopologs of cyclopropenone in space. c-HDC3O is the most promising isotopolog to be found in cold molecular clouds. One of the most sensitive molecular line surveys of such sources is that by Cernicharo et al. (2020) between 31.4 and 50.3 GHz carried out with the Yebes 40 m radio telescope with additional data from the 3 mm region taken earlier with the IRAM 30 m dish. Cernicharo et al. (2020) report the detection of HC3O+ and investigated the chemistry of oxygen-containing molecules in TMC-1. They derived a column density of (4.0 ± 0.2) × 1011 cm−2 for c-H2C3O. The most constraining transition of c-HDC3O in that survey is the 313−212 transition at 37 833.721 MHz. The 3σ upper limit to its intensity in brightness temperature is ~2.6 mK (with corrections for beam dilution and beam efficiency); the corresponding intensity of the 313 −212 ortho transition of c-H2C3O is 42 mK, yielding a 3σ column density ratio of >16 for c-H2C3O to c-HDC3O (J. Cernicharo, priv. comm. to HSPM, Nov./Dec. 2020). This is less constraining than the corresponding ratios of, for example, ~34 and ~25 found for c-C3H2 to c-C3HD (Bell et al. 1986) and l-C3 H2 to l-C3HD (Spezzano et al. 2016), respectively, in TMC-1. However, there are sources with higher degrees of deuteration that may be considered if their column densities of c-H2C3O are sufficiently large. A search for the cyclopropenone isotopomers with one 13C may be more promising in the envelope of Sagittarius B2(N) because the 12 C to 13C ratio in the Galactic center is as low as 20 to 30 (Müller et al. 2008, 2016; Halfen et al. 2017; Jacob et al. 2020).
We determined structural parameters of cyclopropenone which compare very favorably with those of cyclopropenylidene as far as comparison is possible. The CO bond length agrees almost exactly with that of formaldehyde. Relatively large deviations between ourstructural parameters and the earlier substitution structure were traced to misassignments of two transitions to the 13C2 isotopolog which led to an overly large A rotational parameter.
Acknowledgements
We are grateful to José Cernicharo for communication of unpublished results of a search for c-HDC3O in TMC-1. We acknowledge support by the Deutsche Forschungsgemeinschaft via the collaborative research center SFB 956 (project ID 184018867) project B3 as well as the Gerätezentrum SCHL 341/15-1 (“Cologne Center for Terahertz Spectroscopy”). We thank the Regionales Rechenzentrum der Universität zu Köln (RRZK) for providing computing time on the DFG funded High Performance Computing System CHEOPS. J.-C.G. is grateful for financial support by the Centre National d’Etudes Spatiales (CNES; grant number 4500065585) and by the Programme National Physique et Chimie du Milieu Interstellaire (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES. Our research benefited from NASA’s Astrophysics Data System (ADS).
References
- Araki, M., Takano, S., Sakai, N., et al. 2017, ApJ, 847, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Becke, A. D. 1993, J. Chem. Phys., 98, 5648 [Google Scholar]
- Bell, M. B., Feldman, P. A., Matthews, H. E., & Avery, L. W. 1986, ApJ, 311, L89 [Google Scholar]
- Benson, R. C., Flygare, W. H., Oda, M., & Breslow, R. 1973, J. Am. Chem. Soc., 95, 2772 [Google Scholar]
- Berglund, M., & Wieser, M. E. 2011, Pure Chem., 83, 397 [Google Scholar]
- Breslow, R., & Oda, M. 1972, J. Am. Chem. Soc., 94, 4787 [Google Scholar]
- Breslow, R., Pecoraro, J., & Sugimoto, T. 1977, Org. Synth., 57, 41 [Google Scholar]
- Cazzoli, G., Puzzarini, C., & Gauss, J. 2014, A&A, 566, A52 [EDP Sciences] [Google Scholar]
- Cernicharo, J., Marcelino, N., Agúndez, M., et al. 2020, A&A, 642, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costain, C. C. 1958, J. Chem. Phys., 29, 864 [CrossRef] [Google Scholar]
- Dunning, Jr., T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Epple, K. J., & Rudolph, H. D. 1992, J. Mol. Spectr., 152, 355 [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2013, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT [Google Scholar]
- Gauss, J., & Stanton, J. F. 2000, J. Phys. Chem. A, 104, 2865 [Google Scholar]
- Guillemin, J. C., Wlodarczak, G., Lopez, J. C., & Demaison, J. 1990, J. Mol. Spectr., 140, 190 [Google Scholar]
- Halfen, D. T., Woolf, N. J., & Ziurys, L. M. 2017, ApJ, 845, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Harmony, M. D. 1990, J. Chem. Phys., 93, 7522 [Google Scholar]
- Harmony, M. D., & Taylor, W. H. 1986, J. Mol. Spectr., 118, 163 [Google Scholar]
- Hollis, J. M., Remijan, A. J., Jewell, P. R., & Lovas, F. J. 2006, ApJ, 642, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Jacob, A. M., Menten, K. M., Wiesemeyer, H., et al. 2020, A&A, 640, A125 [EDP Sciences] [Google Scholar]
- Kania, P., Hermanns, M., Brünken, S., Müller, H. S. P., & Giesen, T. F. 2011, J. Mol. Spectr., 268, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Kraitchman, J. 1953, Am. J. Phys., 21, 17 [Google Scholar]
- Lee, C., Yang, W., & Parr, R. G. 1988, Phys. Rev. B, 37, 785 [Google Scholar]
- Liévin, J., Demaison, J., Herman, M., Fayt, A., & Puzzarini, C. 2011, J. Chem. Phys., 134, 064119 [Google Scholar]
- Lohilahti, J. 2006, PhD thesis, University of Oulu, Oulu, Finland [Google Scholar]
- Loison, J.-C., Agúndez, M., Marcelino, N., et al. 2016, MNRAS, 456, 4101 [Google Scholar]
- Lykke, J. M., Coutens, A., Jørgensen, J. K., et al. 2017, A&A, 597, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manigand, S., Coutens, A., Loison, J. C., et al. 2021, A&A, 645, A53 [EDP Sciences] [Google Scholar]
- Margulès, L., Motiyenko, R. A., & Demaison, J. 2020, J. Quant. Spectr. Rad. Transf., 253, 107153 [Google Scholar]
- Martin, J. M. L., & Taylor, P. R. 1996, Chem. Phys. Lett., 248, 336 [Google Scholar]
- Martin-Drumel, M. A., van Wijngaarden, J., Zingsheim, O., et al. 2015, J. Mol. Spectr., 307, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Mills, I. M. 1972, Molecular Spectroscopy: Modern Research, eds. K. N. Rao, & C. W. Mathews (New York: Academic Press), 1, 115 [Google Scholar]
- Møller, C., & Plesset, M. S. 1934, Phys. Rev., 46, 618 [Google Scholar]
- Morgan, W. J., Matthews, D. A., Ringholm, M., et al. 2018, J. Chem. Theory Comput., 14, 1333 [CrossRef] [Google Scholar]
- Müller, H. S. P., & Gerry, M. C. L. 1994, J. Chem. Soc., Faraday Trans., 90, 2601 [Google Scholar]
- Müller, H. S. P., Belloche, A., Menten, K. M., Comito, C., & Schilke, P. 2008, J. Mol. Spectr., 251, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Belloche, A., Xu, L.-H., et al. 2016, A&A, 587, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Zingsheim, O., Wehres, N., et al. 2017, J. Phys. Chem. A, 121, 7121 [CrossRef] [Google Scholar]
- Müller, H. S. P., Maeda, A., Thorwirth, S., et al. 2019, A&A, 621, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ordu, M. H., Müller, H. S. P., Walters, A., et al. 2012, A&A, 541, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, K. A., & Dunning, Jr., T. H. 2002, J. Chem. Phys., 117, 10548 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M. 1991, J. Mol. Spectr., 148, 371 [Google Scholar]
- Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [Google Scholar]
- Rudolph, H. D. 1991, Struct. Chem., 2, 581 [Google Scholar]
- Rudolph, H. D. 1995, Advances in Molecular Structure Research, eds. I. Hargittai, & M. Hargittai (Greenwich, CT: JAI Press Inc.), 1, 63 [Google Scholar]
- Spahn, H., Müller, H. S. P., Giesen, T. F., et al. 2008, Chem. Phys., 346, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Spezzano, S., Tamassia, F., Thorwirth, S., et al. 2012, ApJS, 200, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Spezzano, S., Gupta, H., Brünken, S., et al. 2016, A&A, 586, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stanton, J. F., Lopreore, C. L., & Gauss, J. 1998, J. Chem. Phys., 108, 7190 [NASA ADS] [CrossRef] [Google Scholar]
- Tamassia, F., Cané, E., Fusina, L., & Di Lonardo, G. 2016, Phys. Chem. Chem. Phys., 18, 1937 [Google Scholar]
- Wang, H.-J., von Ragué Schleyer, P., Wu, J. I., & Wang, H.-J. 2011, Int. J. Quant. Chem., 111, 1031 [Google Scholar]
- Watson, J. K. G. 1977, Vibrational Spectra and Structure, ed. J. R. Durig (Amsterdam: Elsevier), 6, 1 [Google Scholar]
All Tables
Present and previous experimental spectroscopic parameters (MHz) of the main isotopolog of cyclopropenone and details of the fits in comparison to values calculated at the B3LYP/3a level.
Spectroscopic parameters (MHz) from a minimum parameter set, a maximum parameter set, and initial parameters along with details of the fits of the 13C1, 13C2, and 18O isotopologs of cyclopropenone.
Spectroscopic parameters (MHz) from a minimum parameter set, a full parameter set, and initial parameters along with details on the fits of the mono and doubly deuterated isotopologs of cyclopropenone.
Ground-state rotational parameters Bi,0 of cyclopropenone isotopic species, vibrational corrections ΔBi,v (a), resulting semi-empirical equilibrium rotational parameters 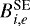 , and inertia defects Δ.(b)
, and inertia defects Δ.(b)
Quantum-chemical and experimental bond lengths (pm) and bond angles (deg) of cyclopropenone.
Equilibrium bond lengths (pm) and selected bond angles (deg) of cyclopropenone in comparison to related molecules.
All Figures
 |
Fig. 1 Model of the cyclopropenone molecule. Carbon atoms are symbolized by gray spheres which are numbered. Hydrogen atoms are indicated by small, light gray spheres and the oxygen atom by a red sphere. |
| In the text | |
 |
Fig. 2 Section of the submillimeter spectrum of c-H2C3O. The Kc = J−1 transitions are approaching oblate pairing, that is, the two lines coalesce at somewhat higher J. Also demonstrated is the 1:3 para to ortho ratio for transitions with Ka being even and odd, respectively; see Sect. 4 for further details. |
| In the text | |
 |
Fig. 3 Section of the millimeter spectrum of cyclopropenone highly enriched in deuterium. Transitions with small but rapidly increasing asymmetry splitting are shown for Ka = 6 of c-HDC3O. We assignedthese transitions first because of their easily recognizable patterns. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


