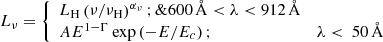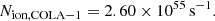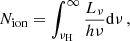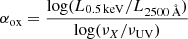| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | L10 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202040107 | |
| Published online | 12 February 2021 | |
Letter to the Editor
Distinguishing AGN from starbursts as the origin of double-peaked Lyman-alpha emitters in the reionization era
1
Département de Physique Théorique, Université de Genève, 24 quai Ernest-Ansermet, 1211 Genève 4, Switzerland
e-mail: hamsa.padmanabhan@unige.ch
2
Astronomy department, Harvard University, 60 Garden Street, Cambridge, MA 02138, USA
Received:
10
December
2020
Accepted:
22
January
2021
We discuss the possible origin of the double-peaked profiles recently observed in Lyman-alpha emitters (LAEs) at the epoch of reionization (z ≳ 6.5) from obscured active galactic nuclei (AGN). In combining the extent of the Lyman-α near-zones estimated from the blue peak velocity offset in these galaxies, with the ionizing emissivity of quasars at z ≳ 6, we forecast the intrinsic UV and X-ray luminosities of the AGN needed to give rise to their double-peaked profiles. We also estimate the extent of the obscuration of the AGN by comparing their luminosities to those of similar quasar samples at these epochs. Future X-ray and radio observations, as well as those with the James Webb Space Telescope, will be valuable tools to test the AGN contribution to the intergalactic-scale ionization zones of high-redshift LAEs.
Key words: dark ages / reionization / first stars / galaxies: high-redshift / quasars: supermassive black holes
© ESO 2021
1. Introduction
The epoch of reionization (EoR), when intergalactic hydrogen transitioned from being neutral to ionized, is within the reach of current galaxy surveys (e.g., Loeb & Furlanetto 2013). The Lyman-α line (rest wavelength 1215 Å) is an important probe of reionization since both its strength and lineshape are sensitive to the amount of neutral hydrogen (for a review, see e.g., Dijkstra 2014). Surveys of Lyman-alpha emitting galaxies, or Lyman-Alpha Emitters (LAEs) at z ∼ 6 can potentially constrain the timing, topology, and sources of reionization (e.g., Stark et al. 2010; Fontana et al. 2010), as well as the properties of the ionized bubbles (e.g., Mason & Gronke 2020). Several LAEs detected at high redshifts (Ouchi et al. 2010; Kashikawa et al. 2006; Hu et al. 2010; Konno et al. 2014) close to the EoR have been used to measure the average neutral fraction of hydrogen. The observed rapid decline in the fraction of LAEs beyond z ∼ 6 (Konno et al. 2014; Sadoun et al. 2017; Matthee et al. 2015; Bagley et al. 2017; Ota et al. 2017; Shibuya et al. 2018) compared to continuum selected galaxies has been used to place constraints on the timing and characteristics of reionization (e.g., Dayal et al. 2009; Bolton & Haehnelt 2013; Tilvi et al. 2014; Mesinger et al. 2015; Choudhury et al. 2015; Weinberger et al. 2018; Mason et al. 2018; Santos et al. 2016; Yang et al. 2020; Whitler et al. 2020), though the modeling is complicated since it may also involve changes in the intrinsic properties of the LAEs with redshift (e.g., Stark et al. 2015; Sobral et al. 2017; Hassan & Gronke 2020). However, the most luminous LAEs show less evolution (Santos et al. 2016; Ota et al. 2017; Zheng et al. 2017; Konno et al. 2018) over the z ∼ 5 − 7 range.
Recently, some extremely luminous LAEs have been detected at z ∼ 6.6, a few of which show evidence for double-peaked line profiles. This is rare among high-redshift galaxies (e.g., Gronke et al. 2020), since the increasing neutral fraction in the intergalactic medium (Hu et al. 2010) almost always leads to the resonant absorption of the blue wing of the line. Its presence, therefore, indicates that the LAE resides in a highly ionized HII region which allows the blue wing to emerge (e.g, Dijkstra 2014), and this can constrain the minimum size of the ionized region in which the galaxy resides (e.g., Matthee et al. 2018; Mason & Gronke 2020). Double-peaked LAEs can also be used to constrain the escape fraction of ionizing photons from the parent galaxy, which has been shown (Verhamme et al. 2015; Izotov et al. 2018) to be tightly correlated with the velocity separation between the red and blue peaks. One of the most studied double-peaked LAEs at z ≳ 6.5 is the galaxy labeled COLA-1, located in the COSMOS field (Hu et al. 2016; Matthee et al. 2018) at z ∼ 6.593. Recently, two other LAEs have also been reported to have double-peaked profiles: NEPLA-4, at z ∼ 6.54 (Songaila et al. 2018), and A370p_z1 in the parallel Frontier Field of Abell 370 (Meyer et al. 2020).
At low redshifts, almost all the luminous LAEs (with log[Lα/ergs/s] > 43.4) are found to be associated with active galactic nuclei (AGN; Konno et al. 2016, though there are also luminous Lyman-α galaxies that show no evidence for AGN, e.g., Marques-Chaves et al. 2020). It is possible that AGN activity makes a contribution to the ionization region and thus the observed double peak of the above high-redshift LAEs (Barkana & Loeb 2003; Matthee et al. 2018; Meyer et al. 2020; Pelliccia et al. 2020) as well1. Unobscured AGN are ruled out in the above scenario due to the narrowness of the observed Lyman-α line. However, obscured AGN (for a review, see, e.g., Hickox & Alexander 2018) are surrounded by an edge-on torus along our line-of-sight, which blocks their broad emission lines. While the AGN’s own broad Lyman-α line is removed from view by the obscuration (e.g., Baek & Ferrara 2013), the UV radiation is able to escape in the perpendicular direction along the torus symmetry axis, creating two ionization cones and thus the observed double peak of the galaxy’s Lyman-α emission. Distinguishing obscured AGN from starbursts at high redshifts (e.g., Pallottini et al. 2015; Pacucci et al. 2017; Matthee et al. 2020) is important for calibrating the as of yet uncertain contribution of AGN to reionization (e.g., Madau & Haardt 2015; Hassan et al. 2018; Mitra et al. 2018).
In this paper, we point out observable signatures of the double-peaked profiles in high-redshift LAEs being the result of obscured AGN, using COLA-1 as an example. If the ionizing emissivity of the quasar is sufficiently high, double-peaked emission can result due to the extent of the quasar’s Lyman-α near zone (Mason & Gronke 2020). We forecast the expected spectra and intrinsic X-ray emission of the AGN in the relevant energy bands, as well as the extent of its obscuration.
2. Conditions for double-peaked profiles from AGN
We start with the formalism of Bolton & Haehnelt (2007) for the ionized near-zones from the spectra of z ∼ 6 quasars. It was found that the maximum radius (in proper megaparsecs, pMpc) of the Lyman-alpha near-zone, that is to say the region around which the ionized bubble becomes optically thick to Lyman-α photons, is given by:
for a quasar with spectral index αν and ionizing emissivity Nion (in s−1), where zα is the redshift of the near-zone boundary2. The above expression assumes that the density of the neutral gas is equal to the cosmic mean at the near-zone boundary, and the IGM temperature in the vicinity of the quasar is 2 × 104 K, a typical value at these epochs (e.g., Bolton et al. 2010). The edge of the near-zone is defined by the last pixel at which the spectrum drops below the normalized flux limit of 10%, corresponding to an optical depth detection limit of τ = 2.3.
We combine the above expression with the findings of Mason & Gronke (2020), who connect the observed blue velocity offset Δvα in double-peaked LAEs to the minimum extent of the underlying Lyman-α near-zone, Rα, min, following their assumption of a single source residing at the center of a large, highly ionized bubble (in contrast to numerous mildly-ionized bubbles and/or neutral IGM scenarios also considered in Matthee et al. 2018). This is given by Rα, min = |Δvα|/H(zs) where H(zs) is the Hubble parameter at the source redshift zs, since the photons must travel a minimum distance of Rα, min so that they redshift out of resonance while still being located within the proximity zone. In the case of COLA-1, the observed Δvα = −250 km s−1 leads to Rα, COLA − 1 = 0.31 pMpc.
Equating the right-hand side of Eq. (1) to Rα, COLA − 1, we can estimate the quasar ionizing emissivity that is required for the observation of the double peak. To do this, we need to invoke a quasar spectral shape. We use the parametrization of Shen et al. (2020) in which the quasar spectrum has a power law having a slope of αν = −1.70 in the 600 Å to 912 Å regime (Lusso et al. 2015), and a power law with an exponential cutoff for wavelengths < 50 Å :
where Ec = 300 keV and E = hν with h being Planck’s constant, αν = −1.7, Γ = 1.9. Here, νH is the ionization frequency of hydrogen (corresponding to 912 Å) and the 600 Å and 50 Å parts of the spectrum are directly connected due to the lack of sufficient observational data3. In the above equation, LH is the luminosity of the quasar at the hydrogen ionizing limit νH, and A is the normalization of the luminosity in the X-ray regime, fixed by scaling the spectrum to the parametrization in Shen et al. (2020).
Using αν = −1.70 in Eq. (1), we find that the required quasar emissivity corresponding to Rα,max,COLA−1 = 0.31 pMpc is
This ionizing emissivity can be used to normalize the spectral shape by using the following relation:
with Lν given by4 Eq. (2). Using Eq. (4) with the value of COLA-1’s ionizing emissivity to normalize Eq. (2), we can plot the flux spectrum of the AGN in the UV to IR regime, shown as the blue line in Fig. 1. We find that this spectrum corresponds to a flux density at 4500 Å of log Lν, 4500 = 45.08 ergs s−1 Hz−1, or a UV magnitude of M1500 = −23.2 for the quasar. We note that this intrinsic magnitude is brighter than the UV magnitude estimated from the COLA-1 galaxy itself (MUV = −21.6; Matthee et al. 2018). The suppression in the observed magnitude to below −21.6 is consistent with the required dust obscuration of the quasar that leads to extinction.
 |
Fig. 1. SED of an AGN consistent with the observed double-peak emission observed in COLA-1. The red downward arrow shows the measured upper limit in X-rays (Jorryt Matthee and João Calhau, priv. comm.), rescaled to 2 keV. The blue horizontal lines indicate the suppression in the flux at 5 keV for various column densities, NH = 1022.75, 1023.25, and 1023.75 cm−2, obscuring the AGN. |
This can now be used to normalize the X-ray portion of Eq. (2), whose integral between 0.5 keV and 7 keV gives the expected luminosity of the quasar in the X-ray regime5. For COLA-1, we find L0.5 − 7 keV = 1044.17 ergs s−1 using the above procedure, which is just below the measured upper limit of 1044.3 ergs s−1 (Jorryt Matthee & João Calhau, priv. comm.). This indicates that by slightly improving the sensitivity of the X-ray observations, it may be possible to confirm or rule out the AGN scenario for COLA-1, unless the obscuring torus has a very large gas column that considerably suppresses the X-rays emission along the line-of-sight.
Using the bolometric correction of Runnoe et al. (2012), this intrinsic X-ray luminosity corresponds to the bolometric luminosity LBol = 1045.9 erg s−1, assuming a radio quiet quasar, or LBol = 1046.0 erg s−1, assuming a radio loud quasar. Both of these luminosities indicate a central black hole of mass MBH ∼ 108 M⊙ accreting at the Eddington limit.
The other two LAEs at z ∼ 6, NEPLA-4 and A370p_z1, can be analyzed by a similar procedure, with NEPLA-4’s spectrum being nearly identical to that of COLA-1 due to the similar size of the near-zone, and that for A370p_z1 being slightly smaller (Rα, A370p_z1 = 0.26 pMpc). We predict the intrinsic 0.5–7 keV emission from the AGN to be 1044.17 and 1044.09 ergs s−1, respectively, for these LAEs.
The lensed galaxy MACS1149-JD1 observed at z ∼ 9.11 (Hashimoto et al. 2018) displays a blue-shifted Lyman-α line relative to its [OIII] 88 μm with a velocity offset of Δvα = −450 km s−1. This corresponds to Rα = 0.37 pMpc, which was difficult to achieve (Mason & Gronke 2020) with the observed faintness of the galaxy (MUV = −18.5). If the ionization zone of the above galaxy arises due to an AGN, we find that the required ionizing emissivity is Nion = 1.34 × 1056 s−1, which corresponds to M1500 = −24.99, or an intrinsic X-ray luminosity of 1044.73 ergs s−1 in the 0.5–7 keV band.
3. Obscuration of the AGN
Since the broad Lyman-α line of the AGN is not detected in the spectra of the LAEs, the AGN source would have to be obscured by a compact torus in its immediate vicinity. We can estimate the extent of this obscuration by comparing the derived properties of the AGN to similar quasars at these redshifts.
Calhau et al. (2020) studied the radio and X-ray properties of ∼4000 LAEs in the COSMOS SC4K field over 2 < z < 6 and found a correlation between the hardness ratio, which determines the level of obscuration, and the X-ray luminosity of X-ray detected LAEs, with the more luminous X-ray LAEs being observed to have smaller hardness ratios. Our estimate for the intrinsic X-ray luminosity of COLA-1 places it above the hardness 0 category when compared to the Calhau et al. (2020) sample, with properties similar to those of obscured AGN discovered in the COSMOS field by Marchesi et al. (2016). It was found that for AGN having log LX/ergs s−1 > 44.1 in the 2–10 keV range, obscured sources are two to three times as abundant as unobscured ones at z ∼ 6 − 6.5 (Marchesi et al. 2016).
We can use the hardness ratio to estimate the column density of the gas surrounding the AGN, using the properties of obscured quasar samples in the literature (e.g., Peca et al. 2021, see Fig. 14). This suggests NH ∼ 1023.5 cm−2 for the obscured AGN, which could lead to a few orders of magnitude reduction in observed flux (Peca et al. 2021). For low-z LAEs, the velocity offset of the red-peak emission line contains information about the neutral hydrogen column density (NHI) of the obscuring material in the vicinity of the galaxy (e.g., Shibuya et al. 2014; Hashimoto et al. 2015). For the systems considered here, this leads to about NHI ∼ 1017 − 1020 cm−2 contributed by the galaxy, which serves as a lower limit to the required obscuration, assuming a non-evolution of the velocity offset-column density relation across cosmic time. Figure 1 shows the decline in the observed flux of the X-ray spectrum of COLA-1 for three representative column densities obscuring the AGN (NH = 1022.75, 1023.25, and 1023.75 cm−2).
4. Discussion and observational prospects
We have studied the possible origin of the double-peaked Lyman-alpha emitters (LAEs), such as COLA-1, NEPLA4, and A370p_z1 at z > 6.5, in the proximity zone of obscured AGN, whose ionizing emissivity leads to the emergence of the blue wing. In particular, we combined the predictions for the extent of the Lyman-α near-zone of z ∼ 6 quasars (Bolton & Haehnelt 2007) with the maximum extent of the near-zone required for the blue peak of LAEs to be visible (Mason & Gronke 2020). In so doing, we find that the required ionizing emissivity may be supplied by AGN with UV magnitudes of MUV ∼ −23 which, assuming typical AGN spectra, correspond to intrinsic X-ray luminosities of ∼1044 ergs s−1 in the 2–10 keV range. These values indicate that by improved X-ray sensitivities in the future, it may be possible to confirm or rule out the AGN scenario. High-resolution imaging by the forthcoming James Webb Space Telescope might also test the expected conical geometry of the obscured AGN scenario, especially in lensed systems.
Due to the observed narrowness of the Lyman-α line, such AGN are likely obscured by the intervening material, making the double peak visible only through the ionization cones. Estimates based on the correlation between the column density and hardness ratio of similar AGN in the Chandra field predict the obscuring column density to be NH ∼ 1023.5 cm−2, which may cause a drop by 1–2 orders of magnitude in the observed X-ray luminosity.
While the stellar emission in A370_pz1 was found to be capable of self-ionizing its own HII bubble (with an escape fraction of fesc ≳ 0.9 for a fraction of its measured age of about 50 Myr), it was found that COLA-1 and NEPLA-4 need additional sources of ionization to keep their bubbles ionized given galaxy lifetimes of a few ten Myr (Meyer et al. 2020). These findings may lend further support to the AGN scenario. Searching for lines such as [NeV] 3347, 3427 with the James Webb Space Telescope will also test this scenario in the future.
Radio observations of LAEs at z ∼ 6 with the LOFAR survey (Gloudemans et al. 2021) have provided upper limits of 1023.90 and 1023.94 W Hz−1 at z ∼ 5.7 and z ∼ 6.6, respectively. In converting the radio upper limits for COLA-1 (Jorryt Matthee & João Calhau, priv. comm.) to their equivalent flux densities assuming a spectral shape with α = −0.8 (Calhau et al. 2020), we find similar values (1024.59 and 1023.91 W Hz−1 at 1.4 GHz and 3 GHz, respectively). Given that only about 10% of AGN are radio loud, these upper limits do not constrain the AGN scenario since these objects could be radio quiet. Infrared observations (1–1000 μm), such as those with ALMA (e.g., Fudamoto et al. 2020), may also be useful, with the caveat that the decline in AGN flux at these wavelengths may be difficult to estimate, particularly if it is obscured (e.g., Fritz et al. 2006).
Bosman et al. (2020) have recently reported the presence of a double-peaked profile in Aerith B, a z ∼ 5.8 Lyman-break selected galaxy, located in the near-zone of a quasar.
Recent work (Wang et al. 2020) may indicate evidence for an increase in Γ at high redshifts, z ∼ 6.
In practice, the contribution from the X-ray section of Eq. (2) is several orders of magnitude lower than that of the 600–912 Å portion.
To normalize the fIux at 0.5 keV, we use the αox parameter corresponding to 2500 Å (Steffen et al. 2006) and defined by:
where νX and νUV are the frequencies corresponding to 0.5 keV and 2500 Å, respectively (e.g., Elvis et al. 2010).
Acknowledgments
We thank Max Gronke, Charlotte Mason, Jorryt Matthee, Fabio Pacucci and Daniel Schaerer for useful discussions and insightful comments on the manuscript, and the referee for a helpful report that improved the presentation. HP acknowledges support from the Swiss National Science Foundation Ambizione Grant PZ00P2_179934 “Probing the Universe: through reionization and beyond”. The work of AL was supported in part by Harvard’s Black Hole Initiative, which is funded by grants from JTF and GBMF.
References
- Baek, S., & Ferrara, A. 2013, MNRAS, 432, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Bagley, M. B., Scarlata, C., Henry, A., et al. 2017, ApJ, 837, 11 [Google Scholar]
- Barkana, R., & Loeb, A. 2003, Nature, 421, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., & Haehnelt, M. G. 2007, MNRAS, 374, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., & Haehnelt, M. G. 2013, MNRAS, 429, 1695 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., Becker, G. D., Wyithe, J. S. B., Haehnelt, M. G., & Sargent, W. L. W. 2010, MNRAS, 406, 612 [Google Scholar]
- Bosman, S. E. I., Kakiichi, K., Meyer, R. A., et al. 2020, ApJ, 896, 49 [Google Scholar]
- Calhau, J., Sobral, D., Santos, S., et al. 2020, MNRAS, 493, 3341 [CrossRef] [Google Scholar]
- Choudhury, T. R., Puchwein, E., Haehnelt, M. G., & Bolton, J. S. 2015, MNRAS, 452, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Ferrara, A., Saro, A., et al. 2009, MNRAS, 400, 2000 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M. 2014, PASA, 31, e040 [Google Scholar]
- Elvis, M. 2010, in Co-Evolution of Central Black Holes and Galaxies, eds. B. M. Peterson, R. S. Somerville, & T. Storchi-Bergmann, IAU Symp., 267, 55 [Google Scholar]
- Fontana, A., Vanzella, E., Pentericci, L., et al. 2010, ApJ, 725, L205 [Google Scholar]
- Fritz, J., Franceschini, A., & Hatziminaoglou, E. 2006, MNRAS, 366, 767 [Google Scholar]
- Fudamoto, Y., Oesch, P. A., Magnelli, B., et al. 2020, MNRAS, 491, 4724 [CrossRef] [Google Scholar]
- Gloudemans, A. J., Duncan, K. J., Kondapally, R., et al. 2021, A&A, in press,, https://doi.org/10.1051/0004-6361/202038819 [Google Scholar]
- Gronke, M., Ocvirk, P., Mason, C., et al. 2020, ArXiv e-prints [arXiv:2004.14496] [Google Scholar]
- Hashimoto, T., Verhamme, A., Ouchi, M., et al. 2015, ApJ, 812, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, T., Laporte, N., Mawatari, K., et al. 2018, Nature, 557, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Hassan, S., Davé, R., Mitra, S., et al. 2018, MNRAS, 473, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Hassan, S., & Gronke, M. 2020, ApJ, submitted [arXiv:2010.00023] [Google Scholar]
- Hickox, R. C., & Alexander, D. M. 2018, ARA&A, 56, 625 [Google Scholar]
- Hu, E. M., Cowie, L. L., Barger, A. J., et al. 2010, ApJ, 725, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, E. M., Cowie, L. L., Songaila, A., et al. 2016, ApJ, 825, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Worseck, G., Schaerer, D., et al. 2018, MNRAS, 478, 4851 [Google Scholar]
- Kashikawa, N., Shimasaku, K., Malkan, M. A., et al. 2006, ApJ, 648, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Konno, A., Ouchi, M., Ono, Y., et al. 2014, ApJ, 797, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Konno, A., Ouchi, M., Nakajima, K., et al. 2016, ApJ, 823, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Konno, A., Ouchi, M., Shibuya, T., et al. 2018, PASJ, 70, S16 [NASA ADS] [CrossRef] [Google Scholar]
- Loeb, A., & Furlanetto, S. R. 2013, The First Galaxies in the Universe [Google Scholar]
- Lusso, E., Worseck, G., Hennawi, J. F., et al. 2015, MNRAS, 449, 4204 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Haardt, F. 2015, ApJ, 813, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesi, S., Civano, F., Salvato, M., et al. 2016, ApJ, 827, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Marques-Chaves, R., Álvarez-Márquez, J., Colina, L., et al. 2020, MNRAS, 499, L105 [Google Scholar]
- Mason, C. A., & Gronke, M. 2020, MNRAS, 499, 1395 [Google Scholar]
- Mason, C. A., Treu, T., Dijkstra, M., et al. 2018, ApJ, 856, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Matthee, J., Sobral, D., Santos, S., et al. 2015, MNRAS, 451, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Matthee, J., Sobral, D., Gronke, M., et al. 2018, A&A, 619, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthee, J., Pezzulli, G., Mackenzie, R., et al. 2020, MNRAS, 498, 3043 [Google Scholar]
- Mesinger, A., Aykutalp, A., Vanzella, E., et al. 2015, MNRAS, 446, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, R. A., Laporte, N., Ellis, R. S., Verhamme, A., & Garel, T. 2020, MNRAS, 500, 558 [Google Scholar]
- Mitra, S., Choudhury, T. R., & Ferrara, A. 2018, MNRAS, 473, 1416 [CrossRef] [Google Scholar]
- Ota, K., Iye, M., Kashikawa, N., et al. 2017, ApJ, 844, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Shimasaku, K., Furusawa, H., et al. 2010, ApJ, 723, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Pacucci, F., Pallottini, A., Ferrara, A., & Gallerani, S. 2017, MNRAS, 468, L77 [Google Scholar]
- Pallottini, A., Ferrara, A., Pacucci, F., et al. 2015, MNRAS, 453, 2465 [NASA ADS] [Google Scholar]
- Peca, A., Vignali, C., Gilli, R., et al. 2021, ApJ, 906, 90 [Google Scholar]
- Pelliccia, D., Strait, V., Lemaux, B., et al. 2020, ApJL, submitted [arXiv:2011.08857] [Google Scholar]
- Runnoe, J. C., Brotherton, M. S., & Shang, Z. 2012, MNRAS, 422, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Sadoun, R., Zheng, Z., & Miralda-Escudé, J. 2017, ApJ, 839, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, S., Sobral, D., & Matthee, J. 2016, MNRAS, 463, 1678 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, X., Hopkins, P. F., Faucher-Giguère, C.-A., et al. 2020, MNRAS, 495, 3252 [Google Scholar]
- Shibuya, T., Ouchi, M., Nakajima, K., et al. 2014, ApJ, 788, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Shibuya, T., Ouchi, M., Harikane, Y., et al. 2018, PASJ, 70, S15 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Matthee, J., Best, P., et al. 2017, MNRAS, 466, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A., Hu, E. M., Barger, A. J., et al. 2018, ApJ, 859, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Chiu, K., Ouchi, M., & Bunker, A. 2010, MNRAS, 408, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Walth, G., Charlot, S., et al. 2015, MNRAS, 454, 1393 [Google Scholar]
- Steffen, A. T., Strateva, I., Brandt, W. N., et al. 2006, AJ, 131, 2826 [NASA ADS] [CrossRef] [Google Scholar]
- Tilvi, V., Papovich, C., Finkelstein, S. L., et al. 2014, ApJ, 794, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Verhamme, A., Orlitová, I., Schaerer, D., & Hayes, M. 2015, A&A, 578, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, F., Fan, X., Yang, J., et al. 2020, ApJ, submitted [arXiv:2011.12458] [Google Scholar]
- Weinberger, L. H., Kulkarni, G., Haehnelt, M. G., Choudhury, T. R., & Puchwein, E. 2018, MNRAS, 479, 2564 [NASA ADS] [CrossRef] [Google Scholar]
- Whitler, L. R., Mason, C. A., Ren, K., et al. 2020, MNRAS, 495, 3602 [Google Scholar]
- Yang, J., Wang, F., Fan, X., et al. 2020, ApJ, 904, 26 [Google Scholar]
- Zheng, Z.-Y., Wang, J., Rhoads, J., et al. 2017, ApJ, 842, L22 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. SED of an AGN consistent with the observed double-peak emission observed in COLA-1. The red downward arrow shows the measured upper limit in X-rays (Jorryt Matthee and João Calhau, priv. comm.), rescaled to 2 keV. The blue horizontal lines indicate the suppression in the flux at 5 keV for various column densities, NH = 1022.75, 1023.25, and 1023.75 cm−2, obscuring the AGN. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} R_{\alpha , \mathrm max}&= 3.14 \left(\frac{N_{\rm ion}}{2 \times 10^{57}\,s^{-1}}\right)^{1/2} \left[\frac{(\alpha _{\nu })^{-1} (\alpha _{\nu } + 3)}{3}\right]^{-1/2} \nonumber \\&\times \left(\frac{1 + z_{\alpha }}{7}\right)^{-9/4} \text{ pMpc} \, , \end{aligned} $$](/articles/aa/full_html/2021/02/aa40107-20/aa40107-20-eq1.gif)