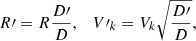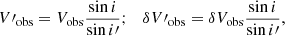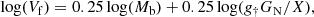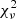| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | L13 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202040101 | |
| Published online | 17 February 2021 | |
Letter to the Editor
A cautionary tale in fitting galaxy rotation curves with Bayesian techniques
Does Newton’s constant vary from galaxy to galaxy?
1
Department of Astronomy, Case Western Reserve University, Cleveland, OH 44106, USA
e-mail: PengfeiLi0606@gmail.com; pxl283@case.edu
2
School of Physics and Astronomy, Cardiff University, Queens Buildings, The Parade, Cardiff CF24 3AA, UK
3
Department of Physics, University of Oregon, Eugene, OR 97403, USA
4
Department of Physics and Astronomy, Sejong University, 209 Neungdong-ro Gwangjin-gu, Seoul 05006, Republic of Korea
Received:
9
December
2020
Accepted:
27
January
2021
The application of Bayesian techniques to astronomical data is generally non-trivial because the fitting parameters can be strongly degenerated and the formal uncertainties are themselves uncertain. An example is provided by the contradictory claims over the presence or absence of a universal acceleration scale (g†) in galaxies based on Bayesian fits to rotation curves. To illustrate this we present an analysis in which the Newtonian gravitational constant GN is allowed to vary from galaxy to galaxy when fitting rotation curves from the SPARC database, in analogy to g† in the recently debated Bayesian analyses. When imposing flat priors on GN, we obtain a wide distribution of GN which, taken at face value, would rule out GN as a universal constant with high statistical confidence. However, imposing an empirically motivated log-normal prior returns a virtually constant GN with no sacrifice in fit quality. This implies that the inference of a variable GN (or g†) is the result of the combined effect of parameter degeneracies and unavoidable uncertainties in the error model. When these effects are taken into account, the SPARC data are consistent with a constant GN (and constant g†).
Key words: galaxies: dwarf / galaxies: spiral / galaxies: irregular / galaxies: kinematics and dynamics / dark matter
© ESO 2021
1. Introduction
Bayesian analysis has been extensively implemented in astronomical studies due to the frequent occurrence of multi-parameter problems. A major philosophy of Bayesian inference is to incorporate reliable priors to break the parameter degeneracies. This is best achieved by imposing physically motivated priors; however, they are not always readily available. The situation becomes even more difficult when the input formal uncertainties are themselves uncertain, as is often the case for heterogeneous collections of data. Thus, any formal outcome of Bayesian analysis should be interpreted with a proper appreciation for both the strengths and limitations of the source data.
One example is the claim of “absence of a fundamental acceleration scale in galaxies” by Rodrigues et al. (2018a) and the follow-up work by Marra et al. (2020). They fitted rotation curves of disk galaxies from the SPARC1 database (Lelli et al. 2016) using the radial acceleration relation (RAR; McGaugh et al. 2016; Lelli et al. 2017. The RAR is a tight empirical relation between the observed kinematic acceleration gobs and the baryonic gravitational field gbar with a characteristic scale g† ≃ 10−10 m s−2. Its asymptotic behaviors agree with the predictions of modified Newtonian dynamics (MOND; Milgrom 1983), hence the RAR can be interpreted as a viable realization of MOND only if the empirical scale g† is a universal constant.
Rodrigues et al. (2018a) tested the universality of g† by fitting the RAR to individual galaxies imposing flat priors on three fitting parameters (acceleration scale g†, galaxy distance, and stellar mass-to-light ratio) and taking formal uncertainties literally for each rotation curve. They obtained a wide distribution of g† and concluded that a universal acceleration scale is ruled out. After substantial criticism about their methodology and interpretation of data (McGaugh et al. 2018; Kroupa et al. 2018; Cameron et al. 2020), they presented a follow-up analysis in Marra et al. (2020) in which they follow Li et al. (2018) in adopting physically motivated Gaussian priors on distance, inclination, and stellar mass-to-light ratio. They persist in using a flat prior on g†, resulting in severe parameter degeneracies. Similar work was presented by Chang & Zhou (2019) using a very broad uninformative prior on g†.
The mere existence and tightness of the RAR and of the baryonic Tully-Fisher relation (BTFR; e.g., Lelli et al. 2019) suggest an empirically motivated Gaussian prior centered around 10−10 m s−2. There cannot be more scatter in g† than there is in the raw forms of these relations prior to any rotation-curve fitting, yet this is exactly what is inferred in analyses where a broad prior on g† is assumed. Degeneracy can cause this parameter to vary widely with other parameters without providing a meaningful improvement in fit quality. This was already pointed out in Li et al. (2018), where we concluded that rotationally supported galaxies are consistent with a single value of g†: there is no value added in allowing it to vary. The same argument applies to pressure supported galaxies (Chae et al. 2020a) and when the MOND external-field effect is taken into account (Chae et al. 2020b).
Comparing the posterior distribution functions of g† from individual galaxy fits implies that one can fully trust the formal uncertainties in each case. The observational uncertainties of SPARC galaxies are surely sensible on average; for example, the mean expected scatter in the RAR from error propagation is comparable with the observed scatter (e.g.,; Lelli et al. 2017). However, taking formal uncertainties of each rotation curve literally is not recommended because they were culled from multiple sources (Lelli et al. 2016). More generally, we can measure the Doppler shift in different parts of galaxies with high accuracy, but dynamical analysis demands knowledge of the circular velocity of a test particle in the equilibrium gravitational potential. The gas rotational velocity is arguably the best possible proxy to the circular velocity, but uncertainties in some individual galaxies (e.g., due to non-circular motions or out-of-equilibrium dynamics) can never be fully under control.
To further illustrate how a blind application of Bayesian statistics with uninformative priors could mislead us, we present a reductio ad absurdum using Newton’s gravitational constant GN as a free parameter in a similar fashion to g†. Choosing GN has a key advantage. Since it is widely accepted as a constant, comparing the Bayesian inference with the expected value provides a clear evaluation on the approach of Rodrigues et al. (2018a) with respect to that of Li et al. (2018). In Sect. 2 we reproduce the results by Rodrigues et al. (2018a) using similar data and priors, but for GN instead of g†. In Sect. 3 we repeat the analysis of Li et al. (2018) exploring different priors on GN. We discuss our results in Sect. 4.
2. Challenging the constancy of the Newtonian gravitational constant
In analogy to previous works (Li et al. 2018; Rodrigues et al. 2018a; Chang & Zhou 2019; Marra et al. 2020), we fit the rotation curves from the SPARC database (Lelli et al. 2016) using the RAR. The SPARC database consists of 175 late-type galaxies with accurate H I/Hα rotation curves and mass modeling from Spitzer photometry at 3.6 μm. The gravitational contributions of different baryonic components (gas disk, stellar disk, and bulge if applicable) are represented as the circular velocity of a test particle (Vgas, Vdisk, and Vbulge, respectively). The total rotation velocity due to baryonic contributions Vbar is then the quadratic sum of these components,
where Υdisk and Υbulge are the stellar mass-to-light ratios for disks and bulges with the fiducial values Υdisk = 0.5 and Υbulge = 0.7 (McGaugh et al. 2016). The RAR relates the observed acceleration gobs to that due to baryons gbar,
where 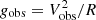 ,
, 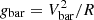 , and g† is the only free parameter. This relation was established by analyzing the data points from 153 galaxies in a statistical sense. We wanted to test the constancy of GN, so we fit Eq. (2) to rotation curves fixing g† = 1.2 × 10−10 m s−2 and varying GN from galaxy to galaxy. We also tried to vary g† and GN simultaneously, and obtained similar results. We show as an example the case that has the same number of fitting parameters as in Rodrigues et al. (2018a).
, and g† is the only free parameter. This relation was established by analyzing the data points from 153 galaxies in a statistical sense. We wanted to test the constancy of GN, so we fit Eq. (2) to rotation curves fixing g† = 1.2 × 10−10 m s−2 and varying GN from galaxy to galaxy. We also tried to vary g† and GN simultaneously, and obtained similar results. We show as an example the case that has the same number of fitting parameters as in Rodrigues et al. (2018a).
We set the likelihood function as 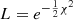 with χ2 given by
with χ2 given by
where gRAR is the expected centripetal acceleration from Eq. (2) and 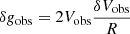 is the uncertainty on the observed acceleration. We impose a flat prior on GN with GN > 0 as Rodrigues et al. (2018a) did for g†. Following the procedure of Rodrigues et al. (2018a), we also impose flat priors on Υ⋆ with a tolerance of a factor of two, though this is not consistent with stellar population synthesis models (Schombert et al. 2019).
is the uncertainty on the observed acceleration. We impose a flat prior on GN with GN > 0 as Rodrigues et al. (2018a) did for g†. Following the procedure of Rodrigues et al. (2018a), we also impose flat priors on Υ⋆ with a tolerance of a factor of two, though this is not consistent with stellar population synthesis models (Schombert et al. 2019).
Galaxy distance affects the fit quality as it is directly related to the contributions of the baryonic components. When the distance D is changed to D′, the galaxy radius R and the contribution of each component 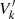 will transform according to
will transform according to
where k denotes gas, disk, or bulge. Rodrigues et al. (2018a) allow galaxy distance to vary freely within 20% of their observational values. This prior does not reflect actual observational errors. Distances measured through Cepheids or the tip magnitude of the red giant branch are highly accurate, so a 20% variation could be larger than 4σ. The Hubble flow method is much less accurate; distances measured using this method could have errors up to 30%, so the imposed 20% free range is even within the 1σ region. Rodrigues et al. (2018a) also ignored the uncertainty on disk inclination. Possible outer asymmetries and warps in the gas disk could mislead the determination of inclinations, as reflected in their uncertainties, which would in turn affect the observed rotation velocities. Despite the shortcomings of the methodology of Rodrigues et al. (2018a), we choose to fit the same parameters (except GN instead of g†) and impose the same priors to achieve the most direct comparison.
We map the posterior distributions of the fitting parameters using the standard affine-invariant ensemble sampler in the Python package emcee (Foreman-Mackey et al. 2013). The Markov chains are initialized with 200 random walkers and iterated for 2000 steps after 1000 burnt-in iterations. We record the best-fit parameters that maximize the probability function for every galaxy.
Figure 1 shows the posterior probability distribution of GN. Though we analyze all the SPARC galaxies, we only include 101 of them in Fig. 1 based on the following quality cuts: we removed galaxies with quality flag Q = 3 (see Lelli et al. 2016), inclination smaller than 30°, or reduced 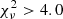 . This is a quality cut similar to that adopted in Rodrigues et al. (2018a), and it retains a similar number of galaxies. Figure 1 shows that the posterior probability distribution of GN presents a wide distribution spanning ∼3.5 dex. We also calculate the 1σ, 2σ, and 3σ credible regions (including 68.3%, 95.4%, and 99.7% of the posterior probability, respectively) from the output of getMargeStats in the Python package GetDist2. It turns out that 34 galaxies out of 101 are incompatible with the expected GN. This is similar to Fig. 1 of Rodrigues et al. (2018a), showing a wide distribution of a0 (which we call g† to distinguish empirical free parameters from physical constants). Rodrigues et al. (2018a) found that 31% of the galaxies are rejected from the global best-fit g† at the 3σ level. Hence, they infer the absence of a fundamental acceleration scale in galaxies. We find that 34% of the galaxies are excluded from the expected value of GN at the 3σ level. Following their argument, we reach the conclusion of the absence of a fundamental Newtonian gravitational constant, ruling out Newtonian gravity and General Relativity.
. This is a quality cut similar to that adopted in Rodrigues et al. (2018a), and it retains a similar number of galaxies. Figure 1 shows that the posterior probability distribution of GN presents a wide distribution spanning ∼3.5 dex. We also calculate the 1σ, 2σ, and 3σ credible regions (including 68.3%, 95.4%, and 99.7% of the posterior probability, respectively) from the output of getMargeStats in the Python package GetDist2. It turns out that 34 galaxies out of 101 are incompatible with the expected GN. This is similar to Fig. 1 of Rodrigues et al. (2018a), showing a wide distribution of a0 (which we call g† to distinguish empirical free parameters from physical constants). Rodrigues et al. (2018a) found that 31% of the galaxies are rejected from the global best-fit g† at the 3σ level. Hence, they infer the absence of a fundamental acceleration scale in galaxies. We find that 34% of the galaxies are excluded from the expected value of GN at the 3σ level. Following their argument, we reach the conclusion of the absence of a fundamental Newtonian gravitational constant, ruling out Newtonian gravity and General Relativity.
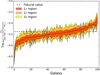 |
Fig. 1. Posterior probability distribution of Newton’s gravitational constant GN for the galaxies in the SPARC database (Lelli et al. 2016). Following a similar analysis by Rodrigues et al. (2018a) for the acceleration scale g†, galaxies are ordered by increasing value of GN and flat priors are imposed on galaxy distances, stellar mass-to-light ratios, and GN (see text for details). Black dots show the maximum of the posterior probability, together with 1σ, 2σ, and 3σ credible regions from the Python package GetDist. The expected value of GN is represented by the dashed line. Of the selected 101 galaxies, 34 are incompatible with the expected GN at the 3σ level. Taken at face value, this would imply that the gravitational constant is not constant. |
There are two interconnected problems here. First, flat priors can give GN too much freedom to go astray. Second, formal uncertainties on circular velocities (as well as distances and inclinations) are themselves uncertain, so the confidence regions from the posterior distribution functions of individual galaxies have to be taken with a grain of salt. With highly accurate observational data (e.g., the orbital data of the planets in the solar system), flat priors are expected to return consistent values of GN. For observational data like galaxy rotation curves, cases can occur where parameters co-vary wildly given the imperfect nature of the input data and their uncertainties (e.g., warped disks, complex non-circular motions). Since a flat prior does not provide any constraints against these effects, the fitting parameters can go astray, beyond the reasonable regions.
3. Confirming the constancy of the Newtonian gravitational constant
To further demonstrate the degeneracy problem, we compare fit qualities imposing different priors on GN. Similar work was done in Li et al. (2018) for g†. In that paper we found that imposing flat and Gaussian priors on g† result in significantly different distributions of its maximum likelihood value, but essentially return the same fit quality. We concluded that adding g† as a fitting parameter does not improve fit quality, thus the data are consistent with a single value of g†. The validity of this argument should be straightforward, but given the recent claims of Chang & Zhou (2019) and Marra et al. (2020), we repeat the analysis of Li et al. (2018) varying GN.
In Li et al. (2018), we include disk inclination as a fitting parameter as it affects the observational rotation velocities and their uncertainties. When the inclination is adjusted from i to i′, the observational rotation velocities and the uncertainties will transform as
where Vobs and δVobs are observational velocities and uncertainties, respectively. We also impose more realistic priors than Rodrigues et al. (2018a) on the fitting parameters: a lognormal prior on the stellar mass-to-light ratio with a standard deviation of 0.1 dex inspired by stellar population synthesis model (e.g., Schombert et al. 2019), and Gaussian priors on galaxy distance and disk inclination with the standard deviations given by their observational uncertainties. The same priors on these nuisance galactic parameters are imposed here.
For GN we follow two different approaches: (1) we impose an uninformative flat prior within [10−8, 10−4] kpc km2 s−2 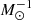 , which is known to give unrealiable results (as shown in the previous section), and (2) we use a lognormal prior following “empirical Bayes” approach. The lognormal prior is centered around the expected value GN = 4.3 × 10−6 kpc km2 s−2
, which is known to give unrealiable results (as shown in the previous section), and (2) we use a lognormal prior following “empirical Bayes” approach. The lognormal prior is centered around the expected value GN = 4.3 × 10−6 kpc km2 s−2 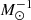 , while its standard deviation is empirically motivated using the BTFR (Lelli et al. 2019). The BTFR is mathematically equivalent to the low-acceleration portion of the RAR (see Sect. 7.1 in Lelli et al. 2017) and can be expressed as
, while its standard deviation is empirically motivated using the BTFR (Lelli et al. 2019). The BTFR is mathematically equivalent to the low-acceleration portion of the RAR (see Sect. 7.1 in Lelli et al. 2017) and can be expressed as
where Vf is the flat rotation velocity, Mb is the total baryonic mass, and X is a factor of order unity that accounts for the cylindrical geometry of disks (McGaugh et al. 2018). Fitting the data from Lelli et al. (2019) in log-log space with LTS_LINEFIT (Cappellari et al. 2013), we find that the best-fit slope is indistinguishable from 0.25 and the vertical intrinsic scatter is 0.02 dex along Vf. This sets a very hard upper limit for the scatter on GN or g† given that galaxy-to-galaxy variations in X may also contribute. Any intrinsic variation in log(GN) or log(g†) just cannot be larger than 0.02 dex. Thus, we consider a standard deviation of 0.02 dex for the lognormal prior on GN. We note that GN and g† enter in Eq. (6) in the same fashion, so the same argument can be applied to g†, as was done in Li et al. (2018).
The left panel of Fig. 2 shows the cumulative distribution function (CDF) of the reduced χ2 for both flat and lognormal priors on GN. We note that 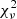 is merely used as a first-order statistic to assess the overall quality of different Bayesian fits, so the arguments against its use outlined in Rodrigues et al. (2018b) do not apply. Moreover, we are not comparing individual galaxy fits, but their average cumulative behavior, which is more robust against the occasional overestimate or underestimate of formal uncertainties. Unsurprisingly, the results shown here are similar to Figs. 6 and 7 in Li et al. (2018), though we are varying GN rather than g†. The CDF shows that imposing flat and lognormal priors essentially gives the same fit quality. For reference, we also include the results with fixed GN (red solid line), which shows a slightly better CDF of
is merely used as a first-order statistic to assess the overall quality of different Bayesian fits, so the arguments against its use outlined in Rodrigues et al. (2018b) do not apply. Moreover, we are not comparing individual galaxy fits, but their average cumulative behavior, which is more robust against the occasional overestimate or underestimate of formal uncertainties. Unsurprisingly, the results shown here are similar to Figs. 6 and 7 in Li et al. (2018), though we are varying GN rather than g†. The CDF shows that imposing flat and lognormal priors essentially gives the same fit quality. For reference, we also include the results with fixed GN (red solid line), which shows a slightly better CDF of 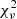 , even though it has one less fitting parameter. This occurs because the rotation-velocity residuals are comparable, so the smaller number of fitting parameters f for the same number N of data points improves the value of
, even though it has one less fitting parameter. This occurs because the rotation-velocity residuals are comparable, so the smaller number of fitting parameters f for the same number N of data points improves the value of 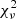 = χ2/ (N − f). Therefore, there is no added value in varying GN.
= χ2/ (N − f). Therefore, there is no added value in varying GN.
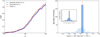 |
Fig. 2. Left: cumulative distribution functions of |
An important thing to note about the CDF in Fig. 2 is that there are too many galaxies with 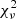 that is too high, and also too many for which it is too low relative to the expected distribution for
that is too high, and also too many for which it is too low relative to the expected distribution for 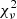 . If we take the cases with high
. If we take the cases with high 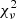 at face value, then the fits are formally rejected at high confidence. However, we have also made fits to the same data with dark matter halos (Li et al. 2020), and obtain CDFs with the same structure for all of the halo types considered (NFW, pseudo-isothermal, Burkert, Einasto, DC14, coreNFW, and Lucky13). The same galaxies have
at face value, then the fits are formally rejected at high confidence. However, we have also made fits to the same data with dark matter halos (Li et al. 2020), and obtain CDFs with the same structure for all of the halo types considered (NFW, pseudo-isothermal, Burkert, Einasto, DC14, coreNFW, and Lucky13). The same galaxies have 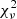 values that are too high for all models of any type. Taking this at face value, neither dark matter nor MOND can explain the data. Rather than conclude that all conceivable models are excluded, we infer that the uncertainties are underestimated in these cases. Similarly, the uncertainties for galaxies with very low
values that are too high for all models of any type. Taking this at face value, neither dark matter nor MOND can explain the data. Rather than conclude that all conceivable models are excluded, we infer that the uncertainties are underestimated in these cases. Similarly, the uncertainties for galaxies with very low 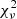 have likely been overestimated. This is a common occurrence in astronomy, where there is often considerable error on the uncertainties.
have likely been overestimated. This is a common occurrence in astronomy, where there is often considerable error on the uncertainties.
The right panel of Fig. 2 shows the different distributions for the maximum-likelihood GN. The lognormal prior gives a very tight distribution around the fiducial value. It appears as a single column in log space and can be resolved by zooming-in on a linear scale. This is essentially consistent with a single value of GN. In contrast, the flat prior results in a wide distribution spanning ∼3.5 dex. This is quite similar to Fig. 1, though we are fitting a different number of parameters and imposing different priors on the galactic parameters. It suggests that the wide posterior distribution is not specific to our case, but a general conclusion of flat priors on GN or g†. Following the same argument made in Li et al. (2018) about g†, we conclude that GN is indeed constant in galaxies. If instead we followed the reasoning of Rodrigues et al. (2018b), we would conclude that GN is not constant, but varies from galaxy to galaxy, just as they conclude for g†. In essence, they believe that there is a meaningful difference between galaxies on one side of the histogram from those on the other, while we do not.
4. Discussion and conclusion
In this paper we presented an inference that Newton’s constant varies as a reductio ad absurdum. This highlights the dangers of degeneracies in parameter estimation from Bayesian fits when the input data are complex and their formal uncertainties cannot be taken too literally. This is motivated by the recent works of Rodrigues et al. (2018a), Chang & Zhou (2019), and Marra et al. (2020), which claim that the acceleration scale g† in the empirical RAR varies from galaxy to galaxy. This conclusion is misleading; if we apply the same logic to GN, we infer that this fundamental constant varies from galaxy to galaxy. Similarly, their conclusion that MOND is ruled out at high statistical significance also applies to fits with dark matter halos (Li et al. 2020): all conceivable models are ruled out if we take the error bars literally.
While the arguments presented here are specific to rotation-curve fits of disk galaxies, they teach us a general lesson about the application of broad priors in Bayesian analyses of astronomical data where there is often considerable uncertainty in the uncertainties. The blind use of Bayesian statistics without properly considering the parameter degeneracy and the uncertain nature of formal errors can lead to absurd conclusions. We use GN in galaxies as an example as it provides a straightforward comparison to the works by Rodrigues et al. (2018a), Chang & Zhou (2019), and Marra et al. (2020). The same issues could arise in other astronomical data sets.
Spitzer Photometry and Accurate Rotation Curves. All data are available at astroweb.case.edu/SPARC.
Acknowledgments
We thank Harry Desmond for useful discussions. This work was supported in part by NASA ADAP grant 80NSSC19k0570. K.-H. C. was supported in part by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2019R1F1A1062477).
References
- Cameron, E., Angus, G. W., & Burgess, J. M. 2020, Nat. Astron., 4, 132 [CrossRef] [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013, MNRAS, 432, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, K.-H., Bernardi, M., Domínguez Sánchez, H., & Sheth, R. K. 2020a, ApJ, 903, L31 [CrossRef] [Google Scholar]
- Chae, K.-H., Lelli, F., Desmond, H., et al. 2020b, ApJ, 904, 51 [CrossRef] [Google Scholar]
- Chang, Z., & Zhou, Y. 2019, MNRAS, 486, 1658 [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Kroupa, P., Banik, I., Haghi, H., et al. 2018, Nat. Astron., 2, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016, AJ, 152, 157 [Google Scholar]
- Lelli, F., McGaugh, S. S., Schombert, J. M., & Pawlowski, M. S. 2017, ApJ, 836, 152 [Google Scholar]
- Lelli, F., McGaugh, S. S., Schombert, J. M., Desmond, H., & Katz, H. 2019, MNRAS, 484, 3267 [NASA ADS] [CrossRef] [Google Scholar]
- Li, P., Lelli, F., McGaugh, S., & Schombert, J. 2018, A&A, 615, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, P., Lelli, F., McGaugh, S., & Schombert, J. 2020, ApJS, 247, 31 [Google Scholar]
- Marra, V., Rodrigues, D. C., & de Almeida, Á. O. F. 2020, MNRAS, 494, 2875 [CrossRef] [Google Scholar]
- McGaugh, S. S., Lelli, F., & Schombert, J. M. 2016, Phys. Rev. Lett., 117, 201101 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., Li, P., Lelli, F., & Schombert, J. M. 2018, Nat. Astron., 2, 924 [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrigues, D. C., Marra, V., del Popolo, A., & Davari, Z. 2018a, Nat. Astron., 2, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrigues, D. C., Marra, V., Del Popolo, A., & Davari, Z. 2018b, Nat. Astron., 2, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J., McGaugh, S., & Lelli, F. 2019, MNRAS, 483, 1496 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1. Posterior probability distribution of Newton’s gravitational constant GN for the galaxies in the SPARC database (Lelli et al. 2016). Following a similar analysis by Rodrigues et al. (2018a) for the acceleration scale g†, galaxies are ordered by increasing value of GN and flat priors are imposed on galaxy distances, stellar mass-to-light ratios, and GN (see text for details). Black dots show the maximum of the posterior probability, together with 1σ, 2σ, and 3σ credible regions from the Python package GetDist. The expected value of GN is represented by the dashed line. Of the selected 101 galaxies, 34 are incompatible with the expected GN at the 3σ level. Taken at face value, this would imply that the gravitational constant is not constant. |
| In the text | |
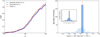 |
Fig. 2. Left: cumulative distribution functions of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



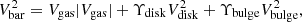
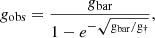
![$$ \begin{aligned} \chi ^2=\sum _R\frac{{[g_{\rm obs}(R)-g_{\rm RAR}(R)]^2}}{\delta g_{\rm obs}^2(R)}, \end{aligned} $$](/articles/aa/full_html/2021/02/aa40101-20/aa40101-20-eq6.gif)