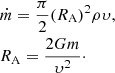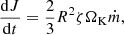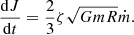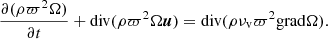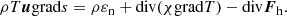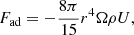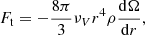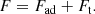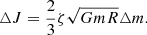| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202037935 | |
| Published online | 12 February 2021 | |
Increasing spin of a B-Star during the common envelope stage
K.A. Barkhatova Astronomical Observatory, B.N. Yeltsin Ural Federal University, Pr. Lenina 51, Ekaterinburg, Russia
e-mail: Evgeny.Staritsin@urfu.ru
Received:
12
March
2020
Accepted:
1
December
2020
Context. In its evolution, the MWC 656 binary system, consisting of a Be star and a black hole, has gone through the common envelope stage. The O and B stars of the early spectral subclasses can be characterised by lower rotational velocities and increased binary frequency. The B star in the MWC 656 system may have undergone rapid rotation during the common envelope stage.
Aims. We study the change in the B star’s state of rotation due to an increase in its angular momentum during the common envelope stage and immediately afterwards.
Methods. We performed one-dimensional numerical calculations of angular momentum transport in the interior of a slightly evolved star on the main sequence with a mass of 16 M⊙. Meridional circulation and shear turbulence are taken into account.
Results. Due to the arrival of angular momentum through the star’s surface, the velocity of the meridional circulation increases by more than six orders of magnitude. Meridional circulation is the main mechanism for the transport of angular momentum into the star’s deep interior. The acquired angular momentum enters the convective core during the common envelope stage if the angular velocity of the accreted matter exceeds half the Kepler value.
Conclusions. The star acquires a rotation typical of classical Be stars if the angular velocity of accreted matter rotation is close to the maximum possible value during the common envelope stage (∼80% of the Kepler value).
Key words: binaries: close / stars: early-type / stars: emission-line / Be / stars: interiors / stars: evolution
© ESO 2021
1. Introduction
Be type stars exhibit the following properties: emission in the Balmer lines of hydrogen, excess radiation in the infrared part of the spectrum, and rapid rotation (Porter & Rivinius 2003). There are several channels by which a Be star can acquire a fast rotation: the process of star birth, the removal of angular momentum from the interior of an isolated star to the exterior during evolution along the main sequence (Meynet & Maeder 2005; Staritsin 2007, 2009; Ekstrom et al. 2008; Granada & Haemmerle 2014; Gagnier et al. 2019), mass and angular momentum exchange in a binary system in the Hertzsprung gap (Pols et al. 1991; Portegies Zwart 1995; Van Bever & Vanbeveren 1997), or the merging of a pair of main sequence stars (Shao & Li 2014).
Massive stars can be characterised by lower rotation velocities and increased binary frequency. The rotational properties of the least-evolved B stars located in Galactic open clusters was analysed by Huang et al. (2010) to obtain a reliable picture about how fast the zero-age main sequence (ZAMS) stars rotate. It was shown that the more massive stars (M > 8 M⊙) tend to be born as slow rotators compared to the less massive stars (M < 8 M⊙). Abt (2009) found that B-stars in open clusters tend to have lower mean cluster rotational velocity and more binary systems. The majority of the O-type stars are also relatively slow rotators. Average velocity of rotation is about 100−125 km s−1 (Vanbeveren et al. 1998). Taking into account macroturbulence and other sources of line-broadening in addition to rotation, Simon-Diaz & Herrero (2014) revised peak in the global distribution of projected rotational velocities in Galactic O- dwarfs downward to 40−60 km s−1. The observed binary fractions of O-type stars and early-type B stars exceed 70% (Chini et al. 2012; Sana et al. 2012). It can be expected that all O-type stars and early-type B stars are born in binaries (Vanbeveren & Mennekens 2017). There is also a significant group of rapidly rotating O-type stars. Many of these stars are runaways. It is likely that they became runaway due to the supernova explosion of the companion or due to the merger of binary components (Vanbeveren 2009; de Mink et al. 2013). Therefore, the formation of Be stars belonging to an early spectral subclass and the phenomenon of duplicity may be closely connected.
Many Be stars create X-ray binary systems paired with compact remnants (Reig 2011). The MWC 656 binary system consists of a Be star with a mass of 10−16 M⊙ and a black hole with a mass of 4−7 M⊙ (Casares et al. 2014). An interesting insight into this system can be obtained from the point of view of a neutron star-black hole pairing, which can coalesce in the Hubble time. According to Grudzinska et al. (2015), the MWC 656 system was created as a result of the passage of a binary system with the initial component masses of ∼41 M⊙ and ∼14 M⊙ through the common envelope stage (CE) at the late stage of a red supergiant. The origin of rapid rotation of less massive star may be either connected to high initial star rotation or to spin-up in CE (or pre-CE mass transfer) phase (Grudzinska et al. 2015). The maximum in the distribution of O and B stars of the early spectral subclass in terms of rotation velocities is ∼100 km s−1 (Vanbeveren & Mennekens 2017). The less massive star of the pair probably did not have a rapid rotation before the common envelope stage. In this paper, we consider the possibility that the binary system’s less massive star spin is increasing during the common envelope evolutionary stage.
Assuming that star rotation is solid, Packet (1981) showed that a star’s spin can reach a critical velocity as a result of accreting ∼3% of the mass with Kepler rotation. The four main processes of angular momentum transport within radiative interiors of stars have been identified up to now: meridional circulation, turbulence driven by instabilities, magnetism, and internal waves (Aerts et al. 2019). The transport of the obtained angular momentum in the accretor’s interior was considered in the particular case of the exchange of matter in a binary system with a massive component possessing a mass of M ≥ 20 M⊙, the evolution of which was accompanied by mixing in the semi-convective region (Staritsin 2019). This earlier paper considered a case where the angular velocity of accreted matter coincides with the angular velocity of the accretor’s surface. Two processes of angular momentum transport within radiative interiors were considered: meridional circulation and shear turbulence. During the accretion stage, a small difference in the angular rotation velocity between the core and the surface of the star is keeping by meridional circulation. So shear turbulence efficiency in angular momentum transport is low. The flux of the angular momentum carried by meridional circulation significantly exceeds the turbulent one. The transport of angular momentum in the depth of the mass gainer is carried out by meridional circulation. An accretor can obtain a rotation typical of Be stars if its mass increases by 30% and the initial rotation velocity is no less than 150 km s−1. In this paper, we consider the capability of meridional circulation and shear turbulence in angular momentum transport in the star’s interior based on the case of accretion in a common envelope environment. Section 2 provides the basic equations and simplifications. Section 3 shows the calculation results. In Sect. 4, we discuss our main results. In Sect. 5, we present our conclusions.
2. Basic equations and simplifications
2.1. Common envelope stage
Over the past 40 years, the hydrodynamics of common envelope escape have been studied in both one-dimensional (Taam et al. 1978; Meyer & Meyer-Hofmeister 1979; Taam 1979) and three-dimensional approximations (Terman et al. 1995; Taam & Sandquist 2000; Taam & Ricker 2010). The placement of a less massive star into a red supergiant’s envelope can be divided into three phases (Podsiadlowski 2001; Ivanova et al. 2013): the loss of co-rotation, dynamical plunge-in, and self-regulated inspiral. The consideration of common envelope escape was presented in a recent paper by Fragos et al. (2019). The placement of a neutron star into the envelope of a red supergiant with a mass of 12 M⊙ was calculated for a period of 20 years. The loss of co-rotation and dynamical plunge-in last for 1.5 years. The self-regulated inspiral phase is the longest. The envelope escapes due to the consumption of the less massive star’s orbital energy and the envelope’s thermal energy: these processes increase the envelope’s gravitational energy and provide it with kinetic energy. According to Fragos et al. (2019), the common envelope stage will last for 50−100 years, after which the remainder of the massive star will retract and the binary system will become detached.
2.2. Accretion
During the dynamical plunge-in phase, and at least at the beginning of the self-regulated inspiral phase, the star moves inside the envelope of the red supergiant with a supersonic velocity (Taam & Sandquist 2000). Due to the effects of spin-up and heating of the envelope, the star’s velocity decreases relative to the envelope and may become subsonic (Terman et al. 1995). In the case of a uniform incident flow of matter, the star accretes matter from the accretion column (Bondi & Hoyle 1944; Ruderman & Spiegel 1971). Density in the red supergiant’s envelope changes vertically. Given the gradient of density in the incident flux, the accretion pattern changes (MacLeod et al. 2017). The material acquires an angular momentum relative to the gravitating object. The angular velocity of the material’s rotation can be 20%–80% of the Kepler one. Therefore, a star can accrete not only mass but also angular momentum.
2.3. Simplifications
The duration of the inspiral may be evaluated according to Livio & Soker (1988):
The accretion rate is given by Bondi (1952):
Here a is the separation, M(a) is the mass in the giant inner to radius a, m is the mass of the secondary, cs is the velocity of sound, ρ is the local density in the common envelope, υ is the relative velocity between the secondary and the common envelope, G – gravitation constant, μ is the Mach number μ = υ/cs, and ζ(μ) is the coefficient in expression of drag force acting on a moving sphere in a gas (Ruderman & Spiegel 1971; Shima et al. 1985).
The density around the secondary is found at an almost constant value throughout the self-regulated regime (Fragos et al. 2019). Excluding the density from expressions (1) and (2) we get the approximate value of the accreted mass
Here η = υ/υK, and υK is the Kepler value of the secondary velocity:
The parameters of the MWC 656 progenitor were determined by population synthesis (Grudzinska et al. 2015): component masses 41 M⊙ and 14 M⊙ and separation – a = 5300 R⊙. After the envelope escapes, the component masses are 13 M⊙ and 14 M⊙, while the separation is a = 142 R⊙. With M(a) = 13 M⊙ and m = 14 M⊙, formula (3) gives the following values of accreted mass: 0.80 M⊙, 1.83 M⊙, and 18.2 M⊙ at three values of the Mach numbers: 1.4, 1.0, and 0.6, respectively, and at η = 1. The values for ζ(μ) were determined according to Shima et al. (1985).
Most of the common envelope stage is taken up by the self-regulated inspiral phase (Fragos et al. 2019). The average value of the accretion rate of mass is assumed to be the same as in this phase. Since the distance between the less massive star and the red supergiant’s core during self-regulated inspiral changes relatively little, we estimate the star’s velocity by distance at the time of envelope escape. The density is assumed to be equal to the average value in the red supergiant’s envelope before the mass exchange stage begins. The red supergiant mass before the mass exchange stage is 17 M⊙ according to Grudzinska et al. (2015). To exclude the uncertainty in mass loss on the red supergiant stage we also consider the limiting case, where the red supergiant mass before the mass exchange is equal to the ZAMS value. The average density is 6 × 10−10 g cm−3 in the first case and 2.4 × 10−9 g cm−3 in the second. The accretion rate of mass is evaluated according to (2) at these two values of the average density and at three values of the Mach number in the case of η = 1 (Table 1).
Accretion rate of mass.
In the case where gradient of density is inherent for the incident flux, the accretion rate of mass was calculated by MacLeod et al. (2017). The results was expressed using classical formulas (Hoyle & Lyttleton 1939):
Here, RA is the accretion radius. Evaluation (4) decreases depending on the RA/Hρ ratio (MacLeod et al. 2017), where Hρ is the height of the scale in terms of density. The accretion rate of mass is ṁ = 0.060 M⊙ yr−1 and ṁ = 0.240 M⊙ yr−1 according to (4) at two values of the average density. The average value of RA/Hρ in the red supergiant’s envelope is ∼1. With this value of RA/Hρ, the rate of mass accretion decreases by an order of magnitude relative to (4) (MacLeod et al. 2017). Assuming the value RA/Hρ ∼ 1 to be typical, we obtain an estimate of the average value of the accretion rate: 0.006 M⊙ yr−1–0.024 M⊙ yr−1.
Formulas (1), (2), (4) are not exact. They only allow evaluate rough values of an accreted mass and a rate of mass accretion. We finally choose an estimate of the accreted mass: △m ≈ 1 M⊙ and the average value of the accretion rate: ṁ ≈ 0.01 M⊙ yr−1. In this case, the duration of the common envelope stage is 100 years, which matches the result obtained by Fragos et al. (2019).
Let the angular velocity of the accreted matter be Ω = ζΩK, where ΩK is the Kepler value of the angular velocity on the star’s surface. Angular momentum flux at the star’s boundary is
where J is the angular momentum of a star, t is time, R is the size of star. Given ΩK = (Gm/R3)0.5, we obtain
The rate of accretion exceeds that one on the thermal timescale. In this case, the accreted layers expand (Ulrich & Burger 1976; Kippenhahn & Meyer-Hofmeister 1977) and interact with the common envelope. Since the expansion does not exceed the accretion radius and the increase in the mass of the star does not exceed ∼7%, we do not consider this interaction; instead, we examine the arrival of angular momentum at rate (5) through the surface of a star with constant mass.
2.4. Transport of angular momentum
The angular momentum transfer in a star’s radiative layers is described by the law of the conservation of angular momentum (Tassoul 1978):
The second term on the left side of the equation describes the transport of angular momentum by meridional circulation: the term on the right side describes turbulent transport. The meridional circulation velocity, u, is determined from the law of the conservation of energy in a stationary form (Maeder & Zahn 1998):
In these equations, ϖ is the distance to the rotation axis, νv is the vertical turbulent viscosity, T is the temperature, s is the specific entropy, εn is the rate of nuclear energy release, χ is the thermal conductivity, and Fh is the horizontal turbulent enthalpy flux. Fh = −νhρT∂s/∂iθ: νh is the horizontal turbulent viscosity (i.e. along the surface of constant pressure).
The radiative envelopes of rotating stars are sites of anisotropic turbulence (Talon & Zahn 1997). The transport properties of turbulence are much stronger in the horizontal direction than in the vertical. Due to the anisotropy of turbulence, the star’s radiative envelope is in a state of shellular rotation (Zahn 1992); that is, the angular velocity of rotation varies slightly on constant pressure surface. Strong horizontal turbulence prevents the creation of a non-spherical distribution of the average molecular weight in a layer with a variable chemical composition. Therefore, meridional circulation in this layer does not stop. Turbulent viscosity coefficients were determined by Talon & Zahn (1997), Maeder (2003), and Mathis et al. (2004). The vertical component of meridional circulation velocity in the case of the star’s shellular rotation can be presented as Ur(r, θ) = U(r)P2(θ) (Zahn 1992), where U(r) is the amplitude of the vertical velocity component of meridional circulation (hereafter, the amplitude of meridional circulation velocity) and P2(θ) is the spherical harmonic of order 2; the higher order harmonics do not contribute to the vertical transport of angular momentum (Mathis & Zahn 2004). Equations (6) and (7) are solved under the assumption of the star’s shellular rotation and by taking into account pointed expansion of the vertical component of the meridional circulation velocity in latitude. It is assumed that the convective core rotates rigidly.
To solve Eq. (6), a difference scheme based on the integro-interpolation method (Samarskij & Popov 1992) was elaborated (Staritsin 1999, 2005, 2007). The method implies an integration of Eq. (6) by a volume of layer located between two sequences of constant pressure. The Eq. (6) after integration gives the low of the conservation of angular momentum for each layer. In the case of an isolated star, the advective and turbulent angular-momentum fluxes at the surface of the star are assumed to be zero. In the case of an accreting star, the influx of angular-momentum through its surface may be defined by Eq. (5).
The transport of angular momentum in rapidly rotating isolated Be stars was studied through one-dimensional (Meynet & Maeder 2005; Staritsin 2007, 2009; Ekstrom et al. 2008; Granada & Haemmerle 2014) and two-dimensional (Gagnier et al. 2019) approximations. The influence of rotation on a star’s structure can be taken into account with Clairaut’s theory (e.g., Staritsin 1999). Even in the case of a critical rotation of the star’s surface, the dense inner layers rotate slowly. The compression of the constant pressure surfaces in the inner layers, which account for more than 99% of the stellar mass, does not exceed 0.05 (Staritsin 2007). Only the outer low-density envelope has a rapid rotation. The one-dimensional (1D) and two-dimensional (2D) approximations offer consistent conclusions about the degree of differential rotation in the radiative envelopes of rapidly rotating isolated stars (Espinosa Lara & Rieutord 2013).
2.5. Initial model
The stellar masses in the binary system from which the MWC 656 system was created differ greatly (Grudzinska et al. 2015). When the massive component reaches the red supergiant stage, the hydrogen content in the core of the less massive component is only slightly decreased. To examine the angular momentum transfer into the star located in the common envelope, we take the model of a slightly evolved star with a mass of 16 M⊙ and an angular momentum of 9.9 × 1051 erg × s (Staritsin 2017). On ZAMS, the rotation velocity has a typical value of 100 km s−1, the difference in the angular velocity of rotation between the core and the surface of the star is ∼18% and the content of hydrogen and heavy elements are 0.70 and 0.02, respectively. By the time of immersion in the common envelope, the hydrogen content in the core decreased to ∼0.60 (Fig. 1). The rotation velocity decreased to 97 km s−1. The difference in the angular velocity of rotation between the core and the star’s surface increased to 34%. In the star’s radiative envelope, there are two cells of circulation with the opposite direction of transport of angular momentum (Fig. 1). The right panel in Fig. 1 presents the use of the radius to resolve a cell of circulation in the outer low density layer. In most of the radiative envelope, U < 0. The advective flux of angular momentum is directed outwards (Fig. 1). In an external cell with a low density, U > 0. This pattern of meridional circulation is typical for massive main sequence stars with slow rotations (Staritsin 2007). In most of the radiative envelope, meridional circulation is the main mechanism of angular momentum transport. In the layer with a variable chemical composition, angular momentum is transported only by meridional circulation (Fig. 1). It is only in the outer cell, where meridional circulation transports angular momentum inwards, that the turbulent flux is stronger: thus, the total angular momentum flux in this layer is also directed outwards (Fig. 1).
 |
Fig. 1. Structure of a star with a mass of 16 M⊙ before the common envelope stage. Distributions of the hydrogen content by mass X (top line), angular velocity of rotation Ω (second line), amplitude of the meridional circulation velocity U (third line), angular momentum flux F (bottom line): turbulent (solid line), advective (dashed line), and full (thick solid line) are shown depending on the mass of the matter inside the isobar (left panel) and the average distance to the isobar (right panel). |
To perform the evolutionary computation taking into account angular momentum transport, we divide the model of a star into the interior part and the exterior part (Paczynski 1970). The boundary condition (5) is applied to the interior part. Only 3.2 × 10−6 M⊙ is included in the exterior part. It is supposed that the exterior part rotates rigidly with the same angular velocity as the upper layer of interior part does.
3. Results
The increase in angular momentum of a star in the envelope of a red supergiant was examined at three values of the parameter ζ: 0.8, 0.5, and 0.2. In this case, the flux of angular momentum at the star’s boundary is 1.0 × 1043, 6.25 × 1042 and 2.5 × 1042 g (cm s−1)2, respectively. Such flux values exceed typical fluxes in the interiors of isolated stars on the main sequence by 106 times (Staritsin 2007). Due to the influx of angular momentum in the star’s outer layer, a cell of circulation, in which the angular momentum is transported inwards, is formed. The meridional circulation velocity in this cell decreases in the direction of the star interior, and the highest velocity is of the order of ∼1 km s−1 (Fig. 2, left panel). Between this cell and previously existing ones, up to seven cells with opposite directions of angular momentum transport are created. The thicknesses of these cells are not large. The highest value of meridional circulation velocity in these cells is much lower than in the outer one and it decreases in the inside direction of the star. The circulation velocity in the pre-existing cells remains almost the same as before the start of the common envelope stage until these cells disappear. Over time, the lower boundary of the outer cell settles down inside the star and reaches the convective core 35 and 56 years after the start of the common envelope stage at ζ = 0.8 and 0.5, respectively. After this, a uniform direction of meridional circulation is established in the star’s radiative envelope. A typical value of circulation velocity is 50 − 150 cm s−1, which is ∼106 times higher than that of isolated stars on the main sequence with the same mass. For ζ = 0.2, the mass of the material in the outer cell at the end of the common envelope stage is ∼5 M⊙ (Fig. 2, left panel).
 |
Fig. 2. Amplitude of the velocity of the meridional circulation U at the common envelope stage and after its completion. The amplitude distribution is shown for ζ = 0.8 (top line), ζ = 0.5 (middle line), and ζ = 0.2 (bottom line) for the following time instants during the common envelope stage (left panel): 1 year (solid line), 10 years (dashed line), 30 years (dash-dotted line), and 100 years (thick solid line). The time instants after its completion (right panel) are 5 × 103 years (solid line), 104 years (dashed line), and 5 × 104 years (dash-dotted line). The velocity values U > 250 cm s−1 are not shown. |
Due to the influx of angular momentum through the star’s surface, the angular velocity of rotation in the star’s subsurface layers increases (Fig. 3, left panel). An increase in the angular velocity of rotation occurs in the outer circulation cell. As the lower boundary of this cell lowers, the angular velocity rises in ever deeper layers of the star. In this case, the increase in the angular velocity of rotation is highest near the star’s surface and decreases towards the lower boundary. The ratio of the angular velocity of rotation of the convective core and the star’s surface decreases (Fig. 4). When ζ = {0.8, 0.5}, the lower boundary of the outer cell reaches the boundary of the convective core: angular momentum begins to flow into the convective core. The higher the value of the flux of the angular momentum at the star’s boundary, the greater the increase in the velocity of rotation of the convective core (Fig. 3, left panel). The ratio of the angular velocities of rotation of the convective core and the star’s surface begins to increase (Fig. 4). The spatial change in the angular velocity of rotation right above the convective core (Fig. 3, left panel) is due to the influence of a layer with a variable chemical composition on meridional circulation velocity.
 |
Fig. 3. Angular velocity of rotation in the star’s interior Ω(m) during the common envelope stage and after its completion. The angular velocity distribution is shown for ζ = 0.8 (top line), ζ = 0.5 (middle line), and ζ = 0.2 (bottom line) for the following time instants during the common envelope stage (left panel): 1 year (solid line), 10 years (dashed line), 30 years (dash-dotted line), and 100 years (thick solid line). The time instants after its completion (right panel) are 103 years (thick solid line), 5 × 103 years (solid line), 104 years (dashed line), and 5 × 104 years (dash-dotted line). |
 |
Fig. 4. Difference in angular velocities of rotation between the convective core and the star’s surface. The ratio of the angular rotational velocities of the convective core and the star’s surface Ωc/Ωs(t) during the common envelope stage (left panel) and after its completion (right panel) is shown for ζ = 0.8 (solid line), ζ = 0.5 (dashed line), and ζ = 0.2 (dash-dotted line). |
After the angular velocity of rotation and the amplitude of the velocity of the meridional circulation are obtained as a result of solving Eqs. (6) and (7), it is then possible to calculate the momentum fluxes – advective Fad, turbulent Ft and total F (Zahn 1994):
The angular momentum is transported inside the star in the outer circulation cell: as the lower boundary of this cell goes down in the case when ζ = {0.8, 0.5}, it extends to the entire radiative envelope of the star (Fig. 5, left panel). Angular momentum begins to enter the convective core only after the lower boundary of the outer circulation cell reaches the boundary of the convective core. The main mechanism of the angular momentum transport in most of the external circulation cell is meridional circulation. Only in the layer where the gradient of the angular velocity of rotation reaches its maximum value is the turbulent transport of angular momentum comparable with the advective one (Fig. 6).
 |
Fig. 5. Flux of the angular momentum in the interior of the star F(m) during the common envelope stage and after its completion. The flux is shown for ζ = 0.8 (top line), ζ = 0.5 (middle line) and ζ = 0.2 (bottom line) for the following points in time during the common envelope stage (left panel): 1 year (solid line), 10 years (dashed line), 30 years (dash-dotted line), and 100 years (thick solid line). The time points after its completion (right panel) are: 103 years (thick solid line), 5 × 103 years (solid line), 104 years (dashed line), and 5 × 104 years (dash-dotted line). |
 |
Fig. 6. Momentum flux in the star’s interior at the common envelope stage for ζ = 0.8. The turbulent flux Ft (solid line), the advective flux Fad (dashed line), and the total flux F (thick solid line) are shown 30 years after the start of the common envelope stage depending on the mass of the matter inside the isobar (left panel) and the average distance to the isobar (right panel). |
As a result of evolution in the common envelope, the star’s angular momentum increases to Jfin: 4.15 × 1052, 2.96 × 1052, and 1.78 × 1052 erg × s with ζ equal to 0.8, 0.5, and 0.2. After escaping the common envelope and the termination of accretion, the meridional circulation velocity in the star’s interior decreases by a factor of 103.
The evolution of the star’s state of rotation is calculated further over the thermal time scale, which is when evolutionary changes in the star’s structure can be neglected. A cell of circulation where meridional circulation transports angular momentum outside is created in the outer layer of the star (Fig. 2, right panel). We note that the right panel of Fig. 2 uses radius to resolve this cell; in mass-coordinates, such a cell would be seen as just a vertical line as it does in Fig. 1, the left panel. The cell of circulation may have appeared due to the cessation of angular momentum transport through the star’s surface. The position of the lower boundary of this cell practically does not change over time. Since the density in this cell is low, the flux of angular momentum is insignificant. We have the inner cell of circulation below.
The inner cell of circulation covers almost the entire radiative envelope of the star if ζ = {0.8, 0.5}. Meridional circulation in this cell still transports angular momentum inside the star. The velocity of meridional circulation is much greater than that of isolated stars on the main sequence with the same mass. The meridional circulation velocity gradually decreases over time (Fig. 2, right panel) as the distribution of the angular velocity of rotation changes (Fig. 3, left panel) due to the transport of angular momentum.
When ζ = 0.2, a similar cell of circulation is located in the middle of the radiative envelope after the end of the common envelope stage. Below this cell, there is a cell of circulation that existed even before the start of the common envelope stage. The boundary between the cells decreases over time inside the star and 3000 years after the end of the common envelope stage, it reaches the convective core and the lower cell disappears. Afterwards, angular momentum also begins to flow into the convective core.
The maximum value of meridional circulation velocity in the inner cell is 6 × 10−3, 10−2, and 2 × 10−2 cm s−1 at the end of the indicated time interval with ζ equal to 0.8, 0.5, and 0.2, respectively. Meridional circulation velocity remains ∼102 times higher than that of isolated stars. The direction of circulation here is opposite to the direction of circulation in isolated stars.
Due to the transport of angular momentum from the star’s outer layers to the inner layers, the angular velocity of the convective core and that of the lower part of the radiative envelope increases: it decreases in the upper part of the radiative envelope (Fig. 3, right panel). After a thermal timescale, the angular velocity of the convective core exceeds the angular velocity of the surface by 8% at ζ = 0.8 and virtually coincides with it at ζ = 0.5. The difference in the angular rotational velocities of the convective core and surface during the evolution of an isolated star on the main sequence increases, depending on its angular momentum (Staritsin 2007). The faster an isolated star rotates, the stronger the displacement of angular momentum from the inner layers to the exterior, and the lower the increase in the differential. The differential, determined by the evolution, at the given stage in an isolated star is expected to be within 18%–34%. Thus, a star that has gone through the common envelope stage can be characterised by a slightly faster rotation of the upper radiative envelope and a slightly slower rotation of the convective core compared to an isolated main sequence star with the same mass, angular momentum, and age. It is for this reason that within the star’s interior, angular momentum continues to be transported from the outer layers to the inner layers after the end of the common envelope stage. The higher is the increase in the star’s angular momentum at the common envelope stage, the fewer differences there are between the state of rotation of the star following the end of this stage and that of the isolated star.
The ratio of the angular rotational velocities of the convective core and the star’s surface at ζ = 0.2 begins to increase immediately after the end of the common envelope stage (Fig. 4) before the gained angular momentum begins to enter the convective core. The ratio of the angular velocities of the convective core and the surface remains the lowest among the cases considered. The rotation of the star in this case is most different from what is considered typical of an isolated star with the same mass, angular momentum, and hydrogen content in the convective core.
The flux of the angular momentum after the end of the common envelope stage is directed inside the star (Fig. 5, right panel). Since the state of rotation of a star after the common envelope stage differs from the evolutionarily determined state of rotation of an isolated star, meridional circulation is the main mechanism of angular momentum transport. This conclusion is similar to the conclusion about the role of meridional circulation in zero-age star models with rotation noticeably different from equilibrium rotation (Staritsin 2005). Only in the outer cell of circulation does the turbulent flux of angular momentum exceed the advective one: thus, the total flux is also directed inwards in this layer of the star (Fig. 7).
 |
Fig. 7. Characteristics of a star with a mass of 16 M⊙ 5 × 104 years after the end of the common envelope stage for ζ = 0.8. Distributions of the angular velocity of rotation Ω(r) (top), the amplitude of the velocity of the meridional circulation U(r) (middle), and the flux of the angular momentum (bottom): turbulent Ft(r) (solid line), advective Fad(r) (dashed line), and full F(r) (thick solid line) are shown depending on the average distance to the isobar. |
The total transport of angular momentum into the star’s deep interior is determined by the velocity of rotation of the accreted matter. With a relatively rapid rotation of the accreted matter where ζ ≥ 0.5, angular momentum occurs in the inner layers of the star mainly during the common envelope stage (Fig. 8). With a relatively slow rotation, where ζ = 0.2, the incoming angular momentum is localised in the upper part of the radiative envelope. Following the end of the common envelope stage, the momentum is transported much less intensively into the star’s interior. There is evident transport intensity dependence on the star’s angular momentum, albeit weak.
 |
Fig. 8. Angular momentum distribution J(m) inside a star with a mass of 16 M⊙. The distribution is shown for ζ = 0.8 (top), ζ = 0.5 (middle), ζ = 0.2 (bottom) for the following time points: 1 year, 10 years, 30 years, 100 years during the common envelope stage, and 5 × 104 years after its completion (solid lines from bottom to top). |
4. Discussion
The equatorial surface rotation velocity of the less massive component of a binary star increases to values exceeding 400 km s−1 as a result of an increase in its angular momentum at the common envelope stage (Fig. 9). Upon completion of this stage, the rotation velocity decreases slightly due to the ongoing transport of angular momentum from the outer parts of the star to the inner ones. The rotation velocity and its relation to the critical velocity depend on how strongly the star’s angular momentum had increased during the common envelope stage.
 |
Fig. 9. Evolution of the surface velocity of rotation of a star with a mass of 16 M⊙. The equatorial rotation velocity Ve(t) (top) and the ratio of this velocity to the critical one Ve/Vc(t) (bottom) during the common envelope stage (left panel) and after its completion (right panel) are shown for ζ = 0.8 ( solid line), ζ = 0.5 (dashed line), and ζ = 0.2 (dash-dotted line). |
If ζ = 0.8 and Jfin = 4.15 × 1052, the increase in the surface rotation velocity is greatest. The ratio of the surface rotation velocity to the critical value increases to 0.98 during the common envelope stage (Fig. 9). In this case, the state of the star’s rotation after the end of the common envelope stage is close to that which was determined in an evolution of isolated star. The ratio of the surface and critical rotation velocities decreases further as the star approaches this state of rotation (Fig. 9). The lowest ratio of the surface and critical rotational velocities of an isolated star in the main sequence with such an angular momentum is ∼0.7 (Staritsin 2007). A similar behaviour on the part of the rotation velocity was obtained in calculating the accretion of matter on a thermal timescale on a chemically homogeneous star with an initial mass of 6 M⊙, when the angular velocity of the accreted matter coincides with the current angular velocity of the star’s surface (Staritsin 2019). After an increase in the star’s mass by 2 M⊙, the surface to critical velocity ratio reaches 0.96. When accretion is over, this ratio decreases, and the lapse of the thermal timescale becomes 0.86: the minimum possible ratio in this case is 0.75. Thus, if a star reaching a critical rotation can provide the reason for the termination of accretion, then even if the star has fast rotation, it is lower than the critical one after the accretion is over. This conclusion was drawn for stars on the main sequence under two different masses and different assumptions about the mass of the accreted matter, the duration of accretion, and the rate of increase in the star’s angular momentum during accretion.
In the MWC 656 system creation scenario, the remainder of a more massive star explodes as SNIb/c 3 × 105 years after the common envelope stage (Grudzinska et al. 2015). The typical synchronisation time of the intrinsic rotation of the B star with an orbital rotation after the end of the common envelope stage is ∼2 × 106 years, according to Tassoul’s mechanism (Tassoul 1987). Therefore, tidal interaction will not affect the B star’s rotation strongly prior to the explosion of the remainder. After the explosion of the remainder, the synchronisation time is approximately half the lifetime of the B star on the main sequence. The star can maintain rapid rotation only during the first part of evolution along the main sequence.
Be stars belonging to the early spectral subclasses have a subcritical rotation, albeit fast. The rotation velocity of stars of this type is, on average, 75% of the critical value (Fremat et al. 2005). The surface and critical rotational velocity ratio ranges from 0.4 − 0.6 to 0.9 − 1.0 according to Cranmer (2005) and exceeds 0.63, according to Huang et al. (2010). Therefore, when Jfin = 4.15 × 1052, the star will have sufficient rotation to demonstrate Be star characteristics during the first part of evolution along the main sequence.
When ζ = 0.5 and Jfin = 2.96 × 1052, the surface and critical rotation velocity ratio becomes less than 0.6 18 000 years after the common envelope stage. The minimum possible ratio for an isolated main sequence star in this case is 0.4 (Staritsin 2007). Thus, the surface and critical rotational velocity ratio falls into the region of the lower boundary for Be stars, according to Cranmer (2005). Given tidal interaction, it is unlikely that a star could exhibit Be characteristics in this case.
When ζ = 0.2 and Jfin = 1.78 × 1052, the surface and critical rotational velocity ratio becomes less than 0.4 after the lapse of the thermal timescale after the common envelope stage. In this case, the state of the star’s rotation differs most from the evolutionarily determined one. The characteristic transport time of angular momentum in the star’s interior ∼R/U is ∼7% of its lifetime along the main sequence. In the future, the state of rotation will be the same as for a star with the same angular momentum that did not pass through the common envelope stage.
The possibility that Be stars will form also depends on how much mass is accreted. In the considered case, the star increase its mass on ∼6%. It is twice more than Packet’s estimation (Packet 1981) because the rotation of accreted mass is limited by 80% of the Kepler value and the transport of angular momentum is not instantaneous. Using Eq. (5), we can get an increase of a star’s angular momentum △J as a function of accreted mass △m:
The increase of stars angular momentum in the case where 5△m/8 is accreted with angular velocity of rotation equal to 80% of Kepler value is the same as in the considered case of ζ = 0.5. Therefore, the decrease of accreted mass twice does not produce the phenomenon of a Be star. In such a case, other mechanisms behind the spinning-up of star should be considered.
5. Conclusions
In this work, we examine the origin of the fast rotation of a Be star in a binary system with the black hole MWC 656. The creation of this system was preceded by evolution in a common envelope (Grudzinska et al. 2015). Detailed insights into this evolution in the common envelope are still lacking. Currently, we have at our disposal only rough information about this stage’s duration, the less massive star’s position in the red supergiant’s envelope, the conditions for the accretion of matter, and the angular momentum. Using the latest results from modelling the evolution of a common envelope (Fragos et al. 2019) and accretion into a star located in a common envelope (MacLeod et al. 2017), we formulated a simplified problem for the evolution of the state of a star’s rotation with an influx of angular momentum through its surface at a constant rate. We studied two processes of angular momentum transport within radiative interiors of a star: meridional circulation and shear turbulence. We found that the main mechanism for the transport of angular momentum entering through the star’s surface into its interior is the circulation of matter in the meridional plane. The turbulent transport of angular momentum is comparable with the advective one only in a relatively narrow layer of the star’s radiative envelope, where the gradient of the angular velocity of rotation is highest. A star can obtain the fast rotation typical of Be stars only if the angular velocity of the rotation of accreted matter is close to 80% of the Kepler value. We should note that this is the highest possible value of the angular velocity of the accreted matter during the common envelope stage, according to MacLeod et al. (2017). Another condition of this case is the increase of the stars mass by no less than 6% during the common envelope stage.
After the end of the common envelope stage, the B-star can be characterised by a lower rotation velocity of the convective core and an increased rotation velocity of the upper radiative envelope in comparison with an isolated star with the same mass, angular momentum, and age. Due to the ongoing transport of angular momentum from the upper part of the radiative envelope to the star’s inner layers, the rotation velocity of the star’s surface decreases slightly. If a star reaching a critical rotation velocity during accretion causes accretion to cease, then such a star will have a fast but subcritical rotation after accretion ends, which is well matched with what has been observed in Be stars belonging to an early spectral subclass.
Acknowledgments
This work was supported by the Ministry of Science and Education, FEUZ-2020-0030 and by the Act no. 211 of the Government of the Russian Federation, agreement no. 02.A03.21.0006.
References
- Abt, H. A. 2009, PASP, 121, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Aerts, C., Mathis, S., & Rogers, T. 2019, ARA&A, 57, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Casares, J., Neguerue, I., Ribo, M., et al. 2014, Nature, 505, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Chini, R., Hoffmeister, V. H., Nasseri, A., Stahl, O., & Zinnecker, H. 2012, MNRAS, 424, 1925 [Google Scholar]
- Cranmer, S. 2005, ApJ, 634, 585 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S., Langer, N., Izzard, R., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Ekstrom, S., Meynet, G., Maeder, A., & Barblan, F. 2008, A&A, 478, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2013, A&A, 552, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fragos, T., Andrews, J., Ramirez-Ruiz, E., et al. 2019, ApJ, 883, 45 [Google Scholar]
- Fremat, Y., Zorec, J., Hubert, A.-M., & Floquet, M. 2005, A&A, 440, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gagnier, D., Rieutord, M., Charbonnel, C., Putigny, B., & Espinosa Lara, F. 2019, A&A, 625, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Granada, A., & Haemmerle, L. 2014, A&A, 570, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grudzinska, M., Belczynski, K., Casares, J., et al. 2015, MNRAS, 452, 2773 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Lyttleton, R. 1939, Proc. Camb. Philos. Soc., 35, 405 [Google Scholar]
- Huang, W., Gies, D., & McSwain, M. 2010, ApJ, 722, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Kippenhahn, R., & Meyer-Hofmeister, E. 1977, A&A, 54, 539 [NASA ADS] [Google Scholar]
- Livio, M., & Soker, N. 1988, ApJ, 329, 764 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, M., Antoni, A., Murguia-Berthier, A., Macias, P., & Ramirez-Ruiz, E. 2017, ApJ, 838, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2003, A&A, 399, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Mathis, S., & Zahn, J.-P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Palacios, A., & Zahn, J.-P. 2004, A&A, 425, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, F., & Meyer-Hofmeister, E. 1979, A&A, 78, 167 [NASA ADS] [Google Scholar]
- Meynet, G., & Maeder, A. 2005, ASP Conf. Ser., 337, 15 [Google Scholar]
- Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
- Paczynski, B. 1970, Acta Astron., 20, 47 [Google Scholar]
- Podsiadlowski, P. 2001, ASP Conf. Ser., 229, 239 [Google Scholar]
- Pols, O., Cote, J., Waters, L., & Heise, J. 1991, A&A, 241, 419 [Google Scholar]
- Portegies Zwart, S. 1995, A&A, 296, 691 [Google Scholar]
- Porter, J., & Rivinius, T. 2003, PASP, 115, 1153 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P. 2011, Ap&SS, 332, 1 [Google Scholar]
- Ruderman, M., & Spiegel, E. 1971, ApJ, 165, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Samarskij, A., & Popov, U. 1992, Raznostnye metody reshenij zadach gazovoy dinamiki (Moscow: Nauka) [Google Scholar]
- Sana, H., de Mink, S., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Shao, Y., & Li, X.-D. 2014, ApJ, 796, 37 [Google Scholar]
- Shima, E., Matsuda, T., Takeda, H., & Sawada, K. 1985, MNRAS, 217, 367 [NASA ADS] [Google Scholar]
- Simon-Diaz, S., & Herrero, A. 2014, A&A, 562, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Staritsin, E. I. 1999, Astron. Rep., 43, 592 [Google Scholar]
- Staritsin, E. I. 2005, Astron. Rep., 49, 634 [Google Scholar]
- Staritsin, E. I. 2007, Astron. Lett., 33, 93 [Google Scholar]
- Staritsin, E. I. 2009, Astron. Lett., 35, 413 [Google Scholar]
- Staritsin, E. I. 2017, Astron. Rep., 61, 450 [Google Scholar]
- Staritsin, E. I. 2019, Ap&SS, 364, 110 [Google Scholar]
- Taam, R. 1979, Astrophys. Lett., 20, 29 [Google Scholar]
- Taam, R., & Ricker, P. 2010, New Astron. Rev., 54, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R., & Sandquist, E. 2000, ARA&A, 38, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R., Bodenheimer, P., & Ostriker, J.-P. 1978, ApJ, 222, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Talon, S., & Zahn, J.-P. 1997, A&A, 317, 749 [Google Scholar]
- Tassoul, J.-L. 1978, Theory of Rotating Stars (Princeton: Princeton University Press) [Google Scholar]
- Tassoul, J.-L. 1987, ApJ, 322, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Terman, J., Taam, R., & Hernquist, L. 1995, ApJ, 445, 367 [CrossRef] [Google Scholar]
- Ulrich, R., & Burger, H. 1976, ApJ, 206, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Van Bever, J., & Vanbeveren, D. 1997, A&A, 322, 116 [Google Scholar]
- Vanbeveren, D. 2009, New Astron. Rev., 53, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Vanbeveren, D., & Mennekens, N. 2017, ASP Conf. Ser., 508, 121 [NASA ADS] [Google Scholar]
- Vanbeveren, D., De Loore, C., & Van Rensbergen, W. 1998, A&ARv, 9, 63 [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1994, Space Sci. Rev., 66, 285 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Structure of a star with a mass of 16 M⊙ before the common envelope stage. Distributions of the hydrogen content by mass X (top line), angular velocity of rotation Ω (second line), amplitude of the meridional circulation velocity U (third line), angular momentum flux F (bottom line): turbulent (solid line), advective (dashed line), and full (thick solid line) are shown depending on the mass of the matter inside the isobar (left panel) and the average distance to the isobar (right panel). |
| In the text | |
 |
Fig. 2. Amplitude of the velocity of the meridional circulation U at the common envelope stage and after its completion. The amplitude distribution is shown for ζ = 0.8 (top line), ζ = 0.5 (middle line), and ζ = 0.2 (bottom line) for the following time instants during the common envelope stage (left panel): 1 year (solid line), 10 years (dashed line), 30 years (dash-dotted line), and 100 years (thick solid line). The time instants after its completion (right panel) are 5 × 103 years (solid line), 104 years (dashed line), and 5 × 104 years (dash-dotted line). The velocity values U > 250 cm s−1 are not shown. |
| In the text | |
 |
Fig. 3. Angular velocity of rotation in the star’s interior Ω(m) during the common envelope stage and after its completion. The angular velocity distribution is shown for ζ = 0.8 (top line), ζ = 0.5 (middle line), and ζ = 0.2 (bottom line) for the following time instants during the common envelope stage (left panel): 1 year (solid line), 10 years (dashed line), 30 years (dash-dotted line), and 100 years (thick solid line). The time instants after its completion (right panel) are 103 years (thick solid line), 5 × 103 years (solid line), 104 years (dashed line), and 5 × 104 years (dash-dotted line). |
| In the text | |
 |
Fig. 4. Difference in angular velocities of rotation between the convective core and the star’s surface. The ratio of the angular rotational velocities of the convective core and the star’s surface Ωc/Ωs(t) during the common envelope stage (left panel) and after its completion (right panel) is shown for ζ = 0.8 (solid line), ζ = 0.5 (dashed line), and ζ = 0.2 (dash-dotted line). |
| In the text | |
 |
Fig. 5. Flux of the angular momentum in the interior of the star F(m) during the common envelope stage and after its completion. The flux is shown for ζ = 0.8 (top line), ζ = 0.5 (middle line) and ζ = 0.2 (bottom line) for the following points in time during the common envelope stage (left panel): 1 year (solid line), 10 years (dashed line), 30 years (dash-dotted line), and 100 years (thick solid line). The time points after its completion (right panel) are: 103 years (thick solid line), 5 × 103 years (solid line), 104 years (dashed line), and 5 × 104 years (dash-dotted line). |
| In the text | |
 |
Fig. 6. Momentum flux in the star’s interior at the common envelope stage for ζ = 0.8. The turbulent flux Ft (solid line), the advective flux Fad (dashed line), and the total flux F (thick solid line) are shown 30 years after the start of the common envelope stage depending on the mass of the matter inside the isobar (left panel) and the average distance to the isobar (right panel). |
| In the text | |
 |
Fig. 7. Characteristics of a star with a mass of 16 M⊙ 5 × 104 years after the end of the common envelope stage for ζ = 0.8. Distributions of the angular velocity of rotation Ω(r) (top), the amplitude of the velocity of the meridional circulation U(r) (middle), and the flux of the angular momentum (bottom): turbulent Ft(r) (solid line), advective Fad(r) (dashed line), and full F(r) (thick solid line) are shown depending on the average distance to the isobar. |
| In the text | |
 |
Fig. 8. Angular momentum distribution J(m) inside a star with a mass of 16 M⊙. The distribution is shown for ζ = 0.8 (top), ζ = 0.5 (middle), ζ = 0.2 (bottom) for the following time points: 1 year, 10 years, 30 years, 100 years during the common envelope stage, and 5 × 104 years after its completion (solid lines from bottom to top). |
| In the text | |
 |
Fig. 9. Evolution of the surface velocity of rotation of a star with a mass of 16 M⊙. The equatorial rotation velocity Ve(t) (top) and the ratio of this velocity to the critical one Ve/Vc(t) (bottom) during the common envelope stage (left panel) and after its completion (right panel) are shown for ζ = 0.8 ( solid line), ζ = 0.5 (dashed line), and ζ = 0.2 (dash-dotted line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



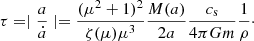
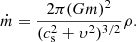
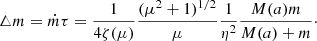
![$$ \begin{aligned} \upsilon _{\rm K}=\left[\frac{G(M(a)+m)}{a}\right]^{1/2}\cdot \end{aligned} $$](/articles/aa/full_html/2021/02/aa37935-20/aa37935-20-eq4.gif)