| Issue |
A&A
Volume 645, January 2021
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202039924 | |
| Published online | 15 January 2021 | |
Comprehensive rotational study and astronomical search for cyclopropanecarboxaldehyde★
1
Instituto de Física Fundamental (IFF-CSIC), Group of Molecular Astrophysics, C/ Serrano 121,
28006 Madrid,
Spain
e-mail: carlos.cabezas@csic.es
2
Departamento de Química Física, Facultad de Ciencias y Tecnologías Químicas, Universidad de Castilla-La Mancha Avda, Camilo José Cela 1B. 13071,
Ciudad Real, Spain
3
Observatorio de Yebes (IGN), Cerro de la Palera s/n,
19141 Yebes,
Guadalajara, Spain
4
Observatorio Astronómico Nacional (OAN-IGN), C/ Alfonso XII 3,
28014 Madrid, Spain
Received:
17
November
2020
Accepted:
2
December
2020
Context. At least a dozen molecules with a formyl group (HCO) have been observed to date in the interstellar medium (ISM), suggesting that other such species exist and remain to be discovered. However, there is still a lack of high-resolution spectroscopic data for simple molecular species of this type that could provide a basis for their detection.
Aims. Cyclopropanecarboxaldehyde, c-C3H5CHO, is a small molecule containing a formyl group and is therefore an interesting candidate for astrophysical detection. The rotational spectrum of cyclopropanecarboxaldehyde has been observed before, but its experimental rotational parameters are not precise enough to allow its detection in the millimetre-wave domain.
Methods. We measured the rotational spectrum of cyclopropanecarboxaldehyde in the frequency ranges 31.5–50 GHz and 72–116.5 GHz using the GACELA (GAS CEll for Laboratory Astrophysics) broadband high-resolution rotational spectrometer constructed at the Yebes Observatory. The spectroscopic study was supported by high-level theoretical calculations which were used in the identification of the vibrational excited states of cyclopropanecarboxaldehyde.
Results. Our analysis of the rotational spectrum of cyclopropanecarboxaldehyde allowed us to obtain accurate rotational parameters for the ground state of both cis and trans isomers, which were used to derive sufficiently reliable predictions up to 300 GHz. In addition to the ground states, we identified 12 and 6 vibrationally excited states for the trans and cis isomers, respectively, including fundamental modes, multiple excitation quanta, and combination states. We find that the gas phase concentration of the trans isomer is almost 1.2 times larger than that of the cis one. These new experimental rotational parameters were employed to search for cyclopropanecarboxaldehyde in the warm molecular clouds Orion KL and Sgr B2(N) using the spectral surveys captured by ALMA (Orion) and IRAM 30 m (Sgr) at 1 and 3 mm, respectively.
Key words: ISM: molecules / methods: laboratory: molecular / molecular data / line: identification
Data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/645/A75
© ESO 2021
1 Introduction
Among the more than 200 molecular species detected so far in the interstellar medium (ISM) or circumstellar shells1, 12 species share a common structural unit, the formyl moiety, HCO. This group of molecules contains seven aldehydes (-CHO), the simplest carboxylic acid, formic acid (HOCHO; Zuckerman et al. 1971), two amides (-NCHO), formamide (Rubin et al. 1971) and N-methyl formamide (Belloche et al. 2019), and two formates (-OCHO), methyl formate (Brown et al. 1975) and ethyl formate (Belloche et al. 2009; Tercero et al. 2013). The interstellar aldehydes discovered so far are formaldehyde (HCHO; Snyder et al. 1969), acetaldehyde (CH3CHO; Gottlieb et al. 1973), cyanoformaldehyde (NCCHO; Remijan et al. 2008), propynal (HC2CHO; Irvine et al. 1988), propenal (H2CHCHO; Hollis et al. 2004), propanal (CH3CH2CHO; Hollis et al. 2004), and glycolaldehyde (HOCH2CHO; Hollis et al. 2000). The relative abundances of some aldehydes are not accurately reproduced by current theoretical chemistry models, and so there are no accepted formation routes in interstellar environments for these molecules. It is therefore not straightforward to make predictions as to which yet-undiscovered species could be abundant in the interstellar medium (ISM). However, given the many HCO-containing molecules detected in space, it is fair to anticipate that others of this type could be present as well.
Five of the seven aldehydes detected in the ISM are alkyl derivatives of the simplest aldehyde, formaldehyde. Hence, one candidate yet to be observed consists of an aldehyde containing a cyclic functional group, either an aliphatic or aromatic ring. While the astrochemical literature on aromatic rings is extensive, less information is available related to aliphatic rings. Cyclopropane, c-C3H6, is the smallest saturated carbon ring; it lacks a dipole moment and therefore cannot be detected by its rotational spectrum. This is not the case with its derived aldehyde, cyclopropanecarboxyaldehyde (c-C3 H5CHO, CPCA hereinafter) which is a good candidate for observation by way of its rotational spectrum. The microwave spectrum of CPCA was observed by Volltrauer & Schwendeman (1971) in the centimeter wave range up to 32 GHz and two different isomers, cis and trans (see Fig. 1), were identified. These measurements included rotational transitions with J ≤ 10 and Ka ≤ 2 and only the rotational constants were determined with large uncertainties. The astronomical search for CPCA at the observational frequency ranges of sensitive radio telescopes becomes difficult using the predictions obtained with these rotational parameters. A more accurate spectral modelling of CPCA with measurements extending into the millimetre-wave region therefore constitutes the first scenario for a robust astronomical detection.
In addition, CPCA was investigated by infrared (IR) and Raman spectroscopy (Durig & Little 1988; Durig et al. 1992; Durig & Shen 2000; Hudson & Coleman 2019) and electron diffraction (Bartell & Guillory 1965). In these works the abundance ratios for both cis and trans isomers were derived and it was found that the cis isomer is more stable in the gas phase while the trans is the only species present in liquid phase, which is in contrast with the rotational spectroscopy study, where the trans species were found to be the most abundant one (Volltrauer & Schwendeman 1971). Quantum chemical calculations (De Mare & Peterson 1983; Durig & Shen 2000) point out some uncertainties in terms of the relative stability of CPCA isomers due to the relative energies of cis and trans species which fluctuate with the calculation method employed. This raises important questions as to the relative abundances of CPCA isomers in the gas phase, which have considerable astrochemical implications.
In this work, we report new rotational spectroscopy measurements for CPCA in the 31.5–50 GHz and 72–116.5 GHz frequency ranges using a high-resolution broadband millimetre-wave spectrometer. The first aim of this investigation is to contribute to the astronomical search for CPCA by providing a better spectral modelling of CPCA isomers, extending the measurements into the millimetre-wave region. This comprehensive study involves the analysis of the rotational spectra in the low-lying vibrational states of CPCA isomers, motivated by the fact that these are found to be considerably populated in the warm environments of the ISM. The analysis of our new data allowed us to very accurately determine the rotational parameters needed to provide reliable predictions to support astronomical observations of CPCA in the warm molecular clouds Orion KL and Sgr B2(N) using the spectral surveys captured by ALMA (Orion) and IRAM 30 m (Sgr) at 1 and 3 mm, respectively. Secondly, this work is also devoted to obtaining insights into the relative stabilities of cis and trans CPCA isomers. To this end, we directly measured the abundance ratio of CPCA isomers in order to ascertain which of the two species, cis or trans, is energetically favoured in the gas phase, and we provide new high-level quantum chemical calculations to predict the theoretical stabilities.
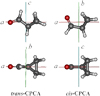 |
Fig. 1 Molecular structures and principal inertial axes for the trans and cis conformers of CPCA. |
Calculated relative energies (in cm−1) for the cis and trans isomers of CPCA at different levels of theory.
2 Quantum chemical calculations
Existing quantum chemical calculations available in the literature include very cheap Hartree Fock (HF; Hartree 1928) methods, small basis sets (Durig et al. 1992), and Møller-Plesset perturbation theory calculations (MP2; Møller & Plesset 1934) combined with Pople’sbasis sets (Frisch et al. 1984), with MP2/6-311++G(d,p) being the highest level of theory employed (Durig & Shen 2000). In order to evaluate the conformational stability of the CPCA isomers, we extended the quantum chemical calculations using two density-functional theory methods, namely Becke 3-parameter Lee-Yang-Parr (B3LYP; Lee et al. 1988) and Grimme’s functional including dispersion (B97D; Grimme 2006), and two post-Hartree Fock methods, namely MP2 and coupled-cluster with single and double excitations (CCSD; Cížek 1969). We combine all these methods with the 6-311++G(d,p) Pople’s basis set (Frisch et al. 1984) and the Dunning’s basis set cc-pVTZ (Dunning 1989) and aug-cc-pVTZ (Woon & Dunning 1995). In addition to the structural optimisation calculations, we carried out harmonic and anharmonic frequency calculations in order to estimate the energy and the rotational constants of the individual vibrationally excited states, facilitating the assignment of the experimental spectrum. These calculations were carriedout at the MP2/6-311++G(d,p) level of theory because this method reproduce the experimental rotational constants very well (see below). The energy calculations for the cis and trans isomers at different levels of theory are shown in Table 1 while a complete list of the vibrational frequencies is given in Table 2. All calculations were carried out using the Gaussian16 (Frisch et al. 2016) program package.
We compared the theoretical constants obtained for each of the levels of theory employed to those determined experimentally in this work. In general, all the methods nicely reproduce the rotational constants for both isomers, with the MP2/6-311++G(d,p) level of theory providing the best agreement with the experiment. The discrepancies for this method are 0.14 and 0.28% for cis and trans isomers, respectively, taking into account the sum of the relative errors for A, B, and C constants. B3LYP/cc-pVTZ, with relative errors of 0.21 and 0.32% for cis and trans, respectively, and CCSD/cc-pVTZ, 0.42 and 0.40%, provide good results as well. The least satisfactory results were found for B97D methods, with relative discrepancies larger than 1.5%.
The MP2/6-311++G(d,p) anharmonic vibrational frequencies (in cm−1) of cis and trans isomers of CPCA.
3 Experimental setup
The emission rotational spectrum of CPCA was recorded using the GACELA (GAS CEll for Laboratory Astrophysics) broadband high-resolution rotational spectrometer constructed at the Yebes Observatory (Spanish National Geographic Institute (IGN)) in the frame of the ERC synergy project Nanocosmos. The GACELA spectrometer is equipped with radio receivers similar to those used in radio astronomy to search for molecular emission in space. The receivers are equipped with 16 × 2.5 GHz FFT spectrometers with a spectral resolution of 38.14 kHz allowing the observation of the rotational transitions in the Q (31.5–50 GHz) and W bands (72–116.5 GHz). The spectrometer performance has been described at length in previous works (Tanarro et al. 2018; Cernicharo et al. 2019; Cabezas et al. 2019, 2020a,b).
The CPCA sample (purity >98%), purchased from Apollo Scientific, was placed into a PyrexTM vacuum Schlenk which was connected directly to the cell of the spectrometer. This latter consists of a stainless steel cylinder of 890 mm length and 490 mm diameter. In order to avoid sample condensation during the experiment, which was carried out in continuous flow mode, the temperature of the sample container, the injection line, and the cell were kept at 350 K using a dry heating tape and a proportional integral derivative (PID) temperature controller. Prior to introduction of the sample, the pressure inside the vacuum chamber was 2.0 × 10−4 mbar and during the experiment the pressure was kept at 6.0 × 10−3 mbar because higher pressures produce undesirable line broadenings. With the selected working pressure, the rotational lines of CPCA have a HWHM of 0.2−0.35 MHz which is well adapted to measuring frequencies with high accuracy. The total observing time to obtain the whole CPCA spectrum in the Q (31.5–50 GHz) and W bands (72–116.5 GHz) was six days. In all these experiments, a frequency switching with a throw of 50 MHz was selected as the observing procedure. This has previously been confirmed as the most suitable mode, as the lines are observed twice and the noise is improved by a factor ![$\sqrt[]{2}$](/articles/aa/full_html/2021/01/aa39924-20/aa39924-20-eq1.png) , allowing us to derive accurate line profiles and intensities for lines of up to 2 MHz full width at half maximum (Cernicharo et al. 2019). With this observing procedure the baseline shows several ripples which can be easily eliminated by applying a FFT filter and removing the corresponding time domain, or by a polynomial baseline removal.
, allowing us to derive accurate line profiles and intensities for lines of up to 2 MHz full width at half maximum (Cernicharo et al. 2019). With this observing procedure the baseline shows several ripples which can be easily eliminated by applying a FFT filter and removing the corresponding time domain, or by a polynomial baseline removal.
4 Rotational spectrum and analysis
The two CPCA isomers are near symmetric tops with moderate dipole moments that have been experimentally determined by Volltrauer & Schwendeman (1971). For the trans isomer, |μa | and |μc | were found to be 3.221 D and 0.493 D, respectively, while the dipole moment components for the cis species are |μa | = 2.019 D and |μb| = 1.856 D. A very rich rotational spectrum is therefore observed for CPCA, which is governed by strong a-type rotational transitions for the trans isomer. Figure 2 shows the typical pattern of a-type R-branch rotational transitions for the ground state of the trans isomer together with weaker b-type Q-branch rotational transitions for the ground state of the cis isomer. For the trans isomer, we measured a total of 208 a-type R-branch transitions with maximum values of J and Ka quantum numbers of 18 and 17, respectively, which were fitted using the SPFIT (Pickett 1991) program with the S-reduction of the Watson’s Hamiltonian in Ir representation (Watson 1977). A list of all the measured transitions is available at CDS. In spite of the fact that the trans isomer also presents a c-type dipole moment different from zero, no c-type rotational transitions could be measured in our spectrum. This can be explained taking into account the fact that the intensity of the rotational transitions is proportional to the square of the dipole moment components, and therefore c-type transitions for the trans species are expected to be about 43 times weaker than the a-type ones. The fit for the trans isomer provided a set of experimental constants, including rotational constants, and four quartic and two sextic centrifugal distortion constants, which are listed in the first column of Table 3.
For the cis isomer, we first measured a-type R-branch transitions and the initial fit of these lines provided a set of refined experimental constants, which were used for new spectral predictions that in turn allowed the identification of b-type R- and Q-branch transitions. The best fit for all these lines was obtained using the S-reduction of Watson’s Hamiltonian in IIIr representation (Watson 1977). This fit was done using the Kisiel’s ASFIT program (Kisiel & Bialkowska-Jaworska 2019) which is best suited when the S-reduction in IIIr representation is required. A total of 819 rotational transitions with maximum values of J and Ka quantum numbers of 79 and 21, respectively, were assigned for the ground vibrational state of the cis isomer. A list of all the measured transitions is available at CDS. The analysis provided a list of experimental constants, shown in Table 4, which includes the rotational constants, and all the quartic and six sextic centrifugal distortion constants.
The spectrum in Fig. 2 shows that each ground-state line of CPCA was accompanied by many satellite lines attributable to rotational transitions in vibrationally excited states, as no other coupling interaction is expected for this closed-shell molecule. As can be seen in Table 2, four vibrational modes are predicted below 500 cm−1, which originate many low-energy vibrationally excited states from overtones and combination states. For the assignment of these satellite lines, the rotational spectra of the lower-energy excited states were modelled on the basis of calculated first-order vibration–rotation constants αi that define the vibrational dependence of rotational constants Bν = Be - ∑i αi (νi + 1/2), where Bν and Be substitute all three rotational constants in a given excited state and in equilibrium, respectively, and νi is the vibrational quantum number. The calculations were carried out with the Gaussian16 program package at the MP2/6-311++G(d,p) level of theory. Our frequency calculations are in agreement with those reported before and with the experimental vibrational assignments (Durig & Little 1988; Durig et al. 1992; Durig & Shen 2000) which point out that the lowest energy vibrational modes are ν27, ν16, ν26 and ν15. These four modes correspond to the asymmetric torsion, the ring CHO in-plane bend, the ring CHO bend, and the CCO bend, respectively. According to this, we searched for the rotational transitions coming from these modes and were able to identify up to 12 and 6 vibrationally excited states for the trans and cis isomers, respectively.
For the trans isomer, in addition to the three fundamental modes ν27, ν16, and ν26, we identified, between the 12 states, the second quanta of ν27, ν16, and ν26 (2ν27, 2ν16 and 2ν26), and the third quanta of ν27 (3ν27), together with some combination states, namely ν27 +ν16, ν27 +ν26, 2ν27+ν16, 2ν27+ν26, and 3ν27+ν16. We note the non-detection of ν15 in spite of it being predicted to lie below other identified modes, such as 2ν16. We scrutinised the rotational spectrum searching for transitions attributable to ν15 but all attempts were fruitless. All the measured rotational transitions for the vibrationally excited states of the trans isomer available at the CDS were analysed using the SPFIT program (Pickett 1991) in the same manner as that used for the ground state, and the derived spectroscopic constants are shown in Table 3. As for the trans ground state, four quartic and two sextic centrifugal distortion constants were determined for all the vibrationally excited states except for 2ν27+ν26, with ΦJK fixed to the ground state value, and 3ν27, whose transitions were very weak and for which only a few parameters could be determined.
The six vibrationally excited states identified for the cis isomer arise from the three lowest energy modes ν27, ν16, and ν26. These three fundamental modes were observed together with the second and third quanta of ν27, 2ν27, and 3ν27, and the combination state ν27 +ν16. The analysis of the rotational lines for all these states was carried out in the same manner as that for the cis ground state, and the spectroscopic constants obtained are collected in Table 4. For ν27, the rotational parameters included the rotational constants and all the centrifugal distortion constants derived for the ground state of the cis isomer, except the h2 constant. For the other five vibrationally excited states, in addition to the rotational constants, only the quartic centrifugal distortion constants could be fitted.
As shown before by Cernicharo et al. (2019), our GACELA spectrometer allows us to determine the concentrations of the different molecular species from the observed line intensities with high accuracy; these concentrations are proportional to the line strength, the partition function, the square of a corresponding component of the electric dipole moment, and the molecular concentration. Therefore, the abundance of each CPCA isomer in the gas phase can be directly determined by relative intensity measurements of their ground-state rotational transitions. In these measurements, we compared the intensities of tens of a-type rotational transitions and we find that the transitions for the trans isomer are 1.1985(37) times more intense than those for the cis isomer. Assuming a temperature for our experiment of 350K, this implies an energy difference between both isomers of 44.05(75) cm−1, with the trans species being the most stable. This result can be compared to those previously reported for the relative stability of CPCA isomers, which seem fairly ambiguous. Durig & Little (1988), Durig et al. (1992) and Bartell & Guillory (1965) in their respective experiments found that the cis isomer was the most stable species in the gas phase, with an energy difference of around 40–60 cm−1, while Hudson & Coleman (2019) showed that the cis/trans ratio was 1:1. On the other hand, Volltrauer & Schwendeman (1971) proposed that in the gas phase the trans species was slightly more stable (10 ± 20 cm−1) than the cis one, but with large uncertainties. In liquid phase, the panorama is completely distinct because the trans isomer was found by Durig & Little (1988) to be the only species present, with an energy gap of 405 cm−1 over the cis isomer. In addition, large discrepancies are encountered when quantum chemical calculations at different levels of theory are used to evaluate the isomer energies. De Mare & Peterson (1983) and Durig & Shen (2000) used HF and MP2 methods combined with modest basis sets and their results indicated that the cis species was the most stable. We carried out additional calculations at different levels of theory and the results, collected in Table 1, show discrepancies as well. Density functional levels of theory, B3LYP and B97D, predict the trans isomer to be more stable than the cis isomer with relative energies of between 12 and 128 cm−1. In contrast, more sophisticated calculation methods, such as MP2 and CCSD, provide totally different results, with the cis isomer being found to be the most stable. In this case, the relative energies also oscillate between 7 and 132 cm−1. In light of this, we can conclude that the small energy difference between cis and trans isomers makes experimental determination of the isomer energies more difficult. However, we find that the trans isomer is moderately more stable than the cis one and therefore both species should be taken into consideration for astronomical implications. Secondly, the use of quantum chemical calculations to estimate the relative energies of CPCA isomers should be handled with caution because these relative energies are near to the level of accuracy of the calculations.
We used the rotational parameters obtained in this work for both cis and trans isomers of CPCA to obtain accurate frequency predictions up to 300 GHz, providing a means for their astronomical detection. These frequency predictions for both CPCA isomers, calculated at T = 300 K, are provided at the CDS. The rotational and vibrational partition functions used in these predictions, at different temperatures, are listed in Table 5. The rotational partition function was calculated considering a maximum value of J = 90, while the vibrational partition function was calculated using the method described by Gordy & Cook (1984) and the anharmonic frequencies from Table 2. The conformational partition function and the conformational abundances were calculated using the energy difference between isomers determined in this work.
 |
Fig. 2 Section of the rotational spectrum of CPCA showing a-type R-branch rotational transitions for the ground state, and ν27 and ν16 vibrationally excited states of the trans conformer, and b-type Q-branch transitions for the ground state of the cis species. The negative spectral features are produced by the folding of the frequency-switched data and appear at ±50 MHz of each rotational transition. |
Spectroscopic constants for the ground- and vibrationally excited states of the trans conformer of CPCA.
Spectroscopic constants for the ground and vibrationally excited states of cis conformer of CPCA.
Rotational, vibrational, and conformational partition functions for both cis and trans isomers of CPCA at different temperatures.
5 Search for cyclopropanecarboxaldehyde in space
Thanks to the improved frequency predictions provided by the present work, we were able to carry out a rigorous search for trans and cis isomers of CPCA in space. For this search, we rely on our line surveys and public data towards different astronomical sources at frequencies above 80 GHz (Cernicharo et al. 2012; Belloche et al. 2013; Tercero et al. 2018, 2015). For these frequencies, the energies of the rotational levels of the CPCA a-type transitions are above 30 K, preventing the detection of CPCA in our IRAM 30 m data of cold clouds at 3 mm (Cernicharo et al. 2012). Therefore, we focused the search on high-mass star-forming regions which show high abundances of acetaldehyde (CH3CHO) such as Orion KL and Sgr B2 (see, e.g. Belloche et al. 2013; Cernicharo et al. 2016). We used the MADEX code (Cernicharo 2012) to exploit the spectroscopic parameters presented in this work and to derive the synthetic spectrum of this species (assuming local thermodynamic equilibrium) according to the physical parameters of the sources (see below) collected in Table 6. The column density was the only free parameter for these models. Corrections for beam dilution were applied to each line depending on its frequency.
Orion KL
Science Verification (SV) data from the Atacama Large millimetre/submillimetre Array (ALMA) interferometer towards Orion KL (Tercero et al. 2015, 2018) were explored to search for CPCA. The ALMA SV data allow us to obtain the spectrum between 213.7 and 246.7 GHz for different positions within the source characterised by different chemistry and physical parameters. We distinguished three positions, two of them presenting high abundances of CH3CHO, namely the south hot core and the MM4 source (Cernicharo et al. 2016). The other location is the compact ridge which shows emission peaks of several complex O-bearing species such as methyl formate, dimethyl ether, and methyl acetate (Favre et al. 2011; Brouillet et al. 2013; Tercero et al. 2018). To model the CPCA emission in these components, we adopted physical parameters according to those derived by Cernicharo et al. (2016) and Tercero et al. (2018). Figure 3 shows selected frequencies and positions within these data together with the model derived by MADEX that demonstrates the lack of CPCA lines above the confusion limit of the data.
Physical parameters of the considered cloud cores.
Column density ratios.
Sgr B2
we also searched for CPCA in public data available for Sgr B2. We did not find this species above the detection limit of the data either in the PRIMOS survey2 (Neill et al. 2012) or in the IRAM 30m data at 3 mm provided by Belloche et al. (2013). To estimate upper limits to the CPCA column density in the region, we adopted the physical parameters derived by Belloche et al. (2013) for CH3CHO (see Table 6). Figure 3 shows the model provided by MADEX together with the IRAM 30 m data of Sgr B2(N). This model is also consistent with the lack of CPCA lines above the detection limit of the PRIMOS data.
Table 7 shows the CH3CHO/CPCA density ratios in Orion KL and Sgr B2. It is worth noting that the lower limit ratios derived agree for the considered Orion cores and for Sgr B2, and they are extremely low (~2–4). As we discuss previously for other species (Bermúdez et al. 2018; Cabezas et al. 2019, 2020b), the CPCA partition function is approximately four times larger than that of CH3CHO at ~100 K. As a result, the CPCA lines appear weaker than those of CH3CHO assuming similar abundances. Therefore, it is reasonable to suggest that the derived lower limit ratio is far from the real abundance ratio between these species in the considered regions.
6 Conclusions
This paper presents an extensive laboratory study of the rotational spectrum of CPCA in its ground- and vibrationally excited states, extending the earlier limited knowledge on the spectroscopic properties of this molecule. Measurements were performed in the 31.5–50 and 72–116.5 GHz frequency regions using a high-resolution broadband spectrometer. From the analysis we obtainedaccurate rotational parameters for the ground state of both cis and trans isomers of CPCA which allowed us to obtain sufficiently reliable frequency predictions up to 300 GHz. In addition to the ground states, we identified 12and 6 vibrationally excited states for the trans and cis isomers, respectively, comprising fundamental modes, multiple excitation quanta, and combination states. By comparison of the observed line intensities, we determined the concentration of both cis and trans isomers in the gas phase with high accuracy. We find that the trans isomer is almost 1.2 times more abundant than the cis isomer, which means that the former is 44.05(75) cm−1 more stable than the latter. Finally, these new laboratory data were employed to search for CPCA in the warm molecular clouds Orion KL and Sgr B2(N) using the spectral surveys captured by ALMA (Orion) and IRAM 30 m (Sgr) at 1 and 3 mm, respectively. We did not find any CPCA above the detection limit of these data and provide upper limits to the column density for the two isomers of CPCA.
 |
Fig. 3 Observed data of Orion KL and Sgr B2 taken with the ALMA interferometer and the IRAM 30 m telescope, respectively (histogram black spectrum), together with the synthetic spectra obtained using the column densities given as upper limits in Table 6 (red and blue thin curves). The synthetic total model for the 30 m data of Sgr B2(N) (see Belloche et al. 2013) is overlaid in green. A vLSR of +9.0 km s−1 and +64.0 km s−1 is assumed for Orion KL and Sgr B2, respectively. |
Acknowledgements
We thank the European Research Council for funding support under Synergy Grant ERC-2013-SyG, G.A. 610256 (NANOCOSMOS). We also thank Ministerio de Ciencia e Innovación for funding support through projects AYA2016-75066-C2-1-P and PID2019-107115GB-C21. B.T. also thanks the Spanish MICIU for funding support from grant PID2019-106235GB-I00. C.B. thanks to Ministerio de Ciencia, Innovación y Universidades for a Juan de la Cierva postdoctoral fellowship (FJCI-2016-27983). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00009.SV. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan) with NRC (Canada), NSC, and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. This work was also based on observations carried out with the IRAM 30-meter telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
References
- Bartell, L. S., Guillory, J. P. 1965, J. Chem. Phys., 43, 647 [CrossRef] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2009, A&A, 499, 218 [Google Scholar]
- Belloche, A., Müller, H. S. P., Menten, K. M., Schilke, P., & Comito, C. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2019, A&A, 628, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bermúdez, C., Tercero, B., Motiyenko, R. A., et al. 2018, A&A, 619, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brouillet, N., Despois, D., Baudry, A., et al. 2013, A&A, 550, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, R. D., Crofts, J. G., Gardner, F. F., et al. 1975, ApJ, 197, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Cabezas, C., Bermúdez, C., Gallego, J. D., et al. 2019, A&A, 629, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabezas, C., Bermúdez, C., Endo, Y., et al. 2020a, A&A, 636, A33 [CrossRef] [EDP Sciences] [Google Scholar]
- Cabezas, C., Bermúdez, C., Tercero, B., &, Cernicharo, J. 2020b, A&A, 639, A129 [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J. 2012, EAS Pub. Ser., 2012, 251, https://nanocosmos.iff.csic.es/?pageid=1619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Kisiel, Z., Tercero, B., et al. 2016, A&A, 587, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Gallego, J. D., López-Pérez, J. A., et al. 2019, A&A, 626, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cížek, J., Advances in Chemical Physics, ed. P. C. Hariharan (New York: Wiley Interscience), 14, 35 [Google Scholar]
- Collins, J. B., Schleyer, P. v. R., Binkley, J. S., & Pople, J. A. 1976, J. Chem. Phys., 64, 5142 [CrossRef] [Google Scholar]
- De Mare, G., & Peterson, M. R. 1983, J. Mol. Strct. Theochem., 104, 115 [CrossRef] [Google Scholar]
- Dunning Jr., T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Durig, J. R., & Little, T. S. 1988, Croat. Chem. Acta, 61, 529 [Google Scholar]
- Durig, J. R., & Shen, S. 2000, Spectrochim. Acta, Part A, 56A, 2545 [CrossRef] [Google Scholar]
- Durig, J. R., Feng, F., Little, T. S., & Wang, A.-Y. 1992, Struct. Chem., 3, 417 [CrossRef] [Google Scholar]
- Favre, C., Despois, D., Brouillet, N., et al. 2011, A&A, 532, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frisch, M. J., Pople, J. A., & Binkley, J. S. 1984, J. Chem. Phys., 80, 3265 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16, revision A.03 [Google Scholar]
- Grimme, S. 2006, J. Comput. Chem., 27, 1787 [CrossRef] [PubMed] [Google Scholar]
- Gordy, W., & Cook, R. 1984, Microwave Molecular Spectra, Techniques of Chemistry (New York: Wiley) [Google Scholar]
- Gottlieb, C. A. 1973, Molecules in the Galactic Environment (New York: Wiley) [Google Scholar]
- Hartree, D. R. 1928, Math. Proc. Cambridge Philos. Soc., 24, 89 [CrossRef] [Google Scholar]
- Hollis, J. M., Lovas, F. J., & Jewell, P. R. 2000, ApJ, 540, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Hollis, J. M., Jewell, P. R., Lovas, F. J., et al. 2004, ApJ, 610, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, R. L., & Coleman F. M. 2019, ACS Earth Space Chem., 3, 1182 [CrossRef] [Google Scholar]
- Irvine, W. M., Brown, R. D., Cragg, D. M., et al. 1988, ApJ, 335, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Kisiel, Z., & Bialkowska-Jaworska, E. 2019, J. Mol. Spectr., 359, 16. [CrossRef] [Google Scholar]
- Lee, C., Yang, W., & Parr, R. G. 1988, Phys. Rev. B, 37, 785 [Google Scholar]
- Møller, C., & Plesset, M. S. 1934, Phys. Rev., 46, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. L., Muckle, M. T., Zaleski, D. P., et al. 2012, ApJ, 755, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M. 1991, J. Mol. Spectr., 148, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2008, ApJ, 675, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, R. H., Swenson, G. W., Jr., Benson, R. C., et al. 1971, ApJ, 169, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, L. E., Buhl, D., Zuckerman, B., & Palmer, P. 1969, Phys. Rev. Lett., 22, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Tanarro, I., Alemán, B., de Vicente, P., et al. 2018, A&A, 609, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Kleiner, I., Cernicharo, J., et al. 2013, A&A, 770, L13 [Google Scholar]
- Tercero, B., Cernicharo, J., López, A., et al. 2015, A&A, 582, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Cuadrado, S., López, A., et al. 2018, A&A, 620, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Volltrauer, H. N., & Schwendeman, R. H. 1971, J. Chem. Phys., 54, 260 [CrossRef] [Google Scholar]
- Watson, J. K. G., Vibration Spectra and Structure, ed. J. Durig (Amsterdam: Elsevier), 6, 1 [Google Scholar]
- Woon, D. E., & Dunning Jr., T. H. 1995, J. Chem. Phys., 98, 1358 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Ball, J. A., & Gottlieb, C. A. 1971, ApJ, 163, L41 [NASA ADS] [CrossRef] [Google Scholar]
CDMS 2020, The Cologne Database for Molecular Spectroscopy: Molecules in the Interstellar Medium or Circumstellar Shells (as of 08/2020), https://cdms.astro.uni-koeln.de/classic/molecules
The 100 m Green Bank Telescope (GBT) PRebiotic Interstellar MOlecule Survey covers a frequency band between 7 and 50 GHz. Access to the entire PRIMOS data set, specifics on the observing strategy, and overall frequency coverage information is available at http://www.cv.nrao.edu/aremijan/PRIMOS/
All Tables
Calculated relative energies (in cm−1) for the cis and trans isomers of CPCA at different levels of theory.
The MP2/6-311++G(d,p) anharmonic vibrational frequencies (in cm−1) of cis and trans isomers of CPCA.
Spectroscopic constants for the ground- and vibrationally excited states of the trans conformer of CPCA.
Spectroscopic constants for the ground and vibrationally excited states of cis conformer of CPCA.
Rotational, vibrational, and conformational partition functions for both cis and trans isomers of CPCA at different temperatures.
All Figures
 |
Fig. 1 Molecular structures and principal inertial axes for the trans and cis conformers of CPCA. |
| In the text | |
 |
Fig. 2 Section of the rotational spectrum of CPCA showing a-type R-branch rotational transitions for the ground state, and ν27 and ν16 vibrationally excited states of the trans conformer, and b-type Q-branch transitions for the ground state of the cis species. The negative spectral features are produced by the folding of the frequency-switched data and appear at ±50 MHz of each rotational transition. |
| In the text | |
 |
Fig. 3 Observed data of Orion KL and Sgr B2 taken with the ALMA interferometer and the IRAM 30 m telescope, respectively (histogram black spectrum), together with the synthetic spectra obtained using the column densities given as upper limits in Table 6 (red and blue thin curves). The synthetic total model for the 30 m data of Sgr B2(N) (see Belloche et al. 2013) is overlaid in green. A vLSR of +9.0 km s−1 and +64.0 km s−1 is assumed for Orion KL and Sgr B2, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


