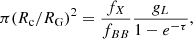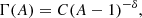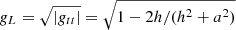EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 644 (December 2020) A&A, 644 (2020) A132 Full HTML
Free Access
Issue
A&A
Volume 644, December 2020
Article Number A132
Number of page(s) 9
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202039158
Published online 11 December 2020

© ESO 2020

1. Introduction

The X-ray emission of active galactic nuclei (AGNs) is thought to be produced via thermal Comptonization of optical/UV photons emitted by the accretion disc in a hot corona (e.g. Haardt & Maraschi 1991). A tight correlation is found between the X-ray and UV luminosity in quasars, indicating the existence of a universal coupling between the disc and the corona (Lusso & Risaliti 2016, 2017). The nature of this coupling is not fully understood (e.g. Arcodia et al. 2019), however a possible physical explanation could be the heating of the corona via reconnection of magnetic fields above the disc (and references therein Lusso & Risaliti 2017).

The geometry of the hot X-ray corona (i.e. its size and location) is poorly known and a matter of debate. Arguably the best constraints can be obtained from the analysis of microlensing variability, although this method is currently limited to a few strongly lensed quasars (e.g. Chartas et al. 2002, 2009, 2016). Another promising method relies on the X-ray spectral-timing properties of nearby bright Seyfert galaxies, especially from the detection of X-ray reverberation lags (Fabian et al. 2009; Cackett et al. 2014; Kara et al. 2016; De Marco & Ponti 2019). Such observational constraints are generally consistent with a compact X-ray source located within a few gravitational radii of the black hole (e.g. Reis & Miller 2013). In a few bright Seyfert galaxies, the spectral modelling of the optical-to-X-ray continuum also yields similar estimates of the coronal size (e.g. Petrucci et al. 2013; Done et al. 2013; Porquet et al. 2019). X-ray polarimetry is also a promising technique to constrain the geometry of the corona, which influences the polarization signal (Tamborra et al. 2018). High-sensitivity polarimetric observations will become possible in the near future thanks to the Imaging X-ray Polarimetry Explorer (IXPE; Weisskopf et al. 2016).

The lamppost geometry is a configuration often used to describe the disc–corona system, where the corona is assumed to be a point-like X-ray source located on the symmetry axis of the disc (e.g. Matt et al. 1991; Martocchia & Matt 1996; Miniutti & Fabian 2004). This could be physically realized by collisions and shocks within an ejection flow or a failed jet (Henri & Pelletier 1991; Henri & Petrucci 1997; Ghisellini et al. 2004). This geometry has been assumed in detailed models for the calculation of reflection spectra (e.g. Dauser et al. 2013; García et al. 2014; Niedźwiecki et al. 2016) and tested in a number of sources showing reflection-dominated spectra, such as the narrow-line Seyfert 1 galaxies 1H 0707-495 (Zoghbi et al. 2010; Fabian et al. 2012; Dauser et al. 2012; Szanecki et al. 2020) and IRAS 13224-3809 (Ponti et al. 2010; Chiang et al. 2015). Interestingly, the observed properties of these objects are consistent with the presence of very compact X-ray sources located close to the black hole. The most extreme spectrum seen from 1H 0707-495 would require a source lying within 1 gravitational radius of the event horizon of a rapidly spinning black hole (Fabian et al. 2012; see also Szanecki et al. 2020).

A small sized corona can also be radiatively compact, meaning a large ratio of luminosity to radius (Guilbert et al. 1983). This in turns implies a large optical depth for pair production. Observational constraints on the coronal parameters so far obtained suggest that pair production and annihilation may act as an effective thermostat controlling the coronal temperature (Fabian et al. 2015, 2017).

However, a Comptonizing corona must intercept a sufficient number of seed photons (per unit time) to explain the observed X-ray flux. This, for a given seed photon flux, implies a constraint on the solid angle subtended by the corona as seen from the disc. Dovčiak & Done (2016; hereafter DD16) developed a method to constrain the coronal size from the observed optical/UV and X-ray fluxes. DD16 developed a relativistic ray-tracing code that estimates the radius of a spherical X-ray source located on the symmetry axis of a standard accretion disc that Comptonizes the soft disc photons. The aim of the present work is to constrain the size of a Comptonizing lamppost corona in a statistically significant sample of AGNs using the DD16 code.

The paper is structured as follows. We present the sample in Sect. 2. In Sect. 3 we discuss the application of the DD16 code and the main results. We summarise our conclusions in Sect. 4.

2. The sample

In order to test the lamppost geometry with the DD16 code, we need good constraints on both the disc luminosity and on the X-ray flux and spectral shape. We therefore focus on bright, unobscured sources with simultaneous high-quality data in the optical/UV and X-ray bands. The simultaneity prevents spurious effects due to inter-band variability. XMM-Newton is the best instrument to perform this kind of analysis because it provides both high-quality X-ray spectra with the EPIC-pn camera (Strüder et al. 2001) and optical/UV data with the optical monitor (OM; Mason et al. 2001). We use the sample of Seyfert 1 galaxies discussed by Petrucci et al. (2018)1. This sample includes 22 objects observed by XMM-Newton, with public data as of April 16, 2014, cross-correlated with the AGNs and quasars catalogue of Véron-Cetty & Véron (2010). The sources are further selected using the criteria of the CAIXA catalogue (Bianchi et al. 2009), namely they are radio-quiet and unobscured (column density NH <  2 × 1022 cm−2). Moreover, each source is detected with at least four OM filters in order to constrain the optical/UV emission. As the black hole mass is a required parameter in our case, our sample includes only the 20 sources for which a measurement of the black hole mass is available (Bianchi et al. 2009), with a total of 96 observations. The basic properties of the sources are reported in Table 1.

Table 1.

Basic data of the Seyfert 1 galaxies in our sample (see also Petrucci et al. 2018).

3. Numerical procedure

The DD16 code assumes a standard accretion disc, producing a multicolor blackbody emission with a Novikov & Thorne (1973) temperature radial profile through the KYNBB model (Dovčiak et al. 2004). The code calculates the photon flux received by the corona, taking into account all relativistic effects: the Doppler energy shift between the comoving disc frame and the corona, the gravitational energy shift, light bending, and aberration (see also Dovčiak et al. 2014). It is assumed that a fraction (1 − e−τ) of the incoming seed photons, where τ is the Thomson optical depth of the corona, become scattered in the X-ray band. The Comptonized spectrum emitted by the corona is calculated with the NTHCOMP model (Zdziarski et al. 1996; Życki et al. 1999). Part of the X-ray photons emitted by the corona illuminate the disc and their reprocessing slightly rises the temperature; however, this has a negligible effect on the photon flux (DD16).

From the observed UV and X-ray fluxes, the DD16 code computes the seed photon flux at the corona fBB (found by integrating over the disc radius) and the X-ray photon flux fX in the local frame of the lamppost. Details of the calculations can be found in DD16. Here we simply reiterate the equation for the coronal radius Rc:

π ( R c / R G ) 2 = f X f BB g L 1 − e − τ , $$ \begin{aligned} \pi (R_{\rm c}/R_{\text{G}})^2 = \frac{f_{X}}{f_{BB}} \frac{g_L}{1-e^{-\tau }} ,\end{aligned} $$(1)

where RG ≡GM/c2 is the gravitational radius and gL is the relativistic energy shift between the corona and the observer2 (see also Dovčiak et al. 2004). The optical depth is computed from the X-ray photon index Γ using the model COMPPS (Poutanen & Svensson 1996), which includes a relativistic treatment for the electron temperature. For a given value of Γ, we use COMPPS to derive the optical depth of a spherical corona that produces a spectrum with that same Γ value, assuming a temperature of 100 keV (see DD16 and Sect. 3.1). For example, photon indices Γ = 1.5, 1.75, and 2 correspond to optical depths τ = 1.8, 1.2, and 0.85, respectively.

The size of a lamppost corona at a given height is therefore constrained by the ratio of the observed photon fluxes. Equation (1) assumes the conservation of the number of photons. Pair production and annihilation are therefore neglected, which is a reasonable approximation for low plasma temperatures (< 511 keV). However, pair processes could still play a role in limiting the maximum temperature that the corona can reach (see Sect. 4).

It must be noted that in NTHCOMP the seed photons illuminate the corona isotropically, which is clearly an approximation given the disc–corona geometry. This limitation was discussed in detail by Zhang et al. (2019), who developed a more self-consistent Monte Carlo radiative transfer code to calculate Comptonized spectra in the Kerr spacetime (MONK). Compared with the DD16 code, Zhang et al. (2019) found slightly larger coronal sizes, depending on the optical depth τ. This small discrepancy can be simply represented by a correction factor. We therefore complemented the DD16 computations with the correction provided by MONK, obtained as follows. For a combination of black hole spin and corona height, we perform several Monk simulations with different values of τ assuming a corona radius of 1 RG (for spherical coronae, the energy spectrum is not sensitive to the size of the corona; see Zhang et al. 2019). Given an observed value of the X-ray photon index Γobs, we find the simulated spectrum that has the same photon index. We then derive the corona radius RDD16 with the DD16 method using the input from the corresponding simulated spectrum. The correction factor is then 1 RG/RDD16 and, in our case, we obtain values in the range 1.1–1.4 and slightly increasing with height.

3.1. Input physical parameters

The crucial parameter determining the coronal size is the ratio between the number of Comptonized X-ray photons and the disc photons seen by the corona (fX/fBB of Eq. (1)). As this ratio increases, the coronal size increases because the corona must intercept a larger number of disc photons. The photon number flux emitted by the disc and the corona can be easily inferred from the corresponding luminosity and spectral shape. For a Novikov-Thorne disc, the spectral shape is set by the inner disc radius, the accretion rate, and the black hole mass. We assume that the inner disc radius is equal to the innermost stable circular orbit (ISCO) in the Kerr metric, which depends on the black hole spin (e.g. Misner et al. 1973). For the hot corona, in the 2–10 keV band the spectral shape is a power law characterized by a photon index Γ. Finally, the main geometric parameter of the corona is the height above the event horizon of the black hole (while the size is computed by the code). A sketch of the lamppost configuration is given in Fig. 1. To summarise, the main input parameters are the black hole mass and spin; the disc luminosity; the X-ray luminosity and spectral shape; and the coronal height. Details of the different parameters are given below.

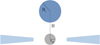thumbnail Fig. 1.

Sketch of the lamppost configuration. The corona has a radius Rc and is located at a height of H − rH above the event horizon.

Black hole mass and spin. For each source, the black hole mass is taken from the CAIXA catalogue (Bianchi et al. 2009). The mass determines the Eddington luminosity LEdd and the spectral shape of the emission from the Novikov-Thorne disc. Concerning the black hole spin a, we tested the two extreme cases a = 0 (Schwarzschild) and a = 0.998 (maximally rotating; Thorne 1974). The inner disc radius is equal to 6 RG for a = 0 and to 1.24 RG for a = 0.998.

Disc luminosity. The disc emission is modelled through the KYNBB code (Dovčiak et al. 2004), which describes a blackbody-like spectrum from an accretion disc around a black hole, assuming a Novikov-Thorne temperature profile. The spectrum is determined by two parameters, namely the black hole mass and the accretion rate or the luminosity in a given energy band. We used the UV luminosity in the 5–7 eV range, roughly covering the bandpass of the UVM2 and UVW2 filters of the XMM-Newton/OM. For such a small energy range, the luminosity is not strongly model-dependent. Therefore, for each source we estimated the 5–7 eV luminosity from the best fits of Petrucci et al. (2018), who assumed a multicolour disc blackbody. We note that Petrucci et al. (2018) subtracted the main non-nuclear contributions, namely those from the host galaxy and the broad-line region; in any case, these components peak in the optical band and do not strongly contribute to the UV emission. For the disc, we also assume an inclination angle of 30 deg to the symmetry axis. However, this parameter does not strongly affect the results (see DD16).

X-ray spectrum and luminosity. The X-ray emission from the corona is modelled through the NTHCOMP code, whose relevant input parameters are: the observed photon index; the electron temperature, fixed at 100 keV (the temperature sets the high energy cut-off, which affects the total X-ray flux especially for low photon indices); the normalization, given by the observed 2–10 keV luminosity; the temperature of the seed photons, estimated as Epeak/2.82 where Epeak is the peak energy of the disc spectrum computed at the corona. This latter parameter sets the low-energy cut-off, which affects the total X-ray flux especially for high photon indices. We used the results of Petrucci et al. (2018), who fitted the XMM-Newton/pn data with NTHCOMP, also assuming a coronal temperature of 100 keV. The optical depths computed by the code are in the range 0.5–2, consistent with values commonly measured applying Comptonization models in spherical geometry (Tortosa et al. 2018; see also Ursini et al. 2019).

Coronal height. The centre of the corona is at a height H above the disc. We performed calculations assuming four different values, namely H = 2.5, 5, 10, and 30 in units of gravitational radii.

3.2. Results

The Eddington ratio. First of all, we checked the consistency between the output physical parameters calculated by the code and the assumed model. In particular, the Eddington ratio ϵEdd = Lbol/LEdd (where Lbol is the bolometric luminosity of the disc) should not exceed unity, as this could conflict with the hypothesis of a standard Novikov-Thorne disc (see Sect. 4). The bolometric luminosity is the total luminosity of the KYNBB component integrated over the disc radius. In Fig. 2 we plot ϵEdd versus the black hole mass. For a given mass, a larger value of the inner disc radius yields a smaller bolometric luminosity, because the disc has a smaller area while the observed UV luminosity is the same. As a result, the Eddington ratio for spin a = 0 is smaller by a factor of two to three than for a = 0.998. However, in both cases we obtain ϵEdd ≤ 1 for 13 sources out of 20. The highest Eddington ratio is found in the narrow-line Seyfert 1 RE 1034+396, with the caveat that the black hole mass is quite uncertain in this source (Czerny et al. 2016).

thumbnail Fig. 2.

Eddington ratio as calculated by the DD16 code, assuming spin a = 0 (left panel) and a = 0.998 (right panel), plotted versus the black hole mass in units of 108 solar masses.

The corona size. In Fig. 3 we show the ratio of the computed coronal radius to the height above the horizon. For spin a = 0, this ratio is greater than 1 for heights H = 2.5 and 5 RG, indicating that in these cases the corona cannot intercept enough seed photons to produce the observed X-ray flux. On the other hand, the corona can almost always fit within 30 RG. For spin a = 0.998, instead, the corona can almost always fit within 5 RG, and even within 2.5 RG in a limited number of sources. One major caveat is that the optical/UV emission of super-Eddington sources might be not well described by a Novikov-Thorne disc, as mentioned above. The coronal radii of those sources with ϵEdd ≤ 1 that are consistent with the lamppost geometry are plotted in Fig. 4. The corresponding light-crossing time t in units of ks is plotted in Fig. 5.

thumbnail Fig. 3.

Ratio of the coronal radius to the height above the event horizon plotted against Eddington ratio.

thumbnail Fig. 4.

Coronal radius Rc, in units of gravitational radii, versus Eddington ratio. We plot only those observations in which the corona can fit within the given height.

thumbnail Fig. 5.

Light-crossing time t of the corona, in units of kiloseconds, versus Eddington ratio.

The photon index. Physical Comptonization models that take into account the energetic coupling between corona and disc predict a relationship between the X-ray spectral index and the Compton amplification factor A, namely the ratio between the total luminosity of the corona and the soft luminosity from the disc that enters the corona (e.g Haardt & Maraschi 1991). In general, the Compton amplification depends crucially on geometry (see also Petrucci et al. 2013, 2018). In the lamppost configuration, there is an inverse relation between the coronal radius and A: for a given luminosity, a bigger corona will intercept more disc photons, meaning that the Compton amplification factor will decrease. This is the basis for a self-consistency check a posteriori of our results. Numerical simulations (Beloborodov 1999a,b; Malzac et al. 2001) show that the relationship between the photon index Γ and the Compton amplification factor is fitted by a simple function:

Γ ( A ) = C ( A − 1 ) − δ , $$ \begin{aligned} \Gamma (A) = C (A-1)^{-\delta } ,\end{aligned} $$(2)

with C ≃ 2 and δ ≃ 0.1. This relationship is obtained assuming a radiatively coupled disc–corona system based on the balance between heating via magnetic dissipation and Compton cooling (see also Haardt & Maraschi 1993).

The Compton amplification is calculated by the DD16 code, from the flux of the disc photons intercepted by the corona. We calculated the expected photon index (labelled Γexp in the following) from Eq. (2) assuming C = 2.33 and δ = 0.1 (Beloborodov 1999a,b)3. The expected photon index can be compared with the observed one (Γobs). As A is computed within the code assuming Γobs, we would expect Γexp ≃ Γobs, with the caveat that Eq. (2) does not take into account general relativistic effects. We plot in Fig. 6Γexp versus Γobs. For a = 0, we mostly have Γobs >  Γexp. On the other hand, for a = 0.998 and a height of 2.5 RG we mostly have Γobs <  Γexp. The best agreement is found in the case a = 0.998 and intermediate heights (5 or 10 RG).

thumbnail Fig. 6.

Expected photon index (from Eq. (2), see Beloborodov 1999b) versus observed photon index. The orange solid line represents the identity Γexp = Γobs, while the dashed and dotted lines correspond to differences ΔΓ = ±0.1, ±0.2 respectively.

To summarise, we consider the lamppost corona on top of a standard disc to be consistent with the observations when: (a) the Eddington ratio is ≤1, (b) the corona fits within at least one of the tested heights, and (c) the difference |Γexp − Γobs| is not too large. A reasonable condition is |Γexp − Γobs|< 0.2, keeping in mind that Γexp is the result of a simple analytical approximation and that the uncertainties on Γobs are in the range 0.01–0.20 (Petrucci et al. 2018). We report in Table 2 the sources that satisfy these constraints for all of their observations considered here. Conditions (a) and (b) are satisfied by eight sources for a = 0 and eleven sources for a = 0.998. Including condition (c) leaves us with only two sources for a = 0 (Mrk 279 and Mrk 509) and five sources for a = 0.998 (Mrk 279, Mrk 509, 1H 0419-577, HE 1029-1401 and NGC 4593).

Table 2.

Sources satisfying different constraints for all of their observations considered here (see Table 1).

4. Discussion and conclusions

The estimates of the DD16 code indicate that, at least for the sub-Eddington sources, the lamppost Comptonizing corona is generally a viable scenario. However, such a corona can only exist beyond a certain height above the event horizon, depending on inner disc radius. If the disc is extended down to the ISCO of a maximally spinning black hole, the corona can be located down to a height of H = 2.5 RG, having a radius smaller than H − rH = 1.44 RG, at least for sources with ϵEdd ≳ 0.1 (see Fig. 3). A coronal height of 5 RG is a physically consistent value in almost all sources analysed here. On the other hand, for a non-spinning black hole, the corona cannot fit within a height of 5 RG. For ϵEdd ≳ 0.04, the corona can be at H = 10 RG, having a radius smaller than H − rH = 8 RG.

The observed spectral shape can also provide some constraints on the coronal geometry, comparing the observed photon index with that predicted from the Compton amplification. The best agreement between observed and expected photon indices is found for maximal spin and heights of 5 RG or larger. This solution is therefore favoured, while assuming a low spin predicts a spectrum mostly flatter than observed for the sources considered here. On the other hand, for a high spin and a height of 2.5 RG the predicted spectrum is mostly steeper than observed. We note that the number of sources with a spectral shape roughly consistent with the expectation, for all of their observations, is not high: if a = 0.998, these sources amount to 5 out of the 11 for which the corona can geometrically fit. This could indicate that a spherical corona on the disc axis might not always represent a good model. Future X-ray polarimetric observations will be crucial to constrain the geometry and distinguish between the possible configurations of the corona (Tamborra et al. 2018; Marinucci et al. 2019).

From the coronal radii, we calculated the dimensionless compactness parameter ℓ ≡ LσT/Rcmec3, where L is the luminosity of the corona (see the plot in Fig. 7). Following Fabian et al. (2015), we computed the luminosity in the 0.1–200 keV band of the NTHCOMP model (very close to a power law with a sharp cut-off at 100 keV). The corona is always consistent with being radiatively compact, in the sense that ℓ is always > 10. We mostly find estimates of ℓ between ∼100 and ∼1000, consistent with the observational constraints that are generally found with NuSTAR (Fabian et al. 2015, 2017). For a given compactness, there exists a maximum temperature below which pair equilibrium is possible; above this temperature, pair production becomes a runaway process. Therefore, especially in the case of large compactness, observation of the X-ray source strongly constrains the temperature, because even a few photons above 511 keV are sufficient to produce runaway pair production. We note that our assumption of a 100 keV temperature is consistent with pair equilibrium, because it would place the sources below the pair runaway line for a spherical corona (Fabian et al. 2015, 2017).

thumbnail Fig. 7.

Compactness ℓ vs. Eddington ratio.

The main limitation of the model used in this work is likely the assumption of a standard, geometrically thin accretion disc. Indeed, super-Eddington sources are thought to be powered by advection-dominated slim/thick discs rather than by standard thin discs (e.g. Paczyńsky & Wiita 1980; Abramowicz et al. 1988; Mineshige et al. 2000; Du et al. 2014; Castelló-Mor et al. 2016). On the other hand, an Eddington ratio much lower than unity might suggest the presence of a radiatively inefficient accretion flow (e.g. Narayan & Yi 1994). However, at least for the sources with ϵEdd in the range 0.01−1, the standard disc assumption is realistic (e.g. Czerny & Naddaf Moghaddam 2018). We note that Petrucci et al. (2018) discuss a physical scenario in which the disc is sandwiched by a warm Comptonizing corona, with a temperature in the range 0.1–1 keV, to account for the soft X-ray excess seen in many unobscured Seyfert galaxies (see also Middei et al. 2019; Ursini et al. 2020). However, the photon rate from the warm corona, and therefore the distribution of seed photons seen by the hot corona, is always dominated by optical–UV photons. Therefore, assuming a standard disc as the illumination source for the hot corona would be a fair approximation also in this case.

We also note that the model does not take into account the disc–corona energetic coupling, in particular the fact that a fraction of the accretion power has to be channelled into the corona to provide its heating, thus reducing the disc flux by the same amount. However, this should not strongly alter our results, because the X-ray luminosity is generally a small fraction (10% or less) of the bolometric luminosity. The coronal radiation reflected by the accretion disc is also not currently computed by the code, and will be implemented in future work. The reflection component can in principle carry significant information on the geometry of the corona. For example, the profile of the ubiquitous Fe K α emission line at ∼6.4 keV can be broadened and skewed (e.g. Nandra et al. 2007, which is often interpreted as a general relativistic effect of reflection off the inner disc (e.g. Tanaka et al. 1995, but see also Miller et al. 2008). Combining spectral and timing analyses of the X-ray continuum and reflection component can yield constraints on the height of the corona, the inner disc radius, and their temporal evolution: for instance, Kara et al. (2019) report a shrinking of the corona in a stellar-mass black hole (but see also Mahmoud et al. 2019; Kajava et al. 2019), while Caballero-García et al. (2020) report coronal height variations in a narrow-line Seyfert 1. Further studies will be needed to understand the dynamical properties of the corona.

Another source of uncertainty is the black hole mass, because the luminosity and the spectral shape of the disc emission, as well as the Eddington ratio, depend crucially on this parameter. Around 50% of the objects in our sample have reverberation-based measurements of the black hole mass, while the other measurements are based on the width of the Hβ emission line (Bianchi et al. 2009; Ponti et al. 2012). The former method yields mass uncertainties of a factor of ≲3 (Peterson et al. 2004), but the latter method yields larger uncertainties (Ponti et al. 2012). This can potentially affect the results. For example, Done & Jin (2016) discussed the case of the narrow-line Seyfert 1 1H 0707-495 in detail. For this source, the spectral-timing models based on relativistic reflection in the lamppost geometry require a high black hole spin (a = 0.998) and a mass of 2 × 106 M⊙ (Fabian et al. 2012). These parameters imply a highly super-Eddington regime. However, Done & Jin (2016) also found a sub-Eddington solution assuming low spin (a = 0) and a mass of 1 × 107 M⊙. In general, we can expect smaller accretion rates if the black hole masses are larger than currently estimated, and so the corona size could in turn be underestimated in these cases. Future extensions of our results will be possible as further, robust measurements of black hole masses become available.

1

Petrucci et al. (2018) performed spectral analyses to test a “two-corona” model. In this scenario, the primary X-ray emission is produced in a hot corona, while the UV and soft X-ray excess below 1–2 keV are produced via Comptonization in a warm (kT ∼ 0.5 keV) corona above a nearly passive disc (see also Różańska et al. 2015; Petrucci et al. 2020). Although this model is different from the standard disc/hot corona assumed here, the sample is perfectly suited for our purpose because the selection criteria are the same.

2

The redshift factor gL is determined by the temporal component of the Kerr metric: gtt = −[1−2r/(r2 + a2 cos θ)] in Boyer-Lindquist coordinates and geometrised units. As the lamppost is at a height h on the symmetry axis (θ = 0), we get g L = | g tt | = 1 − 2 h / ( h 2 + a 2 ) $ g_L = \sqrt{|g_{tt}|} = \sqrt{1 - 2h/(h^2+a^2) } $.

3

Beloborodov (1999a,b) performed calculations of dynamic coronae applying both a simple analytical model and the numerical code of Coppi (1992) in the case of a spherical blob. We obtain very similar results using the parameters of Malzac et al. (2001), who performed more detailed Monte Carlo simulations assuming a cylindrical geometry for the corona.

Acknowledgments

We thank the anonymous referee for comments that improved the manuscript. We also thank S. Bianchi, A. De Rosa and A. Marinucci for useful discussions. MD and WZ acknowledge the financial support provided by the Czech Science Foundation grant 17-02430S and institutional support by the project RVO:67985815. GM acknowledges financial support from the Italian Space Agency under grant n. 2017-14-H.O. POP acknowledges financial support from CNES and the CNRS/PNHE. CD acknowledges the Science and Technology Facilities Council (STFC) through grant ST/P000541/1.

References

  1. Abramowicz, M. A., Czerny, B., Lasota, J. P., & Szuszkiewicz, E. 1988, ApJ, 332, 646 [Google Scholar]
  2. Arcodia, R., Merloni, A., Nandra, K., & Ponti, G. 2019, A&A, 628, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Beloborodov, A. M. 1999a, in High Energy Processes in Accreting Black Holes, eds. J. Poutanen, & R. Svensson, ASP Conf. Ser., 161, 295 [Google Scholar]
  4. Beloborodov, A. M. 1999b, ApJ, 510, L123 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bianchi, S., Guainazzi, M., Matt, G., Fonseca Bonilla, N., & Ponti, G. 2009, A&A, 495, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Caballero-García, M. D., Papadakis, I. E., Dovčiak, M., et al. 2020, MNRAS, 498, 3184 [CrossRef] [Google Scholar]
  7. Cackett, E. M., Zoghbi, A., Reynolds, C., et al. 2014, MNRAS, 438, 2980 [NASA ADS] [CrossRef] [Google Scholar]
  8. Castelló-Mor, N., Netzer, H., & Kaspi, S. 2016, MNRAS, 458, 1839 [NASA ADS] [CrossRef] [Google Scholar]
  9. Chartas, G., Agol, E., Eracleous, M., et al. 2002, ApJ, 568, 509 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chartas, G., Kochanek, C. S., Dai, X., Poindexter, S., & Garmire, G. 2009, ApJ, 693, 174 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chartas, G., Rhea, C., Kochanek, C., et al. 2016, Astron. Nachr., 337, 356 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chiang, C.-Y., Walton, D. J., Fabian, A. C., Wilkins, D. R., & Gallo, L. C. 2015, MNRAS, 446, 759 [NASA ADS] [CrossRef] [Google Scholar]
  13. Coppi, P. S. 1992, MNRAS, 258, 657 [NASA ADS] [CrossRef] [Google Scholar]
  14. Czerny, B., & Naddaf Moghaddam, M. H. 2018, Accretion Processes in Cosmic Sources - II, 6 [Google Scholar]
  15. Czerny, B., You, B., Kurcz, A., et al. 2016, A&A, 594, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Dauser, T., Svoboda, J., Schartel, N., et al. 2012, MNRAS, 422, 1914 [NASA ADS] [CrossRef] [Google Scholar]
  17. Dauser, T., Garcia, J., Wilms, J., et al. 2013, MNRAS, 430, 1694 [NASA ADS] [CrossRef] [Google Scholar]
  18. De Marco, B., & Ponti, G. 2019, Astron. Nachr., 340, 290 [NASA ADS] [CrossRef] [Google Scholar]
  19. Done, C., & Jin, C. 2016, MNRAS, 460, 1716 [NASA ADS] [CrossRef] [Google Scholar]
  20. Done, C., Jin, C., Middleton, M., & Ward, M. 2013, MNRAS, 434, 1955 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dovčiak, M., & Done, C. 2016, Astron. Nachr., 337, 441 [NASA ADS] [CrossRef] [Google Scholar]
  22. Dovčiak, M., Karas, V., & Yaqoob, T. 2004, ApJS, 153, 205 [NASA ADS] [CrossRef] [Google Scholar]
  23. Dovčiak, M., Svoboda, J., Goosmann, R. W., et al. 2014, Proc. RAGtime, 14–16, 51 [Google Scholar]
  24. Du, P., Hu, C., Lu, K.-X., et al. 2014, ApJ, 782, 45 [NASA ADS] [CrossRef] [Google Scholar]
  25. Fabian, A. C., Zoghbi, A., Ross, R. R., et al. 2009, Nature, 459, 540 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  26. Fabian, A. C., Zoghbi, A., Wilkins, D., et al. 2012, MNRAS, 419, 116 [NASA ADS] [CrossRef] [Google Scholar]
  27. Fabian, A. C., Lohfink, A., Kara, E., et al. 2015, MNRAS, 451, 4375 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fabian, A. C., Lohfink, A., Belmont, R., Malzac, J., & Coppi, P. 2017, MNRAS, 467, 2566 [NASA ADS] [CrossRef] [Google Scholar]
  29. García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [NASA ADS] [CrossRef] [Google Scholar]
  30. Ghisellini, G., Haardt, F., & Matt, G. 2004, A&A, 413, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Guilbert, P. W., Fabian, A. C., & Rees, M. J. 1983, MNRAS, 205, 593 [NASA ADS] [CrossRef] [Google Scholar]
  32. Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
  33. Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  34. Henri, G., & Pelletier, G. 1991, ApJ, 383, L7 [NASA ADS] [CrossRef] [Google Scholar]
  35. Henri, G., & Petrucci, P. O. 1997, A&A, 326, 87 [NASA ADS] [Google Scholar]
  36. Kajava, J. J. E., Motta, S. E., Sanna, A., et al. 2019, MNRAS, 488, L18 [CrossRef] [Google Scholar]
  37. Kara, E., Alston, W. N., Fabian, A. C., et al. 2016, MNRAS, 462, 511 [Google Scholar]
  38. Kara, E., Steiner, J. F., Fabian, A. C., et al. 2019, Nature, 565, 198 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lusso, E., & Risaliti, G. 2016, ApJ, 819, 154 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lusso, E., & Risaliti, G. 2017, A&A, 602, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Mahmoud, R. D., Done, C., & De Marco, B. 2019, MNRAS, 486, 2137 [NASA ADS] [CrossRef] [Google Scholar]
  42. Malzac, J., Beloborodov, A. M., & Poutanen, J. 2001, MNRAS, 326, 417 [NASA ADS] [CrossRef] [Google Scholar]
  43. Marinucci, A., Porquet, D., Tamborra, F., et al. 2019, A&A, 623, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Martocchia, A., & Matt, G. 1996, MNRAS, 282, L53 [NASA ADS] [CrossRef] [Google Scholar]
  45. Mason, K. O., Breeveld, A., Much, R., et al. 2001, A&A, 365, L36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Matt, G., Perola, G. C., & Piro, L. 1991, A&A, 247, 25 [NASA ADS] [Google Scholar]
  47. Middei, R., Bianchi, S., Petrucci, P. O., et al. 2019, MNRAS, 483, 4695 [NASA ADS] [CrossRef] [Google Scholar]
  48. Miller, L., Turner, T. J., & Reeves, J. N. 2008, A&A, 483, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Mineshige, S., Kawaguchi, T., Takeuchi, M., & Hayashida, K. 2000, PASJ, 52, 499 [NASA ADS] [CrossRef] [Google Scholar]
  50. Miniutti, G., & Fabian, A. C. 2004, MNRAS, 349, 1435 [NASA ADS] [CrossRef] [Google Scholar]
  51. Misner, C. W., Thorne, K. S., & Wheeler, J. A. 1973, Gravitation (San Francisco: W.H. Freeman and Co.) [Google Scholar]
  52. Nandra, K., O’Neill, P. M., George, I. M., & Reeves, J. N. 2007, MNRAS, 382, 194 [NASA ADS] [CrossRef] [Google Scholar]
  53. Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [NASA ADS] [CrossRef] [Google Scholar]
  54. Niedźwiecki, A., Zdziarski, A. A., & Szanecki, M. 2016, ApJ, 821, L1 [NASA ADS] [CrossRef] [Google Scholar]
  55. Novikov, I. D., & Thorne, K. S. 1973, in Black Holes (Les Astres Occlus), eds. C. Dewitt, & B. S. Dewitt, 343 [Google Scholar]
  56. Paczyńsky, B., & Wiita, P. J. 1980, A&A, 500, 203 [Google Scholar]
  57. Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [Google Scholar]
  58. Petrucci, P.-O., Paltani, S., Malzac, J., et al. 2013, A&A, 549, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Petrucci, P.-O., Ursini, F., De Rosa, A., et al. 2018, A&A, 611, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Petrucci, P. O., Gronkiewicz, D., Rozanska, A., et al. 2020, A&A, 634, A85 [CrossRef] [EDP Sciences] [Google Scholar]
  61. Ponti, G., Gallo, L. C., Fabian, A. C., et al. 2010, MNRAS, 406, 2591 [NASA ADS] [CrossRef] [Google Scholar]
  62. Ponti, G., Papadakis, I., Bianchi, S., et al. 2012, A&A, 542, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Porquet, D., Done, C., Reeves, J. N., et al. 2019, A&A, 623, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Poutanen, J., & Svensson, R. 1996, ApJ, 470, 249 [NASA ADS] [CrossRef] [Google Scholar]
  65. Reis, R. C., & Miller, J. M. 2013, ApJ, 769, L7 [Google Scholar]
  66. Różańska, A., Malzac, J., Belmont, R., Czerny, B., & Petrucci, P.-O. 2015, A&A, 580, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Szanecki, M., Niedzwiecki, A., Done, C., et al. 2020, A&A, 641, A89 [CrossRef] [EDP Sciences] [Google Scholar]
  69. Tamborra, F., Matt, G., Bianchi, S., & Dovčiak, M. 2018, A&A, 619, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Tanaka, Y., Nandra, K., Fabian, A. C., et al. 1995, Nature, 375, 659 [NASA ADS] [CrossRef] [Google Scholar]
  71. Thorne, K. S. 1974, ApJ, 191, 507 [Google Scholar]
  72. Tortosa, A., Bianchi, S., Marinucci, A., Matt, G., & Petrucci, P. O. 2018, A&A, 614, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Ursini, F., Bassani, L., Malizia, A., et al. 2019, A&A, 629, A54 [CrossRef] [EDP Sciences] [Google Scholar]
  74. Ursini, F., Petrucci, P. O., Bianchi, S., et al. 2020, A&A, 634, A92 [CrossRef] [EDP Sciences] [Google Scholar]
  75. Véron-Cetty, M.-P., & Véron, P. 2010, A&A, 518, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Weisskopf, M. C., Ramsey, B., O’Dell, S., et al. 2016, in The Imaging X-ray Polarimetry Explorer (IXPE), SPIE Conf. Ser., 9905, 990517 [Google Scholar]
  77. Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
  78. Zhang, W., Dovčiak, M., & Bursa, M. 2019, ApJ, 875, 148 [CrossRef] [Google Scholar]
  79. Zoghbi, A., Fabian, A. C., Uttley, P., et al. 2010, MNRAS, 401, 2419 [NASA ADS] [CrossRef] [Google Scholar]
  80. Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Basic data of the Seyfert 1 galaxies in our sample (see also Petrucci et al. 2018).

In the text
Table 2.

Sources satisfying different constraints for all of their observations considered here (see Table 1).

In the text

All Figures

thumbnail Fig. 1.

Sketch of the lamppost configuration. The corona has a radius Rc and is located at a height of H − rH above the event horizon.
In the text
thumbnail Fig. 2.

Eddington ratio as calculated by the DD16 code, assuming spin a = 0 (left panel) and a = 0.998 (right panel), plotted versus the black hole mass in units of 108 solar masses.
In the text
thumbnail Fig. 3.

Ratio of the coronal radius to the height above the event horizon plotted against Eddington ratio.
In the text
thumbnail Fig. 4.

Coronal radius Rc, in units of gravitational radii, versus Eddington ratio. We plot only those observations in which the corona can fit within the given height.
In the text
thumbnail Fig. 5.

Light-crossing time t of the corona, in units of kiloseconds, versus Eddington ratio.
In the text
thumbnail Fig. 6.

Expected photon index (from Eq. (2), see Beloborodov 1999b) versus observed photon index. The orange solid line represents the identity Γexp = Γobs, while the dashed and dotted lines correspond to differences ΔΓ = ±0.1, ±0.2 respectively.
In the text
thumbnail Fig. 7.

Compactness ℓ vs. Eddington ratio.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.