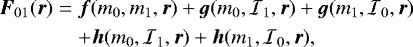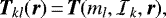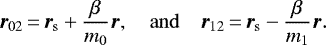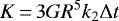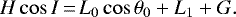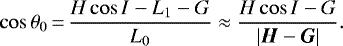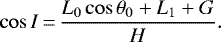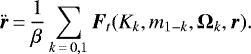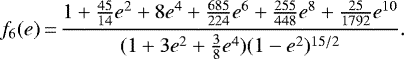| Issue |
A&A
Volume 644, December 2020
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202038858 | |
| Published online | 04 December 2020 | |
Tidal evolution of the Pluto–Charon binary
1
CFisUC, Department of Physics, University of Coimbra,
3004-516
Coimbra,
Portugal
e-mail: acor@uc.pt
2
ASD, IMCCE, Observatoire de Paris, PSL Université, 77 Av. Denfert-Rochereau,
75014
Paris, France
Received:
6
July
2020
Accepted:
26
October
2020
A giant collision is believed to be at the origin of the Pluto–Charon system. As a result, the initial orbit and spins after impact may have substantially differed from those observed today. More precisely, the distance at periapse may have been shorter, subsequently expanding to its current separation by tides raised simultaneously on the two bodies. Here we provide a general 3D model to study the tidal evolution of a binary composed of two triaxial bodies orbiting a central star. We apply this model to the Pluto–Charon binary, and notice some interesting constraints on the initial system. We observe that when the eccentricity evolves to high values, the presence of the Sun prevents Charon from escaping because of Lidov-Kozai cycles. However, for a high initial obliquity for Pluto or a spin-orbit capture of Charon’s rotation, the binary eccentricity is damped very efficiently. As a result, the system can maintain a moderate eccentricity throughout its evolution, even for strong tidal dissipation on Pluto.
Key words: planets and satellites: dynamical evolution and stability / minor planets, asteroids: individual: Pluto / minor planets, asteroids: individual: Charon
© ESO 2020
1 Introduction
In 1978, a regular series of astrometric observations of Pluto revealed that the images were consistently elongated, denouncing the presence of Pluto’s moon, Charon (Christy & Harrington 1978). The orbital parameters determined for this system show that the two bodies evolve in an almost circular orbit with a 6.387-day period, and that the system also shows an important inclination of about 122° with respect to the orbital plane of Pluto around the Sun (e.g., Stern et al. 2018). Charon has an important fraction of the mass of the system (about 12%), and therefore can be considered more as a binary planet rather than a satellite. Indeed, the barycenter of the Pluto–Charon system lies outside the surface of Pluto. Later, it was found that four additional tiny satellites move around the barycenter of the system, also in nearly circular and coplanar orbits (Weaver et al. 2006; Brozović et al. 2015).
The brightness of Pluto varies by some tens of percent with a period of 6.387 days (e.g., Walker & Hardie 1955; Tholen & Tedesco 1994; Buie et al. 2010). Although this period coincides with the orbital period of Charon, it has been identified as the rotation of Pluto, since Charon itself is too dim to account for the amplitude of the variation. Therefore, at present, the rotation of Pluto is synchronous with the orbit of Charon, keeping the same face toward its satellite. The present configuration likely resulted from the action of tidal torques raised on Pluto by Charon. Tidal torques raised on Charon by Pluto are even stronger, and so the satellite is also assumed to be synchronous with Pluto, which corresponds to a final equilibrium situation (e.g., Farinella et al. 1979; Cheng et al. 2014).
From photometric observations, Andersson & Fix (1973) found the angle between the spin of Pluto and its orbit around the Sun to be approximately 90° ± 40°. The uncertainty on this value is significant, but it clearly suggests a high obliquity. Because of the complete tidal evolution that is evident in the system, the obliquity has usually been assumed to be the same as the inclination of the orbital plane of Charon, that is, 122°. Indeed, maps of the surface have been created using HST images and “mutual events” (e.g., Drish et al. 1995; Stern et al. 1997; Young et al. 1999; Buie et al. 2010), and although the authors assumed the above obliquity in the creation of these maps, the solution would not have held together if the obliquity was completely incorrect.
Assuming equal densities, the normalized angular momentum density of the Pluto–Charon pair is 0.45 (McKinnon 1989), exceeding the critical value 0.39, above which no stable rotating single object exists (e.g., Lin 1981; Durisen & Tohline 1985). The proto-planetary disk is not expected to produce such systems, and so alternative theories have been proposed for their origin. Harrington & van Flandern (1979) first suggested that Pluto and Charon could be escaped satellites of Neptune after an encounter with another planet, an unlikely scenario because Triton is on a retrograde orbit (McKinnon 1984). More reliable hypotheses were proposed that take into account the excess of angular momentum in the system, such as binary fission of a rapidly rotating body (e.g., Lin 1981; Nesvorný et al. 2010) or the accumulation process of planetesimals in heliocentric orbits (e.g., Tancredi & Fernández 1991; Schlichting & Sari 2008).
The above-mentioned theories have some limitations and it is more commonly accepted that Charon resulted from the giant collision of two proto-planets in the early inner Kuiper belt (e.g., McKinnon 1989; Canup 2005; Rozner et al. 2020). This scenario provides the system with its large angular momentum and can also explain the additional small moons in the system (Canup 2011). The outward migration of Neptune may have instigated huge perturbations in previously stable zones of the Kuiper belt, and oblique low-velocity collisions between similarly sized objects should have been frequent at the time (e.g., Malhotra 1993). Such a collision probably produced an intact Charon, although it is also possible that a disk of debris orbited Pluto from which Charon later accumulated. The resulting system is a close binary in an eccentric orbit, with the separation at periapse not exceeding many Pluto radii (Canup 2005, 2011).
Most previous studies on the past orbital evolution of the Pluto–Charon system (Farinella et al. 1979; Lin 1981; Mignard 1981; Dobrovolskis et al. 1997; Cheng et al. 2014) assume that both spin axes are normal to the binary orbital plane (2D model), and therefore limit the evolution to the rotations. Although this is the expected outcome of tidal evolution, after a large collision the obliquity of Pluto can take any value (e.g., Dones & Tremaine 1993; Kokubo & Ida 2007; Canup 2011). Previous studies also assume that the Pluto–Charon binary is alone. However, the Sun exerts a torque on the system that causes both the obliquities and the orbital plane of the binary to precess (Dobrovolskis & Harris 1983). For the Earth–Moon system, Touma & Wisdom (1994, 1998) showed that the presence of the Sun is critical to understand its early evolution. Some preliminary work on the Pluto–Charon system (Carvalho 2016) suggests that the obliquity and the Sun may also play a role. Finally, Cheng et al. (2014) showed that the inclusion of the gravitational harmonic coefficient C22 in the analysis allows smooth, self-consistent evolution to the synchronous state. It is therefore important to simultaneously take into account the effect of the obliquity, the Sun, and the residual C22, in order to obtain a more realistic description of the past history of the Pluto–Charon system.
In Sect. 2, we first derive a full 3D model (for the orbits and spins) that is suitable to describe the tidal evolution of a hierarchical three-body system, where the inner two bodies are assumed to be triaxial ellipsoids. In Sect. 3, we determine the initial parameters of the Pluto–Charon system that are coherent with the present observations. In Sect. 4, we perform numerical simulations to study the complete evolution of the Pluto–Charon binary. Finally, we discuss our results in Sect. 5.
2 Dynamical model
In this section, we derive a very general model that is suited to study the system composed of Pluto, Charon, and the Sun. Pluto and Charon are considered as triaxial ellipsoidal bodies, while the Sun is considered a point-mass (see Fig. 1). Our model is valid in 3D for both orbital planes and individual spins. We use Jacobi Cartesian coordinates for the orbits, angular momentum vectors for the spins, and quaternions for the rotations.
2.1 Potential of an ellipsoidal body
We consider an ellipsoidal body of mass m, and have chosen the Cartesian inertial frame (i, j, k) as reference. In this frame, the angular velocity and the rotational angular momentum vectors of the body are given by Ω = (Ωi, Ωj, Ωk) and L = (Li, Lj, Lk), respectively, which are related through the inertia tensor 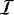 as
as
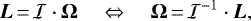 (1)
(1)
The gravitational potential of the ellipsoidal body at a generic position r relative to its center of mass is given by (e.g., Goldstein 1950)
![\begin{equation*} V (m, {{\cal{I}}}, {\bm{r}})\,{=}\,{-} \frac{G m}{r} + \frac{3 G}{2 r^3} \left[ {\bm{\hat{r}}} \cdot {{\cal{I}}} \cdot {\bm{\hat{r}}} - \frac{1}{3} \mathrm{tr}({{\cal{I}}}) \right]\!,\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq6.png) (5)
(5)
where G is the gravitational constant, 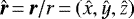 is the unit vector, and
is the unit vector, and 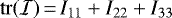 . We neglect terms in
. We neglect terms in 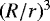 , where R is the mean radius of the body (quadrupolar approximation). Adopting the Legendre polynomial P2 (x) = (3x2 − 1)∕2, we can rewrite the previous potential as
, where R is the mean radius of the body (quadrupolar approximation). Adopting the Legendre polynomial P2 (x) = (3x2 − 1)∕2, we can rewrite the previous potential as
![\begin{eqnarray*} V (m, {{\cal{I}}}, {\bm{r}}) & = & - \frac{G m}{r} + \frac{G}{r^3} \Big[ \big(I_{22}-I_{11}\big) P_2 ({\hat{y}}) + \big(I_{33}-I_{11}\big) P_2 ({\hat{z}}) \nonumber \\ & & + \, 3 \big(I_{12} {\hat{x}} {\hat{y}} + I_{13} {\hat{x}} {\hat{z}} + I_{23} {\hat{y}} {\hat{z}} \big) \Big] .\end{eqnarray*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq10.png) (6)
(6)
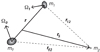 |
Fig. 1 Jacobi coordinates, where r is the position of m1 relative to m0 (inner orbit), and rs is the position of m2 relative to the center of mass of m0 and m1 (outer orbit). The bodies with masses m0 and m1 are considered oblate ellipsoids with angular velocity Ω, and body m2 is considered a point-mass. |
2.2 Point-mass problem
We now consider that the ellipsoidal body orbits a point-mass M located at r. The force between the two bodies is easily obtained from the potential energy of the system U(r) = MV (r) as
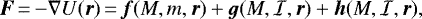 (7)
(7)
For the orbital evolution of the system, we thus obtain
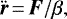 (11)
(11)
where β = Mm∕(M + m) is the reduced mass. The spin evolution of the ellipsoidal body can also be obtained from the force by computing the gravitational torque. In the inertial frame we have
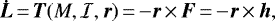 (12)
(12)
Apart from a sphere, in the inertial frame (i, j, k) the inertia tensor (Eq. (2)) is not constant. We let 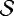 be the rotation matrix, which allows us to convert any vector uB in a frame attached to the body into the Cartesian inertial frame uI, such that
be the rotation matrix, which allows us to convert any vector uB in a frame attached to the body into the Cartesian inertial frame uI, such that 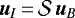 . Thus, we have
. Thus, we have
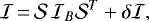 (15)
(15)
where 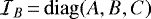 is the permanent deformation inertia tensor in the body frame (expressed in principal axis of inertia), and
is the permanent deformation inertia tensor in the body frame (expressed in principal axis of inertia), and 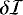 corresponds to the deformation due to the centrifugal and tidal potentials. The equilibrium values for each coefficient of
corresponds to the deformation due to the centrifugal and tidal potentials. The equilibrium values for each coefficient of 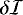 are given by (Correia & Rodríguez 2013):
are given by (Correia & Rodríguez 2013):
 (16)
(16)
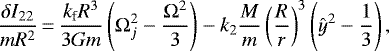 (17)
(17)
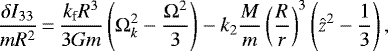 (18)
(18)
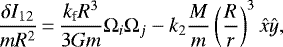 (19)
(19)
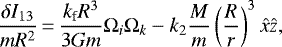 (20)
(20)
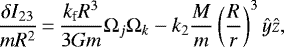 (21)
(21)
where kf and k2 are the fluid and the elastic second Love numbers for potential, respectively (see Sect. 3.4 for more details). The evolution of 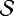 over time is given by
over time is given by
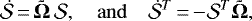 (22)
(22)
In order to simplify the evolution of 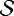 , a set of generalized coordinates can be used to specify the orientation of the two frames. Euler angles are a common choice, but they introduce some singularities. Therefore, here we use quaternions (e.g., Kosenko 1998). We denote q = (q0, q1, q2, q3) the quaternion that represents the rotation from the body frame to the inertial frame. Consequently,
, a set of generalized coordinates can be used to specify the orientation of the two frames. Euler angles are a common choice, but they introduce some singularities. Therefore, here we use quaternions (e.g., Kosenko 1998). We denote q = (q0, q1, q2, q3) the quaternion that represents the rotation from the body frame to the inertial frame. Consequently,
![\begin{equation*} {{\cal{S}}}\,{=}\,\left[\!\! \small \begin{array}{ccc} q_0^2+q_1^2-q_2^2-q_3^2 & 2 (q_1 q_2 - q_0 q_3) & 2 (q_1 q_3 + q_0 q_2) \\[4pt] 2 (q_1 q_2 + q_0 q_3) & q_0^2-q_1^2+q_2^2-q_3^2 & 2 (q_2 q_3 - q_0 q_1) \\[4pt] 2 (q_1 q_3 - q_0 q_2) & 2 (q_2 q_3 + q_0 q_1) & q_0^2-q_1^2-q_2^2+q_3^2 \end{array} \!\! \right] ,\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq35.png) (24)
(24)
To solvethe spin-orbit motion, we need to integrate Eqs. (11), (12), and (25) using the relations (1), (15), and (24).
2.3 Pluto–Charon binary
Pluto and Charon are considered ellipsoidal bodies with masses m0 and m1 and inertia tensors 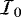 and
and 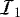 , respectively, that orbit around each other at a distance r from their centers of mass. The total potential energy can be written from expression (5) as
, respectively, that orbit around each other at a distance r from their centers of mass. The total potential energy can be written from expression (5) as
![\begin{equation*} U ({\bm{r}})\,{=}\,{-} \frac{G m_0 m_1}{r} + \frac{3 G}{2 r^3} \left[ {\bm{\hat{r}}} \cdot {{\cal{J}}} \cdot {\bm{\hat{r}}} - \frac{1}{3} \mathrm{tr}({{\cal{J}}}) \right],\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq39.png) (26)
(26)
with 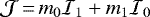 . This potential is very similar to the previous point-mass problem and the equations of motion are simply
. This potential is very similar to the previous point-mass problem and the equations of motion are simply
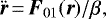 (27)
(27)
 (28)
(28)
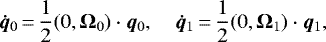 (29)
(29)
and β = m0m1∕(m0 + m1). 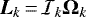 is the rotational angular momentum vector of thebody with mass mk, Ωk is the angular velocity vector, and qk is the quaternion that represents the rotation from the body frame to the inertial frame.
is the rotational angular momentum vector of thebody with mass mk, Ωk is the angular velocity vector, and qk is the quaternion that represents the rotation from the body frame to the inertial frame.
2.4 Effect of the Sun
We now consider that the presence of the Sun, with mass m2, disturbs the Pluto–Charon binary. We use Jacobi canonical coordinates, which are the distance between the centers of mass of Pluto and Charon, r, and the distance between the center of mass of the binary orbit and the Sun, rs (see Fig. 1). The total potential energy can be written from expressions (5) and (26) as
![\begin{equation*} U_T\,{=}\,U({\bm{r}}_{}) + m_2 \, \Big[ V(m_0, {{\cal{I}}}_0, {\bm{r}}_{02}) + V(m_1, {{\cal{I}}}_1, {\bm{r}}_{12}) \Big] ,\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq47.png) (32)
(32)
The equations of motion for the orbits and spins are
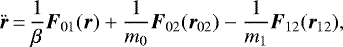 (34)
(34)
![\begin{equation*} {\bm{\ddot{r}}}_{\mathrm{s}}\,{=}\,\frac{1}{\beta_{\mathrm{s}}} \Big[ {\bm{F}}_{02} ({\bm{r}}_{02}) + {\bm{F}}_{12} ({\bm{r}}_{12}) \Big] ,\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq50.png) (35)
(35)
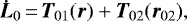 (36)
(36)
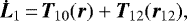 (37)
(37)
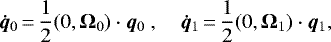 (38)
(38)
where βs = m2(m0 + m1)∕(m0 + m1 + m2), F01 (r) and Tkl (rkl) are given by expressions (30) and (31), respectively, and
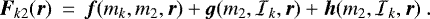 (39)
(39)
2.5 Tidal evolution
The equations of motion derived in Sect. 2.4 conserve the total energy of the system. They already take into account the tidal bulges (Eqs. (16)−(21)), but not tidal dissipation. The dissipation of the mechanical energy of tides inside the bodies introduces a time delay Δt, and hence a phase shift, between the initial perturbation and the maximal deformation. As a consequence, there is an additional net torque on the tidal bulges, which modify the spins and the orbits.
Tidal dissipation is usually modeled through the elastic second Love number k2 and the quality factor Q. The first is related to the rigidity of the body and measures the amplitude of the tidal deformation, while the second is related with the viscosity and measures the amount of energy dissipated in a tidal cycle (e.g., Munk & MacDonald 1960). For a given tidal frequency, σ, the tidal dissipation can be related to this delay through (e.g., Correia & Laskar 2003)
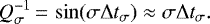 (40)
(40)
The exact dependence of Δtσ on the tidal frequency is unknown. In order to take into account tidal dissipation, we need to adopt a tidal model. A large variety of models exist, but the most commonly used are the constant-Q (e.g., Munk & MacDonald 1960), the linear model (e.g., Mignard 1979), the Maxwell model (e.g., Correia et al. 2014), and the Andrade model (e.g., Efroimsky 2012). Some models appear to be better suited to certain situations, but there is no model that is globally accepted. Nevertheless, regardless of the tidal model adopted, the qualitative conclusions are more or less unaffected, and the system always evolves into a minimum of energy (e.g., Hut 1980).
Here we adopt a viscous linear model for tides (Singer 1968; Mignard 1979). In this model it is assumed that the time delay is constant and independent of the frequency. This choice is motivated by the fact that most of the tidal evolution in the Pluto–Charon binary occurs in just a few million years after formation (see Sect. 4), when the two bodies are likely still mostly melt and fluid. Moreover, the linear tidal model provides very simple expressions for the tidal interactions that are valid forany eccentricity, inclination, rotation, and obliquity.
As in Sect. 2.2, we consider an ellipsoidal body with mass m that orbits a point-mass M located at r. The total tidal force acting on the orbit is given by (e.g., Mignard 1979)
![\begin{equation*} {\bm{F}}_t (K, M, {\bm{\Omega}}, {\bm{r}})\,{=}\,{-} K \frac{M^2}{r^{10}} \Big[ 2 ({\bm{r}} \cdot {\bm{\dot{r}}}) {\bm{r}} + r^2 ({\bm{r}}\,{\times}\,{\bm{\Omega}} + {\bm{\dot{r}}}) \Big],\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq56.png) (41)
(41)
and the tidal torque on the spin
![\begin{equation*} {\bm{T}}_t (K, M, {\bm{\Omega}}, {\bm{r}})\,{=}\,{-} {\bm{r}}\,{\times}\,{\bm{F}}_t\,{=}\,K \frac{M^2}{r^8} \Big[ ({\bm{r}} \cdot {\bm{\Omega}}) {\bm{r}} - r^2{\bm{\Omega}} + {\bm{r}}\,{\times}\,{\bm{\dot{r}}} \Big],\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq57.png) (42)
(42)
contains all the quantities pertaining to the body with mass m. We can now add to Eqs. (34)−(37), the contribution of the tidal evolution of the Pluto–Charon system as
![\begin{eqnarray*} {\bm{\ddot{r}}}_{} &\,{=}\,& \frac{1}{\beta_{}} \Big[ {\bm{F}}_t (K_0, m_1, {\bm{\Omega}}_0, {\bm{r}}_{}) + {\bm{F}}_t (K_1,m_0, {\bm{\Omega}}_1, {\bm{r}}_{}) \Big] \nonumber \\ && + \frac{1}{m_0} {\bm{F}}_t (K_0, m_2, {\bm{\Omega}}_0, {\bm{r}}_{02}) - \frac{1}{m_1} {\bm{F}}_t (K_1, m_2, {\bm{\Omega}}_1, {\bm{r}}_{12}) ,\end{eqnarray*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq59.png) (44)
(44)
![\begin{equation*} {\bm{\ddot{r}}}_{\mathrm{s}}\,{=}\,\frac{1}{\beta_{\mathrm{s}}} \Big[ {\bm{F}}_t (K_0, m_2, {\bm{\Omega}}_0, {\bm{r}}_{02}) + {\bm{F}}_t (K_1, m_2, {\bm{\Omega}}_1, {\bm{r}}_{12}) \Big] ,\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq60.png) (45)
(45)
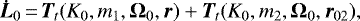 (46)
(46)
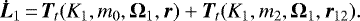 (47)
(47)
3 Initial conditions
The commonly accepted scenario for the formation of the Pluto–Charon binary is a giant impact of two proto-planets (McKinnon 1989; Canup 2005, 2011). The resulting system is a packed binary in an eccentric orbit, with the separation at periapse notexceeding a few Pluto radii (Canup 2005, 2011). In Table 1 we show three possible examples of initial configurations with different initial eccentricities taken from different works.
Although the initial orbits can be quite different, there are some constraints on the system, such that tides can bring it to the present observed configuration (Farinella et al. 1979; Lin 1981; Mignard 1981; Dobrovolskis et al. 1997; Cheng et al. 2014). We use these constraints to determine the starting point of the numerical simulations in Sect. 4.
Possible initial configurations for the Pluto–Charon orbit.
3.1 Angular momentum
If we neglect the effect of the Sun, the total angular momentum of the binary, H, must be conserved. This property can be used to put constraints on the initial spin states of Pluto and Charon, L0 and L1, respectively.We let (Eq. (1))
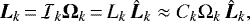 (48)
(48)
with Lk = |Lk|, 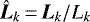 , and Ck being the moment of inertia with respect to the spin axis. The binary orbital angular momentum is
, and Ck being the moment of inertia with respect to the spin axis. The binary orbital angular momentum is
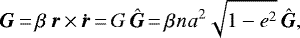 (49)
(49)
where a is the semi-major axis, e is the eccentricity, and n is the orbital mean motion. Consequently,
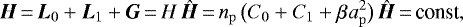 (50)
(50)
where ap and np are the presently observed semi-major axis and mean motion, respectively. We assume that the present spins are aligned with the orbit normal and that both bodies are synchronous, because this corresponds to the last stage of tidal evolution (Hut 1980). We additionally denote θk the obliquity, that is, the angle between the spin and the orbit, such that
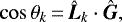 (51)
(51)
and I the inclination between the initial and the present orbit of the binary, such that
 (52)
(52)
The rotational angular momentum of Charon is the smallest contribution in the total angular momentum. We therefore further assume for simplicity that the initial obliquity of Charon is zero, that is, 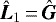 . From expression (50) we have
. From expression (50) we have
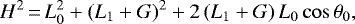 (53)
(53)
The above equations give us two constraints for the initial spins, provided that we know the initial orbit (Table 1). In general, L1 ≪ G, and so we can completely determine the initial spin of Pluto from the initial orbit, characterized by G :
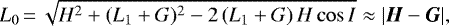 (55)
(55)
In the formation scenarios (Table 1), the inclination between the initial and the present orbit of the binary, I, is not provided. As this parameter is connected with the initial spin of Pluto, in our numerical simulations (Sect. 4) we assume different values for the initial obliquity θ0 and then derive constraints for
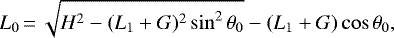 (57)
(57)
3.2 Rotation
The centrifugal breakup period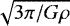 of Pluto and Charon is about 2.5 h, where ρ is the mean density. We can assume this rotation period as the critical value for the initial rotation immediately after formation. Orbital solutions that provide a rotational angular momentum (Eq. (55)) that is not compatible with this critical value can be excluded from the simulations.
of Pluto and Charon is about 2.5 h, where ρ is the mean density. We can assume this rotation period as the critical value for the initial rotation immediately after formation. Orbital solutions that provide a rotational angular momentum (Eq. (55)) that is not compatible with this critical value can be excluded from the simulations.
Assuming principal axis rotation, we can obtain the initial rotation rate from the rotational angular momentum as (Eq. (1))
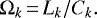 (59)
(59)
For a homogenous sphere we have C∕(mR2) = 2∕5. Adopting a two-layer body with densities of 3.4 and 0.95 g cm−3 for rock andice, respectively, we estimate the core radius (Nimmo et al. 2017) and obtain a more realistic value C∕(mR2) ≈ 0.3. Moreover, for fast-rotatingbodies, the centrifugal potential modifies the mass distribution about the spin axis and introduces a correction in the inertia tensor C = 0.3mR2 + δC, with (Eq. (18))
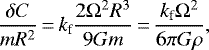 (60)
(60)
where kf is the fluid Love number. For a homogeneous body we have kf = 3∕2, but for differentiated bodies kf is always smaller. Applying the Darwin-Radau relation (e.g., Jeffreys 1976) we obtain kf ≈ 0.73 for the two-layer body. Inserting this into expression (60) we estimate
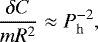 (61)
(61)
where Ph is the rotation period in hours. At present we have Ph ≈ 153 h, and so this correction can be neglected. However, for fast initial rotation periods the correct rotation is obtained by correcting the inertia tensor in the expression of the rotation rate (Eq. (59)), and solving the cubic equation
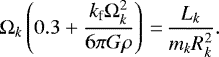 (62)
(62)
We note that the model that we present in Sect. 2 already takes into account these corrections, not only for the centrifuge distortion, but also for the less important tidal one (Eq. (18)).
For Charon we arbitrarily use 6 h for the initial rotation period and zero initial obliquity in all our simulations. The initial L1 is directly obtained from expression (62). These values are not critical, because the rotation of Charon quickly evolves into an equilibrium configuration, while its obliquity undergoes large variations (Sect. 4.5). The initial spin of Pluto is computed from expression (57), which depends on the initial orbit (see Table 1). The initial Ω0 is then obtained by solving Eq. (62).
Geophysical parameters for the Pluto–Charon binary (Nimmo et al. 2017).
3.3 Shape
The images taken during the New Horizons spacecraft encounter were used to determine the mean radius and shapes of Pluto and Charon (Nimmo et al. 2017). While the radius measurements were obtained with good precision (see Table 2), the present-day shapes were inconclusive. Only upper bounds on the flattening of 0.6% (7 km) for Pluto and 0.5% (3 km) for Charon were obtained, consistent with hydrostatic equilibrium. Indeed, from expression (61) and kf = 0.73 we estimate
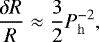 (63)
(63)
which yields present-day distortions smaller than 0.1 km, which is too small to be detectable in the New Horizons images. The absence of significant deformations for Pluto and Charon implies that their interiors must have been warm and/or deformable during the whole orbital evolution of the system.
Assuming a homogeneous density, we can compute the Stokes’ gravity field coefficients from the ellipsoid semi-axes (a ≥ b ≥ c), such that (e.g. Yoder 1995):
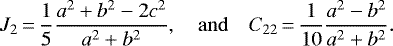 (64)
(64)
We now assume a distortion δR∕R = 10−4 (i.e., δR ≈ 0.1 km) for Pluto and Charon,which is compatible with the hydrostatic residuals (Eq. (63)) and below the observed upper limits (Nimmo et al. 2017). Consequently, using a = R + δR, b = R, and c = R − δR, we obtain J2 = 6 × 10−5 and C22 = 10−5. In our work,we adopt these values as permanent residual deformations for the two bodies.
In the early stages of the system evolution, when the rotations are much faster than today and the two bodies are close to each other, the hydrostatic contributionto J2 and C22 is several orders of magnitude above the present residual values. However, as the system evolves and the bodies cool down, they are expected to freeze at the present deformations. It is then important to keep some permanent deformation in the bodies, even if extremely small, to lock the rotations at the present synchronous state.
3.4 Tidal dissipation
The elastic second Love number for an incompressible homogeneous body is given by (Love 1911)
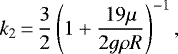 (65)
(65)
where g = Gm∕R2 is the surface gravity and μ is the rigidity. It is common to estimate μ ≈4 GPa for icy bodies (e.g., Nimmo & Schenk 2006), and so we obtain k2 ≈ 0.05 for Pluto and k2 ≈ 0.01 for Charon. As tidal dissipation and evolution only depend on the product k2 Δt (Eq. (43)), we adopt k2 = 0.05 for both bodies and then use different Δt values for Charon.
Our incomplete knowledge of the physics of tides means that the Δt values are unknown. Yet, since Δt is usually small, it only affects the overall timescale of tidal evolution (Eqs. (41) and (42)). As pointed out by previous studies (e.g., Ward & Canup 2006; Cheng et al. 2014), the ratio between tidal dissipations in Charon and Pluto is the important parameter for the tidal evolution history of the Pluto–Charon binary, namely (Eq. (44))
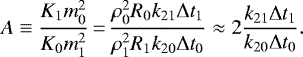 (66)
(66)
For Pluto we adopt Δt0 = 600 s, the same value as that for the Earth (Dickey et al. 1994; Touma & Wisdom 1994), and also the same adopted by a former study of the Pluto–Charon tidal evolution (Cheng et al. 2014), for a better comparison. For Charon we adopt Δt1 = AΔt0∕2 = 300 A s, and vary A from 1 to 16.
3.5 Evolution timescales
The tidal evolution of the spins and orbits of a binary system perturbed by an external body is given by Eqs. (44)–(47). These equations are general, but in the case of the Pluto–Charon system, the Sun is very distant and its tidal effect can be neglected. Therefore, we can drop Eq. (45) and simplify the remaining ones as (k = 0, 1)
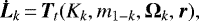 (67)
(67)
Moreover, averaging over the mean anomaly and the argument of the pericenter of the orbit, we get simplified versions of these equations in terms of elliptical elements as (Correia 2009)
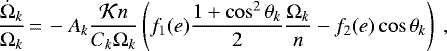 (69)
(69)
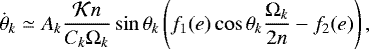 (70)
(70)
![\begin{equation*} \frac{\dot a}{a}\,{=}\,\frac{2 {\cal K}}{\beta a^2} \Big[ \Big(f_2(e) X_0 - f_3(e) \Big) + A \Big(f_2(e) X_1 - f_3(e) \Big) \Big],\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq89.png) (71)
(71)
![\begin{equation*} \frac{\dot e}{e}\,{=}\,\frac{9 {\cal K}}{\beta a^2} \Big[ \Big(\frac{11}{18} f_4(e) X_0 - f_5(e) \Big) + A \Big(\frac{11}{18} f_4(e) X_1 - f_5(e) \Big) \Big],\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq90.png) (72)
(72)
where 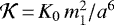 ,
, 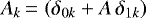 , Xk = cosθk Ωk∕n, and fk (e) are functions that depend solely on the eccentricity and become equal to one for e = 0:
, Xk = cosθk Ωk∕n, and fk (e) are functions that depend solely on the eccentricity and become equal to one for e = 0:
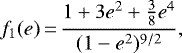 (73)
(73)
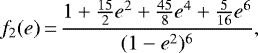 (74)
(74)
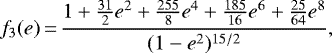 (75)
(75)
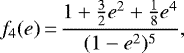 (76)
(76)
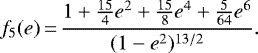 (77)
(77)
Adopting the current final value of ap = 16.5 R0 for the semi-major axis, we estimate the spin evolution timescale of Pluto and Charon, namely,
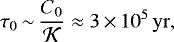 (78)
(78)
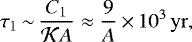 (79)
(79)
respectively,and the orbital evolution timescale
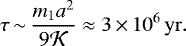 (80)
(80)
These quick estimations agree relatively well with what we observe in the numerical simulations, which are extended up to 107 yr to ensure that the system always ends in the present observed state. We see that we always have τ1 ≪ τ0 < τ, which means that the spins evolve faster than the orbit, and that the spin of Charon evolves much faster than that of Pluto. The equilibrium rotation is obtained when 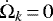 (Eq. (69)) for
(Eq. (69)) for
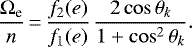 (81)
(81)
As the spin of Charon evolves much faster than anything else, we can replace Ω1 = Ωe with θ1 = 0 in expressions (71) and (72) to get simplified expressions:
![\begin{equation*} \frac{\dot a}{a}\,{=}\,\frac{2 {\cal K}}{\beta a^2} \Big[ \Big(f_2(e) \cos \theta_0 \frac{{\Omega}_0}{n} - f_3(e) \Big) - \frac{7 A}{18} f_6(e) e^2 \Big],\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq103.png) (82)
(82)
![\begin{equation*} \frac{\dot e}{e}\,{=}\,\frac{9 {\cal K}}{\beta a^2} \Big[ \Big(\frac{11}{18} f_4(e) \cos \theta_0 \frac{{\Omega}_0}{n} - f_5(e) \Big) - \frac{7 A}{18} f_6(e) (1-e^2) \Big],\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq104.png) (83)
(83)
For large A values, the eccentricity evolution is dominated by tides raised on Charon, and so the orbit is circularized in the early stages of the evolution (Dobrovolskis et al. 1997). On the other hand, for small A values, the evolution is dominated by tides raised on Pluto, whose rotation decreases slowly, and therefore the eccentricity is allowed to grow to higher values (Cheng et al. 2014). For intermediate A values, the eccentricity may preserve a nonzero but not overly high value for most of the evolution.
3.6 Orbit of the Sun
Previous constraints were derived assuming a two-body problem. However, in our numerical simulations, we additionally consider the presence of the Sun (Sect. 2.4). The final orbit of the Pluto–Charon binary around the Sun is assumed to be exactly the same orbit as today, that is, it has a semi-major axis as = 39.5 au and an eccentricity es = 0.25. More importantly, we assume that the inclination between the present orbit of the binary and the orbit of the Sun is i = 122° (Stern et al. 2018).
The semi-major axis and the eccentricity of the Sun remain almost unchanged throughout the evolution of the Pluto–Charon binary, because we do not include the effect from the remaining planets in our study. However, we note that the initial mutual inclination may change when Pluto has an initial nonzero obliquity (Eq. (58)). We therefore chose the initial mutual inclination between the orbit of the binary and the orbit of the Sun to be i = (122° + I), such that itwill stabilize at the present value at the end of the tidal evolution (when I = 0°).
4 Numerical simulations
In this section we simulate the tidal evolution of the Pluto–Charon binary from the early stages of its formation until the present day configuration. We numerically integrate Eqs. (34)–(38) for the conservative motion of the orbits and spins, and Eqs. (44)–(47) for the tidal dissipation. We use a Runge-Kutta method of order 8 with an embedded error estimator of order 7 due to Dormand & Prince, with step size control (Hairer et al. 1993). The choice of the initial conditions is described in Sect. 3, and here we explore different values for the unknown parameters.
4.1 Tidal dissipation ratio
Distinct tidal evolution behaviors depend on the ratio between the tidal dissipation in Charon and Pluto given by the A parameter (Eq. (66)). In a first set of simulations we therefore vary this parameter from A = 1 to 16.
For a better comparison with the previous work by Cheng et al. (2014), we first adopt orbit #1 (Table 1) for the primoridial system, which places Charon very close to Pluto in a not very eccentric orbit (a∕R0 = 4, e = 0.2). We also assume that the initial obliquities of Pluto and Charon are very close to zero (θ0 = θ1 = 0.001°). For Charon, we assume an initial rotation period of 6 h (Ω1∕n ≈ 3). For Pluto, with expression (57) we compute an initial rotation period of 3.7 h (Ω0 ∕n ≈ 4.5), which is close to the centrifugal breakup limit (Sect. 3.2).
Results are shown in Fig. 2. As expected, since the initial obliquities are nearly zero, our results are in good agreement with those obtained by Cheng et al. (2014). We observe that the full evolution takes less than 10 Myr for all tidal ratios, the final semi-major axis always stabilizes at the present value a∕R0 = 16.5 (except for A = 1, for which a∕R0 = 11.4), the final orbit is circularized, and the rotation for both Pluto and Charon ends up captured in the synchronous resonance.
In the case of Charon, the spin evolution is extremely fast and we observe multiple temporary captures in different spin-orbit resonances, in particular when the orbit is very eccentric. These captures follow more or less the asymptotic equilibrium rotation given by expression (81). Capture in spin-orbit resonances is a stochastic process, and so the output of our simulations for the rotation of Charon is only one among multiple possibilities. However, when the eccentricity becomes higher or lower than a critical value, the resonances always become unstable and the rotation follows its course (Correia & Laskar 2009, 2012).
In the case of Pluto, the evolution can be understood with the averaged equations in Sect. 3.5. For large A values (A ≳ 10), the eccentricity is damped more efficiently to zero because expression (83) can be approximated by its last term (owing to Charon). As a consequence, all fk (e) ≈ 1, and we get for the semi-major axis with θ0 = 0 (Eq. (82)):
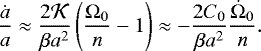 (85)
(85)
We therefore conclude that the semi-major axis always increases, until the rotation is synchronized with the orbit (Ω0 = n). Combining with expression (69), we additionally get
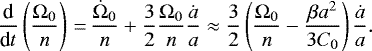 (86)
(86)
For the initial rotation and semi-major axis, we have Ω0∕n ≈ 4.5 and βa2∕3C0 ≈ 1.9, and so the ratio Ω0∕n increases and moves away from synchronous equilibrium. As the orbit expands, there is a turning point after which Ω0 ∕n decreases, for
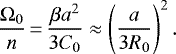 (87)
(87)
Using total angular momentum conservation (Eq. (50)), we have the additional constraint 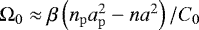 , which gives for the turning point
, which gives for the turning point
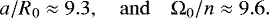 (88)
(88)
We note that the evolution observed for Ω0∕n is essentially due to the semi-major axis variation, because the rotation of Pluto slowly decreases.
For moderate A values (A ~ 7), the eccentricity damping owing to tides raised on Charon is balanced by tides raised on Pluto, which tend to increase the eccentricity (first term in expression (83)). As a result, the eccentricity initially remains approximately constant. As the ratio Ω0 ∕n increases (Eq. (86)), the eccentricity slightly increases, but as soon as the ratio Ω0 ∕n decreases (Eq. (87)), the eccentricity is damped to zero. The overall behavior is that the eccentricity only presents some small oscillations around its initial value throughout the evolution. The semi-major axis and rotation rate evolution are similar to those for larger A values.
For small A values (A ≲ 4), tides raised on Pluto control the orbital evolution (first term in Eqs. (82) and (83)). For initial rotations Ω0 ∕n ≫ 1, both the semi-major axis and the eccentricity rapidly increase to high values. The semi-major axis reaches values much larger than the present value, while the eccentricity may attain values close to one. In these extreme situations, the appocentre distance may approach the Hill sphere radius and the binary can become unstable (Cheng et al. 2014). Interestingly, this is not what we observe. At high eccentricities, there are angular momentum exchanges with the Sun because of Lidov-Kozai cycles that keep the eccentricity at values e ≲ 0.95 and thus prevent the system from being destroyed (see Sect. 4.2).
 |
Fig. 2 Tidal evolution of the Pluto–Charon binary for different values of the tidal parameter A, with initial θ0 ≈ 0° and orbit #1 (Table 1). We show the evolution of the semi-major axis and eccentricity (top), the rotation of Pluto (middle), and the rotation of Charon (bottom). |
 |
Fig. 3 Tidal evolution of the Pluto–Charon binary for different values of the tidal parameter A, with initial θ0 ≈ 0° and orbit #1 (Table 1). We show the evolution obtained including the presence of the Sun (solid line) and withoutthe presence of the Sun (dashed line). We plot the evolution of the semi-major axis and eccentricity (top), the rotation of Pluto (middle), and the rotation of Charon (bottom) on a log scale. |
4.2 Lidov-Kozai cycles
For small A values, the semi-major axis and the eccentricity can grow to extremely high values. In Fig. 2, for A = 1, the semi-major axis becomes so large at some point that it is not shown. Therefore, in Fig. 3, we show again the tidal evolution for orbit #1, but using a logarithmic scale. In addition, we also show the results of a simulation where the Sun is not included, that is, we integrate only a two-body problem (Sect. 2.3).
We observe that, for A = 4, the evolution is similar for the simulations with and without the perturbations from the Sun. However, for A = 1, in the absence of the Sun the semi-major axis increases indefinitely and the eccentricity takes a value of almost one. As a consequence, Charon would be lost. We conclude that the stability of the Pluto–Charon binary can only be correctly addressed by taking into account a three-body problem.
Assuming zero obliquity for Pluto (θ0 = 0), and retaining only the main contributions, the total potential energy (Eq. (32)) can be simplified as (e.g., Correia et al. 2013)
![\begin{eqnarray*} U_T &\,{=}\, & - {\alpha}_1 (1-e_{}^2)^{-3/2} \nonumber \\ && - {\alpha}_2 \Big[ (1 + \tfrac{3}{2} e_{}^2) (1-\tfrac{3}{2} \sin^2 i) + \tfrac{15}{4} e_{}^2 \sin^2 i \cos 2 \omega_{} \Big] ,\end{eqnarray*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq111.png) (89)
(89)
where i is the mutual inclination, ω is the argument of the pericenter of the binary orbit measured from the line of nodes,
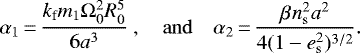 (90)
(90)
The term in α1 results from the oblateness of Pluto owing to rotation, while the term in α2 results from the quadrupole gravitational interactions with the Sun. For close-in orbits, α1 ≫ α2, and so the binary orbit precesses rapidly and the eccentricity remains approximately constant (in the absence of tides). For α1 ~ α2, the two contributions are equivalent, which occurs for
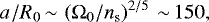 (91)
(91)
with 2π∕Ω0 = 8 h. At this stage, the gravitational interactions with the Sun become important in shaping the dynamics of the system. In particular, the angular momentum of the binary can be transferred to the orbit of the Sun. Indeed, because the two orbits have a mutual inclination of i = 122°, we can observe Lidov-Kozai cycles (Lidov 1962; Kozai 1962). These latter consist in exchanges of eccentricity and mutual inclination, such that
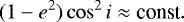 (92)
(92)
Replacing this condition in the expression of the total energy (Eq. (89)) gives us an integrable problem whose dynamics can be easily understood in terms of a (e, ω) diagram. In Fig. 4, we show the level curves of the total energy for different values of the semi-major axis, with 2π∕Ω0 = 8 h and high eccentricity. We observe that, for a∕R0 = 150 (Eq. (91)), there is only a small oscillation in the eccentricity. However, as we increase the semi-major axis (a∕R0 ≥ 200), the interactions with the Sun progressively reduce the minimum eccentricity.
When we use an average smaller eccentricity value in the evolution of the semi-major axis (Eq. (82)), we find that the semi-major axis slows down its expansion rate, and subsequently reverses its evolution. We therefore conclude that Lidov-Kozaicycles act as a protective mechanism.
In order to better understand this interesting scenario, in Fig. 5 we show the critical stages of the evolution in detail for the orbit #1 with A = 1 (corresponding to the same evolution depicted in Figs. 2 and 3). In red color we highlight the evolution during the large semi-major axis and high eccentricity phase, where Lidov-Kozai cycles can occur.
Figure 5a shows the evolution of Pluto’s rotation period as a function of time. We see that it is nearly constant and close to the initial value until the semi-major axis and the eccentricity drop to low values. Figure 5b shows the evolution of the semi-major axis for guidance. Figures 5c and d show the evolution of the mutual inclination and eccentricity as a function of time. We observe significant oscillations of both parameters for large values of the semi-major axis (a∕R0 ≥ 200, red color), corresponding to the Lidov-Kozai cycles. According to expression (92), when cos2i decreases (or increases), the eccentricity also decreases (or increases). Finally, in Fig. 5e, the evolution of the eccentricity is drawn in the diagram (e, ω). We observe that during the large semi-major axis phase, the red points are distributed in agreement with the phase space shown in Fig. 4, confirming that the Lidov-Kozai oscillation is taking place.
The evolution shown in Fig. 5 is not representative of the present system, because the final semi-major axis is below the present value. However, it shows that it is theoretically possible that the initial binary system was formed with a total angular momentum larger than what we observe today, provided that this excess was removed through the interactions with the Sun at periods of high eccentricity.
 |
Fig. 4 Level curves of the total energy (Eq. (89)) for different values of the semi-major axis, with 2π∕Ω0 = 8 h and high eccentricity. The initial condition for all curves is ω = 30°, e = 0.95 and i = 122°. |
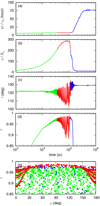 |
Fig. 5 Tidal evolution of the Pluto–Charon binary for A = 1, initial θ0 ≈ 0° and orbit #1 (Table 1). We plot the evolution of Pluto’s rotation period (a), semi-major axis (b), inclination between orbital planes (c), and eccentricity (d) as a functionof time, and the evolution in the (e, ω) diagram (e). The different colors highlight the three evolution stages, initial semi-major axis and eccentricity increase (green), Lidov-Kozaicycles (red), final semi-major axis and eccentricity damping (blue). |
4.3 Distinct initial orbits
We repeat the same experiment from Sect. 4.1, but adopting orbits #2 and #3 for the initial system (Table 1). We assume again that the initial obliquities of Pluto and Charon are close to zero (θ0 = θ1 = 0.001°), and 6 h for the initial rotation period of Charon. Due to the angular momentum conservation, Pluto’s initial rotation period is now 4.1 and 4.7 h for initial orbits #2 and #3, respectively (Eq. (62)). The tidal parameter A is again varied from 1 to 16.
Orbit #2 places Charon still close to Pluto, but in a moderately eccentric orbit (a∕R0 = 6.5, e = 0.5), which gives Ω0∕n ≈ 8.8 and Ω1 ∕n ≈ 6.2 for the initial rotation ratios. On the other hand, orbit #3 places Charon nearly at the present semi-major axis, but in a very eccentric orbit (a∕R0 = 15.8, e = 0.77), which gives Ω0∕n ≈ 29.8 and Ω1 ∕n ≈ 23.5. Results for orbit #2 are shown in Fig. 6, and results for orbit #3 are shown in Fig. 7.
We observe that the main features already present for the simulations with orbit #1 persist: (1) for large A values the eccentricity is quickly damped to zero, while for small A values it can increase to very high values; (2) the semi-major axis always evolves to the present value, except for small A values; (3) for small A values Lidov-Kozai cycles occur and stabilize the system; (4) the spin of Charon quickly evolves into spin-orbit resonances; and (5) the rotation ratio of Pluto (Ω0∕n) initially increases, then decreases towards the synchronous value. Despite these global trends, the individual variations may present a number of subtle differences, either related to the fact that the initial orbit has a larger semi-major axis and a higher eccentricity, or to the spin evolution.
For instance, for orbit #3, we observe that the semi-major axis remains more or less constant throughout the evolution, because the initial value is already close to the present value. On the other hand, as the initial eccentricity is also higher, in order to keep the eccentricity nearly constant during most of the evolution, we need smaller A values (weaker tides on Charon).
An interesting backreaction effect, previously unnoticed for orbit #1, occurs between the spin of Charon and the orbital evolution. For large A values, for which tides raised on Charon dominate the evolution, the semi-major axis and the eccentricity undergo sudden changes. These striking modifications in the orbit result from a change in the spin of Charon, which switches to a different spin-orbit resonance (see Sect. 4.4).
4.4 Spin-orbit resonances
We consider a permanent residual deformation J2 = 6 × 10−5 and C22 = 10−5 in our model (Sect. 3.3), which allows spin-orbit resonances between the rotation rate and the mean motion (e.g., Colombo 1965; Goldreich & Peale 1966; Correia & Delisle 2019). These can be observed for both Pluto and Charon in all plots that show the ratio Ω∕n.
The rotation of Charon quickly evolves into a slow rotation regime for which Ω1 ~ n, while the rotation of Pluto is much faster than the orbital period (Ω0 ≫ n) most of the time. As a consequence, resonant capture for Pluto is only observed towards the end of the evolution and often in the synchronous resonance, because at this point the eccentricity is already close to zero. On the other hand, for Charon we observe a wide variety of resonant captures that follow the eccentricity evolution.
Spin-orbit captures are interesting in the evolution of the Pluto–Charon binary, because they can modify the damping timescale of the eccentricity (Cheng et al. 2014). This backreaction effect was first described for exoplanets (Rodríguez et al. 2012), and it is particularly important when tides raised on Charon control the evolution. Indeed, assuming that Charon is captured in the Ω1 ∕n = p resonance (p is an half integer) with θ1 = 0, for large A values (Eq. (72)) we have
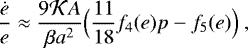 (93)
(93)
which differsfrom what is obtained with Ω1 = Ωe (Eq. (83)):
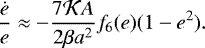 (94)
(94)
In Fig. 8, we show some examples for Charon’s rotation and eccentricity evolution with and without the permanent deformation. We adopt initial orbit #2, Charon’s initial rotation period of 6 h, θ0 = θ1 = 0.001°, and A = 9, 11, and 16 (as in Fig. 6). In the absence of permanent deformation (dashed lines), the rotation of Charon follows the exact equilibrium value given by expression (81). In the case with C22 = 10−5 (solid lines), capture in spin-orbit resonances always occurs at some point. We observe that, just after capture in resonance, the eccentricity evolution is modified. On the other hand, once a spin-orbit resonance is destabilised, the eccentricity evolution immediately slows down. In general, capture in spin-orbit resonances tend to damp the eccentricity more efficiently. At the end of the evolution, the rotation always ends captured in the synchronous resonance and the eccentricity is damped to zero.
 |
Fig. 6 Tidal evolution of the Pluto–Charon binary for different values of the tidal parameter A, with initial θ0 ≈ 0° and orbit #2 (Table 1). |
 |
Fig. 7 Tidal evolution of the Pluto–Charon binary for different values of the tidal parameter A, with initial θ0 ≈ 0° and orbit #3 (Table 1). |
 |
Fig. 8 Tidal evolution of the Pluto–Charon binary for different values of the tidal parameter A and permanent deformation, with initial θ0 ≈ 0° and orbit #2 (Table 1). We show the evolution of Charon’s rotation rate (top) and eccentricity (bottom). Solid lines correspond to J2 = 6 × 10−5 and C22 = 10−5, and dashed lines to J2 = C22 = 0. |
4.5 Initial obliquity of Pluto
The large collision that gave rise to the Pluto–Charon binary likely produced a misaligned system, that is, the orbital plane of Charon and the equatorial plane of Pluto were tilted (Canup 2005, 2011). Therefore, in this section we test the consequences of different initial obliquities for Pluto, θ0. For Charon we always assume an initial rotation period of 6 h and θ1 = 0.001°. We fix the tidal dissipation ratio at A = 4, and run a set of numerical simulations for two initial orbital configurations (Table 1).
Figure 9 shows the results for orbit #1. As expected, regardless of the initial obliquity, in all simulations the orbit is circularised, the final rotation for both Pluto and Charon ends captured in the synchronous resonance, and the obliquities end very close to zero, which corresponds to the final outcome of tidal evolution (Hut 1980; Adams & Bloch 2015). Nonetheless, for all simulations we observe an interesting early excitation of Charon’s obliquity. Pluto is initially very oblate due to fast rotation and its equator is not aligned with the initial orbit of Charon (θ0 > 0°). As a consequence, the gravitational torque of Pluto on Charon induces large obliquity variations, even in the absence of tides. These variations show that the initial choice for the spin of Charon is irrelevant, because its evolution is rapidly controlled by the external torques.
We observe that for initial obliquities θ0 ≲ 30°, the orbital and spin evolution are very similar. This is particularly true for the runs with θ0 = 0° and θ0 = 15°, for which we can only detect changes in the obliquity evolution and in the distribution of Charon’s rotation capture in spin-orbit resonances. Nevertheless, as we increase the initial obliquity of Pluto, a striking difference arises: although we adopt A = 4 in all runs, simulations with higher initial obliquity values resemble those with lower initial obliquities, but with larger A values (see Fig. 2).
For A = 4, the orbital evolution is mainly controlled by tides raised on Pluto, for which the semi-major axis and the eccentricity can grow to high values when the initial obliquity is low (Sect. 4.1). However, we observe that, as we increase the initial obliquity, the semi-major axis and the eccentricity initially decrease. Indeed, for obliquity values close to 90°, we get cosθ0 ≈ 0, and expressions (82) and (83) become always negative. After the obliquity is damped, the semi-major axis and the eccentricity can increase again, but now they restart from a lower value. As a consequence, they cannot reach values as high as in the case of an initial low obliquity.
Another interesting feature is that we cannot choose an arbitrary high initial obliquity. One reason for this is that the initial rotation rate required to conserve the total angular momentum of the system increases with the obliquity (Eq. (57)) and may exceed the rotational breakup limit. However, the main restriction is related to the semi-major axis evolution. We have just seen that high initial obliquities, in particular those with θ0 ≥ 90°, initially reduce the semi-major axis. Thus, the semi-major axis may become so small that the two bodies collide. In the simulation with orbit #1 and A = 4, this limit is around θ0 = 77° (for θ0 = 75° the minimum periapse distance is already 1.9 R0, very close to a physical collision). Since the magnitude of tidal effects is proportional to a−6, initial obliquities close to the limit value are also damped to zero more efficiently (Eq. (70)).
Figure 10 shows the results for initial orbit #2. We observe the same behavior already described for the simulations with orbit #1, but even more pronounced. As this orbit starts with a larger semi-major axis of 6.5 R0, the limit initial obliquity that prevents a collision between Pluto and Charon is higher. We estimate this limit at θ0 ≈ 96°. For initial orbit #2 and A = 4, initially low obliquities resulted in very eccentric orbits, for which the system could only be stabilized owing to Lidov-Kozai cycles (Sect. 4.2). As we increase the initial obliquity, the eccentricity is initially damped and no longer grows to extreme values; exchanges of angular momentum with the Sun no longer occur and therefore the final configuration corresponds to the presently observed system.
We conclude that the initial obliquity is a key variable to take into account in the past history of the Pluto–Charon system; it is as important as the tidal parameter A, because it acts on the eccentricity in a similar way. Indeed, in order to keep the eccentricity small throughout the evolution, it is no longer required that tides raised on Charon dominate the orbital evolution; it is enough that Pluto starts with a high initial obliquity.
5 Conclusion
In this paper we revisit the tidal evolution of the Pluto–Charon binary. We follow the system from its formation until the present-day configuration. We considered a 3D model for the orbits and spins, permanent triaxial deformations, and the presence of the Sun. All these effects prove to be important and modify the evolution of the system under certain conditions.
Previous 2D studies revealed that the orbital evolution of the Pluto–Charon system is essentially controlled by the ratio between tides raised on Charon and Pluto, which is modeled in our study by the A tidal parameter (Eq. (66)). In order to prevent the eccentricity from rising to extremely high values, 2D studies need to adopt large A values, which means that tides raised on Charon dominate the evolution. However, we observed that for high initial obliquities of Pluto (θ0 ≳ 60°), the eccentricity is damped efficiently even for small A values. As a consequence, the eccentricity may preserve a nonzero and not overly high value during most of the evolution, even when tides raised on Pluto dominate the evolution.
Another possible way to damp the eccentricity more efficiently is through capture in spin-orbit resonances. The rotation of Charon quickly evolves into a slow rotation regime (Ω1 ~ n), where capture is possible. We do observe a wide variety of resonant captures, which are enhanced for eccentric orbits. In turn, the eccentricity evolution also depends on the rotation rate of Charon, and so when a capture occurs, we have a backreaction effect in the orbit that modifies its evolution. This effect was first described for exoplanets (Rodríguez et al. 2012), but it is also important in the Pluto–Charon system.
For small A values and low initial obliquity for Pluto, the semi-major axis and the eccentricity can grow to high values. Charon could then approach the Hill sphere radius and escape. Instead, we observe that when the eccentricity is close to 0.95, there are angular momentum exchanges with the Sun through Lidov-Kozai cycles that help the Pluto–Charon binary to remain bounded. It is only possible to observe this interesting scenario with a 3D model, because the mutual inclination between the orbit of the binary and the orbit of the Sun is around 122°. The stability of the four small satellites around the Pluto–Charon binary is difficult to explain within this scenario if they were already present prior to the tidal expansion of Charon’s orbit (e.g., Smullen & Kratter 2017; Woo & Lee 2018). However, it has been shown that these satellites may have formed after the system settled into its present configuration through an impact on Charon (Bromley & Kenyon 2020).
Here we adopted a viscous linear model for tides. Tidal evolution in the Pluto–Charon binary occurs within the first 10 Myr after formation, when the two bodies are likely still mostly melt and fluid, and so this model seems appropriate. This model also provides simple expressions for the tidal evolution that allow us to interpret the output of the numerical simulations more easily. Different and eventually more realistic tidal models could be attempted in future studies (e.g., Renaud et al. 2020). These could modify the evolution timescales and the capture probabilities in spin-orbit resonances, but the main conclusions from this study, enumerated above, should remain valid.
The model described in Sect. 2 of this paper is the most complete model implemented so far for the study of the tidal evolution of the Pluto–Charon system. It is presented here in a very general formulation, and so it can be easily extended to the study of any binary system perturbed by an external body. A straightforward application is the Earth–Moon system, although in this case the evolution timescale is much longer. In order to improve our model for tidal evolution of binary systems, future work should also include planetary perturbations (e.g., Correia & Laskar 2001, 2004).
 |
Fig. 9 Tidal evolution of the Pluto–Charon binary for different values of Pluto’s initial obliquity, θ0, with A = 4 and initial orbit #1 (Table 1). |
 |
Fig. 10 Tidal evolution of the Pluto–Charon binary for different values of Pluto’s initial obliquity, θ0, with A = 4 and initial orbit #2 (Table 1). |
Acknowledgements
We thank T. Boekholt and D. Carvalho for discussions. This work was supported by CFisUC (UIDB/04564/2020 and UIDP/04564/2020), PHOBOS (POCI-01-0145-FEDER-029932), and ENGAGE SKA (POCI-01-0145-FEDER-022217), funded by COMPETE 2020 and FCT, Portugal.
References
- Adams, F. C., & Bloch, A. M. 2015, MNRAS, 446, 3676 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, L. E., & Fix, J. D. 1973, Icarus, 20, 279 [CrossRef] [Google Scholar]
- Bromley, B. C., & Kenyon, S. J. 2020, AJ, 160, 85 [CrossRef] [Google Scholar]
- Brozović, M., Showalter, M. R., Jacobson, R. A., & Buie, M. W. 2015, Icarus, 246, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Buie, M. W., Grundy, W. M., Young, E. F., Young, L. A., & Stern, S. A. 2010, AJ, 139, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Canup, R. M. 2005, Science, 307, 546 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Canup, R. M. 2011, AJ, 141, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Carvalho, D. 2016, Bachelor’s thesis, Universidade de Aveiro, Portugal [Google Scholar]
- Cheng, W. H., Lee, M. H., & Peale, S. J. 2014, Icarus, 233, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Christy, J. W., & Harrington, R. S. 1978, AJ, 83, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, G. 1965, Nature, 208, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M. 2009, ApJ, 704, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., & Delisle, J.-B. 2019, A&A, 630, A102 [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2001, Nature, 411, 767 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2003, J. Geophys. Res. Planets, 108, 5123 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2004, Nature, 429, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2009, Icarus, 201, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2012, ApJ, 751, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., & Rodríguez, A. 2013, ApJ, 767, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., Boué, G., Laskar, J., & Morais, M. H. M. 2013, A&A, 553, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Boué, G., Laskar, J., & Rodríguez, A. 2014, A&A, 571, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickey, J. O., Bender, P. L., Faller, J. E., et al. 1994, Science, 265, 482 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dobrovolskis, A. R., & Harris, A. W. 1983, Icarus, 55, 231 [CrossRef] [Google Scholar]
- Dobrovolskis, A. R., Peale, S. J., & Harris, A. W. 1997, Pluto and Charon, eds. S. A. Stern, & D. J. Tholen (Tucson, AZ: University of Arizona Press), 159 [Google Scholar]
- Dones, L., & Tremaine, S. 1993, Icarus, 103, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Drish, Jr. W. F., Harmon, R., Marcialis, R. L., & Wild, W. J. 1995, Icarus, 113, 360 [CrossRef] [Google Scholar]
- Durisen, R. H., & Tohline, J. E. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews (Tucson, AZ: University of Arizona Press), 534 [Google Scholar]
- Efroimsky, M. 2012, Celest. Mech. Dyn. Astron., 112, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Farinella, P., Milani, A., Nobili, A. M., & Valsecchi, G. B. 1979, Moon Planets, 20, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Peale, S. 1966, AJ, 71, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, H. 1950, Classical Mechanics (Reading: Addison-Wesley) [Google Scholar]
- Hairer, E., Nørsett, S., & Wanner, G. 1993, Solving Ordinary Differential Equations I: Nonstiff Problems, Springer Series in Computational Mathematics (Berlin: Springer) [Google Scholar]
- Harrington, R. S., & van Flandern, T. C. 1979, Icarus, 39, 131 [CrossRef] [Google Scholar]
- Hut, P. 1980, A&A, 92, 167 [NASA ADS] [Google Scholar]
- Jeffreys, H. 1976, The Earth. Its origin, history and physical constitution (Cambridge: Cambridge University Press) [Google Scholar]
- Kokubo, E., & Ida, S. 2007, ApJ, 671, 2082 [NASA ADS] [CrossRef] [Google Scholar]
- Kosenko, I. 1998, J. Appl. Math. Mech., 62, 193 [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C. 1981, MNRAS, 197, 1081 [CrossRef] [Google Scholar]
- Love, A. E. H. 1911, Some Problems of Geodynamics (Cambridge: Cambridge University Press) [Google Scholar]
- Malhotra, R. 1993, Nature, 365, 819 [CrossRef] [Google Scholar]
- McKinnon, W. B. 1984, Nature, 311, 355 [CrossRef] [Google Scholar]
- McKinnon, W. B. 1989, ApJ, 344, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F. 1979, Moon Planets, 20, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F. 1981, A&A, 96, L1 [Google Scholar]
- Munk, W. H., & MacDonald, G. J. F. 1960, The Rotation of the Earth; A Geophysical Discussion (Cambridge: Cambridge University Press) [Google Scholar]
- Nesvorný, D., Youdin, A. N., & Richardson, D. C. 2010, AJ, 140, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Nimmo, F., & Schenk, P. 2006, J. Struct. Geol., 28, 2194 [CrossRef] [Google Scholar]
- Nimmo, F., Umurhan, O., Lisse, C. M., et al. 2017, Icarus, 287, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, J. P., Henning, W. G., Saxena, P., et al. 2020, PSJ, in press [arXiv:2010.11801] [Google Scholar]
- Rodríguez, A., Callegari, N., Michtchenko, T. A., & Hussmann, H. 2012, MNRAS, 427, 2239 [NASA ADS] [CrossRef] [Google Scholar]
- Rozner, M., Grishin, E., & Perets, H. B. 2020, MNRAS, 497, 5264 [CrossRef] [Google Scholar]
- Schlichting, H. E., & Sari, R. 2008, ApJ, 673, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Singer, S. F. 1968, Geophys. J. R. Astron. Soc., 15, 205 [CrossRef] [Google Scholar]
- Smullen, R. A., & Kratter, K. M. 2017, MNRAS, 466, 4480 [Google Scholar]
- Stern, S. A., Buie, M. W., & Trafton, L. M. 1997, AJ, 113, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, S. A., Grundy, W. M., McKinnon, W. B., Weaver, H. A., & Young, L. A. 2018, ARA&A, 56, 357 [CrossRef] [Google Scholar]
- Tancredi, G., & Fernández, J. A. 1991, Icarus, 93, 298 [CrossRef] [Google Scholar]
- Tholen, D. J.,& Tedesco, E. F. 1994, Icarus, 108, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Touma, J., & Wisdom, J. 1994, AJ, 108, 1943 [NASA ADS] [CrossRef] [Google Scholar]
- Touma, J., & Wisdom, J. 1998, AJ, 115, 1653 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. F., & Hardie, R. 1955, PASP, 67, 224 [CrossRef] [Google Scholar]
- Ward, W. R., & Canup, R. M. 2006, Science, 313, 1107 [CrossRef] [Google Scholar]
- Weaver, H. A., Stern, S. A., Mutchler, M. J., et al. 2006, Nature, 439, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J. M. Y., & Lee, M. H. 2018, AJ, 155, 175 [CrossRef] [Google Scholar]
- Yoder, C. F. 1995, in Global Earth Physics: A Handbook of Physical Constants (Washington D.C.: American Geophysical Union), 1 [Google Scholar]
- Young, E. F., Galdamez, K., Buie, M. W., Binzel, R. P., & Tholen, D. J. 1999, AJ, 117, 1063 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Jacobi coordinates, where r is the position of m1 relative to m0 (inner orbit), and rs is the position of m2 relative to the center of mass of m0 and m1 (outer orbit). The bodies with masses m0 and m1 are considered oblate ellipsoids with angular velocity Ω, and body m2 is considered a point-mass. |
| In the text | |
 |
Fig. 2 Tidal evolution of the Pluto–Charon binary for different values of the tidal parameter A, with initial θ0 ≈ 0° and orbit #1 (Table 1). We show the evolution of the semi-major axis and eccentricity (top), the rotation of Pluto (middle), and the rotation of Charon (bottom). |
| In the text | |
 |
Fig. 3 Tidal evolution of the Pluto–Charon binary for different values of the tidal parameter A, with initial θ0 ≈ 0° and orbit #1 (Table 1). We show the evolution obtained including the presence of the Sun (solid line) and withoutthe presence of the Sun (dashed line). We plot the evolution of the semi-major axis and eccentricity (top), the rotation of Pluto (middle), and the rotation of Charon (bottom) on a log scale. |
| In the text | |
 |
Fig. 4 Level curves of the total energy (Eq. (89)) for different values of the semi-major axis, with 2π∕Ω0 = 8 h and high eccentricity. The initial condition for all curves is ω = 30°, e = 0.95 and i = 122°. |
| In the text | |
 |
Fig. 5 Tidal evolution of the Pluto–Charon binary for A = 1, initial θ0 ≈ 0° and orbit #1 (Table 1). We plot the evolution of Pluto’s rotation period (a), semi-major axis (b), inclination between orbital planes (c), and eccentricity (d) as a functionof time, and the evolution in the (e, ω) diagram (e). The different colors highlight the three evolution stages, initial semi-major axis and eccentricity increase (green), Lidov-Kozaicycles (red), final semi-major axis and eccentricity damping (blue). |
| In the text | |
 |
Fig. 6 Tidal evolution of the Pluto–Charon binary for different values of the tidal parameter A, with initial θ0 ≈ 0° and orbit #2 (Table 1). |
| In the text | |
 |
Fig. 7 Tidal evolution of the Pluto–Charon binary for different values of the tidal parameter A, with initial θ0 ≈ 0° and orbit #3 (Table 1). |
| In the text | |
 |
Fig. 8 Tidal evolution of the Pluto–Charon binary for different values of the tidal parameter A and permanent deformation, with initial θ0 ≈ 0° and orbit #2 (Table 1). We show the evolution of Charon’s rotation rate (top) and eccentricity (bottom). Solid lines correspond to J2 = 6 × 10−5 and C22 = 10−5, and dashed lines to J2 = C22 = 0. |
| In the text | |
 |
Fig. 9 Tidal evolution of the Pluto–Charon binary for different values of Pluto’s initial obliquity, θ0, with A = 4 and initial orbit #1 (Table 1). |
| In the text | |
 |
Fig. 10 Tidal evolution of the Pluto–Charon binary for different values of Pluto’s initial obliquity, θ0, with A = 4 and initial orbit #2 (Table 1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{equation*} {{\cal{I}}}\,{=}\,\left[\begin{array}{rrr} I_{11}& I_{12}& I_{13} \\[4pt] I_{12}& I_{22}& I_{23} \\[4pt] I_{13}& I_{23}& I_{33} \end{array}\right],\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq3.png)
![\begin{equation*}{{\cal{I}}}^{-1}\,{=}\,\frac{1}{\Delta {{\cal{I}}}} \left[\!\!\begin{array}{ccc} I_{22} I_{33} - I_{23}^2 & I_{13} I_{23} - I_{12} I_{33} & I_{12} I_{23} - I_{22} I_{13} \\[4pt] I_{13} I_{23} - I_{12} I_{33} & I_{11} I_{33} - I_{13}^2 & I_{12} I_{13} - I_{11} I_{23} \\[4pt] I_{12} I_{23} - I_{22} I_{13} & I_{12} I_{13} - I_{11} I_{23} & I_{11} I_{22} - I_{12}^2 \end{array}\!\!\right],\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq4.png)
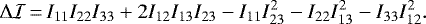
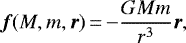
![\begin{eqnarray*} {\bm{g}}(M, {{\cal{I}}}, {\bm{r}}) &=& \frac{15 G M}{r^5} \left[ \frac{I_{22}-I_{11}}{2} \left({\hat{y}}^2 - \frac15 \right) + \frac{I_{33}-I_{11}}{2} \left({\hat{z}}^2 - \frac15 \right) \right. \nonumber \\ && \left. + I_{12} {\hat{x}} {\hat{y}} + I_{13} {\hat{x}} {\hat{z}} + I_{23} {\hat{y}} {\hat{z}} {\vphantom{\frac{I_{22}-I_{11}}{2}}} \right] {\bm{r}} ,\end{eqnarray*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq13.png)
![\begin{eqnarray*} {\bm{h}}(M, {{\cal{I}}}, {\bm{r}}) &\,{=}\,& - \frac{3 G M}{r^4} \Big[ \big(I_{22}-I_{11}\big) {\hat{y}} {\bm{j}} + \big(I_{33}-I_{11}\big) {\hat{z}} {\bm{k}} \nonumber \\ && + I_{12} ({\hat{x}} {\bm{j}} + {\hat{y}} {\bm{i}}) + I_{13} ({\hat{x}} {\bm{k}} + {\hat{z}} {\bm{i}}) + I_{23} ({\hat{y}} {\bm{k}} + {\hat{z}} {\bm{j}}) \Big] .\nonumber \\ \end{eqnarray*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq14.png)
![\begin{eqnarray*} {\bm{T}} (M, {{\cal{I}}}, {\bm{r}}) &=& \frac{3 G M}{r^3} {\bm{\hat{r}}}\,{\times}\,\Big[ \big(I_{22}-I_{11}\big) {\hat{y}} {\bm{j}} + \big(I_{33}-I_{11}\big) {\hat{z}} {\bm{k}} \nonumber \\ && + I_{12} ({\hat{x}} {\bm{j}} + {\hat{y}} {\bm{i}}) + I_{13} ({\hat{x}} {\bm{k}} + {\hat{z}} {\bm{i}}) + I_{23} ({\hat{y}} {\bm{k}} + {\hat{z}} {\bm{j}}) \Big] ,\end{eqnarray*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq17.png)
![\begin{equation*} {\bm{T}}\,{=}\,\frac{3 G M}{r^3} \left[ \begin{array}{c} \big(I_{33}-I_{22}\big) {\hat{y}} {\hat{z}} - I_{12} {\hat{x}} {\hat{z}} + I_{13} {\hat{x}} {\hat{y}} + I_{23} ({\hat{y}}^2 - {\hat{z}}^2) \\[4pt] \big(I_{11}-I_{33}\big) {\hat{x}} {\hat{z}} + I_{12} {\hat{y}} {\hat{z}} + I_{13} ({\hat{z}}^2 - {\hat{x}}^2) - I_{23} {\hat{x}} {\hat{y}} \\[4pt] \big(I_{22}-I_{11}\big) {\hat{x}} {\hat{y}} + I_{12} ({\hat{x}}^2 - {\hat{y}}^2) - I_{13} {\hat{y}} {\hat{z}} + I_{23} {\hat{x}} {\hat{z}} \end{array}\right] .\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq18.png)
![\begin{equation*} {\bm{\tilde{\Omega}}}\,{=}\,\left[\begin{array}{ccc} 0 & - {\Omega}_{k} & {\Omega}_{j} \\[4pt] {\Omega}_{k} & 0 & - {\Omega}_{i} \\[4pt] - {\Omega}_{j} & {\Omega}_{i} & 0 \end{array}\right]\!\! .\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq33.png)
![\begin{equation*} {\bm{\dot{q}}}\,{=}\,\frac{1}{2} (0,{\bm{\Omega}}) \cdot {\bm{q}} \,{=}\, \frac{1}{2} \left[\begin{array}{c} -{\Omega}_{i} q_1 - {\Omega}_{j} q_2 - {\Omega}_{k} q_3 \\[4pt] {\Omega}_{i} q_0 + {\Omega}_{j} q_3 - {\Omega}_{k} q_2 \\[4pt] - {\Omega}_{i} q_3 + {\Omega}_{j} q_0 + {\Omega}_{k} q_1 \\[4pt] {\Omega}_{i} q_2 - {\Omega}_{j} q_1 + {\Omega}_{k} q_0 \end{array}\right] .\end{equation*}](/articles/aa/full_html/2020/12/aa38858-20/aa38858-20-eq36.png)