| Issue |
A&A
Volume 644, December 2020
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202038200 | |
| Published online | 07 December 2020 | |
Rotational spectroscopic study of S-methyl thioformate
A global laboratory analysis of ground and excited torsional states up to 660 GHz★
1
Laboratoire Interuniversitaire des Systèmes Atmosphériques (LISA), UMR CNRS 7583, Université Paris-Est-Créteil, Université de Paris, Institut Pierre Simon Laplace (IPSL),
61 av. du Général de Gaulle,
94010
Créteil,
France
e-mail: kleiner@lisa.ipsl.fr
2
Observatorio Astronómico Nacional (OAN-IGN).
Calle Alfonso XII, 3,
28014
Madrid, Spain
3
Observatorio de Yebes (IGN). Cerro de la Palera s/n,
19141
Yebes,
Guadalajara, Spain
4
Univ. Lille, CNRS, UMR 8523 - PhLAM - Physique des Lasers Atomes et Molécules,
59000
Lille, France
5
Radiospectrometry Department, Institute of Radio Astronomy of NASU,
Kharkov, Ukraine
6
Instituto de Física Fundamental (IFF-CSIC). Calle Serrano 123,
28006
Madrid, Spain
7
Univ. Rennes, Ecole Nationale Supérieure de Chimie de Rennes, CNRS, ISCR-UMR 6226,
35000
Rennes, France
Received:
19
April
2020
Accepted:
13
October
2020
Context. S-methyl thioformate CH3SC(O)H is a monosulfur derivative of methyl formate, a relatively abundant component of the interstellar medium (ISM). S-methyl thioformate being, thermodynamically, the most stable isomer, it can be reasonably proposed for detection in the ISM.
Aims. This work aims to experimentally study and theoretically analyze the ground and first torsional excited states for CH3SC(O)H in a large spectral range for astrophysical use.
Methods. S-methyl thioformate was synthesized as a result of a reaction of methyl mercaptan with acetic-formic anhydride. The millimeter-wave spectrum was then recorded for the first time from 150 to 660 GHz with the solid-state spectrometer located at Lille.
Results. A set of 3545 lines is determined and combined with 54 previously measured lines in the microwave region, belonging to ground state νt = 0 as well as 1391 transitions in the first excited state of torsion ν18 = 1. Some 164 lines were also assigned to ν18 = 2 for the A-species. A global fit was performed using the BELGI-Cs code taking into account the large splitting of A and E lines due to methyl internal rotation motion with a relatively low barrier, V3 = 127.4846(15) cm−1.
Conclusions. Using our spectroscopy work, a deep search of S-methyl thioformate was carried out in the IRAM 30 m and ALMA data of different high-mass star-forming regions (Orion KL and Sgr B2). We derived an upper limit to the CH3SC(O)H column density in these regions.
Key words: line: identification / catalogs / ISM: abundances / submillimeter: ISM / methods: laboratory: molecular
Full Table A.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/644/A102
© A. Jabri et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In recent years, the detection of many complex organic molecules (COMs) in the interstellar medium (ISM) and circumstellar envelopes has been made possible by substantial progress accomplished in astrophysical observation. According to the Cologne Database for Molecular Spectroscopy (CDMS, Endres et al. 2016) and to the recent review of McGuire (2018), around 204 different molecules have been detected, and almost a third of them contain more than five atoms (Herbst & Van Dishoeck 2009). Most of the molecular identifications were accomplished by recording their spectra in the laboratory and comparing them to the interstellar surveys by means of microwave, millimeter- or submillimeter-wave telescopes.
The detection of molecular species in space by microwave, millimeter- and submillimeter-wave telescopes would have been impossible without dedicated studies in the laboratory addressing the high-resolution rotational and rovibrational spectroscopy, both in theory and experimentally, of relevant species. Precise knowledge of the rotational spectra was the key point for the detections of many complex molecules compiled and updated in the existing international databases such as CDMS (Endres et al. 2016), Splatalogue, JPL catalog (Pickett et al. 1998), NIST catalog (Lovas 2004), and Toyama Microwave Atlas for spectroscopists and astronomers. To gain this knowledge, a common strategy is to combine experimental microwave, millimeter- and submillimeter-wave spectroscopy, followed by the analysis of these spectra using appropriate effective quantum mechanical Hamiltonians and ab initio calculations, if no information on the rotational constants is available from previous studies.
In the last decades, several molecules exhibiting internal rotations of the methyl CH3 group have been detected in the interstellar and circumstellar media; for example, methanol (CH3 OH, Ball et al. 1970), methyl formate and its isotopologues (HCOOCH3, Churchwell & Winnewisser 1975; Demyk et al. 2008; Favre et al. 2014; Carvajal et al. 2009; Haykal et al. 2014; Kobayashi et al. 2013), acetaldehyde (CH3 CHO, Fourikis et al. 1974), acetic acid (CH3 COOH, Mehringer et al. 1997; Remijan et al. 2003), and acetamide (CH3 CONH2, Hollis et al. 2006).
Sulfur-bearing molecules are important species when it comes to understanding the chemical evolution of hot cores, and their molecular ratios have previously been used as chemical clocks to obtain information about the age of those hot cores (Wakelam et al. 2004; Charnley 1997). However, the chemistry of interstellar sulfur is still not well understood. The observed abundance of sulfur-bearing species in dense clouds only represents about 0.1% of the abundance of sulfur in diffuse clouds (where it corresponds almost to its solar abundance). There is still some mystery surrounding this missing sulfur and what its reservoir would be (Anderson et al. 2013). About 20 different molecules containing sulfur have been identified in space so far, and among them, only methyl mercaptan (CH3 SH) exhibits observable internal rotation splitting (called A−E splitting) (Linke et al. 1979; Xu et al. 2012; Kolesniková et al. 2014; Zakharenko et al. 2019).
S-methyl thioformate CH3SC(O)H is the sulfur analog of methyl formate CH3OC(O)H, a relatively abundant and ubiquitous molecule in the ISM (Brown et al. 1975; Churchwell & Winnewisser 1975). It is also detected in the comet Hale-Bopp (Bockelée-Morvan et al. 2000) and in low-mass star-forming regions (hot corinos) such as NGC 1333-IRAS4B and IRAS2A (Bottinelli et al. 2007). Methyl thioformate can be thus considered as a potentially detectable species in this medium because most of the abundant oxygen derivatives have the corresponding sulfur derivative detected in the ISM (Cernicharo et al. 1987).
Relatively few laboratory spectroscopic studies exist on internal rotors containing sulfur, and in the case of methyl thioformate those studies mainly concern transitions in the ground torsional state νt = 0. Two isomers exist for methyl thioformate where either the sp3 oxygen atom of methyl formate HCOOCH3 is substituted by a sulfur atom (S-methyl thioformate CH3SC(O)H) or the sp2 oxygen is substituted (O-methyl thioformate CH3OC(S)H). In 2014 Senent et al. (2014) performed high-level quantum chemical calculations to determine the spectroscopic parameters (rotational and centrifugal distortion constants as well as the potential barrier hindering the internal rotation of the methyl group). They also characterized the relative energies for the two isomers, CH3SC(O)H and CH3OC(S)H. Figure 2 of Senent et al. (2014) shows the two isomers with their possible conformers, cis- and trans-, depending on the position of the methyl group relative to that of the C = O or C = S bonds for CH3 SC(O)H and CH3 OC(S)H, respectively. The cis- S-methyl thioformate CH3SC(O)H is determined as the most stable structure at 1134 cm−1 below the trans- CH3SC(O)H, and at 4372.2 and 6335.8 cm−1 below the cis- and trans- configurations of O-methyl thioformate CH3 OC(S)H, respectively.In the present paper, we focus on the spectroscopy of the cis- S-methyl thioformate CH3 SC(O)H as it corresponds to the most stable species.
To our knowledge, only two spectroscopic studies are available for CH3 SC(O)H: Jones et al. (1976) recorded the microwave spectrum between 10 and 41 GHz, as well as an infrared spectrum recorded at low resolution between 50 and 4000 cm−1. Although they measured about 40 lines of the torsional A-species in the R-branch (corresponding to the a-type selection rule) and in the R- and Q-branches (corresponding to the b-type selection rule), their search for the A−E splitting due to internal rotation was unsuccessful because of the poor information about the barrier height to internal rotation V3. Self consistent field (SCF) ab initio calculations allowed them to conclude that their measured lines correspond to the cis- CH3 SC(O)H isomer. Using Stark-effect measurements, they were able to determine the electric dipole moment values μa and μb in the principal axis system to be 1.52 and 0.43 Debye, respectively. Later on, Caminati et al. (1981) recorded the microwave spectrum of CH3 SC(O)H between 10 and 40 GHz with a cold cell at 235 K. They also performed double resonance microwave measurements that allowed them to confirm the identification of the E-species lines. In total, they measured 22 and 15 lines belonging to the internal A- and E-rotation states, respectively, up to J = 20. They fit the 37 lines using 11 parameters. However, their study shows discrepancies up to 5.7 MHz when comparing the observed line positions to the calculated values (see Tables I and II of the ref. Caminati et al. 1981).
In this context, the goal of the present work is to extend, for the first time, the spectroscopic measurements of CH3 SC(O)H in the millimeter- and submillimeter-wave spectral ranges in order to produce a reliable line list of frequencies and intensities to be used for searching the molecule in space. Section 2 presents the experimental details, including the synthesis of the S-methyl thioformate. Section 3 contains a presentation of the theoretical model used for data analysis. The second part of this section is dedicated to assignments and fits of the spectral data. Section 4 presents the intensity calculation and the line lists for astronomers. Section 5 corresponds to the astronomical search for CH3SC(O)H in the ISM. Section 6 is dedicated to the discussion of our results.
2 Experimental details
2.1 Chemical synthesis
To prepare S-methyl thioformate CH3SC(O)H, we modifiedthe synthesis of Hershfield & Schmir (1972). In a Schlenk flask, methanethiol (methyl mercaptan, CH3 SH; 0.1 mol) was slowly added to acetic-formic anhydride (0.1 mol) at a temperature ranging from 5 to 10 °C. The flask was immersed in a liquid nitrogen bath, degassed, and then closed with the stopcock. The mixture was stirred for 36 h at 35 °C. Then, a distillation with a short Vigreux Column (20 cm) gave a first fraction containing the S-methyl thioformate and about 30% of formic and acetic acids. Purification was performed in a vacuum line (0.1 mbar) with a first trap cooled at −50 °C to remove both carboxylic acids, and a second trap cooled at −90 °C to selectively condense the S-methyl thioformate, which was thus obtained in a 37% yield.
2.2 Spectra measurements
The measurements in the frequency range under investigation (150−660 GHz) were performed using the Lille spectrometer (Zakharenko et al. 2015). The absorption cell was a stainless-steel tube (6 cm in diameter, 220 cm in length). The sample pressure during measurements was about 10 Pa and at room temperature, the line width was limited by Doppler broadening. The frequency ranges, 150−330 and 400−660 GHz, were covered with various active and passive frequency multipliers from Virginia Diodes, Inc.(VDI Inc) and an Agilent synthesizer (12.5−18.25 GHz) was used as the source of radiation. As a detector, we used an InSb liquid He-cooled bolometer from QMC Instruments Ltd to improve the sensitivity of the spectrometer. The sources were frequency modulated at 30 kHz. Estimated uncertainties for measured line frequencies are 30 and 50 kHz depending on the observed signal-to-noise (S/N) and the frequency range. Uncertainties of 100 kHz are also given to relatively broad transitions or presenting a weak S/N.
3 Results
3.1 Theoretical model
The S-methyl thioformate contains one methyl group internal rotor with a rather low torsional barrier hindering this motion, which was estimated by Caminati et al. (1981) to be V3 = 147.96 cm−1. Therefore, the rotational analysis of its spectra requires a suitable theoretical model and Hamiltonian to treat the internal rotation splitting between the A- and E-species.
In the present work, we used the BELGI-Cs1 program (Hougen et al. 1994) using the rho-axis method (RAM) with a two-step procedure initially described by Herbst et al. (1984). The BELGI-Cs code was previously applied successfully to a number of interstellar molecules containing an internal methyl rotor and was used in particular for the parent species of the cis- methyl formate (Carvajal et al. 2007) as well as for its 13C isotopic species H13 COOCH3 and HCOO13CH3 (Carvajal et al. 2009), 18O isotopologues HC18 OOCH3 and HCO18OCH3 (Tercero et al. 2012), and deuterated species DCOOCH3 (Duan et al. 2015). The method takes its name from the choice of the axis system, which allows us to minimize the coupling between internal rotation and global rotation in the Hamiltonian, at least in the zeroth order. As it has been described in the literature (Lin & Swalen 1959; Hougen et al. 1994; Kleiner 2010) and applied extensively, we do not repeat it here.
The BELGI-Cs program uses a global approach since it takes into account the A- and E-symmetry states simultaneously, as well as all the νt torsional levels originating from a given vibrational state, up to a truncation level. The interactions between rotation-torsion energy levels are treated explicitly within the Hamiltonian matrix elements. In our approach, only one set of rotational constants and parameters that describe the potential are fit for all the torsional states for a given vibrational state.
In the so-called RAM used in the BELGI-Cs code, we do not use the Principal Axis System (PAS). To simplify the calculations and to get rid at the zeroth order of the torsion-rotation interaction terms, we use a non-principal axis system (called the rho-axis system (RAS); Kleiner 2010). As a consequence, we fit the Dab parameter, which multiplies the PaPb + PbPa off-diagonal operator, where Pa and Pb designate the projection of the total rotational angular momentum on the a and b axes, respectively. The Dab parameter is related to the θRAM angle between the z axis of the PAS and RAS, as described by Kleiner (2010):
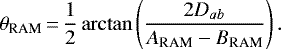 (1)
(1)
Morever, in the BELGI-Cs code, a two-step diagonalisation procedure is used to calculate the energy levels. First, a set of calculations are carried out to diagonalize the torsion part of the Hamiltonian for each K = Ka value. Then in the second step, the rest of the Hamiltonian terms (rotational, centrifugal distortion, and interaction terms between rotation and torsion) are diagonalized. The RAM method has been sucessfully applied to a number of astrophysical internal rotors, such as methyl formate (Carvajal et al. 2007, 2009). As described further in Sect. 4, the BELGI-Cs program also has an option allowing us to calculate the line strengths (using the RAM values for the electric dipole moments).
The torsional frequency mode v18 for the cis- S-methyl thioformate is predicted to lie between 80 and 111 cm−1 depending on the level of theory used (see Tables III and VII of the ref. Senent et al. 2014). Other low-frequency vibrational modes can also be responsible for rotational transitions observed in the spectrum, such as the v17 mode (torsion of the CO group) calculated to be around 250 cm−1, the v12 mode (bending of the CSC bond) observed at 245 cm−1 and the v11 mode (bending of the OCS bond) observed at 320 cm−1 (Senent et al. 2014). However, our present model does not take into account the interactions between the ground state and v17, v12 or v11.
3.2 Millimeter- and submillimeter-wave spectral analysis
First, we performed a preliminary fit using the microwave data measured by Jones et al. (1976) and Caminati et al. (1981) between 10 and 41 GHz in order to obtain the overall rotation and the internal rotation constants in the RAS using the BELGI-Cs program. These preliminary parameters allowed us to obtain a starting prediction of the millimeter-wave spectrum between 150 and 330 GHz in the ground torsional state νt = 0. Eventually, we pursued our assignments up to 660 GHz.
Following Jones et al. (1976), the electric dipole moment is maximal along the a principal axis (μa = 1.52 D; μb = 0.43 D). Therefore, rotational structures of a-type R-branch series were identified with a shift between 2 and 10 MHz for lines with Ka ≤ 5. Then, lines belonging to higher J and Ka values were progressively assigned and added to the fit. After the a-type transitions were analyzed, we also succeeded in assigning some b-type transitions, even though they are approximatively 12 times less intense [(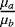 )2 ≈ 12.5]. In this process, we simultaneously assigned A- and E-type transitions, for J values up to 75. The same assignment process was pursued in the first and second excited torsional states νt = 1 and 2.
)2 ≈ 12.5]. In this process, we simultaneously assigned A- and E-type transitions, for J values up to 75. The same assignment process was pursued in the first and second excited torsional states νt = 1 and 2.
The spectrum was recorded at room temperature close to 300 K. For this reason, it was very dense (as shown in Fig. 1) since it contains not only rotational transitions of the ground state but also those belonging to the low-lying excited states, as mentioned earlier in Sect. 3.1.
In total, 5154 rotational transitions were assigned in our model and fit with experimental accuracy for J and Ka values up to 75 and 24, respectively. We weighted all lines into four sets corresponding to differences in measurement accuracy. The first set corresponds to isolated lines with a weight corresponding to 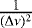 , where Δν is the measurement uncertainty of 30 kHz. The second set is weighted corresponding to the measurement accuracy of 50 kHz since they are blended lines and their energy levels are degenerated. The third given set weighted to 100 kHz corresponds to relatively broad transitions or those with a weak (S/N) ratio. Finally, we weighted the microwave transitions measured in earlier studies by Jones et al. (1976) and Caminati et al. (1981) to 150 kHz. Indeed, in our fit those lines seem to fit with larger residuals than the measurement accuracy of 100 kHz estimated by those authors. The quality of our fit is presented in Table 1, with the unitless standard deviations for each torsional state.
, where Δν is the measurement uncertainty of 30 kHz. The second set is weighted corresponding to the measurement accuracy of 50 kHz since they are blended lines and their energy levels are degenerated. The third given set weighted to 100 kHz corresponds to relatively broad transitions or those with a weak (S/N) ratio. Finally, we weighted the microwave transitions measured in earlier studies by Jones et al. (1976) and Caminati et al. (1981) to 150 kHz. Indeed, in our fit those lines seem to fit with larger residuals than the measurement accuracy of 100 kHz estimated by those authors. The quality of our fit is presented in Table 1, with the unitless standard deviations for each torsional state.
A global unitless standard deviation of 1.01 was obtained by floating 61 parameters for 3599 transitions belonging to the ground state νt = 0, 1391 transitions for ν18 = 1, and 164 transitions for ν18 = 2. Table 2 shows the values of the 61 molecular parameters obtained by the fit using the BELGI-Cs code together with the operators that those parameters multiply. The three rotational constants A, B, and C as well as the quartic centrifugal distortion (ΔJ, ΔJK, ΔK, δJ and δK) and three sextic constants (HJ, HKJ and HK) were determined. As explained in Sect. 3.1, in the RAM we also need to fit a parameter (Dab) that corresponds to the fact that the inertial tensor is not diagonal. The height of the potential barrier V3 was determined as 127.4846(15) cm−1. We note that as we globally fit the data from νt = 0, 1 and 2, wewere also able to determine the value of the internal rotation constant F = 5.332339(21) cm−1, and the second and the third terms in the cosine expansion of the potential (V6 = 24.3418(94) cm−1, V9 = 6.567(21) cm−1). Forty-five interaction parameters between rotation and torsion (such as ρ, c2, c4, k5, k2, k1, etc.), as defined in Table 2, were also necessary to reproduce the observed transitions.
Using the set of parameters of Table 2, the millimeter- and submillimeter-wave spectra measured between 150 and 660 GHz are very well reproduced to experimental accuracies, and the main strong rotational lines are assigned as shown in Fig. 1, where a section of 18 GHz (upper part) is presented with a zoomed portion of 2 GHz (lower part).
The internal rotation effect for the CH3SC(O)H molecule is quite large in comparison with methyl formate. Its barrier height V3 is determined to be relatively low in comparison with its oxygenated analog methyl formate, CH3OC(O)H, for which V3 = 372.6720(42) cm−1 (Ilyushin et al. 2009). As a result, the A−E splittings are larger in our case where, for Ka ≤ 3, differences between A- and E-frequencies vary from −150 to 250 MHz instead of only few MHz for methyl formate for the ground torsional νt = 0 state. Moreover, this splitting between A- and E-levels becomes larger for excited torsional states (ν18 = 1 and ν18 = 2), going up to some GHz. The left panel of Fig. 2 shows the variation of those A−E splittings with increasing J for ground state (upper trace) and for the first excited state (lower trace). Therefore, the use of a suitable theoretical model based on the RAM is needed to predict these rotational lines correctly. Indeed, the global approach used in the BELGI-Cs code allows us to treat all the torsional states together in the fit and to deal with the torsion-rotation interaction terms.
In the right panel of Fig. 2, we also compare the torsional energy levels determined by ab initio calculations (Senent et al. 2014) with those determined using our parameters from the fit. The agreement between our observations and those calculations is quite good.
 |
Fig. 1 Upper panel: section of experimental spectrum between 264 and 282 GHz (in black) compared to calculated spectra obtained from our fit parameters described in Table 2. Lower panel: expanded view of the 271.96−273.96 GHz regionshowing the assignments (A-species of the GS in red, E-species of the GS in blue, A-species of the ν18 = 1 mode in green, E-species of the ν18 = 1 mode in orange, and A-species of the ν18 = 2 mode in magenta). |
 |
Fig. 2 Left plot: variation of A−E splittings with J values for R-type branches of CH3SC(O)H in the ground state (upper trace) and in the first torsional state ν18 = 1 (lower trace). Right plot: obtained energy levels from our BELGI-Cs analysis compared to those determined by Senent et al. (2014) with quantum chemical calculations. |
Overview on the quality of measured lines included in the BELGI-Cs fit, for the ground state (GS) and the two first excited states ν18 = 1 and ν18 = 2.
4 Intensity calculation
For calculations of the line strengths, we used the same procedure as the one described in detail in Sect. 3.2 of Kleiner 2010. This method had been used for different molecules with Cs symmetry containing one methyl rotor such as methyl formate and its isotopologues (Favre et al. 2014; Carvajal et al. 2009, 2007; Haykal et al. 2014; Tercero et al. 2012; Duan et al. 2015) or vinyl acetate (Kolesnikova et al. 2015). We used the BELGI-Cs code to calculate the line strengths, using the energy parameters determined in Table 2. In the same way that the Hamiltonian was used in the calculation and fit of the line positions in the RAM, the calculation of the line strengths also has to be carried out in this same axis system. For this purpose, the components of the dipole moment μa and μb obtained by Stark measurements (Jones et al. 1976) were thus transformed in the RAM system using Eq. (20) of Kleiner (2010) and determined to be 1.527 Debye and −0.404 Debye, respectively. The value of the angle between the PAS and the RAS was calculated using Eq. (1) to be 30.6°.
The line frequencies, line strengths (S.μ2), and lower state energies, as well as the assignments for the observed transitions of CH3SC(O)H in the millimeter-wave and submillimeter-wave ranges are shown in Table A.1. Using a method and a code developed by Favre et al. (2014); Carvajal et al. (2019), we calculated the partition function for an internal rotor, including the torsional contribution. The values of the partition function are presented in Table A.2 for temperatures allowing the search of this molecule in different regions in warm molecular clouds of the ISM.
5 Search for methyl thioformate in space
Using the rotational constants of Table 2 and the MADEX code (Cernicharo 2012), we searched for methyl thioformate in warm molecular clouds. High-mass star-forming regions are the best candidates for this search. On one hand, it is well known that methyl formate is one of the most abundant species in hot cores. In addition, these regions are associated with molecular outflows in which large abundances of sulfur-bearing species arise (see e.g., Esplugues et al. 2013; Crockett et al. 2014; Luo et al. 2019; Belloche et al. 2013). On the other hand, one of the HCOOCH3 derivatives, ethyl formate (HCOOCH2CH3), has only been unambiguously detected in this kind of region (Belloche et al. 2009, 2013; Tercero et al. 2013, 2015, 2018; Rivilla et al. 2017; Marcelino et al. 2018). Therefore, we mainly focused on the available astronomical data of Orion KL and Sgr B2. Our frequency predictions are sufficiently reliable for a-type transitions up to 300 GHz, which is the range of the astronomical search. Nevertheless, owing to the high line density of the data and in orderto ensure the line identification, we restricted our search to transitions with uncertainties in the predicted frequency of less than 0.1 MHz.
We used the ALMA science verification (SV) data of Orion KL between 213.7 and 246.6 GHz (for observations and data reduction, see e.g., Tercero et al. 2018) and the IRAM 30 m, 3 mm survey of Sgr B2 provided by Belloche et al. (2013). In the ALMA data, we concentrated the search in the emission peaks of methyl (MF and ET peaks of Tercero et al. 2018). These positions also seem to be associated with the molecular outflow driven by source I (see Tercero et al. 2018 and references therein).
We did not find this species above the detection limit of both sets of data. To provide upper limits to its column density, we used MADEX to derive the synthetic spectrum of CH3SC(O)H for both sources assuming local thermodynamic equilibrium (LTE) and the same physical parameters as those derived for methyl formate by Tercero et al. (2018) and Belloche et al. (2013) in Orion KL and Sgr B2, respectively. The results are summarized in Table 3.
These results provide an abundance ratio of ![$\frac{[\textrm{HCOOCH}_{3}]}{[\textrm{CH}_{3}\textrm{SC(O)H}]} \, {>} \, 10^{3}$](/articles/aa/full_html/2020/12/aa38200-20/aa38200-20-eq4.png) in the emission peaks of methyl formate within Orion KL (Tercero et al. 2018) and a value > 14−20 for the different methyl formate components of Sgr B2 (Belloche et al. 2013). It is worth noting that the latter value may be greatly underestimated due to the high level of line confusion in the IRAM 30m data of Sgr B2, which leads to a less constrained upper limit for the CH3SC(O)H column density in this region.
in the emission peaks of methyl formate within Orion KL (Tercero et al. 2018) and a value > 14−20 for the different methyl formate components of Sgr B2 (Belloche et al. 2013). It is worth noting that the latter value may be greatly underestimated due to the high level of line confusion in the IRAM 30m data of Sgr B2, which leads to a less constrained upper limit for the CH3SC(O)H column density in this region.
Spectroscopic parameters of CH3SC(O)H in the RAM obtained with the BELGI-Cs program.
S-methyl thioformate column densities.
Comparison of spectroscopic constants of CH3SC(O)H, obtained by BELGI-Cs, fit with those determined in previous experimental and theoretical investigations.
6 Discussion
The values for the rotational constants A, B, and C with the BELGI-Cs code are obtained via the RAM. To compare them directly with the values derived from the previous microwave study (Caminati et al. 1981) or with the values calculated by ab initio methods (Senent et al. 2014), we need to transform them from the RAS to the PAS. This transformation is done with a rotation by an angle θRAM between the z axis of both systems, as described in Sect. 3.1 using Eq. (1) (Kleiner 2010).
Table 4 shows the values of the rotational constants after transforming back to the PAS and comparing with those determined in the literature. The spectroscopic parameters A, B, and C carried out in the present study are more accurate, but they are slightly different from those determined in the previous experimental microwave investigations (Caminati et al. 1981). They also differ from the values determined by previous theoretical calculations (Senent et al. 2014) by 0.5–1%. This could mainly be explained by the fact that we used a different Hamiltonian based on a “global approach”, taking into account both ground state and excited torsional states with a determination of higher order interaction terms between overall and internal rotations (shown in Table 2).
In Fig. 3, we show the torsion-rotation interaction diagrams, which represent the reduced energy levels (E − BJ(J + 1)) in terms of the rotational quantum number J. As shown inFigs. 3a and b for A- and E-species, respectively, the torsional levels in ground state with J ≥16 begin to be mixed, though rotation-torsional interactions or resonances, with those of ν18 = 1 and 2 excited states. Figure 3c presents a zoomed section of Fig. 3a to highlight the complexity of the interaction scheme for J ≥ 56. As shown in Fig. 3d, the interactions often correspond to the rotation-torsion states’ avoided crossings (with large differences in the K values between the interacting energy levels), such as between νt = 0, for values of Ka = 7 and ν18 = 1 for 2 ≤ Ka ≤ 4, and ν18 = 2, Ka ≤ 1.
Our global fit represents a clear improvement on previous work, especially for the ground torsional state and the first excited state, which are fit with 54 and 120 kHz standard deviations, respectively. However our analysis only contains a limited number of rotational transitions within ν18 = 2, with 164 transitions belonging to the A-species. No E-species could be assigned without ambiguity for this state. Presumably the rotational excited torsional states of S-methyl thioformate interact with the levels from other low-frequency vibrational modes, such as the bending of the CSC bond ν12 (a′) observed at 245 cm−1 (Jones et al. 1976) and the torsional mode ν17 of the CO calculated at 253 cm−1 (Senent et al. 2014). A natural next step in the understanding of the rotation-vibrational-torsional spectrum of S-methyl thioformate will be the recording of the far-infrared spectrum at high resolution, in order to measure the torsional fundamental bands at low frequencies. As in the case of methyl formate, the assignment and fit of the higher excited torsional states of S-methyl thioformate will also depend on the global treatment of the various vibrations (Ilyushin et al. 2009). It is possible that the ν18 = 2 and ν18 = 3 analysis willrequire significant extension of the current model to include suspicious perturbations from the ν12 bending mode at 245 cm−1, or ν17 torsion mode at 253 cm−1.
7 Conclusion
This work presents a global fit consisting of pure rotational transitions and rotation-torsion transitions using the BELGI-Cs code for an internal rotor. The present fit makes it possible to reproduce, from microwave to submillimeter-wave domains, data up to 660 GHz with root mean square deviations close to experimental accuracies. Using our spectroscopy work, a deep search of S-methyl thioformate was carried out in the IRAM 30 m and ALMA data of different high-mass star-forming regions (Orion KL and Sgr B2). We derive an upper limit to the CH3SC(O)H column density in these regions.
 |
Fig. 3 (a,b) Torsion-rotation diagrams (reduced energy) [E − BJ(J + 1)] in the ground state, the ν18 = 1 and ν18 = 2 states of torsion for both A-species (left plot) and E-species (right plot). (c) An enlargement of the torsion-rotation diagram for J values between 56 and 70 in order to highlight how energy levels become close to each other. (d) Examples of perturbations between different torsional states (avoided crossings are shown around J = 61 and 62, as well as around J = 66). |
Acknowledgements
This paper makes use of the following ALMA data: ADS/JAO.ALMA #2011.0.00009.SV. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. The results are also based on observations obtained with the IRAM 30 m telescope supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain). We would like to thank Dr. Carvajal for kindly providing us values for the partition functions. A.J. and I.K. also thank the French Groupe de Recherche GDR SPECMO for travel fundings. This work was supported by the Programme National Physique et Chimie du Milieu Intestellaire (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES. B.T. and J.C. thank the ERC for support under grant ERC-2013-Syg-610 256-NANOCOSMOS and the Spanish MINECO for funding support under grants AYA2012-32032 and FIS2014-52172-C2, and the CONSOLIDER-Ingenio program “ASTROMOL” CSD 2009-00038. J.-C.G. thanks the Centre National d’Etudes Spatiales (CNES) for a grant.
Appendix A Additional tables
Excerpt of the line list for CH3SC(O)H in the microwave and millimeter-wave range.
Partition functions of S-methyl thioformate, calculated at different temperatures.
References
- Anderson, D. E., Bergin, E. A., Maret, S., & Wakelam, V. 2013, ApJ, 779, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, J. A., Gottlieb, C. A., Lilley, A., & Radford, H. 1970, ApJ, 162, L203 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2009, A&A, 499, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Müller, H. S. P., Menten, K. M., Schilke, P., & Comito, C. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bockelée-Morvan, D., Lis, D. C., Wink, J. E., et al. 2000, A&A, 353, 1101 [Google Scholar]
- Bottinelli, S., Ceccarelli, C., Williams, J. P., & Lefloch, B. 2007, A&A, 463, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, R., Crofts, J., Gardner, F., et al. 1975, ApJ, 197, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Caminati, W., van Eijck, B. P., & Lister, D. G. 1981, J. Mol. Spectr., 90, 15 [CrossRef] [Google Scholar]
- Carvajal, M., Willaert, F., Demaison, J., & Kleiner, I. 2007, J. Mol. Spectr., 246, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Carvajal, M., Margulès, L., Tercero, B., et al. 2009, A&A, 500, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carvajal, M., Favre, C., Kleiner, I., et al. 2019, A&A 627, A65 [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J. 2012, EAS Pub. Ser., 58, 251 [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Guelin, M., Hein, H., & Kahane, C. 1987, A&A, 181, L9 [Google Scholar]
- Charnley, S. 1997, ApJ, 481, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Churchwell, E., & Winnewisser, G. 1975, A&A, 45, 229 [NASA ADS] [Google Scholar]
- Crockett, N. R., Bergin, E. A., Neill, J. L., et al. 2014, ApJ, 787, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Demyk, K., Wlodarczak, G., & Carvajal, M. 2008, A&A, 489, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duan, C., Carvajal, M., Yu, S., et al. 2015, A&A, 576, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. 2016, J. Mol. Spectr., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Esplugues, G. B., Tercero, B., Cernicharo, J., et al. 2013, A&A, 556, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Favre, C., Carvajal, M., Field, D., et al. 2014, ApJS, 215, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Fourikis, N., Sinclair, M., Robinson, B., Godfrey, P., & Brown, R. 1974, Aust. J. Phys., 27, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Haykal, I., Carvajal, M., Tercero, B., et al. 2014, A&A, 568, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, E., & Van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., Messer, J., De Lucia, F. C., & Helminger, P. 1984, J. Mol. Spectr., 108, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Hershfield, R., & Schmir, G. L. 1972, J. Am. Chem. Soc., 94, 1263 [CrossRef] [Google Scholar]
- Hollis, J., Lovas, F. J., Remijan, A. J., et al. 2006, ApJ, 643, L25 [Google Scholar]
- Hougen, J. T., Kleiner, I., & Godefroid, M. 1994, J. Mol. Spectr., 163, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Ilyushin, V., Kryvda, A., & Alekseev, E. 2009, J. Mol. Spectr., 255, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, G. I., Lister, D. G., Owen, N. L., Gerry, M. C., & Palmieri, P. 1976, J. Mol. Spectr., 60, 348 [CrossRef] [Google Scholar]
- Kleiner, I. 2010, J. Mol. Spectr., 260, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, K., Takamura, K., Sakai, Y., et al. 2013, ApJS, 205, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Kolesniková, L., Tercero, B., Cernicharo, J., et al. 2014, ApJ, 784, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Kolesnikova, L., Peña, I., Alonso, J., et al. 2015, A&A, 577, A91 [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, C. C., & Swalen, J. D. 1959, Rev. Mod. Phys., 31, 841 [CrossRef] [Google Scholar]
- Linke, R., Frerking, M., & Thaddeus, P. 1979, ApJ, 234, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Lovas, F. J. 2004, J. Phys. Chem. Ref. Data, 33, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, G., Feng,S., Li, D., et al. 2019, ApJ, 885, 82 [CrossRef] [Google Scholar]
- Marcelino, N., Gerin, M., Cernicharo, J., et al. 2018, A&A, 620, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGuire, B. A. 2018, ApJS, 239, 17 [Google Scholar]
- Mehringer, D. M., Snyder, L. E., Miao, Y., & Lovas, F. J. 1997, ApJ, 480, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H., Poynter, R., Cohen, E., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Remijan, A., Snyder, L., Friedel, D., Liu, S.-Y., & Shah, R. 2003, ApJ, 590, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Rivilla, V. M., Beltrán, M. T., Martín-Pintado, J., et al. 2017, A&A, 599, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Senent, M., Puzzarini, C., Hochlaf, M., Domínguez-Gómez, R., & Carvajal, M. 2014, J. Chem. Phys., 141, 104303 [CrossRef] [Google Scholar]
- Tercero, B., Margulès, L., Carvajal, M., et al. 2012, A&A, 538, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Kleiner, I., Cernicharo, J., et al. 2013, ApJ, 770, L13 [Google Scholar]
- Tercero, B., Cernicharo, J., López, A., et al. 2015, A&A, 582, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Cuadrado, S., López, A., et al. 2018, A&A, 620, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Caselli, P., Ceccarelli, C., Herbst, E., & Castets, A. 2004, A&A, 422, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, L.-H., Lees, R. M., Crabbe, G. T., et al. 2012, J. Chem. Phys., 137, 104313 [NASA ADS] [CrossRef] [Google Scholar]
- Zakharenko, O., Motiyenko, R. A., Margulès, L., & Huet, T. R. 2015, J. Mol. Spectr., 317, 41 [Google Scholar]
- Zakharenko, O., Ilyushin, V. V., Lewen, F., et al. 2019, A&A, 629, A73 [CrossRef] [EDP Sciences] [Google Scholar]
The source code BELGI for the fit, an example of input data file and a readme file are available at the web site PROSPE, managed by Dr. Zbigniew Kisiel. Extended versions of code are also available by contacting the author I. Kleiner.
All Tables
Overview on the quality of measured lines included in the BELGI-Cs fit, for the ground state (GS) and the two first excited states ν18 = 1 and ν18 = 2.
Spectroscopic parameters of CH3SC(O)H in the RAM obtained with the BELGI-Cs program.
Comparison of spectroscopic constants of CH3SC(O)H, obtained by BELGI-Cs, fit with those determined in previous experimental and theoretical investigations.
Excerpt of the line list for CH3SC(O)H in the microwave and millimeter-wave range.
Partition functions of S-methyl thioformate, calculated at different temperatures.
All Figures
 |
Fig. 1 Upper panel: section of experimental spectrum between 264 and 282 GHz (in black) compared to calculated spectra obtained from our fit parameters described in Table 2. Lower panel: expanded view of the 271.96−273.96 GHz regionshowing the assignments (A-species of the GS in red, E-species of the GS in blue, A-species of the ν18 = 1 mode in green, E-species of the ν18 = 1 mode in orange, and A-species of the ν18 = 2 mode in magenta). |
| In the text | |
 |
Fig. 2 Left plot: variation of A−E splittings with J values for R-type branches of CH3SC(O)H in the ground state (upper trace) and in the first torsional state ν18 = 1 (lower trace). Right plot: obtained energy levels from our BELGI-Cs analysis compared to those determined by Senent et al. (2014) with quantum chemical calculations. |
| In the text | |
 |
Fig. 3 (a,b) Torsion-rotation diagrams (reduced energy) [E − BJ(J + 1)] in the ground state, the ν18 = 1 and ν18 = 2 states of torsion for both A-species (left plot) and E-species (right plot). (c) An enlargement of the torsion-rotation diagram for J values between 56 and 70 in order to highlight how energy levels become close to each other. (d) Examples of perturbations between different torsional states (avoided crossings are shown around J = 61 and 62, as well as around J = 66). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


