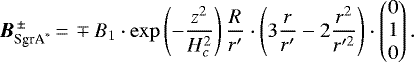| Issue |
A&A
Volume 644, December 2020
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 18 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201936081 | |
| Published online | 01 December 2020 | |
A novel analytical model of the magnetic field configuration in the Galactic center
1
Ruhr University Bochum, Faculty of Physics and Astronomy, RAPP Center, TP IV,
44780,
Bochum,
Germany
e-mail: mehmet.guenduez@rub.de
2
Ruhr University Bochum, Faculty of Physics and Astronomy, RAPP Center, Astronomical Institute (AIRUB),
44780,
Bochum,
Germany
3
IRAP, CNRS, University of Toulouse,
31028
Toulouse Cedex 4, France
Received:
12
June
2019
Accepted:
7
September
2020
Context. Cosmic-ray propagation is strongly dependent on the large-scale configuration of the Galactic magnetic field. In particular, the Galactic center region provides highly interesting cosmic-ray data from gamma-ray maps and it is clear that a large fraction of the cosmic rays detected at Earth originate in this region of the Galaxy. Yet because of confusion from line-of-sight integration, the magnetic field structure in the Galactic center is not well known and no large-scale magnetic field model exists at present.
Aims. In this paper, we develop a magnetic field model, derived from observational data on the diffuse gas, nonthermal radio filaments, and molecular clouds.
Methods. We derive an analytical description of the magnetic field structure in the central molecular zone by combining observational data with the theoretical modeling of the basic properties of magnetic fields.
Results. We provide a first description of the large-scale magnetic field in the Galactic center region. We present first test simulations of cosmic-ray propagation and the impact of the magnetic field structure on the cosmic-ray distribution in the three dimensions.
Conclusions. Our magnetic field model is able to describe the main features of polarization maps; it is particularly important to note that they are significantly better than standard global Galactic magnetic field models. It can also be used to model cosmic-ray propagation in the Galactic center region more accurately.
Key words: ISM: magnetic fields / ISM: structure / cosmic rays / Galaxy: center
© ESO 2020
1 Introduction
Cosmic-ray (CR) propagation is highly influenced by the ambient conditions. Especially the structure and strength of the magnetic field are often modeled in a simplified way. Global models, such as Jansson & Farrar (2012; hereafter JF12), Unger & Farrar (2019), Kleimann et al. (2019), Sun et al. (2008), Jaffe et al. (2013), or the recently published model by Shukurov et al. (2019), do not consider the Galactic center (GC) region due to its complexity. However, a large fraction of the CR flux is supposed to originate from this region. In particular, for the interpretation of spatially resolved gamma-ray data, it is therefore essential to model the transport out of this region correctly. To date no magnetic field model has described both the large-scale structure and strength in this inner region of the Galaxy. Nevertheless, many individual works have been published on the observation of structures and objects in the GC that are known to have a well-defined field structure. This concerns, in particular, the nonthermal radio filaments (Yusef-Zadeh & Morris 1987; Reich et al. 1988; Anantharamaiah et al. 1991, 1999; Lang et al. 1999a,b; LaRosa et al. 2000, 2001, 2005; Yusef-Zadeh 2003; Law et al. 2008) and molecular clouds (Wardle & Königl 1990; Federrath et al. 2016; Kauffmann et al. 2017a). From now on, the localized nonthermal filaments are abbreviated as NTF and the localized molecular clouds MC. Moreover, Chuss et al. (2003) published polarization data within the GC for a longitudinal extent of |y|≤ 50 pc, complemented by Nishiyama et al. (2010) for |y|≤ 250 pc, as well as Mangilli et al. (2019) and Novak et al. (2003) for |y|≤ 220 pc.
In this paper, we offer a description of the magnetic field in the central 200 pc around the GC that is as detailed as possible with current data and with the existing information. We derived a total magnetic field via the superposition of the contributions from four structures: the diffuse inter-cloud medium, localized NFT regions, localized MC regions, and the supermassive black hole at Sgr A*.
This list of chosen objects is based on the relevance of the structures for the large-scale field and the possibility to deduce the directionality and intensity of the field from their parameters. In doing so, we separated the total magnetic field model into poloidal and azimuthal components.
These two components are described by a number of free parameters (four for the poloidal component and five for the azimuthal component).
The results of this work can be used for any CR propagation purpose in the GC region. They are particularly important to extend the spatially resolved modeling of CR interactions. In addition, it also allows for a more detailed modeling of the interaction with the gas as the magnetic field model is based on the gas structure, which also becomes available in this paper. One of the most prominent features detected in recent years concerns the PeVatron seen with H.E.S.S. The detected outflows at γ-ray (Michelson et al. 2010; Su et al. 2010), microwave (Finkbeiner 2004; Dobler 2012), and radio wavelengths (Pedlar et al. 1989) are also in need of proper modeling including the GC magnetic field structure. Further, the γ-ray excess detected with Fermi in the GC region (Ackermann et al. 2017) and its interpretation as a signature of the annihilation of weakly interacting massive dark matter particles (Dobler et al. 2011; Ackermann et al. 2017) can be investigated in more detail. A regular classification of these high-energy features cannot be done without a realistic background magnetic field or gas distribution as many compelling and powerful sources are omnipresent.
This paper is structured as follows. This introduction is followed by a summary to the state-of-the-art research on the environmental conditions in the GC (Sect. 2). Section 3 represents the central part of this work, where we derive a total magnetic field for the GC region. We go through all components individually and explain our reasoning systematically for deriving the field structure or using pre-existing templates for the choice of parameters. Section 4then presents the application of our model using the CR propagation tool CRPropa, which is introduced as well. Here, the results are compared with the propagation in the magnetic field of JF12. The last chapter provides a summary, conclusion, as well as an outlook for the future.
2 The Galactic center
The extreme conditions of the GC make it one of the most exciting regions in our Galaxy. The densest region, also known as the Central Molecular Zone (CMZ), is dominated by molecular gas. The region within a Galactocentric radius of |r| ≃ 430 pc contains about 3–10% of the total gas and star formation in the Milky Way (Kauffmann 2017).
Recent observations by H.E.S.S. reveal nonthermal emission from the GC (Abramowski et al. 2016; Abdalla et al. 2018)indicating a hadronic accelerator, a so-called PeVatron that can accelerate particles up to energies of the first break in the CR energy spectrum, the so-called CR knee. Many exciting and powerful sources are present in the GC region that could be responsible for causing such a high-energy flux, like SgrA* itself or pulsars and supernova remnants (SNRs) in the very central region. The explanation of the large-scale diffuse γ-ray detection byH.E.S.S. inspired this work, since a correct modeling of the spatial dependence is only possible if the propagation of cosmic rays is modeled in a realistic large field configuration.
2.1 Mass distribution
As the local magnetic field strength in the GC cannot be determined by direct measurements except for a few Zeeman measurements, such as by Lin et al. (2000), a correlation between the magnetic field and the gas density and gas dynamics n based on equipartition with gas pressure and kinetic (turbulent) energy will be considered.
This is one reason why we present a detailed state-of-the-art inventory of the mass distribution in this section. The mass distribution is furthermore required for the interpretation of γ-ray observations in terms of hadronic processes. In hadronic processes, γ-rays are produced via CR interaction with the ambient gas. The resulting neutral pions decay into two γ-rays. Thus, even for this interaction process, knowledge on the gas distribution is crucial.
Field lines that pass through MCs are sheared out by the relative motions between MCs and the intercloud medium. Since the Alfvén speed is higher in the intercloud medium than directly in the MCs, where the density is much lower, the shearing is expected to be stronger within the MCs. Although Ferrière et al. (2007) presented the average gas density distribution for the CMZ, this model does not resolve local structures such as MCs or the inner 10 pc. Therefore, this model will only be considered for the diffuse intercloud (IC) medium (ICM). This results in the following concept for deriving an overall density profile of the GC region, which consists of three individual components: firstly, the diffuse component as the diffuse ICM, secondly, localized dense regions in the form of identified MCs, and finally the inner 10 pc, including the known substructures surrounding the supermassive black hole SgrA*. In the following we describe the observations of these three components and how we model them.
2.1.1 Diffuse component
Ferrière et al. (2007) built an analytical 3D model describing the gas distribution in the CMZ. Therefore, in order to determine the diffuse component, we subtract the mass of all MCs that are known to us, as well as the inner 10 pc structure masses from the total mass obtained in Ferrière et al. (2007). The subtracted components will be modeled individually and are therefore not part of the diffuse component. The total mass in the GC is supposed to be ~ 2.05 × 107 M⊙ (Ferrière et al. 2007) which is in the range of recent observation of ~6 × 106 M⊙ for the inner 150 pc (Oka et al. 2019).
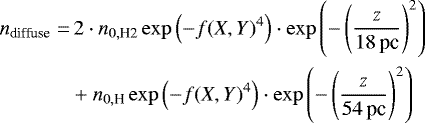 (1)
(1)
In this work, we use Galactocentric Cartesian coordinates (x, y, z) where the x-axis points from the observer at Earth (or equivalently from the Sun) toward the Galactic center, the y-axis corresponds to the direction l = +90°, and the z-axis points toward the North Galactic Pole. The normalization factor after subtracting the substructures, which amounts for ~ 40% of the total mass, yields n0,H2 := 91.1 cm−3 and n0,H := 5.3 cm−3.
2.1.2 Molecular clouds
Kauffmann et al. (2017b) derive the masses and radii from Herschel data, where the target region is obtained with the Submillimetre Common – User Bolometer Array (SCUBA) 850 μm dust emission maps. Here, we consider all MC mentioned in Kauffmann et al. (2017b). Due to the comparatively larger extension of Sgr B2, however, we have decided on an even more detailed and inhomogeneous description given in Goldsmith et al. (1990). Additionally, we treated all MC in the dust ridge region separately. Thus, six different dust ridge MCs are taken into account from Immer et al. (2012), Pillai et al. (2015), and Walker et al. (2015, 2018). It turns out that the source Sgr B1-off has been identified as dust ridge E and F. We assume that the mass of Sgr B1-off is included in the dust ridges and thus neglect this source in our modeling. The MC Sgr D was first identified as an H II region (Wink et al. 1982). The Sgr D molecular cloud is included due to its significant mass. The size and position are taken from LaRosa et al. (2000) and the density is considered as given in Lis et al. (1991). The resulting parameters of the above-described clouds are presented in Table 1.
Molecular cloud parameters.
2.1.3 Inner 10 pc
The central 10 pc around SgrA* are of particularimportance as SgrA* is one of themost interesting candidates for CR acceleration (Abdalla et al. 2018; Abramowski et al. 2016). Thus, the morphology of the mass distribution and magnetic field is highly relevant for CR propagation models. Even if the sources of CRs would mainly lie outside of this inner core, diffusion would lead to the propagation of particles into the central 10 pc and again make a detailed modeling of both the gas distribution and magnetic field configuration important. Ferrière (2012) has constructed a realistic three-dimensional picture of this region by reviewing existing observational studies. Table 2 lists ten components by order of decreasing density that are adopted according to the 3D morphology and density derived in Ferrière (2012).
The locations and sizes are taken from Ferrière (2012). The combined gas density distribution is visualized in Figs. 1 and 2 with and without contours of the diffuse medium, respectively.
2.2 Nonthermal filaments
While the origin of the NTFs is not well understood yet, their presence in the GC region indicates the existence of strong magnetic fields and relativistic electrons. Several reasonable alternatives are describing the formation process. The first scenario (more detailed in Benford 1988, Lesch & Reich 1992, Serabyn & Morris 1994, Uchida et al. 1996 and Staguhn et al. 1998) suggests that the relativistic electrons originate from fast-moving clouds. Hence, the interaction between the background magnetic field and these clouds fulfills both ingredients for generating synchrotron radiation.
The alternative explanation, for example, presented in Yusef-Zadeh (2003) suggests a link to star-formation regions where collective winds of massive WR and OB stars generate shock waves. Thus, within a dense stellar region, particles can be accelerated to relativistic energies.
The third explanation is based on recent MeerKAT observations. Heywood et al. (2019) observed a huge radio bubble (140 pc × 430 pc) extending above and below the GC. These lobes can be seen in both the radio (Heywood et al. 2019) and X-ray (Nakashima et al. 2019; Ponti et al. 2019) parts of the spectrum. The observations indicate an outbursts of relativistic electrons from the central black hole (BH) or from its surroundings. We are interested in NTFs because of their strong non-thermal radio emission and, thus, the connection to the magnetic field. Their expected strong fields, in combination with the known structures, represent an influential contribution to the modeling of the large magnetic field in the GC region.
LaRosa et al. (2000) presented a wide-field 90 cm-VLA image of the GC region. They cataloged the 90 cm flux density, position, and size of NTFs among other objects. Some of the sources were also investigated concerning their 20 cm/90 cm spectral index. Furthermore, isolated NTFs show a constant spectral index of α ≈−0.6, consistent with a relatively flat, first-order-Fermi accelerated electron population. We summarize the properties of these filaments as found in LaRosa et al. (2000) in Table 3. Figure 1 visualizes the NTFs relative to the MC distribution.
 |
Fig. 1 Representation of the combined gas density of the CMZ region in units of cm−3 (color scales). Here and in the figures that follow, the x-axis points fromthe Sun to the GC. The diffuse ICM is shown as red contours. The non-thermal filament objects are presented ascylindrical black colored objects. |
Summary of the gas components of the interstellar gas in the inner 10 pc around SgrA*, ordered by decreasing density.
Summary of the properties of the filaments in the CMZ.
3 Magnetic field in the CMZ
The main application of the global magnetic field models of the Milky Way is the propagation of CR. Divergence-freeness of the JF12 field has been implemented in Kleimann et al. (2019) and Unger & Farrar (2019), which makes the model useful for MHD simulations as well, in which the lack of sources and sinks is of high importance. The JF12 model and its updates, however, do not explicitly take into account the central 1 kpc of the disk component. The use of this field for CR propagation throughout the Galaxy leads to magnetic mirror effects, resulting in the trapping of CRs within 1 kpc (Merten 2015). Interpolating the disk field from further out has been used for CR propagation modeling by Merten et al. (2017). This is a good first approximation for global CR models, but it is doubtful that CR propagation and its signatures in the GC can be studied properly with this simplified approach. Global propagation models can also rely on the field configuration in the GC range – the CR source density is expected to be highest in the central part of the galaxy and local diffusion in the first kpc could also change the global result. The aim of this paper is to answer these open questions by first creating a more sophisticated magnetic field model in the CMZ region (from now on GBFD20) and performing a first comparison with the simplified JF12 extrapolation in the GC region. This section focuses on building the model for the inner radius of 200 pc, while Sect. 4 presents first simulations that compares the two approaches.
3.1 Magnetic field observations in the CMZ
The magnetic field of the diffuse ISM in the GC region has been investigated with different methods, among those are polarization measurements from far-infrared to near-infrared or radio wavelength (Chuss et al. 2003; Novak et al. 2003; Nishiyama et al. 2010). Still, the magnetic field strength and orientation in some regions in the CMZ remain rather uncertain. Nevertheless, the measurements provide us with pieces of information on a general structure and intensity of the field as summarized below for the three different density regions – the MCs, NTFs and the diffuse ICM. Pieces of evidence for the directionality in the CMZ are the following:
- 1.
B ~ poloidal in the diffuse ICM and NTF region:
Nishiyama et al. (2010) present a polarization map deduced from near-infrared wavelength of nearly the whole CMZ that exhibits the existence of a poloidal field for |b| > 0.4 deg.
LaRosa et al. (2005) refer to an approximately poloidal component in the diffuse IC region.
The NTFs can best be described by a poloidal component (LaRosa et al. 2001). One exception is the Pelican region, which reveals a dominantly horizontal orientation (LaRosa et al. 2000), with horizontal being defined as the Br − Bϕ plane.
- 2.
B ~ horizontal in the MC region:
The dense clouds, on the other hand, require a dominant horizontal field component (Ferrière 2009; Nishiyama et al. 2010).
Far-infrared polarization measurements from dust indicate a field which is predominantly parallel to the Galactic Plane for |b| < 0.4 (Nishiyama et al. 2010) where most of the cloud are located. This indicates that the X-field component modeled for the large-scale field in the JF12 paper is subdominant in the CMZ for small Galactic longitudes.
Chuss et al. (2003) (submillimeter observation), Nishiyama et al. (2009) (from far-infrared (FIR) and submillimeter observations), and several other groups suggest a dominant horizontal field component with respect to the Galactic Plane in dense regions.
Evidence for the magnetic field strength are summarized here:
Although the measurement of the field strength at the event horizon of SgrA* is still inaccessible, in simulations, it requires a field strength of about 30–100 G at the event horizon in order to explain the synchrotron radiation (Eatough et al. 2013; Mościbrodzka et al. 2009; Dexter et al. 2010). Therefore, we apply this constraint in our modeling. The field is supposed to be azimuthally sheared by the differential rotation as discussed by Johnson et al. (2015). These authors also found evidence for a partially ordered fields near the event horizon (~6 Schwarzschild radii) as well as an associated variability on the time-scale of an hour.
Simulation results from Peratt (1984) suggest a field strength up to 10 mG inside the inner 10 pc. On average,however, the field might be weaker in order to ensure the stability of the dominant cloud in the Circumnuclear disk (CND; Morris 1990). The highest direct detection of the field strength inside 10 pc was ~ 3 mG (Plante et al. 1995) based on the detection of H I Zeeman splitting.
A field strength of 1 mG has been measured in Sgr B2 based on H I Zeeman measurements (Crutcher et al. 1996).
The dense clouds are thought to have a typical field strength of 1 mG (Ferrière 2009) (see also Table 1).
An average value of ~10 μG with an uncertainty factor of 10 is supposed to be present in the ICM (LaRosa et al. 2005; Ferrière 2009). However, since the field strength in the Galactic disk amounts to ~3 μG a smaller value than ~10 μG seems to be not plausible. This value is from now on defined as
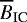 .
.The NTFs also show a field strength up to 1 mG obtained from the related equipartition magnetic field and the radio luminosity (see Table 3).
In summary, the background field in the ICM and the NTF regions1 is predominantly poloidal, whereas the horizontal field dominates in the MC regions. Additionally, each region has a specific field strength with the evidence as discussed above. These pieces of information together with the constraints from electrodynamics, that is ∇ ⋅ B = 0 and a zero net magnetic flux, can be used to develop a first full description of the magnetic field in the CMZ.
3.2 Determination of the magnetic field strength
The highly polarized emission observed (LaRosa et al. 2001) in the NTF regions has an average strength of the order ~ 1 mG (see Table 3) which is derived from radio luminosities.
An average value of 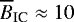 μG determines the field strength in the ICM (LaRosa et al. 2005; Ferrière 2009). Concerning the MCs, only two clouds out of 12 (CND, Plante et al. 1995 and Sgr B2, Crutcher et al. 1996) have direct magnetic field measurements via H I Zeeman splitting. However, it is possible to estimate the field strength in MCs based on a theoretical argument, which assume equipartition between magnetic pressure and turbulent pressure.
μG determines the field strength in the ICM (LaRosa et al. 2005; Ferrière 2009). Concerning the MCs, only two clouds out of 12 (CND, Plante et al. 1995 and Sgr B2, Crutcher et al. 1996) have direct magnetic field measurements via H I Zeeman splitting. However, it is possible to estimate the field strength in MCs based on a theoretical argument, which assume equipartition between magnetic pressure and turbulent pressure.
Equipartition with turbulent pressure
The second method builds on the assumption that the turbulent and magnetic energy are in equilibrium, that is,
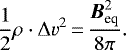 (3)
(3)
Here, Δv represents the turbulent velocity, which is estimated considering cloud line width and presented in Table 4. The magnetic field strength results are also given in Table 4. Here, we interpret Beq as the average field strength 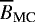 of the MCs.
of the MCs.
3.3 Modeling the magnetic field structure
In this section, we make use of analytical and divergence-free magnetic field components contributing to a total field model and constrain the resulting free parameters by the geometric structure, location and size of the considered regions and objects. The details of this mathematical approach are described below.
Concerning the structure of the field, we start with the introduction of the poloidal field component in Sect. 3.3.1, based on the model presented in Ferrière & Terral (2014), as this can be used to describe both, the IC and NTF regions. A purely poloidal configuration has radial and vertical (vertical = z in cylindrical coordinates) unit vectors. In contrast, a purely horizontal configuration depends on a radial and azimuthal unit vectors. Thepoloidal field does not apply to the MC regions, as the field is predominantly horizontally oriented. Thus, a horizontal field component will be derived for the MCs in the CMZ. The relation between these components will be based on the ambient conditions in the MCs. Therefore, Sect. 3.4 will introduce the horizontal component and constrain the parameters by the boundary conditions also described in the same section. The total magnetic field model is then given by a superposition of all poloidal and horizontal components.
Magnetic field strength for the different objects, derived from equipartition with turbulent pressure is listed.
3.3.1 Poloidal field component
Ferrière & Terral (2014) published an analytical expression of poloidal and x-shaped divergence-free magnetic fields models. A good description of a poloidal field is given by Model C described in Eqs. (80) and (81) in Ferrière & Terral (2014)
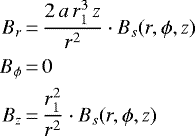 (4)
(4)
Since we are interested in a purely poloidal field, we set the azimuthal component to zero. From now on the magnetic field given by Ferrière & Terral – Model C (FT14-C) is called BC = (Br, 0, Bz). This model has four free parameters: L, m0, B1 and a. Here, L denotes the radial exponential scale length, m is the azimuthal wavenumber (m0 = 0 for axisymmetric, m0 = 1 for bi-symmetric and m0 = 2 quadri-symmetric,... magnetic field). For simplicity and due to the lack of information on the azimuthal wavenumber, we use m0 = 0 for all poloidal fields. B1 is the magnetic field strength normalization factor and a is a strictly positive parameter governing the opening of field lines away from the z-axis. Finally, g(r, z) is a smoothly varying function describing the spiraling of field lines. Those interested in a single global model can use Model C with its azimuthal field component given in Ferrière & Terral (2014). This type of model is easier to handle, but cannot reproduce local but influential configurations, such as those in the NTFs or dense regions in the GC.
3.3.2 Magnetic field in the diffuse inter-cloud medium
As the background field in the ICM is predominantly poloidally oriented, we make use of the poloidal field component described in Eq. (4). The background field in the ICM, from now on 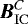 , is assumed to follow the mass distribution in the CMZ as described in Ferrière et al. (2007). There, the semi-major axis corresponds to 250 pc with an axis ratio of 2.5. Transforming this property to an axisymmetric description delivers a radius of RIC = 158 pc. The radial exponential scale length is then obtained by assuming half-max value of B at RIC.
, is assumed to follow the mass distribution in the CMZ as described in Ferrière et al. (2007). There, the semi-major axis corresponds to 250 pc with an axis ratio of 2.5. Transforming this property to an axisymmetric description delivers a radius of RIC = 158 pc. The radial exponential scale length is then obtained by assuming half-max value of B at RIC.
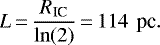 (5)
(5)
The parameter a governing the opening of field lines away from the z-axis will be determined by comparing the configuration obtained by this model and the polarization map of Nishiyama et al. (2013). Here, we consider a region which does not contain any significant NTFs or MCs. In doing so, we assume that we can neglect the field contributed by the NTF and MC regions and just have a dominant background field of the ICM. Therefore, we take the region from − 200 pc < y < − 125 pc into account. Varying a from 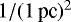 to
to 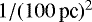 , a best fitting procedure delivers
, a best fitting procedure delivers 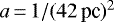 which leads to similar disk thickness as used in Ferrière et al. (2007). Figure 3 displays observed and expected configuration for our best fit value. The map derived from this work is deduced from the direction of the field lines and calculated by the poloidal field model. Thus, it does not correspond to a polarization map in its entirety. Rather, it should only be used as a qualitative comparison with the observation to explain features. Since a single and ordered magnetic field model describes the ICM region, the configuration in the direction of the line of sight does not change.
which leads to similar disk thickness as used in Ferrière et al. (2007). Figure 3 displays observed and expected configuration for our best fit value. The map derived from this work is deduced from the direction of the field lines and calculated by the poloidal field model. Thus, it does not correspond to a polarization map in its entirety. Rather, it should only be used as a qualitative comparison with the observation to explain features. Since a single and ordered magnetic field model describes the ICM region, the configuration in the direction of the line of sight does not change.
The fitting parameter B1 is determined by assuming that the average value of the model needs to match the observed value, here, 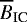
In theIC region, 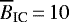 μG is assumed to correspond to the true average value, following the conclusion of Ferrière (2009) and LaRosa et al. (2005) as already discussed above. Within the model, we can determine the average value as
μG is assumed to correspond to the true average value, following the conclusion of Ferrière (2009) and LaRosa et al. (2005) as already discussed above. Within the model, we can determine the average value as
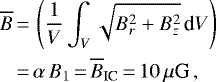 (6)
(6)
with 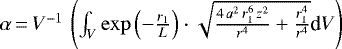 . Here, the integrand in the bracket denotes the average field strength obtained from the model, and V the total volume of the CMZ. Thus, B1 can be determined as
. Here, the integrand in the bracket denotes the average field strength obtained from the model, and V the total volume of the CMZ. Thus, B1 can be determined as
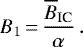 (7)
(7)
Solving this equation delivers α ≈ 0.85 and therefore
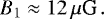 (8)
(8)
Figure 4 illustrates the application of the poloidal magnetic field model in the IC region, projected onto the Y − Z-plane. Due to the symmetry of the equation in Y and X, this graph represents the X−Z-plane as well.
 |
Fig. 3 Magnetic field configuration as derived for BIC is visualizedby black dashes lines and by colored dashed lines as measured by Nishiyama et al. (2013). |
 |
Fig. 4 Magnetic field strength in units of μG in the IC region. The relative length and color of the arrows represent the relative magnetic field strength. |
3.3.3 Magnetic field in the NTF regions
There are observations that prove that NTFs have an almost vertical magnetic field (Yusef-Zadeh 2003; Morris 2015; Mangilli et al. 2019). Using the poloidal field component given by Eq. (4), the opening angle of the field lines (away from the z-axis) is governed by the parameter a. If a is very small, the poloidal field goes to a vertical field, which can then be used for the NTF regions. Outside the filaments, the contributionfrom the NTF magnetic field is much weaker than the contribution from the ICM magnetic field due to the rapid decrease of the NFT field strength. This expectation is exemplified by Sgr C-NTF in Fig. 5, where the field strength outside the filaments decreases rapidly.
An external confining force must be present, otherwise the strong magnetic pressure inside filaments would tend to blow them apart. Considering that the field strength in the NTF regions lies between ~0.1 and 1 mG, the corresponding magnetic pressure lies in the range
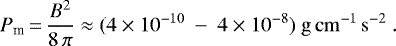 (9)
(9)
A first possibility is confinement by gas pressure,
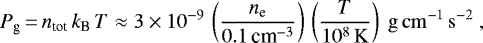 (10)
(10)
where ntot ≈ 2ne is the total number density of particles (protons, helium nuclei, and electrons) and ne is the density of free electrons in the ionized gas. The pressure from the observed hot ICM plasma (Bland-Hawthorn & Reynolds 2000) at a temperature T ~ 106 K and with an electron density ne ~ 0.002 cm−3 is too low to counterbalance magnetic pressure. However, a gas at higher temperature T ~ 108 K and with an electron density ne ~ 0.01 cm−3 has been observed with Chandra (Muno et al. 2004); this gas could very well counterbalance magnetic pressure. A second possibility is that the magnetic field has an azimuthal component, which provides an inward magnetic tension force. A third possibility is that the actual field strength is in fact lower than the assumed strength of 0.1 mG, which is uncertain by a factor ~10. Finally, it could also be that the filaments are not in pressure balance, but in a dynamical state. The only exception is the Pelican NTF, which is rotated by about 90° (LaRosa et al. 2000). Each of the NTFs requires an individual adaption of the free parameters. Similar to Eq. (5), the radial exponential scale length L is given by
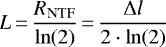 (11)
(11)
where Δl denotes the horizontal extent of the NTF which is presented in Table 3. The parameter a determines the decrease with respectto the z-axis but also theopening of the field lines. Considering the observation, the magnetic field contributed by a NTF should not be dominant outside the NTF region. If the top arms and bottom arm of the poloidal field are pressed together, the upper and lower opening angle of the X decreases around the z-axis. This leads to a monotonous decrease of the magnetic field with respect to the z-coordinate. Since the B-field decreases quadratically with respect to the z, an approximation to the Gaussian distribution is thus close. The vertical Gaussian scale should give us a good value of a for an approximately purely vertical configuration. In this case, the vertical Gaussian scale yields
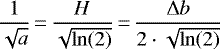 (12)
(12)
where Δb denotes the vertical extent of each NTF and is presented in Table 3. The comparison of the z-profile of the poloidal field model at (x, y) = (0, 0) and the profile of a Gaussian distribution ∝ exp(−b ⋅ z2) is presented in Fig. 6. Applying the poloidal field model to the Sgr C-NTF, the best fit value for the Gaussian parameter b ≈ 0.075 pc2 is approximate the parameter 1∕a2 ≃ 0.061 pc2. Figure 5 shows the field configuration.
The normalization factor B1 is calculated in the same way as presented in Eq. (7). Again, the normalization factor B1 is determined for each NTF individually from the measured values of the average field strength 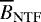 in each NTF presented in Table 3. The volume factor α becomes about the same for all NTFs, i.e. α ≈ 0.256 and thus, the measured value of the average magnetic field in each NTF,
in each NTF presented in Table 3. The volume factor α becomes about the same for all NTFs, i.e. α ≈ 0.256 and thus, the measured value of the average magnetic field in each NTF, 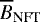 scales linearly with B1:
scales linearly with B1:
 (13)
(13)
The different configuration in the Pelican NTF region has to be considered. As this NTF is perpendicular to all other NTFs, we apply a rotation matrix at the x-axis, which yields
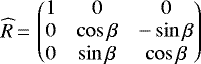 (14)
(14)
is obtained. The total magnetic field in the NTF regions, from now on 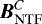 , is given by a superposition of the magnetic field in each NTF region. Figure 7 illustrates the application of the poloidal field model in all NTF regions.
, is given by a superposition of the magnetic field in each NTF region. Figure 7 illustrates the application of the poloidal field model in all NTF regions.
 |
Fig. 5 Magnetic field strength in Sgr C visualized by the related 3D magnetic field configuration. Lower panel: zoomed view. |
 |
Fig. 6 z-profile of the poloidal field strength in units of μG (blue, solid line) in comparison to a Gaussian distribution (red, dashed line). |
 |
Fig. 7 Magnetic field strength in μG is presentedconsidering the NTF components in Table 3. The relative length and color of the arrows represent the relative magnetic field strength. |
3.4 Horizontal field model for the MC regions
The magnetic field in the dense MCs is predominantly parallel to the Galactic plane, that means, it only has radial and azimuthal components, while its vertical component can be neglected.
Here, werelate the azimuthal field component Bϕ to the radialcomponent Br and assume the same constant ratio for all MCs expect for the MC CND, which is highly influenced by the gravitational dynamics of SgrA*.
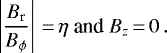 (16)
(16)
The comparison of polarization results of Hildebrand et al. (1990) with the innermost 5 pc MC of the CMZ which is called CND delivers η = 0.77 (Wardle & Königl 1990). For all other MCs, η is not known and therefore will be kept as a free parameter. However, since η determines the azimuthal shearing, a value larger than 1 means a very weak shearing and a value equal zero means a complete azimuthal shearing. Therefore, we show the results for three different values with η ∈ [0, 0.5, 1.0] as examples.
For this purpose, we construct another analytical magnetic field model for the horizontal component considering the Euler potentials, α and β. In doing so, the magnetic field is naturally divergence-free,
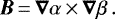 (17)
(17)
Here, we apply ∇ in cylindrical coordinates. Equation (17) produces a field with a vanishing z-component for instance if we choose β = z. In the plane perpendicular to the z-axis, the field lines can be described by
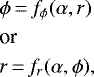 (18)
(18)
where each value of α refers to a field line. Thus, an arbitrary, monotonic function of α, which we call ψ(α), represents the azimuthal angle of the field line at a specific radius ρ. Here, ρ represents the reference radius at which the field line is crossing the reference angle ψ and is a free parameter. This relation will simplify our calculation in order to apply the boundary condition of Eq. (16) for the determination of the field.
With the transformation described in Eq. (18) we obtain
![\begin{equation*} {\vec B}\,{=}\, \begin{pmatrix} \frac{1}{r} \frac{\partial \alpha}{\partial{\psi}}\frac{\partial\psi}{\partial \phi}|_r \\[4pt] -\frac{\partial \alpha}{\partial{\psi}}\frac{\partial\psi}{\partial r}|_{\phi} \\[4pt] 0. \end{pmatrix}\end{equation*}](/articles/aa/full_html/2020/12/aa36081-19/aa36081-19-eq33.png) (19)
(19)
We use η = |Br∕Bϕ| = const. in order to determine ψ:
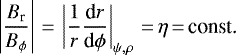 (20)
(20)
![\begin{align*} \mp\;& \frac{\textrm{d}r}{r}|_{\rho} \,{=}\,\eta\,(\textrm{d}\phi|_{\psi})\nonumber\\[4pt] \mp\;& \ln\left(\frac{r}{\rho}\right) \,{=}\,\eta\,(\phi-\psi)\,.\end{align*}](/articles/aa/full_html/2020/12/aa36081-19/aa36081-19-eq35.png) (21)
(21)
As in astrophysical context r extends to many magnitudes, we can transform r→r + b with r ≫ b and still hold a constant ratio of Br and Bϕ. With the same assumption we also transform ρ→ρ + b. This transformation will be necessary for avoiding singularities in the argument of the cosine function in Eq. (25). The free parameters b needs to fulfill r ≫ b and later will be set to a negligible fraction of the MC radius. Thus, the function ψ can be described as
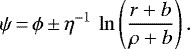 (22)
(22)
The partial derivates become
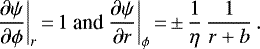 (23)
(23)
Finally, we define ∂α∕∂ψ := ρ ⋅ ξ(ψ) ⋅ h(z) and include an arbitrary function of z which will not destroy the solenoidal property of the field. In doing so, Eq. (19) becomes
![\begin{equation*} \begin{split} \begin{pmatrix} B_{\textrm{r}}\\ B_{\phi}\\ 0 \end{pmatrix}&\,{=}\, \begin{pmatrix} \frac{\rho}{r} \xi({\psi})\cdot h(z) \\[4pt] \mp\eta^{-1}\,\frac{\rho}{r+b}\cdot \xi({\psi})\cdot h(z) \\[4pt] 0 \end{pmatrix}\\&\approx \begin{pmatrix} \frac{\rho}{r}\,\xi(\psi)\cdot h(z)\\[4pt] \mp \eta^{-1}\cdot\frac{\rho}{r}\, \xi(\psi)\cdot h(z) \\[4pt] 0 \end{pmatrix}\,{=}\, {\vec B}_{\,{\pm}\,}. \end{split} \end{equation*}](/articles/aa/full_html/2020/12/aa36081-19/aa36081-19-eq38.png) (24)
(24)
Here, we obtain two solutions B− and B+, as only the absolute value of the ratio between the radial and azimuthal components of the magnetic field is known. This unknown sign transforms into an unknown rotational direction that needs to be constrained by observations, as we discuss later.
The next step will specify ξ(ψ). For this purpose, we assume a simple cosine which yields the same physical results for ϕ = n ⋅ 2π and 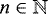 . Moreover, this choice ensures the physical reality of a magnetic field, that is, the net magnetic flux is zero as we show below.
. Moreover, this choice ensures the physical reality of a magnetic field, that is, the net magnetic flux is zero as we show below.
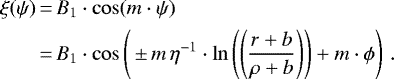 (25)
(25)
Here, m denotes the azimuthal wavenumber as defined before. The field becomes
![\begin{equation*} \begin{split} \begin{pmatrix} B_{\textrm{r}}\\ B_{\phi}\\ 0 \end{pmatrix}\,{=}\,&B_1\cdot\cos\left({\,{\pm}\, m\cdot\eta^{-1}}\cdot\ln\left(\left(\frac{r+b}{\rho+b}\right) \right) +m\cdot{\phi}\right)\\ &\cdot h(z)\cdot\begin{pmatrix} \frac{\rho}{r} \\[4pt] \mp\eta^{-1}\cdot\frac{\rho}{r+b} \\ 0 \end{pmatrix}. \end{split} \end{equation*}](/articles/aa/full_html/2020/12/aa36081-19/aa36081-19-eq41.png) (26)
(26)
The ϕ component of the magnetic field is a continuous function whereas the r component has a singularity at the origin, that means, div B is not well-determined at the origin. However, in mathematical terms, B is divergence-free as
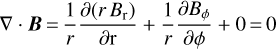 (27)
(27)
for all combinations of r, ϕ and z. In physical terms, the 1∕r dependency in the r component could lead to a divergence so that the field lines are disturbed and not closed and in particular lead to an infinitely large field component in the center of the clouds. We first argue for the case of a physically divergence-free magnetic field and later tackle the question of an infinitely large field in the center of the clouds. A physically divergence-free magnetic field in cylindrical coordinates has a net magnetic flux of zero through the surface of a cylinder with radius R and the length extending from − a to a. The magnetic flux is generally given by
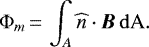 (28)
(28)
In the case of a cylinder, there are three surfaces: lateral, top and bottom
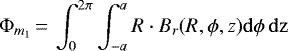 (29)
(29)
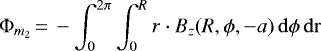 (30)
(30)
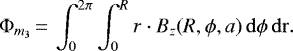 (31)
(31)
Here, 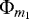 denotes the flux through the side, that is, er.
denotes the flux through the side, that is, er. 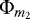 and
and 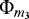 denote the fluxes through the bottom and top surfaces, respectively. As ab initio, Bz (r, ϕ) is zero the expressions
denote the fluxes through the bottom and top surfaces, respectively. As ab initio, Bz (r, ϕ) is zero the expressions 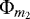 and
and 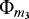 are immediately zero which solely leaves
are immediately zero which solely leaves 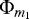 .
. 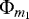 has two possibilities to vanish:
has two possibilities to vanish:
Here, Eq. (32) requires a wavenumber m≠0 and 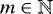 , wherefore we set m = 1 as there is no clue for an explicit value and this ensures the solenoidal property.
, wherefore we set m = 1 as there is no clue for an explicit value and this ensures the solenoidal property.
In this case, the constraint for the choice of h(z) is given by a continuous function and in the simplest case by an odd function, that is
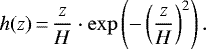 (34)
(34)
In order to constrain ξ(ψ), we rely on the first condition, and thus the choice of h(z) is just restricted by a continuous function. A convenient description which also considers the height of the MCs is given by the Gaussian vertical distribution
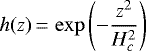 (35)
(35)
with 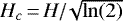 and H as the MC height. Thus, the field in MCs has been constrained to
and H as the MC height. Thus, the field in MCs has been constrained to
![\begin{equation*} \begin{split} {\vec B}\,{=}\,&B_1\cdot\cos\left({\,{\pm}\, m\cdot\eta^{-1}}\cdot\ln\left(\left(\frac{r+b}{\rho+b}\right) \right) + m\cdot{\phi}\right) \\& \cdot\exp\left(-\frac{z^2}{H_c^2}\right)\cdot\begin{pmatrix} \frac{\rho}{r} \\[3pt] \mp\eta \cdot\frac{\rho}{r+b} \\[2pt] 0 \end{pmatrix}\,.\end{split} \end{equation*}](/articles/aa/full_html/2020/12/aa36081-19/aa36081-19-eq60.png) (36)
(36)
The singularity of Br ∝ 1∕r arises from the fact that all field lines meet at r = 0. In order to prevent this unphysical behavior, we modify the expression of B in the innermost region, r < r′, in such a way that all field lines (except for one at each height) avoid the Galactic center.
Therefore, within a radius [0, r′] (r′ ≪ R), we introduce a modified field, which redistributes all incoming and outgoing field lines and therefore also changes the r component. This correction is also already done for nonsolenoidal parts of the Galactic magnetic field model presented in Kleimann et al. (2019) and also in a similar way in Terral & Ferrière (2017). As discussed earlier, the divergence is supported by the factor R∕r in the Br component in Eq. (36). We replace this factor by a differentiable function p(r, r′) at the boundary r = r′. We choose a second order polynomial including three coefficients which is fully determined due to the differentiability condition
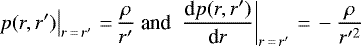 (37)
(37)
plus the request of equating p(0, r′) = 0. In doing so, we obtain
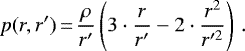 (38)
(38)
With the help of this new function, we can now introduce the new modified field
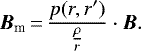 (39)
(39)
In this representation, the modified field becomes non-solenoidal and violates the divergence-free condition. Thus, we have to include an additional term into the ϕ component of the field that keeps the field divergence-free:
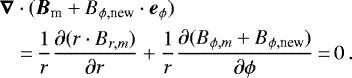 (40)
(40)
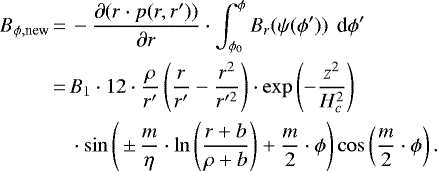 (41)
(41)
Here, ϕ0 occurs as a free parameter which is set to zero in the last step.
Thus, for r > r′, the modified field in the MC regions 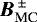 is given by
is given by
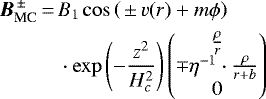 (42)
(42)
with 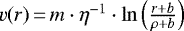 .
.
This final expression of the horizontal magnetic field has five free parameters: 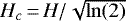 , ρ, η, m and B1. Here, the related Gaussian vertical scale height H, and the reference radius, ρ, are both set to the MC radius, R, η is given by a function of the MC gas density and intrinsic velocity. For ensuring the re-connection of the field lines, as illustrated in Fig. 8 for bisymmetric fields, the wavenumber m is set to 1. In doing so, we prevent the singularity at r = 0. Further, from now on we assume that r′ corresponds to a fraction of the total radius of the MCs, here, r′ = R∕10. The parameter B1 is determined in the same way as done in Sect. 3.3.1 and Eq. (7) where the average field values
, ρ, η, m and B1. Here, the related Gaussian vertical scale height H, and the reference radius, ρ, are both set to the MC radius, R, η is given by a function of the MC gas density and intrinsic velocity. For ensuring the re-connection of the field lines, as illustrated in Fig. 8 for bisymmetric fields, the wavenumber m is set to 1. In doing so, we prevent the singularity at r = 0. Further, from now on we assume that r′ corresponds to a fraction of the total radius of the MCs, here, r′ = R∕10. The parameter B1 is determined in the same way as done in Sect. 3.3.1 and Eq. (7) where the average field values 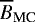 are used to determine the individual B1, that is,
are used to determine the individual B1, that is, 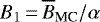 .
. 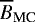 is listed in Table 1 and α depends on the parameter η, thus, [αη = 0, αη = 0.5, αη = 0.77, αη = 1.0] = [59.40, 1.29, 0.91, 0.75].
is listed in Table 1 and α depends on the parameter η, thus, [αη = 0, αη = 0.5, αη = 0.77, αη = 1.0] = [59.40, 1.29, 0.91, 0.75].
3.4.1 Magnetic field at the event horizon of SgrA*
Since the ambient condition around a supermassive black hole is completely different compared to a MC, we are not able to relate the Br and Bϕ component. Thus, we merely consider the ϕ components of the magnetic field for this region and set m = 0 in order to ensure the divergence-free property. For r > r′
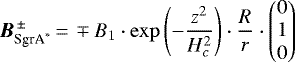 (44)
(44)
In doing so, we ensure Eq. (40), and due to Br = 0 the total magnetic flux remains still zero. Additionally, we fulfill the 1∕r dependency as suggested by Eatough et al. (2013) and Johnson et al. (2015). In this construction the volume factor αSgrA* corresponds to 3.07. The magnetic field reaches a mG field at a radius of 0.024 pc and a 10 μG field at a radius of 2.4 pc. Thus, the magnetic field induced by SgrA* is subdominant at latest after reaching the position of the MC CND, which has a field strength of 3 mG.
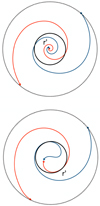 |
Fig. 8 Regularization of a bi-symmetric (m = 1) spiral magnetic field that diverges for r → 0. Upper panel:field as given by Eq. (36), where Br ∝ 1∕r, so that all field lines meet at r = 0. Bottom panel: modified field inside radius r′ = R∕10 (Eq. (43)), so that field lines now avoid the center. |
3.4.2 Application of the horizontal field model to the inner 10 pc
As discussed above, two solutions 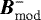 and
and 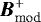 can mathematically describe the horizontal field. The difference between these two is based on the rotational direction, and the observations should constrain the solutions. We therefore apply our model to the central 10 pc around SgrA* and compare the result to the model of Wardle & Königl (1990) who fit their model to the polarization measurements of Hildebrand et al. (1990).
can mathematically describe the horizontal field. The difference between these two is based on the rotational direction, and the observations should constrain the solutions. We therefore apply our model to the central 10 pc around SgrA* and compare the result to the model of Wardle & Königl (1990) who fit their model to the polarization measurements of Hildebrand et al. (1990).
Figure 9 sketches the resulted two configurations of our model using R = 5 pc and η = 0.77 which are the parameters around the CND. The comparison of these configurations reveals the model B+ to fit most suitable to the data of Hildebrand et al. (1990). By assuming that all MCs in CMZ are following the same rotational direction, we adopt B+ for all MCs.
 |
Fig. 9 Vizalization of the MC field. Upper panel: model of Wardle & Königl (1990); middle panel: visualization of B− (left) and bottom panel: visualization of B+ (right). |
3.5 Totalfield and comparison with data
The total field in the CMZ is obtained by a superposition of magnetic field components as derived in Sects. 3.3.1 and 3.4.
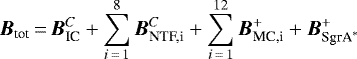 (46)
(46)
Figure 10 shows the total magnetic field strength and the related configuration including the ICM, NTF and MC components for different values of η. Furthermore, the dense MCs and the NTFs are added in Fig. 11.
In order to better recognize the influence of local objects such as the MCs on the field structure, Fig. 12 provides the view of the results also shown in Fig. 10, but shown along the z-axis.
The polarization map of Nishiyama et al. (2013) (see Fig. 16) can be used to cross-check our results with measurements. While these specific structures in dense regions were observed in previous studies (Chuss et al. 2003; Novak et al. 2003), they are not visible in the recent measurements presented by Mangilli et al. (2019), who reported a much smoother field configuration in dense regions in the CMZ. Moreover, Mangilli et al. (2019) did not report any significant change in field orientation at the position of the prominent Radio Arc NTF, where a vertical orientation of the field dominates. These discrepancies further emphasize that this region is not fully understood. In this work, we present a first magnetic field configuration that can be tested against other data in the future.
A qualitative comparison is reached by calculating the deviation of the measured polarization angle αNishiyama from the expected polarization angle αCMZF from our model following Δα = |αNishiyama − αCMZF|. In Fig. 13, N(Δα) represents the relative amount of the deviation Δα which occurs within a specific range (0°−10°, 10°− 20°,..., 80°− 90°) with respectto the total number of polarization measurements. It should be noted that the field orientation from our model is deduced considering the line of sight with a depth of 400 pc. Thus, we do not present the expected polarization from our model, but only the expected field orientation, which makes this study sensitive to the polarization angle only. This comparison should therefore only be considered as a first, qualitative comparison to the data.
The same procedure is also done for the JF12 extrapolation in the GC region and the result are visualized by Fig. 14. What can be learned from this quantitative comparison is that the model developed here follows the polarization map to a better degree (deviations from the measured polarization direction are generally smaller here than for the JF12 field). Also, the choice of η has no significant influence on the results as can be seen from Fig. 13. This indicates that the field model presented here can provide a better representation of the large-scale field than typical global magnetic field models. Figure 15illustrates the field configuration from this work. On this map, all configurations along the line of sight with a depth of 400 pc were added together. Therefore, darker lines represent more frequently appearing configurations along the line of sight.
At first glance, the field configuration measured by Nishiyama et al. (2013) seems to be chaotically distributed and some magnetic structures are not clearly attributable to their physical origin. For a better identification, Fig. 16 visualizes the MCs and NTFs additionally. Figure 17 simplifies the comparison for the reader by an overlay of Figs. 15 and 16. The potential of the model investigated in this work can be seen in the detailed reproduction of the configuration. Many of the field lines seem to be chaotically oriented on first glance, but in fact, even these are caused by some specific components in the CMZ or a superposition of them. A good example is the measured field line configuration at l = 0.6−0.7° and b = −0.1° which is eye-catching due to the circulated configuration. This feature, in reality, is caused by a superposition of Sgr B2’s and ICM’s magnetic field. Many other feature can be explained in the same way.
The development of some discrepancies at higher longitudes, for example, in the corners, can have different reasons:
GBFD20 is mainly based on the mass distribution which decreases at higher longitude and is therefore in these regions subdominant as the CMZ region ends there;
the dynamical effect of the MCs varies due to their orbit within the CMZ (Kauffmann et al. 2017b) and can lead to discrepancies.
However, the most relevant structures in the region |l| < 1.35° and |b| < 0.6° are well described by the model derived in this work and thus indicate that the GBFD20 model is a good representation for the field in the GC.
 |
Fig. 10 Total magnetic field strength in the CMZ for η = 0 (upper panel), η = 0.5 (middle panel) and η = 1.0 (lower panel). Relative length of the arrows/pixels represents the relative magnetic field strength. |
 |
Fig. 11 Same as Fig. 10. Additionally, the figures show the particle densities for the MCs in units of cm−3 and the NTFs are shown schematically. |
 |
Fig. 13 Deviations of polarization vectors from the GBFD20 field model, separated in 10° steps extending from 0° to 90°. The deviation is calculated for a regions extending from − 1.35° < l < 1.35° in the longitude and for two different latitudes: − 0.6° ≤ b ≤ 0.6° and − 0.3° ≤ b ≤ 0.3°. Upper panel:η = 0, middle panel: η = 0.5 and lower panel: η = 1.0 |
 |
Fig. 14 Deviation of the JF12 polarization vectors from the polarization map, separated in 10° steps extending from 0° to 90°. The deviation is calculated for a regions extending from − 1.35° < l < 1.35° in the longitude and for two different latitudes: − 0.6° ≤ b ≤ 0.6° and − 0.3° ≤ b ≤ 0.3°. |
 |
Fig. 15 Magnetic field configuration as derived in this work visualized together with the locations of the MCs and NTFs. |
4 Impacton cosmic-ray propagation – a first comparison
In this section, the impact of the magnetic field configuration on cosmic-ray propagation is tested by comparing the magnetic field model of the CMZ as derived in this paper with the standard field of JF12 and the cosmic-ray propagation presented therein. The JF12 model has been developed in order to have a good description of the global Galactic field model. Updates of this originalfield that improve the divergence-freeness as well as the continuity of the field have been presented recently by Unger & Farrar (2019) and Kleimann et al. (2019). It is expressly mentioned by the authors that the JF12 model is not optimized for propagation in the region of the GC. Nevertheless, we want to present our results with the JF12 field to quantify the influence of the field configurations. Secondly, the JF12 field is often used for global cosmic-ray propagation and that includes the central region in which the source density is high. Some influence of the local field configuration on the large-scale cosmic-ray picture can therefore still be present.
Here wesimulate the propagation of particles with the open-source tool CRPropa (Armengaud et al. 2007; Alves Batista et al. 2016; Merten et al. 2017). CRPropa was written originally for the propagation of extragalactic particles in intergalacticmagnetic fields (Armengaud et al. 2007) and updated with a modern, modular structure in Alves Batista et al. (2016). In its original form, propagation is done in discrete steps by solving the equation of motion. For low-energy particles in the Galacitc magnetic field, that is for example, below energies of 1016 −1017 eV, this method is inapplicable due to the highly diffusive nature and connected to that computationally long propagation times of the particles. Therefore, the tool has been extended by adding an alternative propagation scheme, in which the transport equation is solved viathe method of stochastic differential equations (SDEs; Merten et al. 2017). The latter method works with pseudo-particles and is therefore well compatible with the original CRPropa framework. This software is well suitable for our tests as the propagation environment can be adjusted due to the modular structure of the code.
In each of the simulations presented here, we use the multiparticle picture within the module Diffusion SDE, the solution of the transport equation:
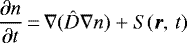 (47)
(47)
with S(r, t) as the source term. In general, the code works with the nonstationary solution of the equation ∂n∕∂t. In this test scenario, we inject particles at the position of SgrA* and propagate them until they leave the Galactic center region, defined by a box of (ΔX × ΔY × ΔZ) = (234 × 234 × 234) pc3. We then produce the figures shown below by adding up the particle density for different time steps with weights as defined in Merten et al. (2017) in order to determine the stationary solution. The code is able to handle arbitrary diffusion tensors 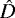 . Here, the standard diffusion coefficient used in this formalism is
. Here, the standard diffusion coefficient used in this formalism is
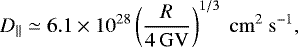 (48)
(48)
where R denotes the rigidity. The perpendicular component of the diffusion coefficient is then determined by assuming a fixed ratio ϵ = D⊥∕D∥ = 0.1. The transport equation is solved in the orthonormal bases corresponding to the background magnetic field such that the parallel diffusion path follows the magnetic field lines.
We perform test simulations for two different magnetic field models: (1) GBFD20 [this work] and (2) JF12. Into this environment, we inject 105 particles in the center of the simulation box, (X, Y, Z) = (0, 0, 0). These particles are propagated in a discrete time step of Δti = 1 pc/c for 234 times. This way, 234 time steps exist and in each time step, the particles start at the position that they had reached the time step before, Δti−1. The maximum distance from the center that can be reached this way by a single particle corresponds to 234 pc, in case of a diffusive influence by the magnetic field, this distance can be significantly shorter. The results are shown in Figs. 18–20 (GBFD20 for η = 0, 0.5, 1..0, respectively) and 21 (JF12). In these figures, the images for each time step (i = 1, …234) are stacked.
The figures reveal that in the JF12 field particles diffuse in an approximately cylindrically symmetric structure, while this work (GBFD20) leads to an approximately dagger-shaped propagation pattern. As an example, at a distance Y = ±100 pc and Z = 0 pc and energiesbetween 1 and 1000 TeV, the JF12 configuration results in a flux level close to zero particles. The GBFD20 with η = 0.5 field, on the other hand, reaches a level of 104 protons at the same energy and distance. This show that diffusion in the Y -direction is therefore much stronger in the field presented in this work. In the JF12 model, the particles rather propagate along the Z-axis. This pictureis further emphasized by Fig. 22, in which random example trajectories are shown for the case of the GBFD20 field (upper panel), the JF12 field (middle panel) and no field at all (lowest panel). All particles start at the (X, Y, Z) = (0, 0, 0). The colors of the trajectories go from dark (early) to light (late times).
It is interesting to note that the diffuse γ-ray detection by H.E.S.S. shows a latitudinal extension up to 220 pc (Abdalla et al. 2018), that is, approximately the same distance which CRs can reach within the GBFD20 model with η = 0.5 model. Further studies are required to show if this broad distribution could be due to the enhanced latitudinal propagation of cosmic rays.
 |
Fig. 16 Visualization of polarization measurement from Nishiyama et al. (2013) together with the MCs and NTFs. |
 |
Fig. 17 Magnetic field configuration as derived in this work is visualized by black dashes lines. The polarization as measured by Nishiyama et al. (2013) is shown as the red colored dashed lines. |
 |
Fig. 18 Density of protons after propagation in the GBFD20 field. Left panel: η = 0 with proton energies between 1 and 1000 TeV; right panel: η = 0 with proton energies between 1 and 100 PeV. |
5 Discussion on the model parameters
Our model is constructed with a certain parametric freedom that can be easily adapted in the future to new observational data. Here, we summarize all parameters related to the different magnetic field components together in modeling the ICM, NTFs and MCs. We also discuss the uncertainties in our results.
In general, the poloidal magnetic field component has four free parameters:
- 1.
B1 is the normalization factor, which is determined by assuming the observed and accordingly, the expected field strength is an average value in the region of interest.
- 2.
L the radial exponential scale length is determined by assuming the half-max value of |B| at the maximum longitudinal extent of the region of interest.
- 3.
The parameter a is governing the opening of field lines away from the z-axis.
- 4.
m is the wavenumber which is set to zero for an axisymmetric description.
The poloidal field is applied to the inter-cloud and non-thermal filament regions:
For the inter-cloud region, the parameter B1 is determined by the expected average field strength of 10 mG based on minimum-energy analysis of the non-thermal sources with an approximate uncertainty of a factor 10 (LaRosa et al. 2005; Ferrière 2009). In the same context, the parameter L is determined by assuming the half-max value of B at the maximum radius RIC = L ⋅ ln2 = 158 pc of the CMZ following the CMZ mass distribution from Ferrière et al. (2007). Here, RIC is in the range of 100−250 pc (Ferrière et al. 2007). The parameter a is determined by a best-fit to the polarization data (Nishiyama et al. 2013). Here, the error is quantified to less than 1% (Nishiyama et al. 2010).
For the NTF region, B1 is determined by the expected field strengths derived from equipartition. The error in the measurement of the flux is approx. 15% (LaRosa et al. 2001) which gives us an error of ~ 5% for the equipartition magnetic field. Here, the systematic uncertainty might be more significant, in particular connected to the assumption of equipartition. The parameter L is determined by assuming the half-max value of B at the maximum radius RNTF = L ⋅ ln2 of the NTFs following the geometry distribution observed by several groups. The error for RNTF is given by the resolution of 24″, corresponding to approximately 0.5 pc (LaRosa et al. 2000). The parameter a is determined by a vertical Gaussian scale assuming the half-max value of B at the vertical edges of each NTF. The vertical sizes are taken as
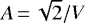 , where V is the vertical size which is taken from LaRosa et al. (2001) with an error of 1.8 pc (a resolution of 43″).
, where V is the vertical size which is taken from LaRosa et al. (2001) with an error of 1.8 pc (a resolution of 43″).
The horizontal magnetic field component has five free parameters:
- 1.
B1 is the normalization factor which is determined by assuming the observed and accordingly, the expected field strength is the average value in the system under consideration.
- 2.
ρ the reference radius at which the field line is crossing the reference angle ψ. In our model for the MCs, this parameter is set to the radius of the cloud.
- 3.
Hc vertical scale length which is determined by assuming the half-max value of |B| at the edges of the MC.
- 4.
m the wavenumber which is set to one for ensuring the solenoidal property.
- 5.
η is the ratio |Br|∕|Bϕ|. In our MC model, it is a free parameter expect for the MC CND.
The horizontal model has been developed in this paper specifically to describe the magnetic field in the MCs. The parameter values have to be set individually and so are the errors. Here is a short discussion of the general range of uncertainties
-
B1: since the normalization factor is proportional to the expected field strength
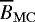 , the associated uncertainty depends on the
, the associated uncertainty depends on the 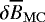 which is listed in Table 1.
which is listed in Table 1. -
The MC radius R: the related uncertainty depends on the detector resolution and is listen in Table 1.
-
The error in the vertical Gaussian scale length is fully determined by the error in the radius, that is,
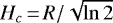 .
. -
η depends on the azimuthal shearing of the field lines and is in the range between zero and one.
-
The azimuthal wave number m is generally not known, but set to one to reach a net magnetic flux of zero which is important for ensuring the solenoidal property.
It should be noted, that for all components an additional degree of freedom comes from the positions of MCs and NTFs.
All these parameters can be adjusted in order to fit specific data. For those who wish a single global model, they can consult the x-shape models of Ferrière & Terral (2014) including the azimuthal component. However, such a model is not appropriate for the GC since they cannot reproduce local configurations which are significant, for example, in NTF regions. All relevant parameters are summarized in Tables 1–3.
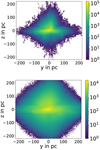 |
Fig. 19 Same as Fig. 18, but with η = 0.5 (upper panel: energies between 1 and 1000 TeV and lower panel: energies between 1 and 100 PeV). |
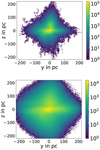 |
Fig. 20 Same as Fig. 18, but with η = 1.0 (upper panel: energies between 1 and 1000 TeV; lower panel: energies between 1 and 100 PeV). |
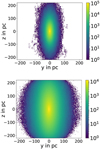 |
Fig. 21 Same as Fig. 18, but using the JF12 field in the energy range 1 and 1000 TeV (upper panel) and 1 and 100 PeV (lower panel). |
6 Summary and conclusion
At first, we summarize molecular cloud surveys from different works and combine them with the proper gas structure in the central 10 pc by Ferrière (2012). Further, we add an adjusted diffuse gas model by Ferrière et al. (2007) and identify this model as the ICM. Putting them all together delivers an accurate 3d gas distribution in the CMZ.
We build a superposition of all components and reconstruct a polarization map considering η = 0.5, which leads to a very good agreement with Nishiyama et al. (2013). The application of the first magnetic field model in the CMZ is carried by the CR propagation tool CRPropa, which delivers the CR trajectories. The results are compared with the extrapolated model in JF12. Throughout this work, the composed model exhibits its power and ability by very good agreement with the measured data.
Future magnetic field models of our Galaxy demand a continuous description without any blank areas. For this purpose, this work can be connected with any previous models such as JF12. For doing so, 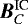 has to be modified and a further azimuthal component has to be included which ensures the continuous differentiability and the divergence-free property at the break point of the former field. At the same time, the average value of 10 μG within the CMZ still has to be maintained.
has to be modified and a further azimuthal component has to be included which ensures the continuous differentiability and the divergence-free property at the break point of the former field. At the same time, the average value of 10 μG within the CMZ still has to be maintained.
 |
Fig. 22 Examples of seven proton trajectories at energies from 1 TeV to 10 PeV with a step length of 0.5 pc: upper: GBFD20 with η = 0.5 (this work), middle: JF12, bottom: (no field). The passed time is proportional to the color batch. |
Acknowledgements
We would like to thank Anvar Shukurov and Jens Kleimann for very helpful discussions. We want to thank LukasMerten for helpful comments on the application of CRPropa. We further acknowledge the support from Rosa-Luxemburg Stiftung.
References
- Abdalla, H., Abramowski, A., Aharonian, F., et al. 2018, A&A, 612, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abramowski, A., Aharonian, F., Benkhali, F., et al. 2016, Nature, 531, 476 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2017, ApJ, 840, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Alves Batista, R., Dundovic, A., Erdmann, M., et al. 2016, J. Cosmol. Astropart. Phys., 1605, 038 [NASA ADS] [CrossRef] [Google Scholar]
- Anantharamaiah, K. R., Pedlar, A., Ekers, R. D., & Goss, W. M. 1991, MNRAS, 249, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Anantharamaiah, K. R., Lang, C. C., Kassim, N. E., Lazio, T. J. W., & Goss, W. M. 1999, ASP Conf. Ser., 186, 507 [Google Scholar]
- Armengaud, E., Sigl, G., Beau, T., & Miniati, F. 2007, Astropart. Phys., 28, 463 [CrossRef] [Google Scholar]
- Benford, G. 1988, ApJ, 333, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., & Reynolds, R. 2000, Gas in Galaxies (Bristol: Institute of Physics Publishing), 2636 [Google Scholar]
- Boehle, A., Ghez, A. M., Schödel, R., et al. 2016, ApJ, 830, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Chuss, D. T., Davidson, J. A., Dotson, J. L., et al. 2003, ApJ, 599, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M., Roberts, D. A., Mehringer, D. M., & Troland, T. H. 1996, ApJ, 462, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., Agol, E., Fragile, P. C., & McKinney, J. C. 2010, ApJ, 717, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G. 2012, ApJ, 750, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., Cholis, I., & Weiner, N. 2011, ApJ, 741, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Eatough, R. P., Falcke, H., Karuppusamy, R., et al. 2013, Nature, 501, 391 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Federrath, C., Rathborne, J. M., Longmore, S. N., et al. 2016, ApJ, 832, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K. 2009, A&A, 505, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrière, K. 2012, A&A, 540, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrière, K., & Terral, P. 2014, A&A, 561, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrière, K., Gillard, W., & Jean, P. 2007, A&A, 467, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finkbeiner, D. P. 2004, ApJ, 614, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., Lis, D. C., Hills, R., & Lasenby, J. 1990, ApJ, 350, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Heywood, I., Camilo, F., Cotton, W. D., Yusef-Zadeh, F., & Abbott, T. D. 2019, Nature, 573, 235 [CrossRef] [Google Scholar]
- Hildebrand, R. H., Gonatas, D. P., Platt, S. R., et al. 1990, ApJ, 362, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Immer, K., Menten, K. M., Schuller, F., & Lis, D. C. 2012, A&A, 548, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaffe, T. R., Ferrière, K. M., Banday, A. J., et al. 2013, MNRAS, 431, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Jansson, R., & Farrar, G. R. 2012, ApJ, 757, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, M. D., Fish, V. L., Doeleman, S. S., et al. 2015, Science, 350, 1242 [Google Scholar]
- Kauffmann, J. 2017, ArXiv e-prints [arXiv:1712.01453] [Google Scholar]
- Kauffmann, J., Pillai, T., Zhang, Q., et al. 2017a, A&A, 603, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., Pillai, T., Zhang, Q., et al. 2017b, A&A, 603, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kleimann, J., Schorlepp, T., Merten, L., & Becker Tjus, J. 2019, ApJ, 877, 76 [CrossRef] [Google Scholar]
- Lang, C. C., Anantharamaiah, K. R., Kassim, N. E., & Lazio, T. J. W. 1999a, ApJ, 521, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, C. C., Morris, M., & Echevarria, L. 1999b, ApJ, 526, 727 [NASA ADS] [CrossRef] [Google Scholar]
- LaRosa, T. N., Kassim, N. E., Lazio, T. J. W., & Hyman, S. D. 2000, AJ, 119, 207 [NASA ADS] [CrossRef] [Google Scholar]
- LaRosa, T. N., Lazio, T. J. W., & Kassim, N. E. 2001, ApJ, 563, 163 [NASA ADS] [CrossRef] [Google Scholar]
- LaRosa, T. N., Brogan, C. L., Shore, S. N., et al. 2005, ApJ, 626, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Law, C. J., Yusef-Zadeh, F., & Cotton, W. D. 2008, ApJS, 177, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Lesch, H., & Reich, W. 1992, A&A, 264, 493 [NASA ADS] [Google Scholar]
- Lin, H., Penn, M. J., & Tomczyk, S. 2000, ApJ, 541, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D. C., Carlstrom, J. E., & Keene, J. 1991, AJ, 380, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Mangilli, A., Aumont, J., Bernard, J. P., et al. 2019, A&A, 630, A74 [CrossRef] [EDP Sciences] [Google Scholar]
- Merten, L. 2015, Master’s thesis, Ruhr-University Bochum, Germany [Google Scholar]
- Merten, L., Becker Tjus, J., Fichtner, H., Eichmann, B., & Sigl, G. 2017, J. Cosmol. Astropart. Phys., 1706, 046 [NASA ADS] [CrossRef] [Google Scholar]
- Michelson, P. F., Atwood, W. B., & Ritz, S. 2010, Rep. Prog. Phys., 73, 074901 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M. 1990, IAU Symp., 140, 361 [Google Scholar]
- Morris, M. R. 2015, Manifestations of the Galactic Center Magnetic Field (Springer), 391 [Google Scholar]
- Mościbrodzka, M., Gammie, C. F., Dolence, J. C., Shiokawa, H., & Leung, P. K. 2009, ApJ, 706, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Muno, M. P., Baganoff, F. K., Bautz, M. W., et al. 2004, ApJ, 613, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Nakashima, S., Koyama, K., Wang, Q. D., & Enokiya, R. 2019, ApJ, 875, 32 [CrossRef] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 690, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Hatano, H., Tamura, M., et al. 2010, ApJ, 722, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Yasui, K., Nagata, T., et al. 2013, ApJ, 769, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Novak, G., Chuss, D. T., Renbarger, T., et al. 2003, ApJ, 583, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T., Geballe, T. R., Goto, M., et al. 2019, ApJ, 883, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Pedlar, A., Anantharamaiah, K. R., Ekers, R. D., et al. 1989, ApJ, 342, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Peratt, A. L. 1984, Sky Teles., 68, 118 [Google Scholar]
- Pillai, T., Kauffmann, J., Tan, J. C., et al. 2015, ApJ, 799, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Plante, R., Lo, K., Crutcher, R., & Killeen, N. 1994, NATO Advanced Science Institutes (ASI) Ser. C, 445, 205 [Google Scholar]
- Plante, R. L., Lo, K. Y., & Crutcher, R. M. 1995, ApJ, 445, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Hofmann, F., Churazov, E., et al. 2019, Nature, 567, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Reich, W., Sofue, Y., Wielebinski, R., & Seiradakis, J. H. 1988, A&A, 191, 303 [Google Scholar]
- Serabyn, E., & Morris, M. 1994, ApJ, 424, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Shukurov, A., Rodrigues, L., Bushby, P. J., Hollins, L., & Rachen, J. P. 2019, A&A, 623, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Staguhn, J., Stutzki, J., Uchida, K. I., & Yusef-Zadeh, F. 1998, A&A, 336, 290 [NASA ADS] [Google Scholar]
- Su, M., Slatyer, T. R., & Finkbeiner, D. P. 2010, ApJ, 724, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X. H., Reich, W., Waelkens, A., & Enßlin, T. A. 2008, A&A, 477, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terral, P., & Ferrière, K. 2017, A&A, 600, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uchida, K. I., Morris, M., Serabyn, E., & Güsten, R. 1996, ApJ, 462, 768 [CrossRef] [Google Scholar]
- Unger, M., & Farrar, G. 2019, in Ultra High Energy Cosmic Rays (UHECR 2018) Paris, France, October 8-12, 2018 [Google Scholar]
- Walker, D. L., Longmore, S. N., Bastian, N., et al. 2015, MNRAS, 449, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, D. L., Longmore, S. N., Zhang, Q., et al. 2018, MNRAS, 474, 2373 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, M., & Königl, A. 1990, ApJ, 362, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Wink, J. E., Altenhoff, W. J., & Mezger, P. G. 1982, A&A, 108, 227 [NASA ADS] [Google Scholar]
- Yusef-Zadeh, F. 2003, ApJ, 598, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., & Morris, M. 1987, Astron. J., 94, 1178 [NASA ADS] [CrossRef] [Google Scholar]
Except for the Pelican region, which particularly has a dominant horizontal component (LaRosa et al. 2000).
All Tables
Summary of the gas components of the interstellar gas in the inner 10 pc around SgrA*, ordered by decreasing density.
Magnetic field strength for the different objects, derived from equipartition with turbulent pressure is listed.
All Figures
 |
Fig. 1 Representation of the combined gas density of the CMZ region in units of cm−3 (color scales). Here and in the figures that follow, the x-axis points fromthe Sun to the GC. The diffuse ICM is shown as red contours. The non-thermal filament objects are presented ascylindrical black colored objects. |
| In the text | |
 |
Fig. 2 Same as Fig. 1, but with the projection along the z-axis and withoutconsidering the ICM. |
| In the text | |
 |
Fig. 3 Magnetic field configuration as derived for BIC is visualizedby black dashes lines and by colored dashed lines as measured by Nishiyama et al. (2013). |
| In the text | |
 |
Fig. 4 Magnetic field strength in units of μG in the IC region. The relative length and color of the arrows represent the relative magnetic field strength. |
| In the text | |
 |
Fig. 5 Magnetic field strength in Sgr C visualized by the related 3D magnetic field configuration. Lower panel: zoomed view. |
| In the text | |
 |
Fig. 6 z-profile of the poloidal field strength in units of μG (blue, solid line) in comparison to a Gaussian distribution (red, dashed line). |
| In the text | |
 |
Fig. 7 Magnetic field strength in μG is presentedconsidering the NTF components in Table 3. The relative length and color of the arrows represent the relative magnetic field strength. |
| In the text | |
 |
Fig. 8 Regularization of a bi-symmetric (m = 1) spiral magnetic field that diverges for r → 0. Upper panel:field as given by Eq. (36), where Br ∝ 1∕r, so that all field lines meet at r = 0. Bottom panel: modified field inside radius r′ = R∕10 (Eq. (43)), so that field lines now avoid the center. |
| In the text | |
 |
Fig. 9 Vizalization of the MC field. Upper panel: model of Wardle & Königl (1990); middle panel: visualization of B− (left) and bottom panel: visualization of B+ (right). |
| In the text | |
 |
Fig. 10 Total magnetic field strength in the CMZ for η = 0 (upper panel), η = 0.5 (middle panel) and η = 1.0 (lower panel). Relative length of the arrows/pixels represents the relative magnetic field strength. |
| In the text | |
 |
Fig. 11 Same as Fig. 10. Additionally, the figures show the particle densities for the MCs in units of cm−3 and the NTFs are shown schematically. |
| In the text | |
 |
Fig. 12 Same as Fig. 10, but with a view along the z-axis. |
| In the text | |
 |
Fig. 13 Deviations of polarization vectors from the GBFD20 field model, separated in 10° steps extending from 0° to 90°. The deviation is calculated for a regions extending from − 1.35° < l < 1.35° in the longitude and for two different latitudes: − 0.6° ≤ b ≤ 0.6° and − 0.3° ≤ b ≤ 0.3°. Upper panel:η = 0, middle panel: η = 0.5 and lower panel: η = 1.0 |
| In the text | |
 |
Fig. 14 Deviation of the JF12 polarization vectors from the polarization map, separated in 10° steps extending from 0° to 90°. The deviation is calculated for a regions extending from − 1.35° < l < 1.35° in the longitude and for two different latitudes: − 0.6° ≤ b ≤ 0.6° and − 0.3° ≤ b ≤ 0.3°. |
| In the text | |
 |
Fig. 15 Magnetic field configuration as derived in this work visualized together with the locations of the MCs and NTFs. |
| In the text | |
 |
Fig. 16 Visualization of polarization measurement from Nishiyama et al. (2013) together with the MCs and NTFs. |
| In the text | |
 |
Fig. 17 Magnetic field configuration as derived in this work is visualized by black dashes lines. The polarization as measured by Nishiyama et al. (2013) is shown as the red colored dashed lines. |
| In the text | |
 |
Fig. 18 Density of protons after propagation in the GBFD20 field. Left panel: η = 0 with proton energies between 1 and 1000 TeV; right panel: η = 0 with proton energies between 1 and 100 PeV. |
| In the text | |
 |
Fig. 19 Same as Fig. 18, but with η = 0.5 (upper panel: energies between 1 and 1000 TeV and lower panel: energies between 1 and 100 PeV). |
| In the text | |
 |
Fig. 20 Same as Fig. 18, but with η = 1.0 (upper panel: energies between 1 and 1000 TeV; lower panel: energies between 1 and 100 PeV). |
| In the text | |
 |
Fig. 21 Same as Fig. 18, but using the JF12 field in the energy range 1 and 1000 TeV (upper panel) and 1 and 100 PeV (lower panel). |
| In the text | |
 |
Fig. 22 Examples of seven proton trajectories at energies from 1 TeV to 10 PeV with a step length of 0.5 pc: upper: GBFD20 with η = 0.5 (this work), middle: JF12, bottom: (no field). The passed time is proportional to the color batch. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



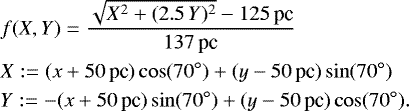
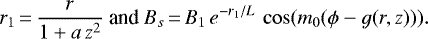
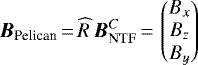
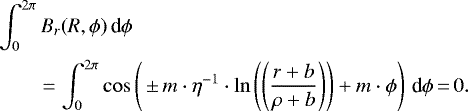
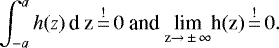
![\begin{equation*} \begin{split} {\vec B}^{\,{\pm}\,}_{\text{MC}}\,{=}&\,B_1\exp\left(- \frac{z^2}{H_c^2} \right)\frac{\rho}{r'}\left(\frac{3r}{r'} -\frac{2r^2}{r'^2}\right)\cos\left(\,{\pm}\, v(r) + m{\phi}\right)\\ &\cdot \begin{pmatrix} 1\\[3pt] \mp \frac{r}{\eta(r+b)}\left(1 +\frac{6(r-r')}{2\, r-3\, r'}\left(\frac{\sin(\,{\pm}\, v(r)+m\phi)-\sin(\,{\pm}\, v(r))}{\cos(\,{\pm}\, v(r)+m\phi)}\right)\right) \\[3pt] 0 \end{pmatrix}. \end{split}\end{equation*}](/articles/aa/full_html/2020/12/aa36081-19/aa36081-19-eq69.png)