EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 643 (November 2020) A&A, 643 (2020) A150 Full HTML
Free Access
Issue
A&A
Volume 643, November 2020
Article Number A150
Number of page(s) 8
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202038290
Published online 18 November 2020

© ESO 2020

1 Introduction

GRS 1758–258 is one of the brightest objects seen in hard X-rays in the close vicinity of the Galactic centre. It was first detected by GRANAT/SIGMA (Sunyaev et al. 1991) and since then this system has enjoyed intense observational coverage at these frequencies over decades from CGRO, RXTE, ROSAT, INTEGRAL, ASCA, Swift, Beppo-SAX, EXOSAT, Chandra, and XMM-Newton (i.e. Lin et al. 2000; Mereghetti et al. 1994, 1997; Smith et al. 2002; Main et al. 1999; Keck et al. 2001; Heindl & Smith 2002; Pottschmidt et al. 2006; Goldwurm et al. 2001; Soria et al. 2011). The source appears to exhibit continuous, variable activity at these wavelengths, spending almost all its time in a hard state. The compact object in GRS 1758–258 is probably a black hole as its X-ray spectrum resembles that of the black hole in Cygnus X-1 (Main et al. 1999). All these characteristics have led to consider GRS 1758–258 as a low mass X-ray binary system (LMXB) with a black hole accreting from a stellar companion. Observations in radio wavelengths show two clearly extended lobes, which suggest that GRS 1758–258 is a prototypical microquasar (Rodríguez et al. 1992; Mirabel et al. 1992). However, the Galactic nature of this system has remained elusive with regard to spectroscopic analysis because of crowded stellar fields, astrometric uncertainties, and significant interstellar extinction towards the Galactic Center in optical and infrared wavelengths (Bignami et al. 1991; Mereghetti et al. 1992; Marti et al. 1998; Eikenberry et al. 2001; Rothstein et al. 2002).

Although a weak stellar counterpart of GRS 1758–258 was finally identified (Muñoz-Arjonilla et al. 2010; Luque-Escamilla et al. 2014), it was not possible to obtain any clear spectral signature even using the 10 m Gran Telescopio Canarias (Muñoz-Arjonilla et al. 2010; Martí et al. 2016). Nevertheless, the system was definitively associated to the Milky Way when large-scale morphological changes were noticed by Martí et al. (2015). These variations in radio shape were attributed to instabilities in the jet and interactions with the interstellar medium, conforming a cocoon observed for the first time in a microquasar, which adds a new aspect of similarity with radio galaxies. A deep inspection of the resulting radio S-shape of GRS 1758–258 revealed it to be a downsized mimic of winged extragalactic radio galaxies, which appear to have some consequences for the black hole merger rate and its corresponding gravitational wave production (Martí et al. 2017).

However, instabilities are not the only mechanisms that could explain the large-scale morphology of astrophysical jets. Precession is often invoked to account for the apparent shape of jets both in extragalactic and Galactic sources. In fact, other known microquasars present observational evidence of jet precession, such as SS 433 (Abell & Margon 1979; Hjellming & Johnston 1981), GRO J1655−40 (Hjellming & Rupen 1995), and 1E 1740.7–2942 (Luque-Escamilla et al. 2015), where the evolution of the large-scale morphology of the jet-lobes is evident over time. Since this mechanism seems to be expected in binary systems similar to GRS 1758–258, due to the torque of the donor star (Larwood 1998) or the relativistic drag from the spinning compact object through Lens-Thirring effect (Bardeen & Petterson 1975), in this paper, we study the possibility that it could be responsible for the changing large-scale radio morphology appearing in GRS 1758–258 at different epochs. In Sect. 2, we show the data and methods we used for fitting the radio jet-lobe changing structures of GRS 1758–258 to a kinematic model, following a similar approach to the one we successfully applied to the case of 1E 1740.7–2942 (Luque-Escamilla et al. 2015). We present a complete set of parameters for the jet precession in Sect. 3 and we analyse the consistency of the results and discuss their consequences in Sects. 4 and 5. We present our conclusions in Sect. 6.

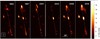thumbnail Fig. 1

Attempt to fit the large-scale radio jets of GRS 1758–258 jets at different epochs using the theoretical kinematic model of Hjellming & Johnston (1981). Horizontal bar shows the scale size and the synthesised beam is on the left-down corner. The vertical scale is expressed in units of the root mean squared noise of each radio map that amounts to 9.3, 8.2, 10.7, 16.0, 7.3, and 4.5 μJy beam−1 for the different epochs, respectively. North is up and east is left.

2 Radio data and precession model fitting

As our intention is to study the evolution of the radio jet morphology of GRS 1758–258, we reused historical records of this source at radio wavelengths from the public archives of the VLA interferometer. This task had already been carriedout for an earlier study of the source, where four maps exhibiting clear morphological variations in time were obtained (see log of observations and detailed calibration methodology in Martí et al. 2015). In this work, we reuse these four “frames” together with a new one that we obtained from a dedicated campaign on GRS 1758–258 with the VLA in C-configuration conducted in 2016 at the 6 cm wavelength (Project ID. 16A-005, on-source time 7659 s). It is remarkable to note the improvement in sensitivity with regard to this latter observation when compared to the previous ones, which was made possible thanks to the GHz bandwidth available since 2011 following the VLA upgrade, although calibration was applied, taking care to produce a map that would be comparable with previous maps. The final five maps are shown in Fig. 1. As we can see, the new radio map confirms thepreviously noticed changes in the large-scale morphology of relativistic jets in GRS 1758–258 (Martí et al. 2015).

However, the possibility that these variations are due to precession has never been raised before in the literature. In considering such a case, we tried to fit the well-known precession kinematic model of Hjellming & Johnston (1981) to our data. We follow a similar approach to that successfully used for the case of 1E 1740.7–2942 (Luque-Escamilla et al. 2015), thus achieving a multi-epoch fit of a relativistic jet from their projected paths for the second time. A detailed description of the fit procedure can be found in this last reference; even though for 1E 1740.7–2942, we deal with a more continuous radio jets and their location could be well established thanks to the so-called “skeleton” of the binary image of the maps (see Luque-Escamilla et al. 2015, for details). Unfortunately, GRS 1758–258 presents less continuous jets, so the position of their projection on the maps in Fig. 1 need to be determined in a different way. For this purpose, we slice the image and look for maxima in the emission profiles. The jet points thus obtained conform analogous to the so-called jet ridge in active galaxy nucleus (AGN). It is worth mentioning that these points correspond to the traces of radio jet in the maps, not only to the hotspots, which do not move ballistically.

Once the jet locations are known, we try to fit these data to the kinematic model previously cited. It is worth mentioning that all jet paths on the five different epochs have to be simultaneously fit to the same set of model parameters. There are eight different parameters in the kinematic model, so the least-squares fitting procedure is a very time-consuming task. To achieve a final result in a reasonable amount of time, we try to narrow the limits on some of the parameters whenever some additional, reliable data is available. For instance, the position angle of the jet axis is easily obtained from the maps with enough accuracy to be around 11°. The distance is known to be less than 12 kpc (Martí et al. 2015), so we let this parameter to vary only up to this value. The inclination i of the jet precession axis with the line of sight cannot be edge-on due to the lack of eclipses in X-ray data, nor completely face-on, because two jets are visible. In order to constrain an inclination value, we can make use of the brightness ratio between approaching and receding continuous, relativistic jets defined as BR = [(1+βcos(i))/(1−βcos(i))]2−α$\textrm{BR}\,{=}\,[(1+\beta \cos(i))/(1-\beta \cos(i))]^{2-\alpha}$. 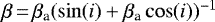Here, α being the spectral index and β the ratio vjet ∕c, which, in turn, may be related to the apparent jet velocity as β = βa(sin(i)+βacos(i))−1$\beta\,{=}\,\beta_{\textrm{a}} (\sin(i) + \beta_{\textrm{a}} \cos(i))^{-1}$. From our deep map obtained by combining all available data at 6 cm, we measure jet brightness at equal angular separation on both sides to estimate the observed BR to be of about 2.5, while α ranges from ~− 0.7 to ~ − 0.3 (Martí et al. 2002). Apparent velocity is at least βa = 0.32 at the end of the jet (Martí et al. 2015). Therefore, the range of possible β ~ 0.32–0.33 while i ~ 51°–56°. These inclination angle values, are in fact, compatible with the lack of Fe Kα line in observed spectra (see e.g. Soria et al. 2011). However, higher β values have been proposed for GRS 1758–258 (Martí et al. 2016), so we let this parameter to exceed the 0.33 limit in our fit, although, according to the reasoning presented just above, it would lead to higher i values.

The fit procedure is performed by varying each parameter value along its range in steps of 10% of the value in the quest of the minimum reduced 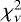χν2$\chi_{\nu}^2$ with 301 degrees of freedom. Once the complete set of parameters has been fully explored, we refine the search in the vicinity of the minimum by reducing the step size. The final best-fit parameters are shown in Table 1, and the result is shown in Fig. 1 over-plotted on the original radio maps. The northern jet is the more conspicuous and so it dominates the fit. The reduced 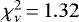χν2 = 1.32$\chi_{\nu}^2\,{=}\,1.32$ is the minimum obtained when exploring a reasonable range of values in the parameter space. It is calculated based on the fit of the eight parameters and the mean error from the synthesised beam. As can be seen in Fig. 1, these parameters provides a reasonable match between observed jet structures and modelled paths, which suggests that studying the precession effects in the morphological evolution of GRS 1758–258 is not out of the scope of this work. The error in each parameter is estimatedwith its 90% uncertainty, obtained as the variation in this parameter which gives an increment of e in the value of the global, non-reduced χ2.

Table 1

Twin-jet kinematic model for GRS 1758–258 radio jets.

3 Reliability of precession model parameters

In order to ensure that precession is taking place on GRS 1758–258, more than an acceptable fitting accuracy is needed. We have to analyse the implications of the values of the parameters in Table 1 and prove them to be reasonable. In this context, the distance here obtained coincides with the usually assumed value of ~ 8.5 kpc in the literature (see e.g. Rodríguez et al. 1992; Mereghetti et al. 1994; Keck et al. 2001; Fender 2001; Grimm et al. 2002; Heindl & Smith 2002; Hardcastle 2005; Pottschmidt et al. 2006; Martí et al. 2017). However, some authors put the microquasar much closer, from 2 kpc (Mereghetti et al. 1992) to 5 kpc (Dunn et al. 2010), while others place it as far as 10 kpc based on the low radio flux and a high accretion rate observed (Mereghetti et al. 1997; McConnell et al. 1996). We can try to constrain the distance to the source a bit more based on an independent approach founded on the relations established between extinction, E(B − V), and distance, d, in the Galaxy (i.e. Lucke 1978; Chen et al. 1999). As E(B − V) cannot be accurately measured from the overly weak companion star in GRS 1758–258, we can derive it from empirical relations to the column density, NH (Güver & Özel 2009; Predehl & Schmitt 1995; Reynoso et al. 2006). As a result, assuming NH ≃ 1.6 × 1022 cm−2 from X-ray data (Soria et al. 2011), the distance to GRS 1758–258 is d ≃ 8−10 kpc and d ≃ 4–7 kpc according to Lucke (1978) and Chen et al. (1999), respectively. Furthermore, taking into account that there is a conspicuous gas cloud possibly related to the jet-ISM interaction in GRS 1758–258 that is located at 8.5 kpc (Martí et al. 2017), the distance value in Table 1 seems reasonable. The existence of such a cloud near the end lobe of the jet could explain a possible slowing down of the jet velocity, lending reliability to the β value obtained in our fitting procedure.

On the other hand, following Soria et al. (2011), M• ≈ 5∕cosi M⊙ for the black hole in GRS 1758–258, while the internal radius of the accretion disc would be Rin ≈ 45∕cosi km. Therefore, a value for the inclination, i, as in Table 1, would lead to M• ≈ 10 M⊙ and Rin ≈ 80 km. It is remarkable that the mass of the black hole in GRS 1758–258 has been derived from X-ray observations and found to be on this order (Keck et al. 2001; Bezayiff 2006; Soria et al. 2011). The internal accretion disc radius Rin may be identified with Rms, the radius of the marginally stable orbit of a Kerr black hole. This last parameter can be expressed in a non-dimensional form as Rms = ξmsRg, with Rg = GM•∕c2 being the gravitational radius. 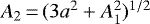A dependence exists between ξms and the dimensionless spin parameter, a, for the black hole such that ξms = 3+A2∓[(3−A1)(3+A1+2A2)]1/2$\xi_{\textrm{ms}}\,{=}\,3&#x002B;A_2\mp[(3-A_1)(3&#x002B;A_1&#x002B;2A_2)]^{1/2}$ (upper sign for prograde rotation), with A1 = 1+(1−a2)1/3[(1+a)1/3+(1−a)1/3]$A_1\,{=}\, 1&#x002B;(1-a^2)^{1/3}[(1&#x002B;a)^{1/3}&#x002B;(1-a)^{1/3}]$ and A2 = (3a2+A12)1/2$A_2\,{=}\,(3a^2&#x002B;A_1^2)^{1/2}$ (see, e.g., Bardeen & Petterson 1975). A radio-quiet source like GRS 1758–258 should not have a rapidly rotating compact object (at least from a theoretical point of view, see Blandford et al. 1990; Davis & Tchekhovskoy 2020) unless a geometric effect, due to the inclination of the source with respect to the observer’s line of sight combined with Doppler boosting, was at work (Motta et al. 2018). However, the above observational constraints of Soria et al. (2011) together with the ξms expression presented above suggest a small to moderate inclination of the GRS 1758–258 system (always i < 60° decreasing with the black hole spin parameter a). Therefore, a tentative a = 0.1 is adopted from this point, which results in Rin ≈ 84 km for a 10 M⊙ black hole, so the assumed value for i appears to be appropriate.

However, the precession period, Pp ~ 7.5 years, derived from our fit is somehow troublesome. On one hand, it seems to be a reasonable value because Pp is somewhere in the range of 10–102 times the orbital period Po proposed for these kinds of sources (see e.g. Larwood 1998), taking into account that the latter is accepted to be Po = 18.45 ± 0.10 days from the X-ray light curve time-series analysis (Smith et al. 2002). On the other hand, no long-term variability greater than ~ 600 days has been reported from such light curves in spite of the extensive X-ray monitoring of GRS 1758–258. In addition, a new orbital period Po ≲ 1 day has been recently proposed based on the optical observation of the companion star (Martí et al. 2016), which would not be compatible with Pp ~ 7.5 years. This new Po value has not been previously reported because it is beyond the typical Nyquist limit in X-ray lightcurves available. What is particularly notable is that this short orbital period clearly appears to be the most usual for LMXB (see the BlackCAT catalogue of stellar black holes in X-ray transients, Corral-Santana et al. 2016). In addition, a significant change within the time frame of the 18.45 day period has been reported from a detailed time-series analysis of RXTE data, ranging from 18.043 to 18.475 days (Hirsch et al. 2020). This is remarkable not only because it would prevent that period from being an orbital modulation,but also because this is the observed behaviour in supra-orbital periods for other known LMXB, such as Her X-1 (with 34 to 36.55 days variability, i.e. Staubert et al. 2013) or SMC X-1 (varying from 45 to 60 days, Dage et al. 2019). Various mechanisms have been suggested to explain such supra-orbital modulations, but not all of them could be at work in GRS 1758–258. For instance, the magnetic warping of the disc (Pfeiffer & Lai 2004) requires a highly magnetic compact object in the system, while GRS 1758–258 appears to harbour a black-hole. A wind-driven tilting of the disc (Schandl & Meyer 1994) has been also proposed, but the plausible A-type companion in GRS 1758–258 is hardly capable of emitting strong enough winds. It is also difficult to relate the ≃ 18.45 day period to a dramatic change in X-ray state change (as the origin of supra-orbital modulations in some sources, e.g. King et al. 1997) because they are not so dramatic nor appeared on such timescales in GRS 1758–258. More likely, the conspicuous periodicity of ≃ 18.45 days could be related to radiation-induced warping of the disc (Ogilvie & Dubus 2001). However, Hirsch et al. (2020) have carefully analysed this possibility and found no definitive evidence for the conclusion that this mechanism is behind the supra-orbital motion observed in GRS 1758–258. Therefore, although we cannot strictly rule out any other mechanisms with the data currently available, precession arises as a promising alternative to account for the (quasi-)periodic behaviour observed in X-ray light curves in GRS 1758–258.

In summary, two possible scenarios arise for GRS 1758–258. The first features an orbital period of Po = 18.45 days and a precession period of Pp ~ 7.5 years, with radio jets approximately following the paths shown in Fig. 1. The most reliable companion star capable of feeding a black hole of M• ≈ 10 M⊙ through Roche lobe overflow would be a K-type giant (Marti et al. 1998; Eikenberry et al. 2001). We refer to this here as the “K-scenario”. On the other hand, the orbital period would be Po ≲ 1 day and the precession period, Pp, would be the conspicuous 18.45 days from the X-ray light curves. In such a case, the donor star would be a main-sequence A5V (Muñoz-Arjonilla et al. 2010; Luque-Escamilla et al. 2014; Martí et al. 2016) and the system could be an intermediate-mass X-ray binary (Martí et al. 2016; Tauris & van den Heuvel 2006). We call this the “A-scenario”, which could not be related to our kinematic model fitting. Although some observational facts support of this latter case (Luque-Escamilla et al. 2014; Martí et al. 2016) and it fits the Pp ∕Po ratio in the literature, certainly no spectroscopic feature has been obtained from the optical or IR counterpart of GRS 1758–258, so the only way to discriminate between these two pictures is to search for any lack of theoretical support.

4 Discerning the true nature of GRS 1758–258

For black holes, two main mechanisms have been proposed as jet drivers: the black hole spin (Blandford & Znajek 1977, hereafter BZ) and thedisc accretion energy (e.g. Blandford & Payne 1982, hereafter BP). According to these two types of jet launching, for jet precession that actually takes place in GRS 1758–258, it would be required to have precession either of the black hole spin axis or instead the disc plane close to the central accretor. For this latter case, the inner part of the disc, where the jet is launched, must be tilted with respect to the whole disc angular momentum. This in turn may be achieved by two mechanisms. One possibility is to have a black hole whose spin axis is misaligned with that of the disc. In such a case, the Bardeen & Petterson (1975) effect can cause a local warping of the disc, forcing it to be perpendicular to the tilted black hole rotation axis. Another possibility is based on the torques that arise via the misalignment of the accretion disc and the orbital plane of the binary (Katz 1973; Papaloizou & Terquem 1995; Papaloizou & Lin 1995; Larwood 1998, 1997).

Therefore, for jet precession driven by BZ, or by BP together with the Bardeen–Petterson effect, a tilted, spinning black hole is needed. Although BZ is probably not behind the precession in our system because of the small angular momentum of the disc compared to that of the black hole (which seems to be the common case, making the precession of black hole spin axes difficult to observe at human timescales; see Nixon & King 2013; Banerjee et al. 2019), observational evidence exists to support the idea that the black hole spin axis could be misaligned with the orbital and accretion disc angular momentum in X-ray binaries (see e.g. Hjellming & Rupen 1995; Maccarone 2002; Caproni et al. 2006). This different spinning axis in accretion disc and black holes may be related to the violent birth of the system together with a corresponding long alignment timescale which has been estimated to be on the order of ≳ 106 years (Maccarone 2002), or even higher (Banerjee et al. 2019); being, thus, greater than, or at least similar to, the system lifetime. On the other hand, jet precession may be due to a disc tilted by an external torque from the companion and a BP launching mechanisms, no matter the black hole spin. Therefore, the existence of precession in a system such as GRS 1758–258 cannot be excluded. In the following, we try to see if this process is, in fact, taking place according to the different mechanisms mentioned above. In this sense, we ought to note that jet precession can also be driven by deflection at the collision point with super-Eddington winds coming from the disc as suggested for SS 433 (Begelman et al. 2006) or other more sophisticated mechanisms (Liska et al. 2018). We cannot discuss these cases in detail for GRS 1758–258 because of the lack of sufficiently precise observations in the vicinity of the launching site.

4.1 Precession due to relativistic local warping

Although the Bardeen–Petterson effect alone may be difficult to relate to precession in black hole binaries (Nixon & King 2013), we try to study its reliability on our particular GRS 1758–258 system. We have to consider precession and viscous timescales, τp and τν, because the Bardeen–Petterson effect is able to align the inner part of the disc to the black hole spin axis if τp ≲ τν at the inner edge of the accretion disc r = Rin (Natarajan & Armitage 1999). They are defined as: 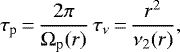τp = 2πΩp(r) τν = r2ν2(r),\begin{equation*} \tau_{\textrm{p}}\,{=}\,\frac{2\pi}{\Omega_{\textrm{p}}(r)} \, \tau_{\nu}\,{=}\,\frac{r^2}{\nu_2(r)}, \end{equation*}(1)

where ν2(r) is the kinematic viscosity of the disc for vertical shear and Ωp(r) = 2GJ•c−2r−3 is the angular velocity due to Lense–Thirring precession (e.g. Wilkins 1972), with 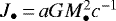J• = aGM•2c−1$J_{\bullet}\,{=}\,a G M_{\bullet}^2 c^{-1}$ as the black hole angular momentum modulus. We do not know ν2(r) but we can assume ν2 ~ ν1, which is theviscosity along the disc, and can be parametrised following the Shakura & Sunyaev (1973) prescription as 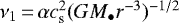ν1 = αcs2(GM•r−3)−1/2$\nu_1\,{=}\,\alpha c_{\textrm{s}}^2 (G M_{\bullet} r^{-3})^{-1/2}$. Here, cs is the local sound speed, which in turn may be written as 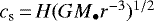cs = H(GM•r−3)1/2$c_{\textrm{s}}\,{=}\,H (G M_{\bullet} r^{-3})^{1/2}$ with H being the disc scale height. So, ifwe associate Rin with the Rms and adopt the above proposed values for GRS 1758–258 we finally obtain: 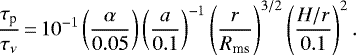τpτν = 10−1(α0.05)(a0.1)−1(rRms)3/2(H/r0.1)2.\begin{equation*} \frac{\tau_{\textrm{p}}}{\tau_{\nu}}\,{=}\,10^{-1} \left(\frac{\alpha}{0.05}\right)\left(\frac{a}{0.1}\right)^{-1} \left(\frac{r}{R_{\textrm{ms}}}\right)^{3/2} \left(\frac{H/r}{0.1}\right)^2. \end{equation*}(2)

Here, we have assumed a very conservative estimate for H∕r in the inner border of the disc. A reduction in one order of magnitude in this last parameter would lead to a decrease in τp ∕τν by two orders of magnitude. Highest values of a would also decrease this ratio.

Thus, this simple estimate suggests that the precession timescale in the inner disc is likely to be shorter than the local viscous timescale, even if H∕r is as high as 0.3 and could be considered a thick disc which would be expected if the black hole is in the hard X-ray state. So, the precession in GRS 1758–258 may be acting due to the Bardeen–Petterson effect even for thicker discs that could be related to jet launching at hard state. It is then possible to calculate the precession period of the disc or jet, taking into account the contribution of the different part of the disc using the following expression (Caproni et al. 2004): Pp = 2πGM•c3∫ξinξoutΣ (ξ)[Φ(ξ)]−1ξ3dξ∫ξinξoutΣ (ξ)Ψ(ξ)[Φ(ξ)]−2ξ3dξ,\begin{equation*} P_{\textrm{p}}\,{=}\,\frac{2 \pi G M_{\bullet}}{c^3}\frac{\int_{\xi_{\textrm{in}}}^{\xi_{\textrm{out}}} \Sigma(\xi)[\Phi(\xi)]^{-1} \xi^3 \textrm{d}\xi}{\int_{\xi_{\textrm{in}}}^{\xi_{\textrm{out}}} \Sigma(\xi) \Psi(\xi)[\Phi(\xi)]^{-2} \xi^3 \textrm{d}\xi},\end{equation*}(3)

where Φ(ξ) = ξ3∕2 + a, 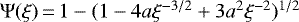Ψ(ξ) = 1−(1−4aξ−3/2+3a2ξ−2)1/2$\Psi(\xi)\,{=}\,1-(1-4 a \xi^{-3/2}&#x002B; 3 a^2 \xi^{-2})^{1/2}$ and Σ(ξ) is the accretion disc surface density. Remember that ξ is the non-dimensional distance rescaled with Rg. We can again take ξin = ξms and assumea potential dependence of the disc density to the distance Σ(ξ) = Σ0 ξs with constant parameters. We consider s ∈{−2, −1, 0} to take into account reasonable decreasing or constant behaviours. As the amplitude of the precession angular velocity decreases with the cube of the distance, the exact value of the outer radius of the accretion disc is not critical and we take ξout = 103ξms as in Martí et al. (2016). We have numerically integrated Eq. (3) and the resulting precession period, Pp, in days is plotted in Fig. 2 as a function of the spin parameter, a. The upper, grey-dotted line represents the 7.5 years precession period of GRS 1758–258 corresponding to the “K-scenario” defined above, while the lower, magenta-dotted line marks the precession period of ~18.45 days proposed in Martí et al. (2016) according to the “A-scenario”. It may be shown that the yearly precession period for GRS 1758–258 can only be reproduced for an overly slow rotating black hole (a ~ 10−3) and assuming a constant density along the disc. On the other hand, the daily precession period can be reached with the here adopted rotation for the black hole (a = 0.1) or even a = −0.2 for a retrograde spin under the same density conditions. A smaller disc will lead to shorter periods and, therefore, to more tiny, unrealistic results. If the outer disc is greater than our estimation, then precession periods grow, and a ξout = 8500 with our assumed black hole spin a = 0.1 and a Sakura–Sunyaev solution 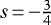s = −34$s\,{=}\,{-}\frac{3}{4}$ would result on the 18.45 days precession period, while the 7.5 years period is only reached if ξout = 1.5 × 105 under the same conditions. These latter value is difficult to reconcile with both the observed emission from the disc and the binary separation. Thus, precession in GRS 1758–258, if indeed caused by the Bardeen–Petterson effect on the disc, would require an extended disc with a surface density slightly dependent on radius, and clearly would favour the “A-scenario” against the “K-scenario”.

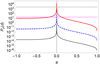thumbnail Fig. 2

Precession period for GRS 1758–258 as a function of the spin parameter. The outer non-dimensional radius of the disc is taken to be ξout = 1000ξms. Different lines correspond to the different power-law slopes of the disc surface density (red-continuous for s = 0; blue-dashed for s = −1, and black-dotted for s = −2). The grey-dotted horizontal line marks the estimated period of precession of approximately 7.5 yr, while the magenta-dotted line marks the 18.48 days precession period proposed in Martí et al. (2016).

4.2 Precession due to external torque

On the other hand, an external torque from the companion could maintain the disc warp and explain the precession in GRS 1758–258. We can follow Papaloizou & Terquem (1995) and assume rigid body precession for a differentially rotating fluid in the accretion disc, and use linear perturbation theory to derive an integral form for the precession frequency. Based on this, Larwood (1998) obtained the ratio between the binary orbital period, Po, and the precession period, Pp, for a non-relativistic, polytropic equation of state with ratio of specific heats of 5∕3, which is: 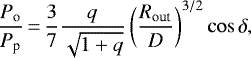PoPp = 37q1+q(RoutD)3/2cosδ,\begin{equation*} \frac{P_{\textrm{o}}}{P_{\textrm{p}}}\,{=}\,\frac{3}{7} \frac{q}{\sqrt{1&#x002B;q}} \left( \frac{R_{\textrm{out}}}{D}\right)^{3/2} \cos \delta,\end{equation*}(4)

where δ is the orbital inclination, D is the orbital separation, and Rout is the outer disc, which is estimated to be a fraction κ of the Roche lobe around the compact object RLc. Here, it is assumed that Rout = κRLc ≫ Rin. This equation differs by a factor of two from the expression given in Katz (1973) because the tidal torque has been averaged over the disc. The extension of the Roche lobe may be approximated through the expression given by Eggleton (1983): 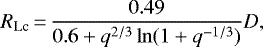RLc = 0.490.6+q2/3ln(1+q−1/3)D,\begin{equation*} R_{\textrm{Lc}}\,{=}\,\frac{0.49}{0.6&#x002B;q^{2/3} \ln(1&#x002B;q^{-1/3})}D, \end{equation*}(5)

so Eq. (4) may be written as: 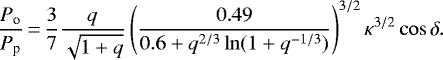PoPp = 37q1+q(0.490.6+q2/3ln(1+q−1/3))3/2κ3/2cosδ.\begin{equation*} \frac{P_{\textrm{o}}}{P_{\textrm{p}}}\,{=}\,\frac{3}{7} \frac{q}{\sqrt{1&#x002B;q}} \left(\frac{0.49}{0.6&#x002B;q^{2/3} \ln(1&#x002B;q^{-1/3}) } \right)^{3/2} \kappa^{3/2} \cos \delta.\end{equation*}(6)

In this model, the inclination δ of the binary orbit with respect to the accretion disc plane gives rise to the observed precession. The jet then subtends a precession cone with a half-opening angle equal to the orbit inclination, so δ = ψ, which we adopt from the model fit (ψ = 1.4°; see Table 1). On the other hand, the κ value was determined by Paczyǹski (1977) for a thin and weakly viscous accretion disc based on the assumption that its size could not exceed the largest orbit with non-intersecting particles in the primary Roche lobe. This parameter depends on the mass ratio, q, although for 0.03< q < 30 the fraction κ = 0.86 and is roughly independentof q. A similar value, κ = 0.88, was obtained from an independent approach by Papaloizou & Pringle (1977) for 0.2 < q < 10. This seems to be the right mass ratio interval for GRS 1758–258 harbouring a ~ 10 M⊙ black hole.

In our “A-scenario” the Po∕Pp = 0.03, which is similar to the theoretical 0.02 derived from Eq. (6). On the other hand, the “K-scenario” gives Po ∕Pp = 0.017, which is half the theoretical value of 0.042 obtained from Eq. (6). In order to find a better discriminant argument between our two possible scenarios, we can estimate thedisc size following the reasoning based on the torque on the accretion disc for a small orbital inclination binary system (Larwood 1998): 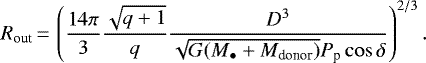Rout = (14π3q+1qD3G(M•+Mdonor)Ppcosδ)2/3.\begin{equation*} R_{\textrm{out}}\,{=}\,\left( \frac{14 \pi}{3} \frac{\sqrt{q&#x002B;1}}{q}\frac{D^3}{\sqrt{G (M_{\bullet} &#x002B; M_{\textrm{donor}})} P_{\textrm{p}} \cos \delta} \right)^{2/3}.\end{equation*}(7)

This result is 22∕3 greater than that proposed in Larwood (1997) and Papaloizou & Terquem (1995), because the considered averaged effect of the donor star tidal torque on the disc. In our “K-scenario”, this would result on Rout ~ 1012 cm, which is of the same order than the Paczyǹski (1977) estimate of Rout = κRLc. This means a non-dimensional ξout ~ 105, which is too high as said before. On the other hand, the “A-scenario” leads to a shorter Rout ~ 1011 cm according both to Eq. (7) and Paczyǹski estimation, which gives ξout ~ 104. We can compare these results to the Rout estimated from the observed delay in brightening and softening events in GRS 1758–258, following Main et al. (1999): 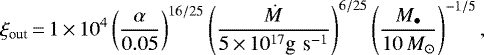ξout = 1 × 104(α0.05)16/25(M˙5 × 1017g  s−1)6/25(M•10 M⊙)−1/5,\begin{equation*} \xi_{\textrm{out}}\,{=}\,1\,{\times}\,10^4 \left( \frac{\alpha}{0.05}\right)^{16/25}\left( \frac{\dot{M}}{5\,{\times}\, 10^{17} \textrm{g}\,\,\textrm{s}^{-1}}\right)^{6/25}\left( \frac{M_{\bullet}}{10\,M_{\odot}}\right)^{-1/5},\end{equation*}(8)

where Ṁ is the accretion rate, which for GRS 1758–258, we assume to be ~ 5 × 1017 g s−1 in accordance with the ~0.02 Eddington observed by Soria et al. (2011) and the value adopted in Main et al. (1999). Equation (8) gives a result which is remarkably compatible with our disc size estimation in the “A-scenario”. Thus, the “K-scenario” seems to be less realistic than the former if this precession model is at work, in addition to the yet commented disagreement to the optical and IR proposed counterpart. Moreover, an accretion disc too large should be more powerful than observed and its emission would be conspicuous at optical and IR wavelengths, in contrast to the observed spectrum (Martí et al. 2016). A smaller disc may be present if GRS 1758–258 system were highly eccentric, which is not expected.

4.3 Considering whether precession is actually taking place on GRS 1758–258

From all theprevious discussions, we can reach as a preliminary conclusion that there seems to be hints of precession in GRS 1758–258 in any case. A precession period on the order of tens of days is favoured over one on the order of years. However, as pointed out above, such a short period would produce jet paths that are too wiggled to explain their changing morphology shown in the radio maps of Fig. 1, unless GRS 1758–258 is assumed to be unexpectedly closed to us. Therefore, we propose that this source is probably configured in the “A-scenario” and that the conspicuous ~ 18.54 day period has to be attributed to precession instead to orbital motion. Thus, as precession could not be responsible for the observed variations inthe paths of the radio jets in GRS 1758–258, we proceed to analyse whether these could be attributed to the growth of instabilities.

5 Instabilities as the source of radio-jet changing morphology

Large-scale morphology changes in GRS 1758–258 have already been attributed to the growth of instabilities (Martí et al. 2015, 2017), as is usual in astrophysical jets structure (e.g. Hardee 2011; Perucho 2012). This certainly seems to be the more promising explanation for our source, as it is evident that a lack of symmetry in the wavy patterns of the jet-counterjet structure of GRS 1758–258 in Fig. 1, in contrast to confident cases of precession jets in microquasars such as SS 433 or 1E 1740.7–2942. This is strongly suggestive of some kind of instability developing at large scales rather than a modulation of the jet at the central source is behind the observed evolution of the GRS 1758–258 radio morphology.

Current-driven (CDI) is one of the possible instabilities developing in the jets if magnetic fields are present. Their azimuthal mode m = 1 kink instability is the most effective one in modifying the magnetised jet structure (Giannios & Spruit 2006; Hardee 2011), leading even to its disruption. An ideal kink mode is characterised by helical displacements of the cylindrical cross sections of a plasma column. It is expected to grow on a dynamical timescale with respect to an Alfvén wave crossing the unstable column. According to simulations of AGN jets (e.g. Mizuno et al. 2012), the timescale for the growth of kink instabilities is on the order of τCDI ~ 10Rjet∕vA, where Rjet is the jet radius and vA the Alfvén speed. For GRS 1758–258, we measured Rjet ~ 0.1 pc (Martí et al. 2015), while vA could be estimated from ultrarelativistic plasma as vA = cB[4π(ukin+pkin)+B2]−1/2$v_{\textrm{A}}\,{=}\,c B [4 \pi (u_{\textrm{kin}}&#x002B;p_{\textrm{kin}})&#x002B;B^2]^{-1/2}$, where ukin is the density of kinetic energy of the particles and pkin is the pressure of the ultrarelativistic plasma (see e.g. Akhiezer et al. 1975). 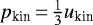With pkin = 13ukin$p_{\textrm{kin}}\,{=}\,\frac{1}{3} u_{\textrm{kin}}$ for this case, and assuming equipartition between the magnetic and particle energy densities (ukin = B2∕8π), we finally have 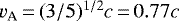vA = (3/5)1/2c = 0.77c$v_{\textrm{A}}\,{=}\, (3/5)^{1/2}c\,{=}\,0.77 c$. Therefore, we find the instability growth timescale to be τCDI ~ 1.5 × 103 days, in Fig. 1 we can estimate that the helical/ribbon-like pattern arises at about ~ 50 arcsec from the core, which for the assumed distance of 8.5 kpc turns out to span a distance of at least dj ~ 2 pc. This would imply a flow velocity dj∕τCDI greater thanc, assuming that the instability starts close to the central engine. Therefore, the CDI kink instabilities do not appear to be responsible of the large-scale structure of GRS 1758–258.

Another possibility is the Kelvin-Helmholtz instability (KHI), which is originated from transverse velocity gradients or discontinuities due to the different kinetic energy between the jet and the typically sub-relativistic ambient medium. Ordinary modes can affect the jet surface or even the whole beam (see e.g. Birkinshaw 1991), leading to shocks, entrainment of ambient material, and eventually the disruption of the jet (Bodo et al. 1998; Martí et al. 2015). KHI seem to produce complex three dimensional helical, ribbon, and thread-like patterns (Hardee 2000; Perucho 2012) with an expected radio emission enhancement of about one order of magnitude. The growth timescale for KHI is of order of τKHI ~ (2Rjet∕vj)η−1∕2, with η being the density contrast between the jet and the medium, and vj the jet bulk velocity (Araudo et al. 2009).

Assuming η ~ 10−1 for GRS 1758–258 (Martí et al. 2015), and vj ~ c for establishing a lower limit, this timescale is τKHI ≳ 800 days, which is even shorter than τCDI. Therefore KHI is even less adequate to explain the surge of the helical patterns from the origin following the same reasoning as before, unless it was triggered far from the central engine because the jet would maintain its stability up to that point.

We can reach the same conclusions with an alternate reasoning as well. The helical pattern observed in the jets in the 1997 map of GRS 1758–258 appears to have a wavelength λ ~ 15 arcsec or λ ~ 0.62 pc at the assumed distance to the source. If the kink CDI starts near the onset of the structure, the flow speed would then be vj ~ λ∕τCDI ~ 0.5c, which seems reasonable. But CDI should start close to the central engine, where the magnetic fields are strong, so it seems unrealistic for them to be responsible for the observations. However, KHI is not compelled to be triggered so near to the core. The same reasoning as before accounts vj ~ λ∕τKHI ~ c for the KHI starting near the onset of the wiggled structure using our τKHI lower limit, which is rather sound.

Recently, another kind of instability that has never before considered in this context was recently proposed to explain the reconfinement and loss of stability in astrophysical jets (Gourgouliatos & Komissarov 2018). The centrifugal force acting on the plasma moving along curved streamlines promotes the so-called centrifugal instability (CFI) that induces stream-oriented features in the flow that disturbs the jet morphology. Such an instability is expected to appear if the flow satisfies the generalised Rayleigh criterion (Gourgouliatos & Komissarov 2018) which, in the case of curved jets confined by an external medium at rest, is always fulfilled.

Therefore, some instabilities seem to be capable of explaining the observed morphological changes in GRS 1758–258 radio jets. The KHI need to start far from the central source and could be triggered by jet precession. The wiggling observed in the South jet could be reminiscent of instability-driven structures which has been found in other microquasars (see e.g. Migliori et al. 2017). This, in addition, strengthens the role that has been attributed to instabilities in the formation of the actual radio structures of GRS 1758–258 (Martí et al. 2015, 2017).

6 Conclusions

In this paper, we have presented a study of the origin of the large scale morphological changes in the relativistic jets of GRS 1758–258. Theoretical and observational arguments led us to reach the following conclusions:

  • 1.

    New radio data confirms that large-scale morphology of GRS 1758–258 indeed changes over time in a matter of years. The observed radio jets clearly exhibit a variable morphology with some structures resembling helical paths;

  • 2.

    A kinematic model has been fit to the observed radio structures. Although some of the derived parameters may make sense, the precession period of ~7.5 years appears problematic. It would need a giant K-type companion which does not agree with previous optical/IR observations. In addition, the corresponding accretion disc would be too large for the observed emission. Therefore, the radio morphology changes in GRS 1758–258 cannot be attributed to precession;

  • 3.

    However, our theoretical considerations allow for the existence of precession in GRS 1758–258. Although we cannot assure its precise origin with the present observational evidence, actual data is compatible with precession in both Bardeen–Petterson and companion torque models. In any case, the favoured scenario is that with an A main-sequence star andan orbital period on the order of a day. This means that the precession period should be on the order of days, which is too short for being compatible with the observed path of the jets;

  • 4.

    We thusexclude precession as the source of the dramatic changes observed in GRS 1758–258. These changes have presumably been attributed to the growth of instabilities, which have shown to form ribbon-like and helical structures. The absence of symmetry in the wiggles of the jets in the large-scale structure of GRS 1758–258 supports this view. According to our analysis, instabilities developing far away from the central source, rather than a modulation of the outflow speed or mass flux at the compact core, appear to explain the radio observations;

As a result, we propose a new physical scenario for GRS 1758–258 system. It could be a close binary composed of a ~ 10 M⊙ black hole and a main-sequence A-type, ~ 2 M⊙ donor star orbiting each other with a period ≲1 day. Although we cannot strictly rule out other mechanisms with currently available data, as precession might certainly be at work on this system, it is suggestive to attribute to it the conspicuous observed period of 18.45 days, which has been assumed as the orbital period up until recently. This is the only scenario compatible with available optical/IR observations and with the precession models we put into test. These properties would made GRS 1758–258 a possible intermediate mass X-ray binary. Such a scenario would explain its X-ray behaviour more easily, as it is more similar to high-mass X-ray binaries than to LMXB. The resulting large-scale morphology of the jets is affected by instabilities that originate the ribbon-like and helical-like structures observed. As has been previously claimed, these instabilities would eventually lead to the disruption of the jet.

Acknowledgements

The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This work was supported by the Agencia Estatal de Investigación grant PID2019-105510GB-C32/AEI/10.13039/501100011033 from the Spanish Ministerios de Ciencia e Innovación y Universidades, and by the Consejería de Economía, Innovación, Ciencia y Empleo of Junta de Andalucía under research group FQM-322, as well as FEDER funds.

References

  1. Abell, G. O., & Margon, B. 1979, Nature, 279, 701 [NASA ADS] [CrossRef] [Google Scholar]
  2. Akhiezer, A. I., Akhiezer, I. A., Polovin, R. V., Sitenko, A. G., & Stepanov, K. N. 1975, Oxford Pergamon Press International Series on Natural Philosophy, 1 [Google Scholar]
  3. Araudo, A. T., Bosch-Ramon, V., & Romero, G. E. 2009, A&A, 503, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Banerjee, S., Chakraborty, C., & Bhattacharyya, S. 2019, MNRAS, 487, 3488 [CrossRef] [Google Scholar]
  5. Bardeen, J. M., & Petterson, J. A. 1975, ApJ, 195, L65 [NASA ADS] [CrossRef] [Google Scholar]
  6. Begelman, M. C., King, A. R., & Pringle, J. E. 2006, MNRAS, 370, 399 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bezayiff, N. 2006, PhD thesis, University of California, Santa Cruz, USA [Google Scholar]
  8. Bignami, G. F., Caraveo, P. A., Mereghetti, S., et al. 1991, Messenger, 66, 10 [Google Scholar]
  9. Birkinshaw, M. 1991, The Stability of Jets, ed P. A. Hughes, 278 [Google Scholar]
  10. Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
  11. Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
  12. Blandford, R. D., Netzer, H., Woltjer, L., Courvoisier, T. J.-L., & Mayor, M., 1990, Active Galactic Nuclei, 97 [Google Scholar]
  13. Bodo, G., Rossi, P., Massaglia, S., et al. 1998, A&A, 333, 1117 [NASA ADS] [Google Scholar]
  14. Caproni, A., Mosquera Cuesta, H. J., & Abraham, Z. 2004, ApJ, 616, L99 [NASA ADS] [CrossRef] [Google Scholar]
  15. Caproni, A., Livio, M., Abraham, Z., & Mosquera Cuesta, H. J. 2006, ApJ, 653, 112 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chen, B., Figueras, F., Torra, J., et al. 1999, A&A, 352, 459 [NASA ADS] [Google Scholar]
  17. Corral-Santana, J. M., Casares, J., Muñoz-Darias, T., et al. 2016, A&A, 587, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Dage, K. C., Clarkson, W. I., Charles, P. A., Laycock, S. G. T., & Shih, I.-C. 2019, MNRAS, 482, 337 [Google Scholar]
  19. Davis, S. W., & Tchekhovskoy, A. 2020, ARA&A, 58, 081817 [Google Scholar]
  20. Dunn, R. J. H., Fender, R. P., Körding, E. G., Belloni, T., & Cabanac, C. 2010, MNRAS, 403, 61 [NASA ADS] [CrossRef] [Google Scholar]
  21. Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
  22. Eikenberry, S. S., Fischer, W. J., Egami, E., & Djorgovski, S. G. 2001, ApJ, 556, 1 [NASA ADS] [CrossRef] [Google Scholar]
  23. Fender, R. P. 2001, MNRAS, 322, 31 [NASA ADS] [CrossRef] [Google Scholar]
  24. Giannios, D., & Spruit, H. C. 2006, A&A, 450, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Goldwurm, A., Israël, D., Goldoni, P., et al. 2001, in AIP Conf. Ser., 587, Gamma 2001: Gamma-Ray Astrophysics, eds. S. Ritz, N. Gehrels, & C. R. Shrader, 61 [Google Scholar]
  26. Gourgouliatos,K. N., & Komissarov, S. S. 2018, Nat. Astron., 2, 167 [NASA ADS] [CrossRef] [Google Scholar]
  27. Grimm, H. J., Gilfanov, M., & Sunyaev, R. 2002, A&A, 391, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Güver, T., & Özel, F. 2009, MNRAS, 400, 2050 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hardcastle, M. J. 2005, A&A, 434, 35 [CrossRef] [EDP Sciences] [Google Scholar]
  30. Hardee, P. E. 2000, ApJ, 533, 176 [Google Scholar]
  31. Hardee, P. E. 2011, in IAU Symp., 275, 41 [Google Scholar]
  32. Heindl, W. A., & Smith, D. M. 2002, ApJ, 578, L125 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hirsch, M., Pottschmidt, K., Smith, D., et al. 2020, A&A, 636, A51 [CrossRef] [EDP Sciences] [Google Scholar]
  34. Hjellming, R. M., & Johnston, K. J. 1981, ApJ, 246, L141 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hjellming, R. M., & Rupen, M. P. 1995, Nature, 375, 464 [NASA ADS] [CrossRef] [Google Scholar]
  36. Katz, J. I. 1973, Nat. Phys. Sci., 246, 87 [NASA ADS] [CrossRef] [Google Scholar]
  37. Keck, J. W., Craig, W. W., Hailey, C. J., et al. 2001, ApJ, 563, 301 [NASA ADS] [CrossRef] [Google Scholar]
  38. King, A. R., Frank, J., Kolb, U., & Ritter, H. 1997, ApJ, 482, 919 [NASA ADS] [CrossRef] [Google Scholar]
  39. Larwood, J. 1998, MNRAS, 299, L32 [NASA ADS] [CrossRef] [Google Scholar]
  40. Larwood, J. D. 1997, MNRAS, 290, 490 [NASA ADS] [Google Scholar]
  41. Lin, D., Smith, I. A., Liang, E. P., et al. 2000, ApJ, 532, 548 [NASA ADS] [CrossRef] [Google Scholar]
  42. Liska, M., Hesp, C., Tchekhovskoy, A., et al. 2018, MNRAS, 474, L81 [NASA ADS] [CrossRef] [Google Scholar]
  43. Lucke, P. B. 1978, A&A, 64, 367 [NASA ADS] [Google Scholar]
  44. Luque-Escamilla, P. L., Martí, J., & Muñoz-Arjonilla, Á. J. 2014, ApJ, 797, L1 [NASA ADS] [CrossRef] [Google Scholar]
  45. Luque-Escamilla, P. L., Martí, J., & Martínez-Aroza, J. 2015, A&A, 584, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Maccarone, T. J. 2002, MNRAS, 336, 1371 [NASA ADS] [CrossRef] [Google Scholar]
  47. Main, D. S., Smith, D. M., Heindl, W. A., et al. 1999, ApJ, 525, 901 [NASA ADS] [CrossRef] [Google Scholar]
  48. Marti, J., Mereghetti, S., Chaty, S., et al. 1998, A&A, 338, L95 [Google Scholar]
  49. Martí, J., Mirabel, I. F., Rodríguez, L. F., & Smith, I. A. 2002, A&A, 386, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Martí, J., Luque-Escamilla, P. L., Romero, G. E., Sánchez-Sutil, J. R., & Muñoz-Arjonilla, Á. J. 2015, A&A, 578, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Martí, J., Luque-Escamilla, P. L., & Muñoz-Arjonilla, Á. J. 2016, A&A, 596, A46 [CrossRef] [EDP Sciences] [Google Scholar]
  52. Martí, J., Luque-Escamilla, P. L., Bosch-Ramon, V., & Paredes, J. M. 2017, Nat. Commun., 8, 1757 [NASA ADS] [CrossRef] [Google Scholar]
  53. McConnell, M., Bennett, K., Bloemen, H., et al. 1996, A&AS, 120, 149 [Google Scholar]
  54. Mereghetti, S., Caraveo, P., Bignami, G. F., & Belloni, T. 1992, A&A, 259, 205 [Google Scholar]
  55. Mereghetti, S., Belloni, T., & Goldwurm, A. 1994, ApJ, 433, L21 [NASA ADS] [CrossRef] [Google Scholar]
  56. Mereghetti, S., Cremonesi, D. I., Haardt, F., et al. 1997, ApJ, 476, 829 [NASA ADS] [CrossRef] [Google Scholar]
  57. Migliori, G., Corbel, S., Tomsick, J. A., et al. 2017, MNRAS, 472, 141 [CrossRef] [Google Scholar]
  58. Mirabel, I. F., Rodríguez, L. F., Cordier, B., Paul, J., & Lebrun, F. 1992, Nature, 358, 215 [NASA ADS] [CrossRef] [Google Scholar]
  59. Mizuno, Y., Lyubarsky, Y., Nishikawa, K.-I., & Hardee, P. E. 2012, ApJ, 757, 16 [Google Scholar]
  60. Motta, S. E., Casella, P., & Fender, R. P. 2018, MNRAS, 478, 5159 [NASA ADS] [CrossRef] [Google Scholar]
  61. Muñoz-Arjonilla, A. J., Martí, J., Luque-Escamilla, P. L., et al. 2010, A&A, 519, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Natarajan, P., & Armitage, P. J. 1999, MNRAS, 309, 961 [CrossRef] [Google Scholar]
  63. Nixon, C., & King, A. 2013, ApJ, 765, l7 [Google Scholar]
  64. Ogilvie, G. I., & Dubus, G. 2001, MNRAS, 320, 485 [NASA ADS] [CrossRef] [Google Scholar]
  65. Paczyǹski, B. 1977, ApJ, 216, 822 [NASA ADS] [CrossRef] [Google Scholar]
  66. Papaloizou, J., & Lin, D. 1995, ApJ, 318 [Google Scholar]
  67. Papaloizou, J., & Pringle, J. E. 1977, MNRAS, 181, 441 [NASA ADS] [CrossRef] [Google Scholar]
  68. Papaloizou, J. C. B., & Terquem, C. 1995, MNRAS, 274, 987 [NASA ADS] [Google Scholar]
  69. Perucho, M. 2012, in Int. J. Mod. Phys. Conf. Ser., 241, 8 [Google Scholar]
  70. Pfeiffer, H. P., & Lai, D. 2004, ApJ, 604, 766 [NASA ADS] [CrossRef] [Google Scholar]
  71. Pottschmidt, K., Chernyakova, M., Zdziarski, A. A., et al. 2006, A&A, 452, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Predehl, P., & Schmitt, J. H. M. M. 1995, A&A, 293, 889 [NASA ADS] [Google Scholar]
  73. Reynoso, E. M., Dubner, G., Giacani, E., Johnston, S., & Green, A. J. 2006, A&A, 449, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Rodríguez, L. F., Mirabel, I. F., & Martí, J. 1992, ApJ, 401, L15 [NASA ADS] [CrossRef] [Google Scholar]
  75. Rothstein, D. M., Eikenberry, S. S., Chatterjee, S., et al. 2002, ApJ, 580, L61 [NASA ADS] [CrossRef] [Google Scholar]
  76. Schandl, S., & Meyer, F. 1994, A&A, 289, 149 [NASA ADS] [Google Scholar]
  77. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  78. Smith, D. M., Heindl, W. A., & Swank, J. H. 2002, ApJ, 578, L129 [NASA ADS] [CrossRef] [Google Scholar]
  79. Soria, R., Broderick, J. W., Hao, J., et al. 2011, MNRAS, 415, 410 [NASA ADS] [CrossRef] [Google Scholar]
  80. Staubert, R., Klochkov, D., Vasco, D., et al. 2013, A&A, 550, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Sunyaev, R., Churazov, E., Gilfanov, M., et al. 1991, A&A, 247, L29 [Google Scholar]
  82. Tauris, T. M., & van den Heuvel, E. P. J. 2006, Formation and Evolution of Compact Stellar X-ray Sources, eds W. H. G. Lewin, & M. van der Klis, 623 [CrossRef] [Google Scholar]
  83. Wilkins, D. C. 1972, Phys. Rev. D, 5, 814 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Twin-jet kinematic model for GRS 1758–258 radio jets.

In the text

All Figures

thumbnail Fig. 1

Attempt to fit the large-scale radio jets of GRS 1758–258 jets at different epochs using the theoretical kinematic model of Hjellming & Johnston (1981). Horizontal bar shows the scale size and the synthesised beam is on the left-down corner. The vertical scale is expressed in units of the root mean squared noise of each radio map that amounts to 9.3, 8.2, 10.7, 16.0, 7.3, and 4.5 μJy beam−1 for the different epochs, respectively. North is up and east is left.
In the text
thumbnail Fig. 2

Precession period for GRS 1758–258 as a function of the spin parameter. The outer non-dimensional radius of the disc is taken to be ξout = 1000ξms. Different lines correspond to the different power-law slopes of the disc surface density (red-continuous for s = 0; blue-dashed for s = −1, and black-dotted for s = −2). The grey-dotted horizontal line marks the estimated period of precession of approximately 7.5 yr, while the magenta-dotted line marks the 18.48 days precession period proposed in Martí et al. (2016).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.