| Issue |
A&A
Volume 642, October 2020
|
|
|---|---|---|
| Article Number | L18 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202038652 | |
| Published online | 22 October 2020 | |
Letter to the Editor
The messy merger of a large satellite and a Milky Way-like galaxy⋆
Kapteyn Astronomical Institute, University of Groningen, Landleven 12, 9747 AD Groningen, The Netherlands
e-mail: koppelman@astro.rug.nl
Received:
13
June
2020
Accepted:
17
September
2020
Aims. About 10 billion years ago the Milky Way merged with a massive satellite, Gaia-Enceladus. To gain insight into the properties of its debris we analyse in detail a suite of simulations that includes an experiment that produces a good match to the kinematics of nearby halo stars inferred from Gaia data.
Methods. We compare the kinematic distributions of stellar particles in the simulations and study the distribution of debris in orbital angular momentum, eccentricity, and energy, and its relation to the mass loss history of the simulated satellite.
Results. We confirm that Gaia-Enceladus probably fell in on a retrograde, 30° inclination orbit. We find that while 75% of the debris in our preferred simulation has high eccentricity (> 0.8), roughly 9% has eccentricity lower than 0.6. Star particles lost early have large retrograde motions, and a subset of these have low eccentricity. Such stars would be expected to have lower metallicities as they stem from the outskirts of the satellite, and hence naively they could be confused with debris associated with a separate system. These considerations seem to apply to some of the stars from the postulated Sequoia galaxy.
Conclusions. When a massive disc galaxy undergoes a merger event, it leaves behind debris with a complex phase-space structure, a wide range of orbital properties, and a range of chemical abundances. Observationally, this results in substructures with very different properties, which can be misinterpreted as implying independent progeny. Detailed chemical abundances of large samples of stars and tailored hydrodynamical simulations are critical to resolving such conundrums.
Key words: Galaxy: formation / Galaxy: halo / Galaxy: kinematics and dynamics / solar neighborhood / galaxies: interactions
Movies associated to Fig. 4 are available at https://www.aanda.org
© ESO 2020
1. Introduction
The ultimate goal of Galactic archaeology is to determine the series of events that have led to the formation of the Milky Way. The arrival of the full phase-space dataset of Gaia (Gaia Collaboration 2016, 2018; Katz et al. 2019) has resulted in many insights that have given a boost to this field. One of these insights is that the local stellar halo formed predominantly through a merger with a massive dwarf galaxy named Gaia-Enceladus (Helmi et al. 2018, or Gaia-Sausage, Belokurov et al. 2018).
It remains unclear, however, which other objects on retrograde orbits have contributed debris to the local stellar halo. Although several smaller retrograde structures have been found that appear to be chemically and dynamically different from Gaia-Enceladus (e.g. Koppelman et al. 2018; Mackereth et al. 2019; Matsuno et al. 2019; Myeong et al. 2019), their origin and linkage are not always clear. For example, Myeong et al. (2019) advocate that several of these structures originate in a single (moderately) massive dwarf galaxy: Sequoia. However, Koppelman et al. (2019) based on their chemistry and orbital properties, suggest that there must be at least two progenitors for the structures.
The debris of a low-mass satellite orbiting in a static potential phase-mixes at roughly constant mean orbital energy (Helmi & White 1999). This makes the integrals of motion powerful tools to identify halo structures and determine the accretion history (Helmi & de Zeeuw 2000; McMillan & Binney 2008). For massive satellites, this picture becomes muddled because of dynamical friction and the tidal interaction between the satellite and host (see e.g. Jean-Baptiste et al. 2017). Dynamical friction is relevant for mergers of a (close to) equal mass-ratio. It affects the mean orbit of a satellite and makes it sink to the centre of the host (Quinn & Goodman 1986). Since a satellite is stripped of its mass mostly in discrete events at its orbital pericentre (and this evolves because of dynamical friction), the result is a complex energy distribution of the debris. For example, the material from the satellite’s outskirts is lost early and hence has high orbital energy. On the other hand, its core sinks to the centre becoming more bound (Tormen et al. 1998; Van Den Bosch et al. 1999). Furthermore, massive satellites with disc-like morphology produce very complex tidal features (Quinn 1984) which must give rise to an intricate structure of the remaining debris. These considerations are pertinent for understanding the left-overs from a system like Gaia-Enceladus.
Further complexity is expected from the chemical perspective, since dwarf galaxies also display chemical gradients (e.g. Kirby et al. 2011; Ho et al. 2015). These gradients are typically negative with radius because the star-formation-rate in the centre of galaxies is more intense due to higher gas density. Moreover, star-formation in the outskirts may be quenched first because this is where gas is stripped more easily. This means that merger debris should probably also reveal chemical gradients. Such a gradient has been found for Sagittarius (Ibata et al. 1994) as its streams have older stellar populations (Bellazzini et al. 2006), and are more metal-poor by ∼0.7 dex than the core (see Dohm-Palmer et al. 2001; Martinez-Delgado et al. 2004; Chou et al. 2007; Hayes et al. 2020 for more references).
Motivated by the above considerations, in this Letter we use numerical simulations to study the dynamical gradients that naturally occur in mergers of massive satellites. The results are particularly important to interpret the debris of Gaia-Enceladus and its relation to the other substructures discovered in the halo, such as the Sequoia galaxy.
2. Methods
We analysed the merger simulations of Villalobos & Helmi (2008, 2009) that originally were designed to study the establishment of a thick disc through heating of a thin disc by a merger. The simulation suite comprises a set of 1:10 and 1:5 mass-ratio mergers of varying orbital inclination, and of spheroidal and discy satellites. After the merger, part of the host’s disc is heated to a plausible thick disc. At the same time, a significant fraction of the original disc (15 − 25%) remains thin and cold. We focus on these simulations because Helmi et al. (2018) noted that the kinematic distribution of the satellite in one of the experiments (denoted here as r30) matches very closely that of nearby Gaia-Enceladus stars.
Since the host galaxy in the simulations is smaller than the Milky Way, and to facilitate comparison to observations, we scale the velocities such that the rotational velocity of the simulated disc at the solar position vϕ, ⊙, sim corresponds to that measured for the Milky Way’s thick disc (vϕ, ⊙ = 170 km s−1, according to Morrison et al. 1990). Following Villalobos & Helmi (2009), we place the Sun at 2.4 RD, and we scale the velocities by the factor vϕ, ⊙/vϕ, ⊙, sim. For example, for the experiment r30, RD ≈ 2.16 kpc (see Fig. 14 of Villalobos & Helmi 2008), vϕ, ⊙, sim∼132 km s−1, and the scaling factor is ∼1.3.
The top left panel of Fig. 1 shows the velocity distribution of a sample of halo stars in Gaia DR2 (see Appendix A.1 for details). Halo stars with vϕ < 75 km s−1 (to the left of the dashed line) are shown as blue dots. For illustrative purposes, we indicate the location of the thin disc with a random subset of 50 000 stars (black dots). The remaining panels in Fig. 1 show the velocity distributions for all the 1:5 mass-ratio simulations, with the stellar particles from the host in black and those from the satellite in blue for discy and red for spheroidal progenitors. These particles are located inside a volume of 2.5 kpc radius centred on the equivalent solar position at the end of the simulations, i.e. 4 Gyr after infall. Because of particle resolution limitations this volume is relatively large compared to that used for the data, especially because it has not been scaled.
 |
Fig. 1. Velocity distribution of the local (< 1 kpc) stellar halo using Gaia data (large panel) and in the Villalobos & Helmi (2008) simulations, where the small panels indicate the orbital inclination (0°, 30° or, 60°) and whether the merger was prograde or retrograde. Stellar particles from the discy (spherical) satellites are shown in blue (red). The distinct velocity distributions of these stars betray the progenitor’s properties and the merger geometry. |
As reported in Helmi et al. (2018), the arch seen in the Gaia data and shown in the top left panel of Fig. 1 is clearly reproduced in the discy simulation with the panel r30, suggesting that the progenitor of Gaia-Enceladus was discy and merged on a retrograde orbit of ∼30° inclination. However, because this simulation was only run for 4 Gyr, to establish the robustness of this conclusion and the arch’s origin we have integrated the simulation for a total of 10 Gyr, which is approximately the time of the merger with Gaia-Enceladus.
3. Results
3.1. Origin of the velocity arch
Figure 2 shows the velocity distribution in a representative solar volume of the r30 simulation 10 Gyr after infall. Although the shape of the distribution depends slightly on the azimuthal location of the volume (because the remnant thick disc in the simulations is somewhat triaxial), the arch structure in velocity space is seen to persist in time. This implies that the conclusions that are drawn on the basis of Fig. 1 still stand.
 |
Fig. 2. Velocity distribution for the discy r30 simulation 10 Gyr after infall. The stellar particles are coloured according to their final eccentricity (left) and energy (Ef, right). The extended arch-like structure (with very negative vϕ) is persistent in time (cf. Fig. 1). |
To characterise the arch we have coloured the stars in Fig. 2 by their final eccentricity e (left panel) and orbital energy Ef (right panel), see Appendix B for details. We note the wide range of values for both quantities and how they appear to correlate with the velocities, although not perfectly. Since its discovery, Gaia-Enceladus has been conflated with stars on very eccentric (e ≳ 0.8) orbits (e.g. Belokurov et al. 2018; Mackereth et al. 2019). Even though this might be true for most of the stars, we find that it is not necessarily true for all of its debris. Roughly 75% of the stars end up on orbits of e > 0.8, while ∼9% have eccentricities e < 0.6.
Figure 3 shows the link between the local structure in velocity space (left) and the orbital properties of all of the debris in e − Lz space. The latter is a function of velocity (Lz = Rvϕ) and is an integral of motion often used to identify Gaia-Enceladus’ debris (e.g. Helmi et al. 2018; Matsuno et al. 2019; Massari et al. 2019). The satellite’s debris displays a large amount of substructure, as shown in the panels on the right, which is clearly linked to that present in velocity space in the solar volume. For example, the arch in velocity space appears to be the local manifestation of the large retrograde structures marked in the middle and bottom rows of Fig. 3. On the other hand, the top row of this figure shows that some stars have relatively prograde angular momentum despite the initially retrograde orbit of the satellite.
 |
Fig. 3. Velocity distribution in a solar volume (left, same as in Fig. 2) and distribution of e − Lz of all satellite stellar particles (right) both at t = 10 Gyr. The colours indicate the location of various selections made in e − Lz following the three clear ridges identifiable in this space. |
We investigate the origin of the structures in e − Lz space in Fig. 4, where we plot the spatial evolution of the satellite between 1–1.7 Gyr after infall. In the first panel (at t ∼ 1 Gyr) most of the satellite’s dark matter has been lost, but the stellar component remains largely bound. A significant fraction of the stars are lost during the second pericentric passage (or shortly after) which takes place at t ∼ 1.5 Gyr (Villalobos & Helmi 2008). The core (traced largely by the magenta points) continues to spiral inwards for two to three more passages, and then fully dissolves. During this process it couples more strongly to the disc and becomes more prograde (as we saw in the top right panel of Fig. 3). To appreciate the high complexity of the mass loss process, an animation of Fig. 4 is made available online.
 |
Fig. 4. Evolution of the satellite around the time of the second pericentric passage, which takes place at t ≈ 1.5 Gyr. The colours distinguish the three structures identified in the final orbital distribution of the debris (see Fig. 3) and evidence the complexity of the mass loss process. This is clearly seen in the bottom two panels, which zoom in on the satellite at two specific times, and where its spin is indicated by a curled arrow. |
When cold rotationally supported disc galaxies merge they produce complex tidal tails (Toomre & Toomre 1972; Eneev et al. 1973; Quinn 1984; Barnes 1988). These tidal tails can be quite different from those originating in spherical dispersion-supported systems. This is also what we find in our simulations, as shown in Fig. 4. The bottom row of this figure zooms in on the discy satellite and reveals that some of the stars in green (i.e. the ridge in the bottom panel of Fig. 3), are lost first. These are followed by some stars in cyan with lower final eccentricity and slightly less retrograde motions since they are part of the ridge in the middle panel of Fig. 3. We also see that there is some alternation in green and cyan stars amongst the material that becomes unbound slightly later.
Since a discy satellite has internal and orbital angular momentum, mass loss depends on the exact configuration of the merger (e.g. inclination, spin) and not only on the internal binding energy of the stars as in the case of a spheroidal system. For example, the presence of a single extended counter-tail can be explained by the alignment of the spins of the two galaxies (Struck & Smith 2012), i.e. although the secondary moves on a retrograde orbit, its sense of rotation is prograde with respect to the primary. A difference in eccentricity also arises from these additional degrees of freedom. For a given internal binding energy stars have a range of internal angular momenta, which translates in debris with high and low orbital angular momentum, resulting respectively in more circular and more radial final orbits (the latter being typical of shell-like features).
In addition to these effects, dynamical friction causes the satellite’s core to spiral inwards. This enhances the prominence of the only tidal arm apparent in Fig. 4, which trails behind the core.
3.2. Some implications
We have just shown that the stars in the velocity arch constitute debris lost early on in the merger. This probably also has implications for the chemical abundances of its stars since dwarf galaxies are known to possess metallicity gradients. For M⋆ ∼ 109.6 M⊙ the gradients have an amplitude ∼ − 0.064 dex kpc−1 according to Ho et al. (2015). Thus, if Gaia-Enceladus had a physical extent of 5 kpc, this could imply a metallicity difference of 0.32 dex between its centre and outskirts.
Myeong et al. (2019) studied some of the stars in the velocity arch, and argued that these stars, together with other retrograde stars, were part of a different accreted galaxy that they named Sequoia. These authors have shown that the stars are more metal poor on average than the debris of Gaia-Enceladus by ∼0.30 dex, which suggests they formed in an object that is ten times smaller (Matsuno et al. 2019). However, an alternative explanation supported by our simulations is that these stars (or some of them) come from the outskirts of Gaia-Enceladus, and their lower metallicities could be explained as being due to internal gradients in Gaia-Enceladus. The lower values of [Mg/Fe] and [Ca/Fe] at similar [Fe/H] in comparison to Gaia-Enceladus reported by Matsuno et al. (2019) could also be due to the typically lower star formation rates found in the outskirts of sizeable galaxies.
This interpretation is tentatively supported by Fig. 5 where we plot [Mg/Fe] versus [Fe/H] for members of Gaia-Enceladus and Sequoia, coloured by their orbital energy E. The chemical abundances are from a cross-match of Gaia DR2 with APOGEE DR16 (Ahumada et al. 2020), using the membership criteria described in Koppelman et al. (2019) (see Appendix A for details). This figure shows that most Sequoia stars are accompanied by a star from Gaia-Enceladus that has very similar orbital energy and chemical abundance values, making it difficult to argue on the basis of this data that the stars have a different origin.
 |
Fig. 5. Chemical abundances for stars in Gaia-Enceladus and Sequoia, identified using selection criteria from Koppelman et al. (2019). The stars are coloured by their orbital energy calculated in the McMillan (2017) potential implemented in AGAMA. The background shows the location of the disc-stars in this diagram with a 2D-histogram. The histogram is coloured by the logarithm of the stars per bin. |
4. Conclusions
We have analysed simulations of the merger between a Milky Way-like galaxy and a massive satellite. On the basis of comparisons to the kinematics of stars in the nearby halo, we confirm the conclusions by Helmi et al. (2018) that the most likely progenitor of Gaia-Enceladus was a discy dwarf galaxy that fell in on a retrograde orbit of ∼30° inclination.
Because of the relative mass of the dwarf galaxy (which implies that it was subject to dynamical friction), and its initial configuration (a cold, rotationally supported disc), its debris shows a rather intricate morphology, quite different from that usually associated with small, spherical, non-rotating satellites. Star particles are found to have a broad range of orbital eccentricities, with 75% having e > 0.8 and 9% e < 0.6. We also find that even though the initial orbital motion of the satellite is very retrograde, some of its debris ends up on prograde orbits. Low-eccentricity and prograde stars originate in the core of the satellite that has sunk in via dynamical friction. We can conclude that a large amount of information about the merger remains encoded in the phase-space structure of the debris.
Because large galaxies have chemical gradients, different portions of the debris may reveal different chemistry. This complicates the interpretation, and can possibly mimic what might be expected for debris from an independent system. For example, some of the stars in the arch (which according to our simulations corresponds to debris that is lost early and forms shells) are dynamically similar to those that have been associated with Sequoia. The abundances of Sequoia stars do not appear to differ much from highly energetic or less bound (and hence potentially lost early) stars from Gaia-Enceladus.
Taken at face value, the simulation predicts that the core of the Gaia-Enceladus dwarf should be found on a mildly prograde, lower eccentricity orbit. However, this prediction depends strongly on whether the configuration of the merger is matched in detail by the simulations. In particular, the simulated host galaxy has a fixed size, which is unrealistic for the Milky Way, which in the last 10 Gyr has grown a very significant cold disc. Simulations with varying orientation of the discs’ angular momentum vectors, and including gas and star formation physics are necessary to fully exploit the data that is currently available, and that which will be collected in the context of upcoming spectroscopic surveys like WEAVE (Dalton et al. 2012), 4MOST (de Jong et al. 2012), SDSS-V (Kollmeier et al. 2017), and DESI (DESI Collaboration 2016). Such a combined approach seems to be necessary as a massive satellite can give rise to substructures that appear to be both chemically and dynamically distinct.
Movies
Movie of Fig. 4 Access here
Movie of Fig. 4 Access here
Movie of Fig. 4 Access here
Movie of Fig. 4 Access here
Acknowledgments
We are grateful to the referee, Curtis Struck, for the constructive report that helped in clarifying the manuscript. This work has been financially supported from a Vici grant and a Spinoza Prize from NWO. We have made use of data from the European Space Agency (ESA) mission Gaia (http://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, http://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. In the analysis, the following software packages have been used: vaex (Breddels & Veljanoski 2018), numpy (Van Der Walt et al. 2011), matplotlib (Hunter 2007), jupyter notebook (Kluyver et al. 2016), pyGadgetReader (Thompson 2014).
References
- Ahumada, R., Allende Prieto, C., Almeida, A., et al. 2020, ApJS, 249, 21 [Google Scholar]
- Barnes, J. E. 1988, ApJ, 331, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M., Newberg, H. J., Correnti, M., Ferraro, F. R., & Monaco, L. 2006, A&A, 457, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belokurov, V., Erkal, D., Evans, N. W., Koposov, S. E., & Deason, A. J. 2018, MNRAS, 478, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Breddels, M. A., & Veljanoski, J. 2018, A&A, 618, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chou, M.-Y., Majewski, S. R., Cunha, K., et al. 2007, ApJ, 670, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Dalton, G., Trager, S. C., Abrams, D. C., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, eds. I. S. McLean, S. K. Ramsay, & H. Takami, Int. Soc. Opt. Photon., 8446, 84460P [CrossRef] [Google Scholar]
- de Jong, R. S., Bellido-Tirado, O., Chiappini, C., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, eds. I. S. McLean, S. K. Ramsay, & H. Takami, Int. Soc. Opt. Photon., 8446, 84460T [Google Scholar]
- DESI Collaboration (Aghamousa, A., et al.) 2016, ArXiv e-prints [arXiv:1611.00036] [Google Scholar]
- Dohm-Palmer, R. C., Helmi, A., Morrison, H., et al. 2001, ApJ, 555, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Eneev, T. M., Kozlov, N. N., & Sunyaev, R. A. 1973, A&A, 22, 41 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayes, C. R., Majewski, S. R., Hasselquist, S., et al. 2020, ApJ, 889, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., & de Zeeuw, P. T. 2000, MNRAS, 319, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., & White, S. D. M. 1999, MNRAS, 307, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, I.-T., Kudritzki, R.-P., Kewley, L. J., et al. 2015, MNRAS, 448, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Jean-Baptiste, I., Di Matteo, P., Haywood, M., et al. 2017, A&A, 604, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, D., Sartoretti, P., Cropper, M., et al. 2019, A&A, 622, A205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirby, E. N., Lanfranchi, G. A., Simon, J. D., Cohen, J. G., & Guhathakurta, P. 2011, ApJ, 727, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, Jupyter Notebooks-A Publishing Format for Reproducible Computational Workflows (IOS Press) [Google Scholar]
- Kollmeier, J. A., Zasowski, G., Rix, H. W., et al. 2017, ArXiv e-prints [arXiv:1711.03234] [Google Scholar]
- Koppelman, H. H., Helmi, A., & Veljanoski, J. 2018, ApJ, 860, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Koppelman, H. H., Helmi, A., Massari, D., Price-Whelan, A. M., & Starkenburg, T. K. 2019, A&A, 631, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L. 2018, Re-normalising the Astrometric Chi-square in Gaia DR2, Tech. rep. [Google Scholar]
- Mackereth, J. T., Schiavon, R. P., Pfeffer, J., et al. 2019, MNRAS, 482, 3426 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Delgado, D., Gomez-Flechoso, M. A., Aparicio, A., & Carrera, R. 2004, ApJ, 601, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuno, T., Aoki, W., & Suda, T. 2019, ApJ, 874, L35 [NASA ADS] [CrossRef] [Google Scholar]
- McMillan, P. J. 2017, MNRAS, 94, 76 [NASA ADS] [CrossRef] [Google Scholar]
- McMillan, P. J., & Binney, J. J. 2008, MNRAS, 390, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, H. L., Flynn, C., & Freeman, K. C. 1990, AJ, 100, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Myeong, G. C., Vasiliev, E., Iorio, G., Evans, N. W., & Belokurov, V. 2019, MNRAS, 488, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Quinn, P. J. 1984, ApJ, 279, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Quinn, P. J., & Goodman, J. 1986, ApJ, 309, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Struck, C., & Smith, B. J. 2012, MNRAS, 422, 2444 [CrossRef] [Google Scholar]
- Thompson, R. 2014, Astrophysics Source Code Library [record ascl:1411.001] [Google Scholar]
- Toomre, A., & Toomre, J. 1972, ApJ, 178, 623 [Google Scholar]
- Tormen, G., Diaferio, A., & Syer, D. 1998, MNRAS, 299, 728 [Google Scholar]
- Van Den Bosch, F. C., Lewis, G. F., Lake, G., & Stadel, J. 1999, ApJ, 515, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [CrossRef] [Google Scholar]
- Vasiliev, E. 2019, MNRAS, 482, 1525 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos, A., & Helmi, A. 2008, MNRAS, 391, 1806 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos, A., & Helmi, A. 2009, MNRAS, 399, 166 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Observational datasets used
A.1. RVS sample
In Fig. 1 we use the subset with full phase-space information from Gaia DR2 as comparison and to interpret the simulations. The dataset, known as the RVS sample, contains 7 224 631 stars. We only consider stars with parallax_over_error > 5, parallax > 1.0 mas, and RUWE < 1.4 (see Lindegren 2018), which leaves 2 784 095 sources.
For this set of stars, we calculate cylindrical space velocities using the transformations implemented in vaex (Breddels & Veljanoski 2018). We place the Sun at X = −8.2 kpc, correct for the motion of the local standard of rest (LSR) using vLSR = 232.8 km s−1 (both based on McMillan 2017), and for the solar motion with respect to the LSR using (U⊙, V⊙, W⊙) = (11.1, 12.24, 7.25) km s−1 (Schönrich et al. 2010). Finally, we use a kinematic selection to filter stars from the disc. All the stars with |V − VLSR|< 210 km s−1 are removed. The resulting set of stars comprises 5371 sources that we label as halo stars.
A.2. Known halo structures and their abundances
The structures that are shown in Fig. 5 originate from Koppelman et al. (2019). In summary, the selection criteria for stars belonging to Gaia-Enceladus and Sequoia are defined as follows:
-
Gaia-Enceladus: −1.5 < En < −1.1 in units of [105 km2 s−2] and −0.20 < circ < 0.13;
-
Sequoia: −1.35 < En < −1.0 in units of [105 km2 s−2] and −0.65 < circ < −0.4.
Here, En is the total energy, using the McMillan (2017) potential and circ is the circularity, defined as 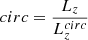 , where
, where 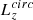 is the angular momentum of a circular orbit with the same energy as Lz. The circularity parameter ranges from −1 to 1 and indicates how circular an orbit is.
is the angular momentum of a circular orbit with the same energy as Lz. The circularity parameter ranges from −1 to 1 and indicates how circular an orbit is.
The abundances shown in the figure come from a cross-match of Gaia DR2 with APOGEE DR16 (Ahumada et al. 2020). Following the work of Hayes et al. (2020), we filter stars with STARFLAG bitmask values of 0, 3, or 4 and ASPCAPFLAG bitmask values of 10 or 23. Furthermore, we only show stars with VERR < 0.2, SNR > 70, and TEFF > 3700, where SNR is the catalogue parameter for the signal-to-noise ratio.
Appendix B: Computation of the orbital parameters for the simulations
To calculate orbital properties (i.e. energy and eccentricity) we fit a static potential to the simulation snapshot at t = 10 Gyr after infall. In this snapshot, the debris of the satellite is sufficiently mixed for the whole system to be approximated by a smooth rigid potential.
We fit the potential with AGAMA (Vasiliev 2019) using a Multipole expansion to approximate each component (dark matter and stellar) of both the host and satellite separately. For the flattened stellar particle distributions we set gridsizeR = gridsizez = 50, mmax = 5, and lmax = 25. We tested using a CylSpline for the flattened stellar systems, but found the Multipole to reproduce the density profile better. The dark matter profile of the host is forced to be spherically symmetric; the other profiles are allowed to be triaxial.
The energy of the particles is computed for this potential at this same time, t = 10 Gyr, and labelled (Ef), as is the angular momentum Lz. The eccentricity is derived by integrating the orbits of the stellar particles for 20 Gyr in this same potential, and is defined as e = (apo − peri)/(apo + peri).
All Figures
 |
Fig. 1. Velocity distribution of the local (< 1 kpc) stellar halo using Gaia data (large panel) and in the Villalobos & Helmi (2008) simulations, where the small panels indicate the orbital inclination (0°, 30° or, 60°) and whether the merger was prograde or retrograde. Stellar particles from the discy (spherical) satellites are shown in blue (red). The distinct velocity distributions of these stars betray the progenitor’s properties and the merger geometry. |
| In the text | |
 |
Fig. 2. Velocity distribution for the discy r30 simulation 10 Gyr after infall. The stellar particles are coloured according to their final eccentricity (left) and energy (Ef, right). The extended arch-like structure (with very negative vϕ) is persistent in time (cf. Fig. 1). |
| In the text | |
 |
Fig. 3. Velocity distribution in a solar volume (left, same as in Fig. 2) and distribution of e − Lz of all satellite stellar particles (right) both at t = 10 Gyr. The colours indicate the location of various selections made in e − Lz following the three clear ridges identifiable in this space. |
| In the text | |
 |
Fig. 4. Evolution of the satellite around the time of the second pericentric passage, which takes place at t ≈ 1.5 Gyr. The colours distinguish the three structures identified in the final orbital distribution of the debris (see Fig. 3) and evidence the complexity of the mass loss process. This is clearly seen in the bottom two panels, which zoom in on the satellite at two specific times, and where its spin is indicated by a curled arrow. |
| In the text | |
 |
Fig. 5. Chemical abundances for stars in Gaia-Enceladus and Sequoia, identified using selection criteria from Koppelman et al. (2019). The stars are coloured by their orbital energy calculated in the McMillan (2017) potential implemented in AGAMA. The background shows the location of the disc-stars in this diagram with a 2D-histogram. The histogram is coloured by the logarithm of the stars per bin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


