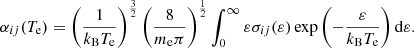EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 642 (October 2020) A&A, 642 (2020) A185 Full HTML
Free Access
Issue
A&A
Volume 642, October 2020
Article Number A185
Number of page(s) 6
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202038266
Published online 20 October 2020

© ESO 2020

1. Introduction

Silicon is the seventh most abundant element in the Universe and the second most abundant element on Earth. Modeling of the silicon emission in astrophysical or laboratory plasmas requires reliable atomic data. The structure of the emission spectra is defined by a charge state distribution in the plasma. Electron-impact ionization along with the radiative and dielectronic recombination define the charge state distribution in the collisionally ionized plasma, such as those formed in the stellar coronae, supernova remnants, galaxies, and the intracluster medium of galaxy clusters. Multiple ionization is important for systems that are suddenly exposed to an abundance of energetic electrons (Müller 1986; Hahn & Savin 2015). On the other hand, the study of multiple ionization is quite complicated (Pindzola et al. 2007; Colgan & Pindzola 2012; Jonauskas et al. 2014; Liu et al. 2018) since it has to deal with the four-body Coulomb problem.

Electron-impact single-ionization cross sections for Si+ were measured and analyzed by Djurić et al. (1993). The semiempirical Lotz formula (Lotz 1968) was adopted to determine the fraction of metastable ions in the parent beam. Additional assessments were taken to eliminate contamination from the N 2 + $ ^{+}_{2} $ and CO+ ions in experimental data since these ions have the same mass-to-charge ratio M/q as Si2+. Theoretical values were calculated using the configuration average distorted wave (CADW) method (Pindzola et al. 1983). A good agreement of the theoretical data with measurements was obtained (Djurić et al. 1993). The study included direct and indirect processes of electron-impact single ionization. Direct ionization (DI) was investigated for the 3s and 3p subshells. The excitations from the 2p and 3s subshells to shells with the principal quantum numbers n = 4, 5 were considered for the indirect process. However, the strong 3s → 3d excitations were missing from the CADW calculations (Djurić et al. 1993). Furthermore, the excitations to the higher shells (n >  5) were not investigated in that work (Djurić et al. 1993). On the other hand, it was demonstrated that the excitations to the high-n shells have to be analyzed to determine the reliable cross sections for the excitation-autoionization (EA) process (Zhang & Kwon 2014; Jonauskas et al. 2015; Kynienė et al. 2015, 2016; Borovik et al. 2016; Jin et al. 2020). As such, a convergence of the cross sections has to be confirmed for the indirect process. The electron-impact single-ionization cross sections for the Si+ ion were later investigated by performing level-to-level distorted wave (LLDW) calculations (Dere 2007). It was noted that the LLDW values showed a fair reproduction of the Si+ cross sections; however, details of the calculations were not provided. It can be assumed that the same type of excitations that was presented in the CADW study (Djurić et al. 1993) were analyzed. The CADW study also omitted the influence of the radiative damping for the doubly excited states of the Si+ ion. The autoionization branching ratio was taken to be unity for all autoionizing configurations. The radiative damping diminishes the EA cross sections since the autoionizing states can also decay through the radiative transitions to the lower states of the Si+ ion.

Therefore, the aim of the current work is to study the electron-impact single-ionization process for the Si+ ion. Excitations to shells with 3 ≤ n ≤ 10 for EA are investigated. Radiative damping is taken into account for all levels above the single-ionization threshold of the Si+ ion. Furthermore, an influence of the correlation effects for the direct and indirect processes of the electron-impact ionization is investigated.

The rest of the paper is organized as follows. Section 2 presents a brief outline of the theoretical approach. In addition, the main channels of the direct and indirect processes are defined. In Sect. 3, the obtained results are discussed. Finally, we end with the conclusions from the present investigation.

2. Theoretical approach

The cross section for the electron-impact single ionization from level i to level f includes direct and indirect processes:

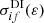σ if ( ε ) = σ if DI ( ε ) + ∑ j σ ij CE ( ε ) B jf a , $$ \begin{aligned} \sigma _{if}(\varepsilon )=\sigma ^{\mathrm{DI} }_{if}(\varepsilon )+\sum _j\sigma _{ij}^{\mathrm{CE} }(\varepsilon )B^\mathrm{a}_{jf}, \end{aligned} $$(1)

where σ if DI ( ε ) $ \sigma^{\mathrm{DI}}_{if}(\varepsilon) $ is the cross section of the direct single collisional ionization process and ε is an energy of the incident electron. The second term in Eq. (1) corresponds to the indirect process: electron-impact excitation with subsequent autoionization. Therefore, 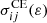σ ij CE ( ε ) $ \sigma_{ij}^{\mathrm{CE}}(\varepsilon) $ is the electron-impact excitation cross section to the intermediate level j of the initial ion, and 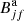B jf a $ B^{\mathrm{a}}_{jf} $ is a branching ratio for the autoionization process from level j to the final level, level f. The autoionization branching ratio diminishes cross sections of the EA process since the autoionizing levels can decay through radiative transitions to the energetically lower levels of the same ion. It defines a part of the population transferred from level j to level f by Auger transition and is expressed by the equation

B jf a = A jf a ∑ m A jm r + ∑ n A jn a , $$ \begin{aligned} B^\mathrm{a}_{jf}=\frac{A_{jf}^\mathrm{a}}{{\sum _m{A_{jm}^\mathrm{r}}}+{\sum _n{A_{jn}^\mathrm{a}}}}, \end{aligned} $$(2)

where Ar and Aa are the radiative and Auger transition probabilities, respectively. The summation in the denominator goes through all levels that can be reached by the radiative and Auger decays from level j.

The direct process studied for the Si+ ion includes collisional ionization from the 3s and 3p subshells:

[ Ne ] 3 s 2 3 p 1 + e − → [ Ne ] { 3 s 2 3 s 1 3 p 1 + 2 e − . $$ \begin{aligned} {[\rm{Ne}}] 3{{\rm{s}}^2}3{{\rm{p}}^1}\; + {{\rm{e}}^ - } \to [{\rm{Ne}}]\left\{ {\begin{array}{*{20}{l}}{3{{\rm{s}}^2}}\\{3{{\rm{s}}^1}3{{\rm{p}}^1}}\end{array} + 2{{\rm{e}}^ - }} \right.. \end{aligned} $$(3)

The collisional ionization from the 2p subshell produces ions above the double ionization threshold, and this mainly leads to states of the Si2+ ion. Therefore, the ionization from the 2p subshell was not included in the study of the single-ionization cross sections. The EA channels for the Si+ ion were determined by excitations from the 2p and 3s subshells to autoionizing levels of the produced configurations:

[ Be ] 2 p 6 3 s 2 3 p 1 + e − → [ Be ] { 2 p 5 3 s 2 3 p 2 2 p 5 3 s 2 3 p 1 3 d 1 2 p 5 3 s 2 3 p 1 n l 2 p 6 3 s 1 3 p 1 3 d 1 2 p 6 3 s 1 3 p 1 n l + e − , $$ \begin{aligned} {[\mathrm{Be}}]\,2\mathrm{p}^{6}3\mathrm{s}^{2}3\mathrm{p}^{1} + \mathrm{e}^{-} \rightarrow [\mathrm{Be}] \left\{ \begin{array}{l} 2\mathrm{p}^{5}3\mathrm{s}^{2}3\mathrm{p}^{2} \\ 2\mathrm{p}^{5}3\mathrm{s}^{2}3\mathrm{p}^{1}3\mathrm{d}^{1} \\ 2\mathrm{p}^{5}3\mathrm{s}^{2}3\mathrm{p}^{1} \; nl \\ 2\mathrm{p}^{6}3\mathrm{s}^{1}3\mathrm{p}^{1}3\mathrm{d}^{1} \\ 2\mathrm{p}^{6}3\mathrm{s}^{1}3\mathrm{p}^{1} \; nl \\ \end{array}+ \mathrm{e}^{-} \right., \end{aligned} $$(4)

where 4 ≤ n ≤ 10, l <  n, and l ≤ 5. The 3s → 3p excitation was not included in calculations since the 3s13p2 configuration is below the single-ionization threshold. Furthermore, the excitations from the 3p subshell of the ground configuration do not contribute to the single ionization since all levels of the produced configurations are below the single-ionization threshold of the Si+ ion. On the other hand, the valence shell excitations can be significant for cross sections close to the ionization threshold (Kwon & Savin 2012).

Energy levels, radiative and Auger transition probabilities, electron-impact excitation, and single-ionization cross sections were studied using Flexible Atomic Code (FAC) (Gu 2008), which implements the Dirac-Fock-Slater (DFS) approach. Continuum orbitals of the incident and scattered electrons were estimated in a potential of the ionizing ion since the obtained cross sections provide better agreement with experimental data (Djurić et al. 1993). The electron-impact excitation and ionization cross sections were investigated using the distorted wave (DW) approximation. Calculations of the single-ionization cross sections using the DW approximation usually provide a good agreement with the experimental data for highly ionized ions (Pindzola & Griffin 1997; Loch et al. 2005; Kwon & Savin 2012; Borovik et al. 2015; Jonauskas et al. 2019). It is well known that the DW approximation often overestimates the single-ionization cross sections for neutral atoms and near neutral ions. Previously, the binary-encounter-dipole (BED) and binary-encounter-Bethe (BEB) models were developed for the direct process to deal with these ionization stages (Kim & Rudd 1994). These models, with the scaled plane-wave-Born cross sections, demonstrated a good agreement with experimental data (Kim 2001; Kim & Desclaux 2002; Kwon et al. 2005, 2006). It was suggested to use the scaled DW cross sections for the atoms and low-ionization ions (Jonauskas 2018; Kynienė et al. 2019a). However, previous DW calculations of the cross sections for the single ionization in Si+ showed good agreement with the measurements (Djurić et al. 1993). Therefore, the same approximation was used in this study.

The Maxwellian rate coefficients were calculated using cross sections obtained for electron-impact direct and indirect ionization processes in the Si+ ion. The rate coefficient αij(Te) for the Maxwellian–Boltzmann electron energy distribution at electron temperature Te was determined by the equation

α ij ( T e ) = ( 1 k B T e ) 3 2 ( 8 m e π ) 1 2 ∫ 0 ∞ ε σ ij ( ε ) exp ( − ε k B T e ) d ε . $$ \begin{aligned} \alpha _{ij}(T_{\rm e}) = \left( \frac{1}{k_{\rm B}T_{\rm e}}\right)^{\frac{3}{2}}\left( \frac{8}{m_{\rm e} \pi }\right)^{\frac{1}{2}}\int _0^\infty \varepsilon \sigma _{ij}(\varepsilon ) \exp \left( -\frac{\varepsilon }{k_{\rm B}T_{\rm e}}\right)\mathrm{d}\varepsilon . \end{aligned} $$(5)

Here, kB is the Boltzmann constant and me is the electron mass.

3. Results

Energy levels of the ground configurations for the Si+, Si2+, and Si3+ ions are presented in Fig. 1. In addition, configurations corresponding to the 3s → 3d, 3s → 4l (l = 0, …, 4) excitations are shown. It can be seen that the energy levels of the 3s13p13d1, 3s13p14s1, and 3s13p14p1 configurations straddle the ionization threshold. The energy levels of the 3s13p2 configuration are below the ionization threshold and, therefore, are not presented in Fig. 1. The theoretical single-ionization threshold for the ground [Ne] 3s23p1 configuration is 15.67 eV. This is slightly below the National Institute of Standards and Technology’s (NIST) recommended value of 16.35 eV (Kramida et al. 2019). On the other hand, the same tendency for the FAC ionization thresholds compared to the NIST data were also determined for other ions (Jonauskas et al. 2015; Konceviiūtė et al., 2018; Jonauskas 2018; Kynienė et al. 2019b).

thumbnail Fig. 1.

Energy levels of the ground configurations for the Si+, Si2+, and Si3+ ions in addition to energy levels of the 3s13p13d1, 3s13p14s1, 3s13p14p1, 3s13p14d1, and 3s13p14f1 configurations. The first excited configuration of Si2+ is also presented. The red represents even configurations and the blue represents odd configurations.

Single-ionization cross sections obtained in a potential of the ionized ion are compared to the CADW calculations and experimental measurements (Djurić et al. 1993) in Fig. 2. The LLDW values are higher than the measurements on the low-energy side. On the other hand, the theoretical cross sections are lower than the experimental ones from the peak to the higher energies of the incident electron. What is more, the DI cross sections obtained using the DFS approximation are lower by approximately a factor of two compared to the CADW values. This is the main reason why the total LLDW cross sections are lower than the CADW calculations at the higher energies.

thumbnail Fig. 2.

Single-ionization cross sections for the ground level of the Si+ ion. The DI cross sections were obtained in the potential of the ionized ion. The solid (green) line represents the total LLDW cross sections, the dashed (green) line represents the LLDW DI cross sections, the dashed-dotted (blue) line represents the total CADW cross sections (Djurić et al. 1993), and the dotted (blue) line represents the DI CADW cross sections (Djurić et al. 1993). Experiment is shown by open circles with error bars (Djurić et al. 1993).

Electron-impact single-ionization cross sections obtained in a potential of the ionizing ion are shown in Fig. 3. The CADW DI cross sections (Djurić et al. 1993) are slightly higher than the LLDW values at higher energies of the incident electron. However, the total LLDW cross sections are well above measurements at the peak values. It should be noted that a good agreement with the experimental values is obtained for the CADW calculations at the lower energies. However, these calculations omit the strong 3s → 3d excitations. The produced 3s13p13d1 configuration has energy levels that straddle the single-ionization threshold (Fig. 1). This configuration may have had an average energy below the ionization threshold in the CADW calculations and, therefore, the excitations to this configuration were not investigated (Djurić et al. 1993). What is more, the excitations to the shells with n >  5 were not included in the previous calculations. Therefore, all omitted EA channels should lead to the much higher values of the total single-ionization cross sections obtained using the CADW approximation. The LLDW cross sections that include the EA channels corresponding to the excitations to the shells with 4 ≤ n ≤ 5 are shown in Fig. 3. The CADW values are slightly above the presented LLDW cross sections starting from the peak. The difference can be explained by the higher CADW DI cross sections compared to the LLDW calculations. A similar situation for the CADW DI cross sections compared to the LLDW ones was previously determined (Zhang & Kwon 2014). Furthermore, the CADW method can provide different EA results for configurations with energy levels that straddle the single-ionization threshold.

thumbnail Fig. 3.

Single-ionization cross sections for the ground level of the Si+ ion. The DI cross sections were obtained in the potential of the ionizing ion. The solid (green) line represents the total LLDW cross sections, the dashed (green) line represents the LLDW DI cross sections, the dashed-dotted-dotted (red) line represents the total LLDW cross sections for excitations to 4 ≤ n ≤ 5, the dashed-dotted (blue) line represents the total CADW cross sections (Djurić et al. 1993), and the dotted (blue) line represents the DI CADW cross sections (Djurić et al. 1993). Experiment is shown by open circles with error bars (Djurić et al. 1993).

Autoionization branching ratios studied for all EA channels lead to diminished cross sections for indirect process by ∼5%. Therefore, radiative damping does not play a significant role when comparing the LLDW and CADW (Djurić et al. 1993) values.

The contribution of the EA channels corresponding to excitations to various shells is presented in Fig. 4. The excitation to the 3d subshell dominates compared to the other channels of indirect process. The excitations to the shells with n >  5 provide ∼14% for the peak value of the EA process. All this shows that the previously omitted EA channels increase the EA cross sections by a factor of two. Therefore, if the total single-ionization CADW cross sections included the excitations to shells with n = 3 and n >  5, it would lead to strongly overestimated values compared to measurements (Djurić et al. 1993).

thumbnail Fig. 4.

Accumulated cross sections of the EA channels contributing to the ionization of the ground level of Si+. The EA channels correspond to excitations to shells with a different principal quantum number.

The EA channels corresponding to excitations to subshells with the orbital quantum number l = 2 dominate for indirect process (Fig. 5). These excitations amount to ∼50% of the EA cross sections. As mentioned above, the main part is provided by the 3s → 3d excitation (Fig. 4). The contribution of the excitations to the subshells with l = 0 or l = 1 is more than a factor of two lower compared to the l = 2 case. What is more, the excitations to the subshells with l = 4 give a negligible contribution to the EA cross sections. It should be noted that the excitations to the subshells with l = 4 are important for ions with the open 4f subshell in the ground configuration (Jonauskas et al. 2015; Kynienė et al. 2015, 2016).

thumbnail Fig. 5.

EA channels corresponding to excitations to various orbitals.

Correlation effects play an important role in the study of energy levels, radiative transitions (Jonauskas et al. 2010), and Auger cascades (Jonauskas et al. 2008, 2011; Palaudoux et al. 2010). What is more, it was demonstrated that the correlation effects have to be included in the analysis of electron-impact ionization cross sections (Kynienė et al. 2019a; Jonauskas et al. 2019). The configuration interaction (CI) strength (Karazija 1996; Kučas et al. 1997; Karazija & Kučas 2013) was previously used to determine the bases of interacting configurations. In this work, the influence of the correlation effects for the direct and indirect ionization processes in the Si+ ion were analyzed using the CI method. The admixed configurations with the largest weight in an expansion of the intermediate wavefunction were determined from the diagonalization of the Hamiltonian matrix. The initial CI bases that were used to determine the main admixed configurations were produced by making one electron excitation up to shells with n = 9 and two electron excitations up to shells with n = 4 from the n = 3 shell of the ground configuration of the Si+ or Si2+ ions.

The 3s23p1, 3p3, 3s13p13d1, 3s24p1, and 3s13p14s1 configurations were used to build a basis of the interacting configurations in the study of the DI process for the Si+ ion. Furthermore, the even parity CI basis consists of the 3s2, 3p2, 3s13d1, 3s14s1, 3d2, and 3p14p1 configurations in Si2+. The odd parity CI basis includes the 3s13p1, 3p13d1, and 4s14p1 configurations. All this leads to a decrease in the cross sections of the direct process by ∼2% for the peak values. Furthermore, since the theoretical single-ionization threshold is slightly below the NIST-recommended value, all energy levels of the Si2+ ion are increased by 0.78 eV for the direct processes in this work. As such, the DI cross sections were decreased by an additional ∼4%.

The basis of interacting configurations consists of the 3s23p1, 3p3, 3s13p13d1, 3s24p1, 3s13p1ns, 3s13p1nd, and 3p1n′s2 (n = 4, 5, 6, n′ = 4, …, 9) configurations for the EA channels corresponding to the 3s → 3d, 3s → ns, and 3s → nd excitations. The inclusion of correlation effects diminishes the EA cross sections by ∼5 × 10−16 cm2 (∼36%). The correlation effects improve the agreement with measurements on the low-energy side and for peak values (Fig. 6). The CADW calculations that omit many EA channels are ∼6% lower than the LLDW cross sections for the values at the peak of the cross sections. However, very good agreement is obtained between the LLDW and CADW values on the high-energy side. Single-configuration cross sections show large discrepancies from the measurements (Fig. 6).

thumbnail Fig. 6.

Single-ionization cross sections for the ground level of Si+. The solid (green) line represents the total CI LLDW cross sections, the dashed-dotted (magenta) line represents the single-configuration cross sections when DI values are obtained in the potential of the ionizing ion, the dashed-dotted-dotted (red) line represents single-configuration cross sections when DI values are obtained in the potential of the ionized ion, and the dotted (blue) line represents the total CADW cross sections (Djurić et al. 1993). Experiment is shown by open circles with error bars (Djurić et al. 1993).

The weight of the 3p3 configuration in expansion of the intermediate wavefunction for levels of the ground configuration amounts to ∼3%. This agrees with the NIST value (Kramida et al. 2019). Therefore, the EA channels corresponding to excitations from the 3p3 configuration were studied for the intermediate wavefunction of the ground configuration. The 3p → nl (n = 3, …, 10, l <  n, l <  5) excitations were investigated for the 3p3 configuration. The contribution to cross sections of the excitations from the 3p3 configuration in expansion of the intermediate wavefunction for the ground level is shown in Fig. 7. These cross sections appear from ∼24 eV. The total single-ionization cross sections are increased by ∼6% and are slightly above the measurements for a peak value. The theoretical cross sections are in better agreement with the measurements compared to the CADW data from 70 eV to high energies of incident electrons.

thumbnail Fig. 7.

Single-ionization cross sections for the ground level of Si+. The solid (black) line represents the total CI LLDW cross sections that include excitations from the 3p3 configuration in the intermediate wavefunction of the ground configuration (see text for explanation), the dashed (green) line represents cross sections without excitations from the 3p3 configuration, the dashed-dotted (magenta) line represents single-configuration cross sections when DI values are obtained in the potential of the ionizing ion, the dashed-dotted-dotted (red) line represents single-configuration cross sections when DI values are obtained in the potential of ionized ion, and the dotted (blue) line represents the total CADW cross sections (Djurić et al. 1993). Experiment is shown by open circles with error bars (Djurić et al. 1993).

The weight of the 3s13p13d1 configuration is ∼2% in the expansion of the intermediate wavefunction of the ground configuration. However, the EA channels corresponding to excitations from the 3s and 3p subshells of this configuration contribute cross sections that are approximately two orders of magnitude lower than the total single-ionization cross sections. It should be noted that the excitations from the 3d subshell have already been included in calculations by considering the excitations from the 3s subshell of the 3s23p1 configuration using the intermediate wavefunction.

The remaining discrepancies among the LLDW cross sections and measurements may be attributed to correlation effects that are missing in our study. A large basis of interacting configurations may help resolve this problem. Furthermore, the electron-impact single-ionization cross sections would have to be diminished by the direct double ionization cross sections if it is assumed that the direct double ionization is formed by the sequential ionization. This effect for the single-ionization cross sections has to appear from the double ionization threshold (47.71 eV). It was previously demonstrated that the single-ionization calculations have to include the diminishing contribution from the direct double ionization to explain the measurements (Pakalka et al. 2018; Jonauskas 2019). What is more, additional measurements may be needed to determine the reason for the discrepancies between the theoretical and experimental data.

A comparison of the contribution from direct and indirect single-ionization processes is made in Fig. 8. The DI cross sections dominate in practically all energy ranges except the low-energy side. The DI from the 3p subshell is ∼10% stronger than the ionization from the 3s subshell for the peak values.

thumbnail Fig. 8.

Comparison of the contribution from the DI and EA channels for the ground level of Si+. Experiment is shown by open circles with error bars (Djurić et al. 1993).

Finally, single-ionization cross sections for direct and indirect single-ionization processes are presented in Table A.1. The corresponding Maxwellian rate coefficients are shown in Table A.2.

4. Conclusions

Electron-impact single-ionization cross sections for the Si+ ion were studied using the DFS approximation. The direct and indirect ionization processes were investigated by considering transitions among energy levels. The contribution of the EA process to the total single-ionization cross sections is larger compared to the DI process obtained in the single-configuration approximation. The DI from the 2p subshell provides a slightly higher contribution than the DI from the 3s subshell. The strongest EA channel corresponds to the 3s → 3d excitation (∼35%). The excitations to shells with n >  5 increases the EA cross sections by ∼14%.

It is demonstrated that correlation effects play a crucial role in explaining measurements. The correlation effects decrease the total single-ionization cross sections by ∼20% for the peak value. The influence of the correlation effects is less pronounced for the DI process. The DI cross sections are diminished by ∼2% when the correlation effects are taken into account. Finally, the theoretical single-ionization cross sections are above the measurements by ∼4% at the peak value and below the experimental values on the high-energy side. On the other hand, additional measurements may help resolve the disagreement between the theoretical and experimental cross sections.

Acknowledgments

Part of computations was performed on resources at the High Performance Computing Center “HPC Saulėtekis” in Vilnius University Faculty of Physics.

References

  1. Borovik, A., Jr., Gharaibeh, M. F., Schippers, S., & Müller, A. 2015, J. Phys. B: At. Mol. Opt. Phys., 48, 035203 [NASA ADS] [CrossRef] [Google Scholar]
  2. Borovik, A., Jr., Ebinger, B., Schury, D., Schippers, S., & Müller, A. 2016, Phys. Rev. A, 93, 012708 [CrossRef] [Google Scholar]
  3. Colgan, J., & Pindzola, M. 2012, Eur. Phys. J. D, 66, 284 [CrossRef] [EDP Sciences] [Google Scholar]
  4. Dere, K. P. 2007, A&A, 466, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Djurić, N., Bell, E. W., Guo, X. Q., et al. 1993, Phys. Rev. A, 47, 4786 [NASA ADS] [CrossRef] [Google Scholar]
  6. Gu, M. F. 2008, Can. J. Phys., 86, 675 [NASA ADS] [CrossRef] [Google Scholar]
  7. Hahn, M., & Savin, D. W. 2015, ApJ, 800, 68 [NASA ADS] [CrossRef] [Google Scholar]
  8. Jin, F., Borovik, A., Jr., Ebinger, B., & Schippers, S. 2020, J. Phys. B: At. Mol. Opt. Phys., 53, 075201 [CrossRef] [Google Scholar]
  9. Jonauskas, V. 2018, A&A, 620, A188 [CrossRef] [EDP Sciences] [Google Scholar]
  10. Jonauskas, V. 2019, J. Quant. Spectrosc. Radiat. Transf., 239, 106659 [CrossRef] [Google Scholar]
  11. Jonauskas, V., Karazija, R., & Kučas, S. 2008, J. Phys. B: At. Mol. Opt. Phys., 41, 215005 [NASA ADS] [CrossRef] [Google Scholar]
  12. Jonauskas, V., Kisielius, R., Kynienė, A., Kučas, S., & Norrington, P. H. 2010, Phys. Rev. A, 81, 012506 [NASA ADS] [CrossRef] [Google Scholar]
  13. Jonauskas, V., Kučas, S., & Karazija, R. 2011, Phys. Rev. A, 84, 053415 [NASA ADS] [CrossRef] [Google Scholar]
  14. Jonauskas, V., Prancikevičius, A., Masys, Š., & Kynienė, A. 2014, Phys. Rev. A, 89, 052714 [NASA ADS] [CrossRef] [Google Scholar]
  15. Jonauskas, V., Kynienė, A., Merkelis, G., et al. 2015, Phys. Rev. A, 91, 012715 [NASA ADS] [CrossRef] [Google Scholar]
  16. Jonauskas, V., Kynienė, A., Kučas, S., et al. 2019, Phys. Rev. A, 100, 062701 [CrossRef] [Google Scholar]
  17. Karazija, R. 1996, Introduction to the Theory of X-ray and Electronic Spectra of Free Atoms (New York: Plenum Press) [CrossRef] [Google Scholar]
  18. Karazija, R., & Kučas, S. 2013, J. Quant. Spectrosc. Radiat. Transf., 129, 131 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kim, Y.-K. 2001, Phys. Rev. A, 64, 032713 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kim, Y.-K., & Desclaux, J.-P. 2002, Phys. Rev. A, 66, 012708 [NASA ADS] [CrossRef] [Google Scholar]
  21. Kim, Y.-K., & Rudd, M. E. 1994, Phys. Rev. A, 50, 3954 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  22. Konceviiūtė, J., Kučas, S., Masys, Š., Kynienė, A., & Jonauskas, V. 2018, Phys. Rev. A, 97, 012705 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kramida, A., Ralchenko, Yu., Reader, J., & NIST ASD Team 2019, NIST Atomic Spectra Database (ver. 5.7.1), [Online]. Available: https://physics.nist.gov/asd [2020, April 10]. National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
  24. Kučas, S., Jonauskas, V., & Karazija, R. 1997, Phys. Scr., 55, 667 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kwon, D.-H., & Savin, D. W. 2012, Phys. Rev. A, 86, 022701 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kwon, D.-H., Rhee, Y.-J., & Kim, Y.-K. 2005, Int. J. Mass Spectrom., 245, 26 [CrossRef] [Google Scholar]
  27. Kwon, D.-H., Rhee, Y.-J., & Kim, Y.-K. 2006, Int. J. Mass Spectrom., 252, 213 [CrossRef] [Google Scholar]
  28. Kynienė, A., Masys, Š., & Jonauskas, V. 2015, Phys. Rev. A, 91, 062707 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kynienė, A., Pakalka, S., Masys, Š., & Jonauskas, V. 2016, J. Phys. B: At. Mol. Opt. Phys., 49, 185001 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kynienė, A., Kučas, S., Pakalka, S., Masys, Š., & Jonauskas, V. 2019a, Phys. Rev. A, 100, 052705 [CrossRef] [Google Scholar]
  31. Kynienė, A., Kučas, S., Masys, Š., & Jonauskas, V. 2019b, A&A, 624, A14 [CrossRef] [EDP Sciences] [Google Scholar]
  32. Liu, P., Zeng, J., & Yuan, J. 2018, J. Phys. B: At. Mol. Opt. Phys., 51, 075202 [CrossRef] [Google Scholar]
  33. Loch, S., Ludlow, J., Pindzola, M., Whiteford, A., & Griffin, D. 2005, Phys. Rev. A, 72, 052716 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lotz, W. 1968, Z. Phys., 216, 241 [NASA ADS] [CrossRef] [Google Scholar]
  35. Müller, A. 1986, Phys. Lett. A, 113, 415 [NASA ADS] [CrossRef] [Google Scholar]
  36. Pakalka, S., Kučas, S., Masys, Š., et al. 2018, Phys. Rev. A, 97, 012708 [NASA ADS] [CrossRef] [Google Scholar]
  37. Palaudoux, J., Lablanquie, P., Andric, L., et al. 2010, Phys. Rev. A, 82, 043419 [NASA ADS] [CrossRef] [Google Scholar]
  38. Pindzola, M. S., & Griffin, D. C. 1997, Phys. Rev. A, 56, 1654 [CrossRef] [Google Scholar]
  39. Pindzola, M. S., Griffin, D. C., & Bottcher, C. 1983, J. Phys. B: At. Mol. Opt. Phys., 16, L355 [CrossRef] [Google Scholar]
  40. Pindzola, M. S., Robicheaux, F., Loch, S. D., et al. 2007, J. Phys. B: At. Mol. Opt. Phys., 40, R39 [CrossRef] [Google Scholar]
  41. Zhang, D.-H., & Kwon, D.-H. 2014, J. Phys. B: At. Mol. Opt. Phys., 47, 075202 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Tables

Table A.1.

Single-ionization cross sections (in 10−20 cm2) for the ground level.

Table A.2.

Maxwellian rate coefficients (in 10−10 cm3 s−1) for the ground level.

All Tables

Table A.1.

Single-ionization cross sections (in 10−20 cm2) for the ground level.

In the text
Table A.2.

Maxwellian rate coefficients (in 10−10 cm3 s−1) for the ground level.

In the text

All Figures

thumbnail Fig. 1.

Energy levels of the ground configurations for the Si+, Si2+, and Si3+ ions in addition to energy levels of the 3s13p13d1, 3s13p14s1, 3s13p14p1, 3s13p14d1, and 3s13p14f1 configurations. The first excited configuration of Si2+ is also presented. The red represents even configurations and the blue represents odd configurations.
In the text
thumbnail Fig. 2.

Single-ionization cross sections for the ground level of the Si+ ion. The DI cross sections were obtained in the potential of the ionized ion. The solid (green) line represents the total LLDW cross sections, the dashed (green) line represents the LLDW DI cross sections, the dashed-dotted (blue) line represents the total CADW cross sections (Djurić et al. 1993), and the dotted (blue) line represents the DI CADW cross sections (Djurić et al. 1993). Experiment is shown by open circles with error bars (Djurić et al. 1993).
In the text
thumbnail Fig. 3.

Single-ionization cross sections for the ground level of the Si+ ion. The DI cross sections were obtained in the potential of the ionizing ion. The solid (green) line represents the total LLDW cross sections, the dashed (green) line represents the LLDW DI cross sections, the dashed-dotted-dotted (red) line represents the total LLDW cross sections for excitations to 4 ≤ n ≤ 5, the dashed-dotted (blue) line represents the total CADW cross sections (Djurić et al. 1993), and the dotted (blue) line represents the DI CADW cross sections (Djurić et al. 1993). Experiment is shown by open circles with error bars (Djurić et al. 1993).
In the text
thumbnail Fig. 4.

Accumulated cross sections of the EA channels contributing to the ionization of the ground level of Si+. The EA channels correspond to excitations to shells with a different principal quantum number.
In the text
thumbnail Fig. 5.

EA channels corresponding to excitations to various orbitals.
In the text
thumbnail Fig. 6.

Single-ionization cross sections for the ground level of Si+. The solid (green) line represents the total CI LLDW cross sections, the dashed-dotted (magenta) line represents the single-configuration cross sections when DI values are obtained in the potential of the ionizing ion, the dashed-dotted-dotted (red) line represents single-configuration cross sections when DI values are obtained in the potential of the ionized ion, and the dotted (blue) line represents the total CADW cross sections (Djurić et al. 1993). Experiment is shown by open circles with error bars (Djurić et al. 1993).
In the text
thumbnail Fig. 7.

Single-ionization cross sections for the ground level of Si+. The solid (black) line represents the total CI LLDW cross sections that include excitations from the 3p3 configuration in the intermediate wavefunction of the ground configuration (see text for explanation), the dashed (green) line represents cross sections without excitations from the 3p3 configuration, the dashed-dotted (magenta) line represents single-configuration cross sections when DI values are obtained in the potential of the ionizing ion, the dashed-dotted-dotted (red) line represents single-configuration cross sections when DI values are obtained in the potential of ionized ion, and the dotted (blue) line represents the total CADW cross sections (Djurić et al. 1993). Experiment is shown by open circles with error bars (Djurić et al. 1993).
In the text
thumbnail Fig. 8.

Comparison of the contribution from the DI and EA channels for the ground level of Si+. Experiment is shown by open circles with error bars (Djurić et al. 1993).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.