| Issue |
A&A
Volume 640, August 2020
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 5 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202037926 | |
| Published online | 25 August 2020 | |
Breakdown curves of CH2(+), CH3(+), and CH4(+) molecules
II. Application to chemical reactions and astrophysical implications
1
Institut de Physique Nucléaire d’Orsay (IPNO), CNRS, Univ. Paris Sud, Université Paris-Saclay,
91406 Orsay, France
e-mail: chabot@ipno.in2p3.fr
2
Institut des Sciences Moléculaires d’Orsay (ISMO), CNRS, Univ. Paris Sud, Université Paris-Saclay,
91405 Orsay, France
3
LERMA, Observatoire de Paris, PSL research university, CNRS, Sorbonne Université,
92186 Meudon, France
4
Laboratoire d’astrophysique de Bordeaux, Université de Bordeaux, CNRS, B18N, allée G. Saint-Hillaire,
Pessac, France
Received:
11
March
2020
Accepted:
15
June
2020
Aims. The aim of this work is to provide semi-empirical branching ratios (BRs) for the kinetic databases used in astrochemistry, such as the KInetic Database for Astrochemistry (KIDA). Our work focuses on the CHy(+) species (y = 2–4) excited by cosmic rays (CR), electrons, and photons (UV), or the intermediate excited complexes CHy(+) resulting from chemical reactions. It also intends to test the sensitivity of benchmark calculations to those new physical inputs in cold quiescent clouds and in photo-dissociation regions (PDRs).
Methods. We constructed semi-empirical breakdown curves (BDCs) based on the collision of CHy+ (y = 2–4) projectiles of constant velocity (250 keV uma−1) with He atoms as explained in a previous paper, where BRs for UV, CR, and electronic processing were also derived. The same BDCs were applied to predict BRs for chemical reactions (bi-molecular neutral and ionic reactions, charge exchange). The effect of the new BRs on the chemical composition of cold dark clouds was tested using the time-dependent Nautilus gas-grain model. The same effect on the chemical composition of PDRs was tested using the Meudon PDR code.
Results. Branching ratio predictions of the model are found to be in good agreement with available BR measurements for charge exchange reactions and the reaction between C and H3+. The chemistry for both cold clouds and PDRs is found to be not strongly affected by this update of BRs.
Key words: astrochemistry / planets and satellites: atmospheres / ISM: abundances / ISM: clouds
© M. Chabot et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Molecules of CH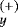 are the precursors of the many carbon-based molecules observed in the interstellar medium (ISM). Therefore the precise knowledge of the kinetic rates of creation and destruction of these species is of the highest importance. The branching ratio (BR) of a chemical reaction may be predicted within the framework of statistical theories with the so-called breakdown curve (BDC). Theses BDCs are BRs of dissociation as a function of internal energy within the intermediate complex (adduct) formed by the reactants. At null temperature the internal energy to be taken into account is simply the difference of formation enthalpy between the reactants and the intermediate complex. At a given temperature of the medium, only the relative translational energy of the reactants has to be added to this formation internal energy since, in the ISM, vibrational and rotational de-excitations are assumed to be fully achieved between two collisions.
are the precursors of the many carbon-based molecules observed in the interstellar medium (ISM). Therefore the precise knowledge of the kinetic rates of creation and destruction of these species is of the highest importance. The branching ratio (BR) of a chemical reaction may be predicted within the framework of statistical theories with the so-called breakdown curve (BDC). Theses BDCs are BRs of dissociation as a function of internal energy within the intermediate complex (adduct) formed by the reactants. At null temperature the internal energy to be taken into account is simply the difference of formation enthalpy between the reactants and the intermediate complex. At a given temperature of the medium, only the relative translational energy of the reactants has to be added to this formation internal energy since, in the ISM, vibrational and rotational de-excitations are assumed to be fully achieved between two collisions.
Even for barrierless reactions like the present reactions, the formation of a real intermediate chemical complex, in particular concerning charge exchange reactions, is questionable. For example, part of the reaction of complex organic molecules colliding with He+ (Cernuto et al. 2017) occurs at large distances between the reactants and part at small distance. Our hypothesis is that, due to the very large number of possible paths leading to the chemical reaction of interest, a statistical treatment not detailing the exact path is possibly valid. The same kind of statistical approach has been shown to be adequate for prediction of BRs in the case of C2H+ + D2 reactions (Chiu et al. 1992). The validity of this statistical approach for chemical reactions, making comparisons with measurements when available, is one of the goals of the present work.
Semi-empirical BDCs of CH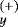 have been recently constructed using the experimental results (dissociation BR and kinetic energy release) of the high velocity collision between CH
have been recently constructed using the experimental results (dissociation BR and kinetic energy release) of the high velocity collision between CH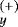 beam and He target (IdBarkach et al. (2019) referred to as Paper I in the following). Detailed structure calculations for CH
beam and He target (IdBarkach et al. (2019) referred to as Paper I in the following). Detailed structure calculations for CH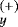 were also used for this purpose (Sanchez et al. 2016). In the same paper in which BDCs were constructed, predictions of photo-dissociation BR’s for different UV flux were performed. The present article continues this work.
were also used for this purpose (Sanchez et al. 2016). In the same paper in which BDCs were constructed, predictions of photo-dissociation BR’s for different UV flux were performed. The present article continues this work.
In a first section predictions of BRs for chemical reactions are given. In the second part of the paper, the influence of this complete, new set of BRs in chemical calculations is analyzed in a translucent cold cloud and in a photo-dissociation region (PDR).
2 Branching ratio predictions for chemical reactions
The full set of fragmentation BRs following CH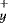 (y = 2–4) of constant velocity (250 keV uma−1) colliding with He atoms has been measured with the multi-detector AGAT near the Andromede facility at Orsay. Kinetic energy distributions of neutral fragments produced in each dissociation channel have also been measured. Using these experimental inputs and theo- retical dissociation energies, semi-empirical BDCs have been constructed. Details on the experimental protocols, experimental results, and methods to construct semi-empirical BDCs are given in Paper I.
(y = 2–4) of constant velocity (250 keV uma−1) colliding with He atoms has been measured with the multi-detector AGAT near the Andromede facility at Orsay. Kinetic energy distributions of neutral fragments produced in each dissociation channel have also been measured. Using these experimental inputs and theo- retical dissociation energies, semi-empirical BDCs have been constructed. Details on the experimental protocols, experimental results, and methods to construct semi-empirical BDCs are given in Paper I.
It is easy to predict BRs from BDCs knowing the internal energy distribution (IED) f(E) contained in the adduct formed by the chemicalreaction (A+B →AB). It is written
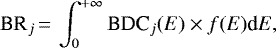 (1)
(1)
where BDCj(E) is the breakdown curve for channel j. At each energy E, BDCs verify,
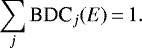 (2)
(2)
In chemical reactions, as mentioned before, the IED is the difference between the enthalpy formations of the reactants and the adduct. These differences (dissociation energies) have been calculated and are given in Paper I (Appendix A). Corresponding IED are delta functions. Equation (1) then becomes
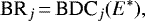 (3)
(3)
where E* is the internal energy.
In case of non-zero temperatures, the adduct internal energy may also originate from internal energies of the two parent reactants (in the form of vibration, rotation, and conformation) and from their relative collision velocity. Since in the ISM the time between two collisions is very long as compared to the very large majority of radiative life times, the internal energy distribution of reactants does not need to be considered. To check the sensitivity of the BRs to the temperature in ISM conditions, we used the Boltzmann relative velocity distributions and we assumed that the cross section formation of the adduct is independent of the velocity. Under these assumptions, no effect is observed upto 6000 K for both exothermic and endothermic reactions with the exception of the reactions with H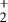 . This last effect is nevertheless a moderate effect (respectively a 10 and 20% variation of the BRs, at respectively 4000 and 6000 K). We thus state that BRs for all reactions producing CH
. This last effect is nevertheless a moderate effect (respectively a 10 and 20% variation of the BRs, at respectively 4000 and 6000 K). We thus state that BRs for all reactions producing CH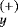 (y = 2–4) adducts are temperature independent in the dilute ISM gas.
(y = 2–4) adducts are temperature independent in the dilute ISM gas.
2.1 Ion-neutral reactions
For ion- neutral reactions (A+ + B) the internal energy E* of the adduct AB+ is the dissociation energy of AB+ in A+ + B. These dissociation energies for CH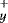 species are given in Tables A.4–A.6 in Paper I. For CH+ reacting with an hydrogen atom, there is only one open channel: CH+ + H → C+ + H2. The reaction of CH
species are given in Tables A.4–A.6 in Paper I. For CH+ reacting with an hydrogen atom, there is only one open channel: CH+ + H → C+ + H2. The reaction of CH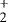 and CH
and CH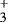 with an hydrogen atom are energetically closed at 0 K by 0.1 and 0.8 eV respectively. Above their temperature of activation the only open channels are CH+ + H2 and CH
with an hydrogen atom are energetically closed at 0 K by 0.1 and 0.8 eV respectively. Above their temperature of activation the only open channels are CH+ + H2 and CH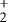 + H2 respectively. It is true up to very high temperatures since the openings of the channels of the three fragments are many electronvolts above the activation energies (see Tables A.5 and A.6 in Paper I), and BRs of channels with H+ or H
+ H2 respectively. It is true up to very high temperatures since the openings of the channels of the three fragments are many electronvolts above the activation energies (see Tables A.5 and A.6 in Paper I), and BRs of channels with H+ or H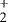 fragments are found to be always very weak.
fragments are found to be always very weak.
Reactions of C+ with a H2 molecule is endothermic at 0 K by 0.4 eV. Above its temperature of activation and up to a very high temperature (4 eV) there is only one open channel, CH+ + H. The same is true for CH+ and CH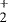 reacting with a H2 molecule where there is only one populated channel: CH
reacting with a H2 molecule where there is only one populated channel: CH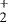 + H, CH
+ H, CH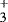 + H.
+ H.
Branching ratios for the reactions of neutral CHy with a H+ ion are displayed in Table 1. The error bars come from the statistics in the measurement and from a systematic error obtained by varying the internal energy of the adduct by a few tens of electronvolts. This variation intends to take into account the errors on the appearance and disappearance slopes of the BDCs. The same table reports on the KIDA15 BRs (Wakelam et al. 2015). They are not so far from the model.
Branching ratios for the reactions of neutral CHy with a H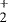 ion are displayed in Table 2. The same table reports on the KIDA15 BRs. Here again they are close to the semi-empirical BRs. Branching ratios for the reactions of neutral CHy with a H
ion are displayed in Table 2. The same table reports on the KIDA15 BRs. Here again they are close to the semi-empirical BRs. Branching ratios for the reactions of neutral CHy with a H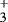 ion are displayed in Table 3. O’Connor et al. (2015) studied the reaction of neutral atomic C with H
ion are displayed in Table 3. O’Connor et al. (2015) studied the reaction of neutral atomic C with H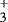 ions using a merged beams apparatus. Branching ratios for the C + H
ions using a merged beams apparatus. Branching ratios for the C + H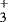 reaction forming CH+ and CH
reaction forming CH+ and CH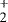 were found to be, below 10 K, of 0.25 and 0.75 respectively. The present semi-empirical BRs are in very good agreement with these experimental values. KIDA15 BRs reported in Table 3 predict H2 as the main channel contrary to the O’Connor et al. (2015) measurements and the present semi-empirical BRs for the C + H
were found to be, below 10 K, of 0.25 and 0.75 respectively. The present semi-empirical BRs are in very good agreement with these experimental values. KIDA15 BRs reported in Table 3 predict H2 as the main channel contrary to the O’Connor et al. (2015) measurements and the present semi-empirical BRs for the C + H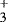 reaction. For the CH + H
reaction. For the CH + H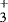 reaction, KIDA15 states that CH
reaction, KIDA15 states that CH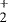 + H2 is the main channel while it is the CH
+ H2 is the main channel while it is the CH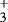 + H channel according to the model.
+ H channel according to the model.
Branching ratios for ion-neutral reactions between CHy and H+.
Branching ratios for ion-neutral reactions between CHy and H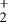 .
.
Branching ratios for ion-neutral reactions between CHy and H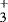 .
.
Adiabatic ionization potentials in electronvolts.
2.2 Charge exchange reactions
Charge exchange reactions usually involve atomic cations that are not able to bind easily with C or H, such as rare gas ions:
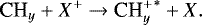 (4)
(4)
Assuming that the neutral atomic product X is produced in its electronic fundamental state and does not have any significant kinetic energy, the internal energy E* of the 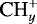 species is written
species is written
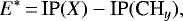 (5)
(5)
where IP is the adiabatic ionization potential of the corresponding species. Table 4 reports on the ionization potentials used in the calculations taken from Sanchez et al. (2016). With these internal energies and the 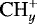 BDC’s (see Figs. 8–10 in Paper I), the BRs of the charge exchange processes are obtained using Eq. (3). Table 5 presents these BRs for the charge exchange with He+ cations.
BDC’s (see Figs. 8–10 in Paper I), the BRs of the charge exchange processes are obtained using Eq. (3). Table 5 presents these BRs for the charge exchange with He+ cations.
Many measurements have been performed for reactions of CH4 with rare gas cations (such as He+, Ar+, and Ne+) (Chatham et al. 1983; Tosi et al. 1995). In all these experiments only BRs for the production of charged fragments have been measured. Table 6 presents the comparison of the model with these measurements for He+. The overall agreement is very good. Nevertheless, experiments observed a small percentage of CH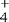 and CH
and CH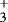 , while the model predicts none. This may be due to limited stabilization with a third body or due to a metastable state since experiments were performed with the gas at room temperature.
, while the model predicts none. This may be due to limited stabilization with a third body or due to a metastable state since experiments were performed with the gas at room temperature.
In Table 5 KIDA15 database values are compared to the model predictions. For the CH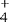 molecule, the KIDA15BRs were taken from experiments given in Table 6. It was assumed that the two body channels and a unique three body channel contribute to the production of charged fragments, while the main channels are in fact three body channels. For the CH
molecule, the KIDA15BRs were taken from experiments given in Table 6. It was assumed that the two body channels and a unique three body channel contribute to the production of charged fragments, while the main channels are in fact three body channels. For the CH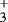 and CH
and CH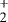 molecules, the same assumption (two body channels only populated by charge exchange with He+) was made. As for charge exchange with He+, model predictions for the charge exchange of CH4 with Ar+ (CH
molecules, the same assumption (two body channels only populated by charge exchange with He+) was made. As for charge exchange with He+, model predictions for the charge exchange of CH4 with Ar+ (CH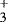 + H : 0.90; CH
+ H : 0.90; CH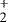 + H2: 0.10) agree with the experiment carried out by Tsuji et al. (1993) (CH
+ H2: 0.10) agree with the experiment carried out by Tsuji et al. (1993) (CH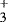 : 0.85; CH
: 0.85; CH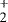 : 0.15).
: 0.15).
Branching ratios for charge exchange reactions between CHy and He+.
Relative yield of charged fragments in charge exchange reaction between CH4 and He+.
Branching ratios for anion-cation reactions between CH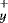 and H−.
and H−.
2.3 Neutral-neutral reactions
All neutral-neutral reactions CHy + Hx with y + x ≤ 4 have a unique, accessible outgoing channel: CHy + H → CHy−1 + H2 and CHy + H2 → CHy+1 + H. This is true for the exothermic and for the endothermic reactions above their activation energy, as well as in the case of the reaction of carbon in its 1D excited state (1.26 eV (NIST)): C(1D) + H2.
2.4 Anion-cation reactions
The reaction of H− with CH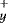 is currently not implemented in KIDA15, because it concerns particular situations. Nevertheless, in Table 7 we present the BRs for this class of reaction, which may be useful in forthcoming studies concerning the role of anions in some ISM locations.
is currently not implemented in KIDA15, because it concerns particular situations. Nevertheless, in Table 7 we present the BRs for this class of reaction, which may be useful in forthcoming studies concerning the role of anions in some ISM locations.
3 Application to interstellar medium chemistry
The influence of the complete set of BRs from this paper and Paper I on the chemical composition is analyzed. It was done in dark clouds and PDRs.
3.1 Dark clouds
We first tested the effect of the new BRs on the chemical composition of cold dark clouds. We used the time-dependent Nautilus gas-grain model from Ruaud et al. (2016). In this model, the gas-phase chemistry is coupled with the grain surface processes. The diffusion of physisorbed species through the Langmuir-Hinshelwood mechanism is computed. When species meet, they have a certain probability to react depending on the energy barrier of the reaction. Physisorbed species are separated into two groups depending on their location: at the surface of the grains (i.e., the two most external monolayers of molecules) or in the bulk (below the surface layers). The diffusion of the species is much faster at the surface than it is in the bulk and only species from the surface are allowed to desorb. Desorption from the surfaces can be induced by the temperature (thermal desorption), by a global heating induced by the collision of the grains with cosmic ray particles (cosmic-ray induced desorption), the impact of UV (direct and indirect) photons (photo-desorption), and the energy released by exothermic surface reactions (chemical desorption). The starting gas-phase chemical is kida.uva.2014 (Wakelam et al. 2015), which we modified to include the BRs published in this paper. The other parameters are the ones described in Ruaud et al. (2016). To test the effect of the new BRs, we ran our model (with and without the modifications) for cold core conditions for 107 yr, starting from an atomic gas (except for H2 initially present): a gas and dust temperature of 10 K, a total proton density of 2 × 104 cm−3, and a high visual extinction (30). Under these conditions, the CH+ abundance drops very quickly after being produced for the first 103 yrs of the simulations. At the typical ages of cold dark clouds (105 –106 yr), its abundance is below 10−13 with respect to the total proton density. Changing BRs increases the CH+ abundance as can be seen in Fig. 1. The effect is stronger between a few 103 and 105 yr but nearly negligible after.
 |
Fig. 1 Abundance of CH+ computed with the Nautilus gas-grain model for cold core conditions before and after the update of the branching ratios. |
3.2 Photo-dissociation region
We also studied the impact of the new BRs on the chemistry of photo-dissociation regions. To test the new BRs presented in this paper and in Paper I, we used the latest version of the Meudon PDR code (version 1.5.41, Le Petit et al. 2006; Goicoechea & Le Bourlot 2007; Le Bourlot et al. 2012). The Meudon PDR code computes the chemical and thermal structure of a stationary slab of gas and dust illuminated by an external radiation field. At each position in the cloud, the code solves the radiative transfer at each wavelength from the far-UV domain to the sub-millimeter domain, the individual heating and cooling mechanisms, as well as the chemistry of several hundred chemical species. In our models, for the computation of H, H2, and CO photo-dissociation rates, the self-shielding is computed using the Federman, Glassgold, and Kwan approximation (Federman et al. 1979). All H2 Lyman and Werner transitions are considered. For key species like C, S, CH, C2, CN, H2 O, and OH, photo-reaction rates are computed by integrating their photo-reaction cross sections times the specific intensity at each position in the cloud and at each wavelength obtained from the resolution of the radiative transfer equation. For other species, we use the classical approximation assuming that photo-reaction rates are equal to the photo-reaction probability at the edge of the cloud, 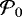 multiplied by an attenuation factor dependent on the visual extinction, exp(−βAV). Photo-reaction cross sections used in the models come from the Leiden photo-reaction database2 (Heays et al. 2017) as well as the two parameters,
multiplied by an attenuation factor dependent on the visual extinction, exp(−βAV). Photo-reaction cross sections used in the models come from the Leiden photo-reaction database2 (Heays et al. 2017) as well as the two parameters, 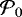 and β. The chemical network considers 240 species linked by 7700 reactions. The chemistry file is available with the Meudon PDR code. The chemical reaction rates are from the KIDA database3 and from the literature. In PDR models, one of the key processes that must be simulated precisely is the H2 formation reaction. Here, H2 formation on grains is simulated using the formalism described in Le Bourlot et al. (2012), which considers Eley-Rideal and Langmuir-Hinshelwood mechanisms. For computing time reasons, we have not used formalisms that consider the stochastic heating of grains by photons and its impact on H2 formation rate and H2 ortho-para conversion on grains (Bron et al. 2014, 2016). For the present study, this is not critical.
and β. The chemical network considers 240 species linked by 7700 reactions. The chemistry file is available with the Meudon PDR code. The chemical reaction rates are from the KIDA database3 and from the literature. In PDR models, one of the key processes that must be simulated precisely is the H2 formation reaction. Here, H2 formation on grains is simulated using the formalism described in Le Bourlot et al. (2012), which considers Eley-Rideal and Langmuir-Hinshelwood mechanisms. For computing time reasons, we have not used formalisms that consider the stochastic heating of grains by photons and its impact on H2 formation rate and H2 ortho-para conversion on grains (Bron et al. 2014, 2016). For the present study, this is not critical.
The chemical network of the Meudon PDR code has been modified to consider the new BRs presented in this paper and in Paper I. We tested the impact of the new data in various conditions from translucent clouds to highly illuminated PDRs. Previously, most of the unknown BRs were proportional to the number of destruction routes. For translucent conditions, we used a constant density model (nH = 100 cm−3), with a size defined by the visual extinction of AV = 1 and illuminated on both sides by the interstellar radiation flield (ISRF). For moderate PDR conditions we used a UV radiation field equals to 100 times the ISRF (Mathis et al. 1983) that illuminates a medium with a constant density nH = 1000 cm−3 corresponding to the order of magnitudes found in the Horsehead nebula. We also ran models of strongly illuminated PDRs using the parameters of the Orion Bar and NGC 7023 NW described in Joblin et al. (2018) in their Table 3. We compared the chemical profiles between the default chemical network of the Meudon PDR code and those obtained with updated chemical reactions presented in this paper and in Paper I.
For all models, the implementation of the new BRs does not significantly change the results. Indeed, the new data presented in this paper provide precise BRs for reactions between CHx species reacting with H+, H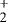 , H
, H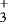 , and He+. In PDRs, the main destruction reactions of CHx species are reactions with H, H2, UV photons, and C+. So, even if the chemical reaction rates of CHx species with ions are faster than neutral-neutral reactions, the number densities of H+, H
, and He+. In PDRs, the main destruction reactions of CHx species are reactions with H, H2, UV photons, and C+. So, even if the chemical reaction rates of CHx species with ions are faster than neutral-neutral reactions, the number densities of H+, H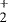 , H
, H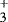 , and He+ are so small in PDRs compared to the number densities of the reactants of the main chemical routes that the updated rates do not change density profiles. The new BRs of Paper I also do not modify the densities of the products compared to previous BRs. Indeed, IdBarkach et al. (2019) provide new BRs for photo-dissociations of CH, CH2, CH3, and CH4. However, in PDRs, the products of these reactions are not significantly formed by these photo-dissociations. For example, CH is mainly formed by the reaction of CH2 with H and dissociative recombinations of CH
, and He+ are so small in PDRs compared to the number densities of the reactants of the main chemical routes that the updated rates do not change density profiles. The new BRs of Paper I also do not modify the densities of the products compared to previous BRs. Indeed, IdBarkach et al. (2019) provide new BRs for photo-dissociations of CH, CH2, CH3, and CH4. However, in PDRs, the products of these reactions are not significantly formed by these photo-dissociations. For example, CH is mainly formed by the reaction of CH2 with H and dissociative recombinations of CH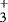 and CH
and CH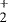 with electrons. Photo-dissociations of CH2, CH3, and CH4 play a minor role compared to these reactions. Another example, CH+, a key species in PDRs, is mainly formed in warm gas by the C+ + H2 reaction, the activation barrier is then bypassed thanks to the kinetic energy of reactants and the internal energy of H2 (Joblin et al. 2018). Figure 2 gives the strongest effect observed as occurring for nH = 1000 cm−3 and χ = 100 × Mathis ISRF. In this plot we see a small difference for CH+ but globally CH+ is not very abundant in this case.
with electrons. Photo-dissociations of CH2, CH3, and CH4 play a minor role compared to these reactions. Another example, CH+, a key species in PDRs, is mainly formed in warm gas by the C+ + H2 reaction, the activation barrier is then bypassed thanks to the kinetic energy of reactants and the internal energy of H2 (Joblin et al. 2018). Figure 2 gives the strongest effect observed as occurring for nH = 1000 cm−3 and χ = 100 × Mathis ISRF. In this plot we see a small difference for CH+ but globally CH+ is not very abundant in this case.
 |
Fig. 2 Density profiles computed with the Meudon PDR code using the old branching ratios (dashed line) and the new branching ratios (solid line). Model parameters correspond to a moderate PDR, nH = 1000 cm−3 and χ = 100 × the ISRF in Mathis units. |
4 Conclusions
Using semi-empirical BDCs of CH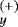 recently constructed in IdBarkach et al. (2019), we predict BRs for chemical reactions involving an adduct of type CH
recently constructed in IdBarkach et al. (2019), we predict BRs for chemical reactions involving an adduct of type CH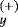 . A comparison of the BR predictions with the few existing measurements in the case of charge exchange and barrierless neutral-ion reactions was found to be very good. Therefore we think that the essential features of the BRs are captured by the model. The new BRs were used to compute chemistry in dark clouds and PDR regions. Some of the previous BRs (as also included in the KIDA database Wakelam et al. 2015) were not based on reliable data. Although the effect of the new BRs does not significantly modify the model results for the two studied interstellar regions, these results depend on the chemical network used. In addition, these new data could have more impact on some other regions such as protoplanetary disks. We thus emphasize the need for current databases and astrochemical models to update their network.
. A comparison of the BR predictions with the few existing measurements in the case of charge exchange and barrierless neutral-ion reactions was found to be very good. Therefore we think that the essential features of the BRs are captured by the model. The new BRs were used to compute chemistry in dark clouds and PDR regions. Some of the previous BRs (as also included in the KIDA database Wakelam et al. 2015) were not based on reliable data. Although the effect of the new BRs does not significantly modify the model results for the two studied interstellar regions, these results depend on the chemical network used. In addition, these new data could have more impact on some other regions such as protoplanetary disks. We thus emphasize the need for current databases and astrochemical models to update their network.
Acknowledgements
This work is performed within the framework of the P2IO LabEx program “Evolution de la matière du milieu interstellaire aux exoplanètes avec le JWST”. It is supported by the Program National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES. The Andromede facility is funded by the program from future investment EQUIPEX, ANR-10-EQPX-23.
References
- Bron, E., Le Bourlot, J., & Le Petit, F. 2014, A&A, 569, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bron, E., Le Petit, F., & Le Bourlot, J. 2016, A&A, 588, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernuto, A., Tosi, P., Martini, L. M., Pirani, F., & Ascenzi, D. 2017, Phys. Chem. Chem. Phys. (Incorporating Faraday Transactions), 19, 19554 [CrossRef] [Google Scholar]
- Chatham, H., Hils, D., Robertson, R., & Gallagher, A. C. 1983, J. Chem. Phys., 79, 1301 [CrossRef] [Google Scholar]
- Chiu, Y.-h., Yang, B., Fu, H., et al. 1992, J. Chem. Phys., 96, 5781 [CrossRef] [Google Scholar]
- Federman, S. R., Glassgold, A. E., & Kwan, J. 1979, ApJ, 227, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Goicoechea, J. R., & Le Bourlot, J. 2007, A&A, 467, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heays, A. N., Bosman, A. D., & van Dishoeck, E. F. 2017, A&A, 602, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- IdBarkach, T., Chabot, M., Béroff, K., et al. 2019, A&A, 628, A75 [CrossRef] [EDP Sciences] [Google Scholar]
- Joblin, C., Bron, E., Pinto, C., et al. 2018, A&A, 615, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Bourlot, J., Le Petit, F., Pinto, C., Roueff, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 500, 259 [NASA ADS] [Google Scholar]
- O’Connor, A. P., Urbain, X., Stützel, J., et al. 2015, ApJS, 219, 6 [CrossRef] [Google Scholar]
- Ruaud, M., Wakelam, V., & Hersant, F. 2016, MNRAS, 459, 3756 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez, J. P., Aguirre, N. F., Diaz-Tendero, S., Martin, F., & Alcamí, M. 2016, J. Phys. Chem. A, 120, 588 [CrossRef] [Google Scholar]
- Tosi, P., Bassi, D., Brunetti, B., & Vecchiocattivi, F. 1995, Int. J. Mass Spectr. Ion Process., 149–150, 345 [CrossRef] [Google Scholar]
- Tsuji, M., Kouno, H., Matsumura, K.-i., et al. 1993, J. Chem. Phys., 98, 2011 [CrossRef] [Google Scholar]
- Wakelam, V., Loison, J.-C., Herbst, E., et al. 2015, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]
Available at http://ism.obspm.fr
KIDA database: http://kida.astrophy.u-bordeaux.fr
All Tables
Relative yield of charged fragments in charge exchange reaction between CH4 and He+.
All Figures
 |
Fig. 1 Abundance of CH+ computed with the Nautilus gas-grain model for cold core conditions before and after the update of the branching ratios. |
| In the text | |
 |
Fig. 2 Density profiles computed with the Meudon PDR code using the old branching ratios (dashed line) and the new branching ratios (solid line). Model parameters correspond to a moderate PDR, nH = 1000 cm−3 and χ = 100 × the ISRF in Mathis units. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


