| Issue |
A&A
Volume 628, August 2019
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201935760 | |
| Published online | 08 August 2019 | |
Breakdown curves of CH2(+), CH3(+), and CH4(+) molecules
I. Construction and application to electron collisions and UV photodissociation
1
Institut de Physique Nucléaire d’Orsay (IPNO), CNRS, Université Paris Sud, Université Paris-Saclay,
91406
Orsay,
France
e-mail: chabot@ipno.in2p3.fr
2
Institut des Sciences Moléculaires d’Orsay (ISMO), CNRS, Université Paris Sud, Université Paris-Saclay,
91405
Orsay,
France
3
Université de Toulouse, UPS-OMP, IRAP,
31028
Toulouse cedex 4,
France
4
Departamento de Química, Módulo 13, Condensed Matter Physic Center (IFIMAC), Institute for advanced Research in Chemical Sciences (IAdChem), Universidad Autónoma de Madrid,
28049
Madrid,
Spain
Received:
24
April
2019
Accepted:
9
June
2019
Aims. The aim of this work is to furnish branching ratios (BRs) to the kinetic databases used in astrochemistry such as the KInetic Database for Astrochemistry (KIDA). This concerns CHy(+) species (y = 2–4) excited by cosmic rays, electrons and photons, or the intermediate excited complexes CHy(+) resulting from a chemical reaction.
Methods. The full set of fragmentation branching ratios following CHy(+) (y = 2,4) of constant velocity (250 keV uma−1) colliding with He atoms has been measured with the multidetector AGAT. Kinetic energy distributions of neutral fragments produced in each dissociation channel have been also measured. With these experimental inputs, and theoretical dissociation energies, semiempirical breakdown curves (BDCs) have been constructed.
Results. Prediction of BRs with the present BDCs is found to agree with available BR measurements for electronic dissociative recombination, collision with fast electron and photodissociation. Dependence of BRs with the various UV fields relevant to interstellar medium and planetary atmospheres is predicted.
Key words: astrochemistry / ISM: molecules / molecular processes
© T. IdBarkach et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The classical scenario of the main hydrocarbon gas phase synthesis in astrochemistry starts with the reaction of C+ ions with a hydrogen atom or molecule (Black & Dalgarno 1973). Then the formed CH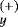 species can react with another C atom or ion to give a heavier hydrocarbon species. Since CH
species can react with another C atom or ion to give a heavier hydrocarbon species. Since CH molecules are the precursors of all the other hydrocarbons, reliable simulations in this field need a precise determination of total reaction rates and branching ratios (BRs; Wakelam et al. 2010).
molecules are the precursors of all the other hydrocarbons, reliable simulations in this field need a precise determination of total reaction rates and branching ratios (BRs; Wakelam et al. 2010).
Many studies have been performed in this context of astrochemistry on CH (e.g., van Dishoeck et al. 1980, 1996, 2006; Bettens & Collins 1998; Blint et al. 1976; Federer et al. 1984; Heays et al. 2017; Kim et al. 1975; Larson et al. 1998; Plasil et al. 2011; Puglisi et al. 2018; Rimmer & Helling 2016; Talbi & Saxon 1992; Thomas et al. 2013; Vejby-Christensen et al. 1997; Zanchet et al. 2016). It is also of interest in planetary atmospheric sciences where CH
(e.g., van Dishoeck et al. 1980, 1996, 2006; Bettens & Collins 1998; Blint et al. 1976; Federer et al. 1984; Heays et al. 2017; Kim et al. 1975; Larson et al. 1998; Plasil et al. 2011; Puglisi et al. 2018; Rimmer & Helling 2016; Talbi & Saxon 1992; Thomas et al. 2013; Vejby-Christensen et al. 1997; Zanchet et al. 2016). It is also of interest in planetary atmospheric sciences where CH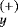 is often an important ingredient (e.g., Gans et al. 2013; Liu & Shemansky 2006; Pei & Farrar 2013; Salehzadeh & Kirchner 2017; Sheehan & St.-Maurice 2004; Tarnovsky et al. 1996; Au et al. 1993; Lecointre et al. 2008), in plasma sciences (e.g., Lecointre et al. 2008, 2009; Deutsch et al. 2000; Irikura 2017; Janev & Reiter 2002; Reiter & Janev 2010), in molecular physics (e.g., Frey & Davidson 1988; Kari & Csizmadia 1967; Jensen et al. 2002; Ren et al. 2015; Samson et al. 1989; Lodriguito et al. 2009; Theodorakopoulos & Petsalakis 1991; van der Wiel et al. 1976), and of course in combustion energy and chemical manufacturing sciences (Baulch et al. 2005). Despite all these efforts, currently BRs are still not accurately documented for all these species.
is often an important ingredient (e.g., Gans et al. 2013; Liu & Shemansky 2006; Pei & Farrar 2013; Salehzadeh & Kirchner 2017; Sheehan & St.-Maurice 2004; Tarnovsky et al. 1996; Au et al. 1993; Lecointre et al. 2008), in plasma sciences (e.g., Lecointre et al. 2008, 2009; Deutsch et al. 2000; Irikura 2017; Janev & Reiter 2002; Reiter & Janev 2010), in molecular physics (e.g., Frey & Davidson 1988; Kari & Csizmadia 1967; Jensen et al. 2002; Ren et al. 2015; Samson et al. 1989; Lodriguito et al. 2009; Theodorakopoulos & Petsalakis 1991; van der Wiel et al. 1976), and of course in combustion energy and chemical manufacturing sciences (Baulch et al. 2005). Despite all these efforts, currently BRs are still not accurately documented for all these species.
The aim of this work is to obtain all the predictable BRs, whatever the chemical or physical process at play, through the construction of what are known as breakdown curves (BDCs) (Vékey 1996). BDCs are energy-dependent branching ratios. This is a microcanonical concept that stipulates that in a finite and isolated system the way to dissipate a given internal energy, on average, only depends on its value. With this concept the way the species is excited is neglected and only the resulting internal energy distribution (IED) is relevant. This BDC concept can be applied to CH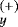 molecules excited by electrons, photons, or heavy swift projectiles or applied to intermediate complexes (adducts) formed during a chemical reaction (e.g., H
molecules excited by electrons, photons, or heavy swift projectiles or applied to intermediate complexes (adducts) formed during a chemical reaction (e.g., H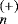 + CHy → [CH
+ CHy → [CH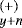 ]* → CH
]* → CH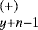 + H).
+ H).
In this paper we first present the experiment performed to retrieve a complete set of BRs for the CH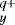 (y = 2–4, q = 0–5) species excited during a high velocity collision (HVC) between a CH
(y = 2–4, q = 0–5) species excited during a high velocity collision (HVC) between a CH species and a single He atom. We also present the method used to get from each fragmentation channel the kinetic energy distribution (KED) of the neutral fragments. In the second part of the paper, starting with the BRs and KEDs for CH
species and a single He atom. We also present the method used to get from each fragmentation channel the kinetic energy distribution (KED) of the neutral fragments. In the second part of the paper, starting with the BRs and KEDs for CH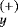 species, we present the general method used to retrieve semiempirical BDC, and for each species we conduct a short discussion. In the third and last part, we compare BR obtained with the semiempirical BDC with BR reported in databases in case of electronic excitation by collisions with electrons. We then predict the BR of photodissociation under different UV fields relevant for the interstellar medium (ISM) or planetary atmospheres.
species, we present the general method used to retrieve semiempirical BDC, and for each species we conduct a short discussion. In the third and last part, we compare BR obtained with the semiempirical BDC with BR reported in databases in case of electronic excitation by collisions with electrons. We then predict the BR of photodissociation under different UV fields relevant for the interstellar medium (ISM) or planetary atmospheres.
In a forthcoming paper, the same semiempirical BDCs will be used to predict BRs in two-body chemical reactions leading to a CH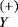 intermediate complex (y = 2–4).
intermediate complex (y = 2–4).
2 Experiment
Experiments were performed from April 2017 to January 2018 at the IPN Orsay ANDROMEDE facility with beams of CH (y = 2,4) of constant velocity (250 keV uma−1) colliding with He atoms.
(y = 2,4) of constant velocity (250 keV uma−1) colliding with He atoms.
2.1 Setup
The cationic CH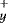 beams were produced with an electron cyclotron resonance (ECR) source from the PANTENIC company (microgam series). The arrangement of the permanent magnets of this source makes a shallow magnetic well and, using low radio frequency power, multifragmentation is scarce. Injecting CH4, all CH
beams were produced with an electron cyclotron resonance (ECR) source from the PANTENIC company (microgam series). The arrangement of the permanent magnets of this source makes a shallow magnetic well and, using low radio frequency power, multifragmentation is scarce. Injecting CH4, all CH species were produced with almost the same nanoampere intensities. This source was placed at the high voltage terminal of a recent electrostatic 4 MV accelerator from the National Electrostatics Corp. (NEC) company named ANDROMEDE. Before acceleration, a Wien filter with moderate resolving power was used to deflect all ions except those of interest, which were injected in the acceleration stages. Downstream of the accelerator, the beam was passing through an electrostatic quadrupole and analyzed at 90° with a magnetic sector. The emittance of the beam was then strongly reduced using two pairs of slits separated by 6 m. The beam size at the entrance of the fragmentation spectrometer AGAT, described later, was on the order of 100 μm for a divergence of approximately 0.02 mrad. Final intensities were on the order of a few thousand incident molecules per second. Before the first slit an electrostatic deflector made of two 15 cm plates separated by 2 mm was used as a fast chopper (0–1 kV), with switching time on the order of few tens of nanoseconds. The aim was to stop the beam during the time of the event recording. The beam diagnostics were done before the slits by two wire beam positioning monitors (BPMs) and faraday cups, and after the slits with a silicon detector. The purity of the beams (i.e., the presence of daughter fragments after the magnetic analysis measured with the silicon detector), was better than 99% for all species.
species were produced with almost the same nanoampere intensities. This source was placed at the high voltage terminal of a recent electrostatic 4 MV accelerator from the National Electrostatics Corp. (NEC) company named ANDROMEDE. Before acceleration, a Wien filter with moderate resolving power was used to deflect all ions except those of interest, which were injected in the acceleration stages. Downstream of the accelerator, the beam was passing through an electrostatic quadrupole and analyzed at 90° with a magnetic sector. The emittance of the beam was then strongly reduced using two pairs of slits separated by 6 m. The beam size at the entrance of the fragmentation spectrometer AGAT, described later, was on the order of 100 μm for a divergence of approximately 0.02 mrad. Final intensities were on the order of a few thousand incident molecules per second. Before the first slit an electrostatic deflector made of two 15 cm plates separated by 2 mm was used as a fast chopper (0–1 kV), with switching time on the order of few tens of nanoseconds. The aim was to stop the beam during the time of the event recording. The beam diagnostics were done before the slits by two wire beam positioning monitors (BPMs) and faraday cups, and after the slits with a silicon detector. The purity of the beams (i.e., the presence of daughter fragments after the magnetic analysis measured with the silicon detector), was better than 99% for all species.
The experimental setup AGAT was detailed in previous publications (e.g., Béroff et al. 2011). It consists of three vacuum chambers. The first contains the effusive He gaseous jet target (Wohrer et al. 2000). The beam and jet crossing point is at the focal point of a time of flight (TOF) MacLaren system ended by two Micro Channel Plate (MCP) detectors. The TOF enables the detection of the target ions produced during the collision with an efficiency of 55%. In order to reach sufficient energy (5 keV) without disturbing the trajectory of the projectile parent and fragments ions, the top part of the TOF was included within an electrostatic sphere at the high voltage point. The sphere was pierced with holes to let the beam pass. The extraction of the recoils was done by a low electric field (100 V cm−1) and the main part of its energy was from the acceleration between the sphere and the low voltage point of the TOF system. Simulations showed that the electric fields viewed by the beam and the fragments were mainly parallel to the trajectory and in opposite direction at the entranceand exit of the sphere then inducing a negligible deflection effect. The second chamber contains an electrostatic deflector made of twoparallel plates of 15 cm long separated by 4 cm. It deflected parent and fragments species with respect to their charge Q to mass M ratio (Q∕M), up to an angle of 20°. The entrance of the deflector was at a distance of 50 cm from the collision point, corresponding at the present beam velocity (250 keV amu−1) to 60 ns. The last chamber contained six planar silicon detectors covering all the Q/M trajectories for the charged fragments: H+, H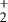 , H
, H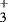 , C+++, C++, CH
, C+++, C++, CH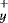 . The charge signal delivered by the preamplifiers attached to each detector (ORTEC 142B) were sent to an eight-channel digitizer. Because this charge is proportional to the kinetic energy of the detected particles, it gives the mass of the impinging fragment(s). To avoid detection of the incident beam by the CH
. The charge signal delivered by the preamplifiers attached to each detector (ORTEC 142B) were sent to an eight-channel digitizer. Because this charge is proportional to the kinetic energy of the detected particles, it gives the mass of the impinging fragment(s). To avoid detection of the incident beam by the CH detector a thin (0.5 mm diameter) rod was placed in front of it. The detection of neutral species was done either by a planar silicon detector or by a dedicated CCD camera from Hamamatsu company (Chabot et al. 2011). In this last case the planar neutral detector was placed on the very near side of the CCD to detect any fragments that might escape from the CCD. The camera CCD electronics must be triggered with an external signal and it was done using either signals from the charged fragment planar detectors or using the MCP signal from the recoil He+ ions. The CCD was read sequentially, so if during the time of reading (≈180 ms) a particle from another event was impinging the CCD, an impact would appear that would pollute the image. The fast chopper was used to avoid such a pile up and to save the statistics.
detector a thin (0.5 mm diameter) rod was placed in front of it. The detection of neutral species was done either by a planar silicon detector or by a dedicated CCD camera from Hamamatsu company (Chabot et al. 2011). In this last case the planar neutral detector was placed on the very near side of the CCD to detect any fragments that might escape from the CCD. The camera CCD electronics must be triggered with an external signal and it was done using either signals from the charged fragment planar detectors or using the MCP signal from the recoil He+ ions. The CCD was read sequentially, so if during the time of reading (≈180 ms) a particle from another event was impinging the CCD, an impact would appear that would pollute the image. The fast chopper was used to avoid such a pile up and to save the statistics.
 |
Fig. 1 Bi-dimensional representation of the coincident events between the CH |
2.2 Data reduction
Figure 1 gives an example of the 2D histogram of the planar neutral detector versus the CH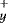 detector charge signal for the CH
detector charge signal for the CH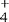 incident beam. Each spot corresponds to a given channel of fragmentation. The top diagonal spots correspond to complete events (i.e., having the same mass as CH4), while in the others the missing H+ fragment(s) is (are) within the H+, H
incident beam. Each spot corresponds to a given channel of fragmentation. The top diagonal spots correspond to complete events (i.e., having the same mass as CH4), while in the others the missing H+ fragment(s) is (are) within the H+, H , or H
, or H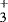 detectors. In the case of channels with more than one atomic neutral fragments (C or H), the state of fragmentation of neutrals cannot be determined from the charge signal. These channels are marked with brackets in the example in Fig. 1. It is why, in addition to the detection of neutral fragments with the planar silicon detector, a CCD camera is necessary. This camera associates the mass and the position information of the fragments, allowing the determination of the neutral pattern of fragmentation within an individual event. The CCD camera does not cover all the possible trajectories of the H atoms, so efficiency corrections have to be performed.
detectors. In the case of channels with more than one atomic neutral fragments (C or H), the state of fragmentation of neutrals cannot be determined from the charge signal. These channels are marked with brackets in the example in Fig. 1. It is why, in addition to the detection of neutral fragments with the planar silicon detector, a CCD camera is necessary. This camera associates the mass and the position information of the fragments, allowing the determination of the neutral pattern of fragmentation within an individual event. The CCD camera does not cover all the possible trajectories of the H atoms, so efficiency corrections have to be performed.
Figure 2 shows an example of the distribution of the positions of the H fragments obtained with an ensemble of events in the channel C+/H/H. The dispersion of the impacts reflects the kinetic energy (KE) distribution of the H fragments produced in the considered channel of dissociation. It is of cylindrical revolution. Under isotropic hypothesis of the collision, the relation between the KE and the radial distribution writes:
![\begin{equation*} f(E,r)= \left\{ \!\!\!\!\!\!\!\!\begin{array}{clcl} &\frac{r}{\sqrt{1-r/r_{90}(E)}} & \textrm{if} & r < r_{90}(E) \\[5pt] & 0 & \textrm{else} & \end{array} \right. \end{equation*}](/articles/aa/full_html/2019/08/aa35760-19/aa35760-19-eq30.png) (1)
(1)
with E the kinetic energy and r the radial distance to the center; therefore, r90(E) is the maximum radius reached for angles of emission perpendicular to the center of mass trajectory:
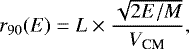 (2)
(2)
where M is the mass of the fragment, L the distance between the collision point and the detection plan (here 1875 mm), and V CM the center of mass velocity, i.e., the beam velocity (250 keV uma−1).
From the Cartesian distribution of the impact in the plane of detection, radial distributions are constructed around the beam center. Figure 3 displays the same events as Fig. 2, but in polar coordinates. Due to the kinematics, the geometrical efficiency of the camera is always one for heavy fragments, but not for H fragments. Correction of the geometrical efficiency is nevertheless easy to perform in polar coordinates. The range of covered KE values for H fragments has been increased by off-axing the beam and the CCD. For multiply-charged species CH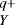 (q = 2,5) not presented here, the KE values are observed to be very high, and the maximum radius covered by the CCD is not large enough. To detect these events, a planar detector covering a radius up to 3 times the maximum radius covered by the CCD (r = 9.7 mm) is placed in front of the CCD. Its drop shadow is 0.5 mm within the active CCD array. Its geometrical efficiency is given in Fig. 3. Then, if needed, interpolation to high radius of the distribution from the CCD may be constrained. In the end, the efficiency corrections obtained in this way are checked twice. The measurements with the neutral planar detector in place of the CCD are 100% geometrically efficient. So, a re-summation of the corrected BR should provide these independent results. The part of the events escaping the neutral detection results in events with incomplete masses. The BRs of those events within a given incomplete mass are constructed. They also compare favorably to those obtained with the corrected BRs and the geometrical efficiencies. Tables A.1–A.6 give the BRs after the corrections. These corrections vary from null to 20–30% in the worse cases. The reported BR errors include errors on this correction, mainly of statistical origin.
(q = 2,5) not presented here, the KE values are observed to be very high, and the maximum radius covered by the CCD is not large enough. To detect these events, a planar detector covering a radius up to 3 times the maximum radius covered by the CCD (r = 9.7 mm) is placed in front of the CCD. Its drop shadow is 0.5 mm within the active CCD array. Its geometrical efficiency is given in Fig. 3. Then, if needed, interpolation to high radius of the distribution from the CCD may be constrained. In the end, the efficiency corrections obtained in this way are checked twice. The measurements with the neutral planar detector in place of the CCD are 100% geometrically efficient. So, a re-summation of the corrected BR should provide these independent results. The part of the events escaping the neutral detection results in events with incomplete masses. The BRs of those events within a given incomplete mass are constructed. They also compare favorably to those obtained with the corrected BRs and the geometrical efficiencies. Tables A.1–A.6 give the BRs after the corrections. These corrections vary from null to 20–30% in the worse cases. The reported BR errors include errors on this correction, mainly of statistical origin.
The radial distributions used for geometrical corrections are also used to measure the KE distribution of the neutral fragments. The relation between the KE distribution KED(E) and the radial distribution G(r) is
 (3)
(3)
with A(r) the distribution of the incident beam spot, here extending on few pixels (1 pixel = 24 μm).
Inversion of this convolution is done by minimizing the difference between experimental radial distribution and calculated ones using parametrized KEDs. In most cases, a single asymmetric Gaussian shape is enough to reproduce observations (see Fig. 3).
The experimental mean KE for the lightest neutral fragment contained in each of the channels is presented in Tables A.1–A.6. For two-fragment channels, it is straightforward to obtain the total kinetic energy release (KER) from energy and momentum conservation laws. For other channels, a mean KER was obtained by summing the mean KEs of all the neutral fragments in the channel. These mean KERs are also presented in Tables A.1–A.6.
Absolute cross sections were measured in the experiments following method of Wohrer et al. (2000). They were found to be consistent, for incident C+, CH+ and CH , with previous measurements performed nearby in another accelerator facility with slightly different velocities (A. Jallat Ph.D., unpublished). Within the error bars (20–30%), no evolutionwith the number of hydrogen atoms contained in the molecule was observed either for capture process or for excitation and ionization processes.
, with previous measurements performed nearby in another accelerator facility with slightly different velocities (A. Jallat Ph.D., unpublished). Within the error bars (20–30%), no evolutionwith the number of hydrogen atoms contained in the molecule was observed either for capture process or for excitation and ionization processes.
 |
Fig. 2 Reconstructed image of the H distribution in the channel C+/H/H with the CCD camera. |
 |
Fig. 3 Reconstructed image of the H distribution in the channel C+/H/H with the CCD camera in polar coordinates (r, θ). Upper panel:projection on the r-axis of the image(solid black line). Also shown are the geometrical efficiency of the CCD (solid red line) and the efficiency of the planar detector (dashed red line; see text). The back points with error bars show the H position distribution after efficiency correction. The dotted line is the result of the adjustment (see text). |
3 Semiempirical BDC construction for CH
3.1 Principles
The construction method has already been detailed in Chabot et al. (2013) where it is applied to the cases of C (n = 2,10), Cn H(+)(n = 2,4), and C3 H
(n = 2,10), Cn H(+)(n = 2,4), and C3 H molecules and in IdBarkach et al. (2018) for the Cn N(+) (n = 2,3) molecules.
molecules and in IdBarkach et al. (2018) for the Cn N(+) (n = 2,3) molecules.
In a microcanonical formulation the branching ratio (BR j) of a decaying channel j, here fragmentation, may be written as
 (4)
(4)
where BDCj(E) is the breakdown curve for the channel j verifying at each energy
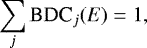 (5)
(5)
and f(E) is the internal energy distribution (IED) of the considered system (molecule or intermediate complex).
The BDCj(E) to be determined are parametrized as
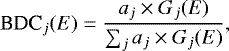 (6)
(6)
where Gj(E) is a generic function associated with each channel and aj is a scaling factor to be adjusted to retrieve experimental BRs from Eq. (4). The Gj (E) functions, ranging between 0 and 1, are defined on five energy domains using four energy parameters. Figure 4 presents an example of this function. It starts at the dissociation energy necessary to produce the considered channel (Eapp). At a certain energy (Esat) it reaches a plateau. For energies higher than the lowest dissociation energy of the fragments contained in the channel the function starts to decrease (Edesap). Beyond a certain energy (Eend) the functionis null.
The values of Eapp and Edesap were obtained from dissociation calculations of Sanchez et al. (2016). Channels containing H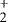 and H
and H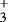 fragments, missing in Sanchez et al. (2016), were calculated with the same level of theory, i.e., geometry optimization at the B3LYP/6-311++G(3df,2p) level of theory and single-point energy over the previously obtained geometry at the CCSD(T)/6-311++G(3df,2p) level. The final values of the energies were corrected with the zero point energy (ZPE), also computed at the B3LYP/6-311++G(3df,2p)) level. All these calculations were performed with the Gaussian09 code (Revision E.01). Dissociation energies calculated in this way are listed in Tables A.1–A.6.
fragments, missing in Sanchez et al. (2016), were calculated with the same level of theory, i.e., geometry optimization at the B3LYP/6-311++G(3df,2p) level of theory and single-point energy over the previously obtained geometry at the CCSD(T)/6-311++G(3df,2p) level. The final values of the energies were corrected with the zero point energy (ZPE), also computed at the B3LYP/6-311++G(3df,2p)) level. All these calculations were performed with the Gaussian09 code (Revision E.01). Dissociation energies calculated in this way are listed in Tables A.1–A.6.
For neutral species energetic barriers were not found (i.e., these channels appear as barrier-less fragmentation pathways). For some specific fragmentation channels of the cation species, small barriers were found and are given in Tables A.4–A.6. They were located by performing a relaxed scan in the potential energy surface, where the distance between the atoms forming the bound to be broken is scanned while the rest of the coordinates are optimized. These barriers have been added to the dissociation energies introduced in the parametrized Gj functions.
The energy of saturation and the energy of disappearing relate to the dissipation of energy by a method different from fragment production, namely fragment translational and rotational motions, and internal vibrational and electronic excitations of the fragments. The appearing extension, (Esat − Eapp) and the disappearing extension (Eend − Edesap) are complementary quantities since disappearing is connected to appearance of a daughter fragment. Canonical values, obtained from theoretical works and found to be valid in previous studies (Chabot et al. 2013; IdBarkach et al. 2018) were used as start values. For the appearing extension (Esat − Eapp) it is 0.1 eV for the first two-body channel, 1 eV for the following two-body channels, and thereafter 3, 5, and 7 eV, respectively, for the 3-, 4-, and 5-body channels. For the disappearing extension (Eend − Edesap) it is 3, 5, and 7 eV, respectively, for the 2-, 3-, and 4-fragment channels. The canonical values were refined using the KE measurements and, in the case of neutral species, BR measurements of electronic dissociative recombination (DR–BR), as is explained below.
The internal energy distribution (IED) f(E) in Eq. (4) depends on the process used. In the present experiments, it is a capture process for the neutral species and electronic excitation for the cationic species. The multiplicity distribution (i.e., distribution in number of fragments) provides an image of the IED. There is a strong relation between the internal energy and the number of produced fragments through formation enthalpies. Practically, using a set of aj scaling factors equal to the experimental BRs within a given number of fragments, multiplicity BDCs (BDCNf) were obtained using Eq. (6) and summing the BDCj values of all channels j having the same number of fragments (Nf). These multiplicity BDCs were found to be not very different from the final BDC obtained using adjusted aj values. On the other hand, experimental BRs within a given number of fragments were summed to get experimental multiplicity distributions. Then, using the same type of relation as in Eq. (4) (but for Nf instead of j), the f(E) functions parametrized with 2 or 3 parameters were determined by minimization. Since excited states of neutral and cationic species have to exist for the process of electron capture or electron excitation to occur, we started the distribution on the low energy side at the energy of the lowest energy excited state. For electron excitation, only states having the same spin as the ground state were considered.
In a given fragmentation channel j, the remaining energy distribution (RED) to dissipate after enthalpy consumption is defined as
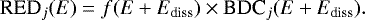 (7)
(7)
From a statistical point of view, the RED has to be shared between KER and vibration, rotation, isomerization, and electronic states of all the fragments. The distribution on these different modes of de-excitation depends a priori very strongly on the involved chemical species and so a direct relation between the KER distribution and IED could not be drawn without help of detailed molecular calculations.In this landscape, nevertheless, the mean KERs give useful semiquantitative tools to check the RED of the model. For the CH4 molecule, Lodriguito et al. (2009) computed the global partition between the translation (KER) and the vibration and rotation for the first excited states. On average, the ratio of KER to RED is 0.4. For smaller systems, this ratio should be higher, the number of vibrational degrees of freedom decreasing rapidly with the size. On this qualitative basis, the mean KERs can be compared to the mean values of RED from the model. If needed (i.e.,in the case of manifest deviation from expected ratios), we can modify the extension of the Gj function as is illustrated below.
In previous studies dealing with neutral Cn and CnH, it was found that semiempirical BDCs were able to predict experimental BR for the electronic dissociative recombination (DR) of C and Cn H+ within the model uncertainties (Chabot et al. 2013). A large part of these uncertainties comes from the imprecision concerning the extension of the Gj functions (i.e., the Esat − Eapp and Eend − Edesap values). In order to reduce the uncertainties on the BDCs, the DR experimental BRs were introduced at the associated energy deposit (taken equal to the adiabatic ionization potential A-IP) in order to constrain the BDCs at this particular position. Practically, canonical values of Esat − Eapp and Eend − Edesap in Gj functions were adjusted when necessary to put the BDCs on the DR measurements. The correction always involved an extension of the Gj function, certainly because canonical values, extracted from theoretical works on Cn clusters (Martinet et al. 2004), pertain to C–C bonds, while here we are dealing with C–H bonds.
and Cn H+ within the model uncertainties (Chabot et al. 2013). A large part of these uncertainties comes from the imprecision concerning the extension of the Gj functions (i.e., the Esat − Eapp and Eend − Edesap values). In order to reduce the uncertainties on the BDCs, the DR experimental BRs were introduced at the associated energy deposit (taken equal to the adiabatic ionization potential A-IP) in order to constrain the BDCs at this particular position. Practically, canonical values of Esat − Eapp and Eend − Edesap in Gj functions were adjusted when necessary to put the BDCs on the DR measurements. The correction always involved an extension of the Gj function, certainly because canonical values, extracted from theoretical works on Cn clusters (Martinet et al. 2004), pertain to C–C bonds, while here we are dealing with C–H bonds.
 |
Fig. 4 Example of the Gj function. |
3.2 CH2
The fundamental state of CH2 is X3B1 (Lau & Ng 2005). Above the dissociation limit (3.25 eV), the first state is a 13 A1 state at 6.28eV (van Dishoeck et al. 1996). We note that there is no state in the range (3.25–4.24) when only C/H2 is energetically opened (Zanchet et al. 2016). Following these considerations on the accessible excited states, the IED was started at 6.0 eV. It consists of a lognormal function peaked on the lowest excited state because the behavior of the capture process, in the high velocity limit, is to populate low excited states. Above 20 eV the IED was set to zero because highly excited nonionizing states would be rare, and if some exist they are populated with very low cross sections.
Due to the small number of fragmentation channels there is obviously not a unique IED making the minimization possible. The IED was chosen in such a way that, in the final result of the minimization, the dispersion of the aj values was as low as possible, leading to a smooth behavior of the BDCs.
The calculated BR for the DR (A-IP = 10.3 eV, Sanchez et al. 2016) are, using the canonical values of the Gj extension, 0.05(±0.05), 0.15(±0.15), and 0.80(±0.15) for respectively the C/H2, CH/H, and C/H/H channels. The errors come mainly from the uncertainty on the appearing and disappearing extensions set to 25% in the Monte Carlo error generation (Chabot et al. 2013). Within the errors it compares favorably to the Larson et al. (1998) experiment at 0 eV: 0.12(±0.03), 0.25(±0.05), and 0.63(±0.05). Increasing the extension of Gj on the high energy side, from 3 to 5 eV for the channels C/H2 and from 3 to 4 eV for the channel CH/H, leads to an almost exact reproduction of the experimental DR-BR.
Figure 5 gives the BDC corresponding to this Gj param- etrization together with the IED used in the minimization procedure. The mean RED (energy to be dissipated after the fragmentation) (see Eq. (7)) are 4.5, 3.6, and 3.1 eV for the C/H2, CH/H, and C/H/H channels. For the two-fragment channels, the ratio between mean KER and mean RED is higher than 50%. Since the system is extremely small, it is normal that the main way to dissipate the energy is the KER. Nevertheless the model predicts more RED and following KER for the channel C/H2 than for the channel CH/H because of the low energy of apparition. It is not the case comparing the mean experimental KER of the C/H2 and CH/H channels. It shows the limitation of using the present Gj almost square form to reproduce real BDCs, but more certainly the limit of constructing IED with a continuous smooth function instead of a structured one. The mean RED for the channel C/H/H, is close to the KER.
 |
Fig. 5 Breakdown curve for the CH2 molecule. The colored dashed lines refer to the different fragmentation channels listed in the box at the top. The full black line is the internal energy distribution used for BDC construction. The internal energy corresponding to DR process (adiabatic ionization potential) is shown by a vertical dashed line. |
3.3 CH3
The fundamental state of CH3 is  (Zanchet et al. 2016). The first theoretically calculated excited states, in the geometry of the CH3 fundamental, are (Zanchet et al. 2016) 3s
(Zanchet et al. 2016). The first theoretically calculated excited states, in the geometry of the CH3 fundamental, are (Zanchet et al. 2016) 3s 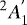 , 3p x,y
, 3p x,y  , and 3p z
, and 3p z  , corresponding to excitation energies of 5.91, 7.0, and 7.66 eV. They are well above the first dissociation limit (CH/H2: 4.48 eV). Following, the IED was started at 5.5 eV and BR for intact CH3 was excluded from the minimization. The log normal shape was used for the IED.
, corresponding to excitation energies of 5.91, 7.0, and 7.66 eV. They are well above the first dissociation limit (CH/H2: 4.48 eV). Following, the IED was started at 5.5 eV and BR for intact CH3 was excluded from the minimization. The log normal shape was used for the IED.
With canonical parametrization of the Gj, the model predicts BR for DR (A-IP = 9.74 eV, Sanchez et al. 2016) to be 0.36(±0.09), 0.07(±0.06), 0.29(±0.10), and 0.28(±0.10) for respectively CH2/H, CH/H2, CH/H/H, and C/H2/H. These values are in agreement with measurements of Vejby-Christensen et al. (1997): 0.40(±0.15), 0.14(±0.10), 0.16(±0.15), and 0.30(±0.08). Increasing the Gj disappearing extension of the channels CH/H2 from 3 to 4 eV and the Gj appearing extension of the channel CH/H/H from 3 to 4 eV would lead to perfect agreement with experimental BR-DR. Since the reported errors for BR-DR are quite large, we kept the canonical Gj parametrization. In Fig. 6 are presented the BDC corresponding to the canonical Gj parametrization together with the IED used in the minimization procedure.
The mean energies of RED of the channels CH2/H and CH/H2 are both equal to 2.9 eV. For the same channels the KER are respectively 1.5 and 1.3 eV. It is around half of the remaining energy going into KER. The mean RED of the channel C/H/H/H is 4.3 eV, in agreement with the KER within the error bar.
3.4 CH4
The fundamental state of CH4 is a X1A1 state (Kato et al. 2002). The calculated first excited states, in the geometry of the CH4 fundamental, are 13T2, 11T2, and 13A1, corresponding to excitation energies of 9.3, 9.6, and 10.3 eV as calculated within time dependent density functional theory (TDDFT) (Table I in Lodriguito et al. 2009). They are above the opening of the three-body dissociation channels. Consequently, the IED was started at 9.0 eV, and BR for intact CH4 was excluded from the minimization. The log normal shape was used for IED.
With canonical parametrization of the Gj function, the model fails to reproduce DR-BR measurements (A-IP = 12.8 eV, Sanchez et al. 2016). It predicts a null population for the two-fragment channels CH3/H and CH2/H2, while in reality they represent 20% (Thomas et al. 2013). At the same time, the mean value of the calculated RED in the channel CH3/H is 5 eV, while the mean KER, representing in theory 40% (Lodriguito et al. 2009), is measured at 3.3 eV. With a strong increase in the Gj disappearing extension for the CH3/H channel from 3 to 10 eV, both issues are solved. The calculated DR-BR values are found to be 0.27, 0, 0.50, 0.02, and 0.21, which agree with the experimental values of 0.18(±0.03), 0.06(±0.01), 0.51(±0.03), 0.02(±0.01), and 0.23(±0.01) respectively for the CH3/H, CH2/H2, CH2/H/H, C/H2/H2, and CH/H2/H channels (Thomas et al. 2013). With this increased extension, the mean value of the calculated RED for the CH3/H channel reaches 6.3 eV, making the KER partition less than 50%, as expected. For the channel CH2/H2 the mean RED is 5 eV, for a KER measurement at 2.2 eV. In Fig. 7 are presented the BDC corresponding to this modified Gj parametrization together with the IED used in the minimization procedure.
As emphasized in the introduction, experimental BRs following photodisociation exist for CH4 near the Lyα. In particular, Gans et al. (2013) observed an inversion of the populations between the CH2/H2 and the CH2/H/H channels passing from 10.2 to 10.5 eV of internal excitation energy. It is remarkable that the BDCs agree with this inversion, even if the exact value of energy where the inversion occurs (10 eV) is found to be slightly lower than the observed value.
3.5 CH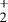
The fundamental state of CH is a X2A1 state (Lau & Ng 2005). The first calculated excited states in the geometry of the CH
is a X2A1 state (Lau & Ng 2005). The first calculated excited states in the geometry of the CH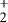 fundamental are (Theodorakopoulos & Petsalakis 1991) 12B1, 12A2, and 12B2, corresponding to excitation energies of 0.84, 6.81, and 7.25 eV. The first state does not contribute to dissociation, the corresponding IED was started at 6.5 eV. We note that there is no state in the energy range were C+ /H2 is the only open channel. An asymmetric Gaussian shape with two different widths for the high and the lowenergy sides was used for the IED. Due to the small number of possible multiplicities (M = 2 or 3), the determination of the IED is not univalent. Photo-absorption cross sections for CH
fundamental are (Theodorakopoulos & Petsalakis 1991) 12B1, 12A2, and 12B2, corresponding to excitation energies of 0.84, 6.81, and 7.25 eV. The first state does not contribute to dissociation, the corresponding IED was started at 6.5 eV. We note that there is no state in the energy range were C+ /H2 is the only open channel. An asymmetric Gaussian shape with two different widths for the high and the lowenergy sides was used for the IED. Due to the small number of possible multiplicities (M = 2 or 3), the determination of the IED is not univalent. Photo-absorption cross sections for CH peak at around 13 eV (Heays et al. 2017). Assuming that dipolar excitations in HVC are those leading to the main part of the excitation, the IED would also peak on the same states around 13 eV. The center of the IED being fixed, the two widths of the Gaussian shapes were adjusted on the experimental multiplicity distribution on the one hand, whereas a small dispersion of aj after the minimization was required on the other hand.
peak at around 13 eV (Heays et al. 2017). Assuming that dipolar excitations in HVC are those leading to the main part of the excitation, the IED would also peak on the same states around 13 eV. The center of the IED being fixed, the two widths of the Gaussian shapes were adjusted on the experimental multiplicity distribution on the one hand, whereas a small dispersion of aj after the minimization was required on the other hand.
With canonical values of extensions in Gj construction, the ratios between mean KERs and mean RED were found to be equal to 1 for channel CH+/H and greater than 1 for the three-fragments channels. This is too much. Adding 1 eV to both appearing and disappearing extensions for this channel leads to better ratios between KERs and mean RED from 0.75 (CH+/H) to 0.95 for the three-fragments channels. The KER of the C+ /H2 channel is small, compared to other channels and mean RED. Consequently, the error on the BDC for the C+ /H2 channel in the opening of IED (6.5 eV) could be large. For the channel CH/H+ the ratio mean KER over mean RED is 0.8. In Fig. 8 are presented the BDC corresponding to the modified (with respect to canonical values) Gj parametrization together with the IED used in the minimization procedure.
 |
Fig. 8 BDC for the CH |
3.6 CH
The fundamental state of CH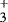 is a
is a  state (Lau & Ng 2005). The calculated first singlet excited states are (Blint et al. 1976):
state (Lau & Ng 2005). The calculated first singlet excited states are (Blint et al. 1976): 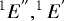 , and
, and 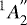 , corresponding to excitation energies of 6.46, 17.3, and 17.4 eV. Accordingly, the IED was started at 6.2 eV. The photo-absorption spectrum of Kari & Csizmadia (1967) peaks at 17.5 eV, and therefore IED too. The two Gaussian widths of IED were adjusted to reproduce the experimental multiplicities, and to lead in the minimization to a small dispersion of the aj adjusted parameters.
, corresponding to excitation energies of 6.46, 17.3, and 17.4 eV. Accordingly, the IED was started at 6.2 eV. The photo-absorption spectrum of Kari & Csizmadia (1967) peaks at 17.5 eV, and therefore IED too. The two Gaussian widths of IED were adjusted to reproduce the experimental multiplicities, and to lead in the minimization to a small dispersion of the aj adjusted parameters.
With canonical Gj, the mean RED of the channel CH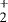 /H is 4.2 eV for a KER of 4.2 eV. The RED has to be increased by increasing the disappearing extension on the high energy size. It is also the case for the channel CH2/H+ (mean REDof 3.2 ev for 4 eV of KER). Putting 11 eV in place of 3 eV for the disappearing extension of both of these channels, leads to mean REDs of 7.9 and 6.3 eV, which agree with the KER representing 50% of the dissipated energy. The mean KER/RED for the two vaporization channels are found equal to 1 as expected.
/H is 4.2 eV for a KER of 4.2 eV. The RED has to be increased by increasing the disappearing extension on the high energy size. It is also the case for the channel CH2/H+ (mean REDof 3.2 ev for 4 eV of KER). Putting 11 eV in place of 3 eV for the disappearing extension of both of these channels, leads to mean REDs of 7.9 and 6.3 eV, which agree with the KER representing 50% of the dissipated energy. The mean KER/RED for the two vaporization channels are found equal to 1 as expected.
In Fig. 9 are presented the BDC corresponding to this Gj parametrization together with the IED used in the minimization procedure. The value of the BDC plateau for the channel CH+/H2, in the energy range 5–9 eV, depends strongly on the IED and on the CH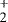 /H extension. The error is nevertheless less than 0.1.
/H extension. The error is nevertheless less than 0.1.
3.7 CH
The fundamental state of CH is a 2T2 state (Liu & Shemansky 2006). The first calculated excited states, in the geometry of the fundamental, are (Frey & Davidson 1988): 2B2 and 2A1, corresponding to excitation energies of 4.57 and 5.76 eV. Accordingly, IED was started at 4.2 eV. The photodissociation spectrum of Heays et al. (2017) is peaked on an A excited states(11 eV), therefore IED too. With canonical Gj, the KER and mean RED are in good ratio for the all two- fragments channels (ratio 0.4) and for the vaporization channels (ratio 1). The KE of the channels CH
is a 2T2 state (Liu & Shemansky 2006). The first calculated excited states, in the geometry of the fundamental, are (Frey & Davidson 1988): 2B2 and 2A1, corresponding to excitation energies of 4.57 and 5.76 eV. Accordingly, IED was started at 4.2 eV. The photodissociation spectrum of Heays et al. (2017) is peaked on an A excited states(11 eV), therefore IED too. With canonical Gj, the KER and mean RED are in good ratio for the all two- fragments channels (ratio 0.4) and for the vaporization channels (ratio 1). The KE of the channels CH /H/H, CH+/H2/H are clearly higher than the others, while it is not the case for the mean REDs. It may indicate that extensions of the Gj for these two channels are underestimated by canonical values, or more certainly than the used IED is too simple.
/H/H, CH+/H2/H are clearly higher than the others, while it is not the case for the mean REDs. It may indicate that extensions of the Gj for these two channels are underestimated by canonical values, or more certainly than the used IED is too simple.
In Fig. 10 are presented the BDC corresponding to canonical Gj parametrization together with the IED used in the minimization procedure. The BDC for the CH exists in the literature. Using photoemission at threshold from neutral CH4, Dutuit et al. (1990) obtained experimental BDCs for charged fragments that compared favorably to BDCs obtained through Rice-Ramsperger-Kassel-Marcus (RRKM) calculations. The present BDCs agree quite well with it.
exists in the literature. Using photoemission at threshold from neutral CH4, Dutuit et al. (1990) obtained experimental BDCs for charged fragments that compared favorably to BDCs obtained through Rice-Ramsperger-Kassel-Marcus (RRKM) calculations. The present BDCs agree quite well with it.
4 Application of semiempirical BDCs to electronic and photonic processes.
With the semiempirical BDCs described in the previous section, it is easy to get BRs for any process that excites the molecule if its associated IED is known. CHy species havebeen widely studied and reliable predictions may be made about IED for electron excitation by electron or photon impact.
4.1 Electron collisions
Collisions with electrons from zero to very high velocity result in electronic excited species. At zero velocity it is the DR process that is efficient in collisions with molecular cations and that we used in the BDC construction. We do not report on it here.
For collision energies higher than the first dissociation energy, but lower than the ionization potential, electronic excitation occurs and leads to fragmentation. As the energy increases, opening new lines in the IED makes the BR evolve quickly. For collision energies higher than the IP, both excitation and ionization may occur. Above the maximum of the electron energy loss cross section (due to electron excitation plus ionization), around 70 eV for outer targetelectrons, the IED for both excitation and ionization becomes almost independent of the projectile velocity andthe BRs should be independent as well (Janev & Reiter 2002). We report on the predicted BRs in this energy domain. Following the notation of the community involved in database construction for fusion (HYDKIN, Reiter & Janev 2010), DE and DI refer to dissociative excitation and to dissociative ionization of neutral CHy, and DE+ and DI+ to the same processes but for charged species CH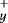 .
.
4.1.1 DE+ and DI+
In the so-called high velocity regime (V proj./ > > 1, i.e., E
> > 1, i.e., E 70 eV) the mass of the projectile is unimportant and only the projectile charge and the relative velocity between the projectile V proj. and the target electron
70 eV) the mass of the projectile is unimportant and only the projectile charge and the relative velocity between the projectile V proj. and the target electron  is physically relevant for predictions of target electronic excitation and ionization. Then, BRs have to be identical in HVC with fast atomic projectiles or in collisions with electrons. In the so-called intermediate velocity regime (V proj. ≳
is physically relevant for predictions of target electronic excitation and ionization. Then, BRs have to be identical in HVC with fast atomic projectiles or in collisions with electrons. In the so-called intermediate velocity regime (V proj. ≳  , i.e.,
, i.e.,  70 eV) differences may occur; in particular, the total cross sections underlying the stopping cross sections are not identical for protons and electrons at these velocities. Nevertheless, since in numerous previous series of experiments with C
70 eV) differences may occur; in particular, the total cross sections underlying the stopping cross sections are not identical for protons and electrons at these velocities. Nevertheless, since in numerous previous series of experiments with C (n = 2–10), Cn H+ (n = 1–4), and Cn N+ molecules we never observed any significant variation in BRs with the collision velocity from 2.0 to 4.5 au, present HVC-BRs are believed to be relevant for fast atomic collisions and also for fast electrons.
(n = 2–10), Cn H+ (n = 1–4), and Cn N+ molecules we never observed any significant variation in BRs with the collision velocity from 2.0 to 4.5 au, present HVC-BRs are believed to be relevant for fast atomic collisions and also for fast electrons.
In Tables 1 and 2 we compare the measured HVC-BRs DE+ with BRs extracted from the online database HYDKIN (2008) (Reiter & Janev 2010). The overall agreement is good with, in particular, the same negligible channels. The HYDKIN BRs are constructed from many measurements of charged fragments. The inclusive yields of charged fragments obtained by summing the BRs of Tables 2 and 1 are given in Table 3 and are compared to the HYDKIN values. We do not report on errors, but they are those of experimental BRs summed quadratically.
For CH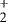 , the inclusive yields from HYDKIN and HVC-DE+ are identical. Nevertheless, H+ production in HVC-DE+ comes mainly from the atomization channel (C/H/H+), while in HYDKIN the CH/H+ channel also contributes. For CH
, the inclusive yields from HYDKIN and HVC-DE+ are identical. Nevertheless, H+ production in HVC-DE+ comes mainly from the atomization channel (C/H/H+), while in HYDKIN the CH/H+ channel also contributes. For CH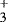 , the inclusive production of H+ is a little bit larger with HVC-DE+ than with HYDKIN. It comes from the vaporization channel, not at all populated in HYDKIN while appearing as a main channel in HVC-DE+. For CH
, the inclusive production of H+ is a little bit larger with HVC-DE+ than with HYDKIN. It comes from the vaporization channel, not at all populated in HYDKIN while appearing as a main channel in HVC-DE+. For CH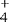 the inclusive distributions agree; instead, C+ is null in HYDKIN, while it is present in HVC-DE+.
the inclusive distributions agree; instead, C+ is null in HYDKIN, while it is present in HVC-DE+.
In Tables 4 and 5 we present the measured BRs for DI+ together with those of HYDKIN. The overall agreement is good. Table 6 gives the yield of charged fragments obtained by the addition of BRs times the occurrence of the fragments in the considered channel. The agreement between the HVC and HYDKIN DI+ yields for the inclusive charged fragments production is very good for all species.
Overall, the agreement is quite good, justifying after the fact the assumption made about the similarity between fast atomic and electronic collisions.
Branching ratio for dissociative excitation (DE+) of CH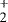 and CH
and CH by fast electrons.
by fast electrons.
Branching ratio for dissociative excitation (DE+) of CH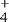 by fast electrons.
by fast electrons.
4.1.2 DEand DI
To predict the BRs of dissociative excitation (DE) of neutral CHy molecules not measured in the HVC collisions, knowledge of the internal energy distribution under fast electron (or atom) bombardment is required.
The internal energy distribution of singly charged hydrocarbon molecular species following HVC-DE+ has been found to weakly depend on the species (see Fig. 11) because the same kinds of orbitals are involved throughout the different species. In addition, the DE IED should be within the dispersion of the DE+ IED, because the same orbitals are involved, even if cationic energies of the first excited states are not the same as neutral species. The calculations were performed with the different IEDs from Fig. 11 with a cut for energies lower than the first excited states found in the cations. In this way the BR with errors were predicted. They are given in Table 7 together with those from HYDKIN. The disagreement is sizeable but no measurement, event partial, supports the HYDKIN values.
For ionization of neutral CHy molecules (I-DI), Irikura (2017) recently proposed an extension of the BEB model to compute the main features of IED following ionization. Figure 12 reports on these distributions for CH2, CH3, and CH4. Calculationswere made for electrons of 66 eV. The resulting lines were then convoluted with a Gaussian shape of 1.2 eV variance. The BEB calculations refer to the fundamental of the neutral species, so the zero energy was taken equal to the A-IP. In Table 8 we list the inclusive yields of charged fragments obtained with these IEDs (model 1). The values have been normalized to the most intense species (intact species here), as is done in mass spectrometry (MS). In the same table, NIST-MS values for the CH4 and HYDKIN predictions for all species are also presented. Differences are observed between HYDKIN/NIST values and values obtained with the BEB IED. Varying slightly the BEB IEDs, as discussed below, provides much better agreement. These modified BEB-IEDs (model 2) are shown in Fig. 12, and yields of charged fragments with model 2 BEB-IED in Table 8.
For CH4, the first component ((1t2)−1) of BEB IEDhas been replaced by the experimental (e,2e) value from Ren et al. (2015). The difference is small, but has some effect because it lies in the abrupt opening of the first dissociation channel (see Fig. 10). The width of the second component ((1t2)−1) has been increased and another component added. It mimics the experimental extension reported by Ren et al. (2015) or van der Wiel et al. (1976). For CH3, the BEB second contribution ((1e )−1)), was moved to lower energies by 0.25 eV. For CH2 the highest component ((2a1)−1)) was reduced by 70%.
)−1)), was moved to lower energies by 0.25 eV. For CH2 the highest component ((2a1)−1)) was reduced by 70%.
In Tables 9 and 10 the BRs from the initial (model 1) and corrected (model 2) IEDs are compared. The overall agreement between model 2 and HYDKIN is acceptable.
Inclusive branching ratio of charged fragments for dissociative excitation (DE+) of CH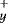 by fast electrons.
by fast electrons.
Branching ratio for dissociative ionization (DI+) and nondissociative ionization (I+) of CH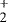 and CH
and CH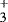 by fast electrons.
by fast electrons.
 |
Fig. 11 Internal energy distributions resulting from HVC dissociative excitation for various cationic molecules. |
Branching ratio for dissociative ionization (DI+) and nondissociative ionization (I+) of CH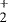 by fast electrons.
by fast electrons.
Inclusive relative yields of charged fragments following single ionization of CH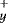 by fast electrons (DI+).
by fast electrons (DI+).
Branching ratios for dissociative excitation (DE) of CHy by fast electrons.
Relative yields of charged fragments for CHy ionized by fast electrons.
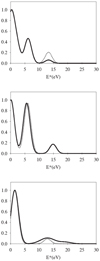 |
Fig. 12 Internal energy distribution following I-DI for CHy. Top panel: CH2, middle panel: CH3, bottom panel: CH4. Dotted line: Irikura (2017) model (model 1), solid line: modified model (model 2) (see text for details). |
4.2 Photodissociation under different UV fields
We already mentioned the good agreement of the present semiempirical predictions with recent measurements of the CH4 photodisociation BR near the hydrogen Lyα by Gans et al. (2013), as well as the good agreement with experimental charged fragments BDCs of CH by Dutuit et al. (1990). We here make predictions of dissociation BRs in the case of CH
by Dutuit et al. (1990). We here make predictions of dissociation BRs in the case of CH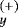 that underwent photodissociation by a broad energy distribution, notably for astrophysical application.
that underwent photodissociation by a broad energy distribution, notably for astrophysical application.
The IED associated with a given UV spectrum I(Eν), is determined by the dissociative photo excitation cross sections σ(Eν). It writes
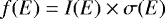 (8)
(8)
with I(E) in s−1 cm−2 ev−1 (the dimension of f(E) is s−1).
The Leiden database (Heays et al. 2017) contains those cross sections for CH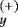 species either from measurements or, when not available, detailed calculations. In this last case all excited states above ionization potentials are assumed to contribute to ionization. We used it to compute the IEDs. In the Leiden database CH
species either from measurements or, when not available, detailed calculations. In this last case all excited states above ionization potentials are assumed to contribute to ionization. We used it to compute the IEDs. In the Leiden database CH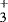 is missing, perhaps because the peak of dissociative excitation is well above the H absorption limit. We recall nevertheless that in HVC experiments we did not observe any significant variation in the dissociative excitation cross sections from one to another CH
is missing, perhaps because the peak of dissociative excitation is well above the H absorption limit. We recall nevertheless that in HVC experiments we did not observe any significant variation in the dissociative excitation cross sections from one to another CH . In order to cover some of the UV spectra diversity in the ISM we used the interstellar radiation fields (ISRF) of Draine (1978), blackbody radiation for three temperatures, and the solar UV field from Heays et al. (2017). Tables 11 and 12 give the BRs obtained with these different IEDs using Eq. (4), and the semiempirical BDCs. The sensitivity of the calculated BRs to the exact BDC appearing and disappearing behavior is weak because IEDs consist of many lines that are often broad. The relative errors of the BR are then only slightly above that on the BR measurements. We do not report on it for clarity. For the neutral species it is on the order of 10 to 25% of the calculated values, while it is on the order of 5 to 20% for the charged species. The relative variations between the UV fields are nevertheless meaningful for values much lower than those errors because it comes from the same BDCs.
. In order to cover some of the UV spectra diversity in the ISM we used the interstellar radiation fields (ISRF) of Draine (1978), blackbody radiation for three temperatures, and the solar UV field from Heays et al. (2017). Tables 11 and 12 give the BRs obtained with these different IEDs using Eq. (4), and the semiempirical BDCs. The sensitivity of the calculated BRs to the exact BDC appearing and disappearing behavior is weak because IEDs consist of many lines that are often broad. The relative errors of the BR are then only slightly above that on the BR measurements. We do not report on it for clarity. For the neutral species it is on the order of 10 to 25% of the calculated values, while it is on the order of 5 to 20% for the charged species. The relative variations between the UV fields are nevertheless meaningful for values much lower than those errors because it comes from the same BDCs.
For the neutral CH2 and CH3 species, there is a little effect on BR of the considered UV spectrum because the cross sections are peaked around energies (~7 eV for CH2, ~8 eV for CH3) between thetwo-fragment channels BDC (see Figs. 5 and 6). The curves are almost flat and changing proportion of the different lines in the IED is of little importance. For CH4, between the coldest and the hotter spectra, the production of two-fragment channels is decreased by a factor of 2 and the ordering of the channels is sensitively changed because the cross section gets a strong component at high energy where two-, three-, and four-fragment channels are competing. Figure 13 displays the IEDs resulting from the different UV fields for illustration purposes.
CationicCH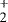 BRs are quite sensitive to the spectrum. It is due to high energy components of the cross section around 14 eV. For the hottest spectrum, atomization of the molecule is the main outgoing channel.
BRs are quite sensitive to the spectrum. It is due to high energy components of the cross section around 14 eV. For the hottest spectrum, atomization of the molecule is the main outgoing channel.
For CH the choice of the UV spectrum does not modify significantly the BRs because the main lines of the cross section cover mainly the three-fragment energy range around 10 eV.
the choice of the UV spectrum does not modify significantly the BRs because the main lines of the cross section cover mainly the three-fragment energy range around 10 eV.
We do not report on CH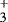 since we didnot find in the literature photodisociation cross sections, as we already mentioned. Nevertheless, the main channels may be identified since the first excited states are known to be at 7 and 17 eV (Blint et al. 1976). They are CH
since we didnot find in the literature photodisociation cross sections, as we already mentioned. Nevertheless, the main channels may be identified since the first excited states are known to be at 7 and 17 eV (Blint et al. 1976). They are CH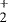 /H, CH+/H/H, and CH/H+/H (see Fig. 9).
/H, CH+/H/H, and CH/H+/H (see Fig. 9).
In Tables 11 and 12, the BRs from the Kinetic Database for Astrochemistry (KIDA) (Wakelam et al. 2015) are given. They could be updated with ISRF values.
Branching ratios for nondissociative and dissociative ionization (I-DI) of CH3 and CH2 by fast electrons.
Branching ratios for nondissociative and dissociative ionization (I-DI) of CH4 by fast electrons.
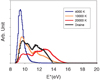 |
Fig. 13 Internal energy distributions of CH4 under various UV fields. |
Photodissociation branching ratio for neutral CHy molecules under various UV fields: ISRF (Draine 1978), blackbody radiation for three temperatures, and solar UV (Heays et al. 2017).
5 Conclusions
In this work we measured the BRs of fragmentation following HVC between CH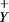 and He atoms. With the BRs and the measured kinetic energy distributions for the neutral fragments we constructed semiempirical BDCs. These BDCs were later used to predict BRs following electron excitation of CH
and He atoms. With the BRs and the measured kinetic energy distributions for the neutral fragments we constructed semiempirical BDCs. These BDCs were later used to predict BRs following electron excitation of CH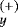 by electronic collision or by photons from different UV fields. All comparisons made with other measurements of BR, where present, were found positive, within the limits of precision and the methodology. In a forthcoming paper, BRs will be predicted with the same semiempirical BDCs for chemical reactions. Effects of the total new sets of BRs in detailed astronomical situations will be also explored.
by electronic collision or by photons from different UV fields. All comparisons made with other measurements of BR, where present, were found positive, within the limits of precision and the methodology. In a forthcoming paper, BRs will be predicted with the same semiempirical BDCs for chemical reactions. Effects of the total new sets of BRs in detailed astronomical situations will be also explored.
Acknowledgements
This work was performed within the framework of the P2IO LabEx program “Evolution de la matiére du milieu interstellaire aux exoplanétes avec le JWST”. It is supported by the Program National “Physique et Chimie du Milieu Interstellaire (PCMI)” of CNRS/INSU with INC/INP co-funded by CEA and CNES. The Andromede facility is funded by the program from future investment EQUIPEX, ANR-10-EQPX-23. We acknowledge the generous allocation of computer time at the Centro de Computacion Cientifica at the Universidad Autonoma de Madrid (CCC-UAM). This work was partially supported by the project CTQ2016-76061-P of the Spanish Ministerio de Economia y Competividad (MINECO).
Appendix A Experimental results
In this appendix we present in Tables A.1–A.6 the experimental dissociation branching ratios (BR), the experimental mean kinetic energies (KE) of neutral fragments and, the mean kinetic energy release (KER), following CHy and CH fragmentation in high velocity
fragmentation in high velocity
collisions (HVC) between CH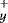 projectiles and He atoms. These data were used to construct the semiempirical breakdown curves (BDCs) of CHy and CH
projectiles and He atoms. These data were used to construct the semiempirical breakdown curves (BDCs) of CHy and CH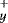 species (y = 2–4). Also reported in Tables A.1–A.6 are theoretical dissociation energies for the various channels, calculated as explained in the text.
species (y = 2–4). Also reported in Tables A.1–A.6 are theoretical dissociation energies for the various channels, calculated as explained in the text.
Experimental branching ratios (BRs) of the dissociation of CH2 molecule are listed in Col. 1.
Experimental branching ratio of the dissociation of CH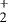 molecule is given in Col. 1.
molecule is given in Col. 1.
References
- Au, J. W., Cooper, G., Burton, G. R., Olney, T. N., & Brion, C. E. 1993, Chem. Phys., 173, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Baulch, D. L., Bowman, C. T., Cobos, C. J., et al. 2005, J. Phys. Chem. Ref. Data, 34, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Béroff, K., van-Oanh, N. T., Chabot, M., et al. 2011, Phys. Rev. A, 84, 032705 [NASA ADS] [CrossRef] [Google Scholar]
- Bettens, R. P. A., & Collins, M. A. 1998, J. Chem. Phys., 108, 2424 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. H., & Dalgarno, A. 1973, Astrophys. Lett., 15, 79 [NASA ADS] [Google Scholar]
- Blint, R. J., Marshall, R. F., & Watson, W. D. 1976, ApJ, 206, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Chabot, M., Martinet, G., Béroff, K., et al. 2011, Rev. Sci. Instrum., 82, 103301 [NASA ADS] [CrossRef] [Google Scholar]
- Chabot, M., Béroff, K., Gratier, P., Jallat, A., & Wakelam, V. 2013, ApJ, 771, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Deutsch, H., Becker, K., Matt, S., & Märk, T. D. 2000, Int. J. Mass Spectrom., 197, 37 [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Dutuit, O., Aït-Kaci, M., Lemaire, J., & Richard-Viard, M. 1990, Phys. Scr., 31, 223 [CrossRef] [Google Scholar]
- Federer, W., Villinger, H., Howorka, F., et al. 1984, Phys. Rev. Lett., 52, 2084 [CrossRef] [Google Scholar]
- Frey, R. F., & Davidson, E. R. 1988, J. Chem. Phys., 88, 1775 [NASA ADS] [CrossRef] [Google Scholar]
- Gans, B., Peng, Z., Carrasco, N., et al. 2013, Icarus, 223, 330 [CrossRef] [Google Scholar]
- Heays, A. N., Bosman, A. D., & van Dishoeck, E. F. 2017, A&A, 602, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- IdBarkach, T., Mahajan, T., Chabot, M., et al. 2018, Mol. Astrophys., 12, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Irikura, K. K. 2017, J. Phys. Chem. A, 121, 7751 [NASA ADS] [CrossRef] [Google Scholar]
- Janev, R. K., & Reiter, D. 2002, Phys. Plasmas, 9, 4071 [CrossRef] [Google Scholar]
- Jensen, P., Wesolowski, S. S., Brinkmann, N. R., et al. 2002, J. Mol. Spectr., 211, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Kari, R. E., & Csizmadia, I. G. 1967, J. Chem. Phys., 46, 1817 [CrossRef] [Google Scholar]
- Kato, M., Kameta, K., Odagiri, T., Kouchi, N., & Hatano, Y. 2002, J. Phys. B At. Mol. Phys., 35, 4383 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J. K., Theard, L. P., & Huntress, Jr. W. T. 1975, J. Chem. Phys., 62, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, Å., Le Padellec, A., Semaniak, J., et al. 1998, ApJ, 505, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, K.-C., & Ng, C. Y. 2005, J. Chem. Phys., 122, 224310 [NASA ADS] [CrossRef] [Google Scholar]
- Lecointre, J., Belic, D. S., Jureta, J. J., Janev, R., & Defrance, P. 2008, Eur. Phys. J. D, 50, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecointre, J., Belic, D. S., Jureta, J. J., Janev, R. K., & Defrance, P. 2009, Eur. Phys. J. D, 55, 569 [CrossRef] [Google Scholar]
- Liu, X., & Shemansky, D. E. 2006, J. Geophys. Res. Space Phys., 111, A04303 [NASA ADS] [CrossRef] [Google Scholar]
- Lodriguito, M. D., Lendvay, G., & Schatz, G. C. 2009, J. Chem. Phys., 131, 224320 [NASA ADS] [CrossRef] [Google Scholar]
- Martinet, G., Díaz-Tendero, S., Chabot, M., et al. 2004, Phys. Rev. Lett., 93, 063401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pei, L., & Farrar, J. M. 2013, J. Chem. Phys., 138, 124304 [NASA ADS] [CrossRef] [Google Scholar]
- Plasil, R., Mehner, T., Dohnal, P., et al. 2011, ApJ, 737, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Puglisi, A., Miteva, T., Kennedy, E. T., et al. 2018, Phys. Chem. Chem. Phys., 20, 4415 [CrossRef] [Google Scholar]
- Reiter, D., & Janev, R. K. 2010, Contrib. Plasma Phys., 50, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Ren, X., Pflüger, T., Weyland, M., et al. 2015, J. Chem. Phys., 142, 174313 [NASA ADS] [CrossRef] [Google Scholar]
- Rimmer, P. B., & Helling, C. 2016, ApJS, 224, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Salehzadeh, A., & Kirchner, T. 2017, Eur. Phys. J. D, 71, 66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samson, J. A. R., Haddad, G. N., Masuoka, T., Pareek, P. N., & Kilcoyne, D. A. L. 1989, J. Chem. Phys., 90, 6925 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez, J. P., Aguirre, N. F., Diaz-Tendero, S., Martin, F., & Alcam., M. 2016, J. Phys. Chem. A, 120, 588 [CrossRef] [Google Scholar]
- Sheehan, C. H., & St.-Maurice, J.-P. 2004, Adv. Space Res., 33, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Talbi, D., & Saxon, R. P. 1992, A&A, 261, 671 [NASA ADS] [Google Scholar]
- Tarnovsky, V., Levin, A., Deutsch, H., & Becker, K. 1996, J. Phys. B At. Mol. Phys., 29, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Theodorakopoulos, G., & Petsalakis, I. D. 1991, J. Mol. Struct. THEOCHEM, 230, 205 [CrossRef] [Google Scholar]
- Thomas, R. D., Kashperka, I., Vigren, E., et al. 2013, J. Phys. Chem. A, 117, 9999 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wiel, M. J., Stoll, W., Hamnett, A., & Brion, C. E. 1976, Chem. Phys. Lett., 37, 240 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Van Der Hart, W. J., & Van Hemert M. 1980, Chem. Phys., 50, 45 [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Beaerda, R. A., & van Hemert M. C. 1996, A&A, 307, 645 [NASA ADS] [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert, M. C. 2006, Faraday Discuss., 133, 231 [Google Scholar]
- Vejby-Christensen, L., Andersen, L. H., Heber, O., et al. 1997, ApJ, 483, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Vékey, K. 1996, J. Mass Spectrom., 31, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Smith, I. W. M., Herbst, E., et al. 2010, Space Sci. Rev., 156, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Loison, J.-C., Herbst, E., et al. 2015, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Wohrer, K., Chabot, M., Fossé, R., & Gardès, D. 2000, Rev. Sci. Instrum., 71, 2025 [CrossRef] [Google Scholar]
- Zanchet, A., Bañares, L., Senent, M. L., & García-Vela, A. 2016, Phys. Chem. Chem. Phys., 18, 33195 [CrossRef] [Google Scholar]
All Tables
Branching ratio for dissociative excitation (DE+) of CH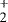 and CH
and CH by fast electrons.
by fast electrons.
Inclusive branching ratio of charged fragments for dissociative excitation (DE+) of CH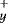 by fast electrons.
by fast electrons.
Branching ratio for dissociative ionization (DI+) and nondissociative ionization (I+) of CH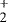 and CH
and CH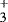 by fast electrons.
by fast electrons.
Branching ratio for dissociative ionization (DI+) and nondissociative ionization (I+) of CH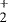 by fast electrons.
by fast electrons.
Inclusive relative yields of charged fragments following single ionization of CH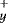 by fast electrons (DI+).
by fast electrons (DI+).
Branching ratios for nondissociative and dissociative ionization (I-DI) of CH3 and CH2 by fast electrons.
Branching ratios for nondissociative and dissociative ionization (I-DI) of CH4 by fast electrons.
Photodissociation branching ratio for neutral CHy molecules under various UV fields: ISRF (Draine 1978), blackbody radiation for three temperatures, and solar UV (Heays et al. 2017).
Experimental branching ratios (BRs) of the dissociation of CH2 molecule are listed in Col. 1.
Experimental branching ratio of the dissociation of CH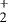 molecule is given in Col. 1.
molecule is given in Col. 1.
All Figures
 |
Fig. 1 Bi-dimensional representation of the coincident events between the CH |
| In the text | |
 |
Fig. 2 Reconstructed image of the H distribution in the channel C+/H/H with the CCD camera. |
| In the text | |
 |
Fig. 3 Reconstructed image of the H distribution in the channel C+/H/H with the CCD camera in polar coordinates (r, θ). Upper panel:projection on the r-axis of the image(solid black line). Also shown are the geometrical efficiency of the CCD (solid red line) and the efficiency of the planar detector (dashed red line; see text). The back points with error bars show the H position distribution after efficiency correction. The dotted line is the result of the adjustment (see text). |
| In the text | |
 |
Fig. 4 Example of the Gj function. |
| In the text | |
 |
Fig. 5 Breakdown curve for the CH2 molecule. The colored dashed lines refer to the different fragmentation channels listed in the box at the top. The full black line is the internal energy distribution used for BDC construction. The internal energy corresponding to DR process (adiabatic ionization potential) is shown by a vertical dashed line. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but for the CH3 molecule. |
| In the text | |
 |
Fig. 7 Same as Fig. 5, but for the CH4 molecule. |
| In the text | |
 |
Fig. 8 BDC for the CH |
| In the text | |
 |
Fig. 9 Same legend as Fig. 8 for the CH |
| In the text | |
 |
Fig. 10 Same as Fig. 8, but for the CH |
| In the text | |
 |
Fig. 11 Internal energy distributions resulting from HVC dissociative excitation for various cationic molecules. |
| In the text | |
 |
Fig. 12 Internal energy distribution following I-DI for CHy. Top panel: CH2, middle panel: CH3, bottom panel: CH4. Dotted line: Irikura (2017) model (model 1), solid line: modified model (model 2) (see text for details). |
| In the text | |
 |
Fig. 13 Internal energy distributions of CH4 under various UV fields. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.